알고리즘: 효율, 분석, 차수

Updated: March 12, 2024

알고리즘

다음 예제를 보자.

$n$개의 수로 구성된 리스트 S를 비내림차순(nondecreasing order)으로 정렬(sort)하시오.
어떤 수 $x$가 $n$개의 수의 리스트 $S$에 있는지 알아보시오.

문제에서 값이 지정되어 있지 않으 변수를 그 문제의 파라미터(parameter)라고 한다. 위 첫 번째 예에서는 $S$와 $n$이 파라미터이고, 두 번째 예에서는 $S, n, x$가 파라미터이다. 특정 입력사례(instance)에 대한 해답(soluion)이란 그 파라미터를 그 입력사례로 지정하여 질문한 문제의 해답이다. 어떤 입력사례가 주어지더라도 해답을 찾아주는 컴퓨터 프로그램을 작성하기 위해서 모든 인수에 대해서 해답을 찾아주는 일반적인 단계별 절차를 명시해야 한다. 이러한 단계별 절차가 바로 알고리즘(algorithm)이고, “문제는 알고리즘으로 푼다(solve)“라고 한다.
알고리즘은 자연어로 표현할 수 있다. 그러나 자연어로 알고리즘을 작성하면 복잡한 알고리즘을 말로 설명하기 쉽지 않고, 말로 표현한 알고리즘에서 컴퓨터 프로그램을 어떻게 만들어낼지가 불투명할 수 있다. 그래서 C++과 비슷하게 생긴 의사코드(pseudocode)를 써서 알고리즘을 표현한다.

효율적인 알고리즘 개발의 중요성

순차검색 vs. 이분검색

다음 순차검색 알고리즘을 보자.

// 문제: 원소가 n개인 배열 S에 원소 x가 있는가?
// 입력(파라미터): 정수 n(>0), 배열 S, 원소 x
// 출력: 원소 x가 위치한 인덱스를 location에 저장

void seqsearch ( int n, const keytype S[], keytype x, index& location){
  location = 1;
  while (location <=n && S[location] != x) {
    location++;
    if (location > n) {
      location = 0;
    }
  }
}

비내림차순으로 정렬된 배열을 이분검색하는 알고리즘은 $x$를 찾고 싶은 경우 먼저 $x$를 배열의 정중앙에 위치한 원소와 비교한다. 만약 같으면, 알고리즘을 끝낸다. 만약 $x$가 그 원소보다 작으면 $x$는 반드시 배열 전반부에 있을 것이므로, 배열 전반부에서 이분검색 절차를 되풀이 한다. 만약 $x$가 배열의 중앙 원소보다 크면, 배열의 후반부에서 이분검색 절차를 되풀이 한다. 이 절차를 $x$를 찾거나, 또는 $x$가 배열에 없음을 확실히 할 때까지 되풀이 한다.

// 문제: 원소가 n개인 정렬된 배열 S에서 원소 x를 찾으시오.
// 입력: 자연수 n, (비내림차순으로) 정렬된 배열 S, 원소 x
// 출력: location, S에서 x가 있는 위치

void binsearch(int n, const keytype S[], keytype x, index& location) {
  index low, high, mid;

  low = 1; high = n;
  location = 0;

  while (low <= high && location == 0) {
    mid = ⌊(low + high)/2⌋;

    if (x == S[mid])
      location = mid;
    else if (x < S[mid])
      high = mid - 1;
    else
      low = mid + 1;
  }
}

일반적으로 순차검색은 크기가 $n$인 배열에서 비교를 $n$번 해야만 $x$가 없음을 확신할 수 있다. 이분검색은 $\log n + 1$번이 최대 비교 횟수이다.

피보나치 수열

피보나치 수열의 $n$번째 수는 다음과 같이 재귀로(recursively) 정의한다.

$f_0 = 0, f_1 = 1, f_n = f_{n-1} + f_{n-2} (n \ge 2)$

// 문제: 피보나치 수열에서 n번째 수를 구하시오
// 입력: 양수 n(0 포함)
// 출력: 피보나치 수열에서 n번째 항

int fib(int n) {
  if( n <= 1)
    return n;
  else
    return fib(n - 1) + fib(n - 2);
}

이 알고리즘은 간단하여 작성하기도 이해하기도 쉽지만, 아주 비효율적이다. 다음 트리구조를 보면 모든 자식마다에서 재귀 호출을 한다.

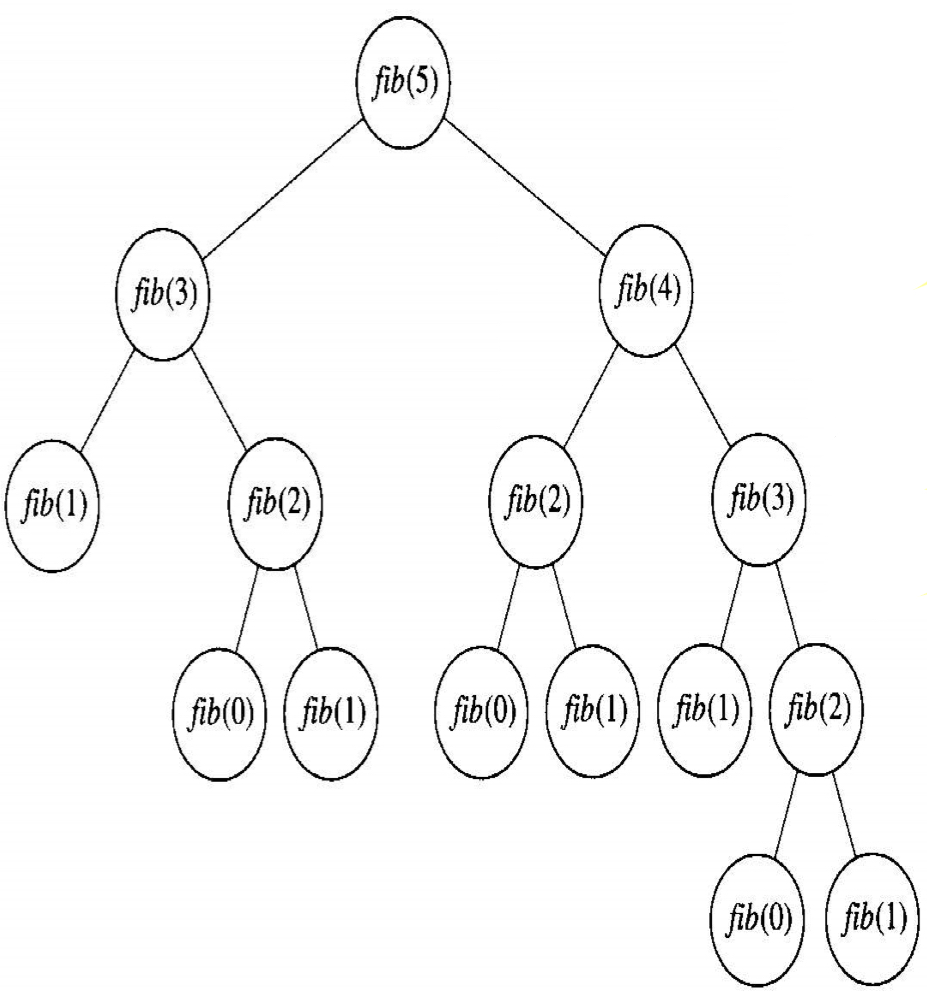
예를 들면, 맨 위에서 fib(5)를 얻기 위해서 fib(4)와 fib(3)을 호출하고, fib(3)을 얻기 위해서 fib(2)와 fib(1)을 호출하고 등등 이런 식이다. 이 트리에서 이 함수는 같은 계산을 중복해서 호출하기 때문에 비효율적이다(느리다). $T(n)$을 $n$에 대한 재귀 나무구조(recursion tree)의 항의 개수라고 하면, $n$이 2 증가할 때마다 항의 개수가 배로 늘어난다면, 다음과 같이 $n$에 대해서 2의 거듭제곱으로 나타나게 된다.

만일 값을 처음 계산하고 그 값을 배열에 저장해두고 나중에 필요할 때마다 쓰면 중복 계산을 피할 수 있다. 다음 알고리즘은 이 전략을 사용한다.

// 문제: 피보니치 수열에서 n 번째 항을 구하시오
// 입력: 양수 n (0포함)
// 출력: fib2, 피보나치 수열에서 n 번째 항

int fib2 (int n) {
  index i;
  int f[n];

  f[0]=0;
  if(n > 0) {
    f[1] = 1;
    for(i = 2; i <= n; i++)
      f[i] = f[i - 1] + f[i - 2];
  }
  return f[n];
}

$fib2(n)$을 구하기 위하여 처음 나오는 $n + 1$개의 항을 각각 한 번씩 계산한다. 즉, $n$번째 피보나치 항을 구하기 위해서 $n + 1$개의 항을 계산한다. 다음 표는 여러 $n$값에 대해서 위 두 식을 비교했다.

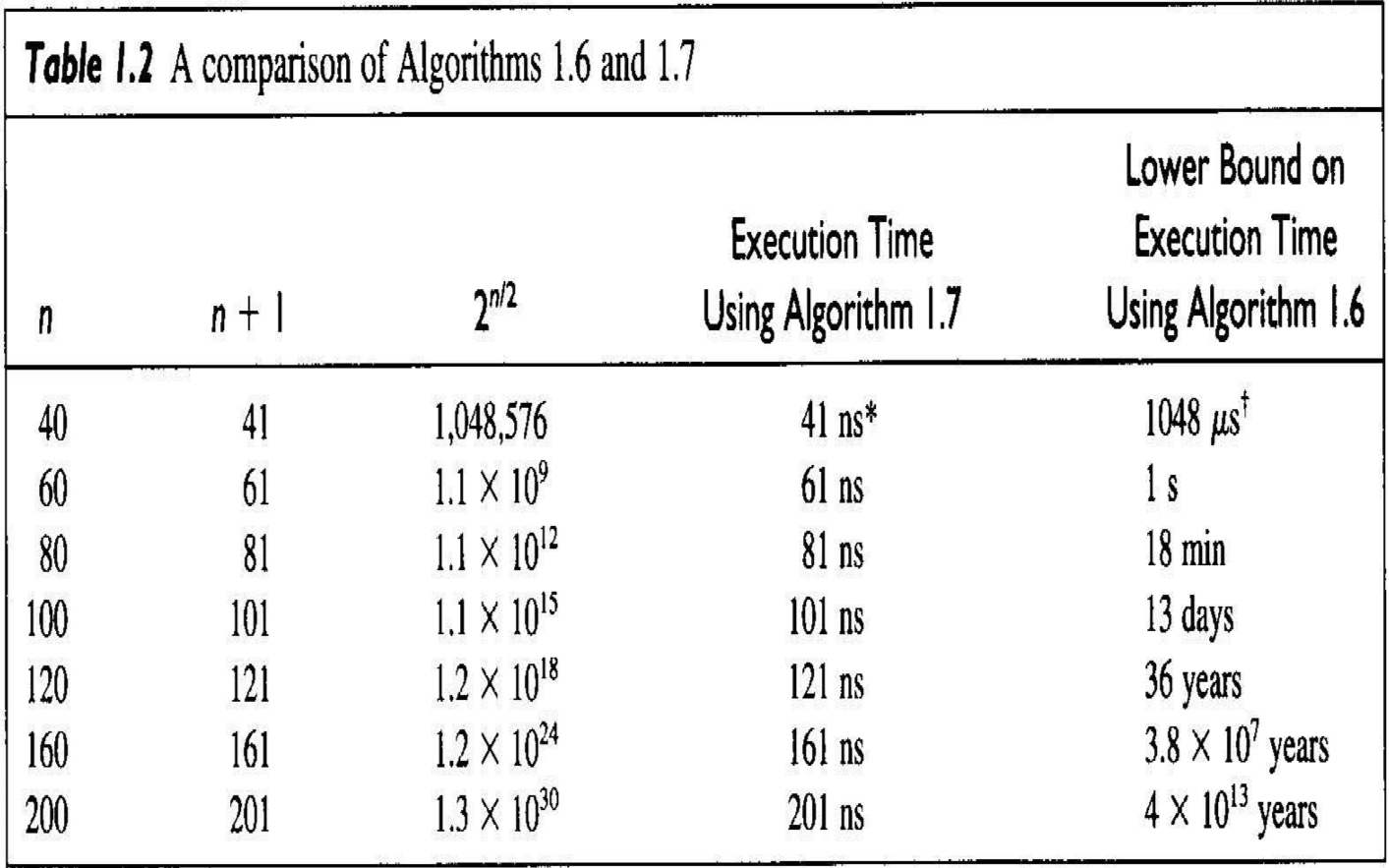
처음 피보나치 알고리즘으로는 $n$이 작은 경우를 제외하고 기다릴 수 없는 만큼의 시간이 걸린다. 반면에 두 번째 알고리즘은 $n$번째 피보나치 항을 거의 즉석해서 계산한다.

알고리즘의 분석

시간 복잡도 분석

일반적으로 알고리즘의 실행시간은 입력의 크기가 커지면 증가하고, 총 실행시간은 단위연산이 몇 번 수행되는가에 거의 비례한다. 따라서 단위연산(basic instruction)이 수행되는 횟수를 입력의 크기(input size)에 대한 함수로 구하여 알고리즘의 효율성을 분석한다. 알고리즘의 시간복잡도 분석(time complexity analysis)은 입력크기를 기준으로 단위연산을 몇 번 수행(실행)되는지 구하는 것이다. 실행 횟수가 일정한 경우 $T(n)$을 입력크기 $n$에 대해서 알고리즘이 단위연산을 실행하는 횟수로 정의한다. 여기서 $T(n)$을 입력크기 $n$에 대해서 알고리즘이 단위연산을 실행하는 횟수로 정의한다. 보통 $T(n)$을 알고리즘의 일정 시간복잡도(every-case time complexity)라고 하고, $T(n)$을 구하는 과정을 일정 시간복잡도 분석이라고 한다. 다음 예를 보자.

// Problem: Add all the numbers in the array S of n numbers.
// Inputs: positive integer n, array of numbers S indexed from 1 to n.
// Outputs: sum, the sum of the numbers in S.
number sum(int n, const number S[]){
  index i;
  number result;
  result = 0;
  for(i = 1; i <= n; i++){
    result = result + S[i];
  }
  return result;
}

배열에 있는 원소의 값에 상관없이 for 루프를 n번 실행한다. 그러므로 단위연산을 항상 n번 실행하여 시간복잡도는 $T(n) = n$이다.

// Problem: Sort n keys in nondecreasing order.
// Inputs: positive integer n, array of keys S indexed from 1 to n.
// Outputs: the array S containing the keys in nondecreasing order.
void exchangesort(int n, keytype s[]){
  index i, j;
  for(i = 1; i <= n - 1; i++){
    for(j = i + 1; j <= n; j++){
      if(S[j] < S[i]){
        exchange S[i] and S[j];
      }
    }
  }
}

for-i 루프를 실행하는 횟수는 항상 $n - 1$번이다. for-j 루프는 $(n - 1)$번, $(n - 2)$번, …, 1번으로 for-j의 $T(n) = (n-1) + (n-2) + \cdots + 1 = \frac{(n-1)n}{2}$이다.

// Problem: Determine the product of two nXn matrices.
// Inputs: a positive integer n, 2D arrays of numbers A and B, each of which has both its rows and columns indexed from 1 to n.
// Outputs: a 2D array of numbers C, which has both its rows and columns indexed from 1 to n, containing the product of A and B.
void matrixmult( int n, const number A[][], const number B[][], number C){
  index i, j;
  for(i = 1; i <= n; i++){
    for(j = 1; j <= n; j++){
      C[i][j] = 0;
      for(k = 1; k <= n; k++){
        C[i][j] = C[i][j] + A[i][k] * B[k][j];
      }
    }
  }
}

for-i 루프는 항상 n번 실행하고, for-i 루프가 한 번 실행할 때마다 for-j 루프는 항상 n번 실행하고, for-j루프가 한 번 실행할 때마다 for-k 루프는 항상 n번 실행한다. 따라서 단위연산을 실행하는 횟수는 $T(n) = n \times n \times n = n^3$이다.
알고리즘을 분석하는 다른 계측방식이 세 가지 더 있다.

$W(n)$: 입력크기 n에 대해서 알고리즘이 실행할 단위연산의 최대 횟수
- 최악 시간복잡도(worst-case time complexity), 최악 시간복잡도 분석
- 만약 T(n)이 존재하면 W(n) = T(n)
$A(n)$: 입력크기 n에 대해서 알고리즘이 수행할 단위연산의 평균 횟수(기대치)
- 평균 시간복잡도(average-case time complexity), 평균 시간복잡도 분석
- 만약 T(n)이 존재하면 A(n) = T(n)
- $A(n)$을 계산하려면 n개의 입력에 확률을 각각 부여해야한다.
$B(n)$입력크기 n에 대해서 알고리즘이 실행할 단위연산의 최소 횟수
- 최소 시간복잡도(best-case time complexity), 최소 시간복잡도 분석
- 만약 T(n)이 존재하면 B(n) = T(n)

이론의 적용

알고리즘 분석 이론을 적용하면서 단위연산 등을 실행하는데 실제로 걸리는 시간들을 고려해야 할 수도 있다. 같은 문제라 할지라도 알고리즘이 다르면 실행횟수는 달라진다.
예를들어, 첫째 알고리즘의 일정 시간복잡도는 $n$이고 둘째 알고리즘의 일정 시간복잡도는 $n^2$이라고 가정하면, 첫째 알고리즘이 궁극적으로는 더 빠를 것이라고 바로 알 수 있다. 그러나 둘째 알고리즘의 단위연산 실행시간보다 첫째 알고리즘의 단위연산 실행시간이 1000배 느리다고 가정하고 둘째 알고리즘의 단위연산 실행시간을 $t$라고 하면, $1000t$는 첫째 알고리즘의 단위연산 실행시간이다. 크기 $n$인 입력에 대해서 실행시간은 첫째 알고리즘의 경우 $n \times 1000t$이고, 둘째 알고리즘의 경우 $n^2 \times t$이다. 따라서 입력의 크기가 1000보다 크지 않은 경우, 둘째 알고리즘이 더 빠르다.

차수

차수의 직관적인 소개

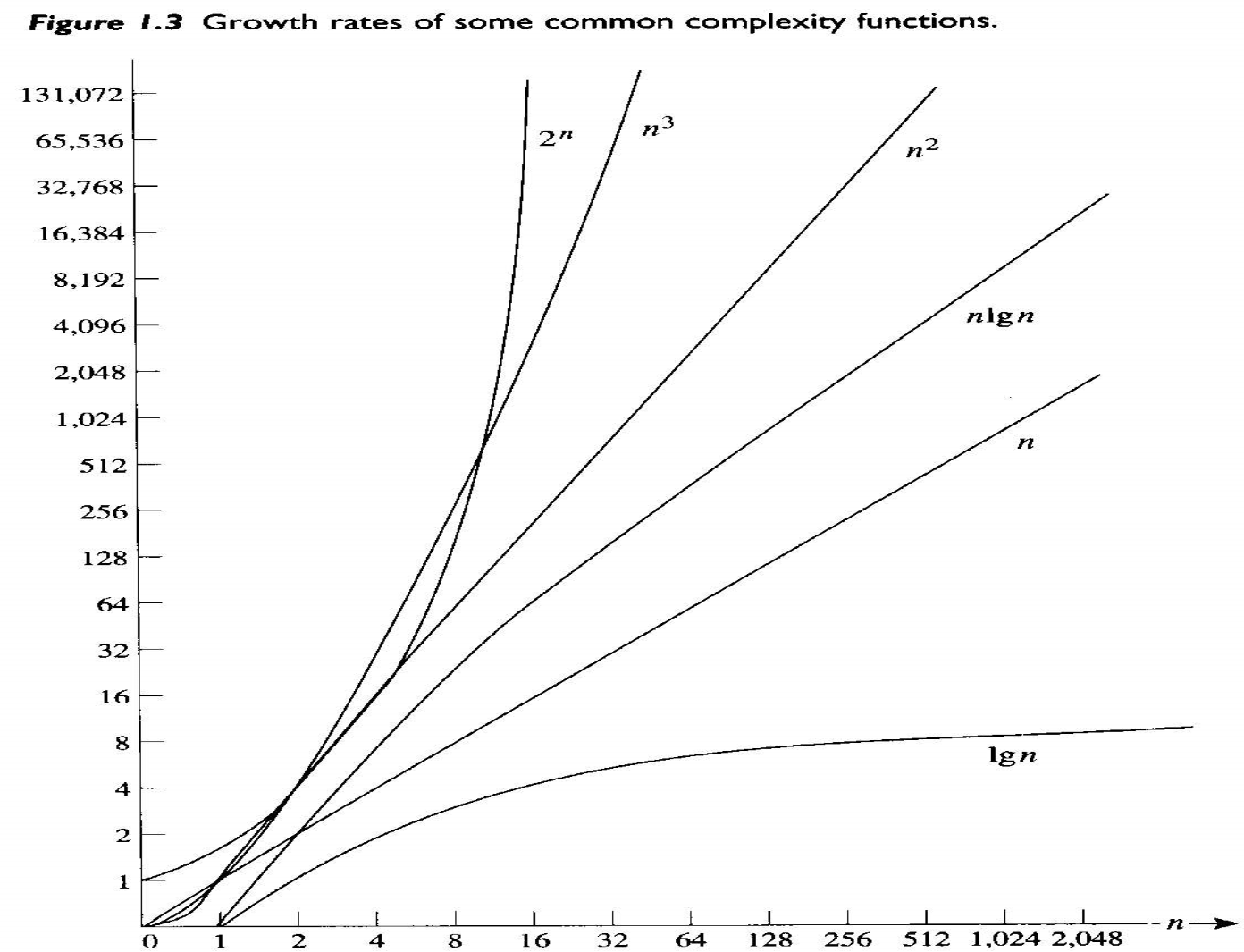
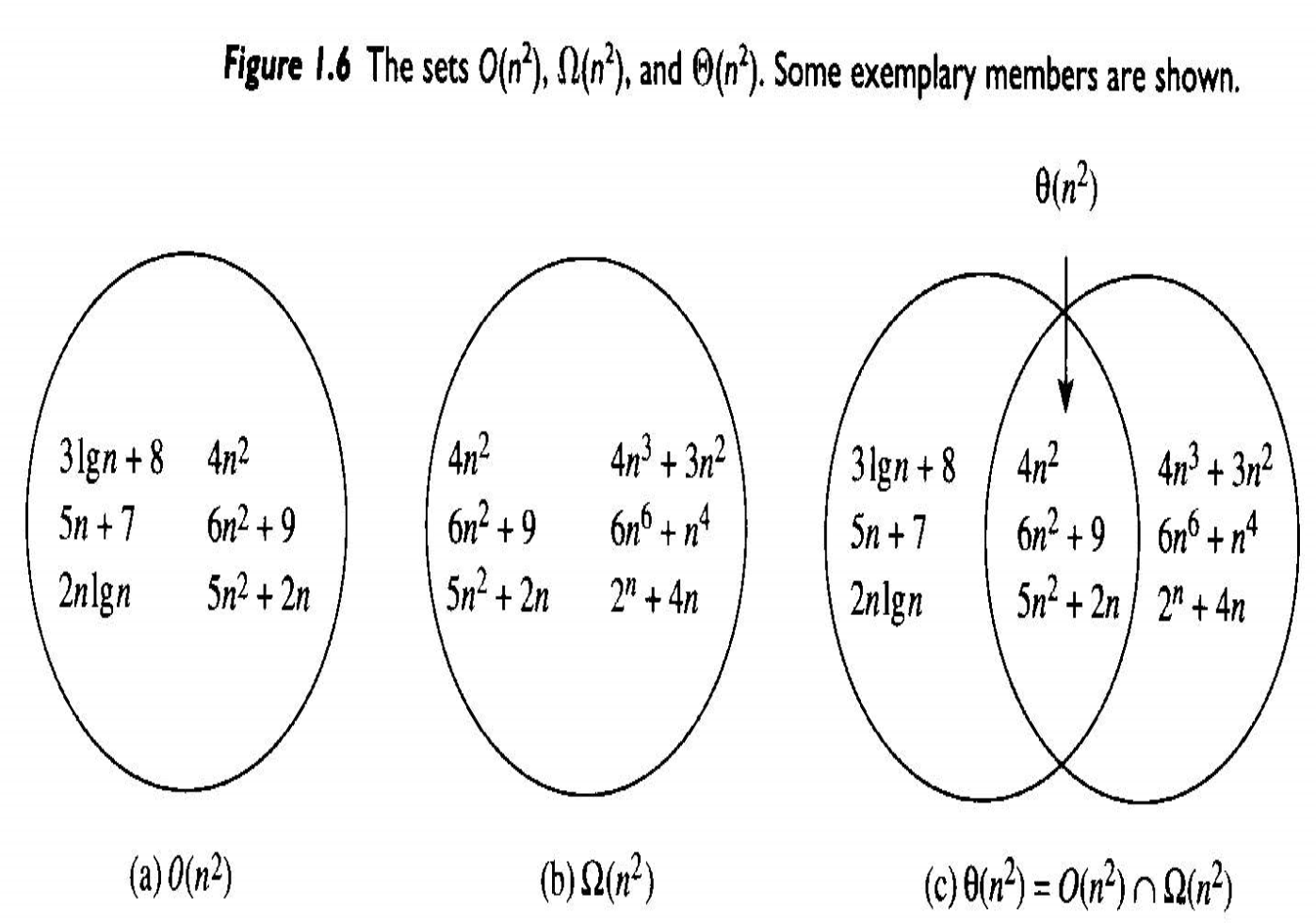
가장 흔히 나타나는 복합도 카테고리(complexity categories)를 보자.

$\theta(\log n)$, $\theta(n)$, $\theta(n \log n)$, $\theta(n^2)$, $\theta(n^3)$, $\theta(2^n)$

이 카테고리들에 속한 가장 간단한 함수들을 그래프로 그리면 다음과 같다.

차수의 정식 소개

Big O는 주어진 복잡도 함수 $f(n)$에 대해서 $O(f(n))$은 정수 $N$이상의 모든 $n$에 대해서 다음 부등식이 성립하는 양의 실수 c와 음이 아닌 정수 $N$이 존재하는 복잡도 함수 $g(n)$의 집합이다.

$g(n) \le c \times f(n)$

만약 $g(n) \in O(f(n))$이면, $g(n)$은 $f(n)$의 Big O이다라고 한다. 다음 예를 보자.

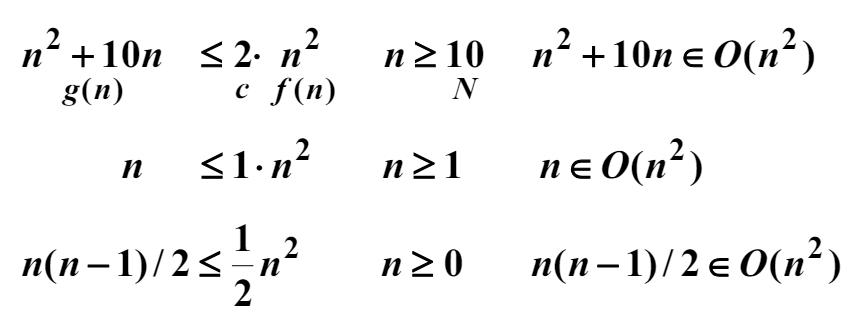
점근적인 하한(asymptotic lower bound, $\Omega$)의 정의는 주어진 복잡도 함수 $f(n)$에 대해서 $\Omega(f(n))$은 $N$ 이상의 모든 $n$에 대해서 다음 부등식을 만족하는 양의 실수 $c$와 음이 아닌 정수 $N$이 존재하는 복잡도 함수 $g(n)$의 집합이다.

$g(n) \ge c \times f(n)$

만약 $g(n) \in \Omega(f(n))$이면, $g(n)$은 $f(n)$의 $\Omega$이다라고 한다. 다음 예를 보자.

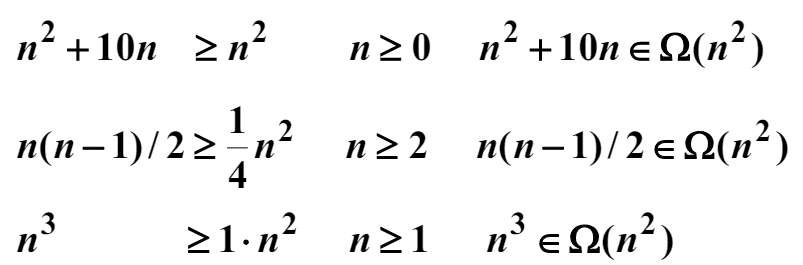
차수의 정의는 주어진 함수 $f(n)$에 대해서 $\theta(f(n)) = O(f(n)) \cap \Omega(f(n))$이면, $\theta(f(n))$는 $N$ 이상의 모든 정수 $n$에 대해서 다음 부등식을 만족하는 양의 실수 $c, d$와 음이 아닌 정수 $N$이 존재하는 복잡도 함수 $g(n)$의 집합이다.

$c \times f(n) \le g(n) \le d \times f(n)$

만약 $g(n) \in \theta(f(n))$이면, $g(n)$은 $f(n)$의 차수(order)이다라고 한다. 다음 예를 보자.

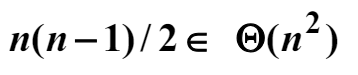
small o의 정의는 주어진 복잡도 함수 $f(n)$에 대해서 $o(f(n))$은 모든 양의 실수 $c$에 대해서 $n \ge N$을 만족하는 모든 $n$에 대해서 다음 부등식을 만족하는 음이 아닌 정수 $N$이 존재하는 모든 복잡도 함수 $g(n)$의 집합이다.

$g(n) \le c \times f(n)$

만약 $g(n) \in o(f(n))$이면, $g(n)$은 $f(n)$의 small o이다라고 한다. 다음 예를 보자.

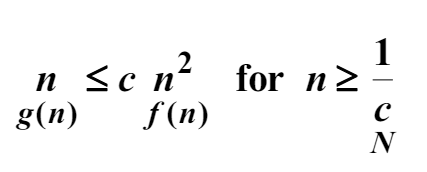
$o(f(n))$과 $O(f(n)) - \Omega(f(n))$은 같은 집합이 아니다. 다음 함수를 보자.

$g(n) = \begin{cases} n, & n\mbox{이 짝수인 경우} \\ 1, & n\mbox{이 홀수인 경우}\end{cases}$

$g(n) \in O(n) - \Omega(n)$이지만 $g(n)$은 $o(n)$에 속하지 않는다. 하지만, 일반적으로 $O(f(n)) - \Omega(f(n))$에 속한 함수는 $o(f(n))$에도 보통 속한다.

Twitter Facebook LinkedIn

MyeongWoo

알고리즘: 효율, 분석, 차수

알고리즘

효율적인 알고리즘 개발의 중요성

순차검색 vs. 이분검색

피보나치 수열

알고리즘의 분석

시간 복잡도 분석

이론의 적용

차수

차수의 직관적인 소개

차수의 정식 소개

공유하기

댓글남기기

참고

8장 인터페이스

7장 상속

6장 클래스

5장 참조 타입