분할정복
Updated:
분할정복(Divide-and-Conquer)은 하향식(top-down) 문제풀이 방식이다. 즉, 문제의 상위 입력사례의 해답은 하위의 작은 입력사례(들)의 해답을 가지고 구한다. 재귀함수가 작동하는 원리가 바로 이렇다. 분할정복 알고리즘을 설계할 때도 보통 알고리즘을 재귀로 작성한다. 후에 재귀 알고리즘은 효율적인 반복 알고리즘으로 변형할 수 있다.
이분검색
이분검색 알고리즘을 재귀(recursion)로 설계해본다.
- (비내림차순으로) 정렬된 배열을 분할정복으로 이분검색을 하기 위해서는 먼저 배열의 정 가운데 원소와 키 $x$를 비교한다. 만일 같으면 원소를 찾았으므로 알고리즘을 종료한다.
- 만약 다르면, 배열을 이미 비교한 원소를 기준으로 반으로 분할한다. 만약 $x$가 가운데 원소보다 작으면, 온쪽 배열에서 찾아야 하고, 그렇지 않으면 오른쪽 배열에서 찾아야한다.
- 왼쪽 또는 오른쪽 중 원소가 있을 해당 반쪽 배열의 정 가운데 원소와 다시 비교하고 위 과정을 $x$를 찾거나 $x$가 그 배열에 없다고 확신할 때까지 이 절차를 계속한다.
다음 예제를 보자.
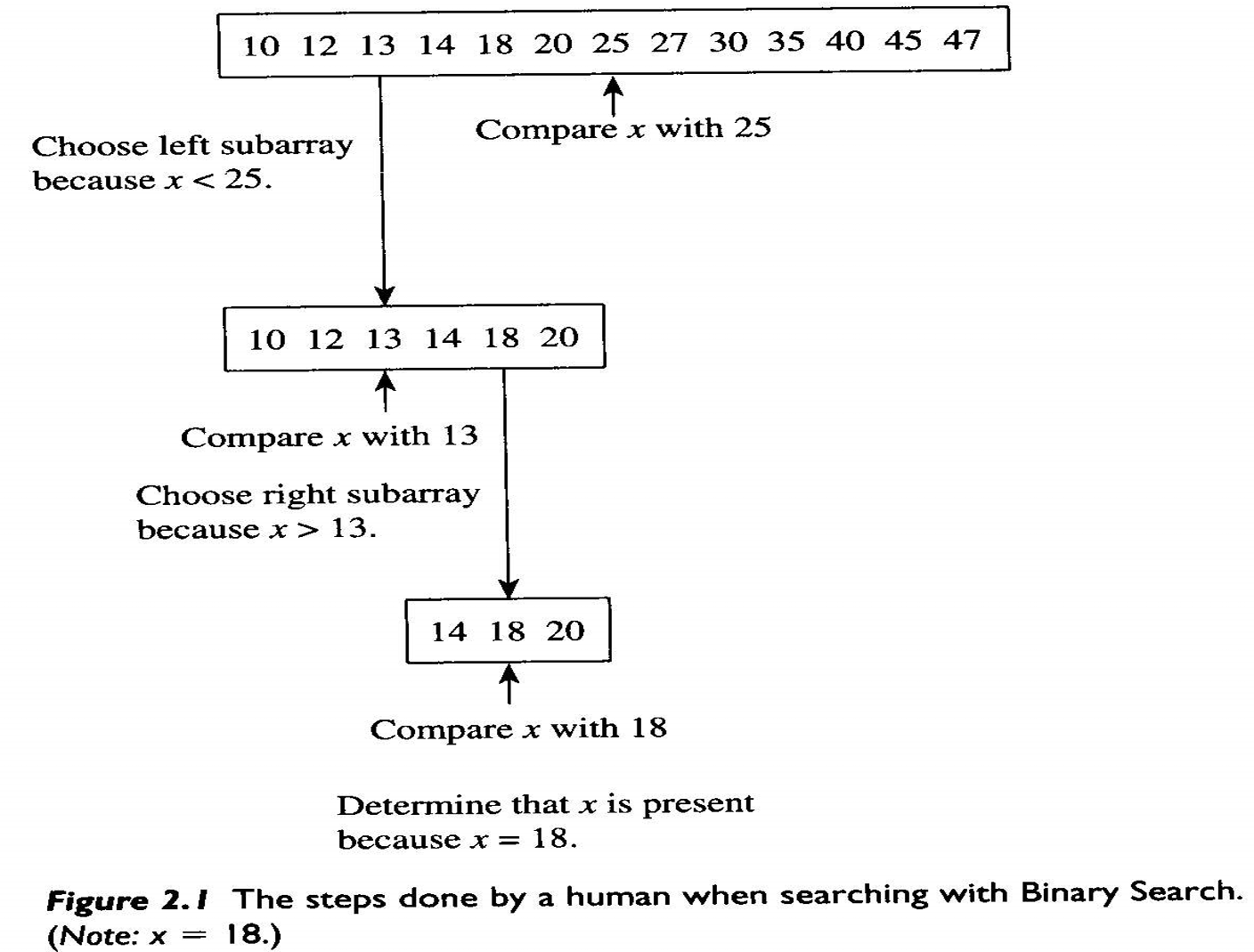
- [분할] 배열을 분할한다. $x < 25$이기 때문에 왼쪽 배열에서 검색한다.
- 10 12 13 14 18 20
- [정복] 왼쪽 배열에 $x$가 있는지 결정한다(왼쪽 배열을 재귀적으로 정복한다).
- $x$는 왼쪽 배열에 있다.
- [취합] 왼쪽 배열에서 얻은 답으로 전체 배열에 대한 답을 구한다.
- $x$는 왼쪽 배열에 있다.
재귀로 작성한 이분검색 알고리즘을 보자.
// 문제: 원소가 n개인 정렬된 배열 S에 검색키 x가 있는가?
// 입력: 양의 정수 n, 정렬된(비내림차순) 배열 S(첨자는 1부터 n까지), 검색키 x
// 출력: location, S에서 x의 위치(만약 x가 s에 없으면 0)
index location(index low, index high){
index mid;
if (low > high){
return 0; // 다 본 경우
} else {
mid = ⌊(low + high) / 2⌋;
if (x == S[mid]){
return mid;
} else if (x < S[mid]){
return location(low, mid - 1);
} else {
return location(mid + 1, high);
}
}
}
이분검색 알고리즘은 최악의 경우를 고려하여 분석한다.

합병정렬
원소가 n개인 배열은 다음과 같은 절차로 합병정렬한다.
- [분할] 배열을 반으로 분할한다. 분할한 배열의 원소는 각각 $n/2$ 개이다.
- [정복] 분할한 배열을 각각 따로 정렬한다(배열에 원소가 2개 이상이면 합병정렬을 재귀 호출하여 정렬한다).
- [취합] 정렬한 두 배열을 합병하여 정렬한다.
다음 예를 보자.
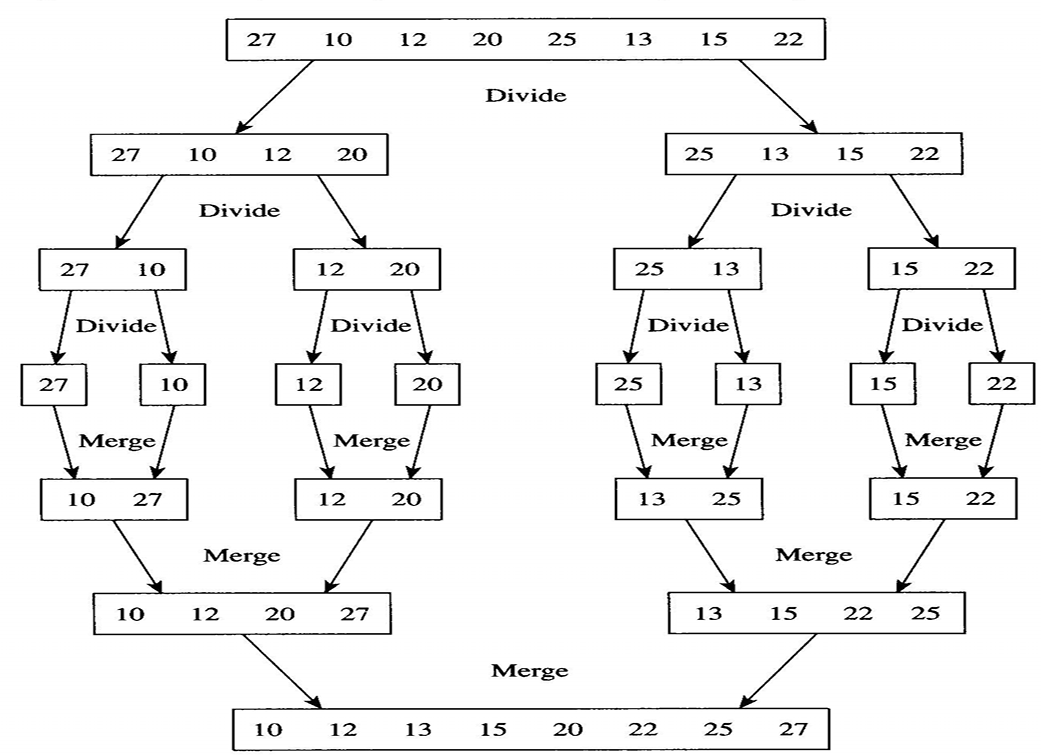
종료조건은 배열의 크기가 1이 된 경우이고, 바로 그 시점에서 합병이 시작된다.
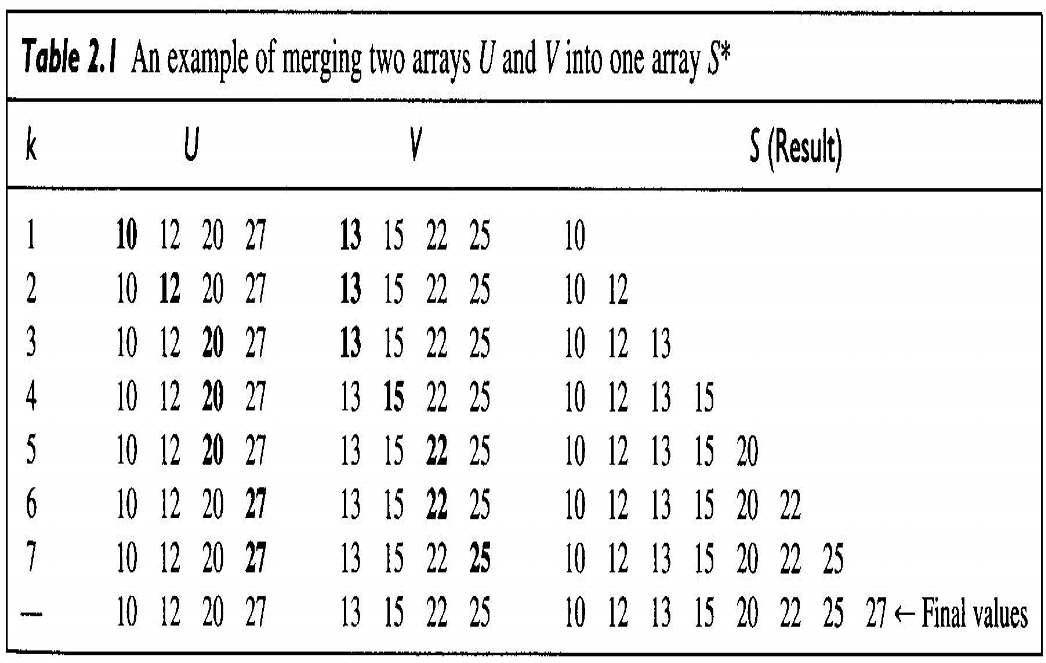
위 표는 크기가 4인 배열 두개를 합병할 때 merge 프로시저는 어떻게 작동하는지 알 수 있다. 재귀로 작성한 합병정렬 알고리즘을 보자.
// 문제: n개의 원소를 비내림차순으로 정렬
// 입력: 양의 정수 n, 배열 S(인덱스는 1부터 n까지)
// 출력: 원소를 비내림차순으로 정렬한 배열 S
void mergesort2 (index low, index high){
index mid;
if(low < high) {
mid = ⌊(low + high) / 2⌋;
mergesort2(low, mid);
mergesort2(mid + 1, high);
merge2(low, mid, high);
}
}
// 문제: 합병정렬 2에서 분할하여 정렬한 배열을 합병
// 입력: 인덱스 low, mid, high, S의 부분배열(인덱스는 low부터 high까지)
// low에서 mid까지 배열의 원소는 이미 정렬되어 있고, mid + 1부터 high까지의 배열에 있는 원소도 정렬되어 있다.
// 출력: 원소가 비내림차순으로 정렬되어 있는 S의 부분배열(인덱스는 low부터 high까지)
void merge2 (index low, index mid, index high) {
index i, j, k;
keytype U[low .. high] // 합병에 필요한 지역 배열
i = low; j = mid + 1; k = low;
while (i <= mid && j <= high) {
if(S[i] < S[j]) {
U[k] = S[i];
i++;
}
else {
U[k] = S[j];
j++;
}
k++;
}
if(i > mid) {
move S[j] through S[high] to U[k] through U[high];
}
else {
move S[i] through S[mid] to U[k] through U[high];
}
move U[low] through U[high] to S[low] through S[high];
}
합병 정렬의 최악 시간복잡도 분석을 해본다.

Quicksort
Quicksort는 기준원소(pivot)를 선정하여 기준원소보다 작은 원소는 모두 왼쪽 배열로, 기준원소보다 크거나 같은 원소는 모두 오른쪽 배열로 가도록 분할한다. 기준원소 선정은 중요하지만, 편의상 일단 배열의 첫 원소를 기준으로 잡는다. 다음 예를 보자.
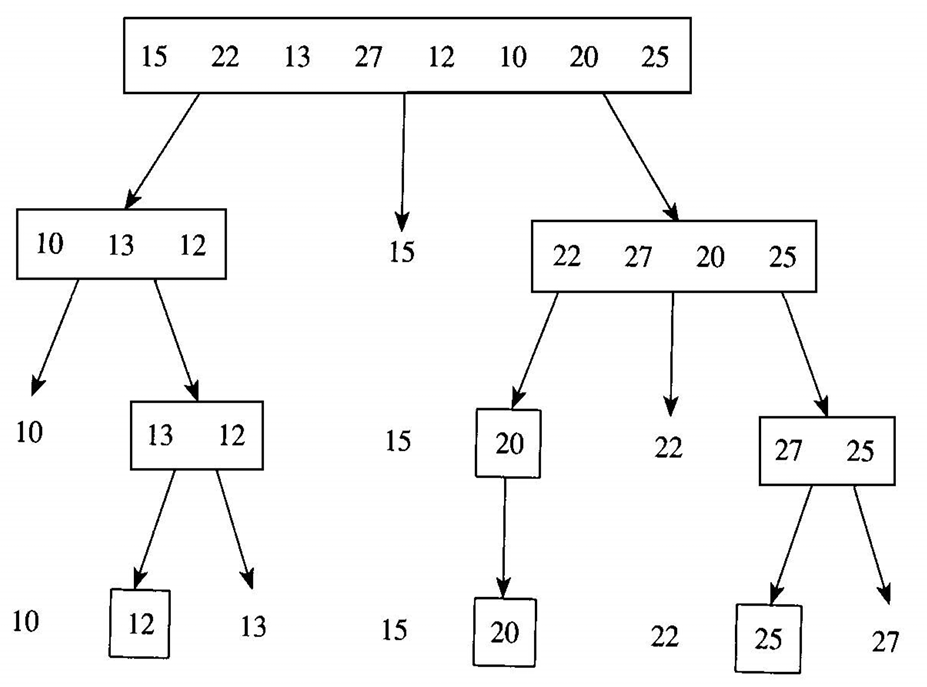
Quicksort는 분할한 두 배열을 각각 재귀 호출하여 정렬한다. 원소가 하나뿐인 배열로 분할될 때까지 재귀 호출을 계속한다. 다음은 알고리즘이다.
// 문제: 비내림차순으로 원소가 n개인 배열을 정렬
// 입력: 양의 정수 n, 배열 S(인덱스는 1부터 n까지)
// 출력: 비내림차순으로 정렬된 배열 S
void quicksort (index low, index high) {
index pivotpoint;
if(high > low) {
partition (low, high, pivotpoint);
quicksort (low, pivotpoint - 1);
quicksort (pivotpoint + 1, high);
}
}
// 문제: quicksort에서 쓸 수 있도록 배열 S를 분할
// 입력: 인덱스 low와 high, 배열 S에서 low부터 high까지의 부분배열
// 출력: low에서부터 high까지 인덱스로 된 S의 부분배열 기준점, pivotpoint
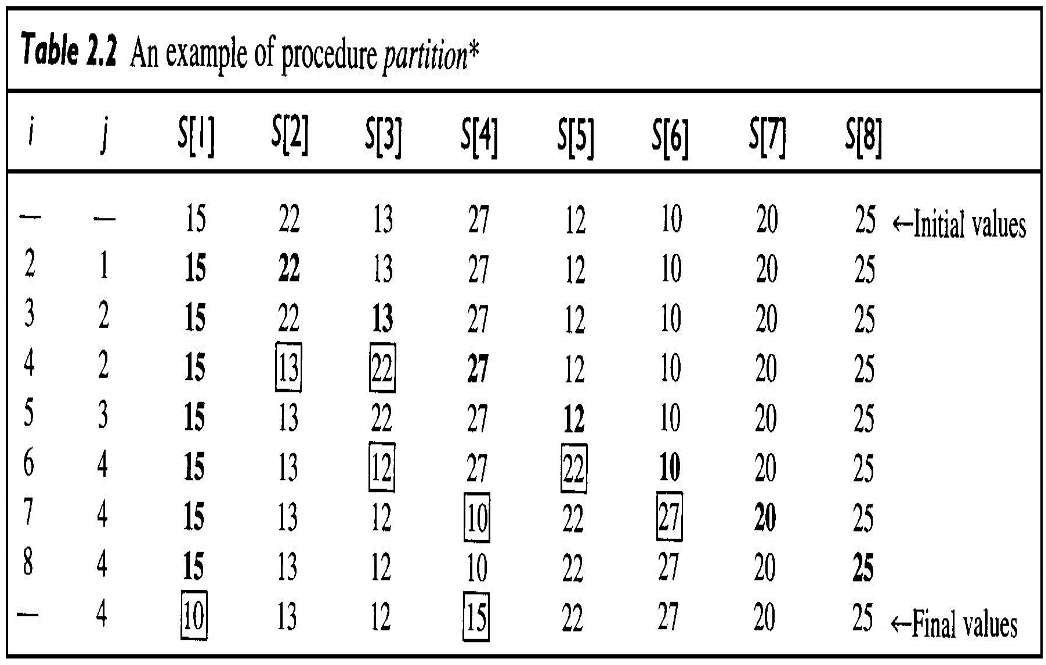
void partition (index low, index high, index& pivotpoint) {
index i, j;
keytype pivotitem;
pivotitem = S[low]; // pivotitem으로 첫 원소 선택
j = low;
for(i = low + 1; i <= high; i++) {
if(S[i] < pivotitem) {
j++;
exchage S[i] and S[j];
}
}
pivotpoint = j;
exchange S[low] and S[pivotpoint]; // pivotitem 값을 pivotpoint에 저장
}
시간 복잡도를 분석해본다. 최악의 경우는 완전히 정렬된 배열을 정렬하는 경우이다. 최악 시간 복잡도 분석은 다음과 같다.

평균의 경우를 따져본다.
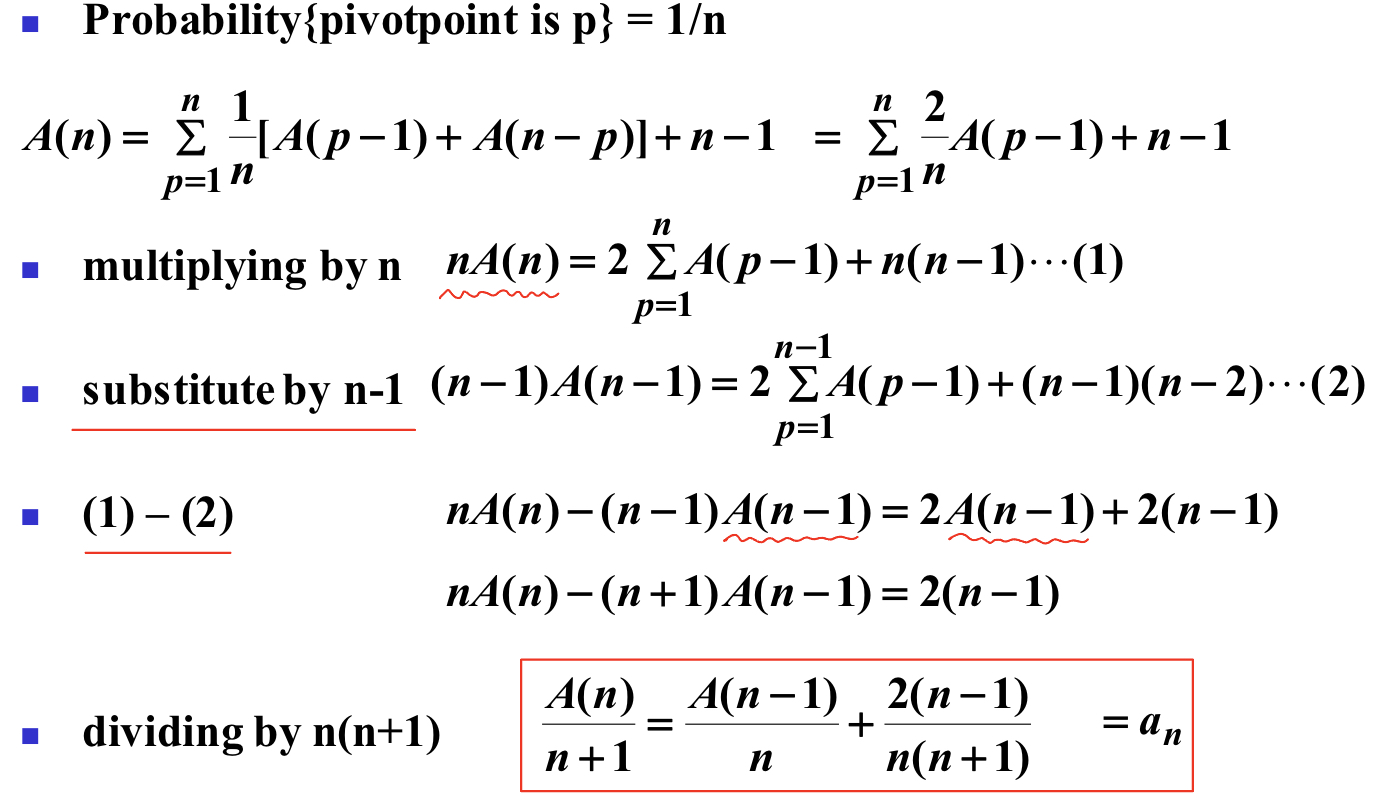
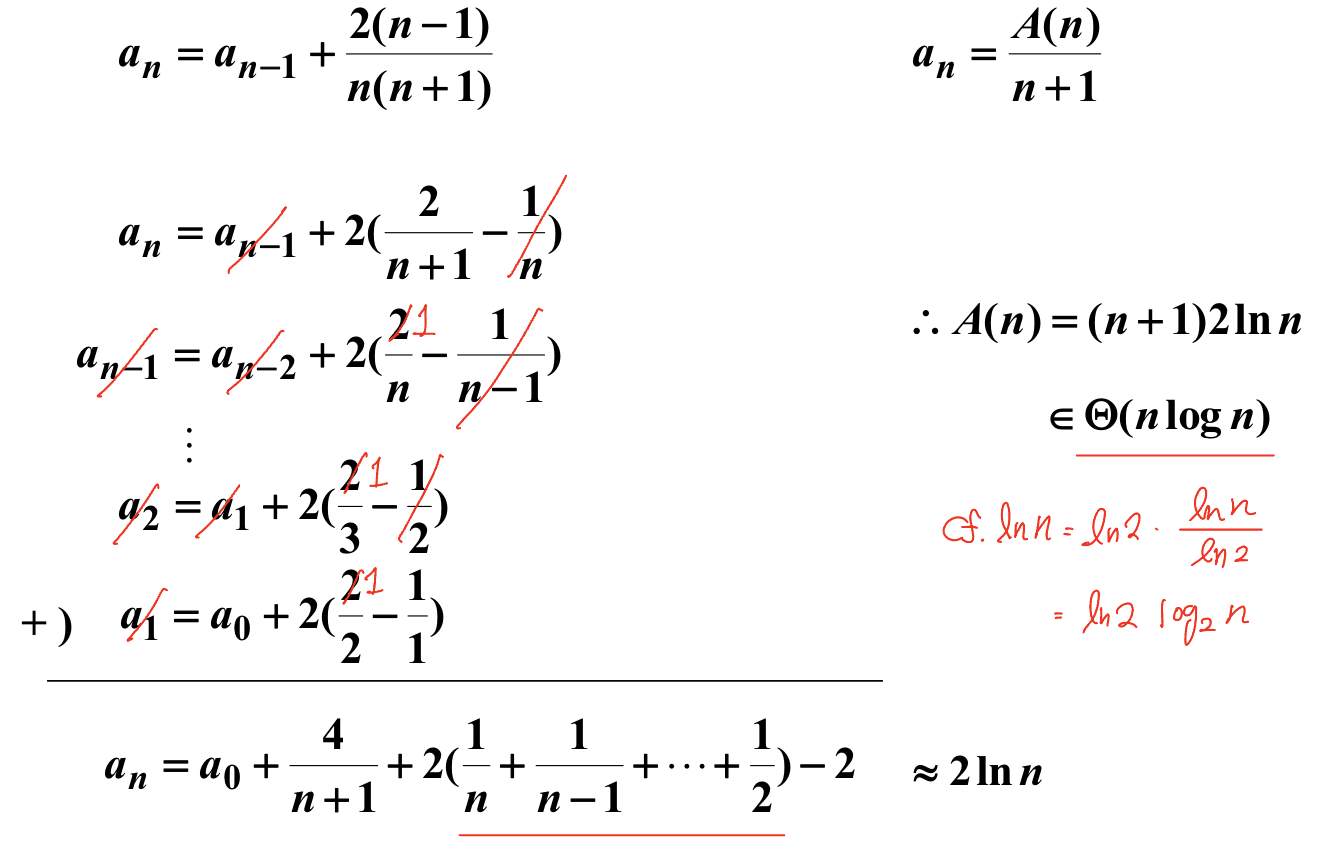
쉬트라쎈의 행렬곱셈 알고리즘
행렬곱셈의 정의를 그대로 따라 두 행렬을 곱하면, 곱셈 횟수를 기준으로구한 시간복잡도는 $n$이 행렬에서 열과 행의 개수일 때 $T(n) = n^3$임을 알 수 있다. 덧셈 횟수를 기준으로 분석하면 시간복잡도는 $T(n) = n^3 - n^2$이다.
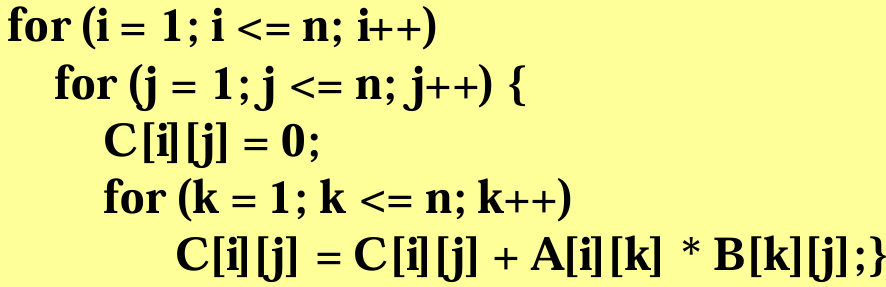
쉬트라쎈(Strassen) 알고리즘은 다음 예와 같다.
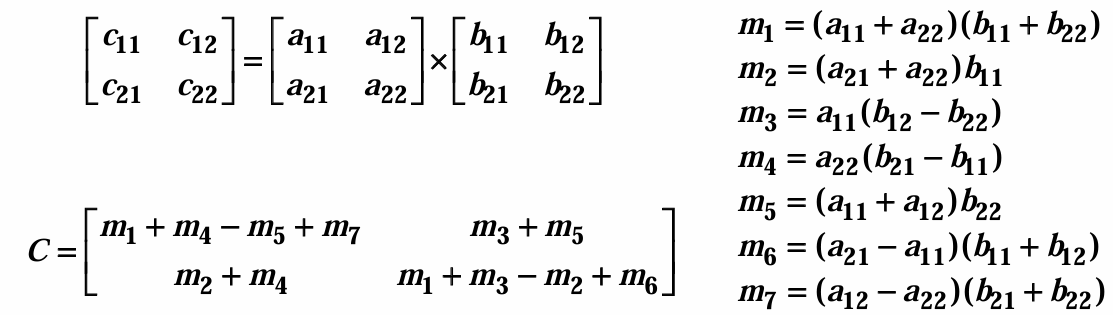
$2 \times 2$ 행렬을 곱할때는 별로 좋아진 것 같아 보이지 않는다. 다음 $4 \times 4$ 예제를 보자.
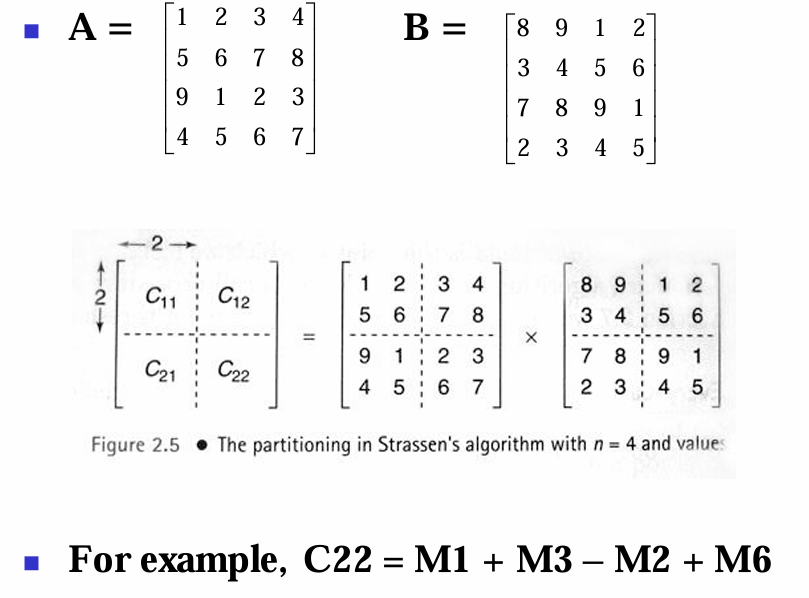
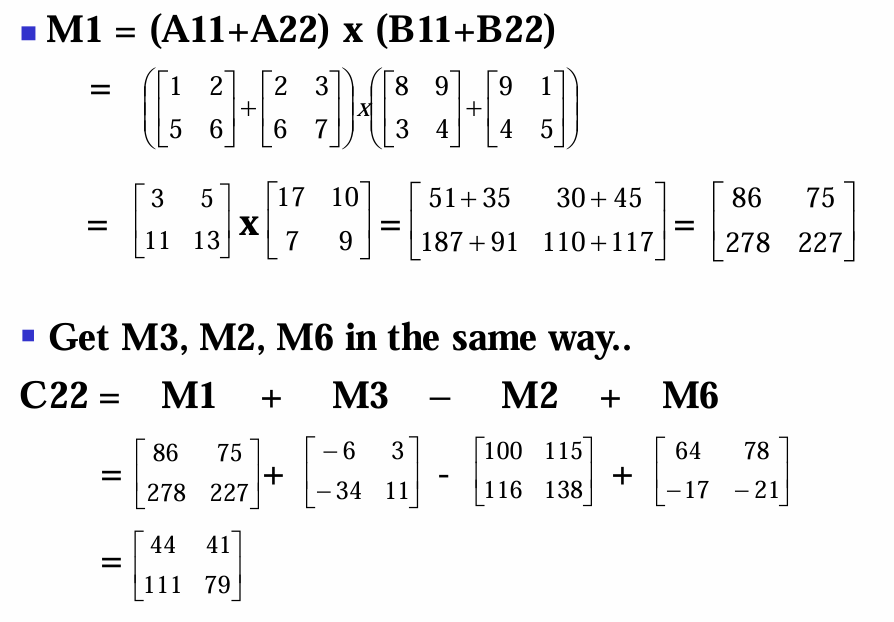
이제 $n$이 2의 거듭제곱일 때 쉬트라쎈의 방법을 이용한 알고리즘을 보자.
// 문제: n이 2의 거듭제곱일 때 2개의 n x n 행렬의 곱을 구하시오.
// 입력: 2의 거듭제곱인 정수 n, 2개의 n x n 행렬 A와 B
// 출력: A와 B의 곱 C
void strassen (int n, nxn_matrix A, nxn_matrix B, nxn_matrix C) {
if(n <= threshold){
표준 알고리즘으로 C = A X B를 계산한다;
}
else {
A를 A_11, A_12, A_21, A_22로 분할한다;
B를 B_11, B_12, B_21, B_22로 분할한다;
쉬트라쎈의 방법으로 C = A X B를 계산한다;
// 재귀 호출의 예제; strassen(n/2, A_11 + A_22, B_11 + B_22, M_1);
}
}
임계점(threshold)은 strassen 프로시저를 재귀 호출하는 것보다 표준 알고리즘을 사용하는 게 더 효과적인 지점이다. 시간 복잡도를 분석해본다.
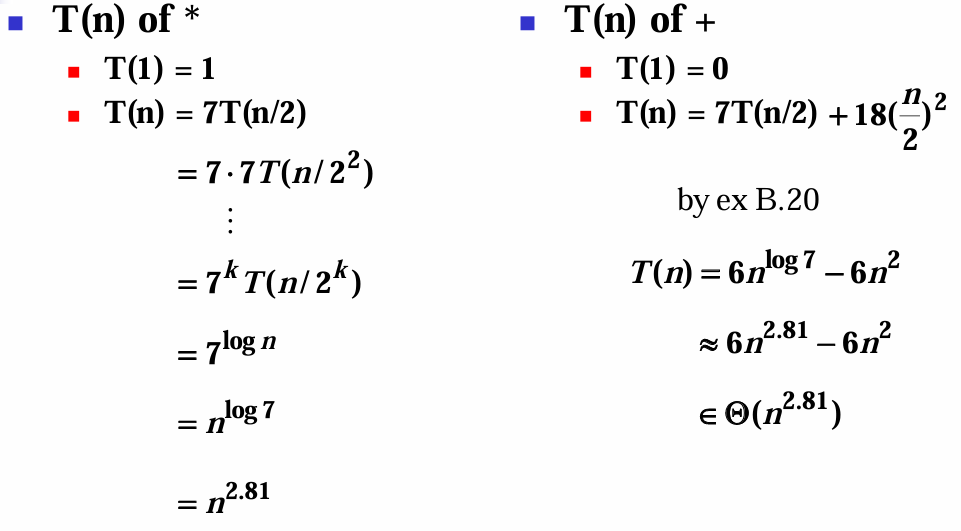
댓글남기기