Hongik University
Mechanical System
Design Engineering,
Computer Engineering

Updated:

  $n$번째 피보나찌 수 구하기알고리즘을 분할정복 알고리즘으로 풀면 재귀 호출의 횟수가 $n$에 대하여 지수($2^n$)로 증가한다. 분할정복은 하향식(top-down) 문제풀이 방식이다. 분할한 입력사례들끼리 서로 관련이 없는 정렬 문제를 푸는 경우 이 방식이 잘 통한다. 분할한 입력사례들은 각각 독립적으로 정렬한배열들이라 서로 관련이 없고 중복도 없다. 그러나 $n$번째 피보나찌 수 구하는 문제는 분할한 입력사례들이 여러 번 중복해서 나타난다.

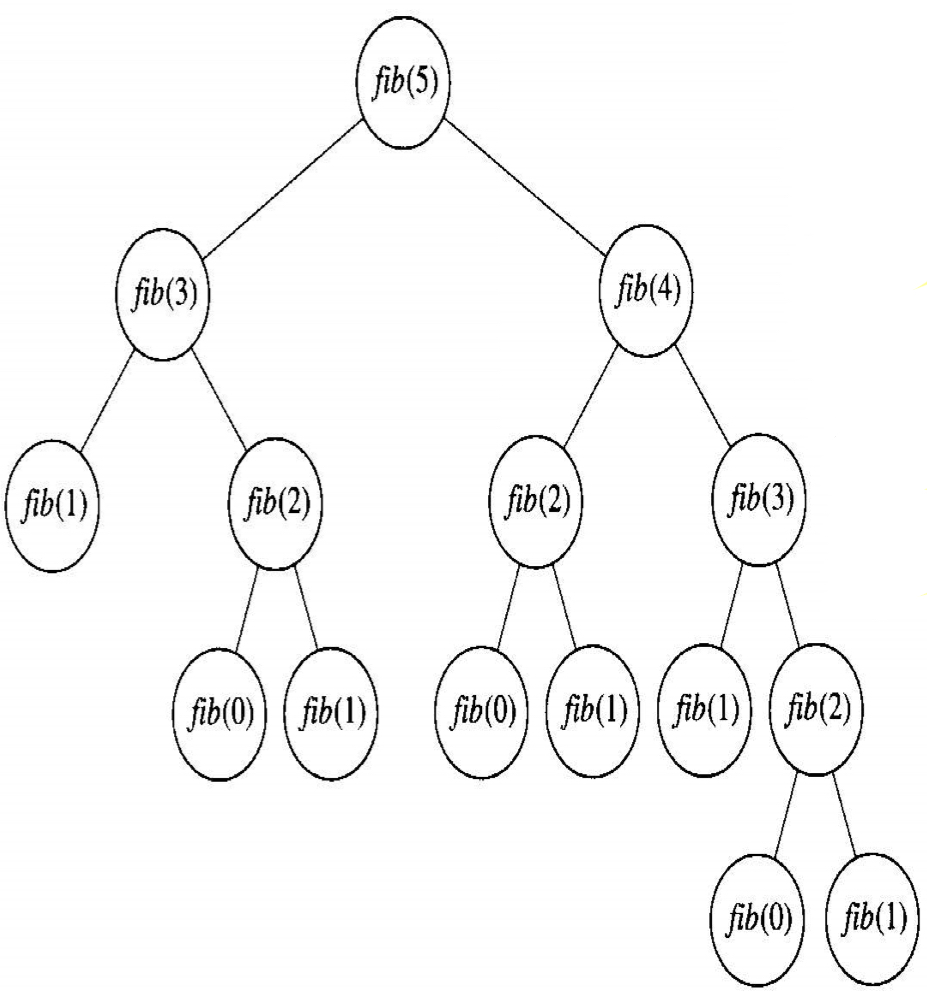
 분할정복 방식으로 이 문제를 풀면 이 두 수를 따로 구하기 때문에 두번째 피보나찌 수는 두 번 이상 중복 계산한다. 분할한 입력사례들이 서로 관련이 있거나 두 번 이상 나타나는 문제를 분할정복 알고리즘으로 풀면 같은 입력사례를 중복 계산하게 되므로 매우 비효율적이다.
 동적계획(Dynamic programming)은 분할정복과 문제해결 방향이 거꾸로다. 동적계획은 문제의 입력사례를 분할하여 문제를 푼다는 점은 분할정복과 비슷하다. 그러나 동적계획은 분할한 입력사례를 재귀 호출하여 답을 얻는 대신, 가장 작은 입력사례의 답을 먼저 구하여 저장해놓고, 필요하면 꺼내 쓴다.
 1장에서 피보나찌 수를 구하는 효율적인 알고리즘은 동적계획을 이용한 전형적인 사례이다. 동적계획 알고리즘은 배열을 이용하여 상향식으로 해답을 구한다. 따라서 동적계획은 상향식(bottom-up) 접근방법이다. 동적계획 알고리즘의 개발절차는 다음과 같다.

  1. 문제의 입력사례에 대해서 해답을 계산하는 재귀 관계식(recursive property)을 세운다.
  2. 작은 입력사례부터 먼저 해결하는 상향식 방법으로 전체 입력사례에 대한 해답을 구한다.

이항계수 구하기

 이항계수(binomial coefficient)는 다음과 같다.

${n \choose k} = \frac{n!}{k!(n-k)!}$ for $0 \le k \le n$

 갑이 큰 $n$과 $k$에 대한 이항계수를 구하는 경우 이 식을 가지고 바로 구하기는 힘들다. 왜냐하면 그리 크지 않은 $n$에 대해서도 $n!$은 꽤 크기 때문이다. 다음 재귀 관계식을 사용하면 $n!$이나 $k!$을 계산하지 않고 이항계수를 구할 수 있다.

${n \choose k} = \begin{cases} {n-1 \choose k-1} + {n-1 \choose k}, & 0< k < n \\ 1, & k=0 \mbox{ or } k=n \end{cases}$

 위 식의 증명과정은 다음과 같다.

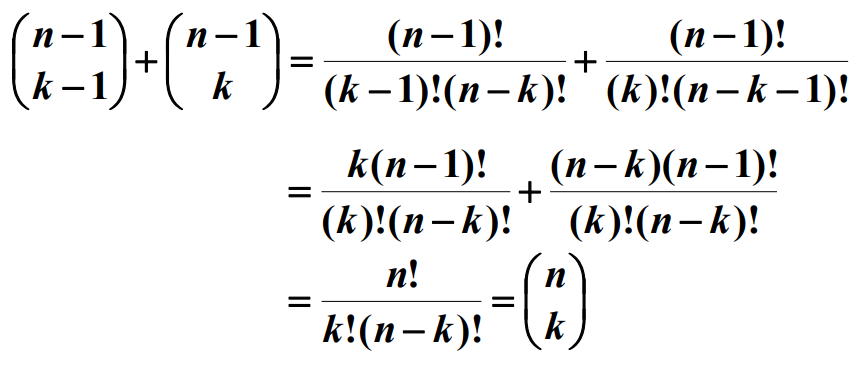
 위 과정을 예로, 배열 $[ a_1, a_2, \ldots a_j, \ldots a_n]$에서 $a_j$를 포함해서 뽑기($n-1$개에서 $k-1$개 뽑기)와 $a_j$를 포함하지 않고 뽑기($n-1$개에서 $k$개 뽑기)를 더한 것이다.

// 문제: 이항계수를 계산하시오.
// 입력: k ≤ n을 만족하는 0 이상의정수 n과 k
// 출력: bin, 이항계수(n k)
int bin (int n, int k) {
    if (k == 0 || n == k){
        return 1;
    }
    else {
        return bin(n - 1, k - 1) + bin(n - 1, k);
    }
}

 위와 같은 알고리즘은 매우 비효율적이다. ${n \choose k}$를 구하기 위해서 이 알고리즘이 계산하는 항의 개수는 다음과 같다.

$2 {n \choose k} - 1$

 문제는 재귀 호출할 때마다 같은 사례를 중복 계산한다는 것이다. 예를 들어, $bin(n - 1, k - 1)$과 $bin(n - 1, k)$는 둘 다 $bin(n - 2, k - 1)$의 계산결과가 필요하고, 이 결과는 각 재귀 호출 시 각각 따로 구한다. 이는 비효율적이다.
 이제 효율적인 알고리즘을 동적계획으로 설계해본다.

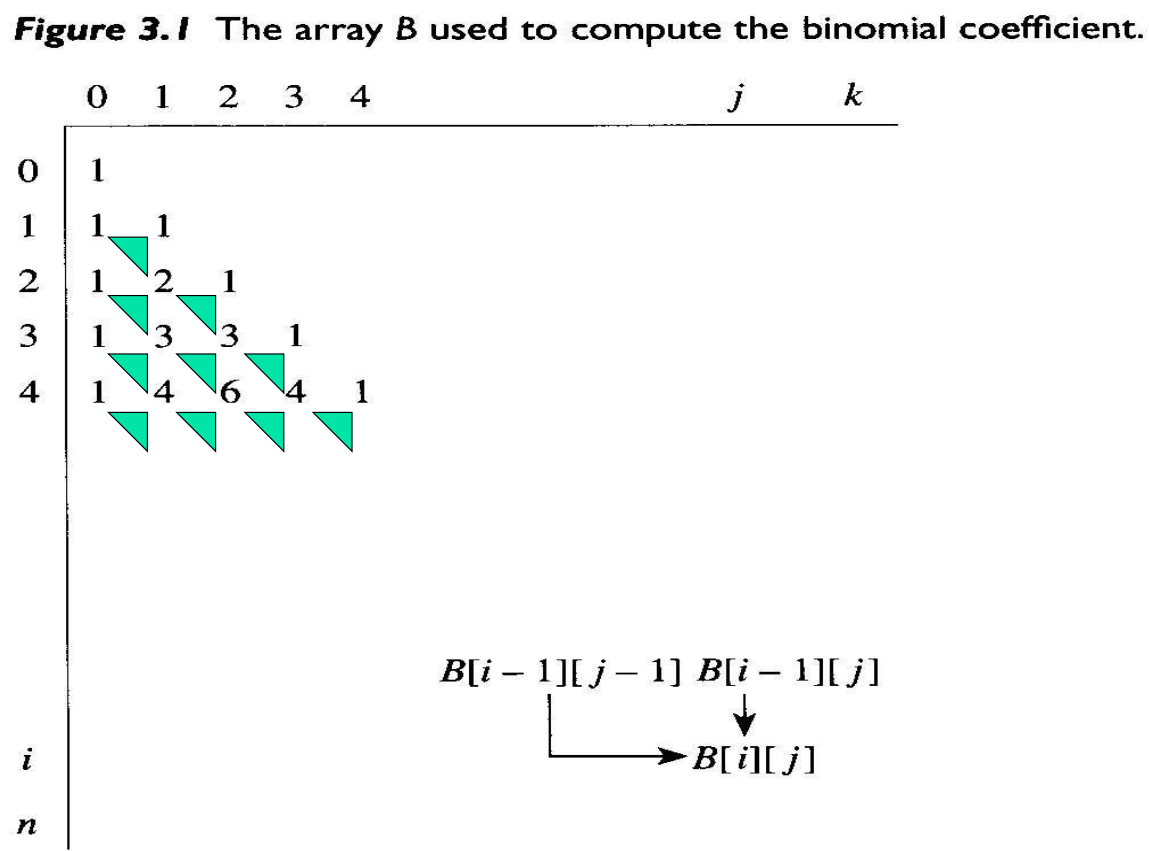
${n \choose k} = \begin{cases} {n-1 \choose k-1} + {n-1 \choose k}, & 0< k < n \\ 1, & k=0 \mbox{ or } k=n \end{cases}$

 이 식으로 $B[i][j]$에 ${i \choose j}$값을 차례로 저장하여 배열 $B$를 구축해 나간다.

  1. 재귀 관계식을 세운다. $B$의 형태로 작성하면 다음과 같다.
    • $B[i][j] = \begin{cases} B[i-1][j-1] + B[i-1][j], & 0< j < i \\ 1, & j=0 \mbox{ or } j=i \end{cases}$
  2. 첫째 행부터 B의 행에 값들을 차례로 계산하여 저장하는 상향식(bottom-up) 방식으로 문제를 푼다.

 다음 그림에서 각 행의 값은 절차 1에서 정립한 재귀 관계식을 적용하여 바로 이전에 계산한 값을 가지고 계산한다.계산한 최종값 $B[n][k]$은 ${n \choose k}$의 값이다.

// 문제: 이항계수를 계산하시오.
// 입력: k ≤ n을 만족하는 0이상의 정수 n과 k
// 출력: bin2, 이항계수 (n k)
int bin2 (int n, int k) {
  index i, j;
  int B[0..n][0..k];

  for(i = 0; i <= n; i++){
    for(j = 0; j <= minimum(i,k); j++){
      if(j == 0 || j == i){
        B[i][j] = 1;
      }
      else{
        B[i][j] = B[i-1][j-1] + B[i-1][j];
      }
    }
  }

  return B[n][k];
}

 $n$과 $k$는 이 알고리즘에서 입력의 크기가 아니다. 입력의 크기는 $n$과 $k$를 코드화(encode)하는데 필요한 심벌의 개수이다. 그러나 답을 구할 때까지 얼마나 작업을 했는지 $n$과 $k$의 함수로 표현하여 알고리즘의 효율성을 대략 알아볼 수는 있다.

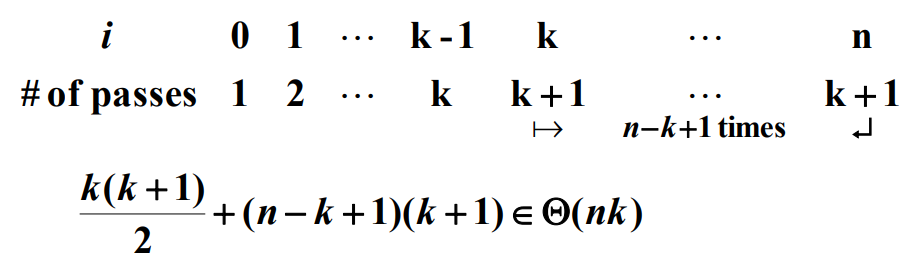
 분할정복 대신 동적계획으로 훨씬 더 효율적인 알고리즘을 설계하였다.

프로이드의 최단경로 알고리즘

 최단경로를 구하는 알고리즘을 설계하기 전에 그래프이론을 알아야 한다. 다음은 가중치가 포함된 방향그래프의 예이다.

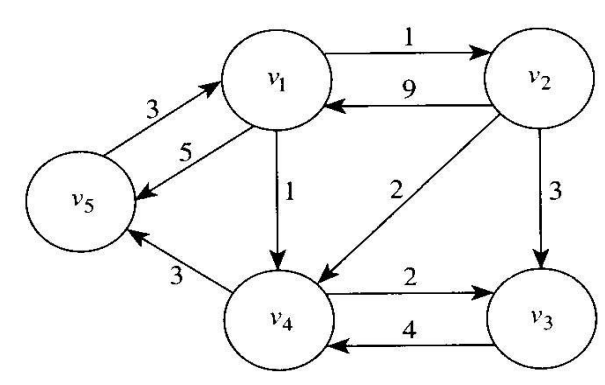
  • 원: 마디(vertex)
  • 선: 이음선(edge)
  • 이음선에 방향이 있는 그래프: 방향그래프(directed graph, digraph)
  • 이음선과 관련된 값: 가중치(weight)
    • 이음선에 가중치가 있는 그래프: 가중치포함 그래프(weighted graph)
    • 가중치는 음이 아니라고 가정한다.
  • 방향그래프에서 다음 마디로 가는 이음선이 있는 마딤의 나열: 경로(path)
  • 어떤 마디에서 그 마디 자신으로 가는 경로: 순환경로(cycle)
    • 그래프에 순환경로가 있으면 순환적(cyclic)이라 하고 그렇지 않으면 비순환적(acyclic)이라고 한다.
  • 같은 마디를 두 번 거치지 않은 경로: 단순경로(simple path)
  • 가중치포함 그래프에서 경로의 길이(length)는 경로 상에 있는 가중치의 합
    • 가중치가 없는 그래프에서 경로의 길이는 경로 상 이음선의 개수

 한 vertex에서 다른 vertex로 가는 최단경로는 하나 이상 있을 수 있기 때문에, 여기서는 그 최단경로들 중에서 하나를 찾는다. 이 문제를 가장 쉽게 푸는 알고리즘은 각 마디에 대해서 그 마디에서 다른 각 마디로 가는 모든 경로의 길이를 구한 후, 그 길이 중에서 최소값을 찾는 것이다. 그러나 이 알고리즘은 지수시간(exponential)보다도 나쁘다. 예를들어, 모든 마디가 이음선으로 서로 연결되어 있다고 가정하면, 한 마디에서 다른 마디로 가면서 나머지 모든 마디를 거쳐서 가는 경로의 총 개수는 $(n-2)(n-3)\cdots 1 = (n-2)!$이다.
 동적계획을 사용하면, 최단경로 문제를 푸는 3차시간(cubic-time) 알고리즘을 만들어낼 수 있다. 우선 최단경로의 길이만 구하는 알고리즘을 설계해본다. $n$개 마디로 된 가중치포함 그래프는 다음과 같이 배열 $W$로 표현한다.

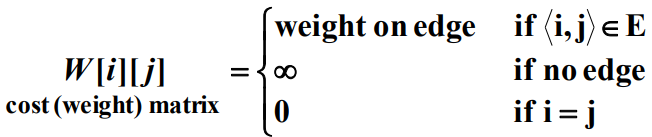
 $v_i$에서 $v_j$로 가는 edge가 있는 경우 $v_i$는 $v_j$에 인접하다(adjacent)라고 하기 때문에 이 배열을 그래프의 인접행렬(adjacent matrix)이라고 한다. 위 그래프를 인접행렬로 표현하면 다음과 같다.

 위 배열에서 D는 그래프 마디 사이의 최단경로의 길이를 나타낸다. 예를 들어, $D[3][5]$는 7인데, $v_3$에서 $v_5$로 가는 최단경로의 길이가 7이기 때문이다. $W$의 값에서 $D$의 값을 계산하는 방법이 바로 최단경로 문제를 푸는 알고리즘이다. 따라서 일련의 $n+1$개의 배열 $D^{k}$를 만든다. 여기서 $0 \le k \le n$이고, $D^k$는 다음과 같이 정의한다.

$D^k[i][j] = \mbox{집합 }{v_1, v_2, \ldots , v_k} \mbox{에 속하는 마디만을 거쳐서 }v_i \mbox{에서} v_j\mbox{로 가는 최단경로의 길이}$

 동적계획을 적용하는 절차는 다음과 같다.

  1. $D^{k-1}$로 부터 $D^k$를 계산하는 재귀 관계식(과정)을 정립한다.
  2. $k=1$부터 $n$까지(1에서 정립한) 과정을 상향식으로 반복하여 문제의 입력사례를 해결한다.
    • $D^0 = W, D^1, \ldots, D^n = D$

 다음 예를 보자.

 $D^n[i][j]$가 다른 모든 마디를 거쳐 가도록 허용하고 계산한 $v_i$에서 $v_j$로 가는 최단 경로의 길이이므로, 그 값은 $v_i$에서 $v_j$로 가는 최단경로의 길이이다. $D^0[i][j]$는 다른 어떤 마디도 거쳐 가지 못하도록 하고 구한 최단경로의 길이이므로, $v_i$에서 $v_j$를 잇는 이음선의 가중치이다.
 $D^{k-1}$로 부터 $D^k$를 계산하는 재귀 관계식(과정)을 정립하기 위해 다음 두가지 경우를 고려한다.

  • 경우1. ${v_1, v_2, \ldots , v_k}$에 속한 마디만 중간마디로 거쳐서 $v_i$에서 $v_j$로 가는 최단경로 중에서 최소한 하나는 $v_k$를 거치지 않는 경우이다. 그러면 등식 $D^k[i][j] = D^{k-1}[i][j]$가 성립힌다.
    • 앞의 그래프에서 $D^5[1][3] = D^4[1][3] = 3$이다.
  • 경우2. ${v_1, v_2, \ldots , v_k}$에 속한 마디만 중간마디로 거쳐서 $v_i$에서 $v_j$로 가는 최단경우는 모두 $v_k$를 거치는 경우이다. 이 경우 어떤 최단경로라도 다음과 같이 된다.

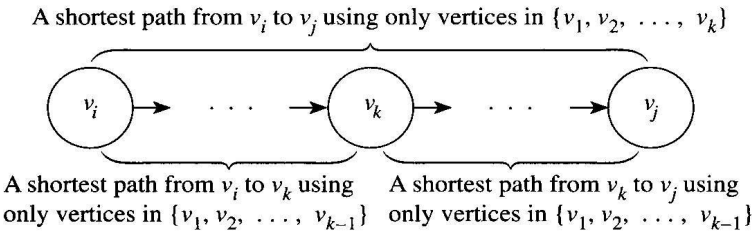
    • $v_k$는 $v_i$에서 $v_k$로 가는 부분경로 상에서 중간마디가 될 수 없기 때문에 그 부분경로는 ${v_1, v_2, \ldots , v_{k-1}}$에 속한 마디만 중간마디로 거치게 된다.($D^{k-1}[i][k]$)
    • 위와 같이, $v_k$에서 $v_j$로 가는 부분경로의 길이는 반드시 $D^{k-1}[k][j]$와 같아야 한다.
    • $D^k[i][j] = D^{k-1}[i][k] + D^{k-1}[k][j]$
    • 앞의 그래프에서 $D^2[5][3] = 7 = D^1[5][2] + D^1[2][3]$

 경우 1이나 경우 2 중 하나는 반드시 성립해야 하므로, $D^k[i][j] = \mbox{min}(D^{k-1}[i][j], D^{k-1})[i][k] + D^{k-1}[k][j]$가 성립한다. 다음 예를 보자.

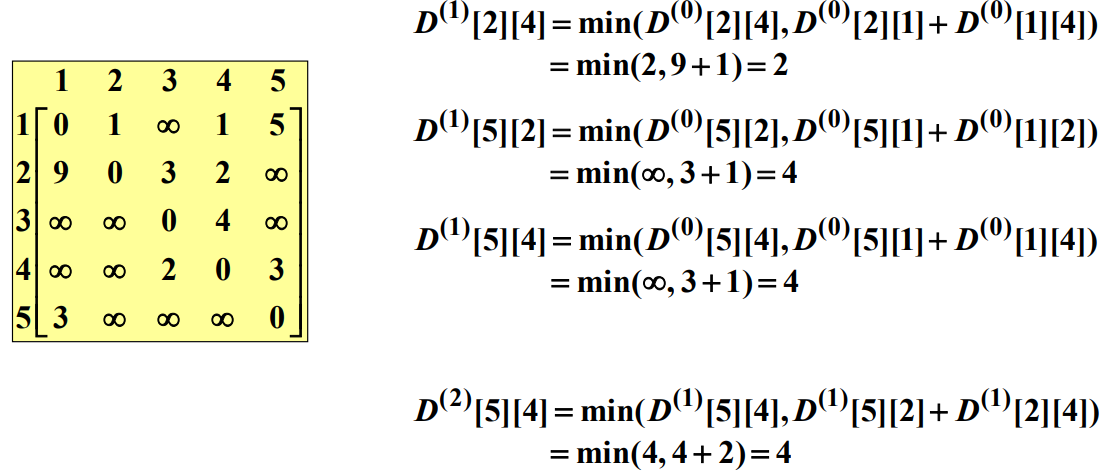
// 문제: 가중치포함 그래프의 각 마디에서 다른 모든 마디로 가는 최단경로를 모두 계산하시오. 여기서 가중치는 음이 아닌 수이다.
// 입력: 마디 개수가 n인 가중치포함 방향그래프, 그래프는 2차원 배열 W로 표현하는데 행과 열의 인덱스 범위는 1부터 n까지이다. 즉, W[i][j]는 정범 i에서 정점 j로 가는 이음선의 가중치이다.
// 출력: 행과 열의 인덱스 범위가 1부터 n까지인 2차원 배열 D, 즉, D[i][j]는 정점 i에서 정점 j로 가는 최단경로의 길이가 된다.
void floyd(int n, const number W[][], number D[]) {
  index i, j, k;
  D = W;
  for(k = 1; k <= n; k++) {
    for(i = 1; i <= n; i++) {
      for(j = 1; j <= n; j++) {
        D[i][j] = minimum(D[i][j], D[j][k] + D[k][j]);
      }
    }
  }
}

 위 알고리즘에서 배열 W이외에 D 배열 하나만 사용하였다. 배열 D 하나만 가지고 계산할 수 있는 이유는 $k$째 행과 $k$째 열에 있는 값들은 루프의 $k$째 반복을 실행하는 동안 변하지 않기 때문이다. 즉, $k$째 반복에서 알고리즘은 D[i][k] = minimum(D[i][k], D[j][k] + D[k][k])과 같은 저장문을 실행하는데 여기서 $D[k][k]$는 항상 0이므로 우변의 값은 의심의 여지가 없이 $D[i][k]$가 된다. 그리고 다음 저장문에서도 D[k][j] = minimum(D[k][j], D[k][k] + D[k][j])에서 $D[k][k]$는 항상 0이므로 우변의 값은 $D[k][j]$가 된다. 시간복잡도는 다음과 같다.

 위 알고리즘을 다음과 같이 수정하면 최단경로를 얻는다. 이 알고리즘에서 P는 다음과 같다.

$P[i][j] = \begin{cases} v_i\mbox{에서 }v_j\mbox{까지 가는 최단경로의 중간에 놓여있는 마디가 최소한 하나 있는 경우, 그 놓여있는 마디 중에서 가장 큰 인덱스} \\ \mbox{최단경로의 중간에 놓여있는 정잠이 없는 경우, 0} \end{cases}$
// 문제: 최단경로 찾는다는 사실을 제외하고는 위 알고리즘과 동일
// 추가적인 출력: 행과 열의 인덱스 범위가 모두 1부터 n까지인 배열 P
void floyd2 (int n, const number W[][], number D[][], index P[][]) {
  index i, j, k;

  for(i = 1; i <= n; i++) {
    for(j = 1; j <= n; j++) {
      P[i][j] = 0;
    }
  }

  D = W;

  for(k = 1; k <= n; k++) {
    for(i = 1; i <= n; i++) {
      for(j = 1; j <= n; j++) {
        if(D[i][k] + D[k][j] < D[i][j]) {
          P[i][j] = k;
          D[i][j] = D[i][k] + D[k][j];
        }
      }
    }
  }
}

// 문제: 가중치포함 그래프에서 한 마디에서 다른 마디로 가는 최단경로 상에 있는 중간 마디들을 출력하시오
// 입력: 배열 P와 그래프 마디의 인덱스 q와 r
// 출력: v_p에서 v_r로 가는 최단경로 상의 중간 마디
void path (index q, r) {
  if(P[q][r] != 0) {
    path (q, P[q][r]);
    cout << "v" << P[q][r];
    path (P[q][r], r);
  }
}

 위 알고리즘을 이용하면 앞 예의 그래프를 활용하여 만든 배열 P는 다음과 같다.

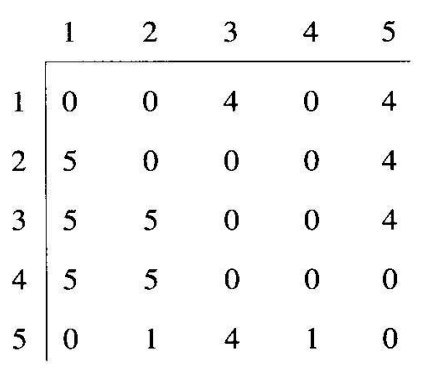
 P를 전역(global)배열로 정의하고 $v_p$에서 $v_r$로 가는 최단경로를 구하는 path의 최상위 호출은 path(q,r)과 같다. 예를 들어, path(5, 3)을 출력하면 $v_1, v_4$가 출력된다. 이 마디들은 $v_5$에서 $v_3$으로 가는 최단경로 상의 중간마디들이다.

동적계획과 최적화 문제

 최적화 문제를 모두 동적계획법으로 풀 수 있는 것은 아니다. 문제에 최적의 원칙(principle of optimality)이 반드시 성립해야 한다. 어떤 문제의 입력사례의 최적해가 그 입력사례를 분할한 부분사례에 대한 최적해를 항상 포함하고 있으면, 그 문제는 최적의 원칙이 성립한다고 한다.
 최단경로 문제에서 $v_k$를 $v_i$에서 $v_j$로 가는 최적경로 상의 마디라고 하면, $v_i$에서 $v_k$로 가는 부분경로와 $v_k$에서 $v_j$로 가는 부분경로도 반드시 최적이어야 한다. 그런데 입력사례의 최적해는 모든 부분사례에 대한 최적 해를 포함하므로 최적의 원칙이 성립힌다.
 최적의 원칙은 어떻게 보면 당연한 것 같지만 동적계획을 적용하여 최적해를 구할 수 있는지 단정하려면 이 원칙이 성립하는지 증명해야 한다. 다음 예는 이 원칙이 성립하지 않는 최적화 문제도 있음을 보여준다.

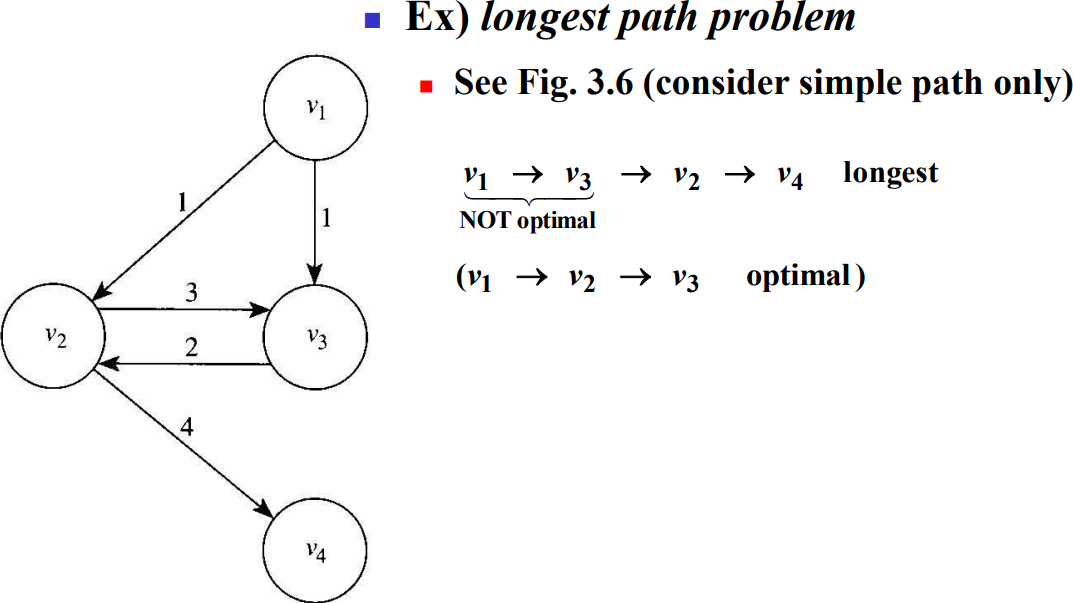
 각 마디에서 다른 모든 마디로 가는 가장 긴 단순경로를 구하는 최장경로 문제(longest path problem)를 생각해보면, 위 그림에서 $v_1$에서 $v_4$로 가는 최장(최적)단순경로는 $[v_1, v_3, v_2, v_4]$이다. 그러나 부분경로인 $[v_1, v_3]$이 $v_1$에서 $v_3$으로 가는 최장(최적)경로가 아니라, $[v_1, v_2, v_3]$이 최장(최적)경로이다.

연쇄 행렬곱셈

 일반적으로, $i \times j$ 행렬과 $j \times k$ 행렬을 곱하면 원소단위 곱셈의 실행 횟수는 $i \times j \times k$번이다. 다음과 같이 4개의 행렬을 곱하는 문제를 생각해보자.

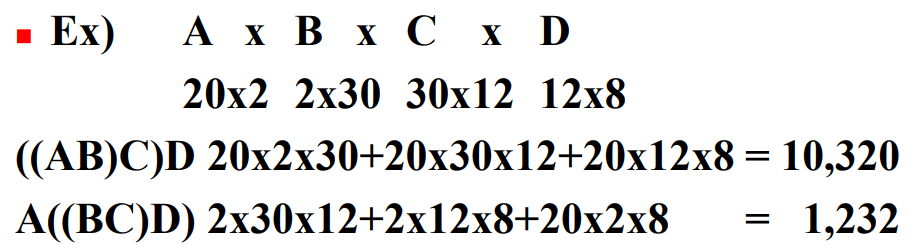
 행렬곱셈은 결합법칙이 성립하므로, 곱셈을 적용하는 순서는 결과에 영향을 미치지 않는다. 4개의 행렬을 곱할 때 5가지 서로 다른 순서로 곱할 수 있는데, 각 순서마다 원소단위 곱셈의 횟수는 다를 수 있다. 위 예에서는 ((AB)C)D가 곱셈 횟수가 젤 많고, A((BC)D)가 곱셈의 횟수가 가장 작으므로 최적의 순서이다.
 그러면 $n$개의 행렬을 곱하는 최적의 순서를 구하는 알고리즘을 설계해본다. 최적의 순서는 행렬의 크기에만 의존한다. 따라서 n과 행렬의 크기가 입력이다. Brute-force로 가능한 모든 순서를 고려해본 다음, 그 중에서 최소값을 주는 순서를 선택하면 된다. Brute-force 알고리즘이 최소한 지수시간이 걸림을 증명해본다.

 이 문제이서 최적의 원칙이 성립하는지를 알아보는 일을 어렵지 않다. 즉, $n$개 행렬을 곱하는 최적의 순서는 $n$개 행렬의 부분집합을 곱하는 최적의 순서를 포함한다. 예를 들어, 6개의 행렬을 곱하는 최적의 순서가 $A_1((((A_2A_3)A_4)A_5)A_6)$이라면 행렬 $A_2$에서 $A_4$까지 곱하는 최적의 순서는 반드시 $(A_2A_3)A_4$와 같다. 이는 동적계획으로 해답을 구할 수 있다는 것을 의미한다.
 최적의 순서를 구하기 위해서 일련의 배열을 사용한다. $1 \le i \le j \le n$인 모든 $i$와 $j$에 대하여 다음과 같이 재귀 관계식을 구축한다.

  • $M[i][j] = i < j$일 때 $A_i$부터 $A_j$까지 행렬을 곱하는데 필요한 원소단위 곱셈의 최소 횟수
  • $M[i][i] = 0$

 이 배열을 어떻게 사용할 지를 알아보기 전에 이 배열 안에 있는 원소의 의미를 알아본다.

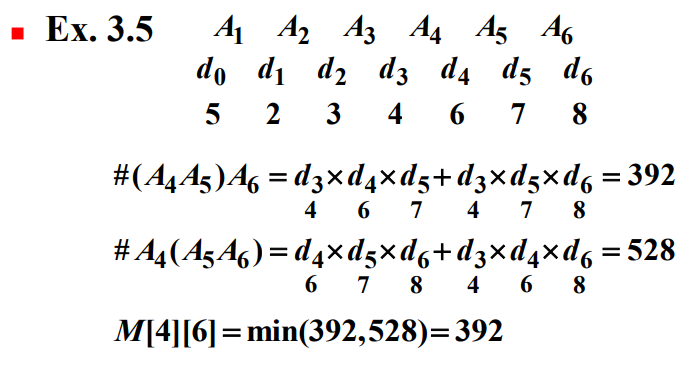
 6개의 행렬을 곱하는 최적의 순서는 다음과 같은 인수분해 중 하나가 되어야 한다.

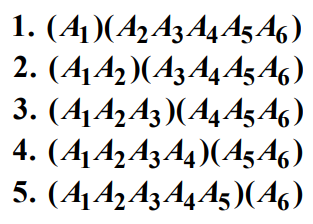
 여기서 각 괄호 안 행렬의 곱은 최적의 순서에 따라 구한 것이다. 이 인수분해 중에서 원소단위 곱셈의 횟수가 되는 것이 최적의 해가 됨이 틀림없다. $k$째 인수분해의 곱셈의 횟수는 각 인수를 구하는데 필요한 최소 원소단위 곱셈의 횟수 더라기 두 인수를 곱하는데 필요한 원소단위 곱셈의 횟수가 된다. 즉, $M[1][k] + M[k+1][6] + d_0d_kd_6$ 이다. 따라서 $M[1][6] = \mbox{min}(M[1][k] + M[k+1][6] + d_0d_kd_6)$이다.
 이를 일반화하면, $1 \le i \le j \le n$인 모든 $i$와 $j$에 대하여 다음이 성립한다.

  • $M[i][j] = \mbox{min}(M[i][k] + M[k + 1][j] + d_{i-1}d_kd_j)$, if $i < j$, $i \le k \le j - 1$
  • $M[i][i] = 0$

 이 관계식에 기초한 분할정복 알고리즘은 지수시간이다. 동적계획법으로 $M[i][j]$의 값을 단계별로 구하는 효율적인 알고리즘을 설계해보자.
 파스칼의 삼각형과 비슷한 형태의 격자를 사용한다. $M[i][j]$ 값은 $M[i][j]$와 같은 행에서 왼쪽에 있는 값 모두와 같은 열의 아래쪽에 있는 값 모두를 가지고 계산한다. 이 특성을 이용하면 $M$의 값을 모두 다음과 같이 계산할 수 있다.

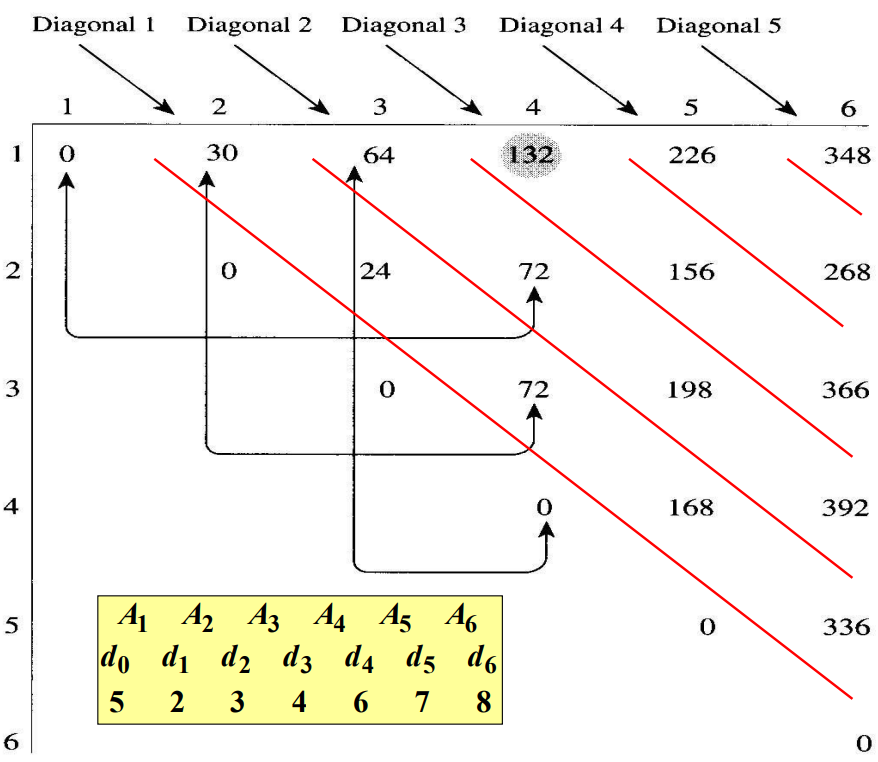
 이제 이 방법을 구현한 알고리즘을 살펴본다.

// 문제: 행렬 n개를 곱하는데 필요한 원소단위 곱셈의 최소 횟수와 최소 횟수로 행렬 곱셉하는 순서를 구하시오.
// 입력: n(행렬의 개수), 인덱스의 범위가 0부터 n까지인 정수 배열 d, 여기서 d[i-1]xd[i]는 i번째 행렬의 크기가 된다.
// 출력: min(n개 행렬을 곱하는데 필요한 원소단위 곱셈의 최소 횟수), P(최적의 순서를 구할 수 있는 이차원 배열)
// 여기서 P의 행의 인덱스는 1부터 n-1까지이고, 열의 인덱스는 1부터 n까지 이다.
// P[i][j]의 값은 i부터 j까지 행렬을 곱할 때 최적의 순서로 갈라지는 기점을 나타낸다.
int minmult (int n, const int d[], index P[][]) {
  index i, j, k, diagonal;
  int M[1...n][1..n];

  for(i = 1; i <= n; i++) {
    M[i][i] = 0;
  }

  for(diagonal = 1; diagonal <= n - 1; diagonal++) {
    for(i = 1; i <= n - diagonal; i++) {
      j = i + diagonal;
      // i <= k <= j - 1
      M[i][j] = min(M[i][k] + M[k + 1][j] + d[i - 1] * d[k] * d[j]);
      P[i][j] = 최소 횟수를 나타내는 k의 값;
    }
  }

  return M[1][n];
}

 위 알고리즘을 분석해본다.

 이제 배열 P에서 최적의 순서를 구하는 방법을 알아본다. 위 알고리즘을 적용하면 배열 P는 다음과 같다.

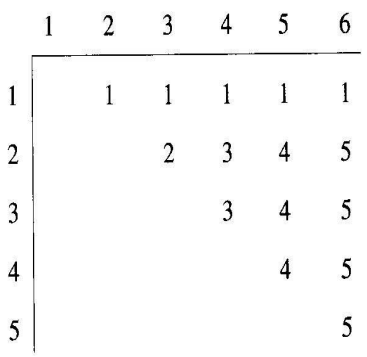
 예를 들어, $P[2][5] = 4$라는 사실은 $A_2$부터 $A_5$행렬을 곱하는데 최적의 순서가 $(A_2A_3A_4)A_5$과 같은 인수분해로 나타남을 뜻한다. 최적의 순서를 구하기 위해서는 먼저 최상위 인수분해를 구하는 $P[1][n]$을 방문해야 한다. $n=6$이고 $P[1][6]=1$이므로, 최적의 순서를 주는 최상위 인수분해는 $A_1(A_2A_3A_4A_5A_6)$이다. 다음 $A_2$부터 $A_6$까지 곱하는 최적의 순서를 구하는 인수분해는 $P[2][6]$을 방문하여 구한다. 이 값이 5이므로, 그 인수분해는 $(A_2A_3A_4A_5)A_6$과 같다. 지금까지의 구한 최적의 순서인 인수분해는 $A_1((A_2A_3A_4A_5)A_6)$이다. 이 과정을 반복하면 최종 답은 $A_1((((A_2A_3)A_4)A_5)A_6)$이다. 다음 알고리즘은 위 과정을 구현한 것이다.

// 문제: n개의 행렬을 곱하는 최적의 순서를 출력하시오.
// 입력: n(양의 정수), P
// 여기서 P[i][j]의 값은 i부터 j까지 헹렬을 곱할 때 최적의 순서로 갈라지는 기점을 나타낸다.
// 출력: 행렬을 곱하는 최적의 순서
void order(index i, index j) {
  if(i == j)
    cout << "A" << i;
  else {
    k = P[i][j];
    cout << "(";
    order(i, k);
    order(k + 1, j);
    cout << ")";
  }
}

최적 이분검색트리

 이분검색트리(binary search tree)는 순서가능집합(ordered set: 순서를 매길 수 있는 원소로 구성된 집합)에 속한 원소(키)로 구성된 이진트리인데, 다음 조건을 만족한다.

  1. 각 마디는 하나의 원소만 가지고 있다.
  2. 마디의 왼쪽하위트리에 있는 원소들은 모두 그 마디의 원소보다 작거나 같다.
  3. 마디의 오른쪽하위트리에 있는 원소들은 모두 그 마디의 원소보다 크거나 같다.  다음 두 이진트리를 보자.

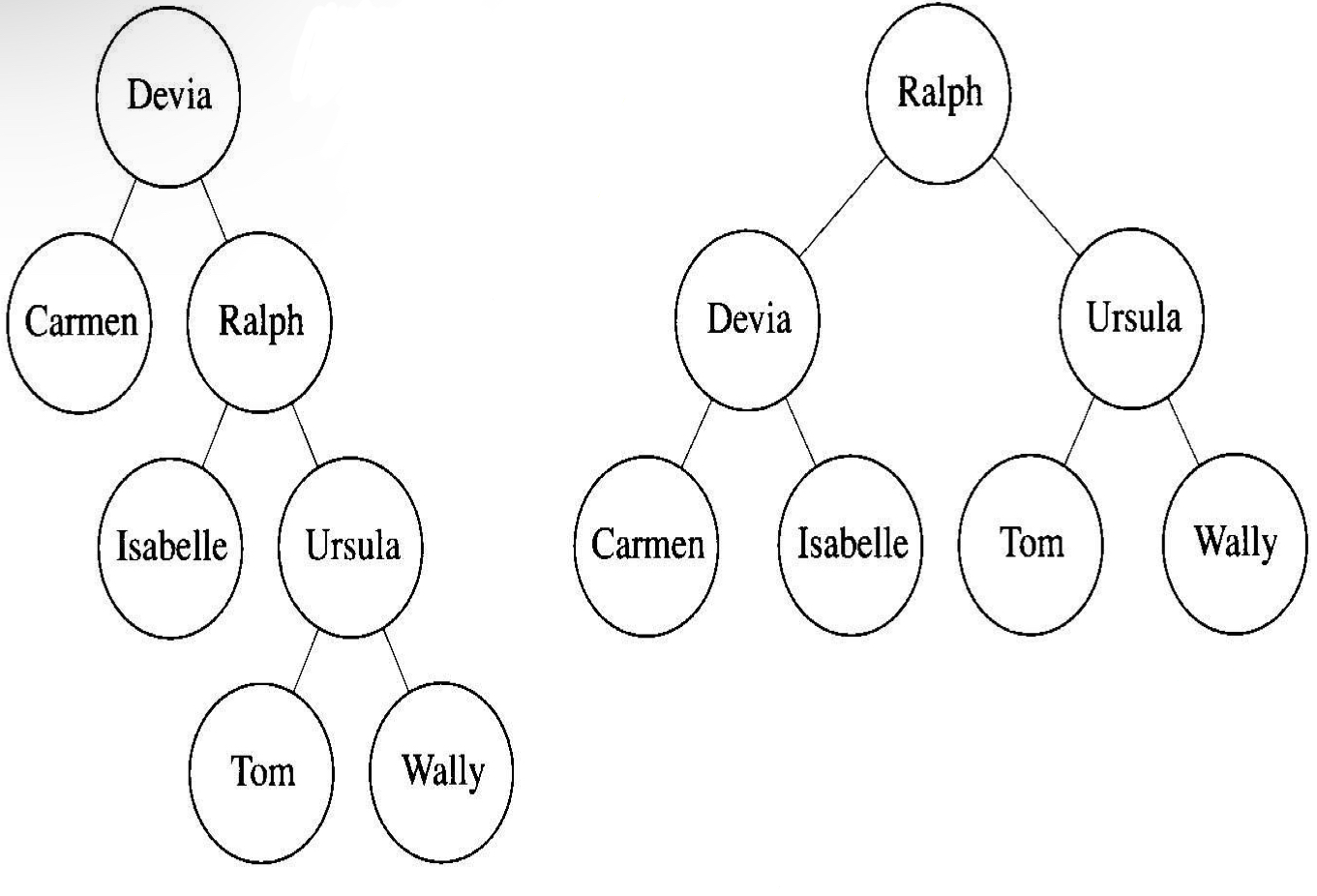
 트리에서 기본적인 개념은 다음과 같다.

  • 마디(terminal)의 깊이(depth): 뿌리(root)에서 마디로 가는 유일한 경로 상에 있는 이음선의 개수
    • 이를 마디의 수준(level)이라고 한다.
    • 위 왼쪽 트리에서 Ursula는 깊이가 2, 수준이 2라고도 한다.
    • 트리의 깊이는 그 트리의 모든 마디의 깊이 중 최대값이다.
  • 균형잡힌 트리(balanced tree): 모든 마디의 두 하위 트리의 깊이가 1 이상 차이나지 않는 트리
  • 최적(optimal): 이분검색트리에서 검색키(search key)와 같은 원소를 찾는데 걸리는 평균시간이 최소가되도록 원소를 잘 정리한 트리

 이제 검색키와 같은 원소가 트리에 있는지 알고 있는 경우를 생각해보자. 알고리즘에서 다음과 같은 데이터구조를 사용한다.

struct nodetype {
  keytype key;
  nodetype* left;
  nodetype* right;
};
typedef nodetype* node_pointer;

 이제 알고리즘을 살펴보자.

// 문제: 이분검색트리에서 검색키와 같은 원소가 있는 마디를 찾으시오, 찾는 원소는 트리에 있다고 가정한다.
// 입력: 이분검색트리를 가리키는 포인터 p와 검색키 keyin
// 출력: 찾은 원소가 있는 마디를 가리키는 포인터 p
void search (node_pointer tree, keytype keyin, node_pointer& p) {
  bool found;

  p = tree;
  found = false;

  while(!found) {
    if(p -> key == keyin)
      found = true;
    else if(keyin < p-> key)
      p = p -> left;
    else
      p = p -> right;
  }
}

 원소를 찾는데 프로시저 search에서 수행한 비교의 횟수를 검색시간(search time)이라 한다. 우리의 목표는 평균검색시간이 최소가 되는 트리를 찾아내는 것이다. $K_1, K_2, \ldots, K_n$을 순서대로 나열한 $n$개의 원소라 하고, $p_i$를 $K_i$가 검색키일 확률이라고 하자. 주어진 트리에서 원소 $K_i$를 찾는데 필요한 비교 횟수를 $c_i$라고 하면 그 트리에 대한 평균검색시간은 $\sum_{i = 1}^n c_ip_i$이고, 이 값이 우리가 최소화하려는 값이다.
 다음 예를보자.

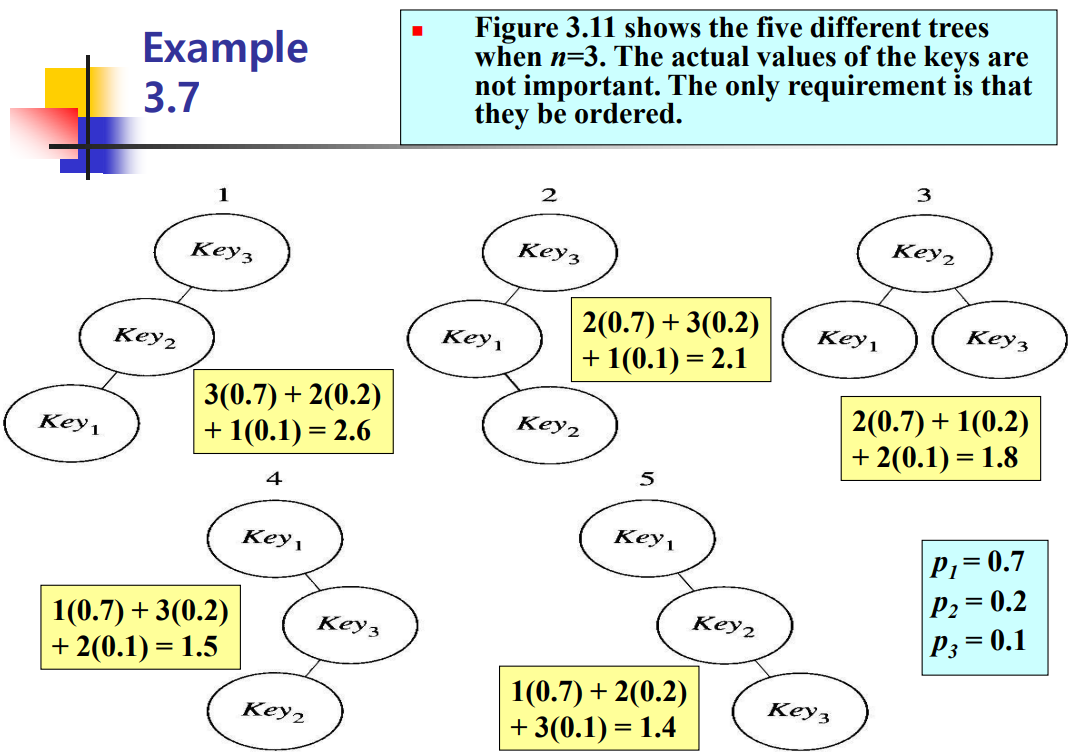
 일반적으로 최적 이분검색트리를 찾기 위해서 가능한 종류의 이분검색트리를 모두 만들어보는 것은 현실적이지 않다. 이는 트리 마디의 개수가 $n$이면, 다른 모양의 이분검색트리의 개수는 최소한 지수개이기 때문이다.
 동적계획으로 더 효율적인 알고리즘을 만들 수 있다. $K_i$에서 $K_j$까지의 원소들을 $\sum_{m = i}^j c_mp_m$의 값이 최소가 되도록 트리에 배치했다고 가정한다. 여기서 $c_m$은 트리에서 $K_m$을 찾는데 필요한 비교 횟수이다. 이러한 트리를 그 원소들에 대한 최적 트리(optimal tree)라 하고, 최적값은 $A[i][j]$로 표시한다. 원소가 하나 있으면 트리에서 워소를 찾는데 비교를 한 번 하므로, $A[i][i] = p_i$이다. 다음 예를 보자.

 일반적으로, 최적트리의 하위트리는 그 하위트리 안에 있는 원소들에 대해서 반드시 최적이어야 한다. 따라서 최적의 원칙이 성립한다.
 트리 1을 $K_1$이 뿌리야 한다는 제한을 가진 최적트리라 하고, 트리 2를 $K_2$가 뿌리야 한다는 제한을 가진 최적트리라고 하며, …, 트리 $n$을 $K_n$이 뿌리야 한다는 제한을 가진 최적트리라 한다. 따라서 이 하위트리들의 평균검색시간은 다음과 같다.

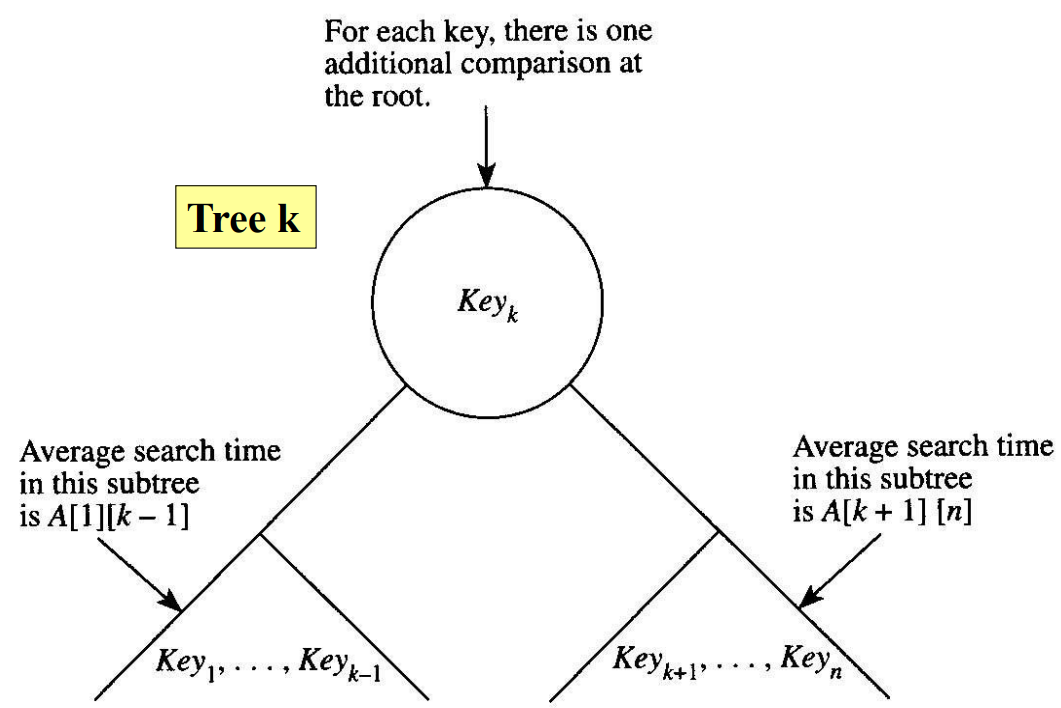
 이 그림을 보면 $m \neq k$인 모든 $m$에 대해서 트리 $k$에서 $K_m$을 찾는데 수행하는 비교 횟수는 그 원소가 있는 하위트리에서 그 원소를 찾는데 수행하는데 비교 횟수보다 정확히 하나 더 많다. 이 한번의 비교 때문에 트리 $k$에서 $K_m$을 찾는 평균검색시간은 $1 \times p_,$ 만큼 늘어난다. 결과적으로 트리 $k$에 대해 평균검색시간은 다음과 같다.

$(A[1][k-1]) + (p_1 + \ldots + p_{k-1}) + (p_k) + (A[k+1][n]) + (p_{k+1} + \ldots + p_n) $
  • $A[1][k-1]$: 왼쪽하위트리에서 평균시간
  • $p_1 + \ldots + p_{k-1}$: 뿌리에서 비교하는데드는 추가시간
  • $p_k$: 뿌리를 검색하는 평균시간
  • $A[k+1][n]$: 오른쪽하위트리에서 평균시간
  • $p_{k+1} + \ldots + p_n$: 뿌리에서 비교하는데드는 평균시간

 위 식을 정리하면 다음과 같다.

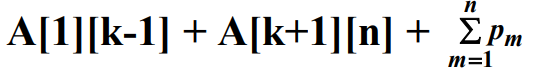
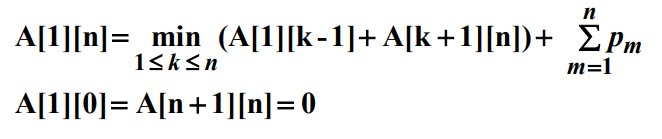
 최종적으로 다음의 일반식을 얻는다.

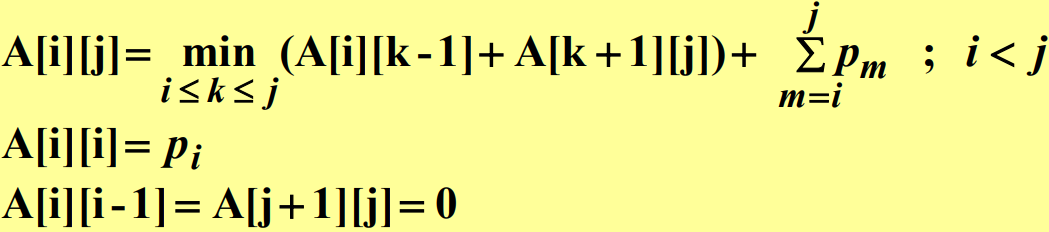
 위 등식을 사용하여 최적 이분검색트리를 구하는 알고리즘을 작성할 수 있다. $A[i][j]$의 값은 $A[i][j]$의 왼쪽 값을 제외한 $i$째 행에 위치한 값들과 $A[i][j]$의 아래 값을 제외한 $j$째 열들의 값들을 가지고 계산하기 때문에 각 대각선에 있는 값들을 차례로 계산해 나간다.

// 문제: 주어진 원소의 집합을 가지고 최적 이분검색트리를 구축한다. 여기서 각 원소에 대해서 검색키가 될 확률이 주어진다.
// 입력: n(원소의 개수), p(인덱스의 범위가 1부터 n까지인 실수 배열)
// 여기서 p[i]는 i째 원소를 찾을 확률이다.
// 출력: 변수 minarg(평균검색시간), 최적트리를 구축할 수 있는 이차원 배열 R
// 여기서 R의 행의 인덱스 범위는 1부터 n + 1까지이고, 열의 인덱스의 범위는 0부터 n까지이다.
// R[i][j]는 i째부터 j째까지 원소를 포함한 최적트리의 뿌리에서 원소의 인덱스이다.
void optsearchtree (int n, const float p[], float& minavg, index R[][]) {
  index i, j, k, diagonal;
  float A[1...n+1][0...n];
  for(i = 1; i < n + 1; i++) {
    A[i][i - 1] = 0;
    A[i][i] = p[i];
    R[i][i] = i;
    R[i][i - 1] = 0;
  }

  A[n + 1][n] = 0;
  R[n + 1][n] = 0;

  for(diagonal = 1; diagonal <= n - 1; diagonal++) {
    for(i = 1; i < n - diagonal; i++) {
      j = i + diagonal;
      A[i][j] = min(A[i][k - 1] + A[k + 1][j]) + ∑_{m = i}^j p_m; // i ≤ k ≤ j
      R[i][j] = 최소값을 주는 k의 값;
    }
  }
  minavg = A[1][n];
}

 위 알고리즘을분석하면 다음과 같다.

 이제 최적 이분검색트리를 구축해본다.

// 문제: 최적 이분검색트리를 구축하시오.
// 입력: n(원소의 개수), n개의 원소를 순서대로 나열한 배열 K, 위 알고리즘의 R
// 여기서 R[i][j]는 i째부터 j째까지 원소를 포함한 최적 트리의 뿌리에서 원소의 인덱스
// 출력: 원소가 n개 최적 이분검색트리를 가리키는 포인터 tree
node_pointer tree (index i, j) {
  index k;
  node_pointer p;

  k = R[i][j];
  if(k == 0) {
    return NULL;
  }
  else {
    p = new_nodetype; // 새로운 마디를 만들어서 그 주소를 p에 저장한다.
    p -> key = K[k];
    p -> left = tree(i, k - 1);
    p -> right = tree(k + 1, j);
    return p;
  }
}

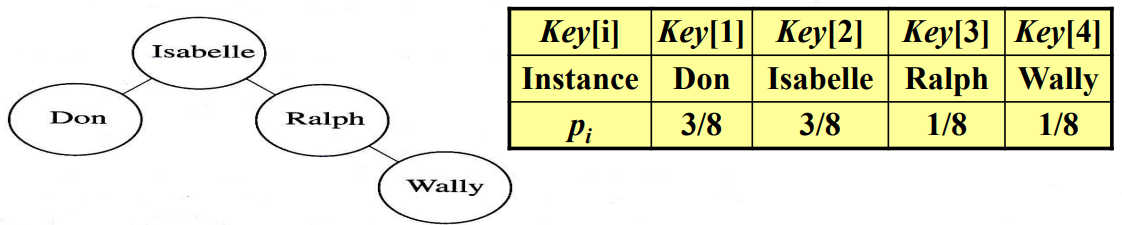
 다음Key[i]들을 입력을 주었을 때 만들어지는 최적 이분검색트리는 왼쪽과 같다.

외판원(Traveling Salesperson) 문제

 방향그래프에서 tour는 한 도시에서 출발하여 다른 모든 도시를 한 번씩만 들리고 출발한 도시로 돌아오는 여행길이다. 가중치포함 방향그래프에서 optimal(최적) tour는 그러한 여행길 중에서 최소거리 여행길이다. 외판원 문제는 최소한 하나의 tour가 존재하는 경우 가중치포함 방향그래프에서 최적tour을 찾는 문제이다. 출발하는 도시가 최적tour의 길이와는 상관없으므로, $v_1$을 출발도시로 잡는다.

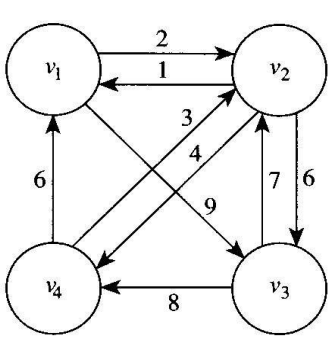
  • length&[v_1, v_2, v_3, v_4, v_1]& = 22
  • length&[v_1, v_3, v_2, v_4, v_1]& = 26
  • length&[v_1, v_3, v_4, v_2, v_1]& = 21

 위에서 마지막 tour가 최적이다. 일반적으로 보면, 각 도시에서 다른 모든 도시로의 이음선이 존재할 수 있다. 가능한 모든 tour을 다 고려하면, 둘째 도시는 $n - 1$개의 도시 중 하나일 수 있고, 셋째 도시는 $n - 2$개의 도시 중 하나일 수 있으므로, 이 과정을 반복하면 총 가지 수는 $(n - 1)(n - 2) \cdots 1 = (n - 1)!$이다. 이는 지수개보다 높다.
 동적계획을 이 문제에 적용할 수 있을까? $v_k$가 optimal tour 상에서 $v_1$ 다음에 오는 첫 번째 도시이면, $v_k$에서 $v_1$로 가는 tour의 부분경로는 다른 도시를 각각 정확히 한 번씩만 거치며 $v_k$에서 $v_1$로 가는 최단경로이어야 한다. 이는 최적원칙이 성립하고, 동적계획을 적용할 수 있음을 의미한다. 몇몇 필요한 용어를 정의한다.

  • $V$ = 모든 도시의 집합
  • $A$ = $V$의 부분집합
  • $D[v_i][A]$ = $A$에 속한 도시를 각 한 번씩만 거쳐서 $v_i$에서 $v_1$로 가는 최단경로의 길이

 위 그래프에서 $V = {v_1, v_2, v_3, v_4}$이고 경로는 $[v_1, v_2, v_3, v_4]$와 같이 표현한다. $A={v_3}$이면, $D[v_2][A]$ = length$[v_2, v_3, v_1]$ = $\infty$이다. $A={v_3, v_4}$이면, $D[v_2][A]$ = min(length$[v_2, v_3, v_4, v_1]$, length$[v_2, v_4, v_3, v_1]$) = min(20, $\infty$) = 20이다.
 집합 $V - {v_1, v_j}$는 $v_1$과 $v_j$를 제외한 모든 도시를 포함하고 있고, 최적원칙이 성립하므로 다음과 같은 식을 얻는다.

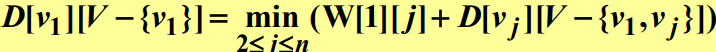
 일반적으로 $i \neq 1$이고 $i$가 $A$에 속하지 않으면, 다음과 같은 관계식을 얻는다.

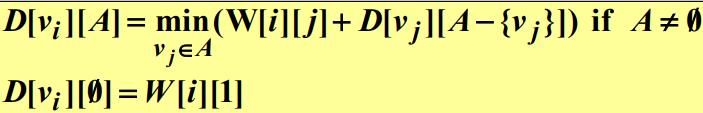
 다음 예를 보자.

 다음은 외판원 문제를 푸는 동적계획 알고리즘이다.

// 문제: 가중치포함 방향그래프에서 optimal tour을 결정하시오. 가중치는 음이 아닌 정수이다.
// 입력: 가중치포함 방향그래프, n(그래프에서 vertex의 개수)
// 그래프는 행과 열의 인덱스의 범위가 모두 1부터 n까지의 2차원 배열 W로 표현한다.
// 여기서 W[i][j]는 i번째 도시에서 j번째 도시를 연결하는 이음선의 가중치이다.
// 출력: 변수 minlength(optimal tour), 2차원 배열 P
// P의 행은 인덱스 범위가 1부터 n까지이고, 열은 인덱스 범위가 $V - {v_1]$의 모든 부분집합이다.
// P[i][A]는 A에 속한 모든 도시를 정확히 한 번만 거쳐서 v_i에서 v_1로 가는 최단경로에서 v_i 다음에 오는 첫 번째 도시의 인덱스이다.
void travel (int n, const number W[][], index P[][], number& minlength) {
  index i, j, k;
  number D[1 .. n][subset of V - {v_1}];

  for(i = 2; i <= n; i++) {
    D[i][∅] = W[i][1];
  }

  for(k = 1; k <= n - 2; k++) {
    for( A ⊆ V - {v_1}를 만족하며 마디가 k개인 모든 부분집합 A) {
      for( i != 1와 v_i ∉ A를 만족하는 모든 i) {
        D[i][A] = min(W[i][j] + D[j][A - {v_j}]);
        P[i][A] = 최소가 되는 j값;
      }
    }
  }
  // 2 ≤ j ≤ n
  D[1][V - {v_1}] = min(W[1][j] + D[j][V - {v_1, v_j}]);
  P[1][V - {v_1}] = 최소가되는 j값;
  minlength = D[1][V - {v_1}];
}

 이 알고리즘을 분석하기 전에 다음과 같은 정리가 필요하다.

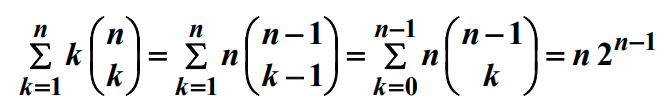
 알고리즘을 분석하면 다음과 같다.

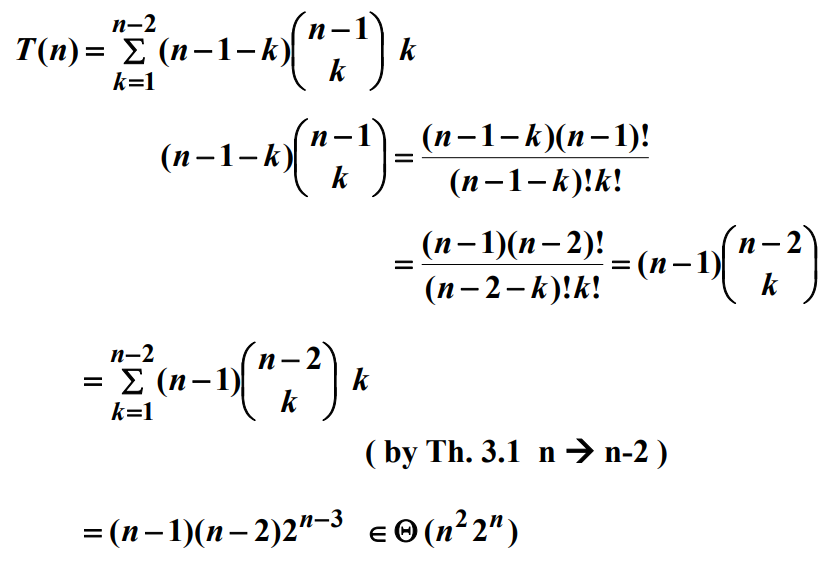
댓글남기기

참고