탐욕 알고리즘
Updated:
탐욕 알고리즘(Greedy Algorithms)은 답을 하나씩 고르는데, 미리 정한 기준에 따라서 매번 가장 좋아 보이는 답을 선택한다. 탐욕 알고리즘은 동적계획과 마찬가지로 최적화 문제를 푸는데 주로 사용한다. 동적계획은 재귀관계식을 세워서 입력사례를 더 작은 입력사례로 분할하는 반면, 탐욕 알고리즘은 입력사례를 분할하지 않는다. 탐욕 알고리즘은 순서대로 답을 하나씩 모아서 최종 답을 구축하는데, 가장 좋아 보이는 답을 선택하여 모은다. 즉, 어떤 선택이든지 선택할 당시(locally)는 최적이다. 따라서 탐욕 알고리즘은 (globally)최적인 해답을 얻는지 확인하는 절차를 반드시 거쳐야 한다.
거스름돈 문제를 푸는 Greedy Algorithm을 알아본다. 거스름돈을 정확히 세어 주는 작업 외에도 동전의 개수가 최소가 되도록 거스름 동전을 선택한다. 즉, 해답은 거슬러 줄 총액에 해당하는 동전의 집합이고, 최적의 해답은 동전의 개수가 최소가 되는 집합이다.
- 처음에는 빈손으로 시작한다.
- 액면가가 가장 높은 동전을 집어 손에 올려놓는다.
- 어느 동전이 가장 좋은지를 결정하는 기준은 동전의 액면가이다.
- 이를 Greedy Algorithm에서 Selection procedure(선택과정)이라고 한다.
- Selection procedure: 집합에 추가할 다음 원소를 고른다. 그 당시 최적을 선택하는 탐욕 기준에 따라 선택한다.
- 손에 있는 거스름돈의 총액이 거슬러주어야 할 액수를 초과하는지 본다.
- 이를 Greedy Algorithm에서 Feasibility check(적절성검사)라고 한다.
- Feasibility check: 새로운 집합이 해답이 되기 적절한지 검사한다.
- 만약 거스름돈의 총액이 거슬러주어야 할 액수와 같은지 검사한다.
- 이를 Greedy Algorithm에서 Solution check(해답점검)라고 한다.
- Solution check: 새로운 집합이 문제의 해답인지 결정한다.
- 만약 같이 않다면 다시 선택과정으로 돌아가서 다른 동전을 찾고 같은 과정을 되풀이 한다.
- 거스름돈의 총익이 거슬러주어야 할 액수와 같든지, 아니면 동전이 떨어질 때(미해결)까지 이 과정을 되풀이한다.
이 절차를 알고리즘으로 정리하면 다음과 같다.
while(동전이 남아있고 문제 미해결) {
가장 가치가 높은 동전을 집는다; // Selection procedure
if (동전을 더하여 거스름돈의 총액이 거슬러주어야 할 액수를 초과) // Feasibility check
동전을 도로 집어 넣는다;
else
거스름돈에 동전을 포함시킨다;
if(거스름돈의 총액이 거슬러주어야 할 액수와 같다) // Solution check
문제 해결;
}
최소비용 신장트리(Minimum Spanning Tree)
먼저 그래프이론 용어를 간단히 복습한다.
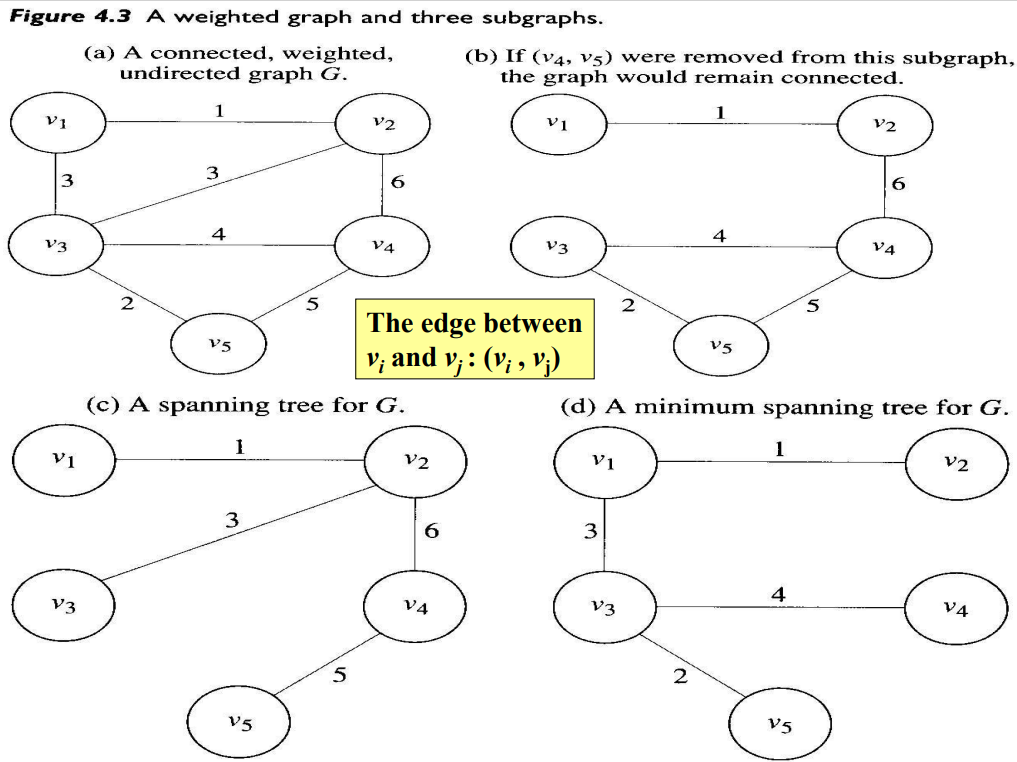
- (a) 가중치포함(weighted), 비방향(undirected) 그래프 G
- weight는 음이 아닌 수로 가정
- edge에 방향이 없으면 undirected
- 비방향그래프에서 경로(path)는 이음선으로 edge로 연결된 vertex의 나열(sequence)이다.
- 비방향그래프에서 모든 마디의 쌍에 대해서 경로가 있으면 연결되어(connected)있다라고 부른다. 만약 (b)에서 $v_2$와 &v_4& 사이의 edge를 제거하면, 이 그래프는 더 이상 연결되어 있다고 할 수 없다.
- 비방향그래프에서 마디에서 자신으로 다시 돌아가는 경로에 최소한 서로 다른 3개의 vertex가 있으면 단순순환경로(simple cycle)라 하고, 단순순환경로가 없는 비방향그래프를 비순환적(acyclic)이라 한다.
- (c)와 (d)는 비순환적인 반면, (a)와 (b)는 비순환적이 아니다.
- 트리는 비순환적이며 연결되어 있는 비방향그래프이다.
연결된, 가중치포함, 비방향그래프 G에서 vertex들은 최소한 모두 연결된 상태로 유지한 채 이음선의 가중치의 합은 가능한 한 최소가 되도록 이음선을 제거하여 부분그래프를 만드는 문제를 풀어본다.
위 그래프들을 보면, (a)의 부분그래프 (b)는 최소 가중치를 가질 수 없다. 왜냐하면, 순환경로 $[v_3, v_4, v_5, v_3]$상의 어떤 edge을 제거하더라도 그 부분그래프는 연결된채로 남아있다. 예를 들어, $v_4$와 $v_5$를 연결하는 edge를 제거하더라도 그 부분 그래프는 연결된 채로 남아있다.
G에 대한 신장트리(spanning tree)는 G의 마디를 모두 포함하면서 트리인 연결된 그래프이다. 그림 (c)와 (d)는 G에 대한 신장트리이다(A spanning tree for G). Weight가 최소가 되는 연결된 부분그래프를 최소비용 신장트리(MST, Minimum Spanning Tree)라고 하고 (d)가 이에 해당한다.
존재하는 신장트리를 모두 찾아보는 무작정 방법으로 MST를 찾으면, 최악의 경우 지수시간보다 나쁘다. Greedy 방법을 사용하면 더 효율적으로 문제를 풀 수 있다. 먼저 비방향그래프의 정의를 보자.
- 비방향그래프(undirected graph) G는 vertex의 유한집합 V와 V에 속한 마디의 쌍의 집합 E로 구성된다. 이 쌍들을 G의 edge라고 한다. G는 $G = (V, E)$ 와 같이 표시한다.
- V의 멤버는 $v_i$로 표시하고, $v_i$와 $v_j$를 연결하는 edge는 $(v_i, v_j)$와 같이 표시한다.
G에 대한 신장트리 T는 G와 같은 마디 V를 가지지만, T의 edge의 집합은 E의 부분집합 F이다. 신장트리는 $T = (V, F)$로 표시한다. 문제는 $T = (V, F)$가 G에 대한 최소비용 신장트리가 되도록 E의 부분집합 F를 찾는 것이다. 이 문제를 푸는 탐욕 알고리즘을 표현하면 다음과 같다.
F = ∅; // Edge의 집합을 공집합으로
while(the instance is not solved) {
부분적으로 최적인 고려사항에 따라 Edge를 선택; // Selection procedure
if(그 Edge을 F에 추가하면 순환경로가 생기지 않음) // Feasibility check
그 Edge를 F에 추가;
if(T = (V, E)가 신장트리)
the instance is solved; // Solution check
}
이 알고리즘은 부분적으로 최적인 고려사항에 따라 Edge를 선택한다라고 단순히 말한다.
Prim` Algorithm
프림 알고리즘(Prim`s Algorithm)은 Edge의 F의 부분집합인 공집합과 임의의 Vertex를 포함하도록 초기화된 마디의 부분집합에서 시작한다. Y는 ${v_1}$으로 초기화한다. Y에서 가장 가까운(nearest) Vertex는 최소 weight를 가진 Edge로 Y에 속한 Vertex를 연결하는 $V - Y$에 속한 Vertex이다. Y에서 가장 가까운 Vertex는 Y에 추가하고, 그 Edge는 F에 추가한다. 같은 가중치가 두 개 이상 있으면, 임의로 선택한다. 이 과정은 $Y = V$가 될 때까지 계속한다. 이 절차를 알고리즘으로 표현하면 다음과 같다.
F = ∅; // Initialize set of edges to empty.
Y = {v_1}; // Initialize set of vertices to contain only the first one.
while(the instance is not solved) {
Y에서 가장 가까운 V-Y애 속한 Edge를 선택 ; // Selection procedure and
그 Vertex를 Y에 추가; // Feasibility check
그 Edge를 F에 추가;
if(Y == V) // Solution check
the instance is solved;
}
$V - Y$에서 새로운 마디를 취해도 순환경로가 생기지 않는다고 보장할 수 있기 때문에 선택절차와 적절성 점검은 같이 이루어진다. 다음 그림은 Prim`s Algorithm이 어떻게 되는지를 보여준다. 각 실행 단계마다 음영 처리된 Vertex는 Y를 나타내고 두껍게 표시된 Edge는 F를 나타낸다.
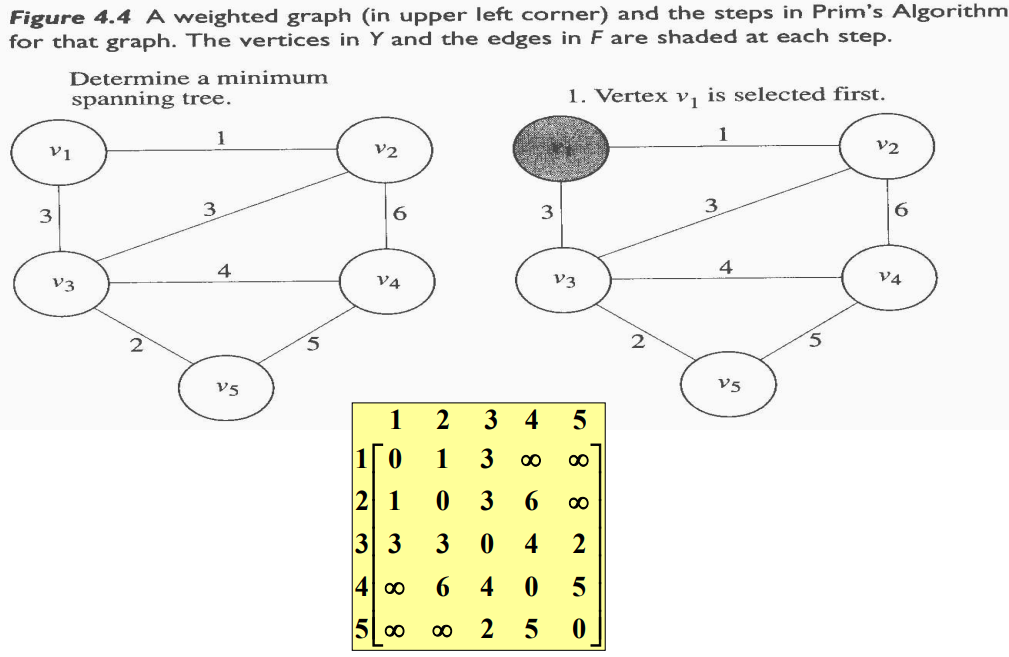
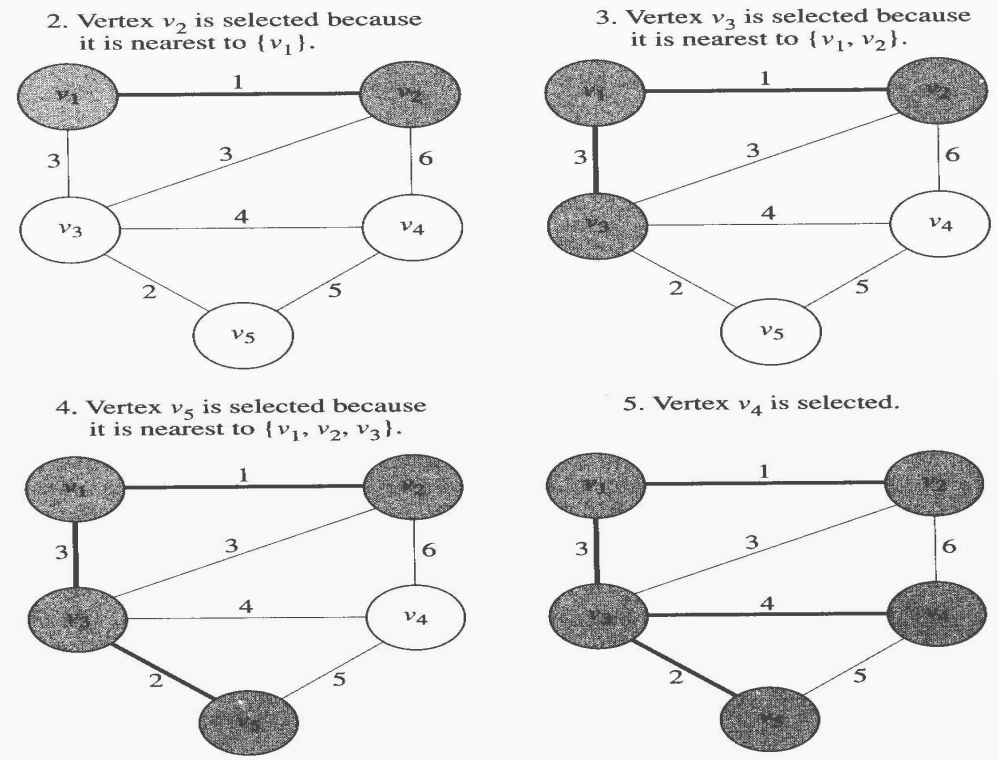
Weight Graph를 인접행렬로 표현한다.
$i= 2, \ldots, n$에 대하여 다음과 같이 정의되는 두 개의 배열 $nearest$와 $distance$를 유지한다.
- $nearest[i] = v_i$에 가장 가까운 Y에 속한 Vertex의 Index
- $distance[i] = v_i$와 $nearest[i]$가 Index인 두 Vertex를 연결하는 Edge의 Weight
시작할 때 $Y = {v_1}$이므로, $nearest[i]$는 1로 초기화하고 $distance[i]$는 $v_1$과 $v_i$를 연결하는 Edge의 Weight로 초기화한다. Vertex들을 Y에 추가하면, 이 두 배열은 Y 바깥에 있는 각 마디에서 가장 가까운 Y 안에 있는 새로운 Vertex를 참조하도록 갱신된다. 어느 Vertex를 Y에 추가시킬지 결정하기 위해 매번 반복할 때마다 $distance[i]$ 값이 최소가 되는 인덱스를 계산한다. 이 인덱스를 $vnear$라고 부른다. $vnear$가 인덱스인 마디는 $distance[vnear]$를 $-1$로 놓음으로서 Y에 추가된다. 다음은 이 알고리즘을 표현한 것이다.
// 문제: 최소비용 신장트리를 구하시오.
// 입력: 정수 n>=2와 Vertex의 개수가 n인 연결된 Weighted undirect graph, 그래프는 행과 열 모두 인덱스의 범위가 1부터 n까지인 2차원 배열 W로 표현한다. 여기서 W[i][j]는 i째 마디와 j째 마디를 연결하는 Edge의 Weight이다.
// 출력: 그래프에 대한 최소비용 신장트리 안에 있는 Edge의 집합 F
void prim(int n, const number W[][], set_of_edges& F) {
index i, vnear;
number min;
edge e;
index nearest[2 .. n];
number distance[2 .. n];
F = ∅;
for( i = 2; i<= n; i++) {
nearest[i] = 1;
// 모든 Vertex에 대하여 Y에 속한 가장 가까운 Vertex (nearest[i])는 v_i로 초기화
distance[i] = W[1][i];
// Y로부터 거리 (distance[i])는 v_i와 v_1을 연결하는 Edge의 Weight로 초기화한다.
}
repeat(n - 1 times) { // n-1개의 마디를 Y에 추가한다.
min = ∞;
// 각 마디에 더하여 distance[i]를 검사하여 Y에 가장 가까이 있는 Vertex(vnear)를 찾는다.
for( i = 2; i <= n; i++) {
if(0 <= distance[i] < min) {
min = distance[i];
vnear = i;
}
}
e = vnear가 index인 Edge를 Y에 추가한다.
add e to F;
distance[vnear] = -1;
// Y에 속하지 않은 각 마디에 대하여 Y로부터의 거리(distance[i])를 갱신한다.
for( i = 2; i <= n; i++) {
if(W[i][vnear] < distance[i]) {
distance[i] = W[i][vnear];
nearest[i] = vnear;
}
}
}
}

repeat-루프 안에 있는 두 개의 for-루프가 있는데, 각각 n - 1회 반복한다. 그 안에 명령문들의 한 번 실행을 단위연산으로 한다. 입력 크기를 n이라고 하면 시간복잡도는 $T(n) = 2(n-1)(n-1) \in \theta(n^2)$이다.
Kruskal` Algorithm
최소비용 신장트리 문제를 풀기 위한 Kruskal` Algorithm은 각 마디마다 자신만 포함하는 V의 서로소 부분집합들을 만드는 걸로 시작한다. 그리고 가중치가 작은 것부터 차례로 Edge를 검사한다(가중치가 같으면 임의로 선택한다). 만약 어떤 Edge가 서로서 부분집합들에 있는 두 Vertex를 연결하면 그 Edge를 추가하고, 두 부분집합을 하나로 합친다. 다음은 이 절차를 표현한 알고리즘이다.
F = ∅;
V의 서로소 부분집합 구축(각 마디마다 하나씩, 그 마디만 포함하도록 한다);
E에 속한 Edge를 Weight가 작은 것부터 차례로 정렬;
while(the instance is not solved) {
다음 Edge를 선택; // Selection procedure
if(Edge가 서로소 부분집합의 두 마디를 연결한다) { // Feaibility check
부분집합을 합침;
그 이음선을 F에 추가;
}
if(all the subsets are merged) // Solution check
the instance is solved;
}
다음을 보면 Kruskal` Algorithm이 어떻게 진행되는지 알 수 있다.
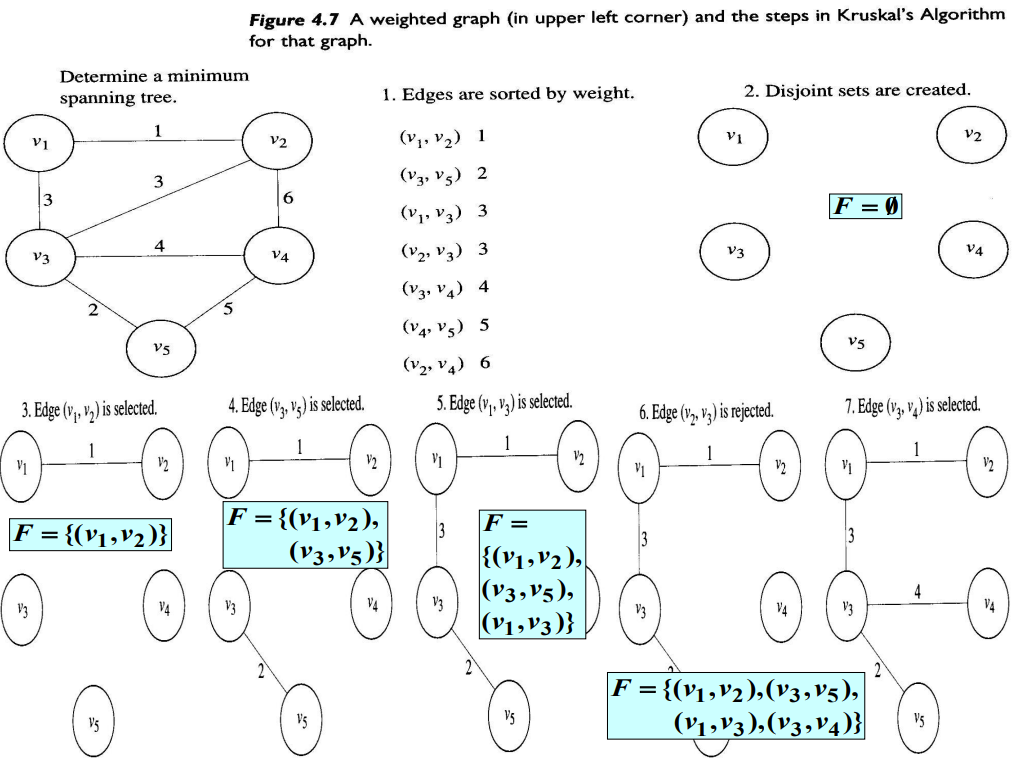
서로소 집합 추상데이터타입은 index와 set_pointer 데이터타입과 initial, find, merge, equal과 같은 연산으로 구성된다.
- index i;
- set_pointer p, q;
- initial(n): n개의 서로소부분집합을 초기화하는데, 각 서로소부분집합은 1부터 n사이의 인덱스 중에서 정확하게 하나만 포함한다.
- p = find(i): p가 인덱스 i를 포함하고 있는 집합을 가리키게 한다.
- merge(p, q): p와 q가 가리키고 있는 두 개의 집합을 하나로 합친다.
- equal(p, q): p와 q가 같은 집합을 가리키면 true를 넘겨준다.
// 문제: 최소비용 신장트리를 구하시오. // 입력: 정수 n(>= 2), 양의 정수 m, n개의 Vertex와 m개의 Edge를 가진 연결된 Weighted undirected graph, 이 그래프는 Weight와 함께 Edge가 포함된 집합 E로 표현한다. // 출력: 최소비용 신장트리에서 Edge의 집합 F void kruskal(int n, int m, set_of_edges E, set_of_edges& F) { index i, j; set_pointer p, q; edge e; E에 속한 m개의 Edge를 Weight가 작은 것부터 차례로 정렬한다; F = ∅; initial(n); // n개의 서로소부분집합을 초기화 while(number of edges in F is less than n - 1) { e = 아직 고려하지 않은 Edge 중 Weight가 최소인 Edge; i, j = e로 연결된 Vertex의 인덱스; p = find(i); q = find(j); if(! equal(p, q)) { merge(p, q); e를 F에 추가; } } }
신장트리에 Edge가 n-1개 있으므로, F에 n-1개의 Edge가 있을 때 while 루프를 빠져나간다. Kruskal`s Algorithm의 시잔복잡도를 분석하면, $\theta(n^2 \log n)$이다.
단일출발점 최단경로 문제를 푸는 다익스트라 알고리즘(Dijkstra`s Algorithm)
다익스트라(Dijkstra)는 관심 있는 Vertex에서 다른 각 Vertex로 가는 최단경로가 존재한다고 가정하고 이 알고리즘을 설명했다. 그렇지 않은 경우를 처리하기 위해서는 조금만 수정을 가하면 된다.
이 알고리즘은 최소비용 신장트리 문제를 푸는 알고리즘과 비슷하다. 최단경로를 구하려고 하는 마디만 포함하도록 집합 Y를 초기화한다(${v_1}$). Edge의 집합 F는 공집합으로 초기화한다. 먼저 $v_1$에서 가장 가까운 마디 $v$를 선택하며 Y에 추가하고, Edge $<v_1, v>$를 F에 추가한다(여기서 $<v_1, v>$는 $v_1$에서 $v$로 가는 방향성 Edge를 의미한다). 이 Edge는 명백하게 $v_1$에서 $v$로 가는 최단경로이다. 다음 $v_1$에서 $V - Y$에 속한 마디로 가는 마디로 가는 경로 중에서 Y에 속한 마디만을 중간에 거쳐 가는 경로를 검사한다. 이 경로들 중에서 가장 짧은 경로가 최단경로이다. 그 경로의 끝에 위치한 Vertex를 Y에 추가하고, 그 경로 상에 그 Vertex로 가는 Edge를 F에 추가한다. Y가 모든 Vertex의 집합인 V와 같아질 때까지 이 과정을 되풀이한다. 이 시점에서 F는 최단경로에 속한 이음선을 포함하게 된다. 다음은 이 과정을 표현한 알고리즘이다.
Y = {v_1};
F = ∅;
while(the instance is not solved) {
Y에 속한 Vertex만 중간에 거쳐 가는 Vertex로 하여 v_1에서의 최단경로를 가진 Vertex v를 V - Y에서 선택한다; // Selection procedure and feasibility check
새로운 Vertex v를 Y에 추가한다;
(최단경로 상에서)v로 가는 이음선을 F에 추가한다;
if(Y == V) // Solution check
the instance is solved;
}
다음은 Dijkstra Algorithm의 실행절차를 예로 설명한다.
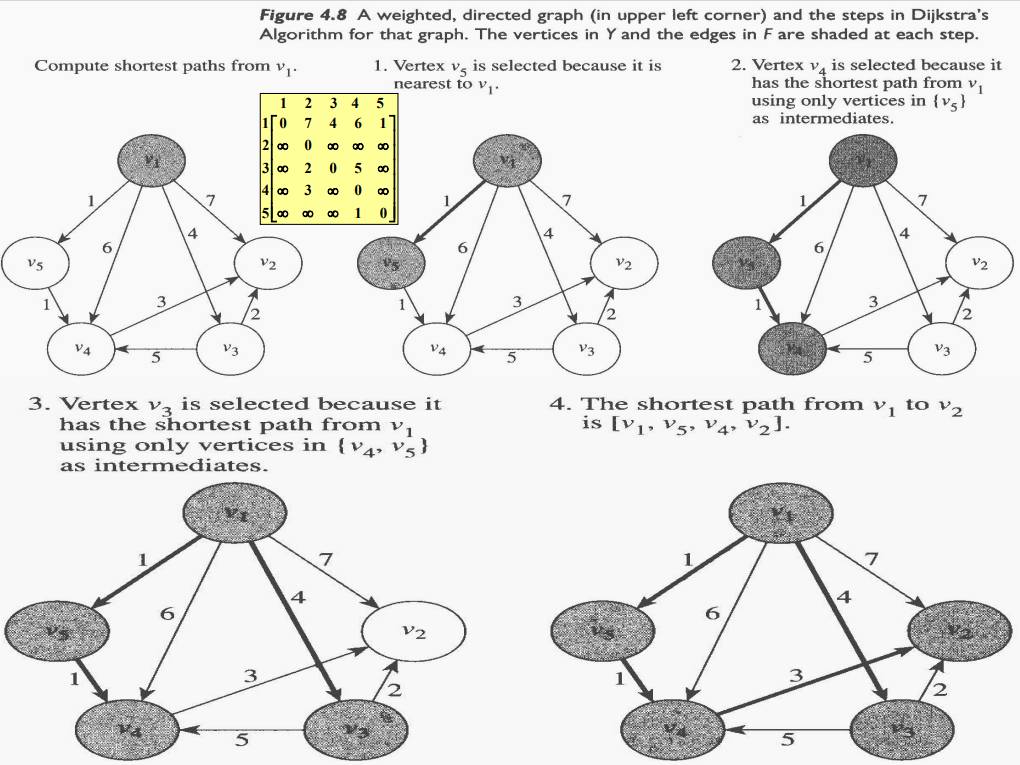
이제 세부적인 알고리즘을 살펴보자. 이 알고리즘에서 가중치 그래프는 이차원배열로 표현한다. 이 알고리즘은 Prim`s Algorithm과 매우 유사하다. $nearest$와 $distance$배열 대신 다음과 같은 $touch$과 $length$ 배열을 사용하는 것이 다르다. 여기서 $i = 2, \ldots, n$이다.
- $touch[i]$: Y에 속한 Vertex들만 중간에 거치도록 하여 $v_1$에서 $v_i$로 가는 현재 최단경로 상의 마지막 Edge를 $<v, v_i>$라고 할 때, Y에 속한 Vertex $v$의 인덱스
- $lengh[i]$: Y에 속한 Vertex들만 중간에 거치도록 하여, $v_1$에서 $v_i$로 가는 현재 최단경로의 길이
이 알고리즘은 다음과 같다.
// 문제: Weighted directed graph에서 v_1에서 다른 모든 마디로 가는 최단경로를 구하시오.
// 입력: 정수 n(>=2)와 Vertex가 n개 있는 연결된 가중치포함 방향그래프, 이 그래프는 이차원 배열 W로 표현되며, 행과 열의 인덱스는 각각 1부터 n까지이다. 여기서 W[i][j]는 i번째 마디에서 j번째 마디를 잇는 이음선 상의 가중치가 된다.
// 출력: 최단경로 상에 놓여있는 Edge의 집합 F
void dijkstra (int n, const number W[][], set_of_edges& F) {
index i, vnear;
edge e;
index touch[2 .. n];
number length[2 .. n];
F = ∅;
// 각 Vertex에 대해서, v_1에서 출발하는 현재 최단경로의 마지막 Vertex를 v_1으로 초기화한다.
// 그 경로의 길이는 v_1에서의 Edge 상의 Weight로 초기화한다.
for(i = 2; i <= n; i++) {
touch[i] = 1;
length[i] = W[1][i];
}
repeat(n-1번) {
min = ∞;
for(i = 2; i <= n; i++) { // 최단경로를 가지는지 각 마디를 점검한다.
if(0 <= length[i] < min) {
min = length[i];
vnear = i;
}
}
e = touch[vnear]가 인덱스인 Vertex에서 vnear가 인덱스인 Vertex로 가는 Edge;
e를 F에 추가;
for( i = 2; i <= n; i++) {
if(length[vnear] + W[vnear][i] < length[i]) {
length[i] = length[vnear] + W[vnear][i];
touch[i] = vnear;
// Y에 속하지 않는 각 마디에 대해서 최단경로를 바꾼다.
}
}
length[vnear] = -1; // vnear가 인덱스인 마디를 Y에 추가한다.
}
}

$v_1$에서 다른 모든 Vertex로 가는 경로가 존재한다고 가정하기 때문에 변수 vnear는 repeat 루프의 각 반복 단계에서 새로운 값을 가지게 된다. 만약 이런 가정이 없다면 이 알고리즘에 쓰여진 대로 repeat 루프의 $n - 1$번 반복이 끝날 때까지 마지막 Edge를 계속해서 추가하게 될 것이다.
이 알고리즘은 최단경로 상의 Edge만 찾는다. 이 경로의 총 길이는 계산하지 않지만 Edge를 가지고 계산할 수있다. 대안으로 알고리즘을 조금 수정하면 길이를 구하여 저장하게 할 수 있다.
이 알고리즘의 시간복잡도는 $T(n) = 2(n - 1)^2 \in \theta(n^2)$이다.
Scheduling
- Time in the system: Time spent both waiting and being served.
- Objective: Minimize total time.
시스템 내부의 총 시간의 최소화
다음 예를 보자.
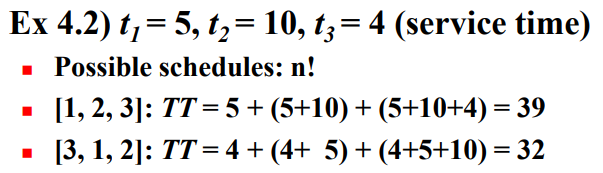
1, 2, 3의 순서로 스케줄을 짠다면 이 작업 3개를 완료하는데 시스템 내부에서 걸리는 시간 $TT = 5 + (5 + 10) + (5 + 10 + 4) = 39$이다. 이 예제에서 최적 스케줄(Scheduling)은 3, 1, 2 순이다. 이 방법을 탐욕 알고리즘으로 표현하면 다음과 같다.
작업시간 별로 작업을 비내림차순으로 정렬한다;
while(the instance is not solved) {
다음 작업을 스케줄에 넣는다; // Selection procedure and Feasibility check
if(작업이 더 이상 없다) // Solution check
the instance is solved;
}
시간복잡도는 $W(n) \in \theta(n \log n)$이다. 이 알고리즘이 만들어 낸 스케줄이 최적일 수밖에 없다는 것을 증명한다.

이 알고리즘을 복수작업자 Scheduling 문제(multiple-server scheduling problem)를 푸는 알고리즘으로 일반하하기는 쉽다.
- 작업자가 m명 있다고 가정해보자. 작업자의 순서는 무작위이다.
- 작업시간별로 작업을 비내림차순으로 정렬한다.
- 첫째 작업자는 첫째 작업을 하고, 둘째 작업자는 둘째 작업을 하고, …, m째 작업자는 m째 작업을 한다.
- 첫째 작업자는 $(m + 1)$째 작업을 하게된다. 비슷하게 둘째 작업자는 $(m + 2)$째 작업을 하게되고, 같은 식으로 계속된다.
이 방법은 다음과 같다.
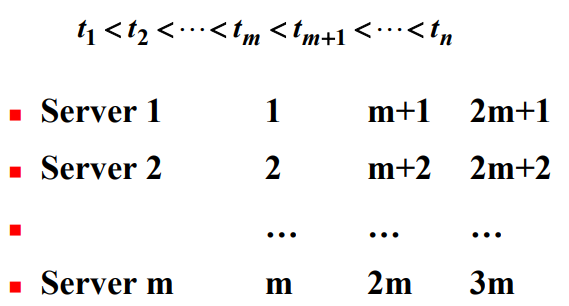
작업은 결과적으로 1, 2, …, m, 1 + m, 2 + m, …, m + m, 1 + 2m, … 순서로 처리하게 된다. 즉, 서비스시간별로 비내림차순으로 처리된다.
마감시간이 있는 스케줄 짜기
마감시간이 있는 Schedulinh 문제에서 각 작업을 끝내는데 1의 단위시간이 걸리고, 마감 시간과 보상이 할당되어 있다. 작업을 마감시간 전이나 마감시간에 마친다면 보상을 받는다. 목표는 총 보상액이 최대가 되게 작업 스케줄을 짜는 것이다. 모든 작업을 스케줄에 포함시킬 필요는 없다. 마감시간 후의 작업은 보상이 없으므로 아예 작업을 하지 않는 것과 마찬가지이다. 그러한 스케줄은 불가능(impossible)한 스케줄이라고 한다. 다음 예를 보자.
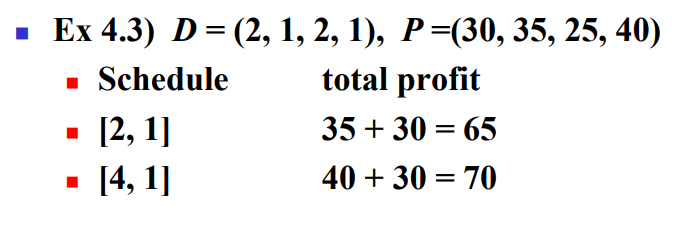
- D: 마감시간, P: 보상
- 가능한 스케줄 $[1, 3], [2, 1], [2, 3], [3, 1], [4, 1], [4, 3]$ 중에서 스케줄 $[4, 1]$이 총 보상이 70이 되며 최적임을 알 수 있다.
모든 스케줄을 다 따지면 계승시간이 걸린다. 이 문제를 푸는 웬만한 탐욕 알고리즘은 보상이 큰 것부터 차례로 작업을 먼저 정렬하게 될 것을 암시할 수 있다. 각 작업을 순서대로 검사하여 그 작업이 가능한 작업이면 스케줄에 포함시킨다. 알고리즘을 작성하기 전에 몇 가지를 정의한다.
- 작업 순서상의 모든 작업들을 마감시간 내에 시작하면, 그 순서를 적절한 순서(feasible sequence)라고 한다.
- 작업의 집합에서 최소한 하나의 적당한 순서가 존재하면 그 집합은 적절한 집합(feasible set)이라고 한다.
- 목표는 총 보상을 최대로 하는 적절한 순서를 찾는 것이다. 그러한 순서를 최적 순서(optimal sequence)라 하고, 그 순서에 속한 작업의 집합을 작업의 최적 집합(optimal set of jobs)이라고 한다.
이제 알고리즘을 살펴본다.
작업을 보상이 큰 것부터 차례로 정렬한다;
S = ∅;
while(the instance is not solved) {
select next job; // Selection procedure
if(이 작업을 추가하면 S가 적절하다) // feasibility check
이 작업을 S에 추가;
if(there is no more jobs) // Solution check
the instance is solved;
}
다음 예를 보자.
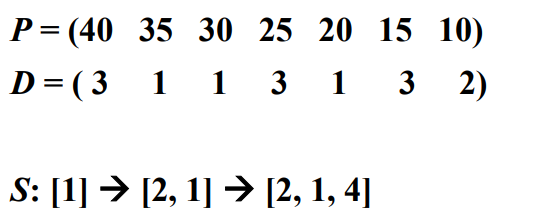
- S를 ∅으로 놓는다.
- 순서 $[1]$이 적절하므로 S를 ${1}$로 놓는다.
- 순서 $[2, 1]$이 적절하므로 S를 ${1, 2}$로 놓는다.
- ${1, 2, 3}$은 적절한 순서가 존재하지 않으므로 기각한다.
- 순서 $[2, 1, 4]$가 적절하므로 S를 ${1, 2, 4}$로 놓는다.
- ${1, 2, 4, 5}$은 적절한 순서가 존재하지 않으므로 기각한다.
- ${1, 2, 4, 6}$은 적절한 순서가 존재하지 않으므로 기각한다.
- ${1, 2, 4, 7}$은 적절한 순서가 존재하지 않으므로 기각한다.
- S의 최종값은 ${1, 2, 4}$가 되고, 이 집합에 대한 적절한 순서는 $[2, 1, 4]$가 된다. 작업 1과 4는 모두 마감시간이므로 3이므로, 적절한 순서인 $[2, 4, 1]$을 대신 사용할 수 있다.
이제 알고리즘을 살펴보자. 작업들은 알고리즘에 전달되기 전에 이미 보상이 큰 것부터 차례로 정렬되어 있다고 가정한다. 보상은 작업을 정렬하기 위해서만 필요하므로, 알고리즘의 파라미터에는 빠져있다.
// 문제: 각 작업을 마감시간에 마칠 수 있도록 스케줄을 짠 경우에만 보상을 얻을 수 있을 때 총 보상이 최대가 되도록 스케줄을 짜시오.
// 입력: 작업의 수 n과 정수 배열 deadline(인덱스는 1부터 n), 여기서 deadline[i]는 i 째 작업의 마감시간, 배열은 보상이 큰 것부터 차례로 정렬되어 있다.
// 출력: 작업의 최저 순서 J
void schedule(int n, const int deadline[], sequence_of_integer& J) {
index i;
sequence_of_integer K;
J = [1];
for(i = 2; i <= n; i++) {
K = J에다가 deadline[i]의 값이 작은 것부터 차례로 i를 추가;
if(K is feasible)
J = K;
}
}
다음 예를 보자.

이 알고리즘의 시간 복잡도를 분석하면 $W(n) \in \theta (n^2)$이다.
Huffman Code
데이터 압축(data compression)문제는 데이터 파일을 코드화(encode)하는 효율적인 방법을 찾는 것이다. 허프만 코드(Huffman code)라고 하는 코드화 방식과 주어진 파일을 허프만 코드화하는 탐욕 알고리즘을 알아본다.
데이터 파일은 통상적으로 이진코드(binary code)로 표현한다. 각 문자는 코드워드(code word)라고 하는 유일한 이진 문자열로 표현한다. 길이가 고정된 이진 코드(fixed-length code)는 각 문자를 표현하는 비트(bit)의 개수가 일정하다. 예를 들어, 문자의 집합이 ${a, b, c}$라고 하면, 이 경우 두 비트만으로 각 문자를 코드화 할 수 있다.
- a: 00
- b: 01
- c: 11
이 코드화 공식을 ababcbbbc에 적용하면 000100011101010111이 된다.
길이가 변하는 이진 코드(variable-length binary code)를 사용하면 공간을 덜 사용하는 효율적인 코드화 방식을 만들어낼 수 있다. 이 코드화 방식은 각 문자마다 표현하는 비트의 개수가 다르다. b가 가장 빈번히 나오므로 b를 0으로 코드화하면 다음과 같다.
- a: 10
- b: 0
- c: 11
이 코드화 공식을 ababcbbbc에 적용하면 1001001100011이 된다. 이 코드화 방식을 이용해 18개 비트가 필요한 이전 방식을 13개 비트만으로 표현했다. 최적 이진코드(optimal binary code) 문제는 주어진 파일에 있는 문자들을 이진코드로 표현하는데 필요한 비트의 개수가 최소가 되는 이진문자코드를 찾는 것이다.
전치코드
길이가 변하는 이진코드의 특수 형태의 하나로 전치코드(prefix code)가 있다. 전치코드에서는 한 문자의 코드워드가 다른 문자의 코드워드의 앞부분이 될 수 없다(01이 ‘a’의 코드워드라면 011은 ‘b’의 코드워드가 될 수 없다).
전치코드는 잎이 코드문자로 구성된 이진트리로 표현이 가능하다.
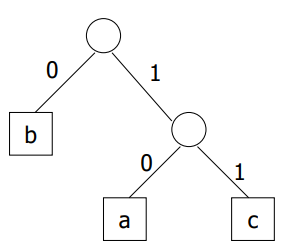
전치코드의 장점은 파일을 parse할 때 현쟈 parse하고 있는 지점의 앞부분을 미리 볼 필요가 없다는 것이다. 파일에서 한 비트씩 차례로 훑어가고, 0이 나오는지 1이 나오는지에 따라서 트리의 마디에서 왼쪽 또는 오른쪽으로 간다. leaf node에 도달하면 그 leaf에 있는 문자를 취한다. 다음은 파일을 코드화하는데 사용 가능한 3가지 다른 코드도 나열한다.
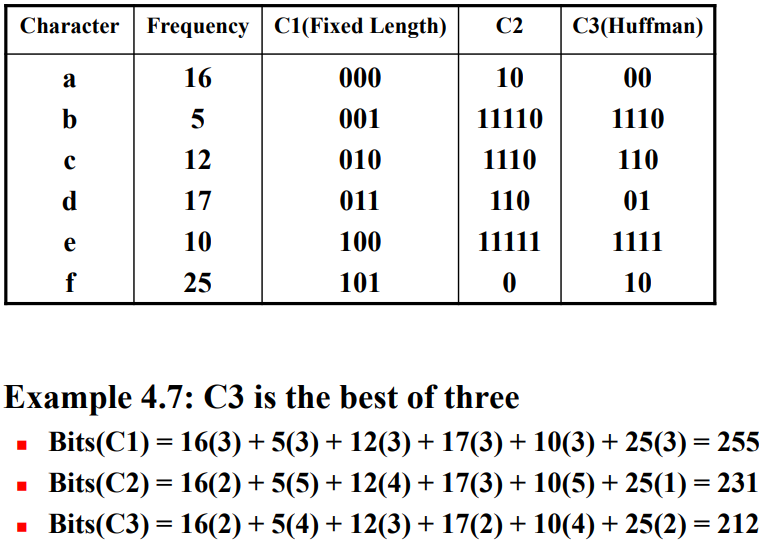
코드 C2는 C1보다 좋지만, C3는 C2보다도 더 좋음을 알 수 있다.
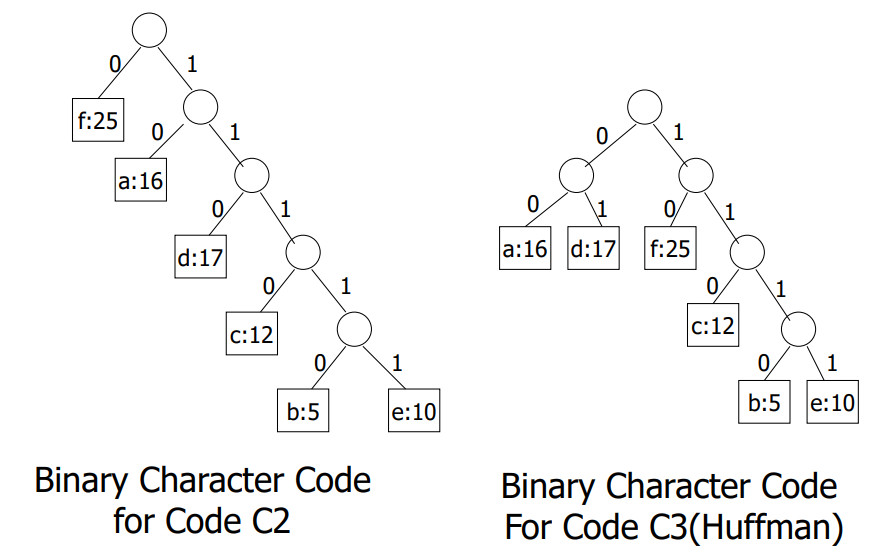
이진트리 T가 주어지고 파일을 코드화 했을 때 차지하는 비트의 수는 다음과 같이 계산할 수 있다.
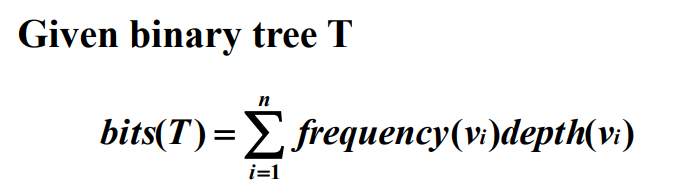
여기서 ${v_1, v_2, \ldots, v_n}$는 파일에 있는 문자의 집합이고, $frequency(v_i)$는 $v_i$가 파일에 나타나는 횟수이고, $depth(v_i)$는 $T$에서 $v_i$의 깊이이다.
허프만 알고리즘
허프만 코드(Huffman`s code)란 최적 코드에 해당하는 이진트리를 구축하여 최적 이진문자코드를 만들어내는 탐욕 알고리즘이다. 먼저 타입 선언을 보자.
struct nodetype {
char symbol; // 문자값
int frequency; // 파일에 있는 문자의 빈도수
nodetype* left;
nodetype* right;
}
여기서는 우선순위 대기열(priority queue)을 사용한다. Priority queue에서는 우선순위가 가장 높은 요소가 항상 먼저 빠져나간다. 우선순위가 가장 높은 원소는 파일에서 빈도수가 가장 낮은 문자이다. 허프만 알고리즘(Huffman`s Algorithm)은 다음과 같다.
- n: 파일에서 문자의 개수
- PQ(Priority queue)에서 $nodetype$ 레코드를 가리키는 포인터 n개를 다음과 같이 배열한다.
- p -> symbol = 문자
- p -> frequency = 문자의 빈도수
- p -> left = p -> right = NULL 우선순위는 빈도수에 좌우되는데, 낮은 빈도수가 높은 우선순위를 가진다.
for(i = 1; i <= n - 1; i++) {
remove(PQ, p);
remove(PQ, q); // Selection procedure
r = new nodetype;
r -> left = p;
r -> right = q;
r -> frequency = p -> frequency + q -> frequency;
insert(PQ, r);
}
remove(PQ, r);
return r;
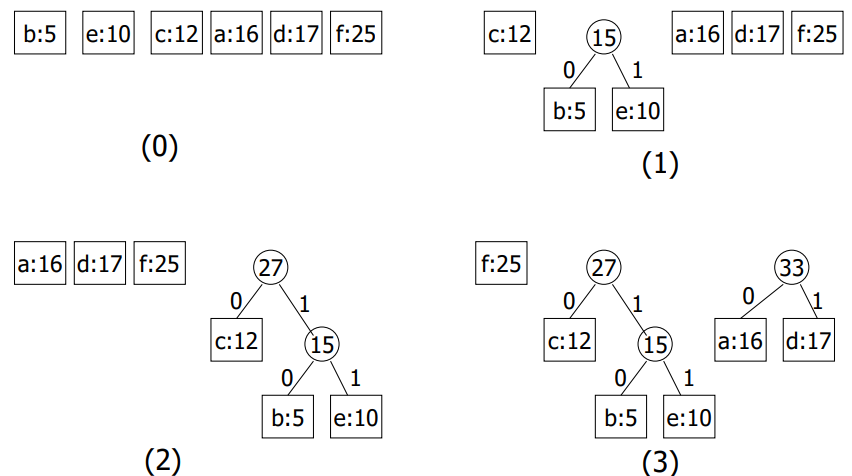
Huffman`s Algorithms의 과정은 다음과 같다.
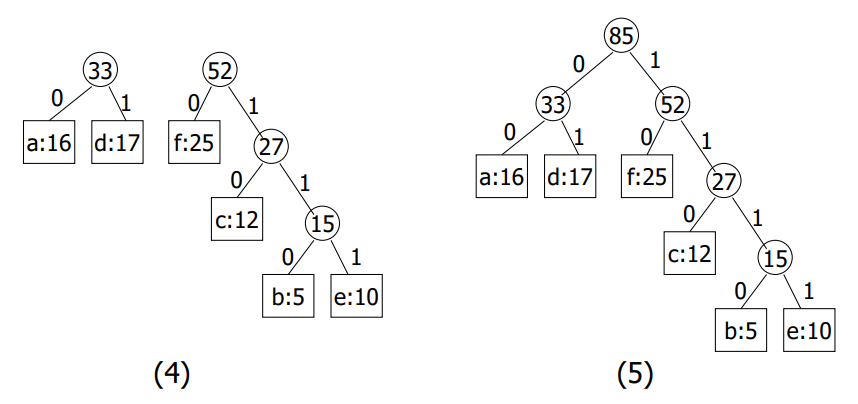
The Knapsack Problem
0-1 배낭 채우기 문제의 탐욕적인 해법
- item $i$: profit $p_i$, weight $w_i$
- W: knapsack capacity(배낭의 용량)
- If a fraction $x_i(0 \le x_i \le 1)$ of item i is placed in the knapsack, then a profit of $p_i x_i$ is earned.
목표는 $\Sigma_{item_i \in A} w_i \le W$를 만족하면서 $\Sigma_{item_i \in A} p_i$를 최대가 되는 아이템들의 부분집합을 구하는 것이다.
가장 쉬운 탐욕적인 전략은 가장 값어치가 높은 아이템을 먼저 채우는 것이다. 즉, 값어치가 높은 순서로 채우는 것이다. 그러나 이 전략은 가장 값어치가 많이 나가는 아이템이 그 값어치에 비해서 무개가 많이 나가는 경우 좋지 않을 수 있다. 또 다른 탐욕적인 전략은 가장 가벼운 아이템부터 채우는 것이다. 이 전략은 가벼운 아이템이 무게에 비해서 값어치가 별로 나가지 않는 경우 좋지 않다.
이 두 탐욕 알고리즘의 단점을 극복하기 위한 좀 더 복잡한 탐욕 알고리즘은 무게 당 값어치가 가장 높은 아이템을 우선 채우는 것이다. 하지만 다음 예를 보면 0-1 knapsack problem은 Greedy Approach로는 풀 수 없다.
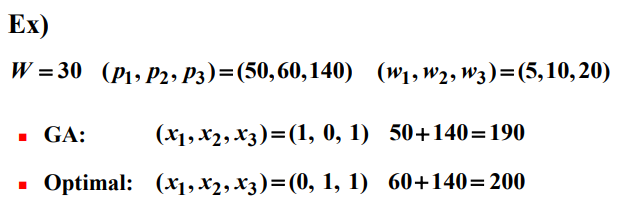
0-1 배낭 채우기 문제를 푸는 동적계획법
최적의 원칙이 적용된다고 증명할 수 있다면 동적계획법으로 0-1 배낭 채우기 문제를 풀 수 있다. A를 n개의 아이템들 중에서 최적을 이루는 부분집합이라고 하면, A가 아이템 n을 포함하는 경우와 포함하지 않는 경우 두 가지로 나눌 수 있다. 만약 A가 아이템 n을 포함하고 있지 않다면 A는 처음 $n-1$개 아이템들 중에서 최적을 이루는 부분집합과 같다. 만약 A가 아이템 n을 포함하고 있다면 A에 속한 아이템들의 총 이익은 총 무게가 $W - w_n$을 초화할 수 었다는 제약조건 하에서 처음 $n - 1$개 중에서 아이템들을 선택할 때 얻는 최적의 이익에다 $p_n$을 더한 것과 같다. 따라서 최적의 원칙이 적용된다.
위 결과를 일반화할 수 있다. $i > 0$과 $w > 0$인 경우 총 무게가 $w$를 초과할 수 없다는 제약조건 하에서 처음 $i$개 아이템에서만 선택할 때 얻는 최적의 이익을 $P[i][w]$라 하면 다음과 같은 식을 얻는다.
최대 이익은 $P[n][W]$와 같다.
0-1 배낭 채우기 문제를 푸는 동적계획법 알고리즘의 개선
이 알고리즘을 최악의 경우 계산한 엔트리의 개수가 $\theta(2^n)$이 되도록 개선할 수 있다. 1과 $W$사이에 모든 $w$에 대해서 $i$째 행에 있는 엔트리는 계산할 필요가 없다는 사실을 기초로 개선을 시도한다. $n$번째 행에서는 $P[n][W]$만 계산하면 된다. 따라서 $(n - 1)$째 행에서는 $P[n][W]$를 계산하는데 필요한 엔트리만 계산하면 된다. $P[n][W]$는 다음과 같은 식으로 표현할 수 있다.
다음 예를 보자.
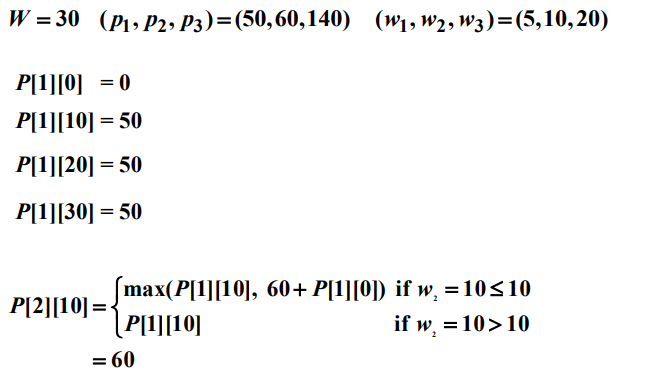
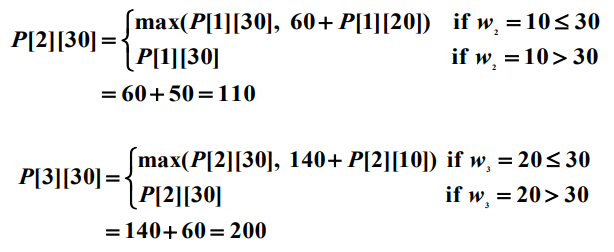
댓글남기기