되추적
Updated:
The Backtracking Technique
Backtracking은 임의의 집합(set)에서 주어진 기준(criterion)대로 원소의 순서(sequence)를 선택하는 문제를 푸는데 사용한다. Backtracking은 트리의 변형된 깊이우선검색(DFS, Depth-First Search)이다. Preorder(부모마디우선) 트리검색은 트리의 깊이우선검색이다. 이는 뿌리마디(root)를 먼저 방문한 후, 그 뿌리마디(node)의 후손들을 모두 방문한다.
깊이우선검색을 하는 간단한 재귀 알고리즘이 있다. 이 알고리즘은 자식마디를 방문하는 순서에 대해 언급하지는 않았지만, 왼쪽에서 오른쪽으로 방문하도록 한다.
void depth_first_tree_search (node v) {
node u;
visit v;
for(each child u of v)
depth_first_tree_search(u);
}
내려 가봐야 해답이 없는 마디를 만나는 순간, 그 마디의 검색을 중단하고 그 마디의 부모마디로 돌아가서 다른 자식마디의 검색을 계속하는 과정이 Backtracking이다. 해답이 될 가능성이 없는 마디를 유망하지 않다(nonpromising)고 한다. 그렇지 않으면 유망하다(promising)고 한다. 요약해 보면 Backtracking은 상태공간트리(A State Space Tree)를 깊이우선검색하여 각 마디가 promising한지를 검사하고, 만약 nonpromising하지 않으면 그 마디의 부모마디로 Backtracking한다. 이 절차를 상태공간트리를 가지친다(pruning)고 하고, 유망한 마디만으로 구성된 부분트리를 가지친 상태공간트리(pruned state space tree)라고 한다. Backtracking의 일반적인 알고리즘은 다음과 같다.
void checknode (node v) {
node u;
if(promising(v)){
if(there is a solution at v)
write the solution;
else{
for(each child u of v)
checknode(u);
}
}
}
상태공간트리의 뿌리마디는 호출할 때 파라미터로 checknode에 전달된다. 마디를 방문하면 일단 그 마디가 promising한지를 먼저 점검한다. 만약 그 마디가 promising하고 그 마디에 해답이 있으면, 해답을 프린트한다. promising한 마디에 해답이 없으면, 그 마디의 자식마디를 방문한다.
Backtracking Algorithm이 트리를 실제로 구축할 필요는 없다. 대신, 조사 중인 해당 가지(branch)의 값만 알고 있으면 된다. 즉, 상태공간트리가 알고리즘에서 묵시적으로(implicity) 존재한다.
Backtracking Algorithm(checknode)에 비효율적인 부분이 있다. 마디를 프로시저에 전달한 후 마디의 유망여부를 점검한다. 이는 활성레크드 스택에 유망하지 않는 마디의 활성레코드를 불필요하게 쌓아 놓음을 뜻한다. 마디를 전달하기 전에 마디의 유망성을 점검하면 이 비효율성을 제거할 수 있다. 이를 적용시킨 일반 알고리즘은 다음과 같다.
void expand (node v) {
node u;
for(each child u of v) {
if(promising(v)){
if(there is a solution at u)
write the solution;
else
expand(u);
}
}
}
알고리즘에 파라미터로 전달된 마디는 뿌리이다. 이 알고리즘을 expand라고 하는 이유는 유망한 마디를 확장(expand)할 때 이 프로시저를 호출하기 때문이다. 이 알고리즘을 프로그램으로 구현하면 활성레코드 스택에 유망하지 않은 마디의 활성레코드를 쌓아놓지 않고 그 유망하지 않은 마디에서 backtracking한다.
The n-Queens Problem
The n-Queens Problem은 여왕말을 서로 잡아먹지 않게 두어야 한다. 같은 행과 열, 대각선에 두 말을 놓을 수 없다. 예를 한번 보자.
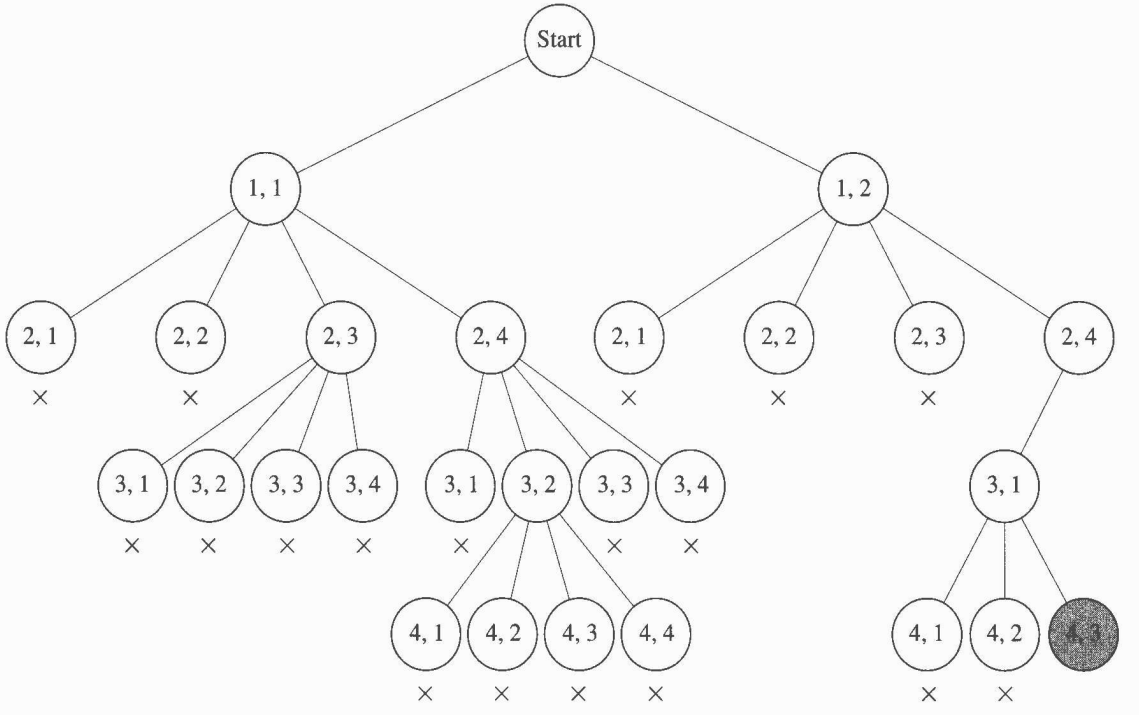
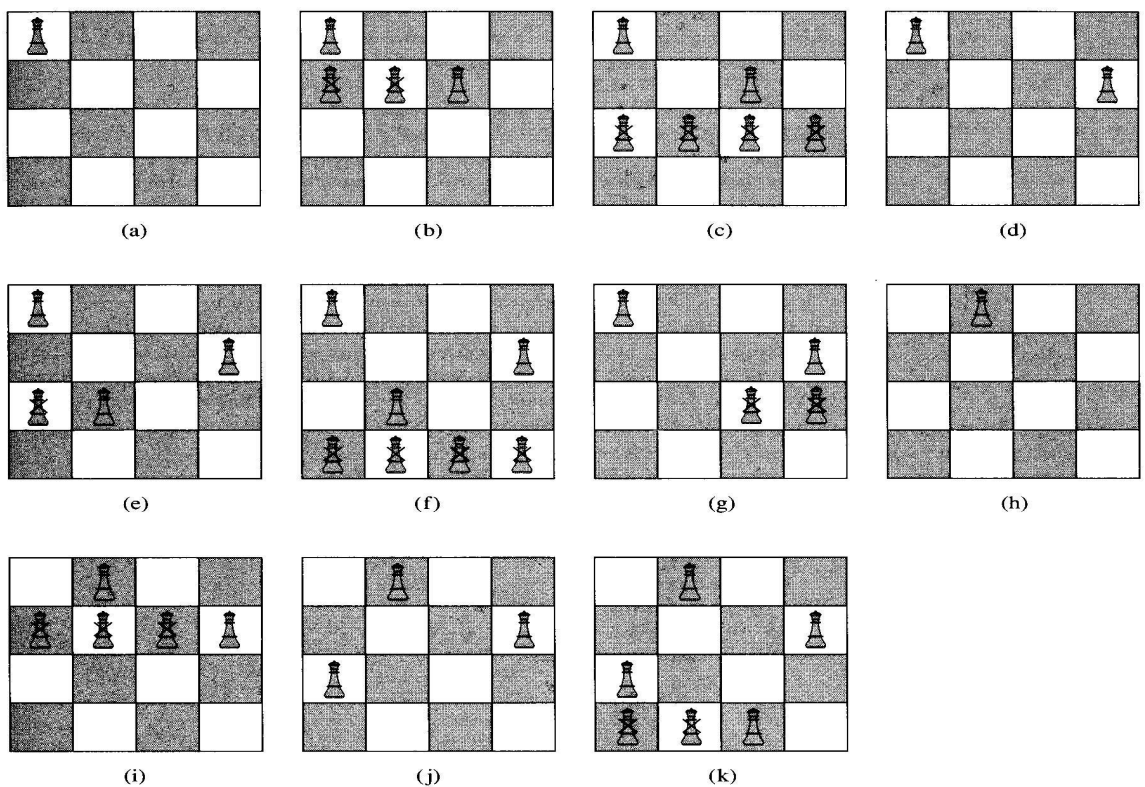
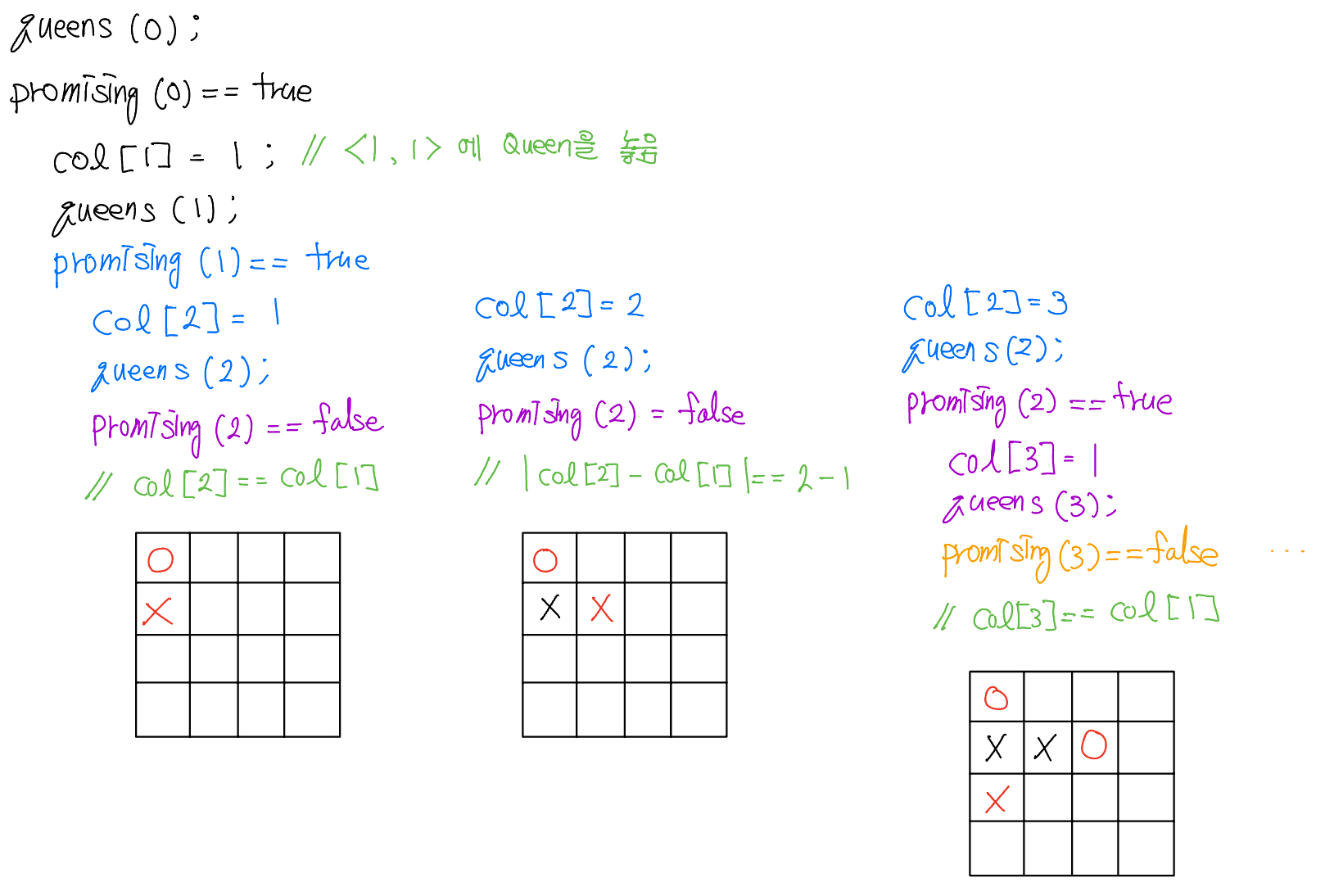
- $<1, 1>$은 유망하다.
- 여왕말 1이 두는 첫째 말이기 때문이다.
- $<2, 1>$은 유망하지 않다.
- 여왕말 1이 열 1에 있기 때문이다.
- $<2, 2>$은 유망하지 않다.
- 여왕말 1이 왼쪽 대각선에 있기 때문이다.
- $<2, 3>$은 유망하다.
- $<3, 1>$은 유망하지 않다.
- 여왕말 1이 열 1에 있기 떄문이다.
- $<3, 2>$은 유망하지 않다.
- 여왕말 2가 오른쪽 대각선에 있기 때문이다.
- $<3, 3>$은 유망하지 않다.
- 여왕말 2가 열 3에 있기 때문이다.
- $<3, 4>$은 유망하지 않다.
- 여왕말 2가 왼쪽 대각선에 있기 때문이다.
- $<1, 1>$로 backtracking
위와 같게 계속 추적하다보면 해답을 알 수 있다.
The n-Queens Problem에서 유망함수는 두 여왕말이 같은 열이나 대각선에 있는지 검사해야 한다. 만약 $col(i)$를 $i$째 행에서 여왕말이 놓어있는 열이라고 하면, $k$째 행에 있는 여왕말이 같은 열에 있는지 검사하기 위해서 식 $col(i) = col(k)$이 성립하는지 검사해야 한다($i > k$).
대각선의 경우를 보면, 행 $k$에 있는 여왕말은 행 $i$에 놓여있는 여왕말에 의해서 어느 한쪽 대각선으로 위협받고 있으면, 식 $col(i) - col(k) = i - k$ 또는 $col(k) - col(i) = k - i$가 성립한다. 이제 알고리즘을 살펴보자.
// 문제: 체스판에 어떤 두 여왕말도 같은 행, 열, 대각선에 있지 않도록 n개 여왕말을 놓으시오.
// 입력: 양의 정수 n
// 출력: n x n 체스판에 n개 여왕말을 서로 위협받지 않고 놓을 수 있는 가능한 모든 방법. 각 출력은 인덱스 범위가 1부터 n까지인 정수배열 col로 이루어진다.
// 여기서 col[i]는 i번째 행에 있는 여왕말이 놓여있는 열이다.
void queens (index i) {
index j;
if(promising(i)){
if(i == n)
cout << col[1] through col[n];
else{
for(j = 1; j <= n; j++){
col[i + 1] = j;
queens(i + 1);
}
}
}
}
bool promising (index i) {
index k;
bool switch;
k = 1;
switch = true;
while(k < i && switch) {
if(col[i] == col[k] || abs(col[i] - col[k]) == i - k)
switch = false;
k++;
}
return switch;
}
만약 $n$과 $col$이 전역변수로 정의된다면, queens의 최초 호출은 $queens(0)$;이다.
이 알고리즘을 분석하기 위해서 검사하는 마디의 수를 여왕말의 개수인 $n$의 함수로 나타내야 한다. 트리에서 마디 개수의 상한은 전체 마디의 개수를 세어 구할 수 있다.
만약 $n = 8$인 경우, 상태공간트리의 마디 개수는 19173961마디가 된다. 하지만 이렇게 알고리즘을 분석하는 것은 진정한 분석이 아니다. Backtracking의 목적은 알고리즘을 실행하기 전에 알고리즘이 효율적인지를 결정하는 데 있다. 다음 몬테칼로 기법을 사용하면 어떻게 backtracking algorithm의 효율을 추정할 수 있는지 알 수 있다.
몬테칼로 알고리즘을 사용한 Backtracking Algorithm의 효율성 추정
몬테칼로 알고리즘(Monte Carlo Algorithms)은 실행할 명령이 무작위로 결정되는 확률 알고리즘(probabilistic algorithm)이다. 결정 알고리즘(deterministic algorithm)은 그렇지 않다. 지금까지 공부한 알고리즘은 모두 결정 알고리즘이다. 몬테칼로 알고리즘은 표본공간의 무작위 표본의 평균치를 가지고 표본공간에서 정의된 무작위변수의 기대치를 추정한다. 추정치가 실제 기대치에 근접하리라는 보장은 없지만 알고리즘을 오래 실행할수록 실제 기대치에 근접할 확률은 증가한다. 몬테칼로 알고리즘을 사용하여 특정 사례에 대한 backtrackin algorithm의 효율을 추정할 수 있다.
이 기술을 적용하기 위해서 알고리즘은 다음 조건을 반드시 만족해야 한다.
- 상태공간트리의 같은 수준의 모든 마디에서 같은 유망함수를 사용해야 한다.
- 상태공간트리에서 같은 수준에 있는 마디들은 모두 자식마디의 개수가 같아야 한다.
The n-Queens problem은 이 조건을 만족한다. $m_i$를 수준 $i$에서 마디들의 유망한 자식마디의 평균 개수의 추정치, $t_i$를 수준 $i$에서 어떤 마디의 자식마디의 총 개수라고 하면, 어떤 마디 $t_i$개의 자식마디를 모두 검사하고 $m_i$개의 유망한 자식만 검사한 자식마디이기 때문에 backtracking algorithm이 해답을 모두 찾기 위해서 검사한 마디의 총 개수 추정치는 다음과 같다.
이 추정치를 계산하는 일반 알고리즘은 다음과 같다. 이 알고리즘에서 변수 $mprod$는 각 수준에서 만들어진 $m_0m_1 \cdots m_{i-1}$을 표현하는데 쓴다.
// 문제: 몬테칼로 알고리즘을 사용하여 backtracking algorithms의 효율을 추정하시오.
// 입력: Backtracking algorithm이 풀려고 하는 문제의 사례
// 출력: 알고리즘이 만들어 내는 가지친 상태공간트리에서 마디의 개수 추정치.
// 그 사례에 대하여 알고리즘이 해답을 모두 찾기 위하여 검사하는 마디의 개수가 됨.
int estimate () {
node v;
int m, mprod, t, numnodes;
v = 상태공간트리의 뿌리;
numnodes = 1;
m = 1;
mprod = 1;
while(m != 0) {
t = v의 자식마디의 개수;
mprod = mprod * m;
numnodes = numnodes + mprod * t;
m = v의 유말한 자식마디의 개수;
if(m != 0)
v = v의 무작위로 선택한 자식마디의 개수;
}
return numnodes;
}
다음 알고리즘은 The n-Queens problem에 대한 몬테칼로 추정치를 구하는 알고리즘이다.
// 문제: The n-Queens problem의 효율 추정
// 입력: 양의 정수 n
// 출력: The n-Queens problem이 만들어 내는 가지친 상태공간트리에서 마디의 개수 추정치.
// 두 여왕말이 서로 위협하지 않도록 체스판에 n개의 여왕말을 놓는 방법을 모두 찾기 전에 알고리즘이 검사하는 마디의 개수가 됨
int estimate_n_queens (int n) {
index i, j, col[1 .. n];
int m, mprod, numnodes;
set_of_index prom_children;
i = 0;
numnodes = 1;
m = 1;
mprod = 1;
while(m != 0 && i != n) {
mprod = mprod * m;
numnodes = numnodes + mprod * n;
i++;
m = 0;
prom_children = ∅;
for(j = 1; j <= n; j++) {
col[i] = j;
if(promising(i)) {
m++;
prom_children = prom_children ⋃ {j};
}
}
if(m != 0) {
j = prom_children에서 무작위로 선택;
col[i] = j;
}
}
return numnodes;
}
몬테칼로 알고리즘을 사용할 때 두 번 이상 실행하여 추정치를 구해야 하고, 그 결과의 평균을 실제 추정치로 사용해야 한다. 통계학에서 표준으로 쓰이는 방법을 사용하면 시도한 결과로 검사한 마디의 실제 개수에 대한 신뢰구간을 결정할 수 있다. 경험으로 보면 20번 정도 시도하면 보통 충분하다. 몬테칼로 알고리즘을 여러 번 실행시키면 좋은 추정치를 구할 확률이 높아지지만, 결과가 항상 좋은 추정치라는 보장은 결코 없다는 걸 주의해야 한다.
The Sum-of-Subsets Problem
부분집합의 합 구하기 문제에서는 양의 정수(무게) $w_i$가 $n$개, 양의 정수 $W$가 있다. 목표는 합이 $W$가 되는 정수의 부분집합을 모두 찾는 것이다. 다음 예를 보자.
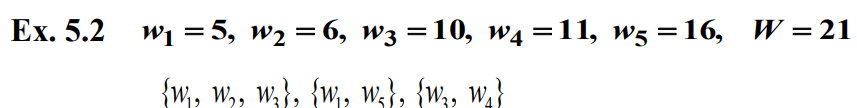
큰 $n$ 값에 대해서 체계적인 접근 방법이 필요하다. 상태공간트리를 만들어 푸는 방법이 하나 있다. 검색하기 전에 증가하는 순으로 가중치를 정렬한다면, 마디가 유망하지 않음을 분명하게 알려주는 표시가 존재한다. 가중치가 이렇게 정렬되어 있으면 $w_{i + 1}$은 $i$수준에서 남아있는 가장 가벼운 무게가 된다. weight를 수준 $i$의 마디까지 포함된 무게의 합이라 하면, $w_{i+1}$이 weight의 값을 $W$를 넘기게 한다면, 그 이후에 어떤 다른 무게도 $W$를 넘길 것이다. 따라서 weight가 $W$와 같지 않으면, $weight + w_{i+1} > W$,수준 $i$의 마디는 유망하지 않다.
어떤 주어진 마디에서 남아있는 아이템의 무게의 총 합에다 weight를 더해서도 최소한 $W$와 같아지지도 않으면, 그 마디 이후로 아무리 확장하더라고 $W$와 같아질 수 없다. 이는 total이 남은 아이템의 총 무게일 때, $weight + total < W$를 만족하면 이 마디는 유망하지 않음을 의미한다. 다음 예를 보자.
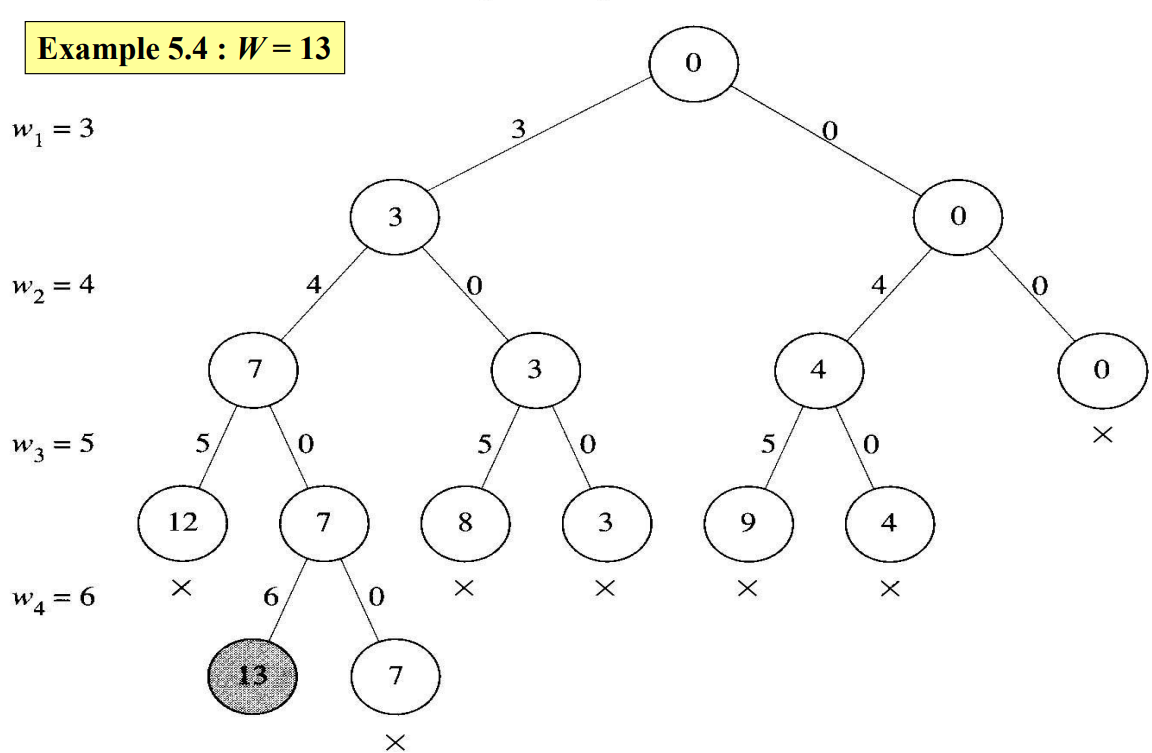
- 12, 8, 9를 포함하는 마디들은 다음 무게(6)을 추가하면 weight의 값이 W를 초과하기 때문에 유망하지 않다.
- 7, 3, 4, 0을 포함하는 마디들은 남은 무게의 총합이 weight의 값을 W까지 올리기에 충분하지 않기 때문에 유망하지 않다.
- 해답을 포함하지 않은 상태공간트리에서 leaf는 자동적으로 유망하지 않다.
어떤 마디까지 포함된 무게의 합이 $W$와 같으면, 그 마디에 해답이 있다. 그러므로 아이템을 더 추가시킨다고 또 다른 해답을 구할 수는 없다. 이는 만약 $W = weight$가 성립하면 해답을 프린트하고, 되추적해야 한다. 이제 알고리즘을 살펴보자. 이 알고리즘은 배열 $include$를 사용하는데 $w[i]$를 포함하면 $include[i]$가 ‘yes’값을 가지고, 그렇지 않으면 ‘no’값을 가진다.
// 문제: n개 양의 정수(무개)와 양의 정수 W를 가지고,합이 W가 되는 모든 정수의 조합을 모두 구하시오.
// 입력: 양의 정수 n, 감소하지 않는 순으로 정렬된 양의 정수 배열 w(범위는 1부터 n)
// 출력: 합이 W가 되는 모든 정수의 조합
void sum_of_subsets (index i, int weight, int total) {
if(promising(i)){
if(weight == W)
cout << include[1] through include[i];
else {
include[i + 1] = "yes";
sum_of_subsets(i + 1, weight + w[i + 1], total - w[i + 1]);
include[i + 1] = "no";
sum_of_subsets(i + 1, weight, total - w[i + 1]);
}
}
}
bool promising(index i) {
return (weight + total >= W) && (weight == W || weight + w[i + 1] <= W);
}
$n, w, W, include$는 전역적으로 정의하여 sum_of_subsets의 최초 호출은 sum_of_subsets(0, 0, total)이 된다.
Graph Coloring
Graph Coloring(m-coloring) 문제는 비방향그래프에서 서로 인접한 정점이 같은 색을 갖지 않도록 최대 m개의 다른 색으로 칠하는 방법을 모두 찾는 문제이다. 다음 에를 보자.
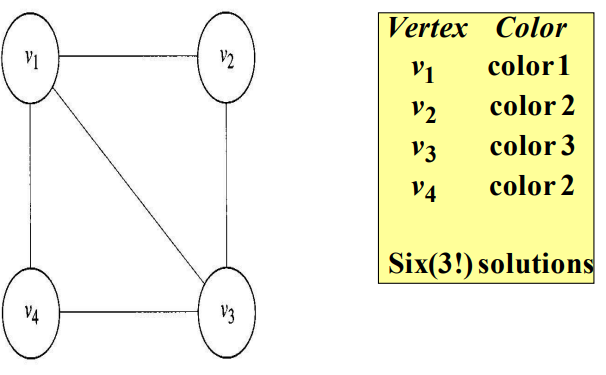
이 그래프에서 최대 2개의 다른 색까지만 사용할 수 있다면, 인접한 정점이 같은 색을 갖지 않도록 정점을 색칠하기는 불가능하기 때문에 2-coloring 문제의 해답은 없다. 이 그래프에서 3-coloring 문제의 해답 중 하나는 위와 같다. 이 그래프에서 3-coloring 문제의 해답은 총 $3!$개 이다. 이는 색이 조합된 방법만 다를 뿐이다.
Graph Coloring의 주요 응용분야는 지도 색칠하기이다. 두 개의 Edge가 서로 교차하지 않도록 그린 그래프를 평면그래프(planar graph)라고 한다. 다음은 평면 그래프이다.
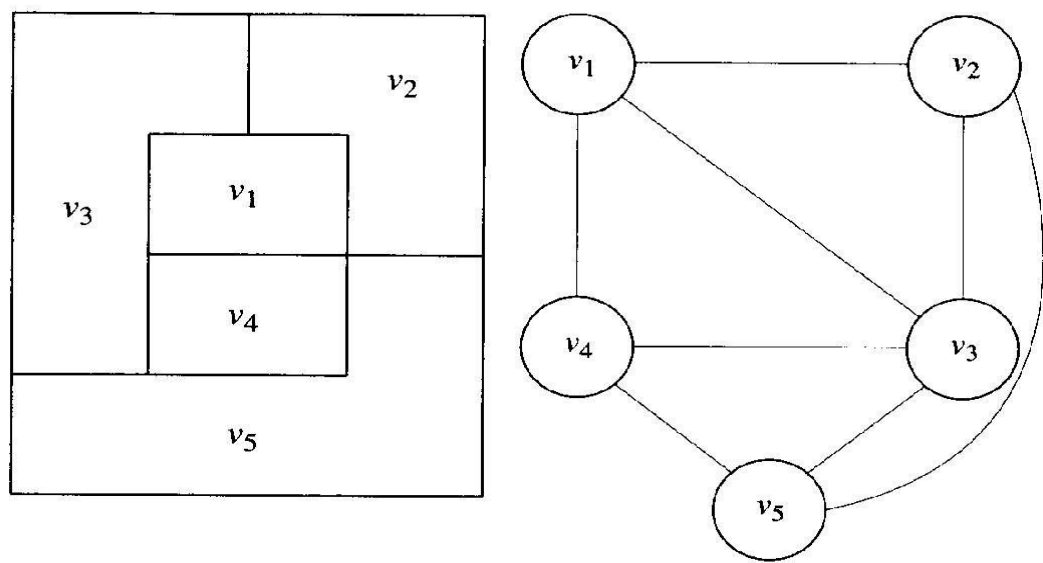
그러나 Edge $(v_1, v_5)$와 $(v_2, v_4)$를 추가하면 더 이상 평면그래프가 아니다. 모든 지도는 그에 상응하는 평면그래프가 존재한다. 지도에서 각 지젹은 정점에 해당한다. 만약 한 지역이 다른 지역과 인접해 있으면, 그에 해당하는 정점들은 Edge로 연결한다.
이 문제에서 Backtracking할 수 있는데, 어떤 마디에서 색칠한 Vertex와 인접한 Vertex가 이미 그 마디에 사용된 색인 경우 nonpromising하기 때문이다. 다음은 첫 예에서 3-coloring하는데 backtracking 전략을 적용하여 만들어진 가지친 상태공간 트리를 보여준다.
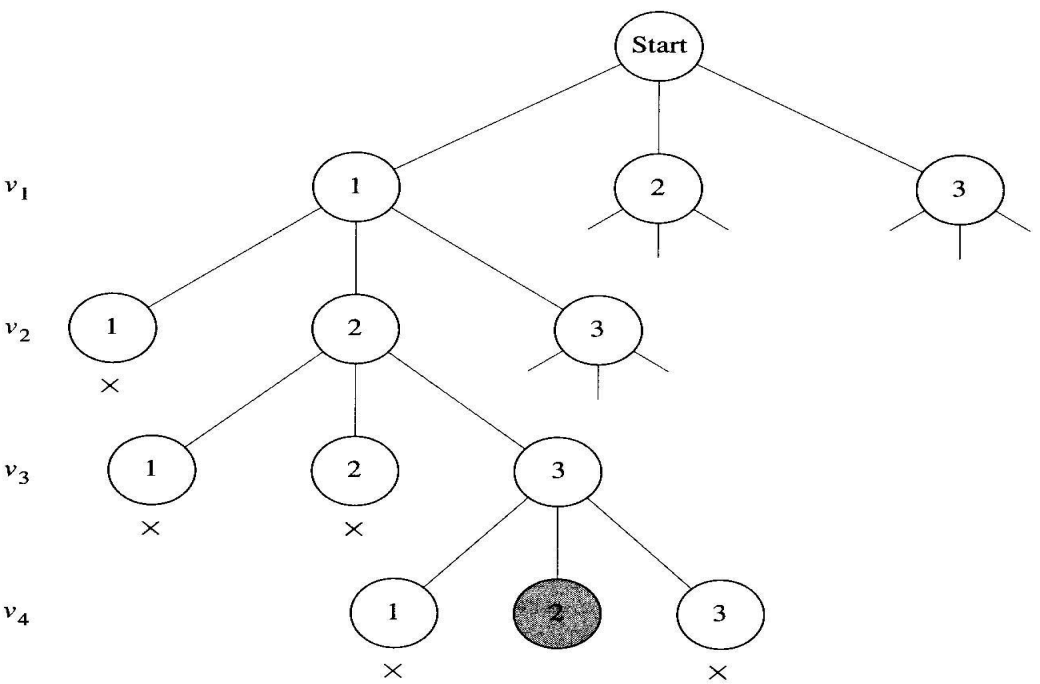
이제 모든 m값에 대한 m-coloring 문제를 푸는 알고리즘을 살펴본다. 이 그래프에 가중치가 없기 때문에 두 정점을 잇는 Edge의 존재여부에 따라서 행렬의 각 엔트리는 true나 false가 된다.
// 문제: 비방향그래프에서 m개의 색만 사용하여 인접한 정점이 같은 색이 되지 않게 정점을 색칠할 수 있는 모든 방법을 구하시오.
// 입력: 양의 정수 n과 m, 그리고 n개의 정점을 가진 비방향그래프. 그래프는 행과 열의 인덱스가 모두 1부터 n까지인 2차원 배열 W로 표현된다. 여기서 i번째 정점과 j번째 정점 사이에 Edge가 존재하면 W[i][j]는 true이고, 그렇지 않으면 false이다.
// 출력: 최대로 m개의 색을 가지고 인접한 정점이 같은 색이 되지 않게 그래프에 색칠하는 가능한 모든 경우. 출력은 인덱스가 1부터 n까지인 배열 vcolor이다. 여기서 vcolor[i] 값은 i번째 정점에 할당된 색(1부터 m사이의 정수)이다.
void m_coloring (index i) {
index color;
if(promising(i)){
if(i == n)
cout << vcolor[1] through vcolor[n];
else {
for(color = 1; color <= m; color++) { // 다음 정점에 모든 색을 시도해 본다.
vcolor[i + 1] = color;
m_coloring(i + 1);
}
}
}
}
bool promising (index i) {
index j;
bool switch;
switch = true;
j = 1;
while(j < i && switch) {
// 인접한 정점에 이 색이 이미 칠해져 있는지 점검한다.
if(W[i][j] && vcolor[i] == vcolor[j])
switch = false;
j++;
}
return switch;
}
알고리즘을 구현할 때 이 루틴들은 $n, m, W, vcolor$를 전역적으로 정의한다. m_coloring의 최상위 수준 호출은 m_coloring(0)으로 하면 된다. 이 알고리즘을 위 예제에 적용하면 다음과 같다.
이 알고리즘의 상태공간트리에 있는 마디의 개수는 $1 + m + m^2 + \cdots + m^n = \frac{m^{n + 1} - 1}{m - 1}$개 이다.
The Hamiltonian Circuits Problem
외판원 문제에서 n개의 도시 전체를 더 빨리 다녀올 수 있는 사람이 외판원 자리를 차지하게 되었다. 시간복잡도는 동적계획 알고리즘을 사용할 경우 $T(n) = (n - 1)(n - 2)2^{n - 3}$이 된다. Brute-force로 하게 된다면 n!가지 여행경로 길이를 모두 계산한다. 하지만 $n = 40$일 때 동적계획으로도 도시를 여행하는 최단 여행경로를 구하려면 엄청난 시간이 걸리게 된다.
연결된 비방향그래프에서 해밀튼 회로(Hamiltonian Circuits, 여행 경로)는 한 Vertex에서 출발하여 그래프에 있는 모든 Vertex를 각각 정확히 한 번씩만 방문하고, 다시 출발한 Vertex로 돌아오는 경로이다. 다음 예를 보자.
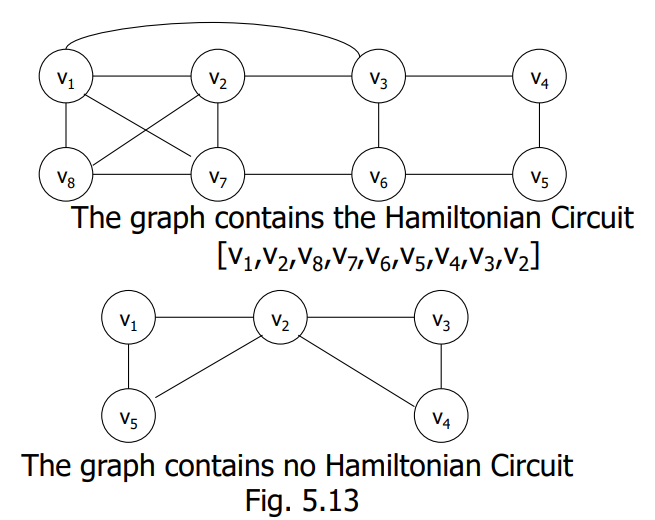
위 그래프에서는 Hamiltonian circuit $[v_1, v_2, v_8, v_7, v_6, v_5, v_4, v_3, v_1]$이 존재하고, 아래의 경우 해밀튼 회로가 존재하지 않는다.
이 문제를 풀기 위한 상태공간트리는 다음과 같다.
- 트리의 수준 0에서 출발 Vertex를 놓고, 그 Vertex를 경로의 0째 Vertex라고 부른다.
- 수준 1에서는 출발 Vertex를 제외한 각 Vertex을 출발 Vertex 다음에 오는 첫째 Vertex으로 고려한다.
- 수준 2에서는 앞에서와 같은 Vertex들을 각각 둘째 Vertex로 고려한다.
- 마지막으로 수준 $n - 1$에서 앞에서와 같은 Vertex들을 각각 $(n - 1)$째 Vertex으로 고려한다.
이 상태공간트리에서 backtracking하기 위해서 다음 사항을 고려한다.
- 경로 상의 $i$째 Vertex은 그 경로에서 $(i - 1)$째 Vertex과 반드시 인접해 있어야 한다.
- $(n - 1)$째 Vertex는 0째 Vertex(출발 Vertex)와 반드시 인접해 있어야 한다.
- $i$째 Vertex는 그 앞에 오는 $i - 1$개의 Vertex들 중 하나가 될 수 없다.
다음 알고리즘은 위의 사항을 고려하여 backtracking한다. 이 알고리즘은 $v_1$을 출발 Vertex로 고정시킨다.
// 문제: 연결된 비방향그래프에서 해밀튼 회로를 모두 구하시오.
// 입력: 양의 정수 n과 Vertex이 n개인 비방향그래프. 그래프는 2차원 배열 W로 표현한다. 이 배열의 행과 열의 인덱스는 1부터 n까지이다.
// 여기서 i째 Vertex과 j째 Vertex을 잇는 이음선이 있으면 W[i][j] 값은 true이고, 그렇지 않으면 false이다.
// 출력: 주어진 Vertex에서 출발하여 그래프상의 각 Vertex을 정확히 한 번씩 방문하고, 출발 Vertex으로 돌아오는 모든 경로.
// 각 경로의 출력은 인덱스가 0부터 n - 1까지인 인덱스의 배열 vindex이다.
// 여기서 vindex[i]는 경로상에서 i째 Vertex의 인덱스이다. 출발 Vertex의 인덱스는 vindex[0]이다.
void hamiltonian (index i) {
index j;
if(promising(i)) {
if(i == n - 1)
cout<< vindex[0] through vindex[n - 1];
else {
for(j = 2; j <= n; j++){ // 모든 Vertex의 다음 Vertex을 시도해 본다.
vindex[i + 1] = j;
hamiltonian(i + 1);
}
}
}
}
bool promising (index i) {
index j;
bool switch;
if(i == n - 1 && !W[vindex[n - 1]][vindex[0]]) // 첫째 Vertex를 마지막 Vertex와 인접
switch = false;
else if (i > 0 && !W[vindex[i - 1]][vindex[i]]) // i째 Vertex는 (i - 1)째 Vertex와 인접
switch = false;
else {
switch = true;
while(j < i && switch) { // Vertex가 이미 선택되는지를 검사
if(vindex[i] == vindex[j])
switch = false;
j++;
}
}
return switch;
}
변수 $n, W, vindex$들은 전역적으로 정의하면 hamiltonian 프로시저의 최초 호출은 $index[0] = 1;, hamiltonian(0);$이다. 이 알고리즘의 상태공간트리에서 마디의 개수는 $1 + (n - 1) + (n - 1)^2 + \cdots + (n - 1)^{n - 1} = \frac{(n - 1)^{n - 1}}{n - 2}$개 이다. 이는 지수 결과보다 더 나쁘다. 이는 몬테칼로 기술을 사용할 수 있는 조건을 만족하므로 이를 사용하여 효율을 추정할 수 있다. 해밀튼 회로는 하나만 필요하므로 첫째 회로를 찾은 후 알고리즘이 멈추게 할 수 있다.
The 0/1 Knapsack Problem
0-1 배낭 채우기 문제를 푸는 Backtracking Algorithm
이 문제에서 아이템의 집합이 있고, 각 아이템은 무게와 값어치를 가지고 있다. 무게와 값어치는 양의 정수이다. 이 문제의 목표는 총 무게 W를 초과할 수 없고 총 값어치가 최대가 되는 아이템의 집합을 구하는 것이다.
이는 Sum of subsets problem에서 사용한 것과 정확히 똑같은 상태공간트리를 가지고 이 문제를 풀 수 있다. 즉, 첫째 아이템을 넣으면 뿌리에서 왼쪽으로 가고, 뺴면 오른쪽으로 간다. 같은 방법으로 둘째 아이템을 넣으면 수준 1의 마디에서 왼쪽으로 가고, 빼면 오른쪽으로 가고, 등등 이런 식으로 계속한다. 뿌리에서 잎까지의 경로는 각각 해답 후보가 된다.
이 문제는 최적화 문제(optimization problem)라는 점에서 이 장에서 다룬 다른 문제들과 다르다. 이는 검색이 완전히 끝날 때까지 마디가 해답을 포함하고 있는지 알지 못한다는 뜻이다. 따라서 backtracking을 조금 다른 방식으로 한다. 어떤 마디까지 넣은아이템이 지금까지 최고 해답보다 값어치의 총액이 크다면, 지금까지의 최고 해답의 값을 바꾼다. 그러나 그 마디의 후손 중 한 마디에서 더 좋은 해답을 찾을 수도 있다. 그러므로 최적화 문제에서는 유망한 마디의 자식마디들을 항상 방문한다. 다음은 최적화 문제의 경우 일반 backtracking algorithm이다.
void checknode (node v) {
node u;
if(value(v)가 best보다 좋다)
best = value(v);
if(promising(v)) {
for(v의 각 자식마디 u)
checknode(u);
}
}
이 기술을 0-1 knapsack problem에 적용시켜 보자. 먼저 마디가 유망하지 않다고 알려주는 표시를 살펴본다. 마디가 유망하지 않음을 알려주는 분명한 표시는 배낭에 더 이상 아이템을 넣을 공간이 남아있지 않은 경우이다. 따라서 $weight$를 어떤 마디까지 넣은 아이템 무게의 합이라고 할 때 $weight >= W$가 성립하면 그 마디는 유망하지 않다(“유망”이란 자식마디로 더 팽창해야 함을 의미하므로, 같은 경우도 유망하지 않다).
탐욕적 방법의 고려사항을 사용하여 살펴본다. 먼저 $p_i / w_i$의 값에 따라서 큰 것부터 아이템을 정렬한다. $profit$을 그 마디까지 넣은 아이템의 값어치의 합이라 하고, $weight$는 그 아이템들의 무게의 합이라고 한다. 변수 $bound$와 $totweight$는 $profit$과 $weight$ 값으로 각각 초기화한다. 다음은 Greedy하게 아이템들을 취하는데, 그 값어치는 $bound$에 더하고 무게는 $totweight$에 더한다. 이 과정은 $totweight$가 $W$를 초과하게 되는 아이템을 집을 때까지 계속된다. 이때 남은 공간이 허용하는 무게만큼만 그 아이템의 일부분을 취하고, 그 일부분의 값어치를 bound에 더한다. 어떤 마디가 수준 $i$에 위치하고 있다고 하고, 수준 $k$에 위치한 마디는 무게의 합이 $W$가 넘어가는 마디라고 하면 다음과 같다.
- $(profit + \sum\limits_{j=i+1}^{k-1} p_j)$: 처음 $k-1$개 아이템의 값어치
- $(W - totweight)$: $k$번째 아이템에 가용한 용량
- $\frac{p_k}{w_k}$: $k$번째 아이템의 단위무게 당 값어치
$maxprofit$을 지금까지 찾은 최고 해답에서 값어치의 값이라고 하면, $bound \le maxprofit$이 성립하면 수준 $i$에서 위치한 마디는 유망하지 않다. 다음 예를 보자.
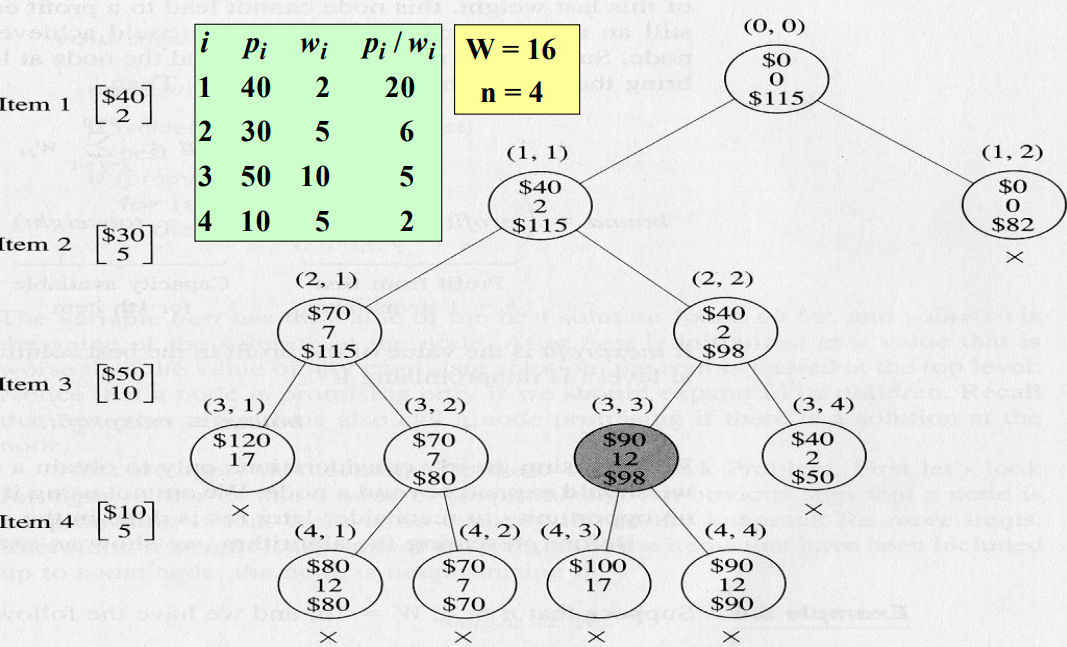
$p_i / w_i$ 값에 따라서 이미 정렬된 상태로 시작한다. 최대 이익은 음영 처리된 Vertex에서 찾을 수 있다. 이것을 찾는 과정을 살펴보자.
- $maxprofit$을 $0으로놓는다.
- Node (0, 0), 뿌리를 방문한다.
- $profit = 0$, $weight = 0$
- $2 + 5 + 10 = 17 > W = 16$이므로, 셋째 아이템을 취하면 무게의 합이 $W$를 넘는다. 따라서 $k=3$이고 $totweight = 0 + (2 + 5) = 7$, $bound = (0 + 40 + 30) + (16 - 7) \times 5 = $ $115가 된다.
- $weight < W$, $bound >maxprofit$이 성립하므로, 이 마디는 유망하다고 결정한다.
이런 과정을 거치면 음영 처리된 Vertex가 최대 이익임을 알 수 있다. 이 과정에서 가지친 공간트리에서 마디가 13개 있는 반면, 전체 트리에는 마디가 31개 있다. 이제 알고리즘을 살펴보자.
// 문제: 무게와 값어치가 주어진 n개의 아이템이 있다고 하자. 무게와 값어치는 양의 정수이다. 게다가 양의 정수 W도 주어진다. 무게의 합이 W가 넘지 못한다는 제약 하에서 총 값어치가 최대가 되는 아이템의 집합을 구하시오.
// 입력: 양의 정수 n과 W, 배열 W와 p. 인덱스의 범위는 1부터 n까지이고, 각 배열은 p[i]/w[i]값에 따라서 큰 수부터 차례로 정렬된 양의 정수를 포함한다.
// 출력: 배열 bestset. 여기서 인덱스의 범위는 1부터 n까지이고, bestset[i]의 값은 i번째 아이템이 최적의 해에 포함되어 있으면 'yes'이고, 그렇지 않으면 'no'이다.
// 최대 값어치를 나타내는 정수 maxprofit.
void knapsack(index i, int profit, int weight) {
if(weight <= W && profit > maxprofit) { // 지금까지는 이 집합이 최고이다.
maxprofit = profit;
numbest = i; // numbest를 고려한 아이템의 개수
bestset = include; // bestset을 이 해답으로 놓는다.
}
if(promising(i)) {
include[i + 1] = "yes"; // w[i+1] 포함
knapsack(i + 1, profit + p[i + 1], weight + w[i + 1]);
include[i + 1] = "no"; // w[i+1] 비포함
knapsack(i + 1, profit, weight);
}
}
bool promising(index i) {
index j, k;
int totweight;
float bound;
if(weight >= W) // 자식마디로 확장할 수 있을 때만 마디는 유망하다.
return false; // 자식마디에 쓸 공간이 남아 있어야 한다.
else {
j = i + 1;
bound = profit;
totweight =weight;
while(j <= n && totweight + w[j] <= W) { // 가능한 한 많은 아이템을 취한다.
totweight = totweight + w[j];
bound = bound + p[j];
j++;
}
k = j; // 앞 예에서 k를 썼기 때문에 k사용
if(k <= n) // k째 아이템의 일부분을 취함
bound = bound + (W - totweight) * p[k]/w[k];
return bound > maxprofit;
}
}
변수 $n, w, p, W, maxprofit, include, bestset, numberbest$는 전역적으로 정의하면, 다음 코드는 최대 수익과 그 수익을 만들어 주는 아이템의 집합을 내준다.
- numbest = 0;
- maxprofit = 0;
- Knapsack(0, 0, 0);
- cout << maxprofit; // 최대 값어치를 출력
- for(j = 1; j <= numbest; j++) // 최적이 되는 아이템의 집합을 보여준다.
- cout << bestset[i];


댓글남기기