분기한정법

Updated: June 05, 2024

분기한정(BB, Branch-and-Bound) 알고리즘은 Backtracking 알고리즘을 개선한 것이다. 분기한정 설계전략은 상태공간트리를 사용하여 문제를 푼다는 사실이 backtracking과 매우 비슷하다. 차이점으로 BB는 트리 횡단방법에 구애받지 않고, 최적화 문제를 푸는데 만 쓰인다. BB는 어떤 마디가 유망한지를 결정하기 위해서 그 마디에서 수(한계값)를 계산한다. 이 수는 그 마디 아래로 확장하여 구할 수 있는 해답 값의 한계(bound)를 나타낸다. 그 한계값이 그때까지 찾은 최고 해답 값보다 더 좋지 않으면 그 마디는 유망하지 않다(nonpromising), 그렇지 않으면 그 마디는 유망하다(promising)라고 한다.
마디가 유망한지를 결정하기 위해 한계값을 사용하는 것 외에도 유망한 마디들의 한계값을 비교하여 그 중에서 가장 좋은 한계값을 가진 마디의 자식마디를 방문한다. 이렇게 하면 미리 정한 순서대로 마디를 방법론적으로 방문하는 것보다 더 빨리 최적해에 도달할 수 있다. 이 방법을 분기한정 가지치기 최고우선검색(Best-first search with Branch-and-Bound pruning)이라고 한다. 이 방법은 분기한정 가지치기 너비우선검색(Breadth-first search with Branch-and-Bound pruning)이라고 하는 또 다른 하나의 방법론적인 접근법을 간단히 수정하여 구현할 수 있다.
먼저 너비우선검색을 알아본다. 트리의 경우 너비우선검색(Breadth-first search)은 뿌리마디를 먼저 방문하고, 다음에 수준 1의 마디를 모두 방문하고, 다음에 수준 2의 마디를 모두 방문하고, 등등 이런식으로 계속한다. 다음은 왼쪽에서 오른쪽으로 진행하는 경우 트리의 Breadth-first search를 보여준다.

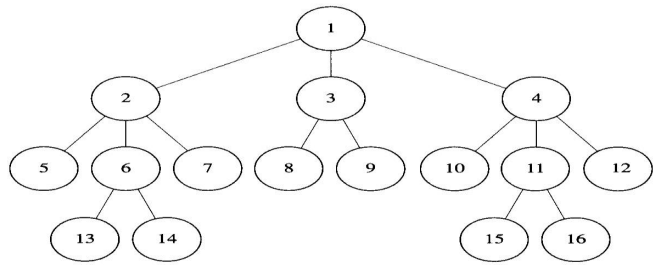
깊이우선검색과는 달리 너비우선검색을 하는 재귀 알고리즘은 작성하기 어렵다. 그러나 대기열(queue)을 사용하여 아래 알고리즘과 같은 방식으로 구현할 수 있다. enqueue라는 프로시저로 대기열의 뒤에 아이템을 붙여 넣고, dequeue라는 프로시저로 앞에서 아이템을 제거한다.

void breadth_first_tree_search(tree T) {
    queue_of_node Q;
    node u, v;

    initialize(Q);  // Q를 빈 대기열로 초기화
    v = root of T;
    visit v;
    enqueue(Q, v);

    while(!empty(Q)) {
        dequeue(Q, v);

        for(each child u of v) {
            visit u;
            enqueue(Q, u);
        }
    }
}

분기한정을 0-1 배낭 채우기 문제로 설명하기

먼저 node 구조체를 정해준다.

struct node {
    int level;  // use level instead of i in BB
    int profit, weight;
}

다음 예에서 다음과 같은 사례를 사용한다.

weight와 profit은 그 마디에 오기까지 포함되었던 아이템의 총 무게와 총 이익으로 한다. 마디가 유망한지를 결정하기 위해서 totweight와 bound를 weight와 profit으로 각각 초기화하고, 그 다음 totweight가 W를 초과하게 하는 아이템에 도달할 때까지 Greedy하게 아이템을 취하여 그 무게와 이익을 totweight와 bound에 각각 더한다. 배낭에 넣을 수 있는 만큼만 그 아이템의 일부분을 취하여 그 부분의 weight를 totweight에 더한다. 이런식으로 bound는 그 마디에서 확장하여 얻을 수 있는 이익의 상한이 된다. 만약 그 마디가 수준 $i$에 위치하고 있고, 수준 $k$에 위치한 마디는 무게의 합이 $W$가 넘어가는 마디라고 하면 다음과 같은 식을 얻는다.

$totweight = weight + \sum\limits_{j=i+1}^{k-1} w_j$ $bound = (profit + \sum\limits_{j=i+1}^{k-1} p_j) + (W - totweight) \times \frac{p_k}{w_k}$

지금까지 찾은 최고 해답에서의 값인 maxprofit보다 이 한계값이 작거나 같으면($bound \le maxprofit$) 그 마디는 유망하지 않고 $weight \ge W$가 성립해도 유망하지 않다.
분기한정 알고리즘은 어떤 마디에서 확장 여부를 결정할 때 지금까지 구한 답 중에서 가장 좋은 값보다 한계값이 더 좋은지 검사한다. 따라서 가중치가 W보다 작지 않아서 마디가 유망하지 않게 되면 한계값을 0으로 놓는다. 이런 식으로 하면 한계값이 지금까지 구한 답보다 더 좋을 수 없다고 보증할 수 있다.

Breadth-First Search with Branch-and-Bound Pruning

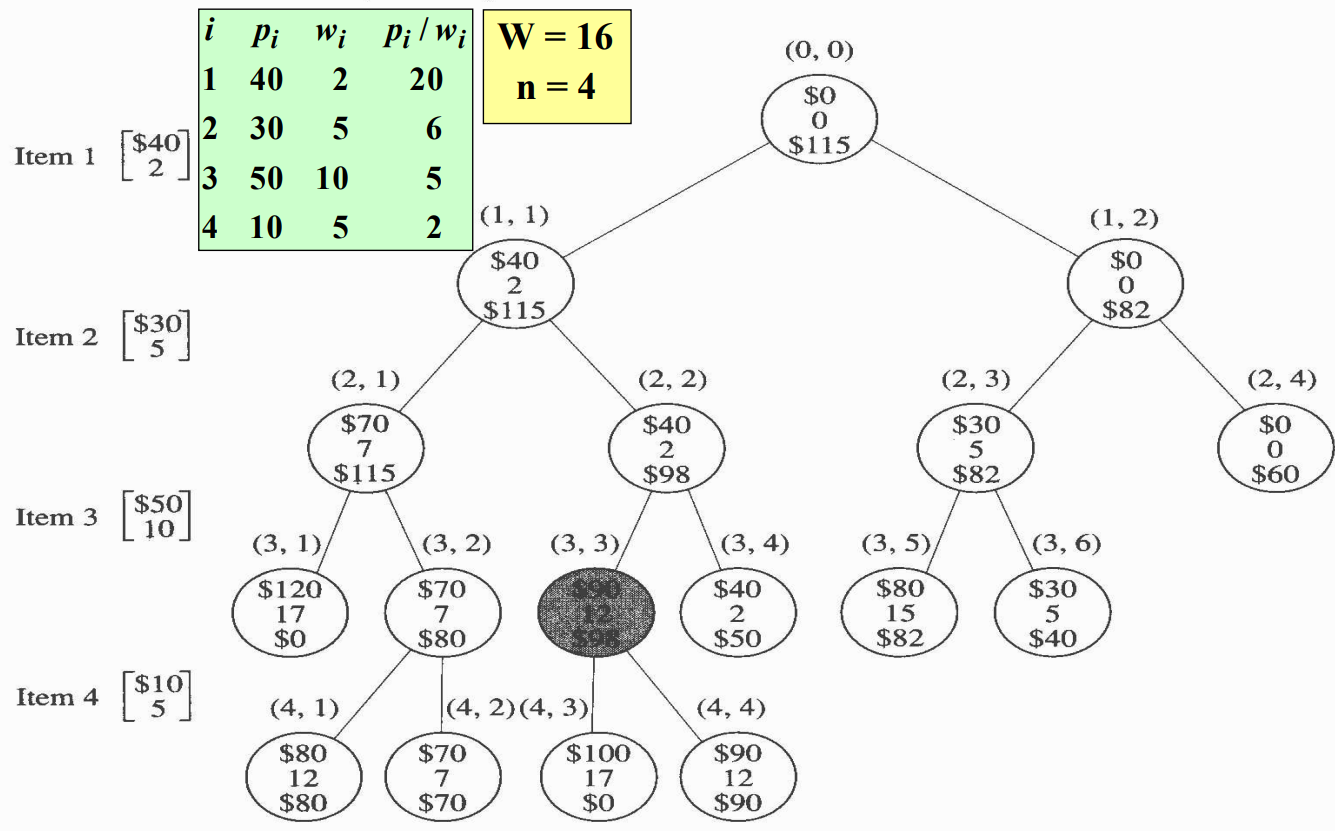
이 문제를 가지고 DFS를 할 때 마디 $(1, 2)$가 유망하지 않음을 알아냈고, 그 마디 이상으로는 확장하지 않았다. 그러나 BFS의 경우 이 마디는 3번째 마디가 된다. 이 마디를 방문할 때 maxprofit의 값은 40이고, 이 시점에 한계값 82가 maxprofit 값을 넘기 때문에 그 마디 이후에도 계속 확장한다.
분기한정 가지치기 단순 너비우선검색에서는 어떤 마디의 자식마디를 방문해야 할지는 그 마디를 방문할 때 결정한다. 즉, 자식마디로 뻗는 가지는 그 마디를 방문할 때 친다. 따라서 마디 $(2, 3)$을 방문할 때 그 마디의 한계값은 82인 반면 maxprofit 값은 70밖에 되지 않기 때문에 그 자식마디를 방문하기로 결정한다. DFS와는 달리 BFS에서는 maxprofit 값이 자식마디를 실제로 방문하는 때에 변해버릴 수 있다. 이렇게 되면 이 자식 마디를 검사하는 시간을 낭비하게 된 셈이다.
분기한정 가지치기 BFS를 하는 일반 알고리즘을 살펴본다. 이 문제의 파라미터는 이 알고리즘의 실제 입력이고, 상태공간트리 T를 구한다.

void breadth_first_branch_and_bound (state_space_tree T, number& best) {
  queue_of_node Q;
  node u, v;

  initialize(Q);  // Q는 빈 대기열로 초기화
  v = root of T;  // 뿌리마디를 방문

  enqueue(Q, v);
  best = value(v);

  while(! empty(Q)) {
    dequeue(Q, v);

    for(each child u of v) {  // 각 자식마디를 방문
      if(value(u)가 best보다 좋다)
        best = value(u);
      if(bound(u)가 best보다 좋다)
        enqueue(Q, u);
        }
    }
}

이 알고리즘에서는 마디의 한계값이 당시 최고 해답의 값보다 좋은 경우에만 그 마디에서 계속 확장한다. 당시 최고 해답의 값(변수 best)은 뿌리 마디에서의 해답의 값으로 초기화한다. 경우에 따라서 해답을 얻기 위해서 상태공간트리의 leaf까지 도달하기도 해야 하기 때문에 뿌리마디에 해답이 없는 경우도 있다. 그런 경우에는 best값을 어떤 해답보다도 나쁜 값으로 초기화한다. breadth_first_branch_and_bound를 어디에 사용하는가에 따라서 함수 bound와 value는 달라진다.
이제 0-1 배낭 채우기 문제를 푸는 알고리즘을 살펴본다.

// 문제: 무게와 이익이 주어진 n개의 아이템, 양의 정수 W가 있다고 하자. 무게와 이익은 양의 정수이다.
// 무게의 합이 W가 넘지 못한다는 제약 하에서 총 이익이 최대가 되는 아이템의 집합을 구한다.
// 입력: 양의 정수 n과 W, 양의 정수 배열 w와 p. 인덱스의 범위는 1부터 n까지.
// 각 배열은 p[i]/w[i]값에 따라서 큰 수부터 차례로 정렬되어 있다.
// 출력: 최적의 집합에 있는 이익의 합을 나타내는 정수 maxprofit.
void knapsack2 (int n, const int p[], const int w[], int W, int& maxprofit) {
  queue_of_node Q;
  node u, v;

  initialize(Q);  // Q를 반 대기열로 초기화
  v.level = 0; v.profit = 0; v.weight = 0;  // v가 뿌리마디가 되게 초기화
  maxprofit = 0;
  enqueue(Q, v);

  while(!empty(Q)) {
    dequeue(Q, v);
    u.level = v.level + 1;  // u를 v의 자식마디로 놓음
    // u를 다음 아이템을 포함하는 자식마디로 놓음
    u.weight = v.weight + w[u.level]; 
    u.profit = v.profit + p[u.level];

    if(u.weight <= W && u.profit > maxprofit)
      maxprofit = u.profit;
    if(bound(u) > maxprofit)
      enqueue(Q, u);
    // u를 다음 아이템을 포함하지 않는 자식마디로 놓음
    u.weight = v.weight;
    u.profit = v.profit;

    if(bound(u) > maxprofit)
      enqueue(Q, u);
  }
}

float bound(node u) {
  index j, k;
  int totweight;
  float result;

  if(u.weight >= W)
    return 0;
  else {
    result = u.profit;
    j = u.level + 1;
    totweight = u.weight;

    while(j <= n && totweight + w[j] <= W) {  // 가능한 한 많은 아이템을 취한다.
      totweight = totweight + w[j];
      result = result + p[j];
      j++;
    }
    k = j;
    if(k <= n)
      result = result + (W - totweight) * p[k]/w[k];
    return result;
  }
}

함수 bound는 5장의 함수 promising과 본질적으로 같다. 차이는 분기한정 알고리즘을 만들기 위한 지침에 따라서 bound를 작성했고, 따라서 bound는 정수를 넘겨주는 반면, 함수 promising은 backtracking 알고리즘의 지침을 따라서 작성했으므로 boolean 값을 넘겨준다.
위 알고리즘으로 아이템의 최적 집합이 만들어지지 않는다. 단지 최적의 집합에 속한 이익의 합만 구한다. 알고리즘은 최적의 집합을 만들어 내도록 수정할 수 있다.

각 마디에서 그 마디에 이르기까지 포함된 아이템의 집합인 items라는 변수를 저장하고, 당시 최고 아이템의 집합을 타나내는 변수 bestitems를 유지한다.
maxprofit을 u.profit과 같게 놓으면 bestitems도 u.items와 같게 놓는다.

Best-First Search with Branch-and-Bound Pruning

일반적으로 BFS 전략은 DFS보다 좋은 점이 없다. 그러나 마디의 유망성 여부를 결정하는 것 이외에 추가적인 용도로 한계값을 사용하면 검색을 향상시킬 수 있다. 주어진 어떤 마디의 모든 자식마디를 방문한 후 유망하면서 확장하지 않은 마디들을 모두 살펴보고 그 중에서 가장 좋은 마디를 우선적으로 확장한다. 지금까지 찾은 최고 해답보다 그 한계값이 더 좋다면 그 마디는 유망하다. 미리 정해 놓은 순서대로 무작정 검색을 진행하는 것보다 이런 식으로 하면 최적해를 더 빨리 찾게 된다. 다음 예를 보자.

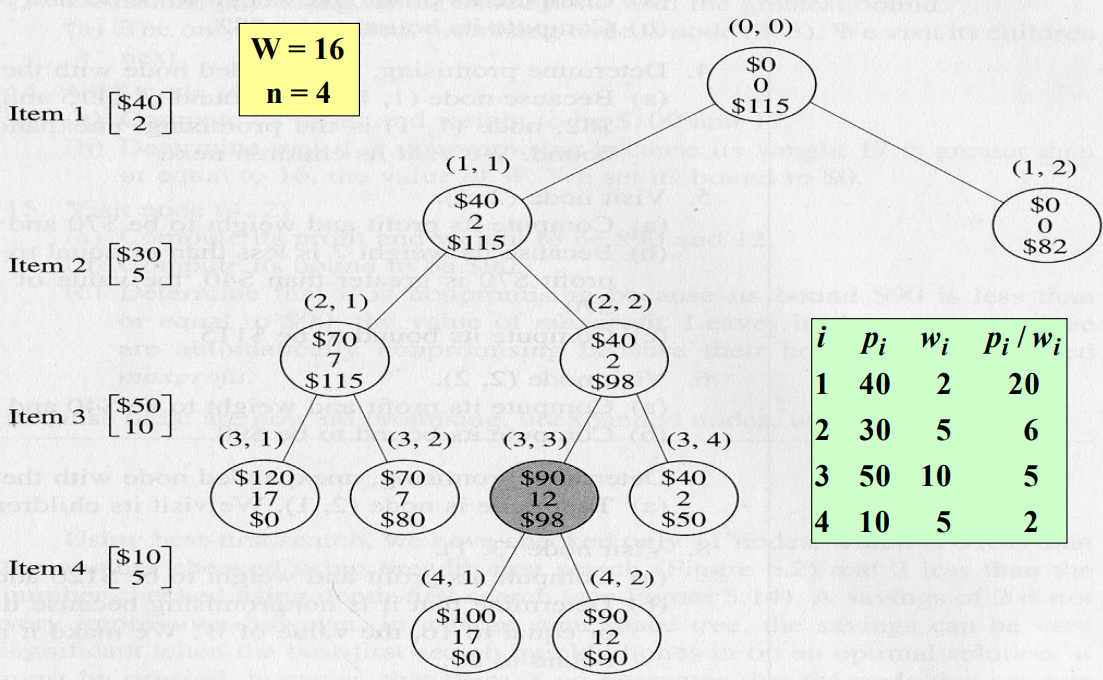
마디 $(0, 0)$를 방문한다.
- 이익과 무게를 각각 0으로 놓는다.
- 한계값을 계산하면, 115가 된다.
- maxprofit을 0으로 놓는다.
마디 $(1, 1)$를 방문한다.
- 이익과 무게는 각각 40, 2가 된다.
- 무게 2는 W의 값 16보다 작거나 같고, 이익 40은 0보다 크므로, maxprofit의 값을 40으로 놓는다.
- 한계값을 계산하면 115가 된다.
마디 $(1, 2)$를 방문한다.
- 이익과 무게는 각각 0이 된다.
- 한계값을 계산하면, 82가 된다.
아직 확장하지 않은 마디 중에서 가장 큰 한계값을 가진 유망한 마디를 구한다.
- 마디 $(1, 1)$은 한계값이 115이고, 마디 $(1, 2)$는 한계값이 82이므로 마디 $(1, 1)$이 한계값이 가장 크면서 유망하고, 확장하지 않은 마디이다.
- 그 마디의 자식마디를 다음에 방문한다.

위와 같은 방식으로 검색을 진행하면 11개 마디만 검사한다. 이는 BFS보다 검사한 마다의 수가 6개 작고, DFS보다 2개 작다.
최고우선검색은 BFS를 조금 변형시켜서 구현하면 된다. queue를 사용하는 대신, priority queue를 사용한다. 우선순위 대기열(priority queue)에서 우선순위가 높은 구성요소를 항상 먼저 제거한다. Best-Fitst Search를 하면 우선순위가 높은 구성요소가 최고의 한계값을 가진 마디가 된다. Priority queue는 linked list로 구현할 수 있지만 힙(heap)으로 더 효율적으로 구현할 수 있다.

최고우선검색의 일반 알고리즘은 다음과 같다. $insert(PQ, v)$는 priority queue PQ에 v를 추가시키는 프로시저이고, $remove(PQ, v)$는 최고 한계값을 가진 마디를 제거하고, 그 값을 v에 대입한다.

void best_first_branch_and_bound (state_space_tree T, number& best) {
  priority_queue_of_node PQ;
  node u, v;

  initialize(PQ); // PQ를 빈 대기열로 초기화
  v = root of T;
  best = value(v);
  insert(PQ, v);
  
  while(! empty(PQ)) {  // 최고 한계값을 가진 마디를 제거
    remove(PQ, v);

    if(bound(v) is better than best) {  // 마디가 아직 유망한지 점검
      for(each child u of v) {
        if(value(u) is better than best)
          best = value(u);
        if(bound(u) is better than best)
          insert(PQ, u);
      }
    }
  }
}

대기열 대신에 우선순위 대기열을 사용하는 이외에 우선순위 대기열에서 마디를 제거한 후 마디의 한계값이 best보다 아직 좋은지를 결정하는 검사를 추가한다. 어떤 마디를 방문한 후 그 마디가 유망하지 않게 되는지 이렇게 결정한다.
다음은 0-1 배낭 채우기 문제를 푸는 세부 알고리즘이다. 마디를 추가하고 제거할 때 그리고 우선순위 대기열에서 마디의 순서를 매기기 위해서 한계값이 필요하므로, 그 한계값을 마디에 기록한다. 마디의 타입은 다음과 같다.

struct node {
  int level, profit, weight;
  float bound;
}

이제 알고리즘을 살펴본다.

// 문제: 무게와 이익이 주어진 n개의 아이템이 있다. 무게와 이익은 양의 정수이다. 게다가 양의 정수 W도 주어진다.
// 무게의 합이 W가 넘지 못한다는 제약 하에서 총 이익이 최대가 되는 아이템의 집합을 구한다.
// 입력: 양의 정수 n과 W, 양의 정수 배열 w와 p, 인덱스의 범위는 1부터 n까지이다.
// 각 배열은 p[i]/w[i] 값에 따라서 큰 수부터 차례로 정렬되어 있다.
// 출력: 최적의 집합에 있는 이익의 합을 나타내는 정수 maxprofit.
void knapsack3 (int n, const int p[], const int w[], int W, int& maxprofit) {
  priority_queue_of_node PQ;
  node u, v;

  initialize(PQ); // PQ를 빈 대기열로 초기화
  v.level = 0; v.profit = 0; v.weight = 0;  // v가 뿌리가 되게 초기화
  maxprofit = 0;
  v.bound = bound(v);
  insert(PQ, v);

  while(! empty(PQ)) { 
    remove(PQ, v);  // 최고의 한계값을 가진 마디 제거

    if(v.bound > maxprofit) { // 마디가 아직 유망한지 검사
      u.level = v.level + 1;
      u.weight = v.weight + w[u.level];
      u.profit = v.profit + w[u.level];

      if(u.weight <= W && u.profit > maxprofit)
        maxprofit = u.profit;
      u.bound = bound(u);

      if(u.bound > maxprofit)
        insert(PQ, u);
      u.weight = v.weight;
      u.profit = v.profit;

      if(u.bound > maxprofit) {
        insert(PQ, u);
      }
    }
  }
}

외판원 문제

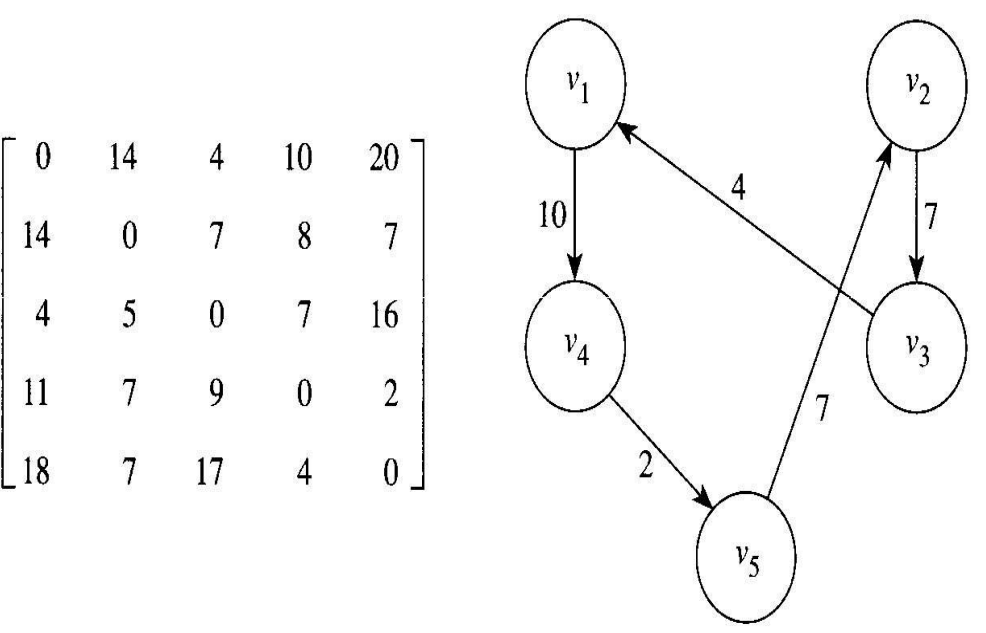
방향그래프의 주어진 정점에서 출발하여 그래프에 있는 각 정점을 정확하게 한 번씩만 방문하고, 출발한 정점으로 돌아오는 최단경로를 찾는 것이 이 문제의 목표이다. 그러한 경로를 최적경로(optimal tour)라고 한다. 출발정점이 어디인지는 상관이 었으므로 출발하는 정점은 단순히 첫째 정점이 될 수 있다. 다음은 5개의 Vertex가 모두 서로 연결되어 있는 그래프를 표현해 놓은 인접행렬과 그 그래프의 최적 여행경로가 있다.

이 문제를 풀기 위하여 상태공간나무는 출발 정점을 제외한 각 Vertex는 수준 1에 속한 첫째 정점으로 채택하고, 출발 정점과 수준 1에서 선택한 정점을 제외한 각 정점은 수준 2에 속한 둘쩨 정점으로 채택하고, 등등 이런 식으로 계속해서 구축한다. 다음은 상태공간트리의 일부분을 보여준다.

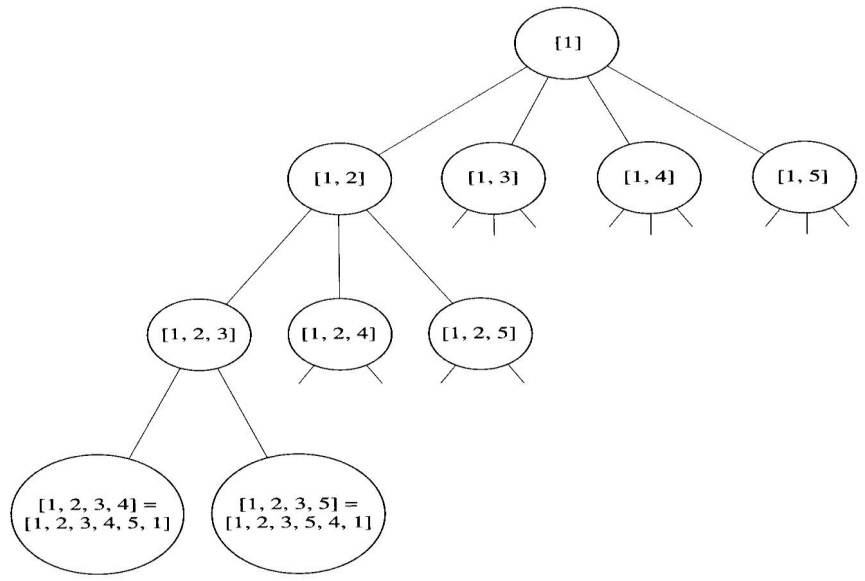
각 leaf는 여행경로를 나타낸다. 따라서 최적 여행경로가 포함된 leaf를 찾아야 한다. 마디에 기록된 경로에 정점이 4개 있으면 다섯째 정점은 선택의 여지없이 하나뿐이기 때문에 트리 구축을 멈춘다.
최고우선검색을 사용하기 위해서 각 마디의 한계값을 구할 수 있어야 한다. 이 문제이서는 주어진 마디에서부터 뻗어나가서 얻을 수 있는 여행경로 길이의 하한을 구할 필요가 있다. 그리고 당시 최소경로길이보다 한계값이 작은 경우에 그 마디를 유망하다고 한다. 먼저 한계값을 구해본다.

Vertex를 떠날 때 선택한 Edge의 길이는 그 Vertex에서 나오는 가장 짧은 Edge의 길이만큼은 최소한 길다.
정점 $v_1$을 떠나는 비용(선택한 이음선의 길이)의 하한은 인접행렬의 첫째 행에서 0이 아닌 모든 값 중에서 최소값이 된다.
$v_2$를 떠나는 비용의 하한은 둘째 행에서 0이 아닌 모든 값 중에서 최소값이 되고, 등등 이런 식으로 계속하면 된다.
5개의 정점을 떠나는 비용의 하한은 다음과 같다.
- $v_1 minimum(14, 4, 10, 20) = 4$
- $v_2 minimum(14, 7, 8, 7) = 7$
- $v_3 minimum(4, 5, 7, 16) = 4$
- $v_4 minimum(11, 7, 9, 2) = 2$
- $v_5 minimum(18, 7, 17, 4) = 4$

각 여행경로는 정점을 정확히 각각 한 번씩 떠나야 하기 때문에 여행경로 길이의 하한은 이 최소값들의 합이다. 따라서 여행경로의 길이의 하한은 $4 + 7 + 4 + 2 + 4 = 21$이다. 이 길이의 여행경로가 있다는 말은 아니다. 이보다 더 짧은 여행경로가 있을 수 없다는 말이다.
Edge $[1, 2]$를 포함한 마디를 방문했다고 가정하자. 이 경우 이미 $v_2$를 여행경로의 둘째 정점으로 선택하였고, $v_2$까지 가는데 든 비용은 14가 된다. 따라서 이 마디 이후에 확장하여 구한 여행경로의 정점들은 떠나는 비용의 하한은 다음과 같이 구한다.

$v_1 = 14$
$v_2 minimum(7, 8, 7) = 7$
- $v_2$에서 $v_1$으로 돌아갈 수 없기 때문에 $v_1$으로 가는 이음선을 포함하지 않는다.
$v_3 minimum(4, 7, 16) = 4$
- $v_2$는 이미 들렸기 때문에 $v_2$로 가는 이음선을 포함하지 않는다.
$v_4 minimum(11, 9, 2) = 2$
$v_5 minimum(18, 17, 4) = 4$
$14 + 7 + 4 + 2 + 4 = 31$

$[1, 2, 3]$을 포함하고 있는 마디를 방문했다고 가정하자. $v_2$를 둘째 정점으로, $v_3$를 셋째 정점으로 하기로 이미 정했다. 이 마디 이후에 확장하여 구한 여행경로는 정점들을 떠나는 비용의 하한을 가진다.

$v_1 = 14$
$v_2 = 7$
$v_3 minimum(7, 16) = 7$
$v_4 minimum(11, 2) = 2$
$v_3 minimum(18, 4) = 4$
$14 + 7 + 7 + 2 + 4 = 34$

이제 한 예를 보자.

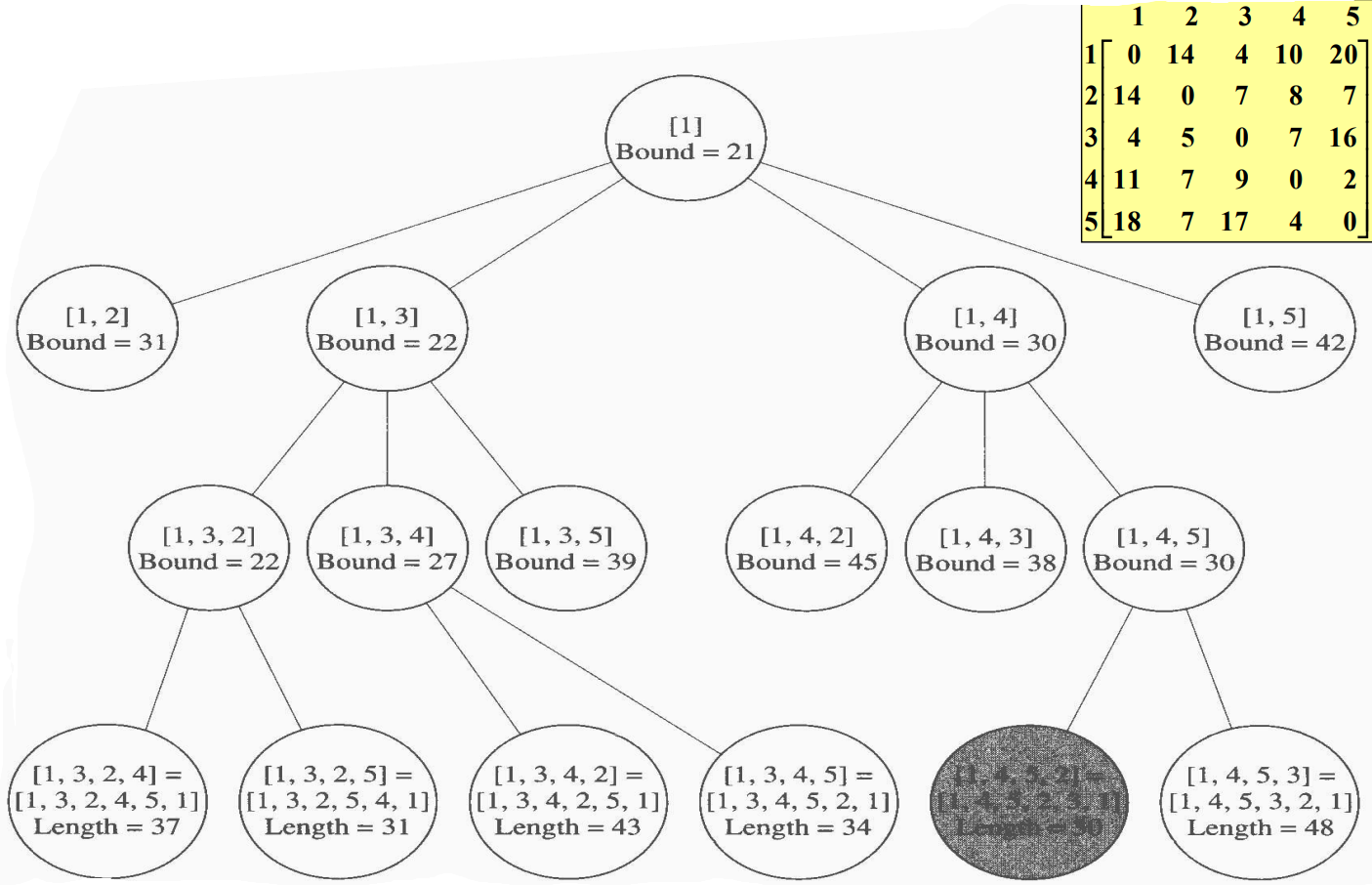
$[1]$을 포함하는 마디를 방문한다.
- $Bound = 21$
- $minlength = \infty$
$[1, 2]$를 포함하는 마디를 방문한다.
- $Bound = 31$
$[1, 3]$를 포함하는 마디를 방문한다.
- $Bound = 22$
$[1, 4]$를 포함하는 마디를 방문한다.
- $Bound = 30$
$[1, 5]$를 포함하는 마디를 방문한다.
- $Bound = 42$
한계값이 가징 작은 유망하고 확장하지 않은 마디를 결정한다.
- $[1, 3]$부터 방문한다.
위과 같은 방식으로 $[1, 3, 2, 4]$를 포함하는 마디를 방문한다.
- 이 마디는 leaf이므로, 여행경로의 길이를 계산하면 37이 된다.
- 길이 37은 $minlength$보다 작으므로, $minlength = 37$로 놓는다.
- $[1, 5]$와 $[1, 3, 5]$를 포함하는 마디들은 그들의 한계값 42와 39가 $minlength$보다 크거나 같기 때문에 유망하지 않게 된다.
$[1, 3, 2, 5]$를 포함하는 마디를 방문한다.
- 이 마디는 leaf이므로, 여행경로의 길이를 계산하면 31이 된다.
- 길이 31은 $minlength$보다 작으므로, $minlength = 31$로 놓는다.
- $[1, 2]$를 포함하는 마디들은 그들의 한계값 31이 $minlength$보다 크거나 같기 때문에 유망하지 않게 된다.
한계값이 가장 작은 유망하고 확장하지 않은 마디를 결정한다.
- $[1, 4]$부터 방문한다.

위과 같은 방식으로 계속 진행하면 $[1, 4, 5, 2, 3, 1]$이 최적 여행경로이고, 최적 여행경로의 길이는 30이다. 이와 같은 방식으로 전체 마디의 개수 41개$(1 + 4 + 4 \times 3 + 4\times3\times2)$를 17개로 줄였다.
알고리즘을 구현할 때 다음과 같은 데이터타입을 사용한다.

struct node {
  int level;  // 트리에서 마디의 수준
  order_set path;
  number bound;
}

알고리즘은 다음과 같다.

// 문졔: 가중치포함 방향그래프에서 최적일주여행길을 결정하시오. 가중치는 음이 아닌 정수이다.
// 입력: 가중치포함 방향그래프, n(그래프에서 정점의 개수). 그래프는 2차원 배열 W로 표현한다.
// 출력: 변수 minlength(최적일주여행딜의 길이), 변수 opttour(최적 여행경로)
void travel2(int n, const number W[][], ordered_set& opttour, number& minlength) {
  priority_queue_of_node PQ;
  node u, v;

  initialize(PQ); // PQ를 빈 대기열로 초기화
  v.level = 0; v.path = [1]; v.bound = bound(v);  // 첫째 정점을 출발정점으로 놓음
  minlength = ∞;
  insert(PQ, v);
  
  while(! empty(PQ)) {
    remove(PQ, v);

    if(v.bound < minlength) {
      u.level = v.level + 1;

      for(all i such that 2 <= i <= n && i is not in v.path) {
        u.path = v.path;
        put i at the end of u.path;

        if(u.level == n - 2) {  // 다음 정점에서 여행을 마치는지 검사
          put index of only vertex not in u.path at the end of u.path;
          put 1 at the end of u.path; // 첫째 정점을 마지막 정점으로 둠

          if(length(u) < minlength) {
            minlength = length(u);  // 함수 length는 여행경로의 길이를 계산
            opttour = u.path;
          }
        }
        else {
          u.bound = bound(u);

          if(u.bound < minlength)
            insert(PQ, u);
        }
      }
    }
  }
}
// 함수 bound와 length 작성

Twitter Facebook LinkedIn

MyeongWoo

분기한정법

분기한정을 0-1 배낭 채우기 문제로 설명하기

Breadth-First Search with Branch-and-Bound Pruning

Best-First Search with Branch-and-Bound Pruning

외판원 문제

공유하기

댓글남기기

참고

8장 인터페이스

7장 상속

6장 클래스

5장 참조 타입