계산복잡도와 다루기 힘든 정도: NP 이론의 소개
Updated:
효율적인 알고리즘을 만들기 불가능한 문제를 “다루기 힘든(intractable) 문제”라고 한다.
다루기 힘든 정도
다차시간 알고리즘(polynomial-time algorithm)은 최악 시간복잡도의 상한이 입력크기의 다항식 함수가 되는 알고리즘이다. 즉, n이 입력크기이면, $W(n) \in O(p(n))$을 만족하는 다항식(polynomial) &p(n)$이 존재한다. 다음 예를 보면, 위 최악 시간복잡도를 가진 알고리즘은 모두 다차시간이지만, 아래에 있는 최악 시간복잡도를 가진 알고리즘은 다차시간이 아니다.
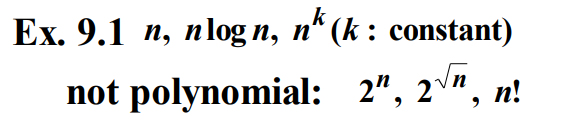
컴퓨터과학에서 어떤 문제를 다차시간 알고리즘으로 풀 수 없으면, 그 문제를 다루기힘들다(intractable)라고 한다. 다루기 힘든 정도는 문제를 푸는 어떤 특정 알고리즘의 성질이 아니라 문제의 성질이라는 사실을 알아야 한다. 다루기 힘든 문제가 되려면 그 문제를 푸는 다차시간 알고리즘이 없어야 한다.
입력크기: 재고
알고리즘에서 보통 $n$을 입력크기로 보았다. 그러나 $n$이 무조건 알고리즘의 입력크기가 되는 건 아니다. 다음 양의 정수 $n$이 소수인지 검사하는 알고리즘을 보자.
bool prime(int n) {
int i; bool switch;
switch = true;
i = 2;
while(switch && i <= ⌊ n^{1/2} ⌋) {
if(n % i == 0)
switch = false;
else
i++;
}
return switch;
}
이 알고리즘에서 while 루프의 실행 횟수는 $\theta (n^{1/2})$이다. 파라미터 n이 알고리즘의 입력이긴하지만, 입력크기라고 할 수는 없다. 즉, n 값은 입력 사례일 뿐이다. 입력을 작성하는데 필요한 문자를 세어보기 위해서 어떻게 부호화(encode)가 되는지 알 필요가 있다. 예를 들어, 컴퓨터에서 사용하는 이진수로 부호화가 있다.
“합당한(reasonable)” 부호화 방법을 쓰기만 하면, 어떤 부호화 방법을 사용하는지는 알고리즘이 다차시간인지 결정하는데 영향을 미치지 않는다. “합당성”을 만족할 만한 정의가 정식으로 존재하는 것 같지는 않지만, 대부분 알고리즘에서 무엇이 합당한지에 대해서 보통 의견일치를 본다.
입력크기를 정확하게 따지면 알고리즘이 다차시간으로 남아있을까를 증명해보자. 입력크기를 정확하게 따지기 전에 최악 시간복잡도를 정확하게 따져야 한다. 알고리즘의 최악 시간복잡도 $W(s)$는 입력크기 $s$에 대하여 그 알고리즘이 실행한 단위연산의 최대 개수이다. 단위연산은 비교연산 또는 저장연산으로 정한다. 앞 정의에 따르면, 알고리즘이 실행한 단위연산의 개수를 모두 세어야 한다. 책의 과정을 살펴보면, 입력크기를 정확히 따지면 교환정렬이 다차시간을 유지함을 볼 수 있다. 부정확한 입력크기를 사용하여 다차시간임을 확인한 알고리즘에 대해서도 비슷한 결과가 나온다. n이 입력 데이터 크기를 재는 척도일 때 단순히 n을 입력크기로 해도 빋을만한 시간복잡도를 알아낼 수 있음을 알았다. 따라서 n을 그대로 입력크기로 사용해도 문제없다.
하지만 소수검사 알고리즘으로 돌아가면, 단위연산의 총 개수는 최소한 루프의 실행 횟수와 같으므로 시간복잡도는 다차시간이 아니다. 소수검사 알고리즘 같은 알고리즘에서 n을 입력의 절대크기(magnitude)라고 한다. 절대크기로 시간복잡도가 다차시간이지만 크기로는 다차시간이 아닌 다른 알고리즘도 볼 수 있다. n번째 피보나찌 항을 계산하는 알고리즘의 시간복잡도는 $\theta (n)$이다. n이 입력의 절대크기이고, lg n이 입력크기이므로 알고리즘의 시간복잡도는 절대크기로 1차시간이지만, 크기로는 지수시간이다. 0-1 Knapsack문제에 대한 동적계획 알고리즘의 시간복잡도는 $\theta (nW)$이다. 이 알고리즘에서 n은 입력 아이템의 개수이므로 크기를 재는 척도이다. 그러나 W는 배낭의 최대용량이므로 절대크기가 되고, lg W은 W의 크기를 재는 척도이다. 이 알고리즘의 시간복잡도는 절대크기와 크기로 다차시간이지만 크기만 가지고는 지수시간이다.
최악 시간복잡도의 상한이 크기와 절대크기로 모두 다차시간이 되는 알고리즘을 의사다차시간(pseudopolynomial-time)이라 한다. 이러한 알고리즘은 지나치게 큰 수인 사례를 처리할 때만 비효율적이므로 꽤 유용하게 쓸 수 있는 경우가 종종 있다. 예를들어, 0-1 Knapsack문제에서 W가 지나치게 크지 않은 경우 문제없이 쓸 수 있다.
문제의 3가지 일반적인 분류
다루기 힘든 정도(intractability)로 분류한 문제의 세 가지 일반적인 카테고리를 알아본다.
다차시간 알고리즘을 찾은 문제
다차시간 알고리즘을 찾은 문제는 모두 이 카테고리에 속한다.
다루기 힘들다고 증명된 문제
이 카테고리에 속하는 문제는 두 가지 종류가 있다.
- 지수이상 크기의 출력을 요구하는 문제
- Hamiltonian circuits: $(n - 1)$!
- 이 문제를 푸는 알고리즘은 해밀톤 회로를 모두 출력해야 하는데, 이는 현실적이지 않다. 하지만, 하나의 해답만 출력하도록 이 알고리즘을 수정하기는 쉽다. 이는 다루기 힘든 문제가 아니다.
- Hamiltonian circuits: $(n - 1)$!
- 요구가 현실적이고(지수시간 이상 크기의 출력을 요구하지 않고), 문제를 다차시간에 풀 수 없다고 증명할 수 있는 경우: 이는 별로 존재하지 않다.
- 진위판별불가능(undecidable) 문제: 푸는 알고리즘이 없다고 증명할 수 있는 문제
- 멈춤 검사 문제(Halting Problem): 임의의 알고리즘과 임의의 입력을 받아서 받은 알고리즘에 받은 입력을 적용했을 때 알고리즘이 멈추는지를 판별하는 문제이다.
- 진위판별 문제(Decision problem): 항상 “예” 또는 “아니오”로만 대답한다. 문제의 요구 출력 크기는 분명히 적당한다.
- 프레스버거 산술문제(Presburger Arithmetic)
- 진위판별불가능(undecidable) 문제: 푸는 알고리즘이 없다고 증명할 수 있는 문제
지금까지 다루기 힘들다고 증명된 문제는 모두 NP집합에 속하지 않는다고 증명되었다. 그러나 다루기 힘들것처럼 보이는 문제는 대부분 NP집합에 속한다.
다루기 힘들다고 증명되지고 않았고, 다차시간 알고리즘도 찾지 못한 문제
다차시간 알고리즘을 찾지 못했지만, 그렇다고 다차시간 알고리즘이 불가능하다고 증명하지도 못한 문제는 모두 이 카테고리에 속한다. 이러한 문제는 많이 있다. 예를 들어, 0-1 Knapsack, TSP, sum-of-subsets 등등이 있다. 즉, 사례를 임의의 제한된 부분집합에서 취할 때 단위연산을 수행하는 횟수의 한계를 정하는 n에 대한 다항식(polynimial)이 존재한다. 그러나 모든 사례에 대하여 다항식이 존재하는 것은 아니다. 이를 보여주기 위해서 단위연산을 수행하는 횟수의 한계를 정하는 n에 대한 다항식이 없는 무한개의 사례들을 찾기만 하면 된다.
NP 이론
처음부터 문제를 진위판별 문제로만 제한하면 이론을 전개하기가 훨씬 더 쉽다. 진위판별 문제에 대한 해답은 단순히 “예” 또는 “아니오” 중 하나이다. 최적화 문제란 답이 최적해라는 말인데, 최적화 문제는 모두 각각에 대응되는 진위판별 문제가 존재한다.
- 외판원 문제(TSDP): 임의의 양수 d가 주어지고, 총 거리가 d보다 길지 않은 여행경로가 있는지 판별하는 문제이다. 이 문제는 최적화 문제의 파라미터에다가 추가로 d를 파라미터로 사용한다.
- 0-1 Knapsack: 임의의 가치액수 P가 주어지고, 총 무게가 W가 넘지 않으면서 총 수익이 최소한 P가 되도록 배낭을 채울 수 있는지 판별하는 문제이다. 이 문제는 0-1 Knapsack 문제의 파라미터에대가 추가로 P를 파라미터로 사용한다.
- Graph coloring: 임의의 정수 m이 주어지고, 최대한 m가지 색을 사용하여 인접한 두 마디가 같은 색이 되지 않도록 그래프를 색칠할 수 있는지를 판별하는 문제이다. 이 문제는 그래프 색칠하기 최적화 문제의 파라미터에다가 추가로 m을 파라미터로 사용한다.
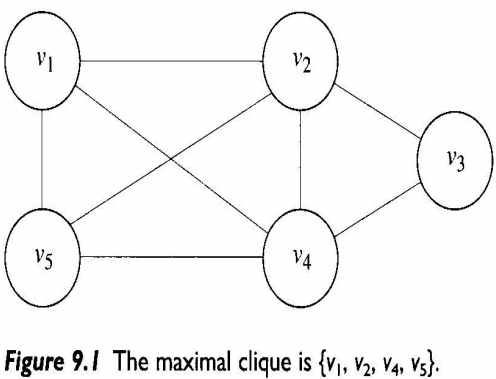
- 파벌(Clique) 문제
- 비방향그래프 $G = (V, E)$에서 파벌(clique)은 각 마디가 다른 모든 마디에 인접해 있는 $V$의 부분집합 $W$이다.
- ${v_2, v_3, v_4}$는 파벌이지만, ${v_1, v_2, v_3}$는 $v_1$이 $v_3$에 인접해 있지 않으므로 파벌이 아니다.
- 최대 파벌(maximal clique)은 파벌 중에서 크기가 가장 큰 파벌이다. 위 그림에서는 ${v_1, v_2, v_4, v_5}$이다.
- 파벌 최적화 문제(Clique Optimization Problem)는 임의의 그래프에서 최대 파벌의 크기를 구하는 문제이다.
- 파벌 진위판별 문제(Clique Decision Problem)는 임의의 양의 정수 k가 주어지고, 마디의 개수가 최소 k개가 되는 파벌이 존재하는지 판별하는 문제이다. 이 문제는 파벌 최적화 문제의 파라미터에다가 추가호 k를 파라미터로 사용한다.
위의 문제들에 대해서 진위판별 문제와 최적화 문제는 모두 다차시간 알고리즘을 아직 찾지 못했다. 그러나 어느 하나라도 최적화 문제에 대한 다차시간 알고리즘을 찾을 수 있다면, 그에 대응하는 진위판별 문제에 대한 다차시간 알고리즘도 존재할 것이다. 왜냐하면, “최적화 문제에 대한 해답을 구하면, 그에 상응하는 진위판별 문제에 대한 해답은 쉽게 얻을 수 있기” 때문이다.
P와 NP집합
P는 다차시간 알고리즘으로 풀 수 있는 모든 진위판별 문제의 집합이다. 다차시간 알고리즘이 있는 진위판별 문제는 모두 확실히 P에 속한다. 예를 들어, 아이템이 배열 안에 있는지 판별하는 문제와 다차시간 알고리즘을 찾은 3장과 4장의 최적화 문제에 대응하는 진위판별 문제들은 모두 P에 속한다. 다차시간 검증가능성의 개념을 더 상세히 기술하기 위해 비결정 알고리즘(nondeterministic algorithm)의 개념을 도입한다. 비결정 알고리즘은 두 단계로 구성되어 있다고 볼 수 있다.
- (비결정) 추측 단계(Gussing (nondeterministic) stage): 문제의 사레를 가지고 단순히 임의의 문자열 S를 만들어 낸다. 만든 문자열은 추측한 해답으로 보면된다. 사실 전혀 무의미한 문자열이어도 상관없다.
- (결정) 검증 단계: 입력은 문제 사례와 추측한 문자열 S이다. 이 단계는 일반적인 결정 실행방식으로 다음과 같이 진행된다.
- 궁극적으로 “true”의 출력을 내주면서 멈춘다.
- “false”의 출력을 내주면서 멈춘다.
- 멈추지 않는다.
다음 예를 보자.
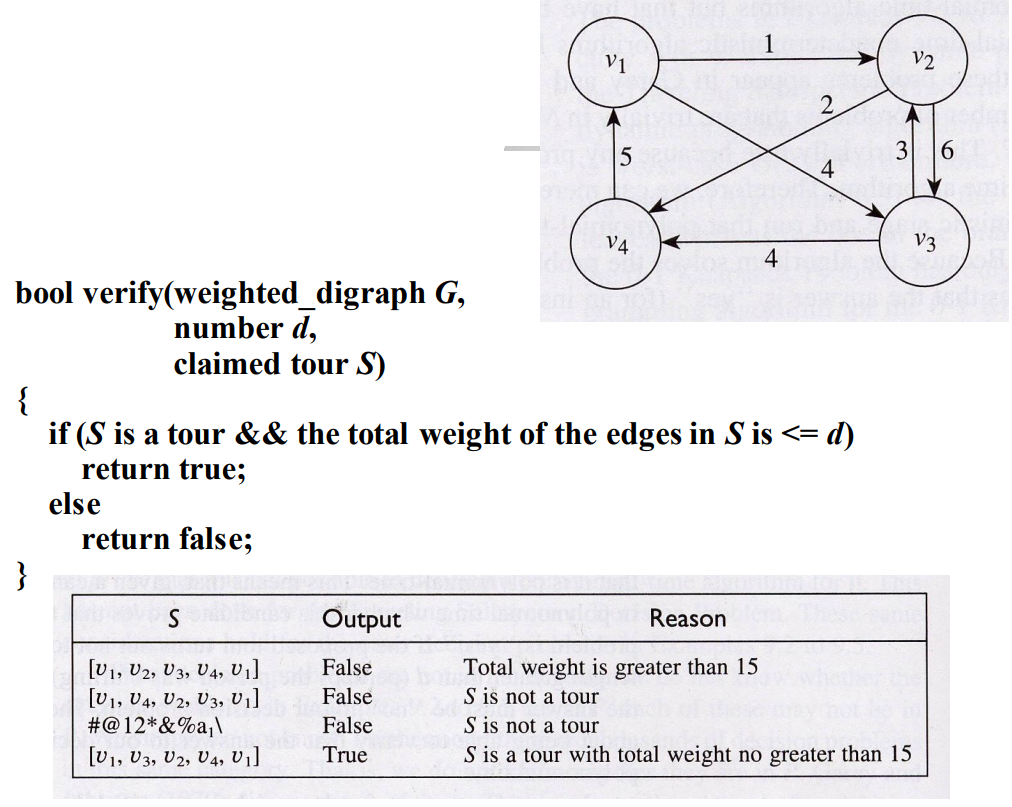
verify함수는 외판원 진위판별 문제의 검증단계에 해당하며, 결정 알고리즘이다. 비결정적이 되는 부분은 추측 단계로서 어떻게 해답을 만들어내는지 명시하지 않으므로 비결정(nondeterministic)단계라고 한다. 이 단계에서는 오히려 아무 문자열이나 임의로 만들어도 된다. “비결정 단계”는 다차시간 검증가능성의 개념을 정립하기 위한 치장도구에 불과할 뿐이며, 진위판별 문제를 풀기 위한 현실적인 방법은 아니다.
비결정 알고리즘을 실제로 문제를 푸는데 절대 사용할 수 없지만, 다음 두 조건을 만족하면 비결정 알고리즘이 진위판별 문제를 “푼다(solve)”고 한다.
- 해답이 “예”가 되는 사례에 대하여 검증단계의 결과가 “true”가 되는 문자열이 있다.
- 해답이 “아니오”가 되는 사례에 대하여 검증단계의 결과가 “true”가 되는 문자열이 없다.
위 그림의 표를 보면 사례가 그래프이고, d가 15일 때, 입력 문자열 S를 verify함수에 적용한 결과를 나열한다. 셋째 입력은 S가 전혀 무의미한 문자열이어도 상관없음을 보여준다. 추측 단계에서 단순히 문자열을 생성하고 검증 단계에서 verify 함수를 호출하는 비결정 알고리즘은 외판원 결정문제를 “푼다”고 할 수 있다. 이제 다차시간 비결정 알고리즘(polynomial-time nondeterministic algorithm)을 정의하면 검증단계가 다차시간 알고리즘인 비결정 알고리즘이다.
이제 집합 NP(Nondeterministic Polynomial)를 정의하면 다차시간 비결정 알고리즘으로 풀 수 있는 모든 진위판별 문제의 집합이다. 진위판별 문제가 NP에 속하기 위해서는 다차시간에 검증을 하는 알고리즘이 반드시 존재해야 한다. 예를들어, 외판원 진위판별 문제는 검증하는 다차시간 알고리즘이 있으므로 NP에 속한다.
다차시간 알고리즘이 있는지 아직 모르지만 문제를 푸는 다차시간 비결정 알고리즘은 있기 때문에 NP애 속함이 증명된 진위판별 문제가 수천개 이상 존재한다. 마지막으로, 따져볼 것도 없이 사소하게 NP에 속하는 문제도 상당히 많다. 즉, “P에 속하는 문제는 모두 NP에도 속한다.” P에 속한 문제는 모두 다차시간 알고리즘으로 풀 수 있으므로 따져볼 것 없이 사소하게 사실이다. 비결정 단계에서 아무 문자열이나 생성하고, 결정 단계에서 다차시간 알고리즘을 실행한다.
다음은 모든 진위판별 문제의 집합을 보여준다.
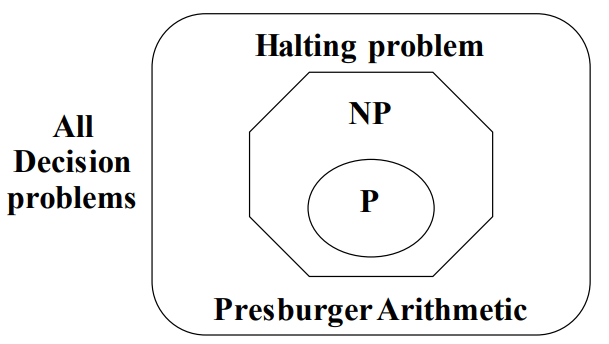
위 그림에서 NP는 P를 진부분집합으로 포함하고 있는 걸로 그려져 있다. 그러나 그렇지 않을지도 모른다. 즉, NP에 속하면서 P에 속하지 않는 문제가 아직 있다고 증명하지 못했기 때문이다.
NP-Complete 문제
NP-Complete를 이해하기 위해 다음을 먼저본다.
- CNF-Satisfiability Problem
- $x$가 논리 변수이면, $\bar{x}$는 $x$의 부정(negation)이다.
- 절(clause)은 논리 연산자 or($\lor$)를 사이사이에 끼운 나열이고 CNF(Conjunctive Normal Form)는 논리식(logical expression)으로 논리 연산자 and($\land$)를 사이사이에 끼운 절의 나열이다.
- $(\bar{x_1} \lor x_2 \lor \bar{x_3}) \land (x_1 \lor \bar{x_4}) \land (\bar{x_2} \lor x_3 \lor x_4)$
- CNF-Satisfiability 진위판별 문제는 주어진 CNF 논리식을 true로 만드는 참값 대입이 존재하는지 판별하는 문제이다.
- Transformation
- 진위판별 문제 A를 풀려고 하고, 진위판별 문제 B를 푸는 알고리즘이 있다고 가정하자. 그리고 문제 B를 푸는 알고리즘이 $y$에 대해서 “예”라고 답하면 문제 A에 대한 답도 “예”가 되도록 문제 A의 모든 사례 $x$에서 문제 B의 사례 $y$를 만들어내는 알고리즘을 작성할 수 있다고 가정하자.
- 변환 알고리즘(transformation algorithm)은 문제 A의 모든 사례를 문제 B의 사례로 실제로 매핑하는 함수이다. 이 함수는 $y = tran(x)$와 같이 표현한다.
- 문제 B를 푸는 알고리즘을 가지고 이 변환 알고리즘을 적용하여 문제 A를 푸는 알고리즘을 만들어낸다.
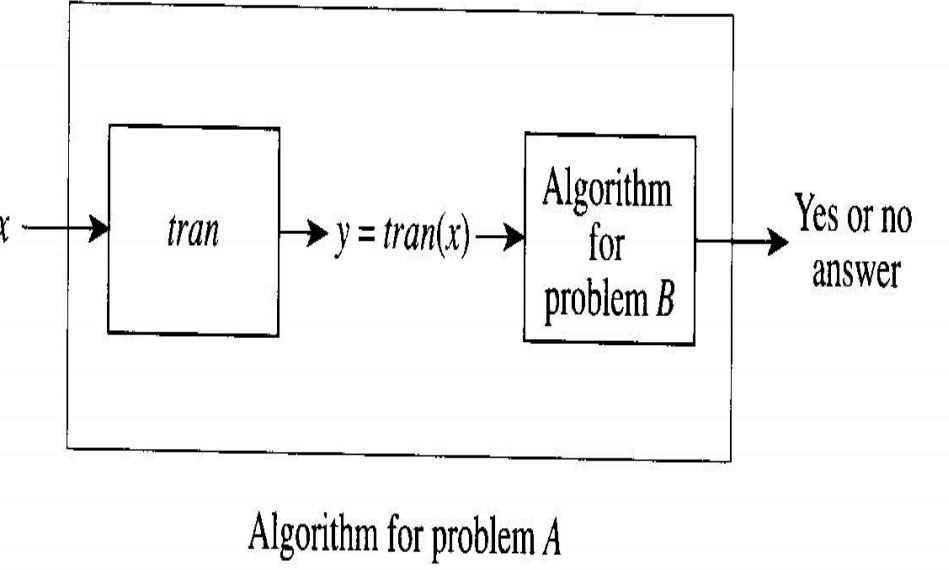
진위판별 문제 A를 진위판별 문제 B로 변환하는 다차시간 변환 알고리즘이 존재하면, “문제 A는 문제 B로 다차시간 다일 축소변환가능(polynomial-time many-one reducible)“하다(“문제 A는 문제 B로 축소 변환된다.”). 이는 $A \varpropto B$로 표현한다. “다일”이라고 한 이유는 변환 알고리즘이 문제 A의 많은 사례에 문제 B의 하나의 사례로 매핑하는 함수이기 때문이다.
이제 NP-Complete를 정의한다. 문제 B는 다음 조건을 만족하면 NP-Complete라고 한다.
- NP에 속한다.
- NP에 속한 모든 다른 문제 A에 대하여 $A \varpropto B$이 성립한다.
쿡의 정리에 따르면, CNF-Satisfiability는 NP-Complete이다. 또한 문제 C는 다음 두 조건을 만족하면 NP-Complete이다.
- C는 NP에 속한다.
- 다른 NP-Complete 문제 B에 대해서 $B \varpropto C$가 성립한다.
- B가 NP-Complete이므로, NP에 속한 임의의 문제 A에 대해서 $A \varpropto B$가 성립한다. 따라서 $A \varpropto C$가 성립한다. C는 NP에 속하므로, C는 NP-Complete라고 결론지을 수 있다.
P는 NP의 진부분집합(proper subset)으로 보이지만, 동일한 집합일 수도 있다. NP-Complete문제의 집합을 보면, NP-Complete 집합은 NP의 부분집합이다. 따라서 NP에 속하지 않는 다른 진위판별 문제는 NP-Complete가 아니다. NP에는 속하지만 NP-Complete에는 속하지 않는 진위판별 문제는 무조건 “예”라고 대답하는(또는 “아니오”) 사소한 진위판별 문제이다. 사소하지 않은 진위판별 문제를 사소한 진위판별 문제로 축소변환이 불가능하므로 사소한 진위판별 문제는 NP-Complete가 아니다.
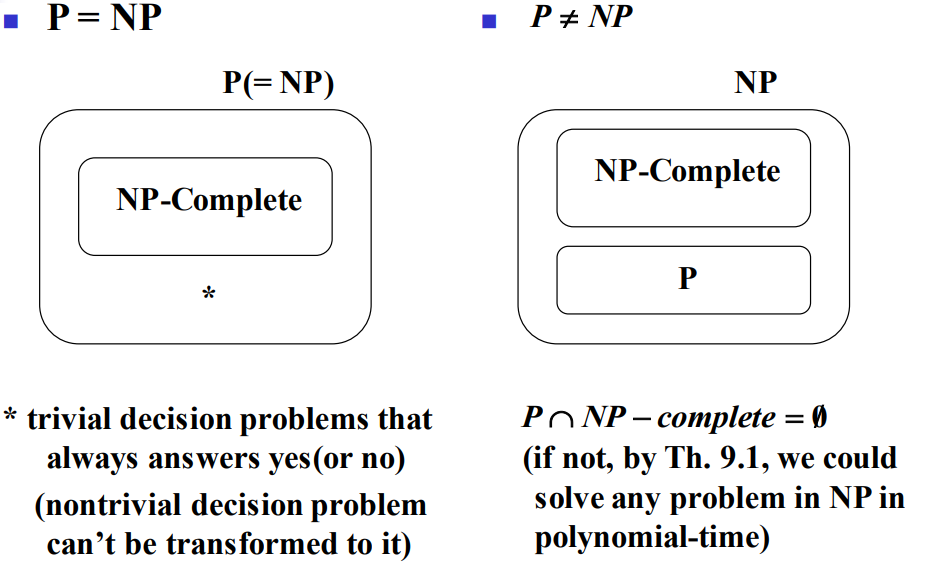
$P = NP$라고 가정하면, 왼쪽 그림이 맞다. $P \neq NP$이면 오른쪽 그림이 맞다. 즉, $P \neq NP$이면, $P \cap NP-Complete = \varnothing$이 성립한다.
NP-Hard 문제
위에서 배운 결과를 일반(nondecision) 문제로 확장하여 적용해본다. 문제 B를 푸는 가상 다차시간 알고리즘을 사용하여 문제 A를 다차시간에 풀 수 있다면, 문제 A는 문제 B로 다차시간 튜링 축소변환가능(polynomial-time Turing reducible) 하다고 한다. 기호로는 $A \varpropto_T B$로 쓴다. 문제 B를 푸는 다차시간 알고리즘이 있으면 문제 A도 다차시간에 풀 수 있다는 것을 말하는 것이다. A와 B가 모두 진위판별 문제이면, “$A \varpropto B$이면 $A \varpropto_T B$이다”는 분명히 성립한다.
이제NP-Complete의 개념을 일반 문제로 확장한다. 임의의 NP-Complete 문제 A에 대해서 $A \varpropto_T B$가 성립하면, 문제 B는 NP-Hard하다고 한다. 따라서 NP 문제는 모두 NP-Hard 문제로 축소변환 가능하다. 다시 말해서, “NP-Hard 문제를 푸는 다차시간 알고리즘이 존재하면 $P = NP$가 성립한다”는 의미가 된다.
NP-Complete 문제는 분명히 모두 NP-Hard 문제이다. 최적화 문제를푸는 다차시간 알고리즘이 있으면, 그에 상응하는 진위판별 문제를푸는 다차시간 알고리즘은 거저 얻을 수 있다. 따라서 “NP-Complete 문제에 상응하는 최적화 문제는 모두 NP-Hard이다.“
사실, “NP-Hard가 아님을 증명한 문제가 있다면, $P \neq NP$를 증명한 것과 다름이 없다.” 그 이유는 $P = NP$이면 NP 문제를 모두 다차시간 알고리즘으로 풀 수 있을 것이기 때문이다. 또한 “다차시간 알고리즘이 있는 문제를 NP-Hard라고 증명할 수 있다면, $P = NP$를 증명한 것과 다름이 없다.” 그 이유는 어떤 NP-Hard 문제를 푸는 가상이 아닌 실제 다차시간 알고리즘이 있을 것이기 때문이다. 그러므로 NP문제를 NP-Hard 문제로 튜링 축소변환하여 다차시간에 NP문제로 모두 풀 수 있게 된다.
댓글남기기