3장 동적 응답

Laplace 변환의 개관

　선형 시불변 시스템(LTI system: linear time-invariant system)의 다음 두 가지 특성은 선형 시불변 시스템에 적용되는 거의 모든 해석 기법의 기본이 된다.

• 선형 시스템의 응답은 중첩(superposition)의 원리를 따른다.
• LTI 시스템의 응답은 입력과 시스템의 단위충격응답의 콘벌루션(convolution)으로 표현될 수 있다.

콘벌루션에 의한 응답

　중첩의 원리는 만약 시스템이 여러 신호의 합으로 표현될 수 있는 입력을 가질 때, 시스템의 응답은 각 신호에 대한 개별적인 응답의 합으로 표현될 수 있다는 것이다. 중첩은 수학적으로 나타낼 수 있다. 입력이 $u$, 출력이 $y$인 시스템을 고려하자. 또한 정지상태의 시스템에 입력 $u_1(t)$를 인가하면 출력 $y_1(t)$를 얻을 수 있다고 가정하자. 다시 정지상태로 복원된 시스템에 두 번째 입력 $u_2(t)$를 인가하면 $y_2(t)$를 얻을 수 있다고 하자. 이때 복합 입력 $u(t) = \alpha_1u_1(t) + \alpha_2u_2(t)$를 시스템에 인가한다. 중첩의 원리에 의하면 시스템의 응답은 $y(t) = \alpha_1y_1(t) + \alpha_2y_2(t)$가 될 것이다. 중첩의 원리는 선형 시스템에대해서만 성립한다.
　시불변(time invariant) 시스템의 경우에 만약 입력이 지연 혹은 전이되면, 출력은 정확히 동일한 시간만큼 전이되는 것 이외에 다음 변화가 없다. 수학적으로 이를 표현하면, $y_1(t)$가 입력 $u_1(t)$에 의한 출력이면 $y_1(t-\tau)$는 $u_1(t-\tau)$에대한 응답이 될 것이다. 다음 예제를 살펴보자.

$\dot{y} + ky = u$

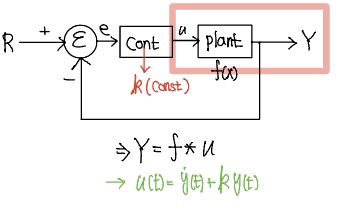
　$u = \alpha_1u_1 + \alpha_2u_2$와 $y = \alpha_1y_1 + \alpha_2y_2$라고 하면 $\dot{y} = \alpha_1\dot{y_1} + \alpha_2\dot{y_2}$이 된다. 이 식들을 시스템 방정식에 대입하면 $\alpha_1\dot{y_1} + \alpha_2\dot{y_2} + k(\alpha_1y_1 + \alpha_2y_2) = \alpha_1u_1+ \alpha_2u_2$가 되고, 이로부터 다음 식을 얻는다.

$\alpha_1(\dot{y_1} + ky_1 - u_1) + \alpha_2(\dot{y_2} + ky_2 - u_2) = 0$

　만약 $y_1$이 입력 $u_1$의 해이고 $y_2$가 입력 $u_2$의 해이면 위 식은 만족되고 시스템의 응답은 개별적인 응답의 합이 되므로 중첩의 원리가 성립한다.
　만약 $\dot{y_1}(t) + k(t)y_1(t) = u_1(t)$ 그리고 $\dot{y_2}(t) + k(t)y_2(t) = u_1(t - \tau)$ 이고 $\tau$는 일정한 전이이다. $y_2(t) = y_1(t-\tau)$이라고 가정하면 ${dy_1(t-\tau) \over dt} + k(t)y_1(t-\tau) = u_1(t-\tau)$이다. 변수 $t-\tau = \eta$로 치환하면 ${dy_1(\eta) \over d\eta} + k(\eta + \tau)y_1(\eta) = u_1(\eta)$이다.
　$\tau = 0$이거나, $k(\eta + \tau) = k = $상수인 경우에 ${dy_1(\eta) \over d\eta} + ky_1(\eta) = u(\eta)$이고 $\dot{y} + ky = u$와 동일하다. 그러므로 만약 시스템이 시불변이면 $y(t-\tau)$는 $u(t-\tau)$의 답이다. 즉, 입력이 $\tau$초만큼 지연되면 출력 또한 $\tau$초만큼 지연된다.

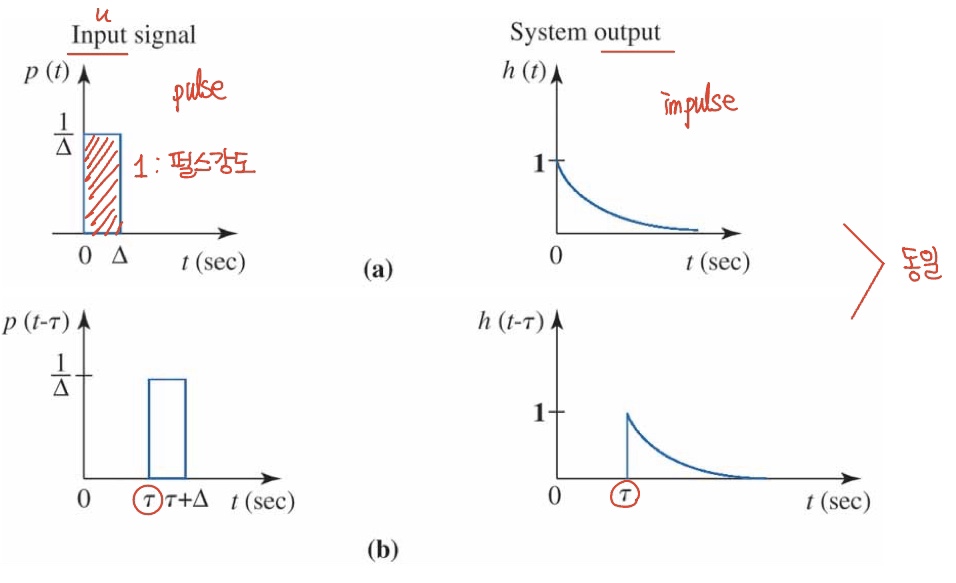
　LTI 시스템의 입력신호가 짧은 펄스 $u_1(t) = p(t)$이고, 이때 출력신호가 (a)와 같이 $y_1(t) = h(t)$라고 가정하자. 만약 입력이 $u_1(t) = u(0)p(t)$로 스케일되면 중첩의 스케일링 성질에 따라 출력응답은 $y_1(t) = u(0)h(t)$가 될 것이다. 만약 짧은 펄스신호가 $\tau$만큼 지연된다면 입력은 $u_2(t) = p(t-\tau)$가 되고 출력응답은 역시 (b)와 같이 $y_2(t) = h(t-\tau)$처럼 동일하게 지연될 것이다.

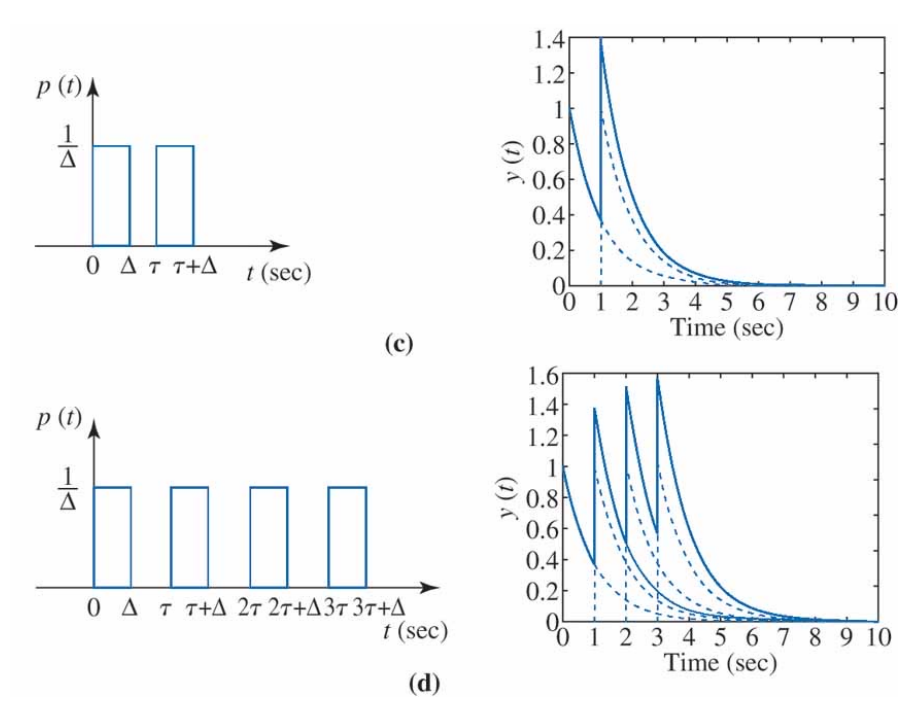
　이제 중첩의 원리에 의해 두 개의 짧은 펄스에 대한 응답은 (c)와 같이 각 출력의 합이 될 것이다. 만약 네 개의 펄스를 입력한다면 출력은 (d)와 같이 네 개의 응답의 합이 될 것이다. 임의의 입력신호 $u(t)$가 다음과 같이 연속된 펄스신호로 근사화될 수 있다고 하자.

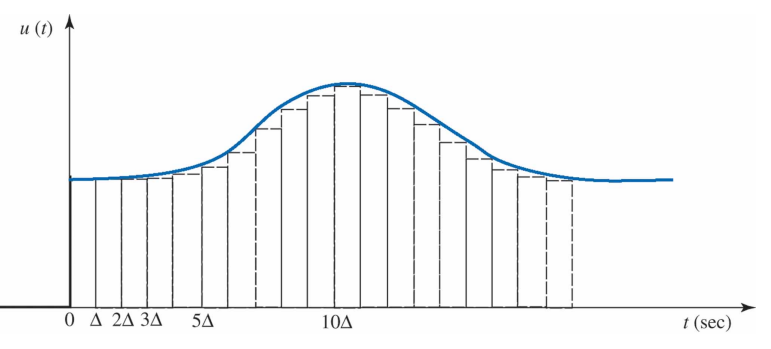
　짧은 펄스 $p_{\Delta}(t)$를 (a)와 같이 단위면적을 가진 직사각형 펄스로 정의하자.

$p_{\Delta}(t)=\begin{cases} \frac{1}{\Delta}, & 0\le t\le \Delta \\ 0, & \mbox{elsewhere} \end{cases}$

　$p_{\Delta}(t)$에 대한 시스템응답을 $h_{\Delta}(t)$로 정의하면 중첩에 의해 시간 $t$에서의 연속된 짧은 펄스에 대한 총 응답은 다음과 같다. $y(t) = \lim\limits_{\Delta \to 0}$ {$u(0)h_{\Delta}(t) + u(\Delta)h_{\Delta}(t-\Delta) + u(2\Delta)h_{\Delta}(t-2\Delta) + \cdots$} $= \lim\limits_{\Delta \to 0} \sum\limits_{k=0}^\infty u(k\Delta)h_{\Delta}(t-k\Delta)$
　이때 충격신호(impulse signal) $\delta(t)$의 개념을 이용하면 연속신호를 다룰 수 있게 된다.
　이 경우 $y(t) = \int_{0}^{\infty}u(\tau)h(t-\tau)\,d\tau$ $(\lim\limits_{\Delta \to 0} h_{\Delta}(t) = h(t) \mbox{: 충격응답(impulse response)})$ 이다.
　위의 적분은 콘벌루션(convolution) 적분이다.
　물리학자 Paul Dirac은 충격(impulse) $\delta(t)$라는 수학적 개념으로 나타낼 수 있다고 제안하였으며, 이것은 다음의 성질을 만족한다.

$\delta (t) = 0 (t \neq 0), \int_{-\infty}^{\infty} \delta (t)\, dt = 1$

　시불변 시스템에서 일반적 입력에 대한 출력은 적분 $y(t) = \int_{-\infty}^{\infty} u(\tau)h(t-\tau) \, d\tau$으로 주어진다.
　변수 $\tau_1 = t - \tau$로 치환하면 $y(t) = \int_{\infty}^{-\infty} u(t - \tau_1)h(\tau_1) \, (-d\tau) = \int_{-\infty}^{\infty} h(\tau)u(t-\tau) \, d\tau = h(t)*u(t)$이 된다. 이것이 콘벌루션 적분(convolution integral)이다. 다음 예제를 보자.
　다음 미분방정식으로 표현된 시스템의 충격응답을 구하라.

$\dot{y}(t) + ky(t) = u(t)$, $y(0) = 0$

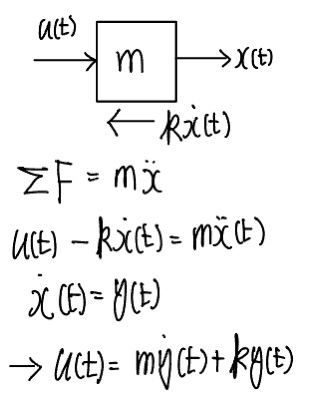
　충격응답 $y(t)$는 $\dot{y}(t) + ky(t) = \delta(t)$를 통해 얻을 수 있다.

전달함수와 주파수응답

　콘벌루션 적분에 대한 유도는 어려울 수 있기 때문에 다음 Laplace변환을 사용하여 간접적으로 유도되었다.

$Y(s) = \int_{-\infty}^{\infty} y(t)e^{-st} \, dt$

　이 변환을 콘벌루션에 적용하면 $Y(s) = \int_{-\infty}^{\infty}[ \int_{-\infty}^{\infty} h(\tau)u(t-\tau)]e^{-st} \, dt$이다. 그런 다음 적분 순서를 바꾸어서 t에 대한 적분을 먼저 수행한 뒤 $t - \tau = \eta$로 내부 적분의 변수를 치환하면 다음과 같다.

$Y(s) = \int_{-\infty}^{\infty} [ \int_{-\infty}^{\infty} u(\eta)e^{-s(\eta + \tau)} \, dt] h(\tau) \, d\tau$, $Y(s) = [ \int_{-\infty}^{\infty} u(\eta)e^{-s\eta} \, d\eta ] \int_{-\infty}^{\infty} h(\tau)e^{-s\tau} \, d\tau$

$Y(s) = U(s)H(s)$

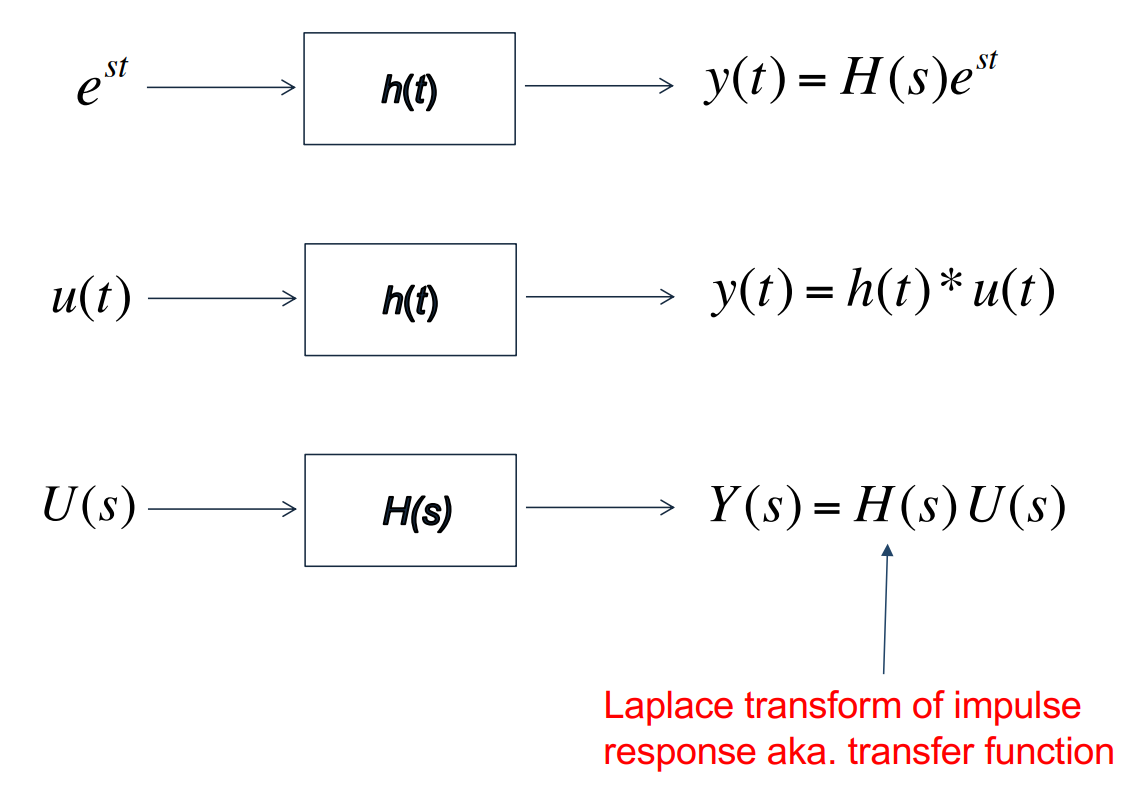
　위 풀이에서 $U(s)$는 입력함수의 Laplace 변환이고, 충격응답의 Laplace 변환인 $H(s)$는 전달함수(transfer function)라고 정의된다.
　콘벌루션의 결과로 $e^{st}$형태의 입력은 출력 $H(s)e^{st}$를 만든다. 입력과 출력 모두 지수 시간함수이고, 출력은 크기 $H(s)$만큼 입력과 다르다는 점에 주목하자. $H(s)$는 시스템의 전달함수로 정의된다. 상수 $s$는 복소수가 될 수 있으며 $s = \sigma + j\omega$로 표현한다. 따라서 입력과 출력 모두 복소수가 될 수 있다. 만약 $u(t) = e^{st}$일때 다음과 같다.

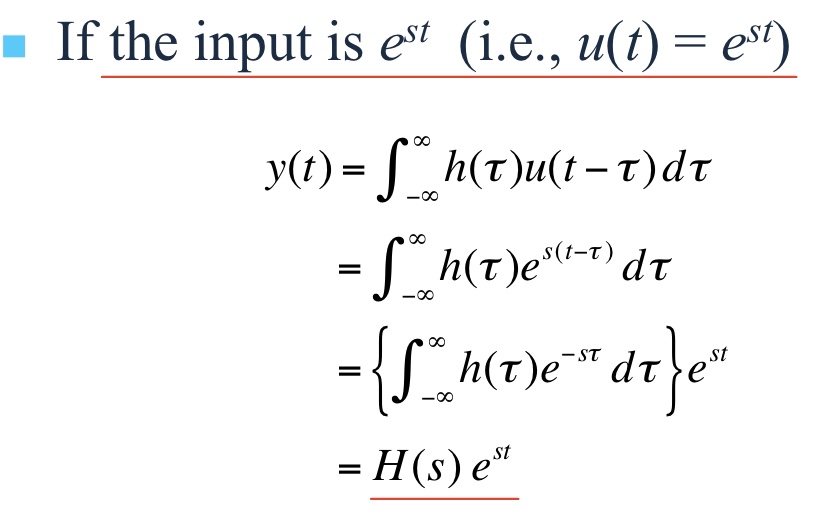
　여기서 $H(s) = \int_{-\infty}^{\infty} h(\tau)e^{-s\tau} \, d\tau$이다.
　$t<0$일 때 $h(t)=0$인 실제 인과적 시스템에서 적분의 극한은 0부터 $\infty$까지로 정해진다.

$H(s) = \int_{0}^{\infty} h(\tau)e^{-s\tau} \, d\tau$

　인과 시스템에서 $y(t) = \int_{0}^{\infty} h(\tau)u(t-\tau) \, d\tau$로 간략하게 표현된다.
　전달함수 $H(s)$는 $U(s)$에서 $Y(s)$까지의(입력에서 출력까지의) 전달 이득(gain) 함수이다. 이것은 입력의 Laplace 변환과 출력의 Laplace 변환의 비이다. 시스템의 모든 초기조건이 $0$이라는 핵심적인 가정하에 다음과 같다.

$Y(s) = H(s)U(s), \frac{Y(s)}{U(s)} = H(s)$

　만약 입력$u(t)$가 단위충격함수 $\delta(t)$라면 $y(t)$는 단위충격응답이다. $u(t)$의 Laplace 변환$U(s) = 1$이고 $y(t)$의 변환 $Y(s) = H(s)$이다. 즉, 전달함수 $H(s)$는 단위충격응답 $h(t)$의 Laplace 변환이다. 다음 예제를 보자

$\mathcal{L}$_Laplace 변환

단방향(일면의) Laplace 변환은 적분의 하한이 $0^-$이 된다. $\mathcal{L}$_{$f(t)$} $= F(s)$로 표현되는 $f(t)$의 $\mathcal{L}$_Laplace 변환은 복소 변수 $s = \sigma + j\omega$의 함수이다.

$F(s) = \int_{0^-}^{\infty} f(t)e^{-st} \, dt$

　단위충격함수의 Laplace 변환을 알아 보자. 단위충격함수 $\delta (t)$는 $0$일 때만 존재하고 $t=0$일 때 $e^{-st} = 1$이므로 다음과 같이 쓸 수 있다.

$F(s) = \int_{0^-}^{\infty} \delta (t)e^{-st} \, dt = \int_{0^-}^{0+} \delta (t) \, dt = 1$

　정형파 함수의 Laplace 변환을 알아 보자.

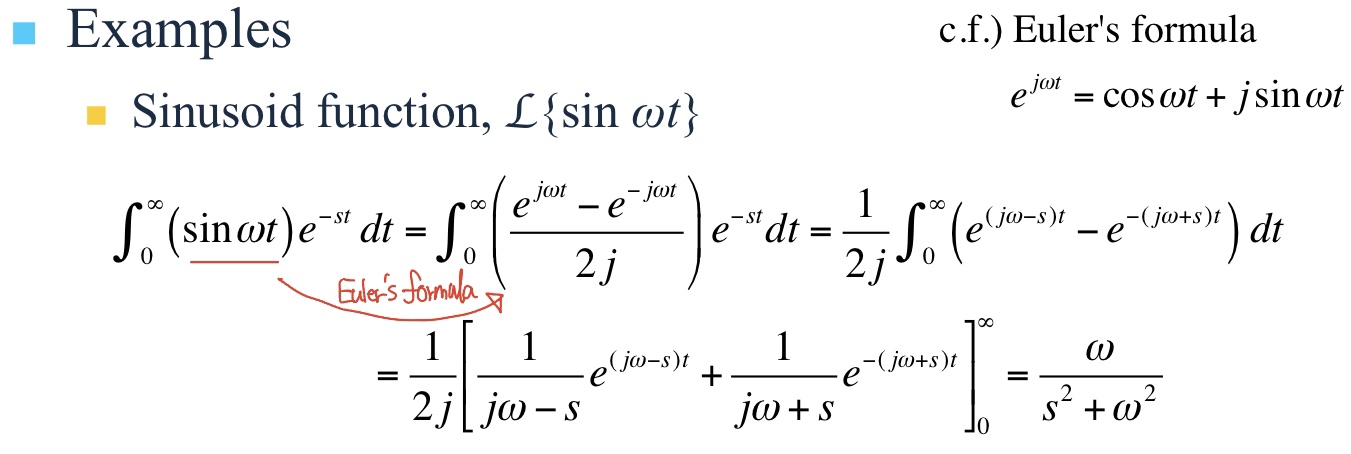
Laplace 변환의 성질

시간 지연
　함수 $f(t)$가 $\lambda > 0$만큼 지연된다고 가정하자($f_1(t) = f(t - \lambda)$). 이에 대한 Laplace 변환은 다음과 같다.

$F_1(s) = \int_{0}^{\infty} f(t - \lambda)e^{-st} \, dt = e^{-s\lambda}F(s)$

　이를 통해 $\lambda$만큼의 시간 지연은 변환에 $e^{-s\lambda}$을 곱한 것이라는 것을 알 수 있다.

시간 스케일링
　만약 시간 $t$가 $a$로 스케일링된다면 $f_1(t) = f(at)$이고, 시간 스케일링 된 신호의 Laplace 변환은 다음과 같다.

$F_1(s) = \int_{0}^{\infty} f(at)e^{-st} \, dt = \frac{1}{|a|} F(\frac{s}{a})$

미분

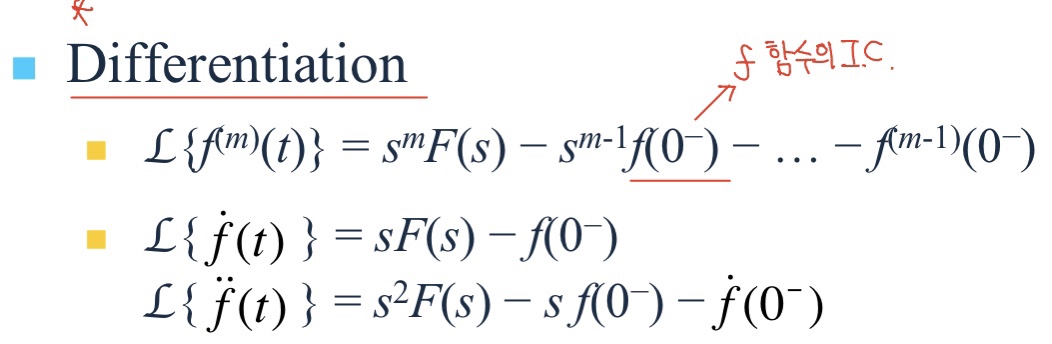
적분
　시간함수 $f(t)$의 적분에 대한 Laplace 변환은 다음과 같다: $f_1(t) = \int_{0}^{t} f(\xi) \, d\xi$.

$F_1(s) = \mathcal{L}${$\int_{0}^{t} f(\xi) \, d\xi$} $=\frac{1}{s}F(s)$

이는 함수의 Laplace 변환에 $\frac{1}{s}$를 곱하는 것과 같다.

콘벌루션
　입력과 시스템의 충격응답을 콘벌루션하거나, 입력의 Laplace 변환과 전달함수를 곱하여 시스템응답을 구한다. $\mathcal{L}${$f_1(t)$} $= F_1(s)$, $\mathcal{L}${$f_2(t)$} $= F_2(s)$라 가정하면 다음과 같다.

$\mathcal{L}${$f_1(t)*f_2(t)$} = $\int_{0}^{\infty} f_1(t)*f_2(t)e^{-st} \, dt = F_1(S)F_2(S)$

　이때 $*$은 콘벌루션 연산자이다. 이것은 다음을 의미한다.

$\mathcal{L}^{-1}${$F_1(s)F_2(s)$} $= f_1(t)*f_2(t)$

　다음 예제를 보자.

부분분수 전개에 의한 역 Laplace 변환

　Laplace 변환 $F(s)$로부터 $f(t)$를 찾는 가장 쉬운 방법은, $F(s)$가 유리함수라고 가정하면 $F(s)$를 표에서 찾을 수 있는 간단한 항들의 합으로 전개하는 것이다. 이러한 과정을 위한 기본 방법을 부분분수 전개라고 한다. 두 다항식의 비로 구성된 유리함수 $F(s)$에 대한 일반적인 형태를 고려하자.

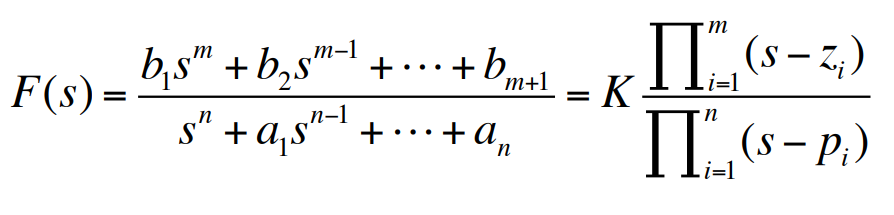
　먼저 극점이 서로 다른 경우에 대해 고려해 보자. 임의의 물리적 시스템의 응답을 나타내는 변환 $F(s)$에 대해 $m \le n$이다.

• $s=z_i$일 때, $s$는 함수의 영점(zero)라고 한다.
• $s=p_i$일 때, $s$는 함수의 극점(pole)이라고 한다.

　극점{$p_i$}가 서로 다른 실수 혹은 복소수라고 가정하면, $F(s)$를 부분분수로 다음과 같이 표현할 수 있다.

$F(s) = \frac{C_1}{s-p_1} + \frac{C_2}{s-p_2} + \cdots + \frac{C_n}{s-p_n}$

　그다음 단계로 상수 집합{$C_i$}를 결정한다. 위 식의 양변에 $s-p_1$를 곱하여 다음을 얻는다.

$(s-p_1)F(s) = C_1 + \frac{s-p_1}{s-p_2}C_2 + \cdots + \frac{s-p_1}{s-p_n}C_n$

　위 식의 양변에서 $s=p_1$이라 하면 첫 항을 제외한 모든 $C_i$가 $0$이 된다.

$C_1 = (s-p_1)F(s)|_{s=p_1}$

　다른 계수들도 유사한 형태로 표현될 수 있다.

$C_i = (s-p_i)F(s)|_{s=p_i}$

　이 방법은 도포법(cover-up method)이라고 부른다. 이 과정이 완료되면 시간함수는 다음과 같이 표현된다.

$f(t) = \sum\limits_{i=1}^{n} C_ip^{p_it}1(t)$

　이 이유는 $F(s) = \frac{1}{s-p_i}$이면 $f(t) = e^{p_it}1(t)$이기 때문이다. 다음 예제를 보자.

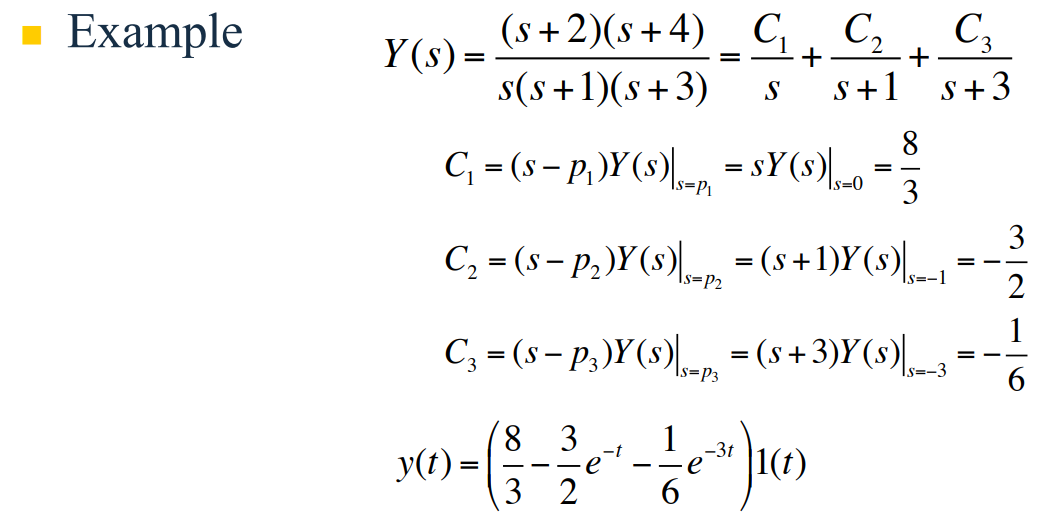
최종값 정리

　만약 $sY(s)$의 모든 극점이 $s$-평면의 좌반평면(lefr-half plane)에 있다면 다음이 성립한다.

$\lim\limits_{t \to \infty} y(t) = \lim\limits_{s \to 0} sY(s)$

　이 정리는 또한 시스템의 DC이득을 구할 때 사용될 수 있다. DC이득(DC gain)은 모든 과도항이 사라진 후 입력(상수)과 시스템 출력의 비이다. DC이득을 찾기 위해 단위계단입력($U(s)= 1/s$)을 가정하고 출력의 정상상태값을 계산하기 위해 최종값 정리를 사용한다. 따라서 시스템 전달함수 $G(s)$에 대해 DC이득은 다음과 같다.

DC gain $= \lim\limits_{s \to 0}sG(s)\frac{1}{s} = \lim\limits_{s \to 0} G(s)$

미분방정식을 풀기 위해 Laplace 변환 사용하기

　다음 예제를 살펴보자

극점 및 영점

　유리수 전달함수는 $s$를 변수로 하는 두 다항식의 비로 표현될 수 있다.

$H(s) = \frac{b_1s^m + b_2s^m + \cdots + b_{m+1}}{s^n + a_1s^{n-1} + \cdots + a_n} = \frac{N(s)}{D(s)} = K\frac{\prod_{i=1}^{m}(s-z_i)}{\prod_{i=1}^{n}(s-p_i)}$

　$K$는 전달함수 이득(transfer function gain)이다.
　분모의 근 $p_1, p_2, …, p_n$은 시스템의 극점(pole)이라고 한다. 극점은 $s$-평면에서 전달함수의 크기가 무한대가 되는 지점에 위치한다. 만약 $s=p_i$이면 다음과 같다.

$|H(s)|_{s=p_i} = \infty$

　시스템의 극점은 시스템의 안전성을 결정한다. 또한 시스템 모드(mode)라고 불리는 시스템의 고유 또는 비가진(unforced) 거동을 결정한다.
　분자의 근 $z_1, z_2, …, z_m$은 시스템의 유한 영점(zero)이라고 한다. 만약 $s=z_i$라면 다음과 같다.

$H(s)|_{s=z_i} = 0$

　영점은 시스템의 신호 전달을 막는 성질을 가지고 있어서 시스템의 전달 영점(transmission zeres)이라고도 불린다. 또한 영점들은 시스템의 과도응답에 중요한 영향을 미친다.
　극점과 영점의 위치는 피드백 제어 설계의 핵심이고, 제어시스템 설계에 있어서 매우 중요한 실제적 내용을 포함하고 있다. 만약 $m < n$이면 $s$가 무한대로 향할 때 전달함수는 $0$이 되기 때문에 시스템은 무한대에서 $n - m$개의 영점을 가진다고 말한다. 만약 무한대의 영점 갸수도 포함해서 센다면 시스템은 같은 수의 영점과 극점을 가질 것이다. 어떤 물리적 시스템도 $n < m$이 될 수 없다. 그렇지 않으면 $\omega = \infty$에서 무한대 응답을 가지게 될 것이다. 만약 $z_i = p_j$이면 전달함수에서 상쇄(cancellation)가 일어나고, 이는 원하지 않는 시스템의 성질을 야기하게 될 수도 있다.

시스템 모델링 선도

블록선도

　각 구성여서의 전달함수는 네모박스 안에 위치하고, 구성요소 간의 입력-출력 관계식은 선과 화살표로 표시한다. 그러면 우리는 대수적 연산보다 쉽고 더 많은 정보를 가진 도식적 간략화를 이용하여 방정식을 풀 수 있다. 다음 그림은 세 가지 기본 블록선도이다.

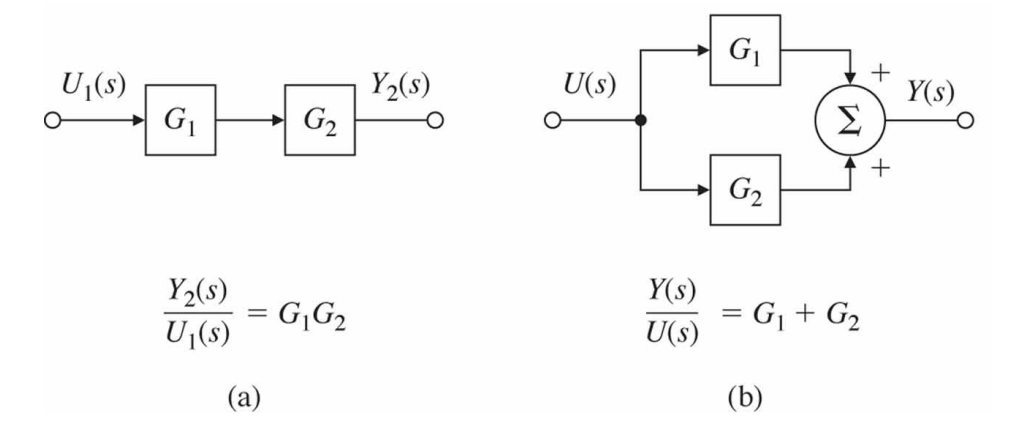
　블록 사이의 연결은 여러 신호가 합해지는 합점(summing point)들을 포함한다. 합점들은 내부에 $\sum$기호가 그려진 원으로 표시한다. 위 그림의 (a)에서 전달함수 $G_1(s)$블록이 전달함수 $G_2(s)$블록과 직렬로 연결되어 있으며, 이떄 전체 전달함수는 곱 $G_2G_1$이 된다. (b)에서 두 시스템은 병렬로 출력과 연결되어 있으며, 이때 전체 전달함수는 합 $G_1 + G_2$이다.
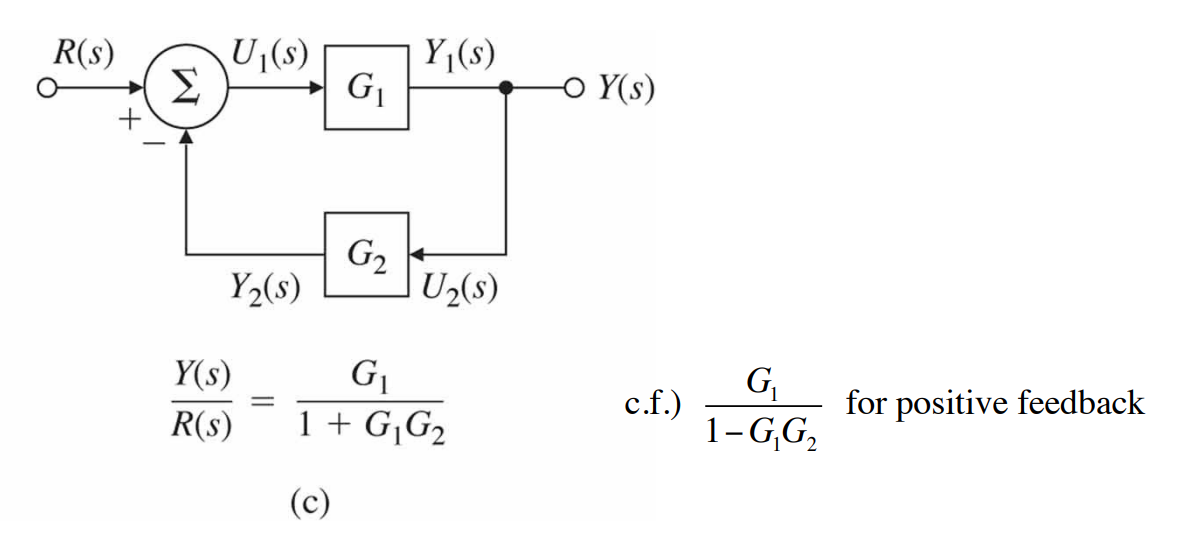
　(c)는 좀 더 복잡한 경우를 보여 준다. 두 블록이 피드백 배열로 연결되어 각 블록이 다른 블록의 입력이 된다. 피드백 $Y_2(s)$를 빼는 것을 음의 피드백(negative feedback)이라고 부른다. 음의 피드백은 보통 시스템 안전성을 위해서 필요하다. (c)의 방정식은 다음과 같다.

$U_1(s) = R(s) - Y_2(s), Y_2(s) = G_2(s)G_1(s)U_1(s), Y_1(s) = G_1(s)U_1(s)$

　위 식의 해는 다음과 같다.

$Y_1(s) = \frac{G_1(s)}{1 + G_1(s)G_2(s)}R(s)$

　우리는 다음 규칙을 통해 해답을 표현할 수 있다.
　단일루프 음의 피드백 시스템의 이득은 전향이득을 (1 + 루프이득)으로 나눈 것이다.
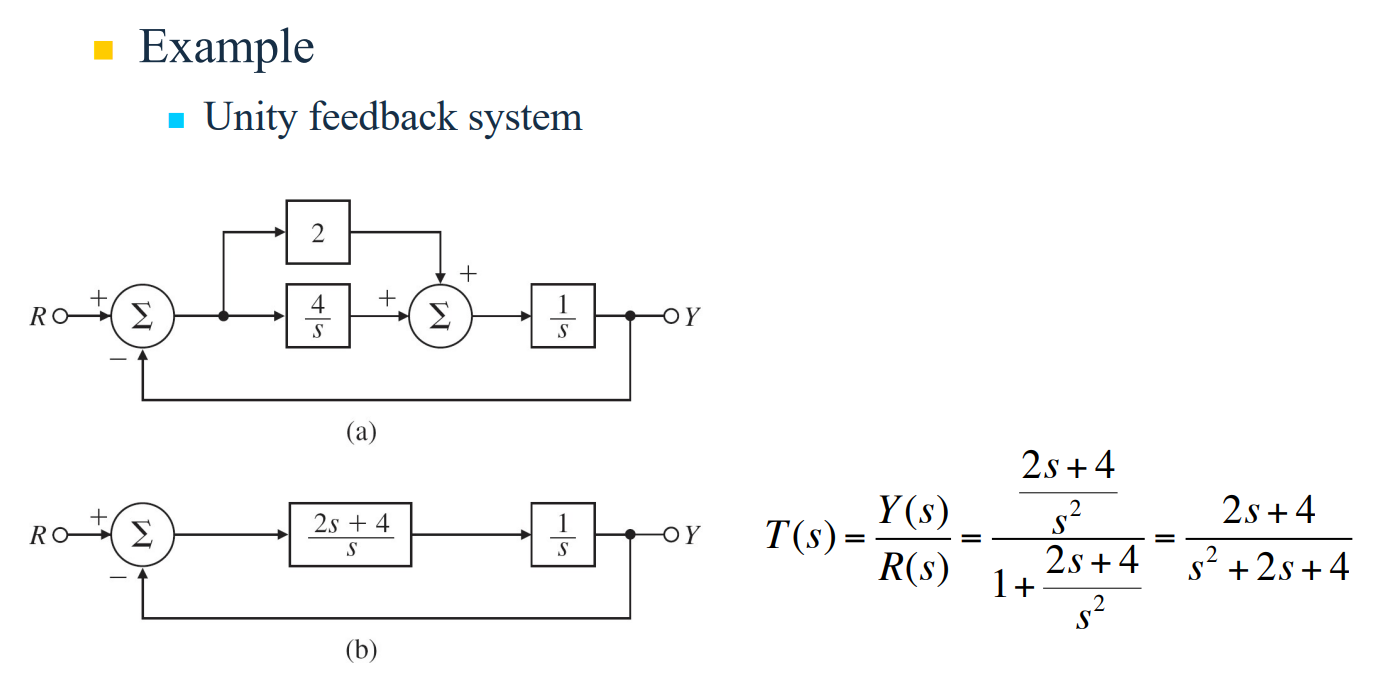
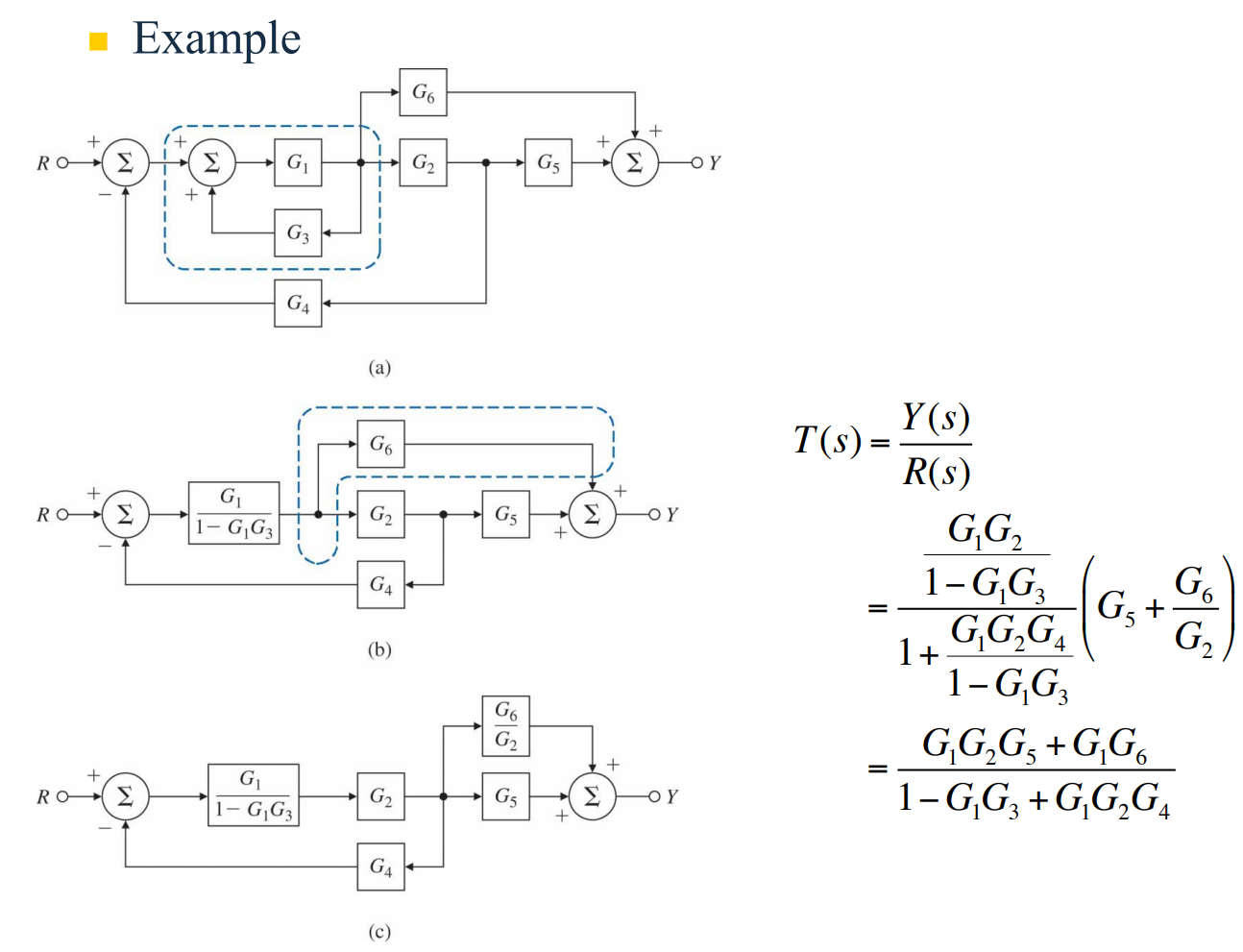
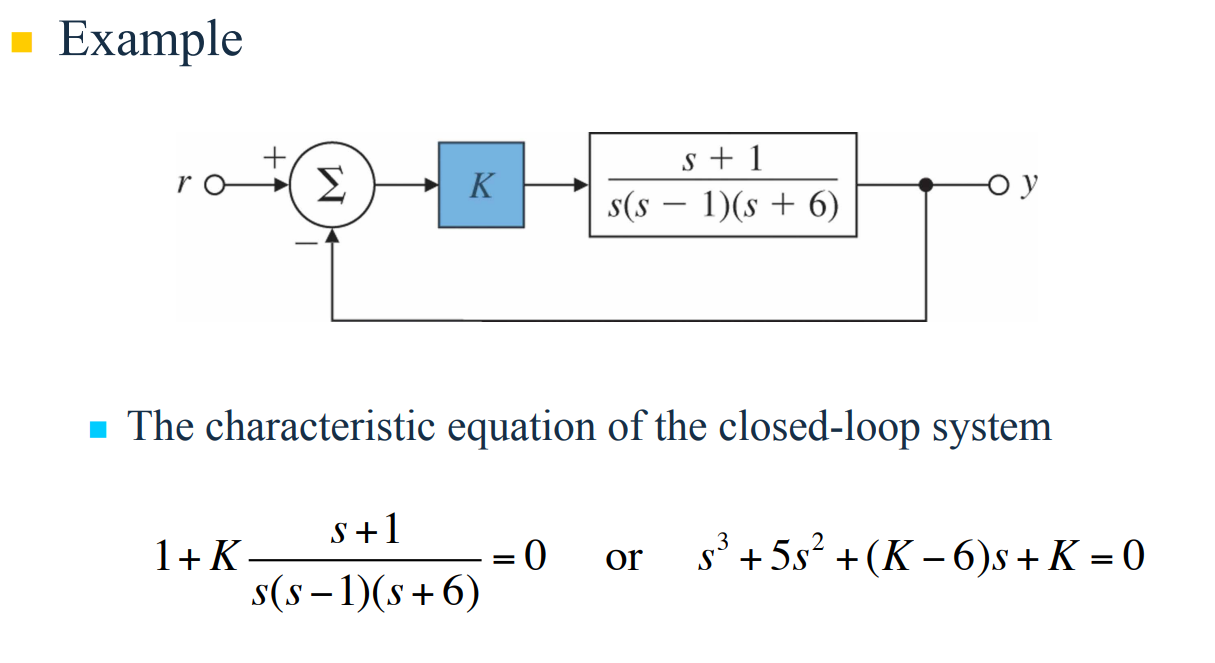
　다음 예제를 살펴보자.

극점 위치의 효과

　일단 전달함수가 정해지면 그 전달함수가 나타내는 시스템의 응답에 대한 해석을 시작할 수 있다. 시스템 방정식이 연립 상미분방정식(ODE)일 때, 전달함수는 다항식의 비가 될 것이다. 즉, $H(s) = b(s) / a(s)$ 이다. 만약 $a(s) = 0$ 이 되는 s의 값은 $H(s)$ 가 무한대가 되는 점이 될 것이다. 이러한 $s$ 값을 $H(s)$ 의 극점이라고 한다. $b(s) = 0$ 이 되는 $s$ 의 값은 $H(s) = 0$ 인 점이고, 이에 해당하는 s의 위치를 영점이라고 한다.
　충격응답은 전달함수에 대응되는 시간함수이므로 충격응답을 시스템의 고유응답(natural reponse)이라고 부른다. 대응하는 시간응답을 계산하기 위해 극점과 영점을 사용할 수 있고, $s$ -평면에서 극점의 위치로 시간응답을 식별할 수 있다. 예를 들어, $H(s)$의 부분분수 전개에서 극점들은 충격응답에 포함된 신호의 종류를 구별한다.
　1차 극점에 대해 $H(s) = \frac{1}{s+\sigma}$ 이고 이는 $h(t) = e^{-\sigma t}1(t)$ 와 같다. $\sigma > 0$ 일 때, 극점은 $s < 0$에 위치하고, 지수항은 감쇠하며, 충격응답은 안정하다(stable). $\sigma < 0$ 이면 극점은 $s > 0$에 있고, 지수항이 사간에 따라 증가하기 때문에 충격응답은 불안정하다(unstable). 다음 그림은 전형적인 안정한 응답을 나타내고 있으며 시상수(time constant)를 $\tau = 1 / \sigma$로 정의한다.

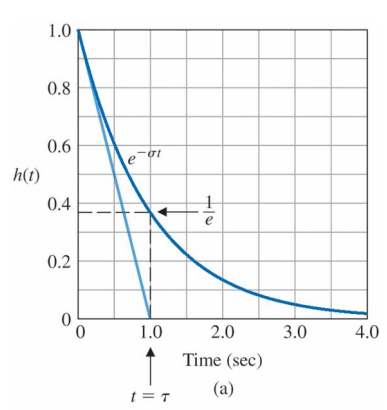
　이는 응답이 초기값의 $1/e$배 되는 시간이다. 그러므로 이것은 감쇠속도의 지표이다. 직선은 $t = 0$에서 지수곡선에 접하며 $t = \tau$에서 종료된다. 지수 표현의 이러한 특징은 시간선도를 그리거나 계산결과를 확인하는 데 유용한다. 다음 예제를 보자.

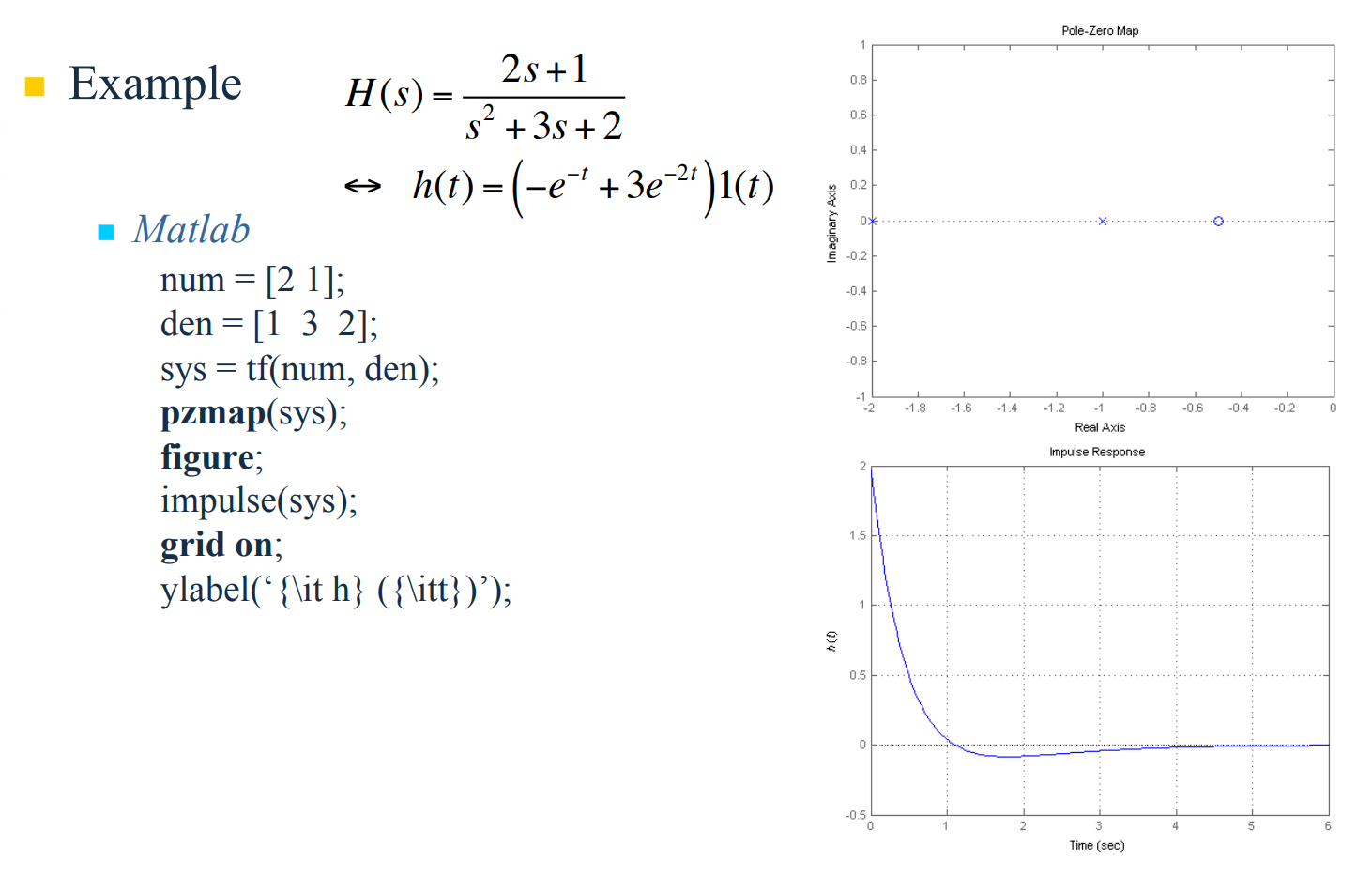
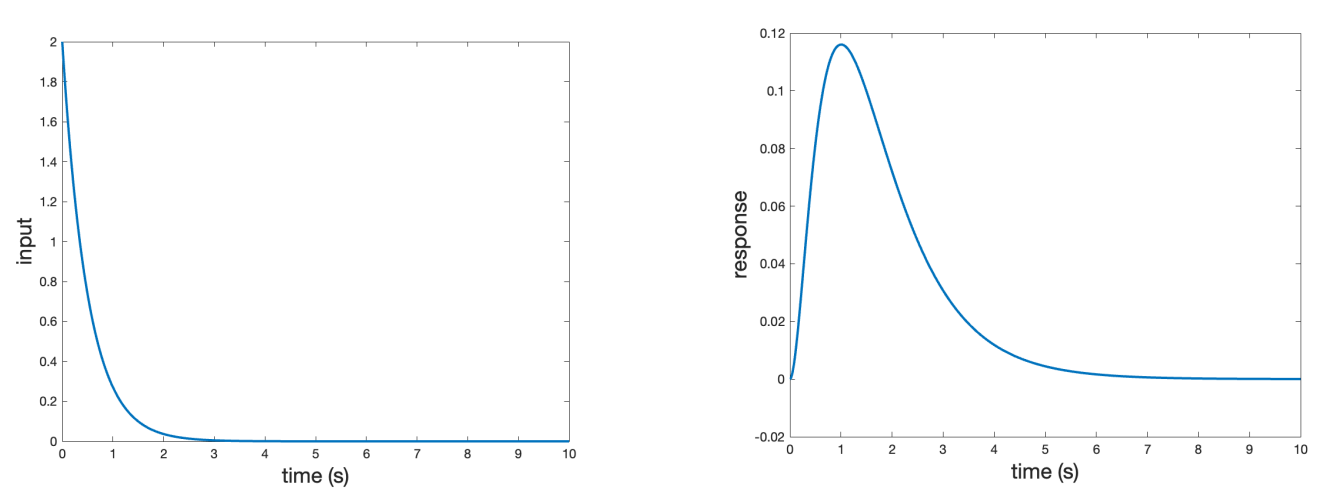
　위에서 아래 그래프는 빠른 $3e^{-2t}$ 항이 시간응답의 초기를 지배하고, $-e^{-t}$ 항이 시간응답의 후반에 주요한 영향을 주는 것을 보여준다.
　다음은 복소수를 포함한 극점의 위치와 그에 대응하는 고유응답에 대한 개략도가 나와 있다.

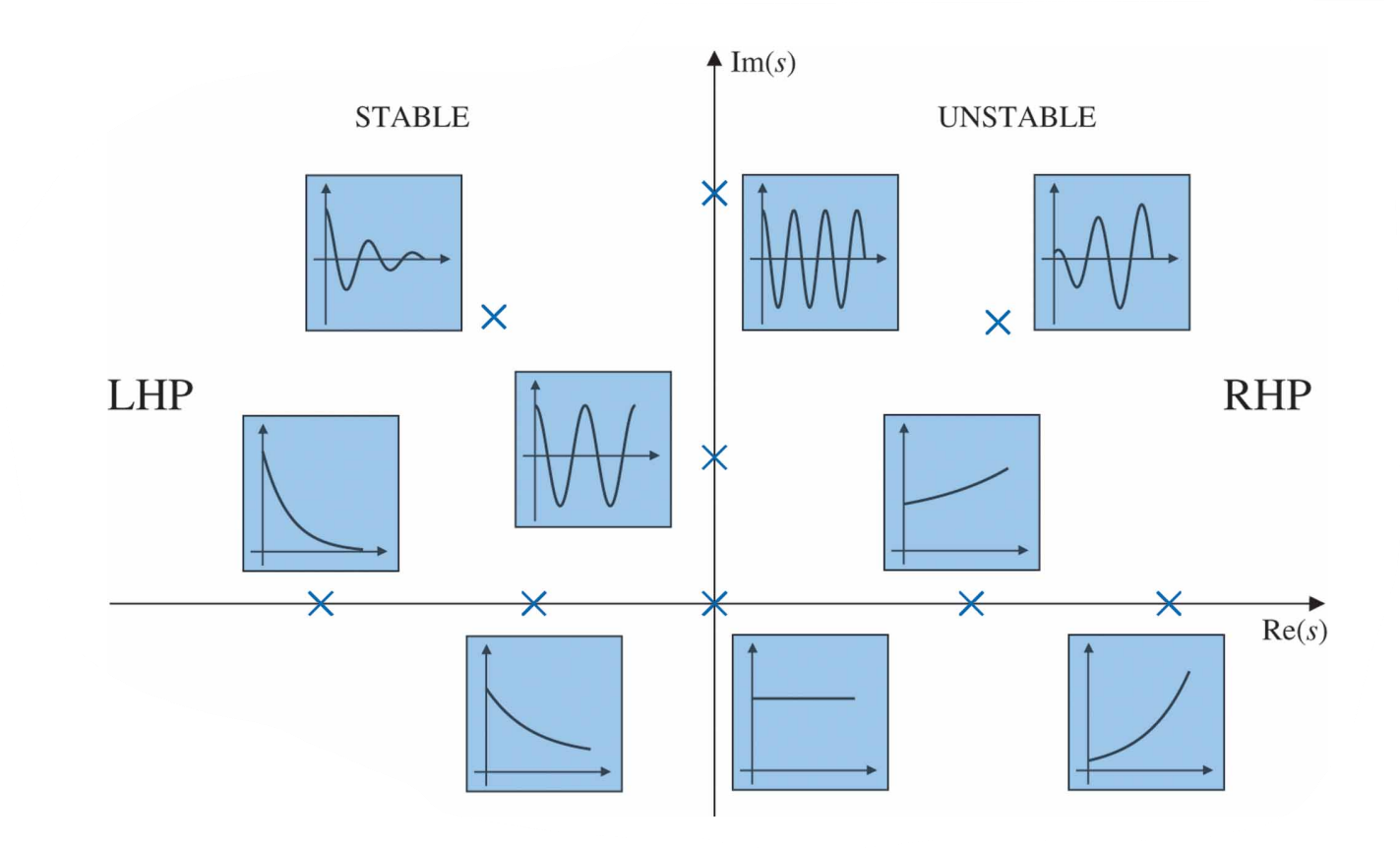
　복소수 극점은 다음과 같이 실수부와 허수부로 정의된다.

$s = -\sigma \pm j\omega_d$

　복소수 극점은 항상 공액복소수를 또 다른 극점으로 가지므로, 복소수쌍에 해당하는 분모는 다음과 같다.

$a(s) = (s + \sigma - j\omega_d)(s + \sigma +j\omega_d) = (s + \sigma)^2 + \omega_d^2$

　2차 미분방정식으로부터 전달함수를 구할 때 보통 다음의 다항식 형태를 사용한다.

$H(s) = \frac{\omega_n^2}{s^2 + 2\zeta\omega_ns + \omega_n^2}$

　위 $a(s)$ 를 $H(s)$ 의 분모 계수와 비교함으로써 다음과 같은 대응관계를 찾을 수 있다.

$\sigma = \zeta\omega_n, \omega_d = \omega_n \sqrt{1 - \zeta^2}$

　여기서 $\zeta$는 감쇠비(damping ratio)이고 $\omega_n$은 비감쇠 고유주파수(undamped natural frequency)이다. 이 전달함수의 극점은 $s$ -평면에서 반경 $\omega_n$, 각도 $\theta = sin^{-1}\zeta$에 위치한다.

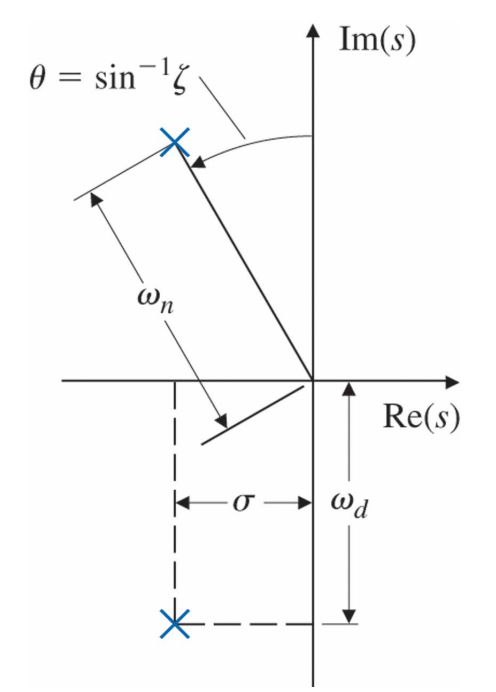
　직각좌표계에서 극점은 $s = -\sigma \pm j\omega_d$ 에 위치한다. $\zeta = 0$ 일 때 감쇠는 일어나지 않고($\theta = 0$) 감쇠 고유주파수 $\omega_d = \omega_n$(비감쇠 고유주파수)를 가진다. $H(s)$ 는 다음과 같이 쓸 수 있다.

$H(s) = \frac{\omega_n^2}{(s + \zeta\omega_n)^2 + \omega_n^2(1 - \zeta^2)}$

　그러므로 위의 충격응답은 다음과 같음을 알 수 있다.

$h(t) = \frac{\omega_n}{\sqrt{1 - \zeta^2}}e^{-\sigma t}(\sin\omega_dt)1(t)$

　세 극점의 위치가 다음과 같이 주어진다.

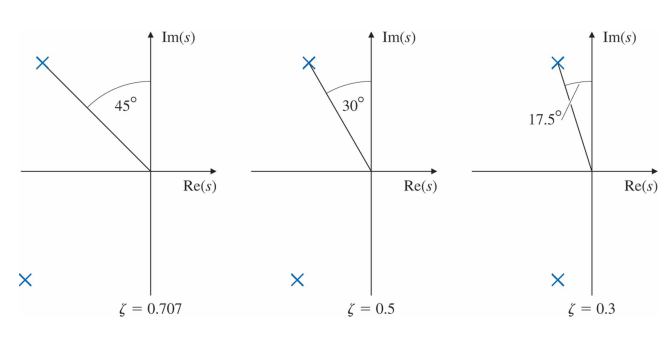
　극점의 음의 실수부 $\sigma$ 는 정현파와 곱해지는 지수외피(exponential envelop)의 감쇠율을 결정한다.

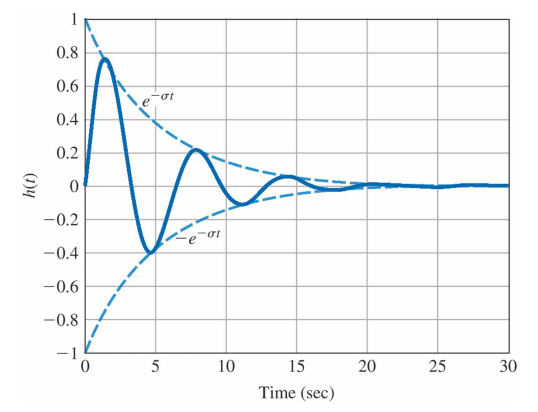
　만약 $\sigma < 0$ 이면 고유응답은 시간에 따라 증가하게 되고, 이미 정의한 바와 같이 시스템은 불안정하다고 말한다. 만약 $\sigma = 0$ 이면 고유응답은 증가하지도 감소하지도 않게 되며 이 경우 안정성은 정의할 수 없게 된다. 만약 $\sigma > 0$ 이면 고유응답은 감소하고 시스템은 안정하다.
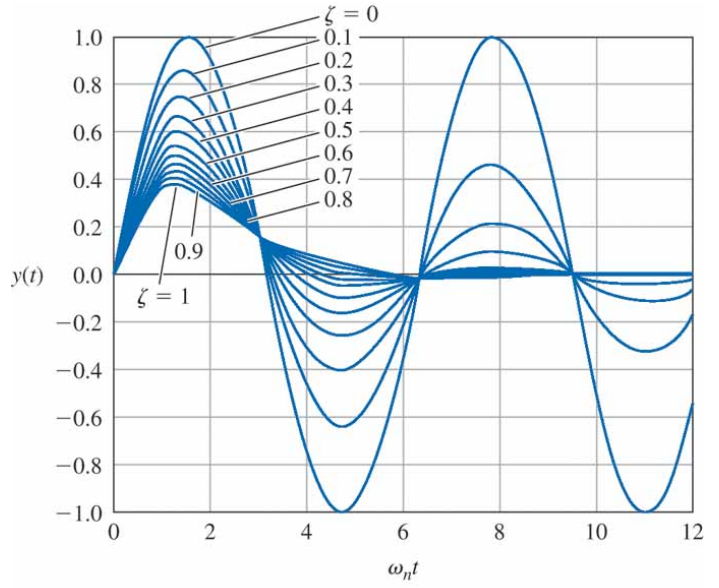
　여러 $\zeta$ 값에 대한 $y(t)$ 의 그림은 다음과 같다.

시간영역 사양

　제어시스템 설계를 위한 성능 사양은 때로 시스템의 시간응답과 관련된 요구사항들을 포함하고 있다. 계간응답에 대한 요구사항은 다음과 같이 설명된 표준량으로 표현된다.

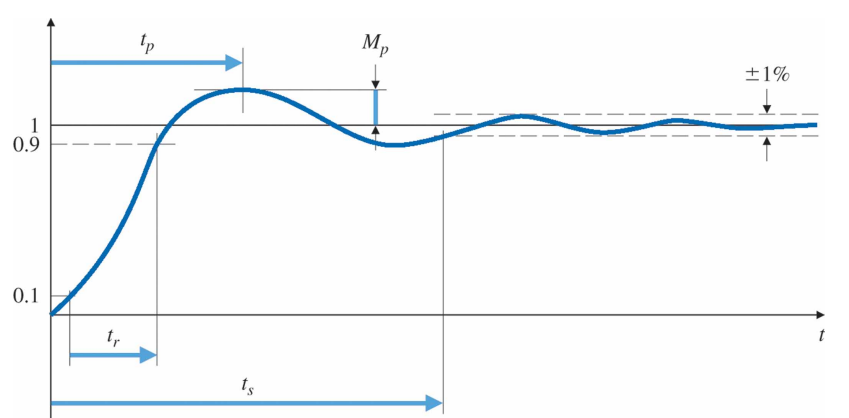
• 상승시간(rise time, $t_r$): 시스템이 새로운 설정값 근처에 도달할 때 걸리는 시간
• 정착시간(setting time, $t_s$): 시스템의 과도응답이 감소하는 데 걸리는 시간
• 오버슈트(overshoot, $M_p$): 최종값을 초과하는 시스템의 최대값을 그 최종값으로 나눈 것(때로 퍼센트로 나타낸다.)
• 최고시간(peak time, $t_p$): 시스템이 최대 오버슈트점에 도달하는 데 걸리는 시간

상승시간

　거의 모든 곡선은 거의 같은 시간에 상승한다. 만약 $\zeta = 0.5$ 의 곡선을 평균으로 고려한다면, $y = 0.1$ 부터 $y = 0.9$ 까지 상승하는데 걸리는 시간은 대략 $\omega_n t_r = 1.8$ 이다. 따라서 다음과 같이 말할 수 있다.

$t_r \cong \frac{1.8}{\omega_n}$

　이 식은 영점이 없는 2차 시스템에서만 정확히 성립한다. 다른 시스템에 대해서는 위 식은 $t_r$ 과 $\omega_n$ 사이의 관계에 대한 근사화가 된다.

오버슈트와 최고시간

　표준형 2차 시스템 계단응답은 다음과 같다.

$y(t) = 1 - \frac{e^{-\sigma t}}{\sqrt{1-\zeta^2}}\cos (\omega_dt-\beta)$

　$y(t)$ 가 최대값일 때 그 미분은 0이 될 것이다. 이는 $\sin \omega_d t = 0$이 성립하고 $\omega_d t_p = \pi$이다. 따라서 다음과 같다.

$t_p = \frac{\pi}{\omega_d}$

　위 식을 $y(t)$에 대한 식에 대입하면 다음과 같은 식을 얻는다.

$y(t_p) = 1 + M_p = 1 + e^{-\sigma\pi / \omega_d}$

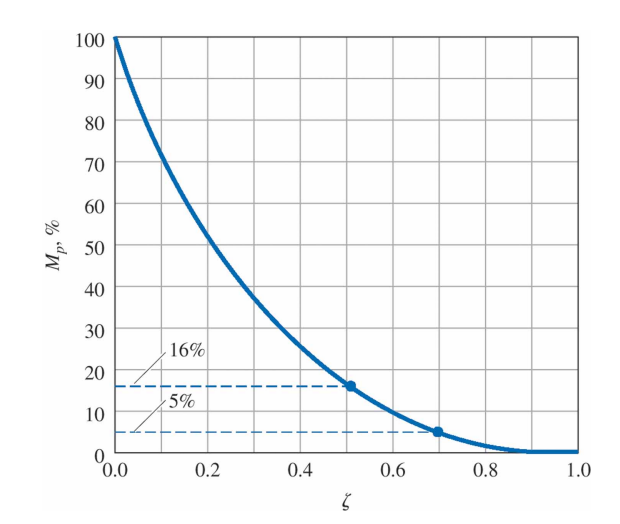
　따라서 다음의 공식을 얻는다.

$M_p = e^{-\pi\zeta / \sqrt{1-\zeta^2}}$, $0 \leq \zeta < 1$

　이 곡선에서 자주 사용되는 두 개의 값은 $\zeta = 0.5$일 때 $M_p = 0.16$ 그리고 $\zeta = 0.7$일 때 $M_p = 0.05$인데, 각각 16%와 5%의 오버슈트이다.

정착시간

　과도응답에서 관심 있는 마지막 파라미터는 정착시간 $t_s$이다. 이것은 과도응답이 아주 작은 값으로 감쇠하여 $y(t)$ 가 거의 정상상태에 도달하는 데 걸리는 시간이다. 이 오차의 기간은 본질적으로 과도지수(transient exponential) 항에 의해 결정되므로, 정착시간을 감쇠지수가 1%에 도달했을 때 $t_s$값으로 정의한다.

$e^{-\zeta\omega_nt_s} = 0.01$,　$\zeta\omega_nt_s=4.6$,　$t_s = \frac{4.6}{\zeta\omega_n}=\frac{4.6}{\sigma}$

　설계를 할 때, 우리는 $t_r, M_p, t_s$를 결정하고 실제 응답이 이러한 사양들과 동일하거나 유사할 수 있게 만드는 극점의 위치를 파악하기를 원한다. 주어진 $t_r, M_p, t_s$ 값에 대해 설계방정식은 다음과 같다.

$\omega_n \ge \frac{1.8}{t_r}$,　$\zeta \ge \zeta(M_p)$,　$\sigma \ge \frac{4.6}{t_s}$

　이 방정식들은 $s$-평면에서 그래프로 그려질 수 있으며 동적 응답 관련 제어시스템 사양을 만족시키기 위한 극점 및 영점 위치의 선택을 돕는 데 사용된다. 다음 예제를 보자.

영점과 추가 극점의 영향

　과도응답 해석의 단계에서, 영점은 극점에 의해 그 형태가 결정되는 지수항의 계수를 수정하는 데 영향을 미친다. 다음 동일한 극점을 가지지만 서로 다른 영점을 가지는 두 전달함수를 고려해보자.

$H_1(s) = \frac{2}{(s+1)(s+2)} = \frac{2}{s+1} - \frac{2}{s+2}$

$H_2(s) = \frac{2(s+1.1)}{1.1(s+1)(s+2)} = \frac{2}{1.1}(\frac{0.1}{s+1} - \frac{0.9}{s+2}) = \frac{0.18}{s+1} + \frac{1.64}{s+2}$

　$(s+1)$항의 계수는 $H_1(s)$의 2에서 $H_2(s)$의 0.18로의 감소는 $H_2(s)$에 있는 $s = -1.1$에서의 영점으로 인하여 발생하며 이 영점은 $s = -1$의 극점을 거의 상쇄하는 효과를 가진다. 만약 영점을 정확히 $s = -1$에 두면 이 항은 완전히 없어질 것이다. 일반적으로 극점 근처에 있는 영점의 전체 응답에서 그 극점항의 영향을 감소시킨다. 부분분수 전개에서 대응하는 계수에 대한 방정식으로부터 $C_1 = (s - p_1)F(s)|_{s=p_1}$이고, 만약 $F(s)$가 $s = -p_1$의 극점 근처에서 영점을 가지면, $F(s)$의 값은 $s$의 값이 0에 가까워지기 때문에 작아질 것이다. 그러므로 응답에서 그 항이 얼마나 크게 나타나는지를 반영하는 계수 $C_1$은 작게 될것이다.
　제어시스템을 설계할 때 영점이 과도응답에 미치는 영향을 고려하기 위해 두 개의 복소수 극점과 한 개의 영점을 가진 전달함수를 고려하자. 여러 가지 경우에 대해 그림을 그리는 것을 쉽게 하기 위해 다음과 같이 표준화된 시간과 영점 위치를 갖는 형태로 변환하여 사용한다.

$H(s) = \frac{(s/\alpha\zeta\omega_n) + 1}{(s/\omega_n)^2 + 2\zeta(s/\omega_n) + 1}$

　영점은 $s = -\alpha\zeta\omega_n = -\alpha\sigma$ 에 위치한다. 만약 $\alpha$가 크면 영점은 극점에서 멀어질 것이고, 영점은 응답에 거의 영향을 미치지 않을 것이다. 만약 $\alpha \cong 1$ 이면 영점은 극점의 실수부와 매우 가깝게 되고, 응답에 상당한 영향을 미칠 것이라고 예상할 수 있다. 몇몇 $\alpha$ 값에 대해 $\zeta = 0.5$ 일 때의 계단응답 곡선은 다음과 같다.

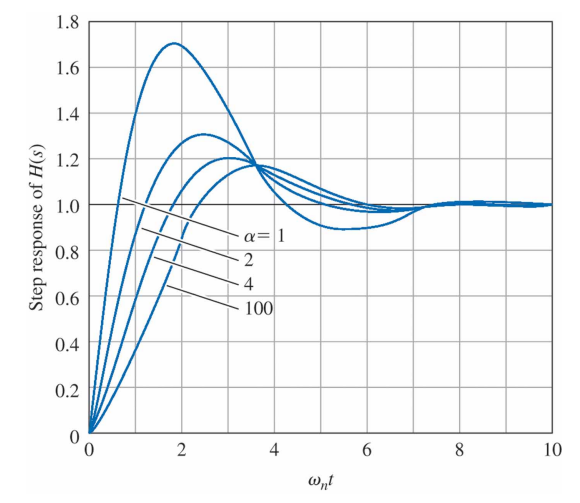
　영점의 주요한 영향은 오버슈트 $M_p$를 증가시키고 상승시간 $t_r$을 감소시키는 반면 정착시간에는 거의 영향을 미치지 않는다. $M_p$ 와 $\alpha$ 사이의 관계를 보여 주는 그림은 다음과 같다.

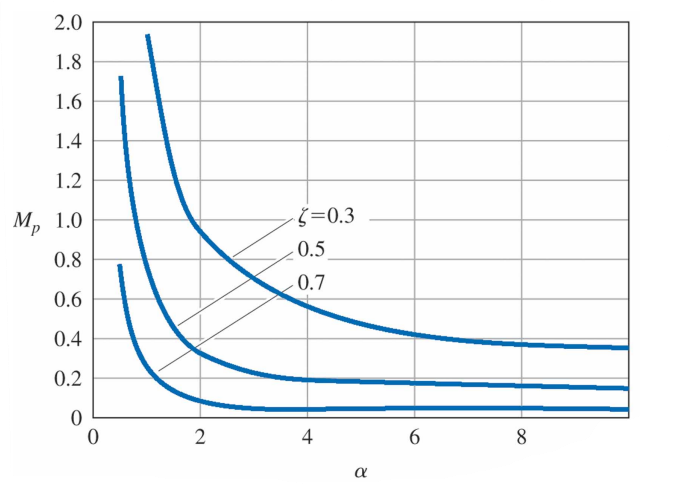
　위 그림에서 $\alpha > 3$ 이면 영점은 $M_p$에 거의 영향을 미치지 않지만, $\alpha$가 3보다 작아지면, 특히 $\alpha = 1$ 혹은 그 이하인 경우, 영점은 $M_p$ 에 큰 영향을 미친다는 것을 알 수 있다.
　위 그래프는 Laplace 변환으로 해석이 가능하다. 먼저 $s$ 로 $s/\omega_n$을 치환한다.

$H(s) = \frac{s/\alpha\zeta + 1}{s^2 + 2\zeta s + 1}$

　이는 전달함수의 주파수를 표준화하며, 해당 계단응답에서 시간을 표준화하는 효과를 가진다. 위 전달함수를 다음과 같이 두 항의 합으로 다시 쓸 수 있다.

$H(s) = \frac{1}{s^2 + 2\zeta s + 1} + \frac{1}{\alpha\zeta} \frac{s}{s^2 + 2\zeta s + 1}$

　첫 번째 항 $H_0(s)$ 은 기본항(유한 영점이 없는)이고 영점에 의해 만들어진 두 번째 항 $H_d(s)$ 는 기본항에 $(1/\alpha\zeta)$ 와 $s$ 를 곱한 값이다. 위 식을 Laplace 변환을 하면 다음과 같다.

$y(t) = y_0(t) + y_d(t) = y_0(t) + \frac{1}{\alpha\zeta} \dot{y_0}(t)$

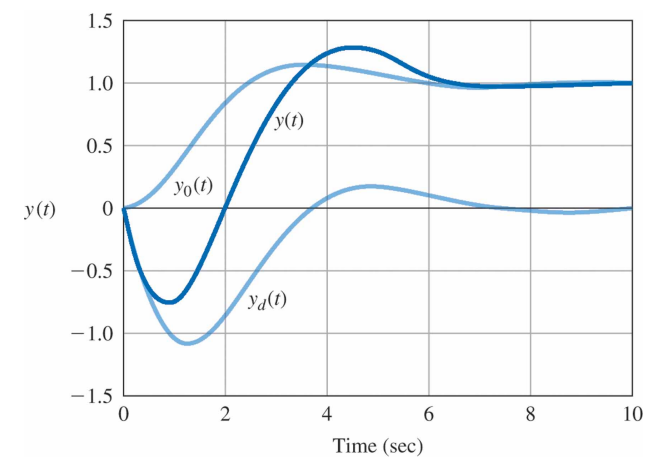
　$y_0(t)$와 $y_d(t)$로 나타낸 $H_0(s)$ 와 $H_d(s)$의 계단응답들은 다음과 같다.

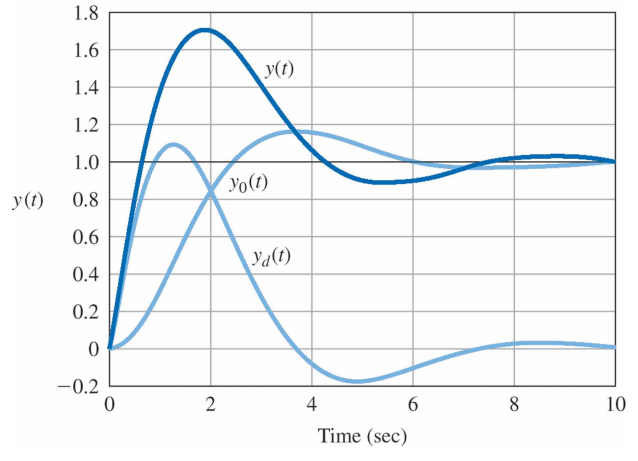
　이 곡선들을 보면, 왜 영점이 오버슈트를 증가시키는지 알 수 있다. 미분항은 곡선 시작부분에서 큰 진폭을 가지게 되고 이것이 $H_0(s)$ 응답에 더해지면 $H(s)$ 전체 응답이 상승하여 오버슈트를 발생시킨다. 이 해석은 $\alpha < 0$ 이고 영점이 RHP에 있을 경우($s > 0$)에 대해서도 매우 유용하다. 이 경우, 미분항을 더하지 않고 빼게 된다. 대표적인 경우는 다음과 같다.

　표준 2차 계단응답에 영향을 미치는 부가극점(extra pole)의 효과를 고려하는 것 또한 유용하다. 이 경우 다음의 전달함수를 고려한다.

$H(s) = \frac{1}{(s/\alpha\zeta\omega_n + 1)[(s/\omega_n)^2 + 2\zeta(s/\omega_n) + 1]}$

　몇몇 $\alpha$에 대해 $\zeta = 0.5$ 일 때 위 전달함수에 대한 계단응답 선도는 다음과 같다.

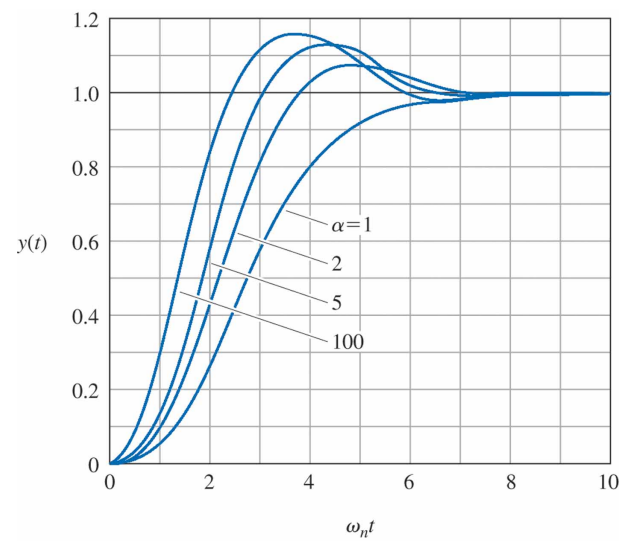
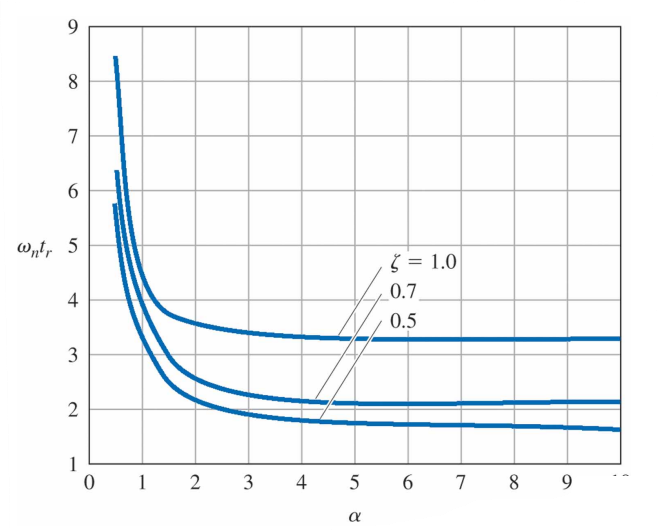
　이 경우, 주요 효과는 상승시간이 증가되는 것이다. 상승시간과 $\alpha$ 사이의 관계는 몇몇 $\zeta$ 값에 대해서 다음과 같이 주어져 있다.

안정도

　전달함수 분모다항식의 모든 근이 음수 실수부를 가지면(즉, 모두 $s$-평면의 좌반에 있으면) LTI 시스템은 안정하고, 그렇지 않으면 불안정하다. 만약 초기조건들이 0으로 수렴하면 시스템은 안정하고, 발산하면 불안정하다. LTI(상수 파라미터) 시스템은 만역 시스템의 모든 극점이 확실하게 s의 좌반평면 내에 있으면(즉, 모든 극점이 음의 실수부,$s = -\sigma + j\omega, \sigma > 0$,를 가지면) 안정하다(stable). 만약 시스템의 어떤 극점에 s의 우반평면에 있으면(즉, 양의 실수부, $s = -\sigma + j\omega, \sigma < 0$,를 가지면) 시스템은 불안정하다(unstable).

한정입력-한정출력 안정도

　만약 모든 한정입력이 한정출력을 만든다면(시스템으로 무엇이 들어오든지 상관없이) 시스템은 한정입력-한정출력 안정도(bounded input-bounded output stability,BIBO)를 가진다고 말한다. 이 특성에 대한 시험은 시스템응답이 콘벌루션에 의해 주어질 때 손쉽게 가능하다. 만약 시스템이 입력 $u(t)$, 출력 $y(t)$, 충격응답 $h(t)$ 를 가진다면 다음과 같다.

$y(t) = \int_{-\infty}^{\infty} h(\tau)u(t - \tau) \, d\tau$

　만약 $u(t)$ 가 한정된다면 $|u| \le M < \infty$ 를 만족하는 상수 $M$ 이 존재한다고 할 수 있으므로 출력은 다음과 같이 한정된다.

$|y| = |\int hu\, d\tau| \le \int |h||u| \, d\tau \le M\int_{-\infty}^{\infty} |h(\tau)| \, d\tau$

　따라서 만약 $\int_{-\infty}^{\infty} |h| \, d\tau$ 가 한정되면 출력은 한정될 것이고 만약 다음 적분이 한정되면 출력 입력 $h(t)$ 를 가진 시스템은 BIBO-안정하다.

$\int_{-\infty}^{\infty} |h(\tau)| \, d\tau < \infty$

　일반적으로 허수축이나 RHP에 극점을 가지는 LTI 시스템의 응답은 BIBO-안정하지 않다. 만약 모든 극점이 LHP 안에 있으면 응답은 BIBO-안정할 것이다. 따라서 이러한 시스템에 대해 전달함수의 극점 위치는 안정성을 확인하기 위해 사용될 수 있다.

LTI 시스템의 안정도

　전달함수 분모다할식이 다음의 특성방정식으로 표현되는 LTI 시스템을 고려하자.

$s^n + a_1s^{n-1} + a_2s^{n-2} + \cdots + a_n = 0$

　시스템의 모든 극점들이 확실하게 LHP에 있을 때 시스템이 안전되는데 이를 내부안정도(internal stability)라 한다. 그러므로 시스템의 안정도는 특성방정식의 근들의 위치를 계산하고 모든 근이 LHP에 있는지를 확인함으로써 판별할 수 있다. 만약 시스템이 RHP에 있는 극점을 가진다면 그 시스템은 불안정하다(unstable). 그러므로 $j\omega$ 축은 점근적인 안정성과 불안정한 응답 사이의 안정성 경계이다. 만약 시스템이 $j\omega$축에 중복되지 않는 극점을 가진다면 중립적으로 안정하다(neutally stable)고 한다. 만약 $j\omega$축에서 중복되는 극점을 가지면, 이 시스템은 불안정하다(unstable)($te^{\pm j \omega_i t}$ 항 때문에 발생한다).

Routh 안정도 판별법

　이 방법은 다항식의 계수가 문자(비수치)인 경우에 안정성을 보장할 수 있는 계수들의 범위를 구하는 문제에 유용하게 사용된다. 다음 $n$차 시스템의 특성방정식을 고려하자.

$a(s) = s^n + a_1s^{n-1} + a_2s^{n-2} + \cdots + a_{n-1}s + a_n$

　시스템의 안정도를 위한 필요조건은 위 식의 모든 근이 음의 실수부를 가지는 것이고, 이것은 모든 ${a_i}$가 양수임을 요구한다.

안정도를 위한 필요조건(충분조건은 아니다)은 특성다항식의 모든 계수가 양수가 되는 것이다.

　Routh 공식은 ${a_i}$의 함수인 삼각형 형태의 배열을 계산할 필요가 있다. Routh는 안정도를 위한 필요충분조건은 이 배열의 첫 번째 열에 있는 모든 요소가 양이어야 한다는 것을 보였다.

Routh 배열의 첫 번째 열에 있는 모든 요소가 양수이면 시스템은 안정하다.

　$a(s) = s^6 + 4s^5 + 3s^4 + 2s^3 + s^2 + 4s +4$ 를 예로들어보자.

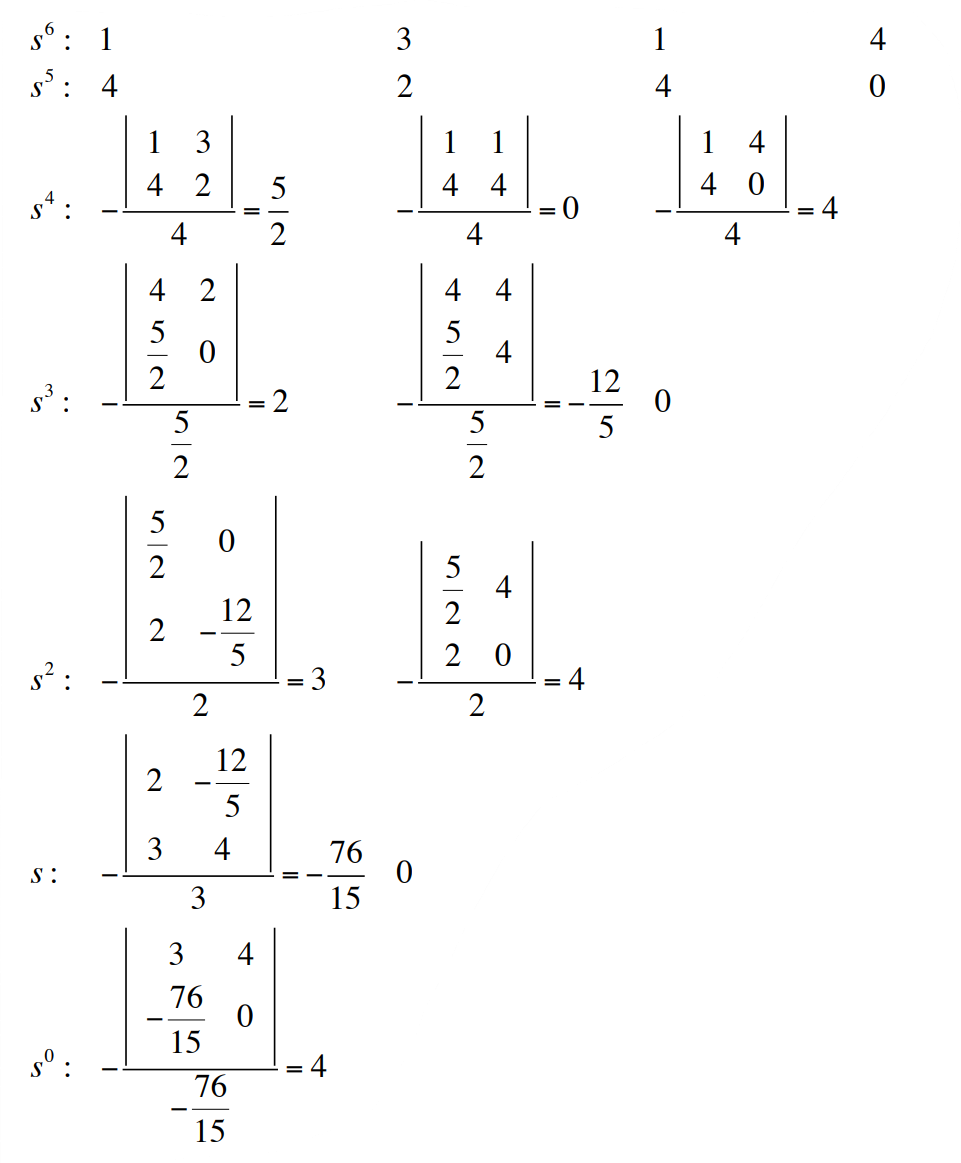
　위는 두번의 부호변화가 있었기 때문에 RHP에 두 개의 극점이 존재한다. 다음 예제를 보자.