4장 피드백에 관한 첫 해석
Updated:
제어의 기본 방정식
다음과 같은 개루프 시스템에서 플랜트 입력에 외란이 가해지면 출력은 다음과 같이 주어진다.
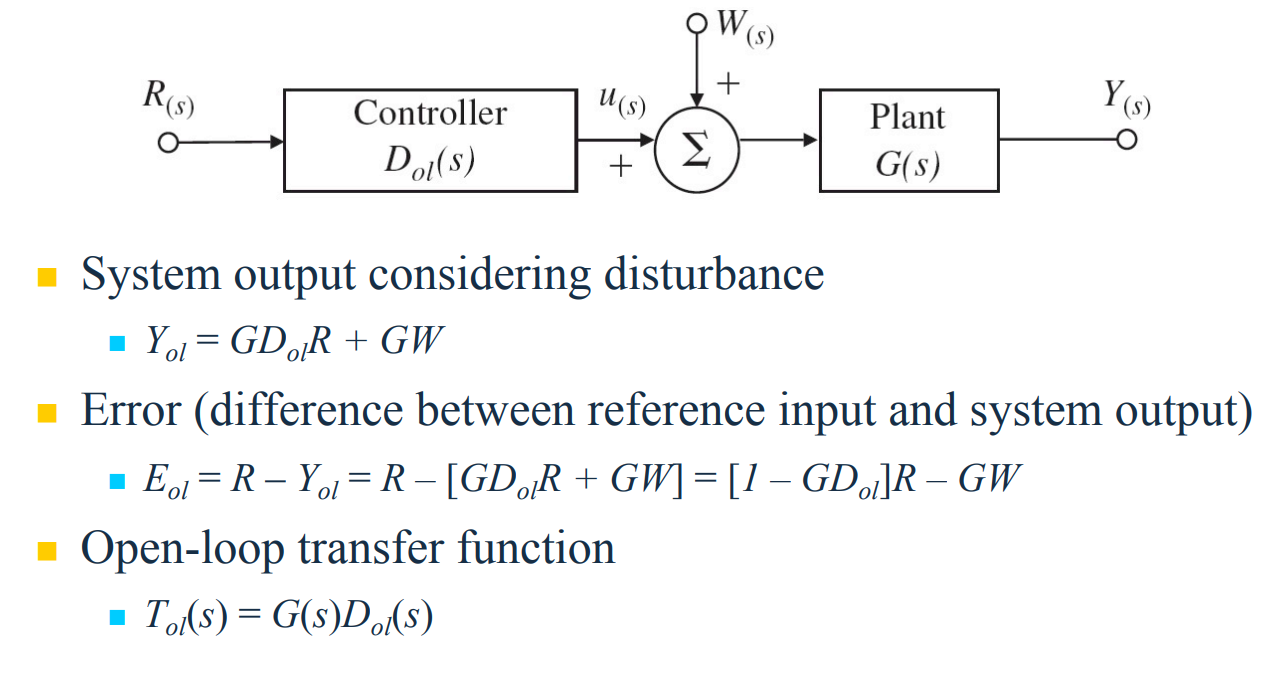
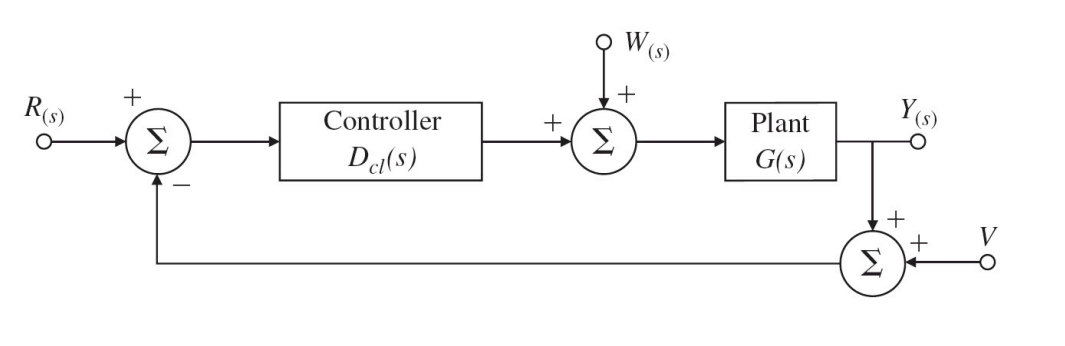
피드백 제어에서 다음은 기본적인 단일 피드백 구조를 보여준다.
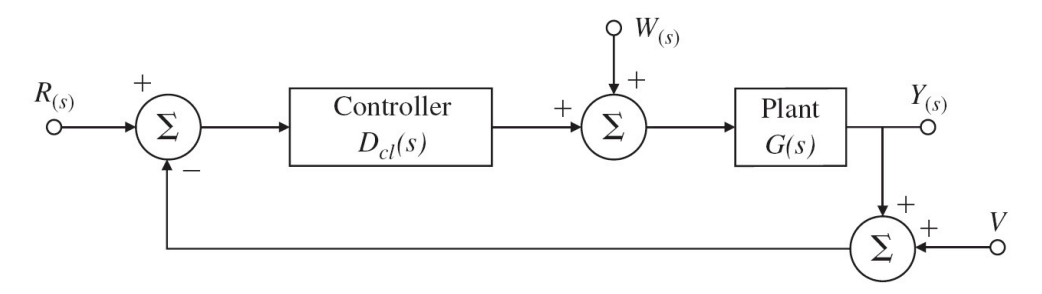
여기서 세 가지 외부입력이 있다.
- 기준입력(R, Reference): 출력이 추종하기를 원함
- 플랜트 외란(W, Plant disturbance): 제어를 통해 출력이 영향을 주지 않을 것이라고 여겨짐
- 센서잡음(V, Sensor noise): 제어기가 무시해야 함
위 피드백 블록선도에서 출력과 제어에 대한 방정식은 다음과 같이 세 가지 입력과 각각에 대한 출력의 합으로 주어진다.

이 방정식들을 이용하여 개루프 및 폐루프의 네 가지 기본 목적인 안정도, 추적성, 조절성, 민감도를 탐구할 것이다.
안정도
안정도의 요구조건은 전달함수의 모든 극점이 좌반면(LHP)에 있어야 한다. 식 $Y_{ol} = GD_{ol}R + GW$의 개루프의 경우, 이는 $GD_{ol}$의 극점이다. 전달함수 $T_{ol}(s) = G(s)D_{ol}(s) = \frac{b(s)}{a(s)} \frac{c(s)}{d(s)}$로 표현한다. 이 식에서 안정도 조건은 $a(s)$와 $d(s)$가 우반면(RHP)에 근을 가지지 않아야 하는 것이다. 만약 $a(s)$ 가 RHP에 근을 가져서 불안정할 경우 $c(s)$와 $d(s)$ 의 영점으로 이 극점을 상쇄한다면 안정화될수 있다고 믿을 수 있지만, 불안정한 극점은 남아 있고 약간의 잡음 또는 외란으로 출력이 포화에 의해 멈추거나 시스템이 고장 날 때까지 켜질 것이다. 따라서 개루프 구조는 불안정한 플랜트를 안정되게 만들 수 없으므로 플랜트가 불안정하게 되면 사용할 수 없다.
식 $E_{cl} = \frac{1}{1 + GD_{cl}} R - \frac{G}{1 + GD_{cl}} W + \frac{GD_{cl}}{1 + GD_{cl}} V$ 의 피드백 시스템에서 시스템 극점은 $1 + GD_{cl} = 0$ 의 근이다. 특성방정식은 다음과 같다.
만약 플랜트가 불안정하고 $a(s)$가 RHP에 극점을 가지는 경우 피드백 제어기는 시스템을 안정화할 수 있다. 예를 들어, $G(s) = \frac{1}{s^2 - 1}$에서 $b(s) = 1$이고 $a(s) = s^2 -1 = (s + 1)(s - 1)$이다. 만약 $D_{cl}(s) = \frac{K(s + \gamma)}{s + \delta}$이면 특성방정식은 다음과 같다.
이 경우에 간단한 해법은 $\gamma = 1$로 두고 (안정한) 공통 항을 상쇄하는 것이고 결과는 $(s - 1)(s + \delta) + K = 0$이다. 남은 두 개의 극점을 원하는 위치에 놓음으로써 최종 2차 방정식은 쉽게 풀 수가 있다.
다항식 입력에 대한 정상상태 오차의 제어: 시스템 형태
추적에 대한 시스템 형태
추적 문제는 출력이 가능한 기준입력과 가깝게 추적할 수 있도록 하는 것이다.

위의 단위 피드백의 경우 시스템 오차는 $E_{cl} = \frac{1}{1 + GD_{cl}} R - \frac{G}{1 + GD_{cl}} W + \frac{GD_{cl}}{1 + GD_{cl}} V$ 로 주어진다. 기준 입력만 추적하고 $W = V = 0$으로 한다면 오차 방정식은 단순히 $E = \frac{1}{1 + GD_{cl}} R$ 이다.
다항식의 입력들을 고려하기 위해 입력 $r(t) = \frac{t^k}{k!} 1(t)$로 하며 그 변환은 $R(s) = \frac{1}{s^{k+1}}$ 이다. 기계적 시스템을 일반적인 기준 명칭의 근거로 삼으면 실제적인 신호의 단위에도 불구하고 $k = 0$인 계단입력을 ‘위치’ 입력, $k = 1$인 경사입력을 ‘속도’ 입력, $k = 2$인 입력을 ‘가속도’ 입력이라고 한다. 오차 공식에 최종값 정리를 적용하면 다음 결과를 얻는다.
우선 $GD_{cl}$이 원점에 극점을 가지고 있지 않고 적분기가 없고 $R(s) = 1/s$ 인 계단 입력이 가해진 시스템에 대해 생각해보자. 이 경우 위 식은 다음과 같이 표현된다.
여기서 $r_{ss} = \lim\limits_{t \to \infty} r(t) = 1$ 이다. 이 시스템을 0형이라고 정의하고 $\lim\limits_{s \to 0}GD_{cl} = K_p$를 위치 오차상수(position constant)로 정의한다.
만약 $GD_{cl}$ 에 적분기가 한 개 있다면 $R(s) = 1/s^2$이고 $e_{ss} = \lim\limits_{s \to 0} s \frac{1}{1 + GD_{cl}} \frac{1}{s^2} = \frac{1}{\lim\limits_{s \to 0} sGD_{cl}} = \frac{1}{K_v}$이다. 상수 $K_v$는 속도상수라고 부르고 시스템은 1형이라고 분류한다.
만약 $GD_{cl}$ 에 적분기가 두 개 있다면 $R(s) = 1/s^3$이고 $e_{ss} = \lim\limits_{s \to 0} s \frac{1}{1 + GD_{cl}} \frac{1}{s^3} = \frac{1}{\lim\limits_{s \to 0} s^2GD_{cl}} = \frac{1}{K_a}$이다. 상수 $K_a$는 가속도상수라고 부르고 시스템은 2형이라고 분류한다.
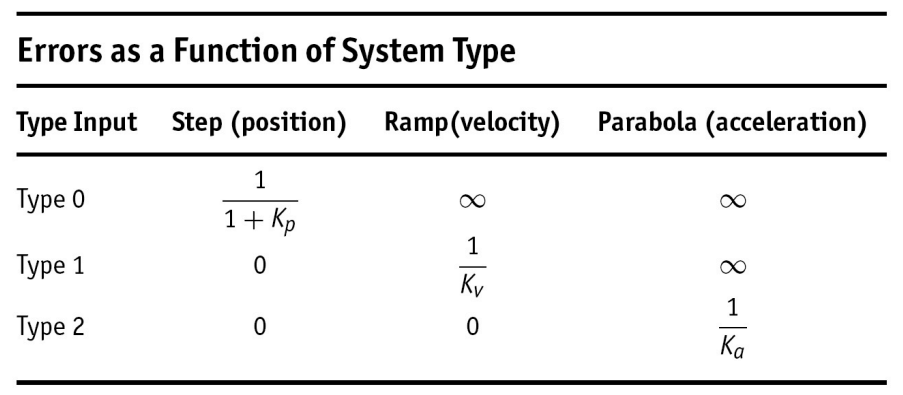
시스템 형태의 정의는 다항식을 추적하는 시스템의 능력을 빨리 파악하는 데 도움을 준다. 단위 피드백 구조에서 1형 시스템에서 원점에 있는 극점을 제거하지 않고 프로세스 파라미터가 변한다면 속도상수는 변하지만 상수 입력에 대한 정상상태 오차는 없으며 여전히 1형 시스템이다. 2형 또는 그 이상 형태의 시스템에 대해서도 마찬가지이다. 그러므로 시스템 형태는 단위 피드백 구조에서 파라미터 변화에 대한 강인한 특성(robust property)이라고 말할 수 있다. 다른 종류의 제어구조보다 단위 피드백을 더 선호하는 주요한 이유는 강인성 때문이다.
다음 모터 축에 회전속도계(tachometer)가 고정되어 있고 회전속도계의 전압이 제어의 한 부분으로서 피드백되는 비단위 피드백(non-unity feedback) 시스템의 전기모터 위치제어 예제를 보자.
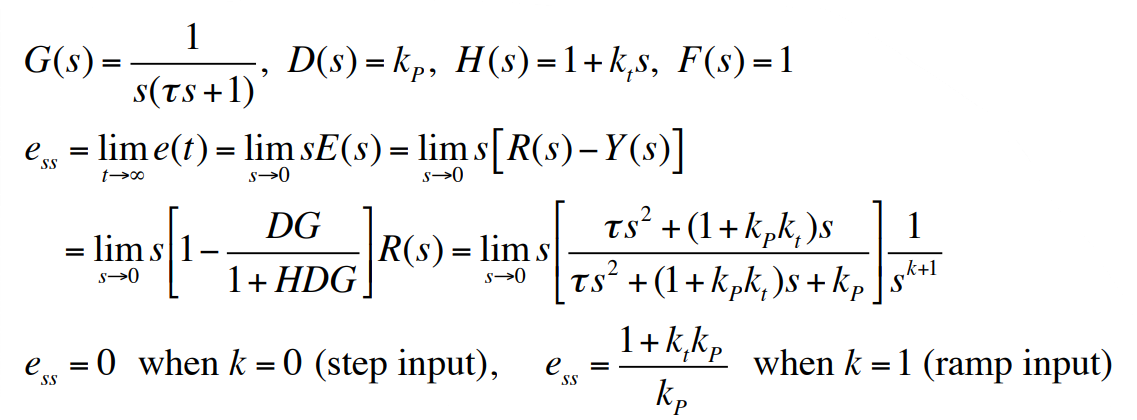
그러므로 시스템은 1형이고 속도상수는 $K_v = \frac{k_p}{1 + k_tk_p}$이다.
다음과 같은 DC모터의 단순화된 모델에 대해 생각해 보자.
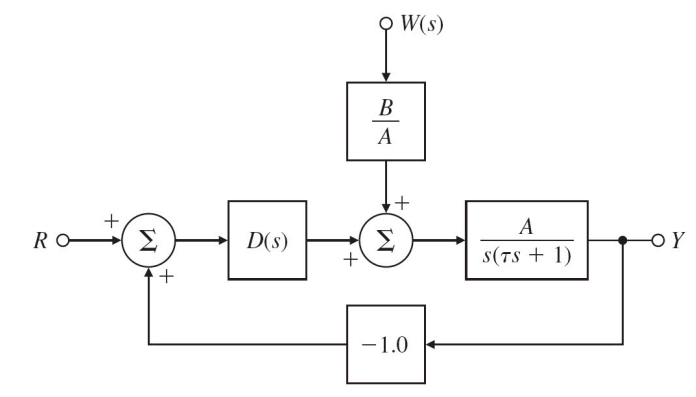
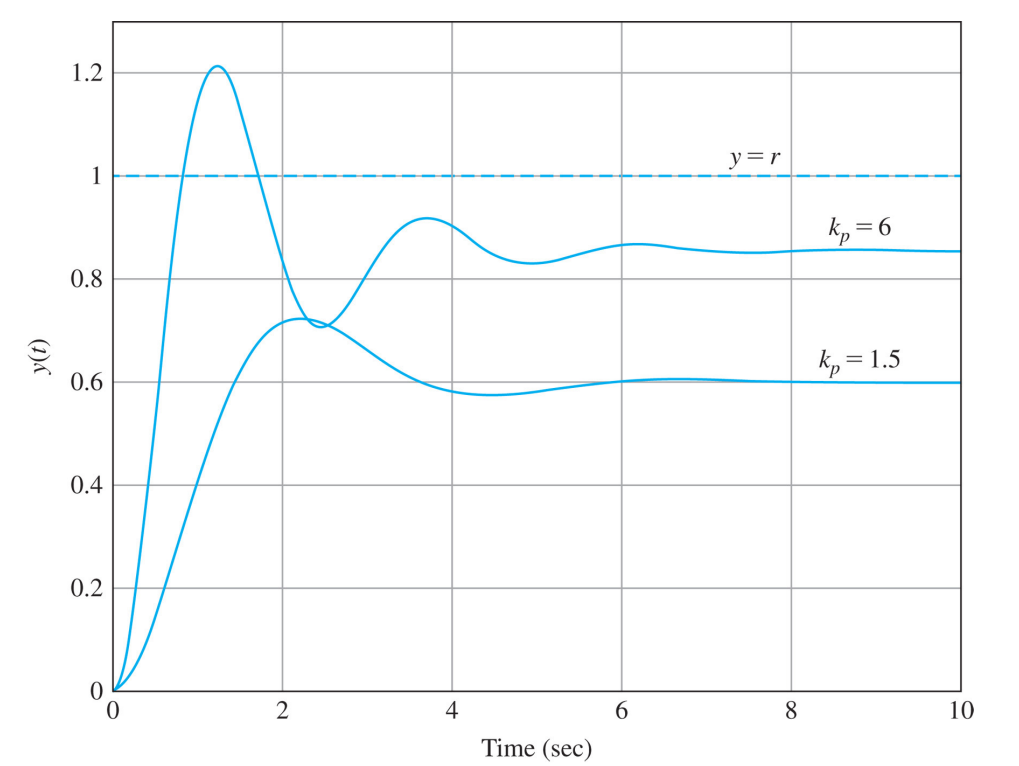
위 시스템에서 비례(P) 제어(proportional controller)를 사용하면 $D_{cl}(s) = k_P$이고 외란 입력(disturbance inputs)에 대한 시스템 타입을 고려하자.
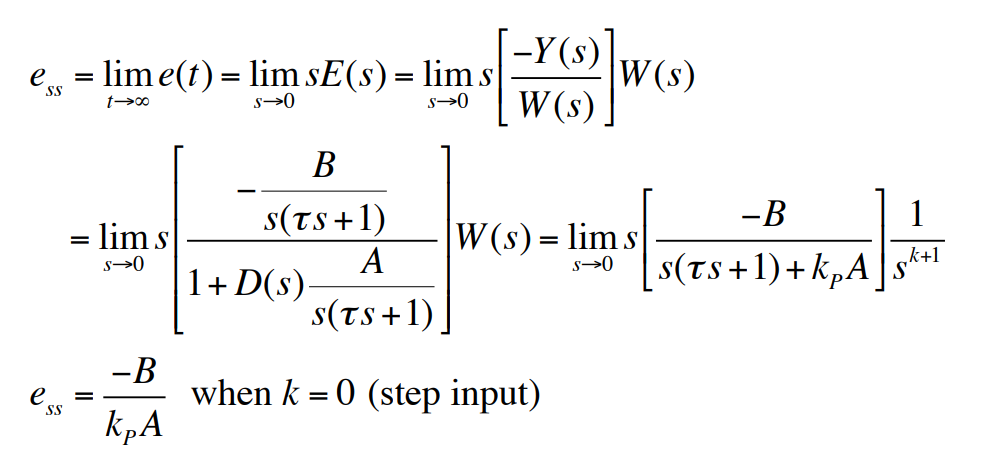
위 시스템은 0형이고 단위계단 토크입력(disturbance inputs)에 대한 정상상태 오차는 위와 같음을 알 수 있다. 또한 이 시스템의 기준입력(reference inputs)에 대해 1형이다. 같은 시스템이라도 다른 입력에 대해서는 시스템의 형태가 다를 수 있다.
위 시스템에서 비례적분(PI) 제어(proportional plus integral controller)를 사용하면 $D_{cl}(s) = k_P + \frac{k_I}{s}$이고 외란 입력에 대한 시스템 타입을 고려하자.

그러므로 시스템은 1형이다.
3항 제어기: PID 제어
비례적분미분(PID, proportional plus integral plus derivative) 제어 방정식의 변환 함수는 다음과 같다.
비례(P) 제어
피드백 제어신호가 시스템 오차에 선형적으로 비례하도록 만들어질 때, 이를 비례 피드백(proporional feedback)이라고 한다.
만약 플랜트가 2차 시스템이면 플랜트 전달함수는 다음과 같이 쓸 수 있다.
이 경우 비례제어를 포함한 특성방정식은 다음과 같다.
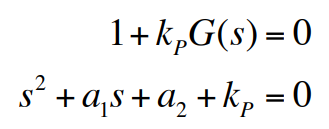
$k_P$는 비례게인(proportional gain)으로 불린다. 설계자는 이 방정식에서 $k_P$를 조정하여 상수항 $(a_2 + k_PA)$을 제어할 수 있다. $k_P$는 고유진동수를 바꾸지만 감쇠항 $a_1$는 $k_P$에 독립적이기 때문에 바꿀 수 없다. 예를 들어 $s^2 + 2\zeta\omega_n s + \omega_n^2 = 0$에서 설계자는 natural frequency를 제어할 수 있지만, damping을 제어할 수 없다.
적분(I) 제어
피드백 제어 신호가 시스템 오차의 적분값에 선형적으로 비례할 경우, 이 결과를 적분 피드백(integral feedback)이라고 부른다. 적분제어의 목표는 정상상태 추종오차와 외란으로부터의 정상상태 출력응답을 최소화하는 것이다. 적분제어 방법은 다음과 같은 식을 가진다.
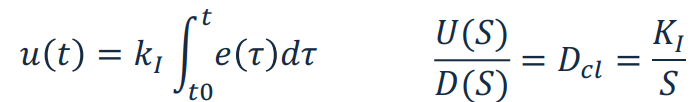
$k_I$는 적분게인(integral gain)이라고 한다. 이 제어방법은 시간마다 가해지는 제어신호가 그 시간까지 추종오차의 모든 합임을 의미한다. 따라서 제어동작은 시스템 오차의 ‘기록(history)’에 기반하게 된다.
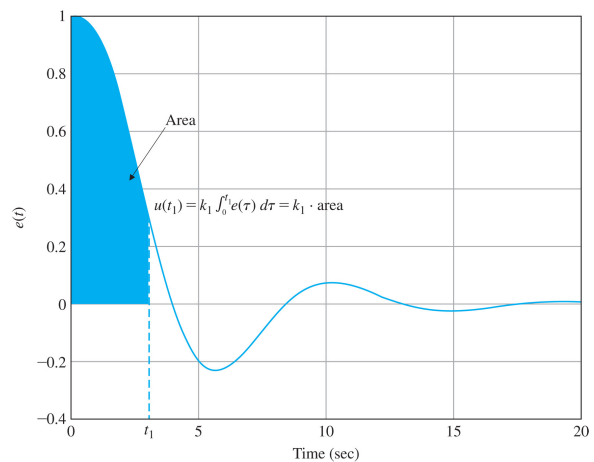
다음 그림을 통해 매시간의 제어신호가 시스템 오차 곡선 아래의 면적과 비례함을 알 수 있다.
다음 플랜트 $G(s)$에 적분제어를 적용해 보자.

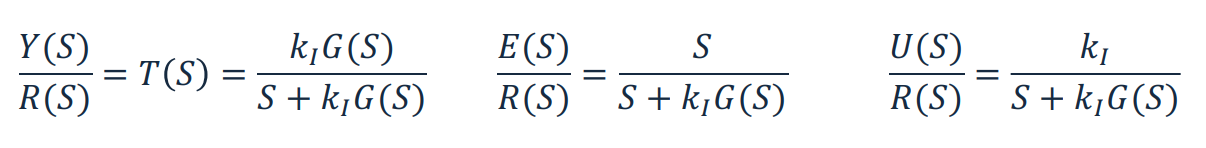
이제 단위계단 기준입력 $R(s) = 1/s$를 넣어보자. 위 식에 최종값 정리($G(0) = 1$)를 사용하면 다음과 같다.
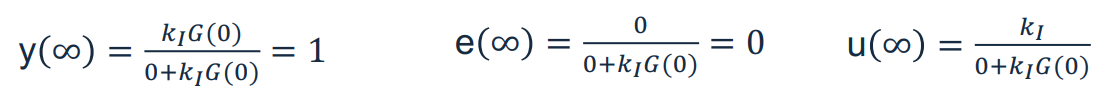
비례제어기에서는 $k_P$의 값이 무엇이든 간에 항상 추종오차가 있지만, 적분제어기에서는 $k_I$가 어떤 값이든 간에 정상상태 추종오차는 0이 된다.
외란입력에 대한 출력과 제어신호는 다음과 같다.

이제 단위계단 외란입력 $W(s) = 1/s$를 넣어보자. 위 식에 최종값정리를 사용하면 다음과 같다.
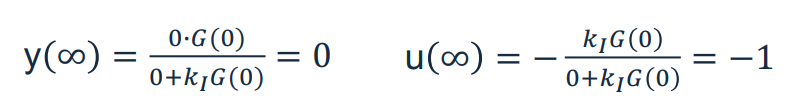
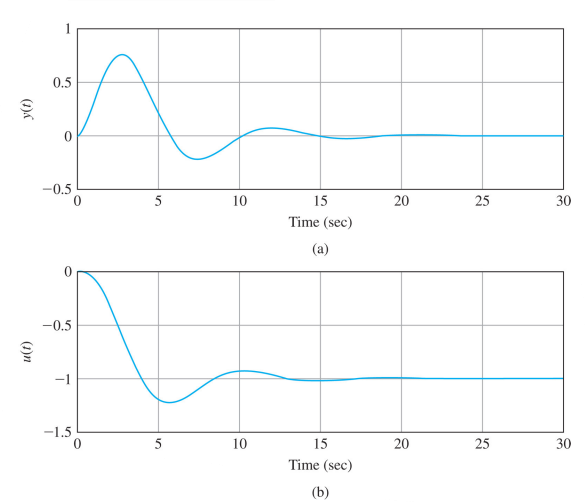
위 두 식은 출력에서 정상상태 오차가 0이고 외란을 완벽하게 제거하도록 하는 제어신호의 최종값을 보여준다. 다음은 $k_I = 0.5$일 때의 시스템의 응답을 나타낸다.
비례적분(PI) 제어
더 작은 정상상태 오차를 얻기 위해 비례제어기에 적분항을 추가하여 시간영역에서 비례적분(PI, proportional plus integral)제어 방정식은 다음과 같이 만든다.
다음 예제를 보자.

만약 플랜트가 2차 시스템이면 다음과 같이 표현된다.

미분(D) 제어
고전 제어기의 마지막 항은 미분 피드백(derivative feedback)이며, 이는 비율 피드백(rate feedback)으로도 불린다. 미분 피드백의 목표는 폐루프 시스템의 안정도를 증가시키는 것뿐만 아니라 과도응답의 속도를 상승시키는 것과 오버슈트를 감소시키는 것이다. 따라서 안정도를 증가시켜야 한다면 미분 피드백을 사용하는 것이 요구된다. 미분 피드백의 제어식은 다음과 같다.

위 식에서 $k_D$는 미분게인(derivative gain)이며, 제어신호는 시스템 오차의 변화율(혹은 미분)에 비례한다.
미분제어는 거의 단독으로 사용되지 않고 보통 비례제어와 같이 사용된다. 핵심 이유는 미분값은 목표하는 최종값에 대한 정보를 제공하지 않기 때문이다. 또한 $e(t)$가 상수를 유지한다면 미분제어기의 출력은 0이 될 것이고 비례제어기 또는 적분제어기가 이 순간 제어신호를 공급해 주어야 한다.
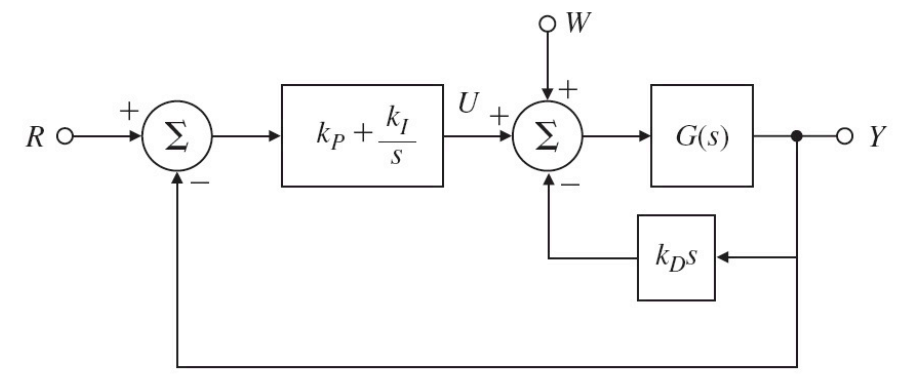
미분항의 중요한 효과는 갑자기 변하는 신호에 대해 빠른 응답을 제공한다는 점이다. 이 때문에 위처럼 미분항은 계단 기준입력에 대한 과도응답을 제어하기 위해 때때로 피드백 경로에 사용된다. 이것은 표준 제어기의 일부일 수도 있고, 또는 모터의 축에 있는 회전속도계와 같은 속도센서를 묘사할 수도 있다. 위 경우에서 기준입력에 대한 출력의 전달함수의 영점(zero)들은 다르다는 것을 인지해야 한다. 피드백 경로에 미분항을 넣으면, 기준입력은 미분되지 않는다. 이는 기준입력의 갑작스러운 변화로 인해 발생하는 바람직하지 않은 응답을 피하는 방법이 된다. 다음 예제를 보자.

비례적분미분(PID) 제어
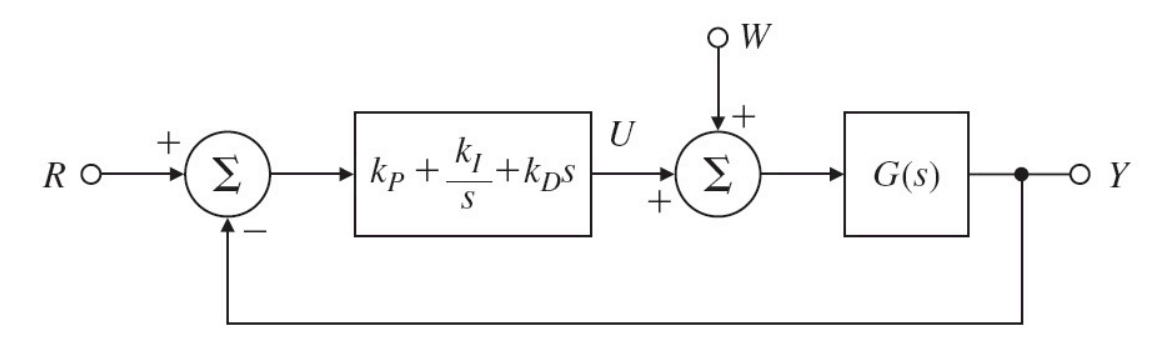
세 가지 항(비례, 적분, 미분)을 모두 추가하면 시간영역에서 비례적분미분(PID: proportional plus integral plus derivative) 제어 방정식의 변환은 다음과 같다.
PID 제어의 효과를 알아보기 위해 2차 플랜트에 대한 속도제어를 생각해 보자. 이 경우 $1 + GD_{cl} = 0$으로부터 나온 특성방정식은 다음과 같다.
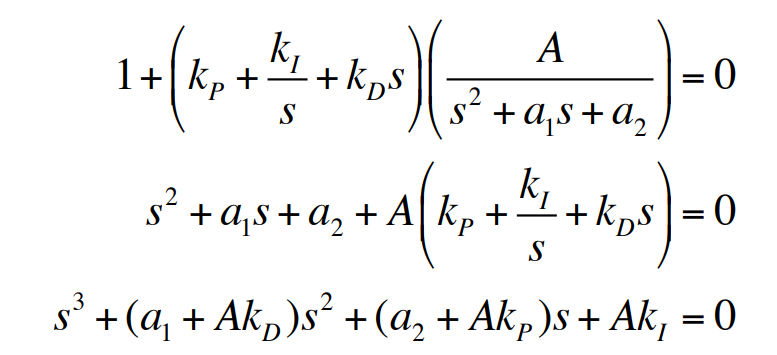
여기서 이 방정식의 세 근이 시스템의 동적 응답 특성을 결정하고, 이 방정식은 $k_P, k_I, k_D$에서 세 개의 자유 파라미터를 가지고 있으며, 이 파타미터들을 선정함으로써 이론적으로 근들이 유일하고 임의적으로 결정될 수 있다는 것이다. 미분항이 없다면, 세 개의 근에 대해 단지 두 개의 파라미터가 있으므로 특성방정식의 근 선정에 제약을 받게 된다.
다음과 같이 단위 피드백을 갖는 DC-DC 변환기의 제어를 생각해 보자.
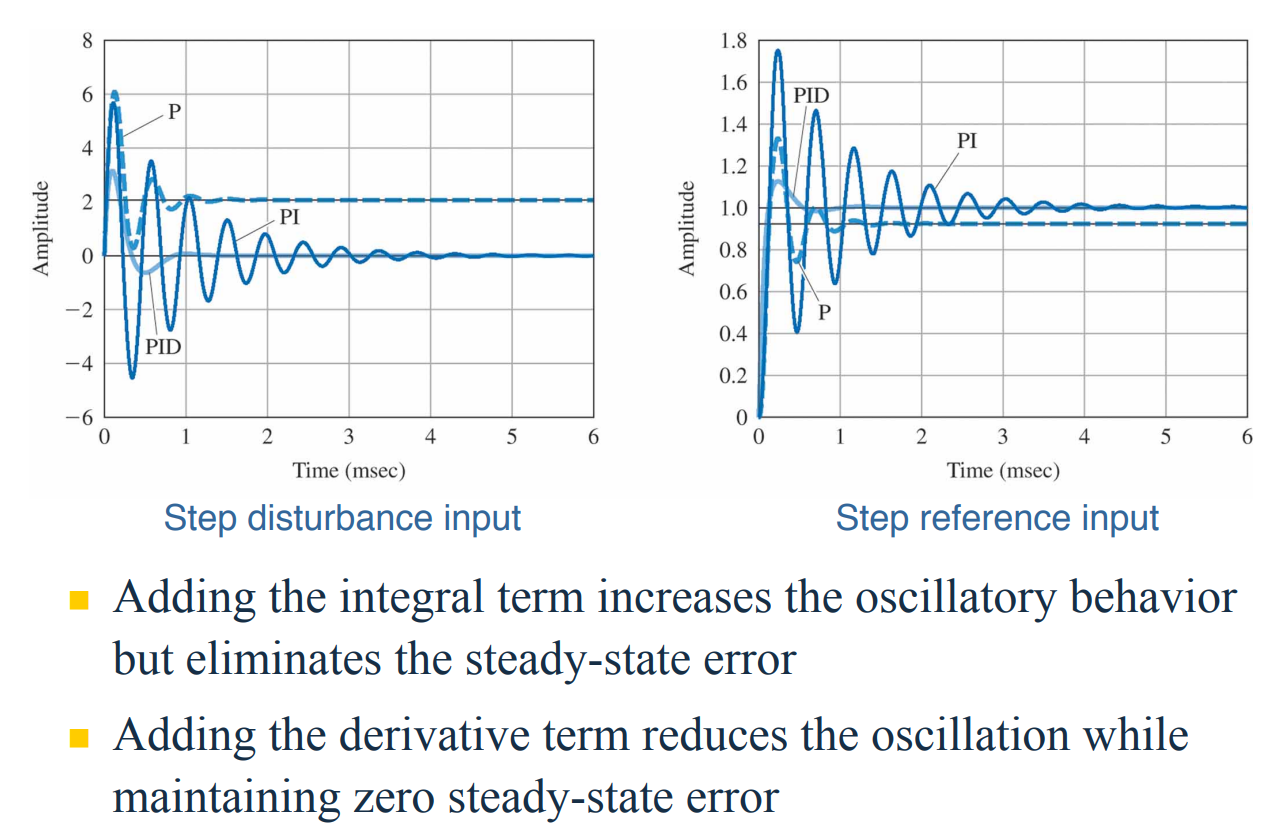
다음 예제를 보자.
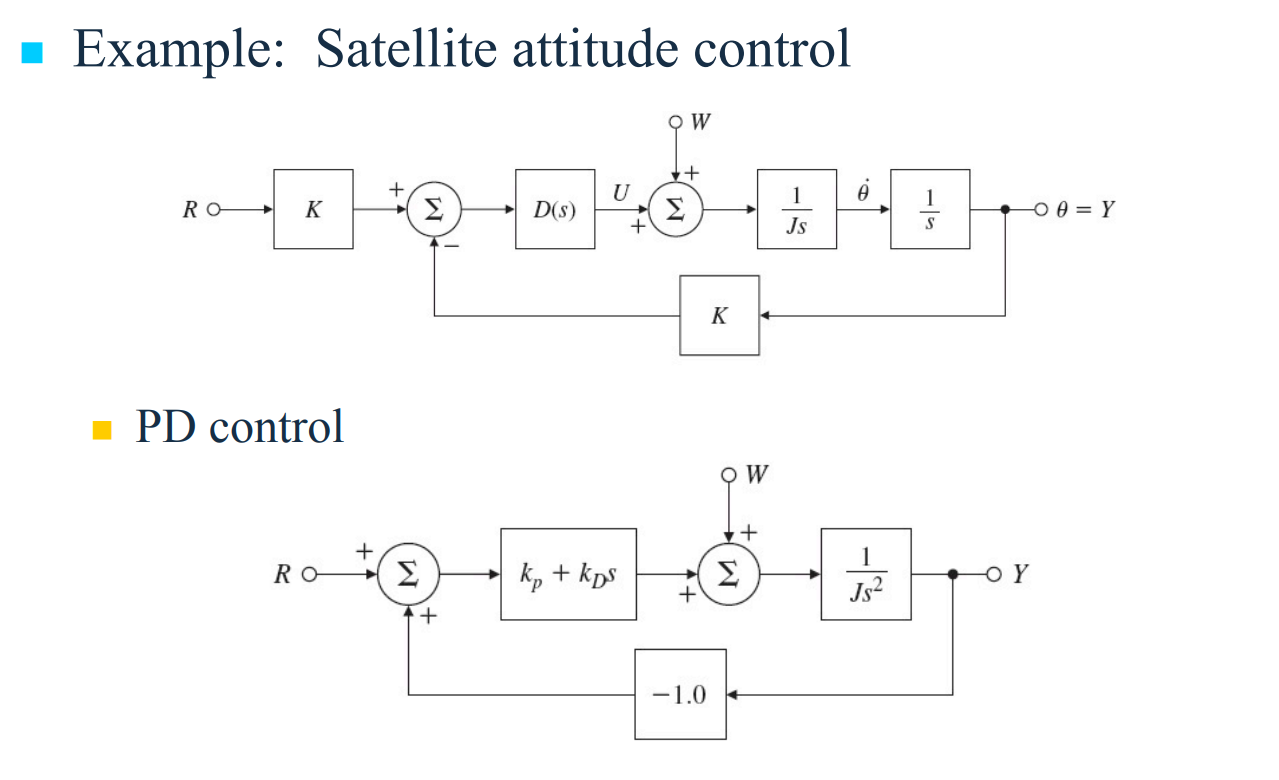

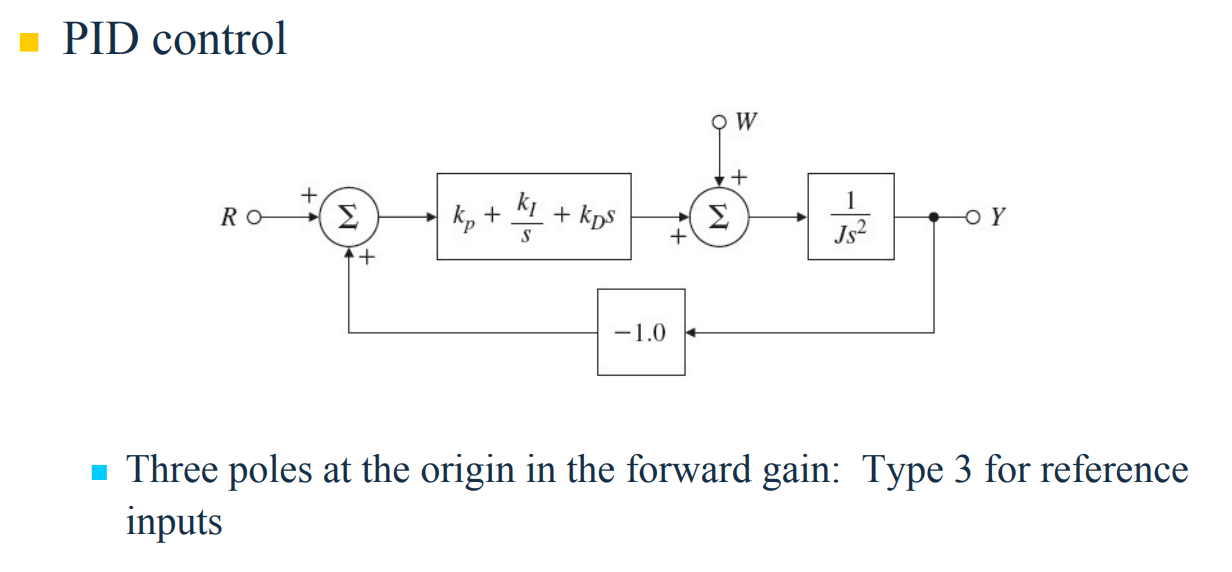

댓글남기기