5장 근궤적 설계법
Updated:
Review of Complex Variable
복소수의 기본 개념은 다음과 같다.
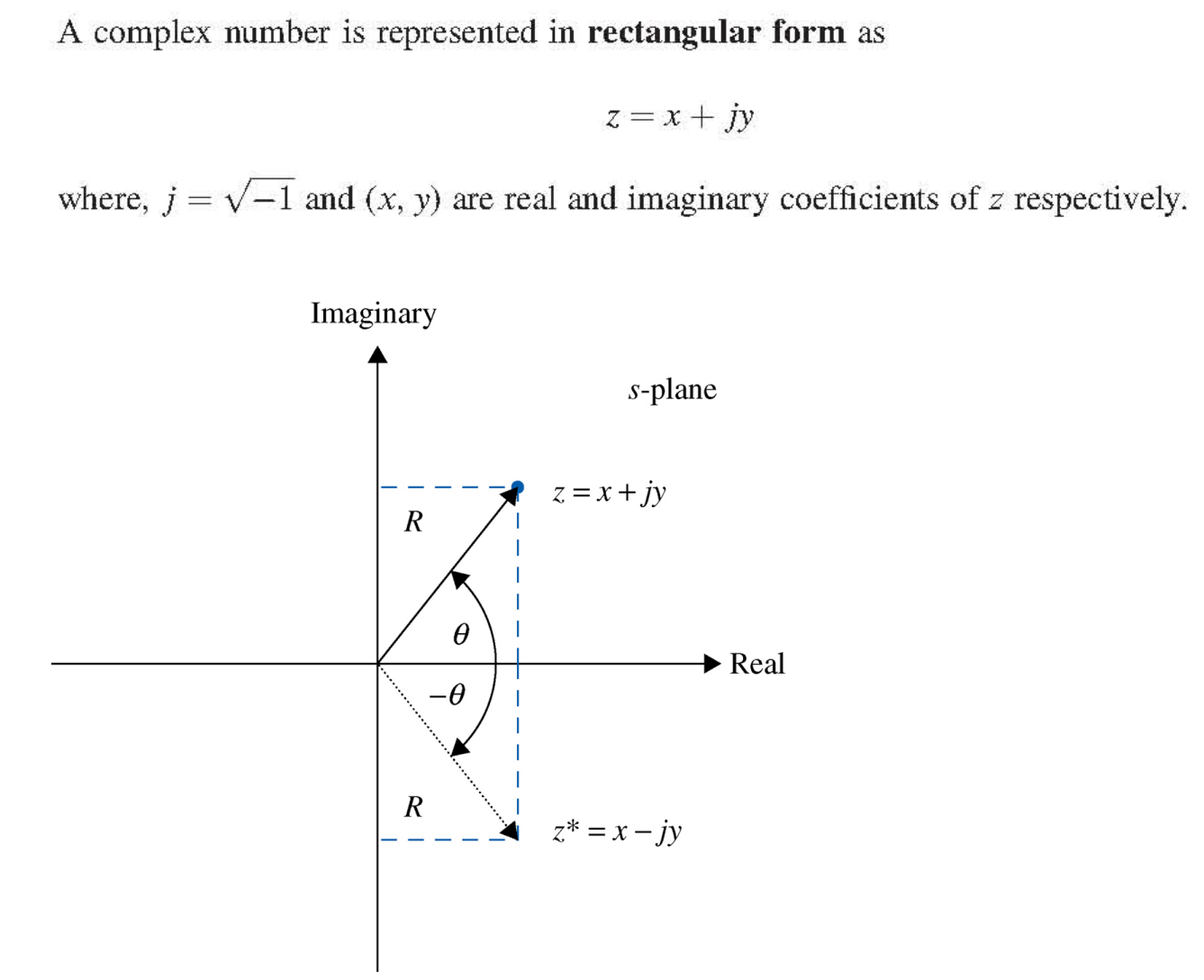

다음은 복수수 연산의 예이다.
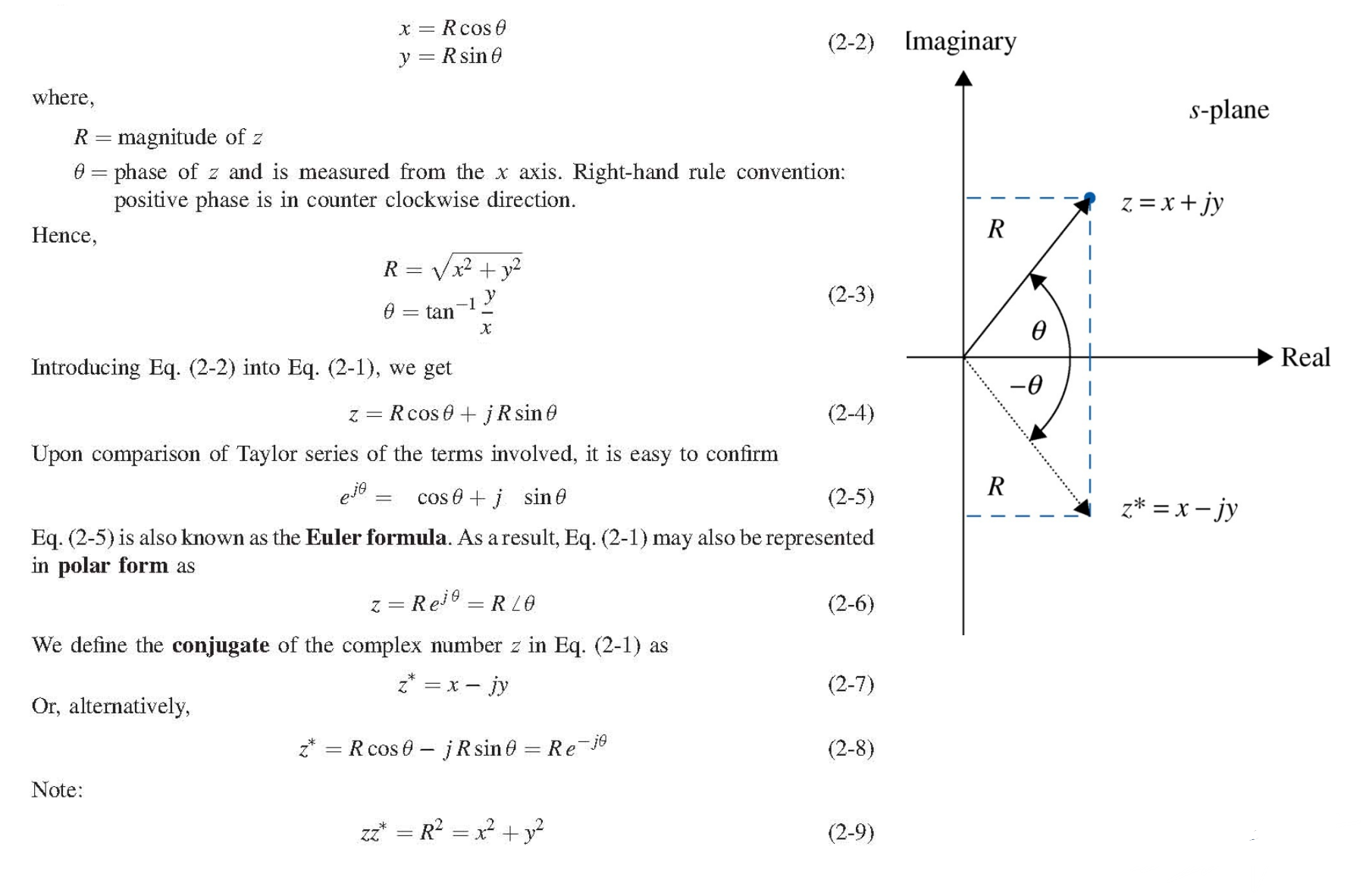
복소함수의 개념은 다음과 같다.

다음과 같이 $G(s)$의 polar representation로 변환해보자.
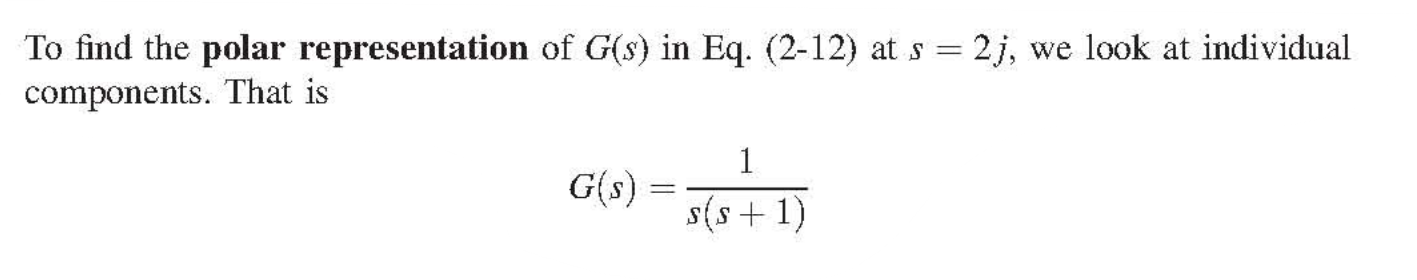
$z_1=s$, $z_2=s+1$이라 하면, 테일러 급수 $e^{j\theta} = \cos{\theta} + j\sin{\theta}$를 이용하여 $z_1=2e^{j \frac{\pi}{2}}$, $z_2=\sqrt{5}(\frac{1}{\sqrt{5}} + \frac{2}{\sqrt{5}}j)=\sqrt{5} e^{j\theta_2}$ $(\theta_2=\tan^{-1}{2})$이므로 $z_1z_2=2\sqrt{5}e^{j(\frac{\pi}{2} + \theta_2)}$, $G(s) = \frac{1}{2\sqrt{5}} e^{-j(\frac{\pi}{2} + \theta_2)}$로 나타낼 수 있다. 다음 예를 보자.
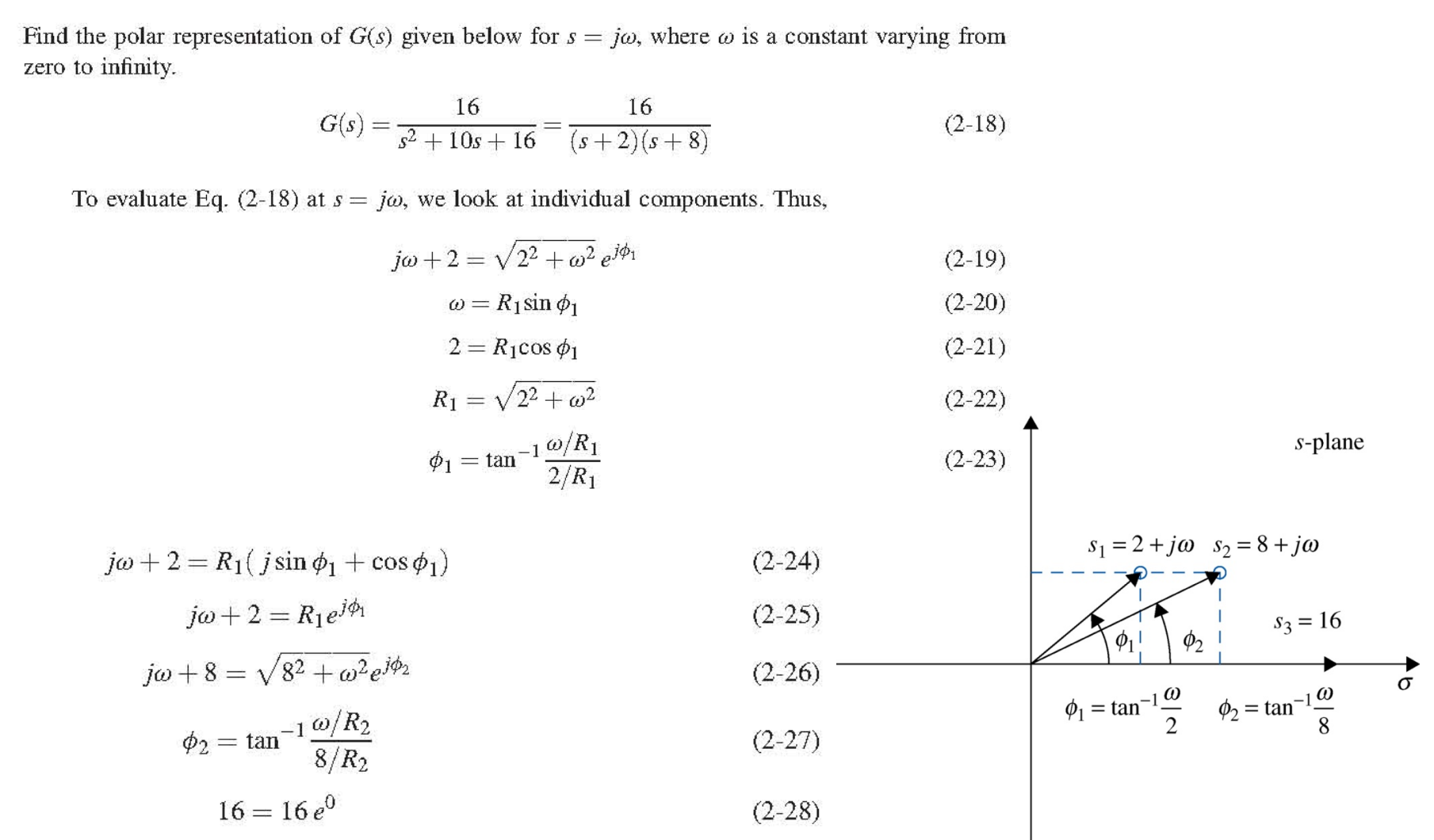


위 과정을 일반화하면 다음과 같다.

기본 피드백 시스템의 근궤적
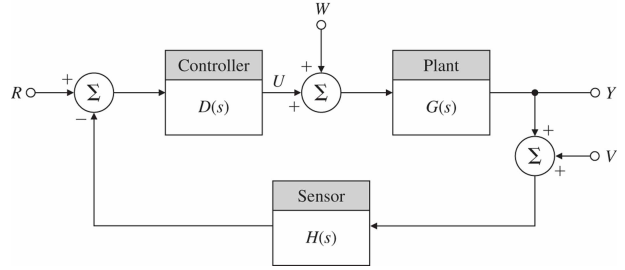
다음과 같은 기본 피드백 루프는 갖는 시스템의 폐루프 전달함수와 특성방정식은 다음과 같다.
특성방정식의 근이 전달함수의 극점이다. 파라미터 변화에 따른 근 위치변화 연구를 위한 알맞은 형태로 식을 변환하기 위해 먼저 다항식을 만든 후, 관심 대상 파라미터를 선택하고 이를 $K$라 하고, 특성다항식을 $a(s) + Kb(s)$ 형태로 만들 수 있는 각 요소 다항식 $a(s)$, $b(s)$에 대해 전달함수 $L(s)=b(s)/a(s)$라 하면 특성방정식은 다음과 같이 쓸 수 있다.
많은 경우 $K$는 제어기(Controller)의 게인이고 이 경우 $L(s)$는 단순히 $D(s)G(s)H(s)$에 비례한다. $K$가 0부터 무한대까지 변할 때 위 식의 모든 가능한 근을 그리고, 그것을 사용해 가장 알맞은 $K$값을 선택한다. 또한 이 그래프에 추가된 극점과 영점의 효과를 연구함으로써 루프의 보상기(Compensation)로서 $D(s)$에 추가될 동특성의 결과를 결정할 수 있게된다. 따라서 특정한 파라미터값을 선정하는 것뿐 아니라 동적 보상기를 설계할 때도 이 방법을 사용할 수 있다. 파라미터 $K$에 대한 모든 근의 그래프를 근궤적(root locus)라하고, 이 궤적을 만들기 위한 방법을 근궤적법이라 한다.
전달함수 $L(s)$의 분자는 $m$차 모닉다항식(monic polynimial)인 $b(s)$이고, 분모는 $n$차 모닉다항식인 $a(s)$이다. 여기서 $n \ge m$이다. $m$은 영점의 개수, $n$은 극점의 개수이다. 모닉다항식은 $s$의 최고차항의 계수가 1임을 의미한다. 다항식은 다음과 같이 인자들의 곱 형태로 나타낼 수 있다.
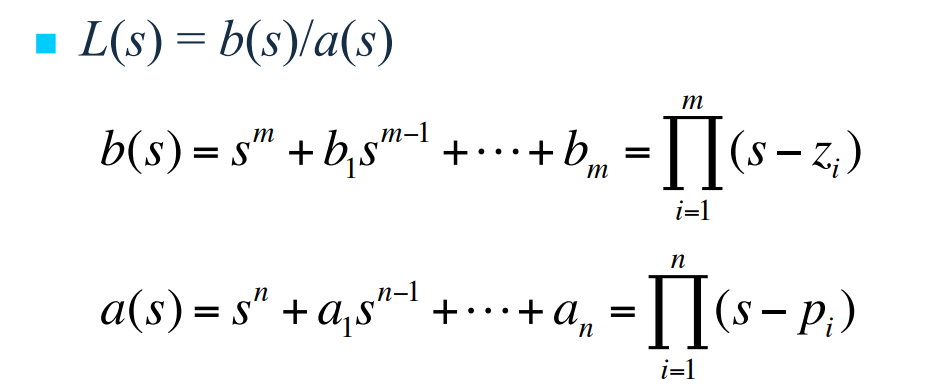
$b(s)=0$의 근은 $L(s)$의 영점이고 $z_i$로 표기되며, $a(s)=0$의 근은 $L(s)$의 극점이 되고 $p_i$로 표기된다. 특성방정식은 다음과 같이 표현할 수 있다.
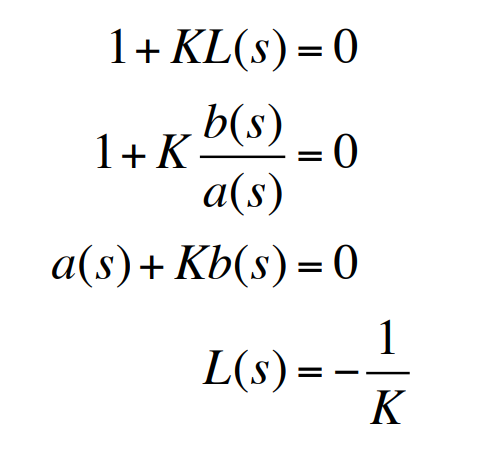
위 식들은 특성방정식의 근궤적형이라고 한다. 위 식의 해는 폐루프 시스템 특성방정식의 근이며 동시에 폐루프 시스템의 극점이기 때문에, 근궤적법은 $K$의 변화에 따른 폐루프 시스템의 동특성을 추론하는 방법이다. 다음 예를 보자.
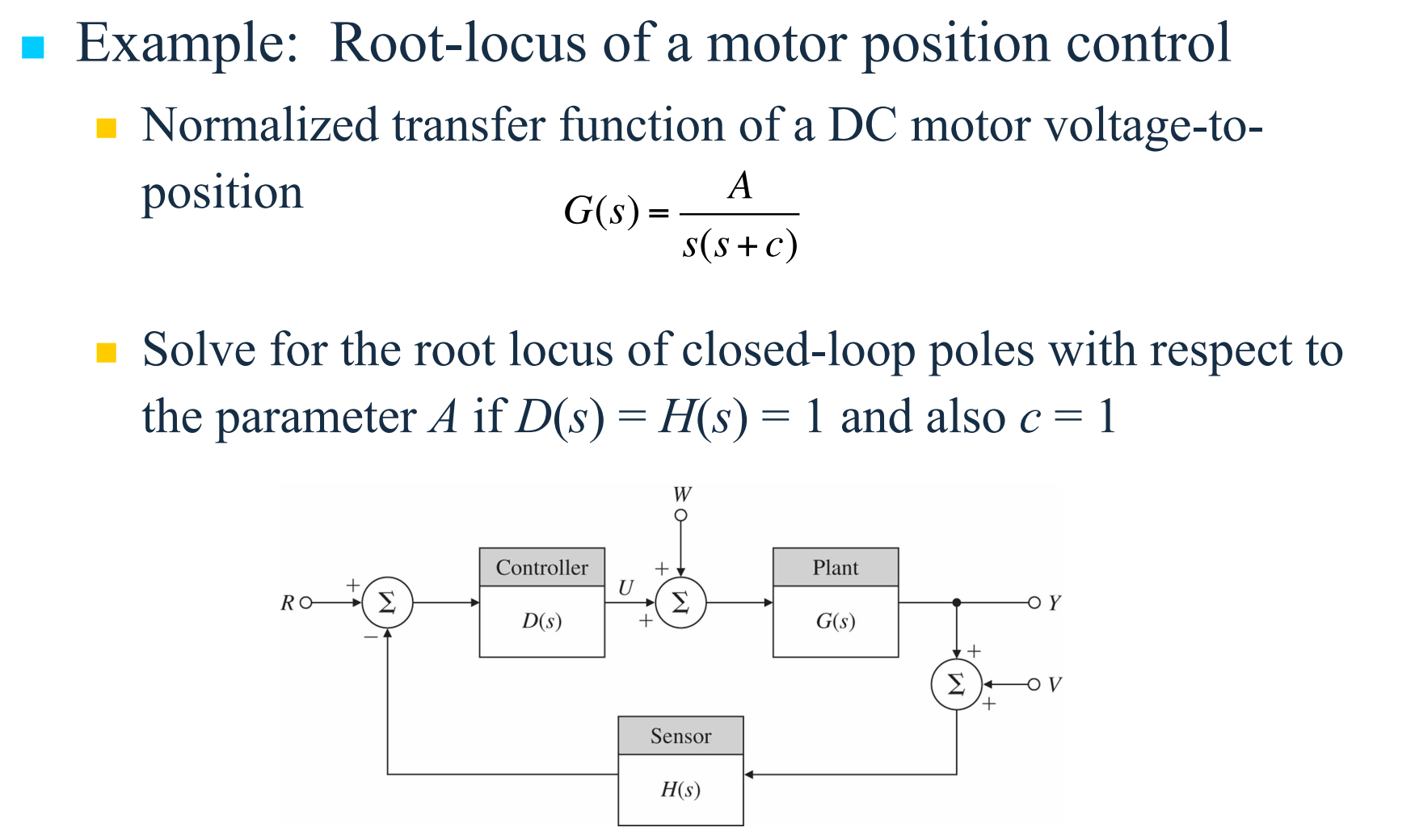
$G(s)=\frac{A}{s(s+c)}$에서 $A=K$, $c=1$이므로, $L(s)=\frac{1}{s(s+1)}$이고, 특성방정식은 $1 + \frac{K}{s(s+1)} = 0$, root locus(근궤적형)는 $s^2 + s + K = 0$이다. 근의 공식을 이용하여 근을 구하면 $r_1, r_2 = -\frac{1}{2} \pm \frac{\sqrt{1-4K}}{2}$이다. 해당 root locus는 다음과 같다.
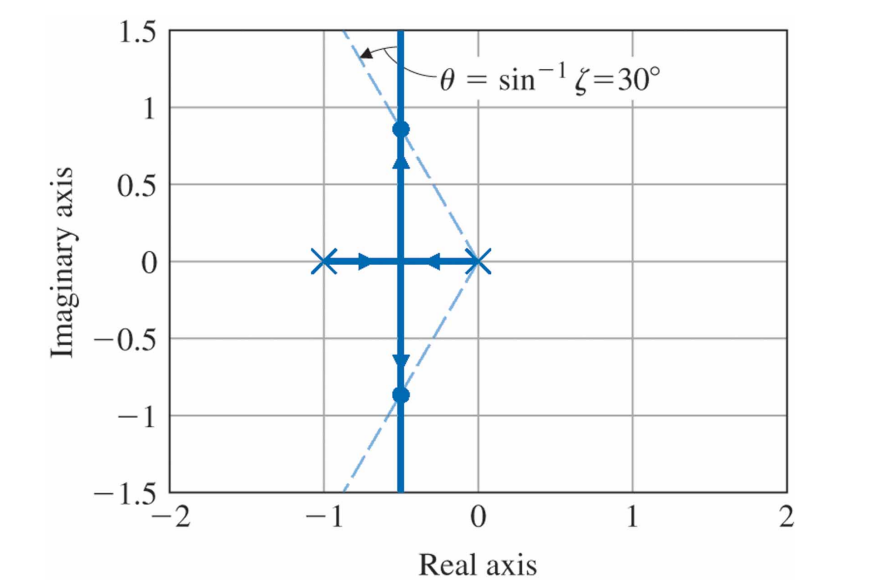
$0 \le K \le 1/4$이면 근은 $-1$과 $0$사이의 실수이다. $K=1/4$이면 $-1/2$에 근이 두 개 있다. 그리고 $K > 1/4$이면 근은 복소수가 되어 실수부는 $-1/2$이고 허수부는 $K$의 제곱근에 비례하여 증가한다. 위 root locus에서 점선은 감쇠비 $\zeta = 0.5$일 때의 근에 해당한다. 감쇠비 $\zeta = 0.5$이면 $\theta = \sin^{-1} 0.5 = 30^{\circ}$이므로 $\frac{\sqrt{1 - 4K}}{2} = \frac{\sqrt{3}}{2}$이므로 $K=1$이다.
위 예에서 $K=0$에서부터 $K$가 증가함에 따라 근이 서로를 향해 움직이고 $K=1/4$에서 만나고 이때 $s=-1/2$이다. 이 점은 이탈점(breakaway point)이라하고 근은 같은 실수부를 가지면서 무한대로 이동한다. 그리고 두 근의 합은 항상 $-1$이다. 다음 예를 보자.
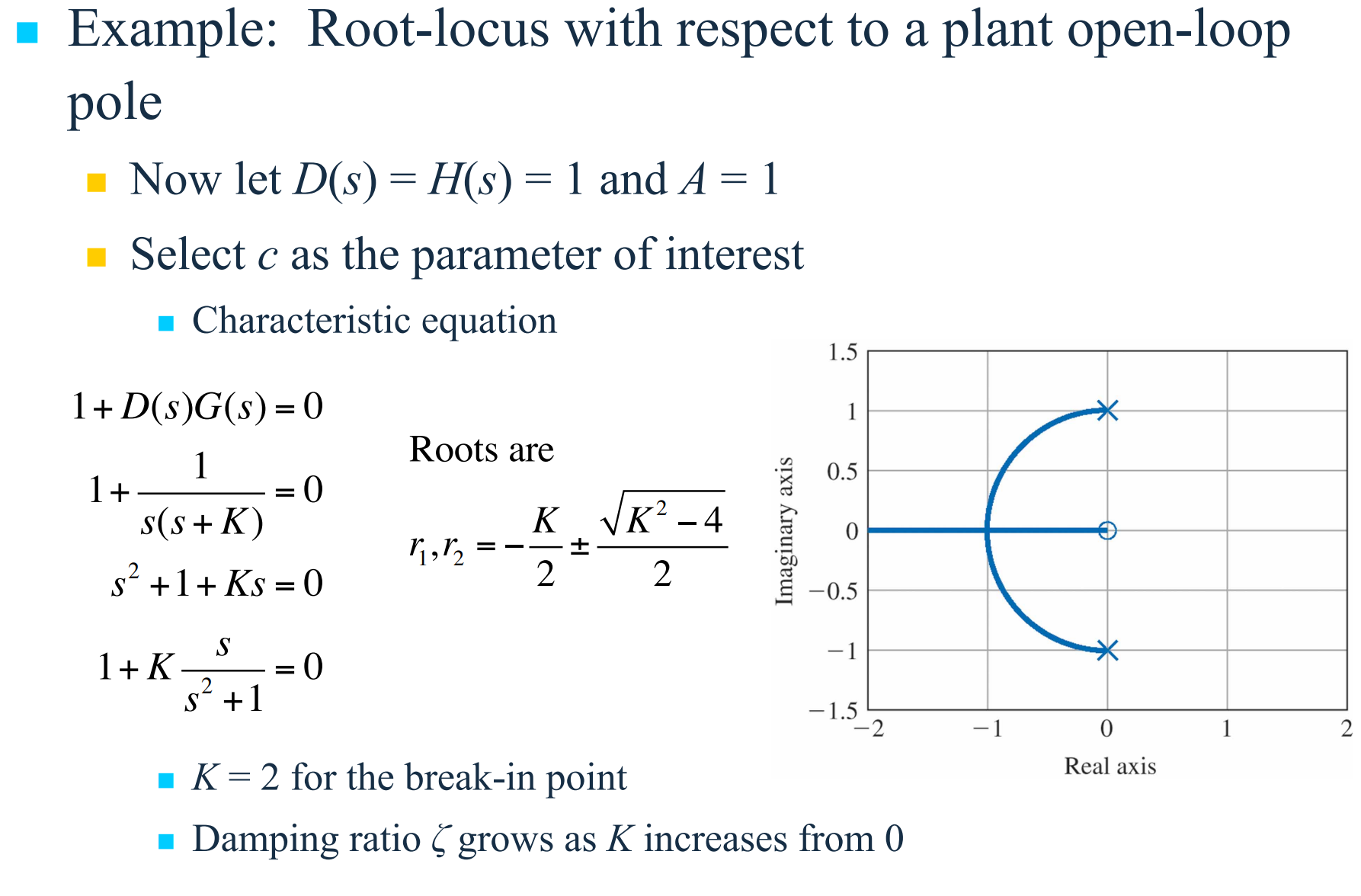
먼저 관심이 있는 파라미터를 $c$로 선택하면 $1 + G(s)=1 + \frac{1}{s(s + K)} = 0$, $s^2 + Ks + 1 = 0$이므로 해 $r_1, r_2 = -\frac{K}{2} \pm \frac{\sqrt{K^2 - 4}}{2}$이다. 두 개 또는 이상의 근이 실수축에서 모이는 중근점 $K=2$을 break-in-point(복귀점)이라한다. $s^2 + Ks + 1 = 0$을 root locus로 표시하면 $1 + K \frac{s}{s^2 + 1} = 0$이다. $K$가 0부터 증가함에 따라 감쇠비 $\zeta$는 점점 증가한다.
MATLAB에서 rlocus(sys)명령으로 root locus를 그릴 수 있다. 그러나 제어설계에 있어서 특정한 궤적뿐만 아니라 좋은 제어성능을 보장하는 동적 응답 특성을 갖도록 시스템 동역학을 어떻게 수정해야 하는지도 관심대상이다. 이러한 목적 때문에 또 다른 보상기의 성능을 평가할 수 있도록 궤적의 개략적인 도시를 할 수 있는 것이 매우 중요하다.
근궤적을 결정하는 지침
근궤적의 공식적인 정의로부터 시작한다.
정의I. 근궤적은 실수 파라미터 K가 0에서 +$\infty$로 변할 때, $1 + KL(s)=0$을 만족하는 $s$의 집합이다. $1 + KL(s)=0$은 시스템의 특성방정식이며, 궤적상의 근은 시스템의 폐루프 극점이다.
$L(s) = - \frac{1}{K}$를 보면, K가 실수이며 양수인 경우 $L(s)$는 실수이며 음수여야 한다. 즉, $L(s)$를 크기와 위상을 갖는 극좌표 형태로 표시하면 $L(s)$의 위상은 $180^{\circ}$가 되어야 한다. 따라서 근궤적을 다음과 같이 위상조건(phase condition)으로 정의할 수 있다.
정의II. $L(s)$의 근궤적은 s-평면상에서 $L(s)$의 위상이 $180^{\circ}$가 되는 점의 집합이다. s-평면 내의 점이 궤적 위에 존재하는지의 여부를 시험하기 위해 시험점과 영점이 이루는 각을 $\psi_i$, 그리고 시험점과 극점이 이루는 각을 $\phi_i$라 정의하면 정의II는 정수 $l$에 대해 식 $\Sigma\psi_i - \Sigma\phi_i = 180^{\circ} + 360^{\circ}(l - 1)$을 만족시키는 s-평면상의 점이라 할 수 있다.
정의II의 가장 큰 장점은 고차 다항식은 풀기가 매우 어려운 반면, 전달함수의 위상의 계산은 비교적 쉽다는 점이다. 일반적으로 $K$는 양의 실수이고, 이 경우를 양(positive) 또는 $180^{\circ}$궤적이라 부른다. $K$가 음의 실수인 경우에는 $L(s)$가 위상이 $0^{\circ}$인 양의 실수여야만 한다. 이 특수한 경우는 음(negative) 또는 $0^{\circ}$궤적이라 부른다.
정의II로부터, 위상을 측정하여 위상이 $180^{\circ}$가 되는 점들을 표시함으로써 복소수 전달함수의 근궤적을 대체로 도시할 수 있다. 다음 예를 보자.
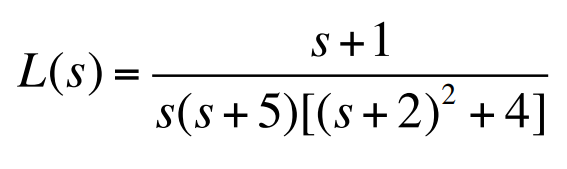
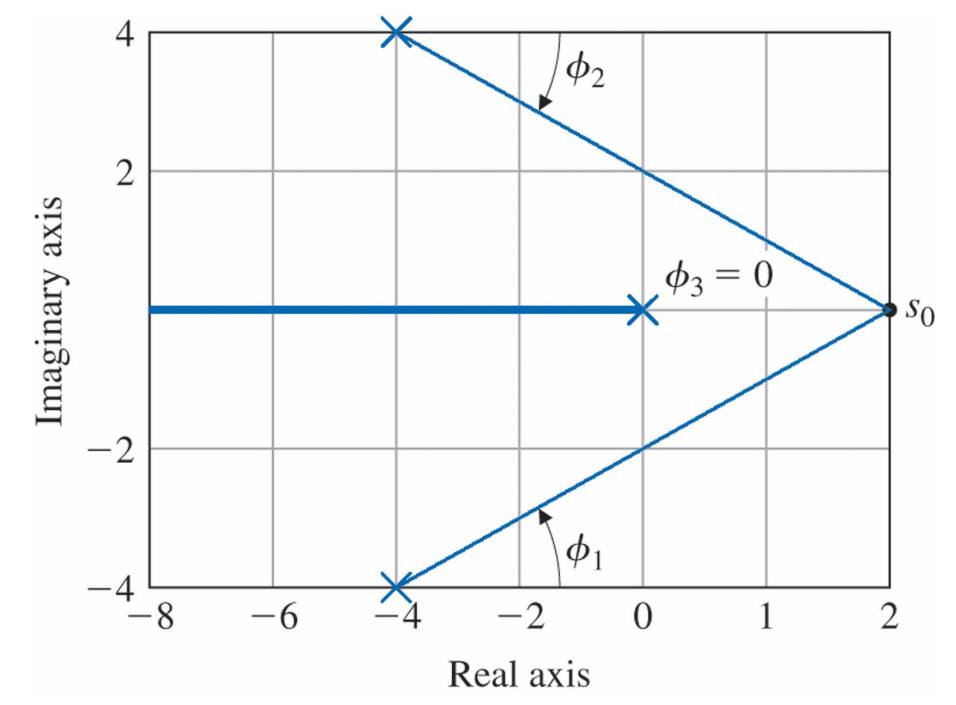
다음 그림에서 $L(s)$의 극점은 $\times$로 표시되고 영점은 $\bigcirc$으로 표시되었다.
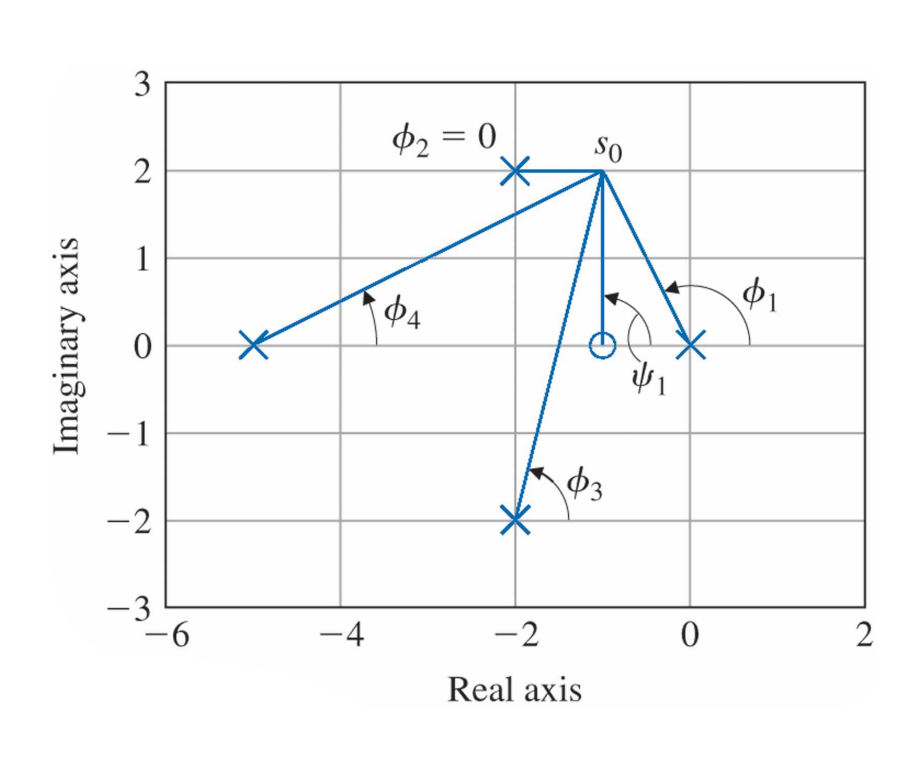
$s_0= -1 + 2j$를 시험점으로 선택하고 K의 어떠한 값에대해 $s_0$가 근궤적상에 있는지 없는지 알아본다. 이 점이 궤적상에 있기 위해서는 어떤 정수 $l$에 대해 $\angle L(s_0) = 180^{\circ} + 360^{\circ}(l - 1)$인 조건을 만족하거나 $\angle (s_0 + 1) - \angle s_0 - \angle (s_0 + 5) - \angle [(s_0 + 2)^2 + 4] = 180^{\circ} + 360^{\circ}(l - 1)$을 만족해야 한다.
영점항인 $s_0 + 1$로부터의 각도는 영점 위치인 $-1$에서 시험점 $s_0$까지 선을 그려서 계산할 수 있다. 복소수 극점 $-2 \pm 2j$로부터 $s_0$까지의 두 벡터의 각은 $\phi_2$와 $\phi_3$로 표시된다. 위 식으로부터 $s=s_0$에서의 $L(s)$의 전체 위상은 영점의 위상들의 합에서 극점에 해당하는 분모항의 위상을 뺀 것에 해당된다.
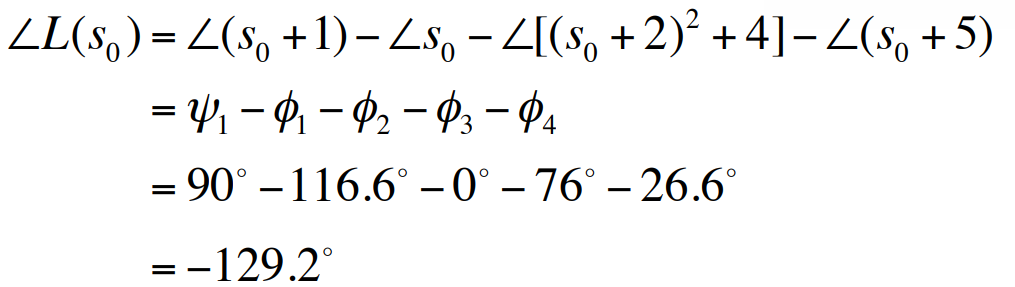
$L(s)$의 위상이 $180^{\circ}$가 아니므로 $s_0$는 근궤적상의 점이 아니라는 것을 알 수 있다. 그러므로 다른 점을 선택하여 다시 시험을 해야 한다.
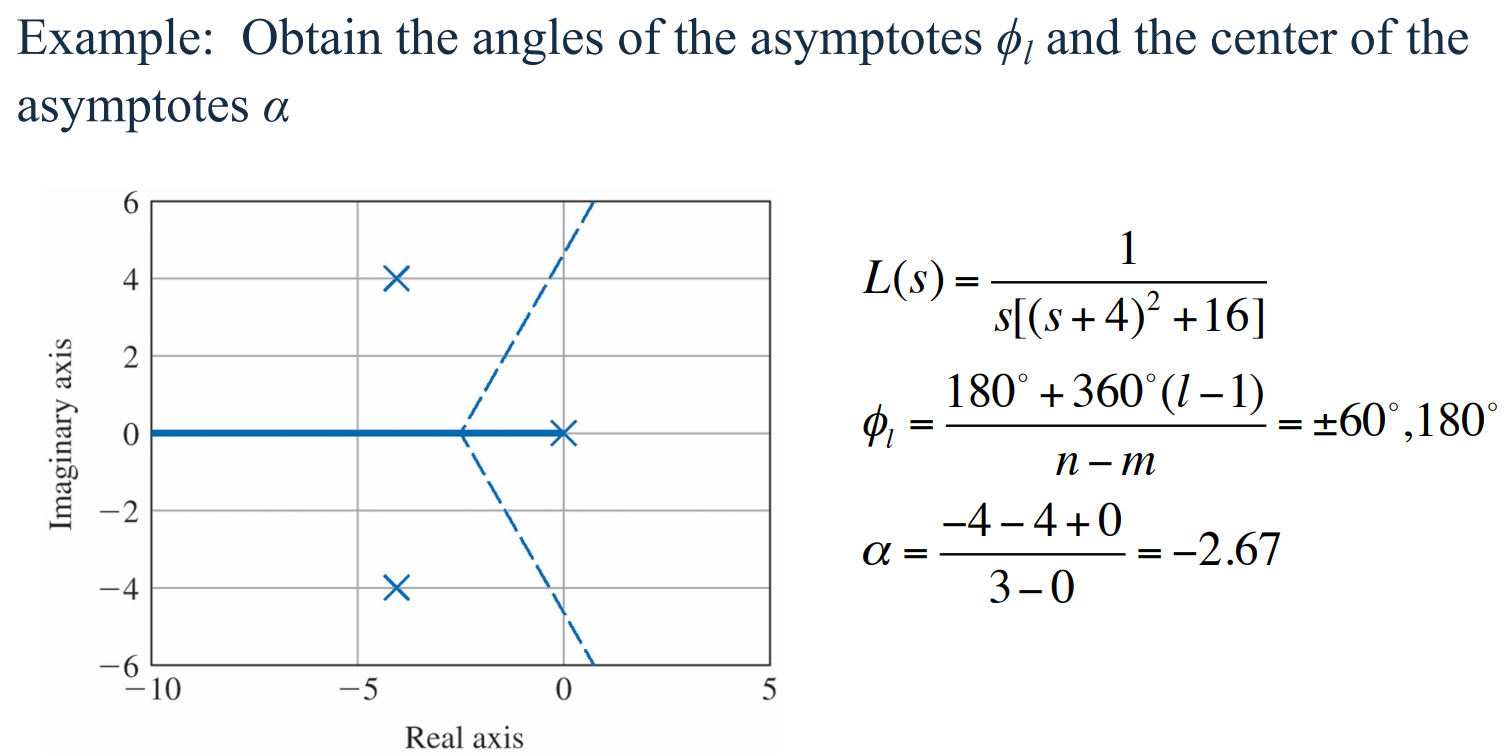
$L(s) = \frac{1}{s[(s + 4)^2 +16]}$으로 양의 궤적을 고려해 다음을 살펴본다.
양($180^{\circ}$)의 근궤적 그리는 지침
규칙 1. 궤적의 n개의 분지들은 $L(s)$의 극점에서의 출발하고 그중 $m$개의 분지들은 $L(s)$의 영점에서 끝난다. 식 $a(s) + Kb(s) = 0$에서 $K=0$이라면, $a(s)=0$이 되고 근은 극점이 된다. $K$가 무한대가 되면 $s$는 $b(s)=0$이 되게 하거나 $s\rightarrow \infty$ $(n > m)$여야 한다. $m$개의 영점에서는 $b(s)=0$이므로 $m$개의 분지는 영점에서 끝난다.
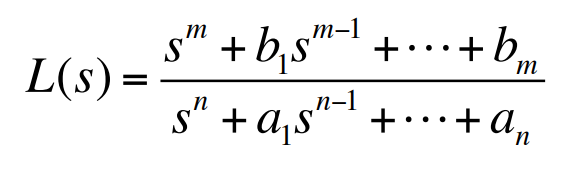
규칙 2. 궤적은 영점과 극점 개수의 합이 홀수인 부분의 왼쪽에 있는 실수축이 된다.
위 그래프에서 $s_0$와 같은 실수축상의 점을 시험점으로 선택하면 두 복소수 극점의 각도인 $\phi_1$과 $\phi_2$는 서로 상쇄된다. 실수 극점과 영점의 각도는 시험점이 극점 또는 영점의 오른쪽에 있으면 $0^{\circ}$이고, 왼쪽에 있으면 $180^{\circ}$가 된다. 그러므로 각의 총합이 $180^{\circ} + 360^{\circ}(l - 1)$이 되기 위해서는 위 그림처럼 시험점이 실수축상의 극점과 영점 개수의 합이 홀수가 되는 부분의 왼쪽에 있어야만 한다.
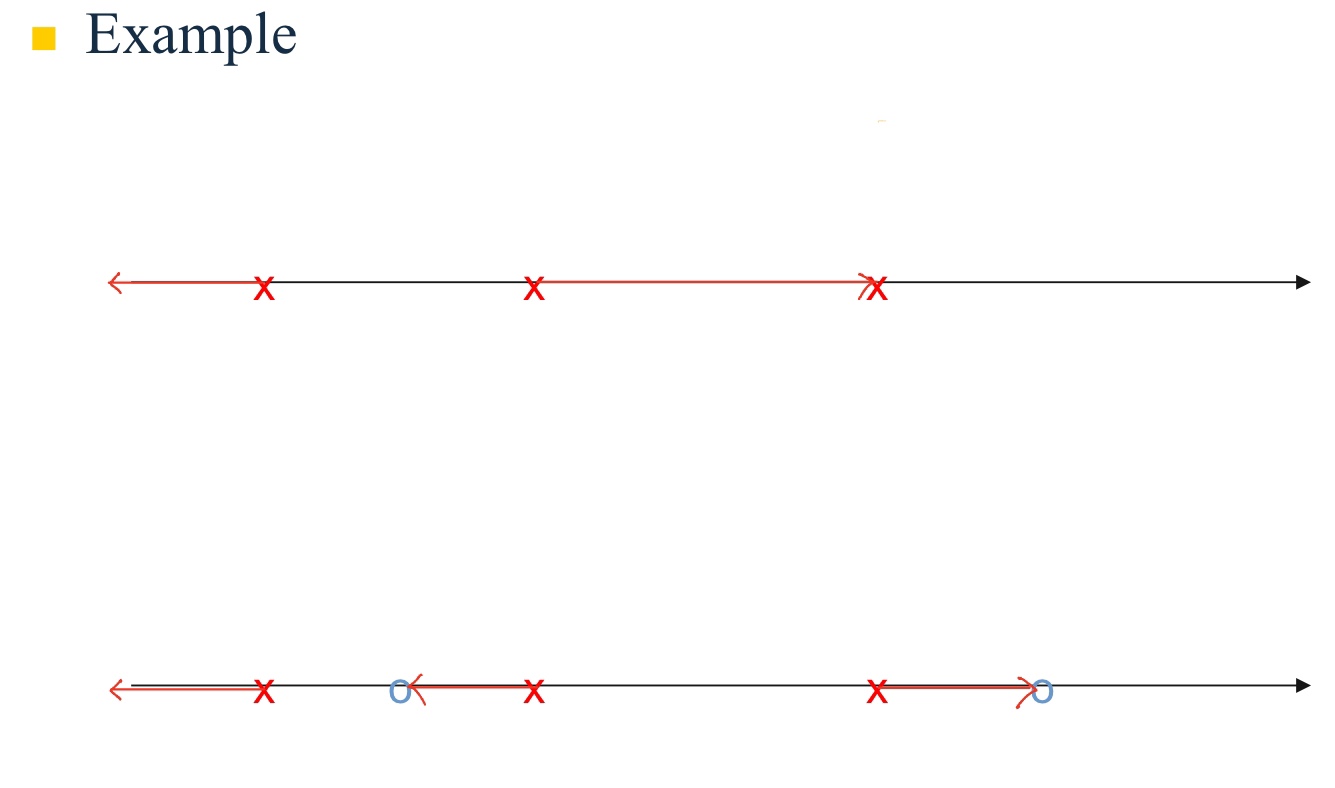
위 예에서 빨간 부분이 조건을 만족하는 시험점이 위치하는 영역이다.
규칙 3. $s$와 $K$가 큰 경우에는 $n-m$개의 궤적의 분지들이 실수축상의 한 점 $s = \alpha$에서 각 $\phi_l$으로 뻗어 나오는 직선에 점근적으로 접근하게 된다.
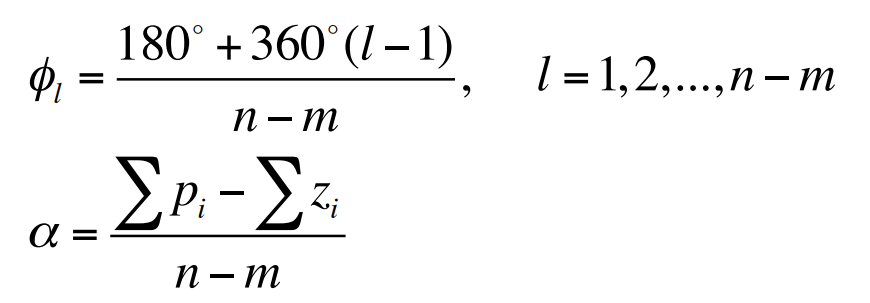
$K$값이 무한대로 감에 따라 $L(s) = 0$일 때만 $L(s) = -\frac{1}{K}$을 만족하는데, 이는 명확히 다른 두 가지 방법으로 생길 수 있다.
- 규칙 1에서 언급하였듯이 m개의 근들이 $L(s)$의 영점에 접근하게 되는 것이다.
- $n > m$ 가정하에서 $s$가 무한대로 가는 경우이다.
점근선은 이 $n - m$개의 근들이 어떻게 $s\rightarrow \infty$로 접근하는가를 나타낸다.
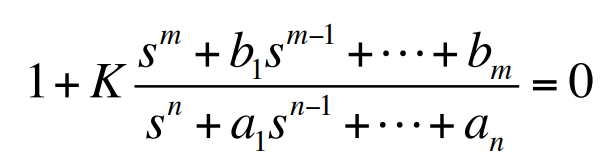
s가 클 경우 위 식은 다음과 같이 근사화될 수 있다.
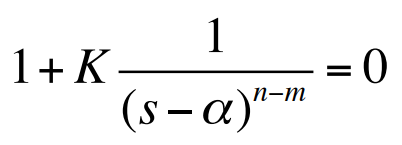
이는 $n - m$개의 극점이 $s = \alpha$에 모두 모여 있는 시스템의 방정식이다. 이러한 간단한 시스템의 모든 극점이 한군데 모여 있으므로 각각 $\phi_l$인 모든 $n-m$개의 각을 더하여 $180^{\circ}$가 되면 이 전달함수의 각도는 $180^{\circ}$가 된다. 따라서 $\phi_l$은 임의의 정수 $l$에 대해 $(n-m)\phi_l = 180^{\circ} + 360^{\circ}(l - 1)$과 같이 주어진다. 그러므로 근궤적의 점근선은 다음과 같은 $n-m$개의 각도를 가지는 방사상으로 뻗어 나오는 선이 된다.
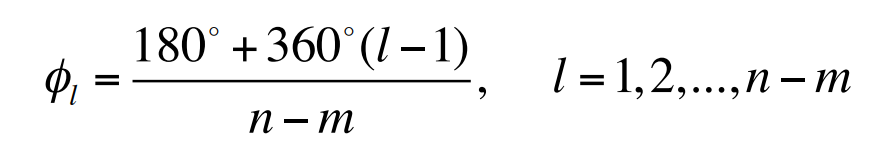
식 $L(s) = \frac{1}{s[(s + 4)^2 +16]}$의 경우 $n - m = 3$이며 $\phi_{1, 2, 3} = 60^{\circ}, 180^{\circ}, 300^{\circ}$이다.
계수가 $a_i$이고 근이 $p_i$인 모닉다항식(monic polynomial)을 인수분해 형태의 다항식으로 나타내면 다음과 같다.
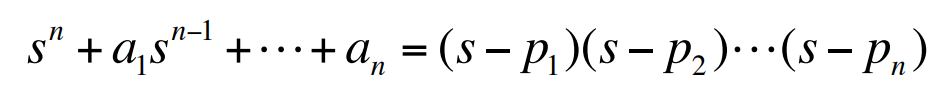
위 식의 우변의 괄호를 벗기면 $s^{n-1}$의 계수는 $-p_1-p_2 - \cdots - p_n$이 된다는 것을 알 수 있다. 죄변의 이 항은 $a_1$이다. 따라서 $a_1 = - \Sigma p_i$, 즉 모닉다항식의 두 번째 높은 차수의 항의 계수는 근의 음의 합이다. 이 결과를 다항식 $b(s)$에 적용하면 영점의 음의 합이 $b_1$이라는 것을 알게 된다. 이 결과는 다음과 같이 쓸 수 있다.
이 결과를 이용하면 다음과 같은 식을 얻을 수 있다.
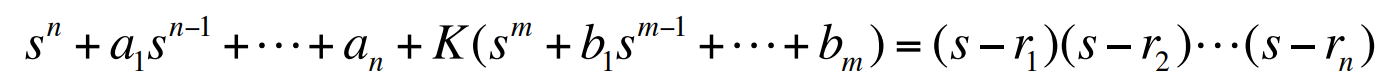
위 식의 근들의 합은 $s^{n-1}$계수의 음수이며, 만약 $m < n-1$이면 $K$와 관계가 없다. 그러므로 만약 $L(s)$가 영점보다 극점이 적어도 두 개 많다고 할 때 $a_1 = -\Sigma r_i$가 된다. 이렇게 하여 $m < n -1$이면 근의 중심점은 $K$에 따라 변하지 않으며, 개루프와 폐루프의 합은 $-a_1$로 동일하며 다음과 같이 쓸 수 있다.
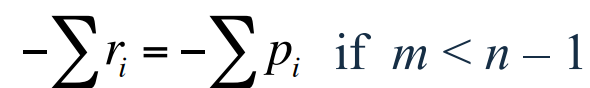
모든 근들의 합은 무한대로 뻗는 근들과 $L(s)$의 영점으로 가는 근들의 총합으로 된다는 것을 알 수 있다.
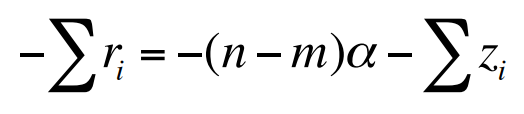
위 식을 $\alpha$에 대해 풀면 $\alpha = \frac{\Sigma p_i - \Sigma z_i}{n - m}$가 된다. 복소수 극점과 영점은 항상 공액복소수 형태로 나타나므로 $\Sigma p_i$과 $\Sigma z_i$에서 허수부는 항상 합해서 0이 되므로 오직 실수부 정보만 필요로 한다. 다음 예를 보자.
규칙 4. 단일극점으로부터의 궤적 분지점의 이탈각은 $\phi_{dep} = \Sigma \psi_i - \sum\limits_{i \neq l, dep} \phi_i - 180^{\circ}$이며, 여기서 $\Sigma \phi_i$는 나머지 극점까지의 각도의 합이고 $\Sigma\psi_i$는 모든 영점까지의 각도의 합이다. 차수 $q$의 다중극점에서의 이탈각은 $q\phi_{l, dep} = \Sigma \psi_i - \sum\limits_{i \neq l, dep} \phi_i - 180^{\circ}- 360^{\circ}(l - 1)$이고 여기서 $l$은 정수이고 $1, 2, \cdots, q$의 값을 가진다. $q$번 반복되는 $q$차 다중극점이 있다면 그 극점에서부터 출발하는 궤적의 분지는 $q$이다. 마찬가지로 차수 $q$를 가지는 다중영점에서의 분지의 도착각은 $q\psi_{l, arr} = \Sigma \phi_i - \sum\limits_{i \neq l, arr} \psi_i + 180^{\circ}+ 360^{\circ}(l - 1)$이다. 여기서 $\Sigma \phi_i$는 모든 극점까지의 각도의 합이고 $\Sigma \psi_i$는 나머지 영점까지의 각도의 합이며 $l$은 $1, 2, \cdots, q$의 값을 갖는다. 따라서 영점에 도달하는 궤적의 분지는 $q$개가 된다.
극점들 중 하나로부터 출발하는 궤적의 분지의 각을 계산하기 위해 극점과 아주 가까운 근처에 시험점 $s_0$를 선택하고, 극점과 시험점이 이루는 각을 $\phi_1$로 정의하고 식$\Sigma \psi_i - \Sigma \phi_i = 180^{\circ} + 360^{\circ}(l - 1)$의 모든 다른 항을 우변으로 이항한다. 이 과정은 $-4 + 4j$에 있는 극점 근처에 시험점을 선택하고 $L(s_0)$의 각도를 계산함으로써 알 수 있다.
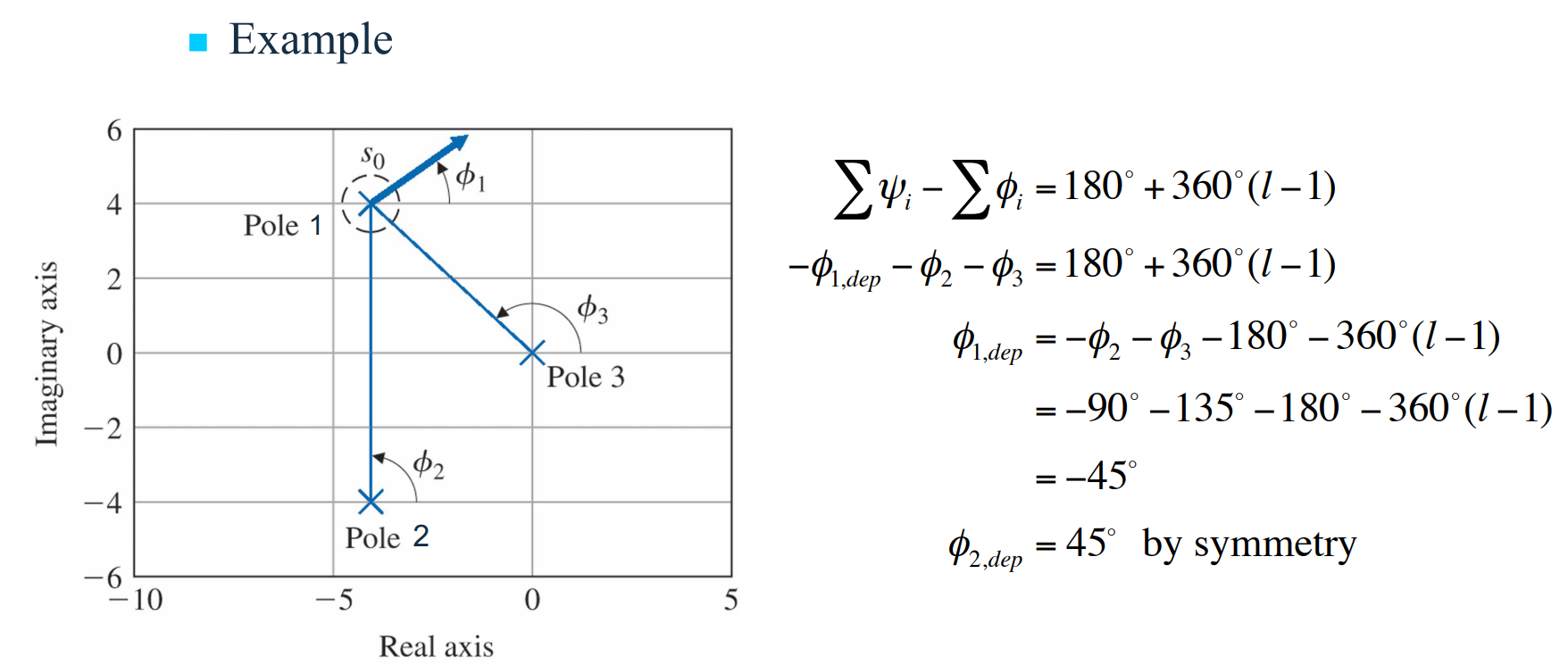
이 규칙은 시스템이 허수축 근처에 극점을 갖는 경우 특별히 유용한데, 그 이유는 극점으로부터의 궤적 분지가 안정한 좌반평면(LHP)으로 이동하는지 아니면 불안정한 우반평면(RHP)으로 향하는지를 보여주기 때문이다.
규칙 5. 궤적은 궤적상의 점에서 중근을 가질 수 있다. 그리고 분지들은 $\frac{180^{\circ} + 360^{\circ}(l - 1)}{q}$의 각도로 차수 $q$의 중금점으로 접근하고, 또 동일한 각도로 이탈한다.
다른 다항식과 마찬가지로 1차 이상의 차수의 특성다항식이 중근을 작는 것은 가능하다.
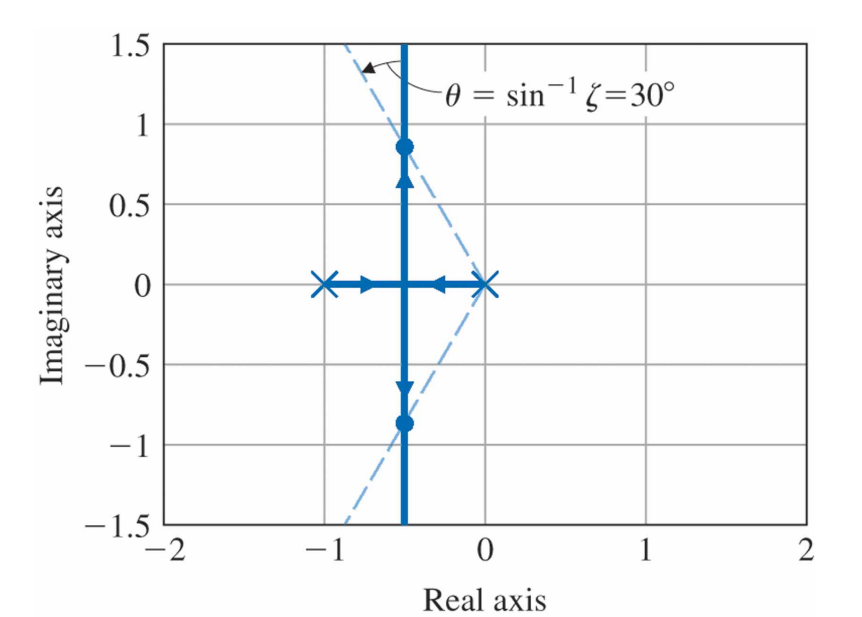
위 그림에서 $K=1/4$일 때 $s=-1/2$에는 두 개의 근이 있다. 이 점에서 궤적의 수평분지들이 만나고 실수축으로부터 수직분지가 이탈하며, $K > 1/4$에서 복소수가 된다. 궤적은 $0^{\circ}$와 $180^{\circ}$로 도착하고 $+90^{\circ}$와 $-90^{\circ}$로 이탈한다.
증근점에서 도착각과 이탈각을 계산하기 위해서는 연속궤적(continuation locus)이라는 기법을 사용하는 것이 효과적이다. $K$의 초기범위 $0 \le K \le K_1$에 대한 근궤적을 작성한다 하면, $K = K_1 + K_2$으로 놓인 최초의 궤적의 연속된 궤적인 파라미터 $K_2$에 대한 새로운 궤적이 그려질 수 있으며, 이 궤적의 시작 극점은 최초 시스템의 $K = K_1$일 때의 근이 된다. 예를 들어, 식 $s^2 + s + K = 0$에서 $K_1=1/4$인 이탈점에 해당하는 값으로 놓는다. 그리고 $K = 1/4 + K_2$으로 놓는다면 궤적 방정식은 $s^2 + s +1/4 + K_2=0$ 또는 $(s + \frac{1}{2})^2 + K_2 = 0$이 된다. 이 궤적을 그리는 규칙은 앞의 식의 궤적의 초기이탈이 식 $s^2 + s + K = 0$의 궤적의 이탈점에 해당되는 것을 제외하고는 다른 경우와 같다. $s=-1/2$의 이중극점에 이탈각 규칙을 적용하면 다음과 같다.
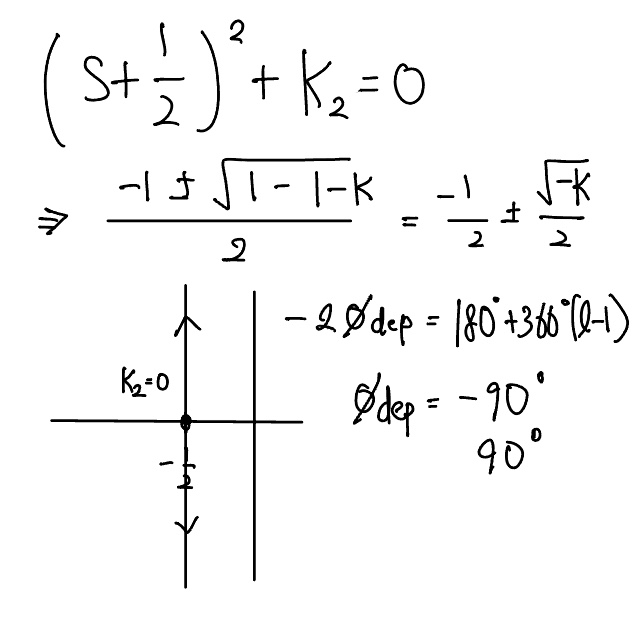
이 경우 원래의 근궤적으로부터 $s=-1/2$로의 도착각은 실수축을 따르며 명백히 $0^{\circ}$와 $180^{\circ}$이다.
파라미터값의 선택
양의 근궤적은 양의 실수값 $K$에 대한 방정식 $1 + KL(s) = 0$의 근을 모든 가능한 위치를 나타낸 그림이다. 설계의 목적은 동적인 성능조건 및 정적인 성능조건을 만족시키는 특정한 $K$값을 선택하는 것이다.
궤적의 정의II를 사용하여 $L(S)$의 위상만으로 근궤적을 그리는 규칙이 개발되었다. 방정식이 $L(s)$의 위상이 $180^{/circ}$인 곳에 근을 갖는다면 크기조건 또한 틀림없이 만족되어야 한다. 이 조건식은 $L(s) = -\frac{1}{K}$이며, 다시 정렬하면 $K = -\frac{1}{L(s)}$이다. 근궤적상의 $s$값들에 대해서 $L(s)$의 위상은 $180^{\circ}$이므로 크기조건은 $K = \frac{1}{|L|}$이다. 다음 예를보자.
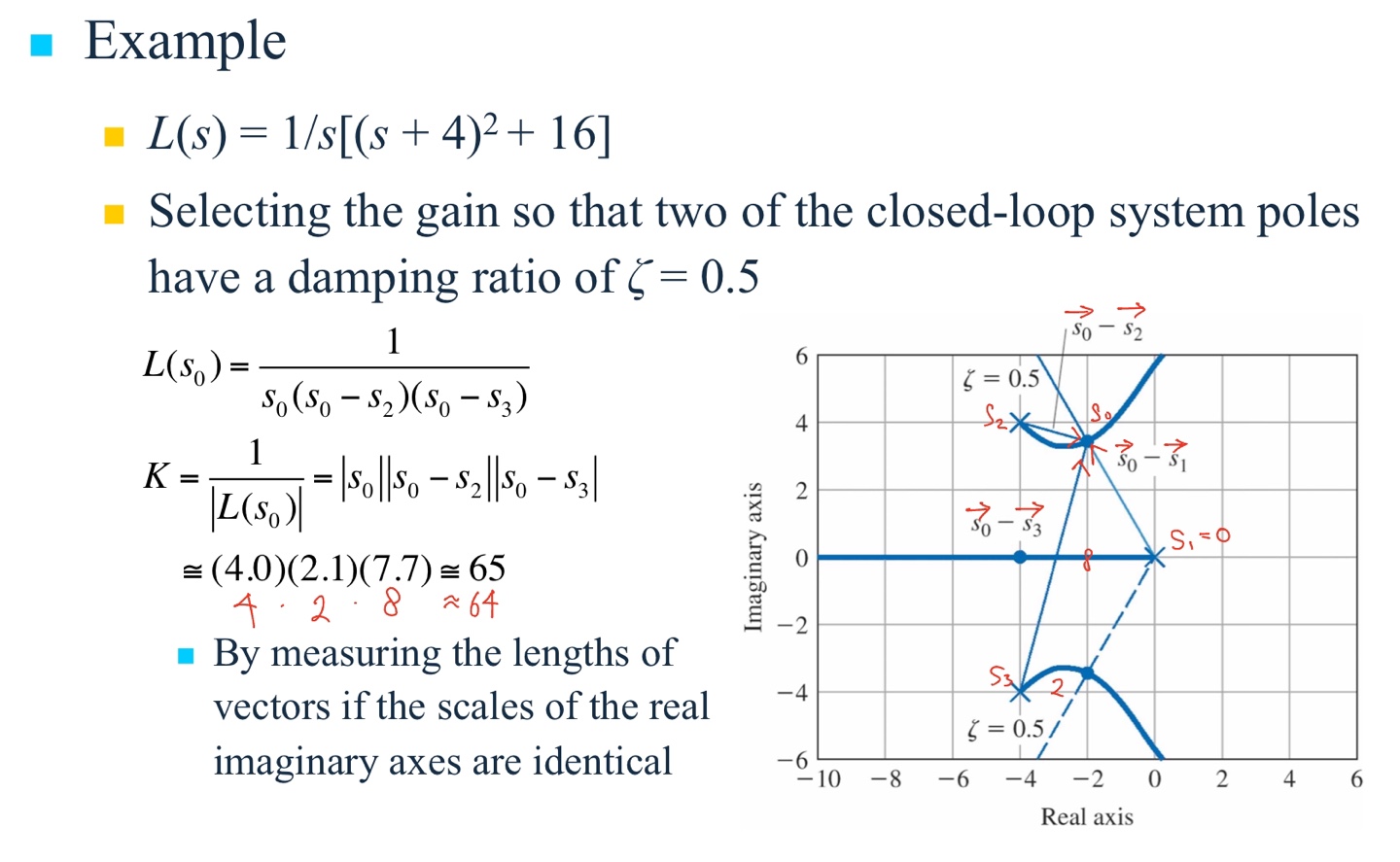
만약 $K$가 65로 선정되면 $1 + KL$의 근은 감쇠비가 0.5가 되는 $s_0$에 위치하게 된다. 또 다른 근은 $s_0$의 공액복소수 위치에 있다. 세 번째 근은 음의 실수축을 따라서 존재한다.
근궤적의 실증적인 몇 가지 예제
많은 중요한 제어 문제는 간단한 이중적분기 전달함수($G(s)=\frac{1}{s^2}$)를 갖는 프로세스로 특정지어진다. 만약 이 플랜트에 비례제어기를 갖는 단일 피드백 시스템을 구성하면 제어기 게인에 대한 근궤적은 $1 + k_p\frac{1}{s^2}$이다. 이는 어떠한 $k_p$에 대해서도 진동하는 과도응답이 얻어진다. 비례적분 제어기의 사용으로 더 유용한 설계결과를 얻을 수 있다.
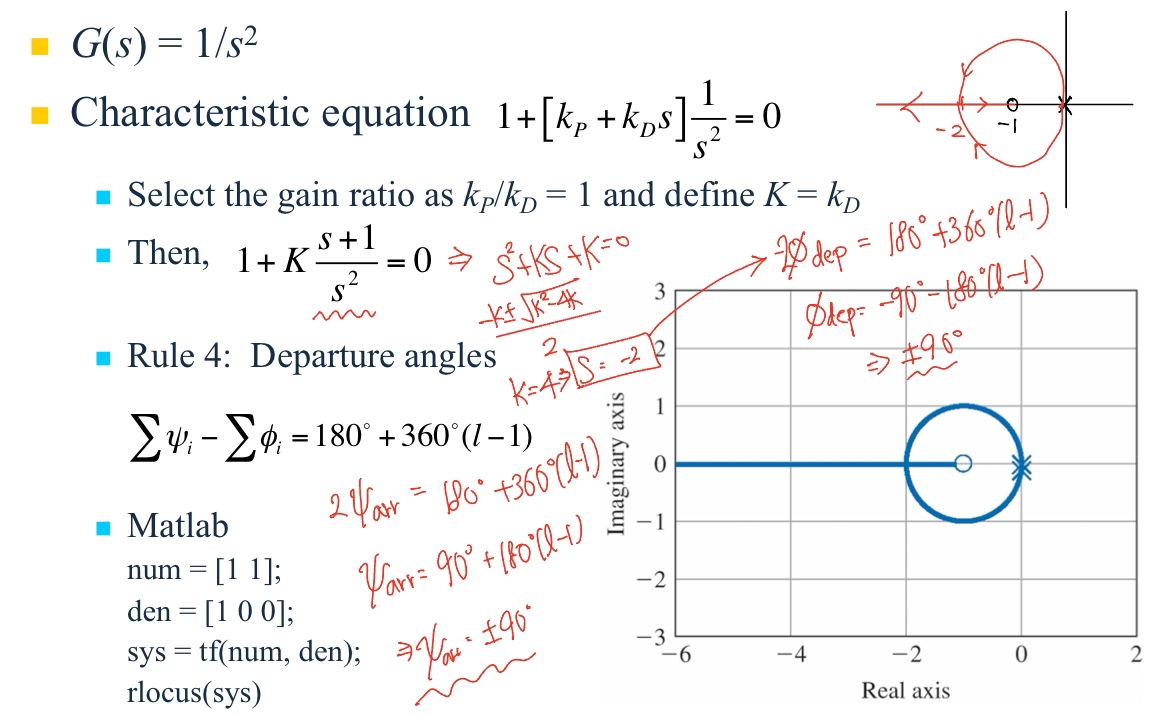
예제 5.3 PD제어기를 사용한 인공위성 자세제어의 근궤적
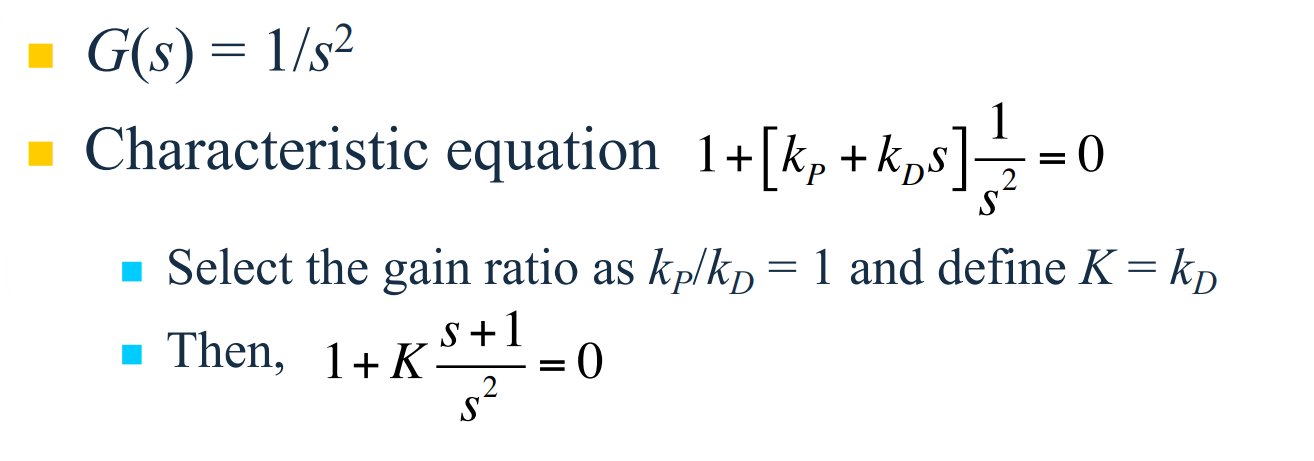
- 규칙1. $s=0$에서 출발하는 두 개의 분지가 있으며, 하나는 영점 $s=-1$에서 끝나고 하나는 무한대로 접근한다.
- 규직2. $s=-1$의 왼쪽 실수축에 궤적이 있다.
- 규칙3. $n - m = 1$이기 때문에 음의 실수축을 따라서 한 개의 점근선이 있다.
- 규칙4. $s=0$의 이중극점으로부터의 이탈각은 $\pm90^{\circ}$이다.
- 규칙5. 규칙 1~4로부터 궤적은 영점을 감아 돌아 영점 왼쪽의 실수축에서 다시 만나고 규칙 1에서 언급한 대로 영점에서 끝나게 됨을 알 수 있다. $s=-2$에서 궤적들이 실수축과 만나므로 중근점이 형성된다. 이 점에서 도착각을 계산해보면 분지들이 $\pm90^{\circ}$의 각도로 도착하게 됨을 알 수 있다. 복귀점에서 한 분지는 서쪽으로 무한대를 향하고 다른 하나는 동쪽으로 향해 $s=-1$에서 만난다.
이 예를통해, 영점의 추가는 좌반평면으로 궤적을 끌어당기며 이는 보상기 설계에서 중요한 특성임을 알 수 있다.
실제 PD제어기는 다음과 같이 근사화 될 수 있다.
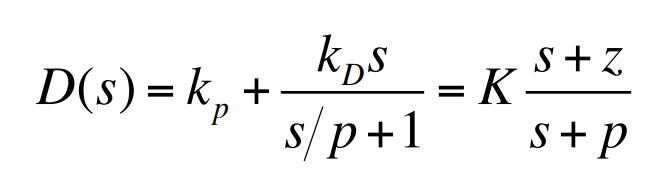
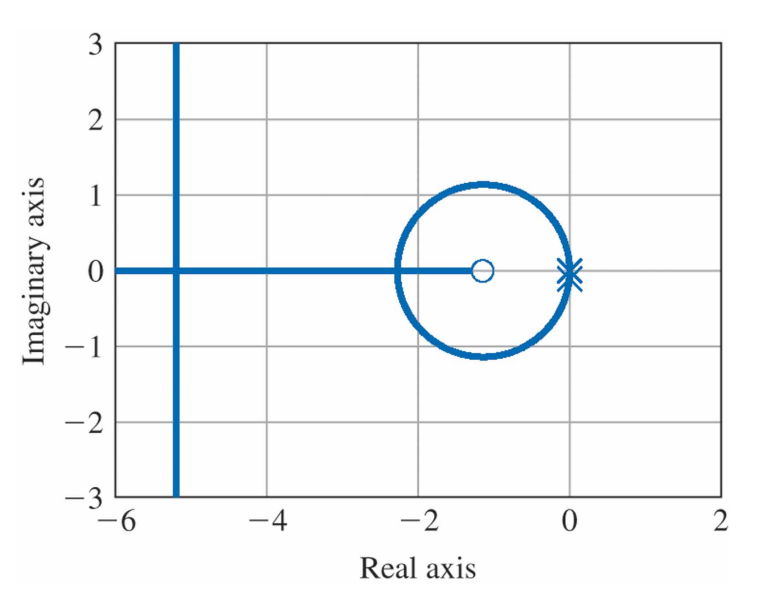
예제 5.4 수정된 PD 또는 앞섬보상을 사용한 인공위성 제어의 근궤적

- 규칙1. $s=0$에서 출발하는 두 개의 분지와 $s=-12$에서 시작되는 한개의 분지로 이루어진 세 개의 분지가 있다. 하나는 영점 $s=-1$에서 끝나고 두 개는 무한대로 접근한다.
- 규칙2. $-12 \le s \le -1$사이의 실수축 구간이 궤적의 영역이다.
- 규칙3. $n-m=3-1=2$개의 점근선이 있으며 점근선의 중심은 $\alpha = \frac{-12 + 1}{3 - 1} = -5.5$이고, 각은 $\phi = \frac{180^{\circ} + 360^{\circ}(l - 1)}{3 - 1} = \pm90^{\circ}$이다.
- 규칙4. $s=0$에서 이탈각은 $\pm 90^{\circ}$이다. $s=-12$에 있는 극점에서의 이탈각은 $0^{\circ}$이다.
예제 5.5 상대적으로 작은 값의 극점을 갖는 앞섬보상을 사용한 인공위성 제어의 근궤적

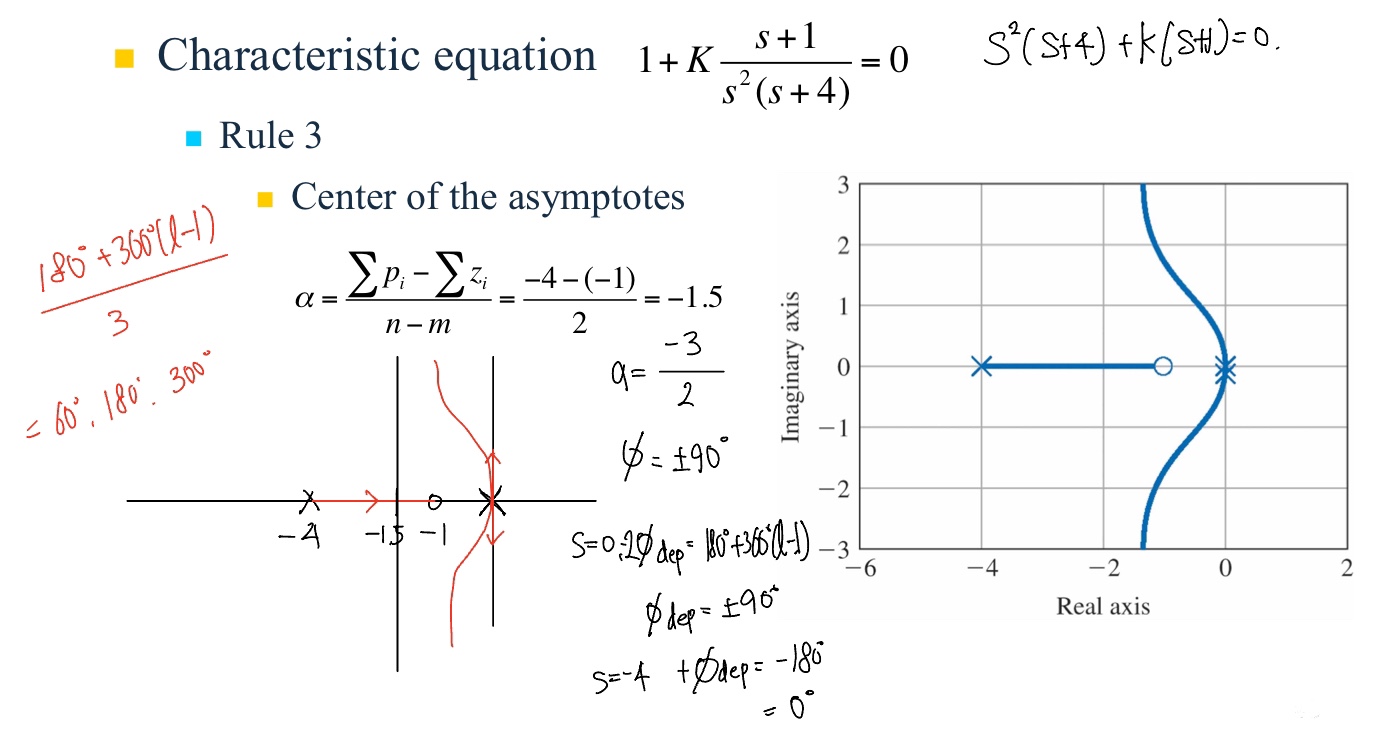
예제 5.6 중간값 극점을 갖는 인공위성의 근궤적

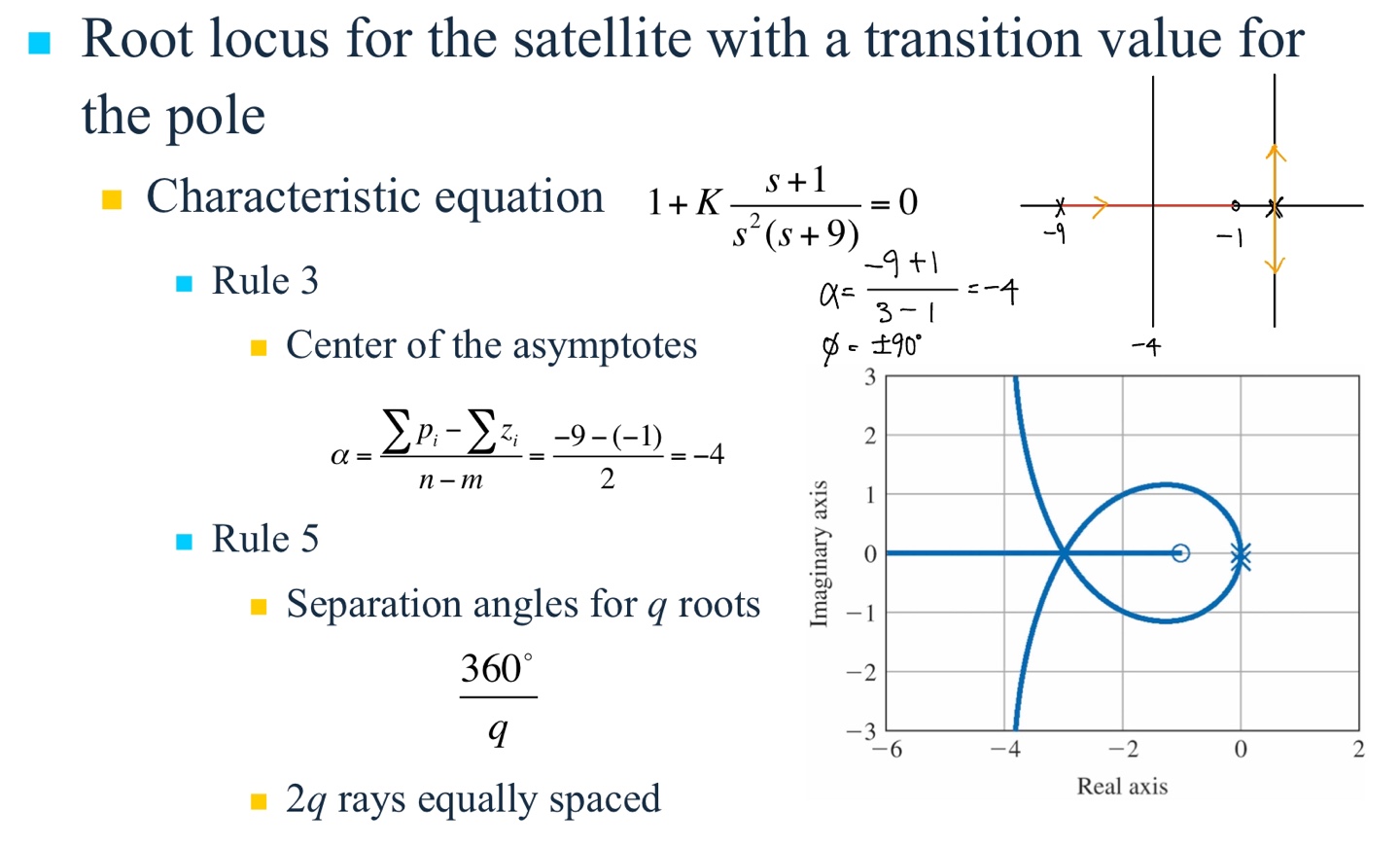
Root-Locus Examples
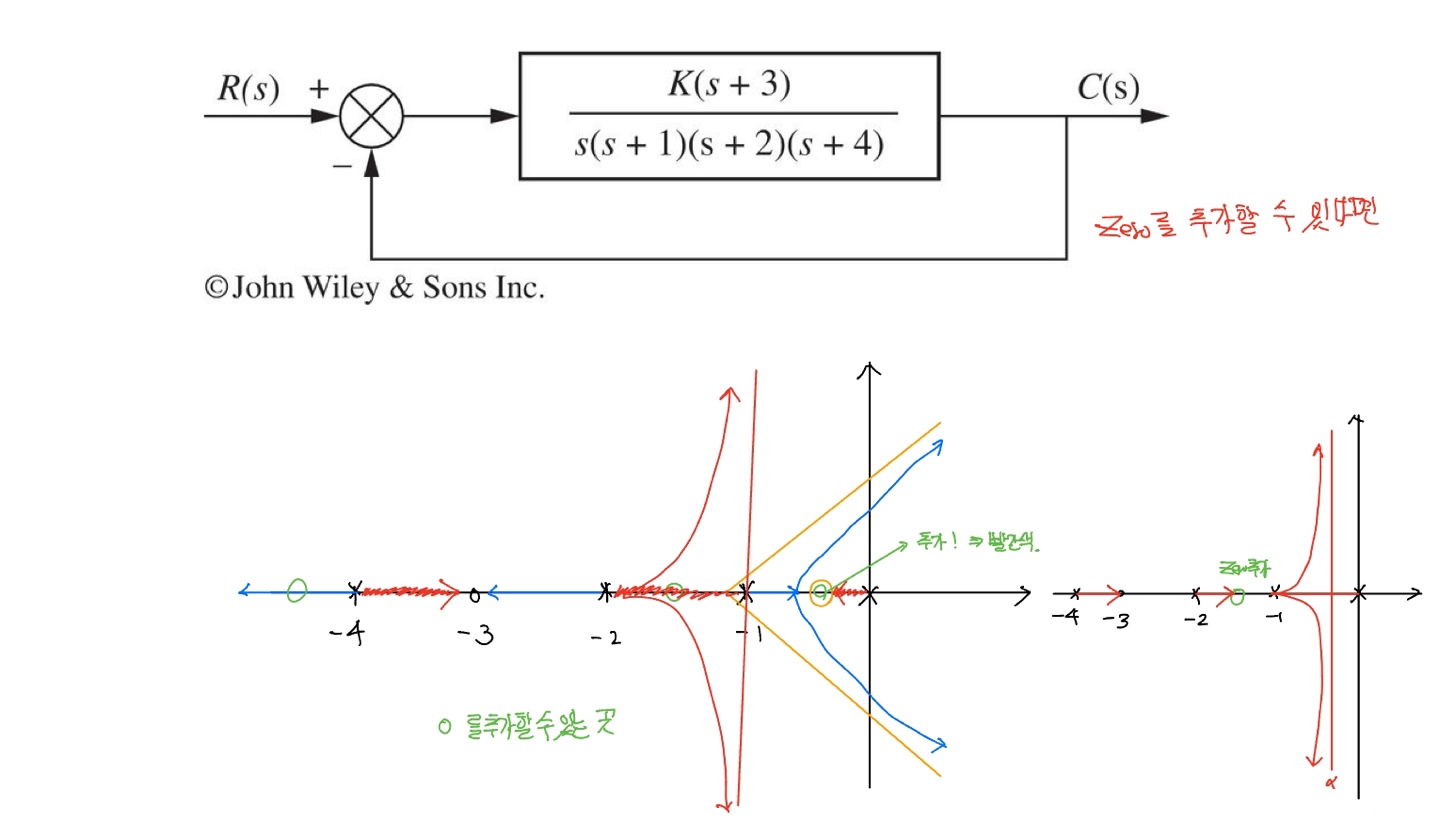
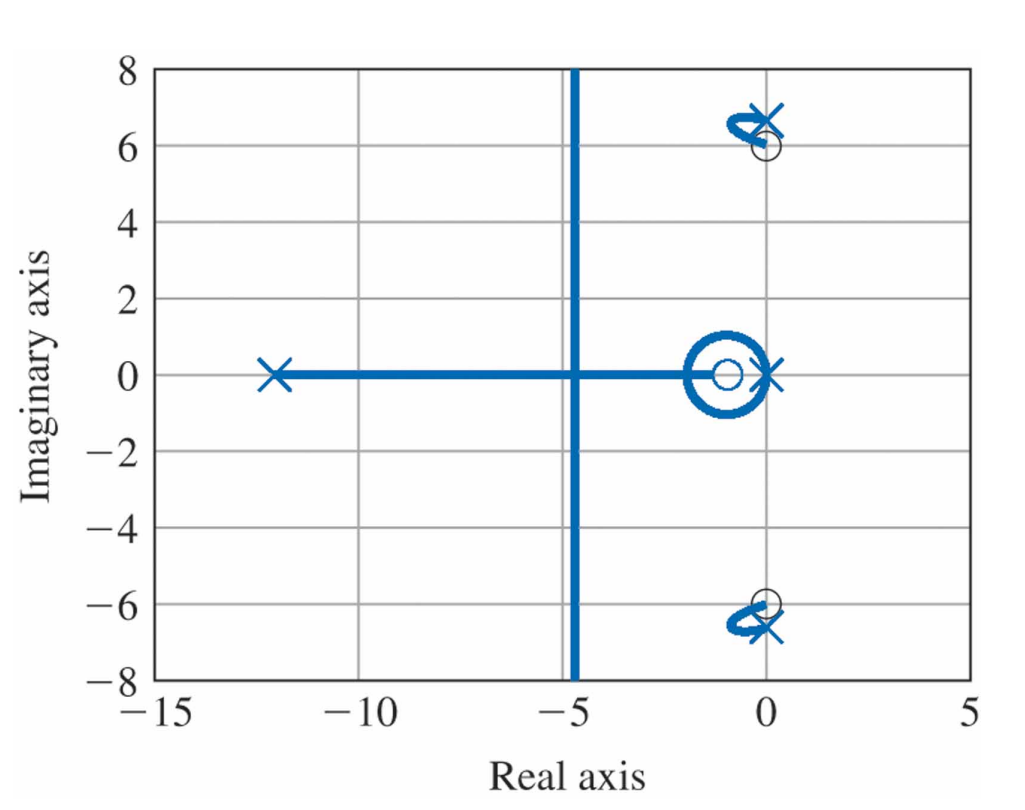
예제 5.8 연관된 유연성을 가진 인공위성 제어의 근궤적
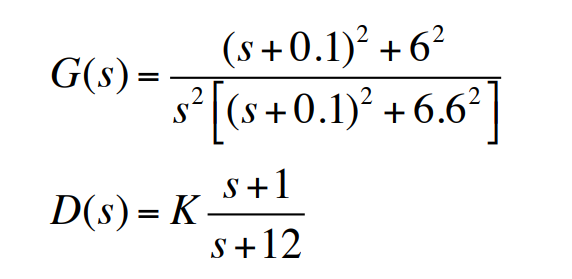
- 규칙1. 궤적에는 다섯 개의 분지가 있으며 세 개는 유연한 영점으로, 두 개는 점근선으로 근접한다.
- 규칙2. 실수축 구간 $-12 \le s \le -1$사이에 궤적이 존재한다.
- 규칙3. 두 점근선의 중심은 $\alpha = -5.5$이고 점근선의 각은 $\pm 90^{\circ}$이다.
- 규칙4.
- $s=-0.1+j6.6$에 있는 극점으로부터 이탈각을 계산하면 $\phi_1 = -217.4^{\circ} = 142.6^{\circ}$이다.
- 따라서 근은 극점 왼쪽위를 향해 출발하여 안정영역으로 위치하게 된다.
- $s=-0.1+j6$에 위치한 영점에서의 도착각을 계산하면 $\psi_1 = 126^{\circ}$이다.
- $s=-0.1+j6.6$에 있는 극점으로부터 이탈각을 계산하면 $\phi_1 = -217.4^{\circ} = 142.6^{\circ}$이다.
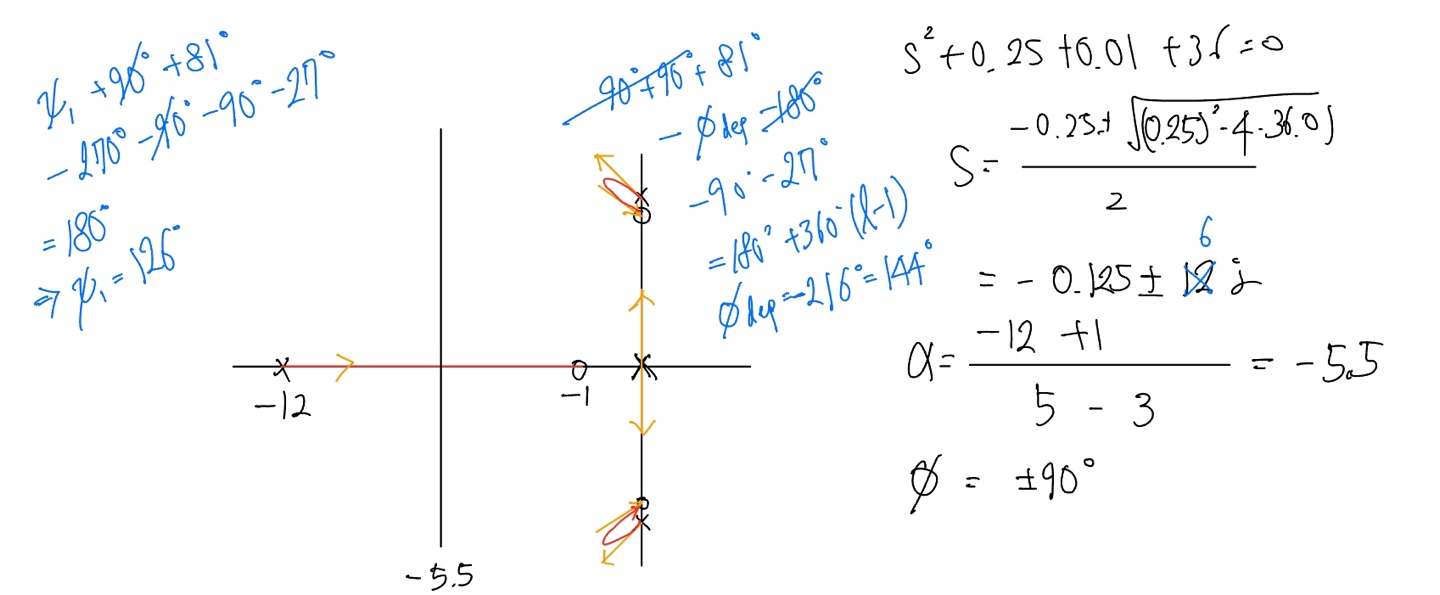
다음은 $D(s)$에서 $p$를 달리 함으로 달리지는 root locus를 보여준다.
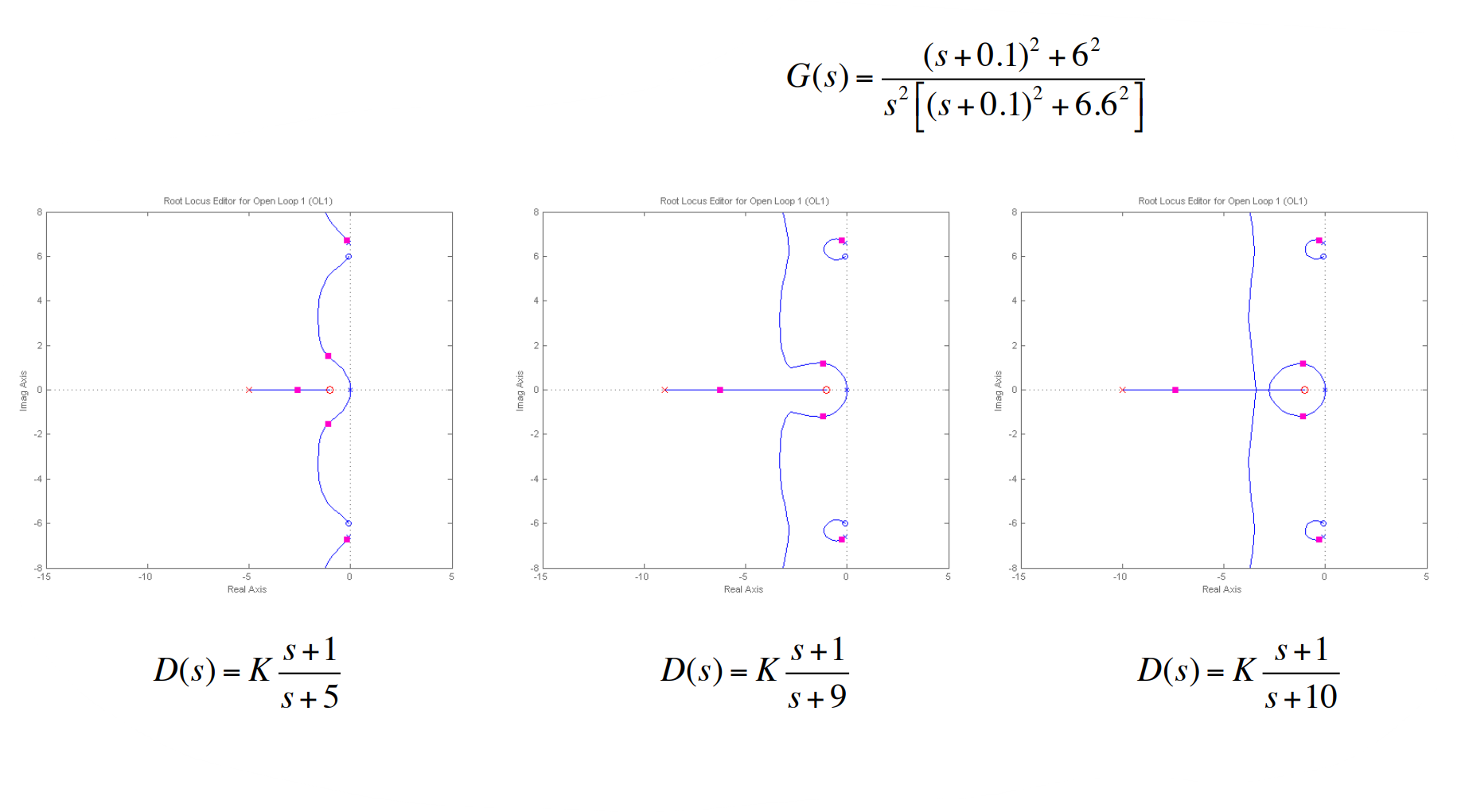
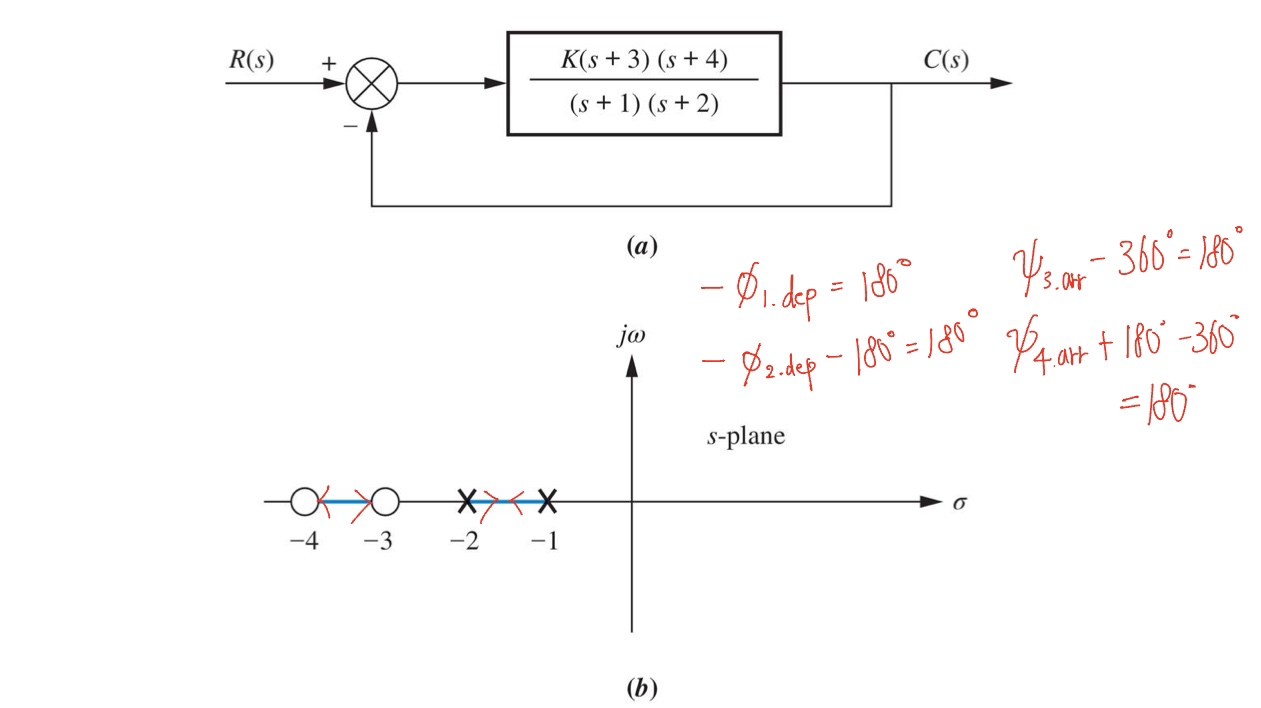
예제 5.9 비연관 경우의 근궤적
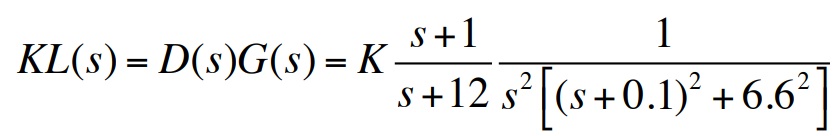
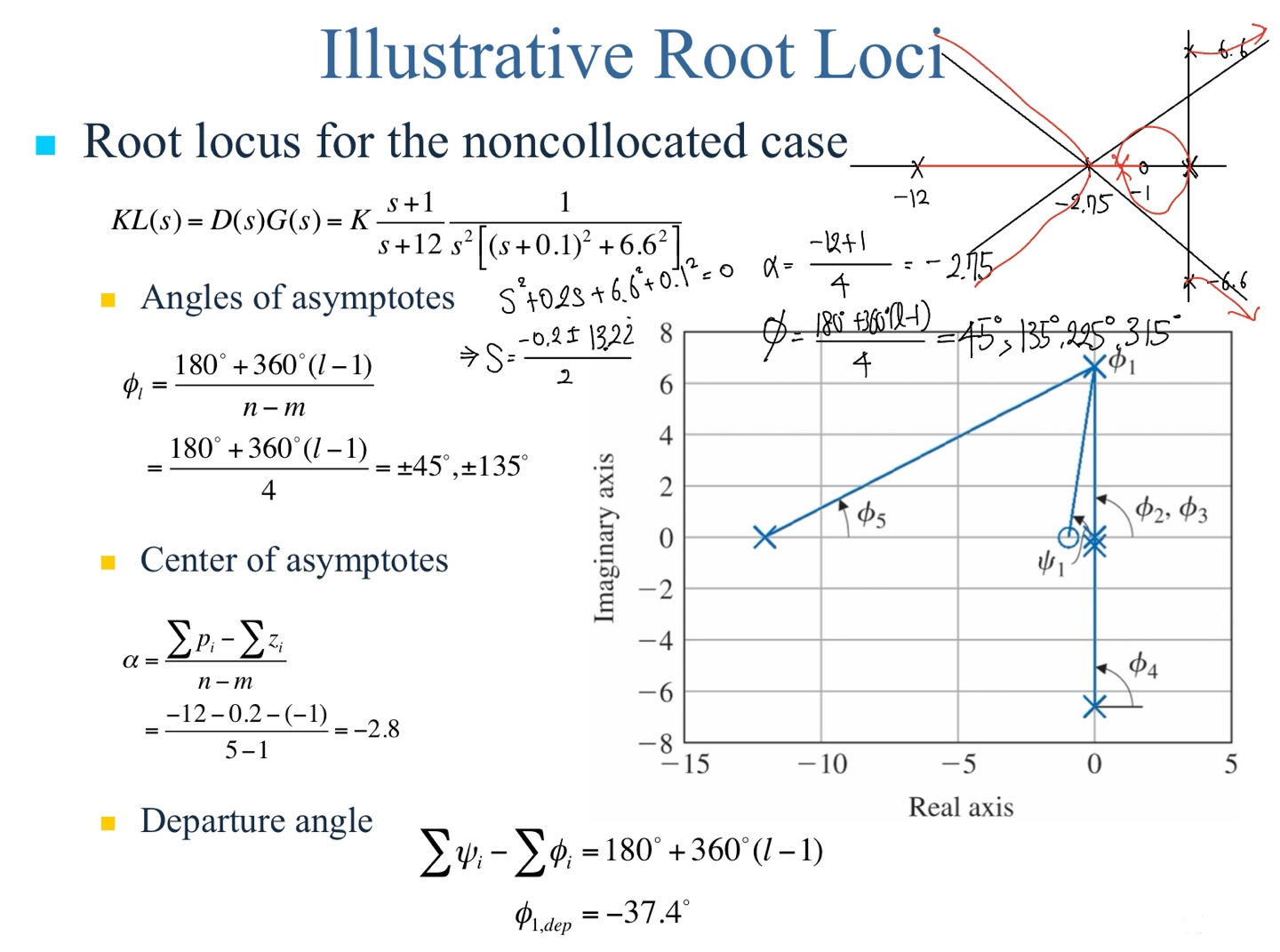
위 root locus애서 두 폴은 unstable이므로 depart angle이 왼쪽으로 가게 zero를 추가해 주어야 한다. 다음은 다른 비연관 경우의 근궤적을 보여준다.
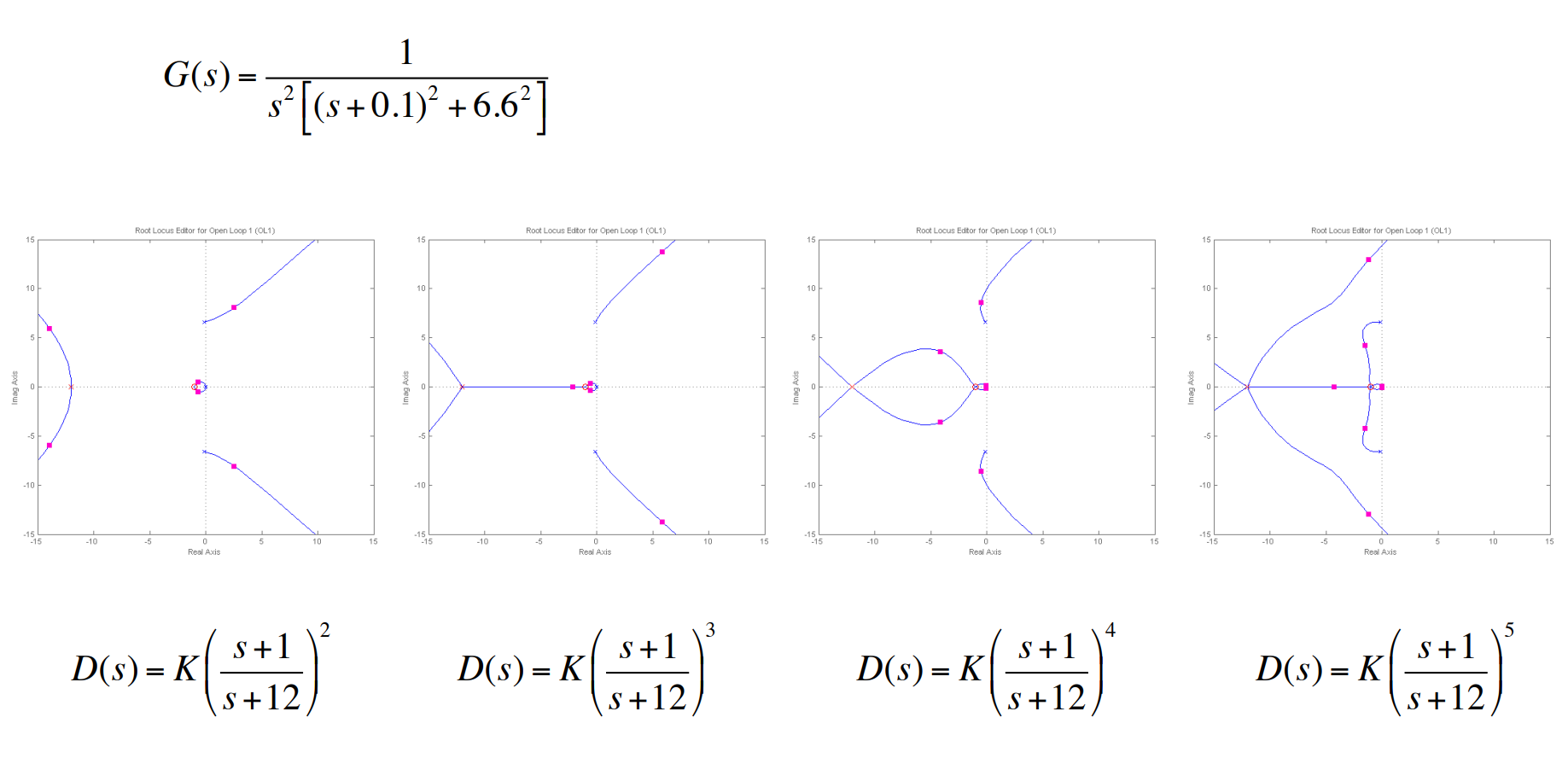
동적 보상을 이용한 설계
제어기의 설계는 공정 자체에 대한 설계로부터 시작된다. 공정을 설계하는 과정에서 잠재적인 제어 문제를 초기단계에 고려하는 것과 구동기(actuator)나 센서를 선정하는 것은 매우 중요하다. 예를들어, 유연성 제어를 더 쉽게 하기 위해 구조물에 강성이나 감쇠를 추가하는 것과 같이 공정 자체를 바꾸도록 제안하는 제어 연구의 첫 단계는 드물지 않다. 이러한 요소를 고려하고 나면 제어기이 설계가 비로소 시작된다. 공정의 동적 특성이 비례게인만으로는 만족할 만한 시스템의 설계가 이루어질 수 없는 상황이라면 동적 특성에 약간의 수정이나 보상이 필요하다. 보상방법은 여러 가지가 있지만, 다음의 세 가지 방법이 특별히 간단하고 효과적임이 판명되었다.
- 앞섬보상(lead compensation)
- PD 제어기의 기능과 유사하며, 주로 상승시간과 과도기 오버슈트를 감소시켜 응답을 빠르게 하는 작용을 한다.
- 뒤짐보상(lag compensation)
- PI 제어기의 기능과 유사하며, 시스템의 정상상태의 정확도를 개선하기 위해 사용한다.
- 노치보상(notch compensation)
- 비연관된, 즉 같은 곳에 위치하지 않는 구동기와 센서를 가지고 있는 인공위성 자세제어의 문제처럼, 저감쇠된 유연한 모드 시스템의 안정성을 확보하는 데 사용된다.
앞섬보상을 이용한 설계
$G(s)=\frac{1}{s(s+1)}$에 $D(s)=K$인 비례제어(실선)와 $D(s)=K(s+2)$인 비례미분 제어기(점선)를 사용한 경우 근궤적도는 다음과 같다.
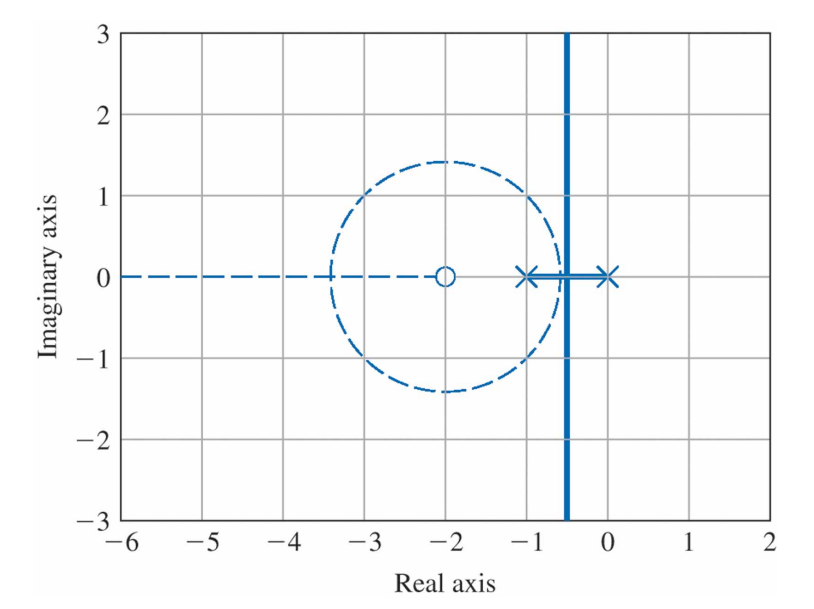
앞선 예제들에서 본 것과 같이 영점의 효과는 궤적을 왼쪽, 즉 s-펼면의 좀 더 안정한 영역으로 움직이게 한다. 만약 응답속도 사양이 $\omega_n \cong 2 \mathrm{rad/sec}$라면, 근을 요구되는 $\omega_n$에 위치시킬 때 비례제어($D=K$)만으로는 매우 낮은 감쇠비 $\zeta$가 얻어지게 된다. 따라서 요구되는 게인에서 과도 오버슈트가 매우 클 것이다. 그러나 PD 제어기의 영점을 추가함으로써 $\omega_n = 2\mathrm{rad/sec}$와 $\zeta \ge 0.5$의 위치에 폐루프 근이 놓이도록 궤적을 움직일 수 있다. 다음은 참고로 알아둬야 하는 내용이다.
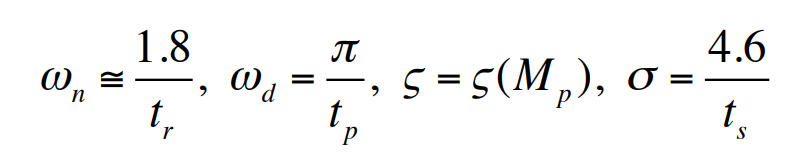
앞에서 보았듯이 미분에 의해 센서잡음이 증폭되기 때문에 순수한 미분제어는 일반적으로 실용적이지 않으므로 근사화시켜야 한다. 앞섬보상의 극점을 $\omega_n$설계범위 밖에 멀리 위치시켰다면 앞섬보상이 설계의 동적 응답을 많이 변화시키지는 못할 것이라고 예상된다. 예를들어, 다음과 같은 앞섬 보상을 고려한다.
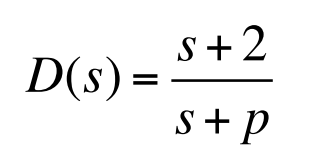
$p=10$과 $p=20$일 때의 두 가지 경우의 근궤적이 PD 제어의 궤적과 함께 다음과 같이 나타나 있다.
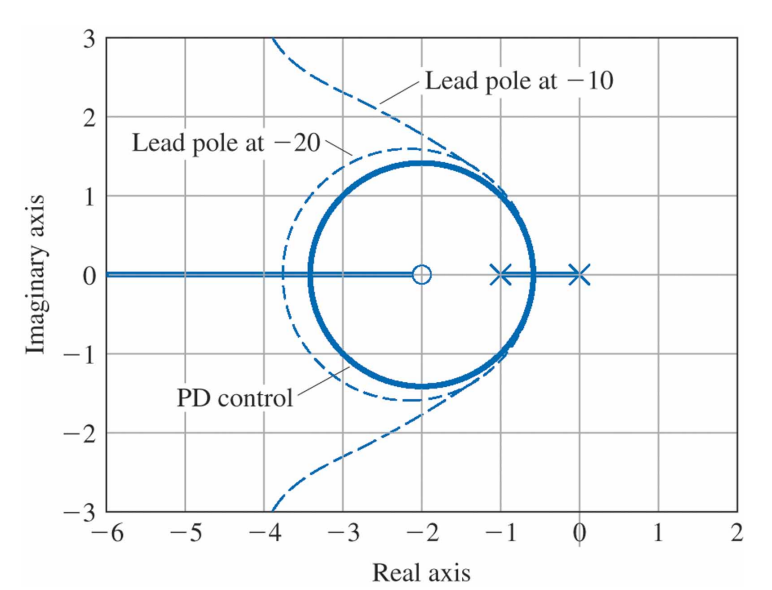
이 궤적들에 대한 중요한 사실은, 게인이 작은 경우 실근이 $-p$에서 출발하여 $-2$로 도달하기 전에는 앞섬제어의 궤적은 $D(s)=K(s+2)$의 궤적과 거의 동일하다는 것이다. 극점의 효과는 감쇠를 낮추는 것이지만, $p>10$이라면 궤적의 시작부분에서 극점의 영향을 크지 않다.
식 $D(s) = K\frac{s+z}{s+p}$의 $z$와 $p$의 정확한 값은 일반적으로 시행착오법에 의헤 결정되며, 경험에의해 반복횟수를 줄일 수 있다. 일반적으로 영점은 상승시간 또는 정착시간을 결정하는 폐루프 $\omega_n$의 근처에 놓이고, 극점은 영점 위치 값의 5배 내지 25배 되는 위치에 놓인다. 극점의 정확한 위치선정은, 작은 $p$가 필요한 잡음제어와 큰 $p$가 필요한 보상의 효율의 상반되는 효과 사이에서 절충하여 결정된다. 일반적으로 극점이 영점과 너무 가까이 있으면 근궤적이 보상되지 않은 형상으로부터 그다지 많이 움직이지 않게 되어 영점이 그 역할을 제대로 수행하지 못한다. 반면에 극점이 지나치게 좌반면 깊이 위치할 경우 $D(s)$의 출력에 나타나는 센서잡음의 크기가 매우 커서 모터 또는 다른 구동기가 제어신호 $u(t)$의 잡음 에너지에 의해 과열될 수 있다. 다음 예를 보자.
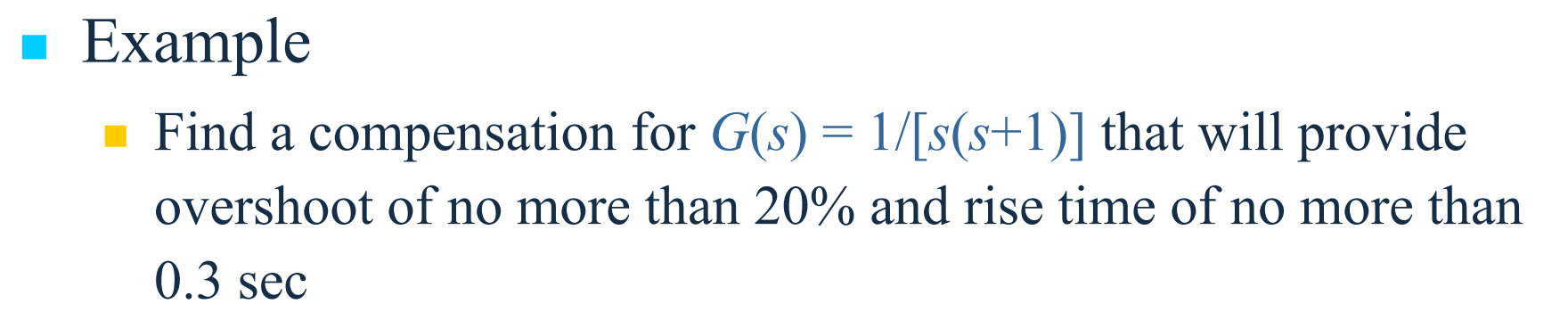
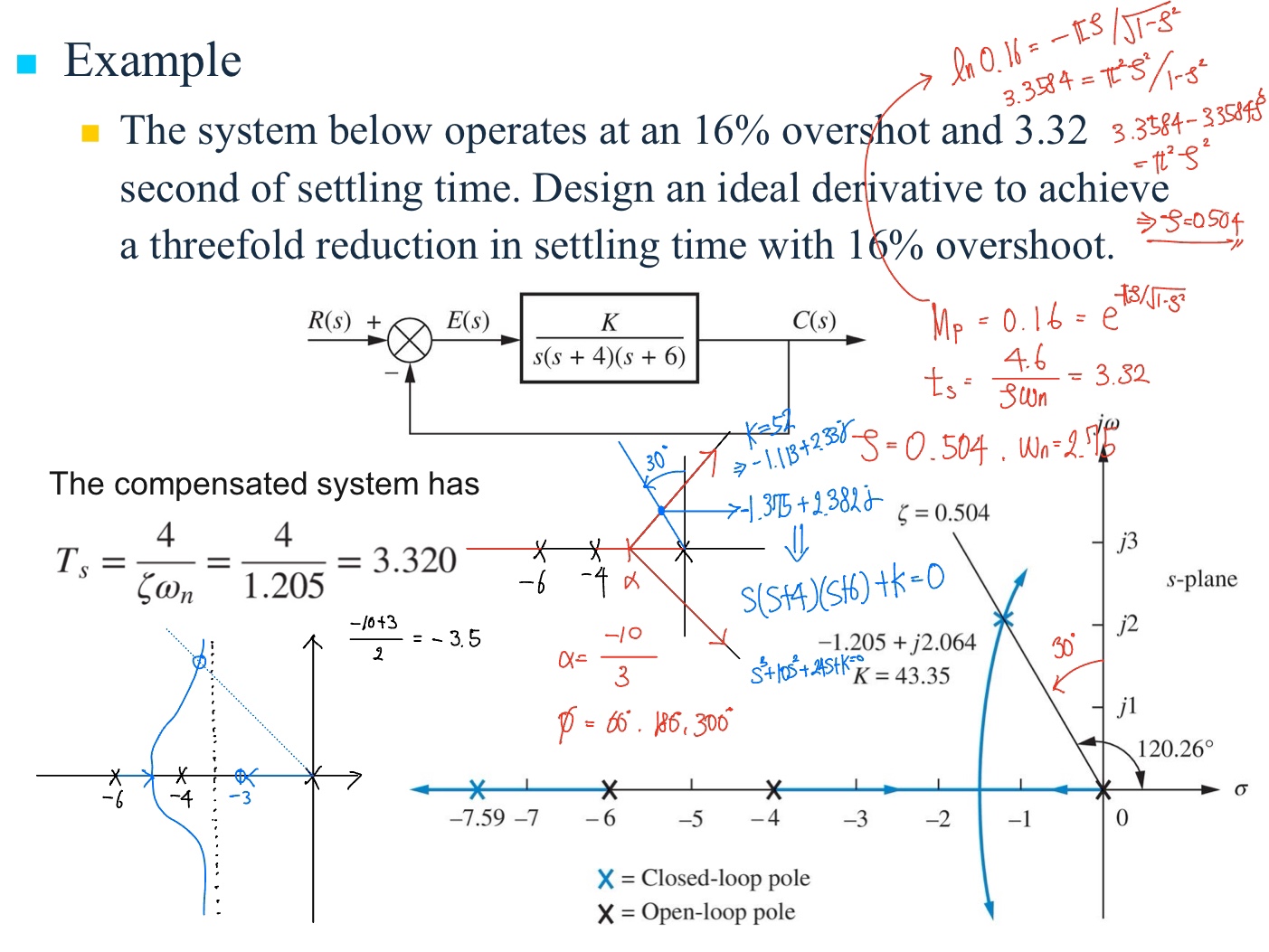
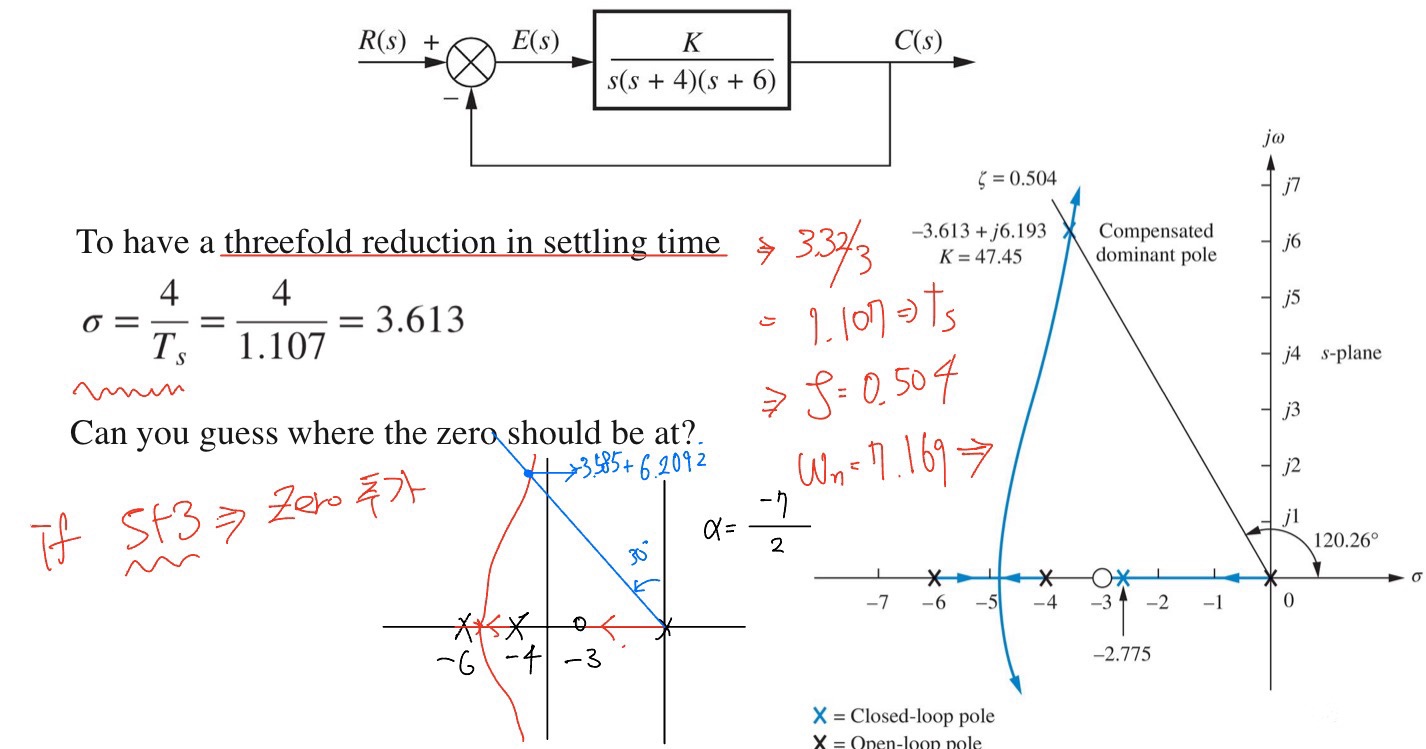
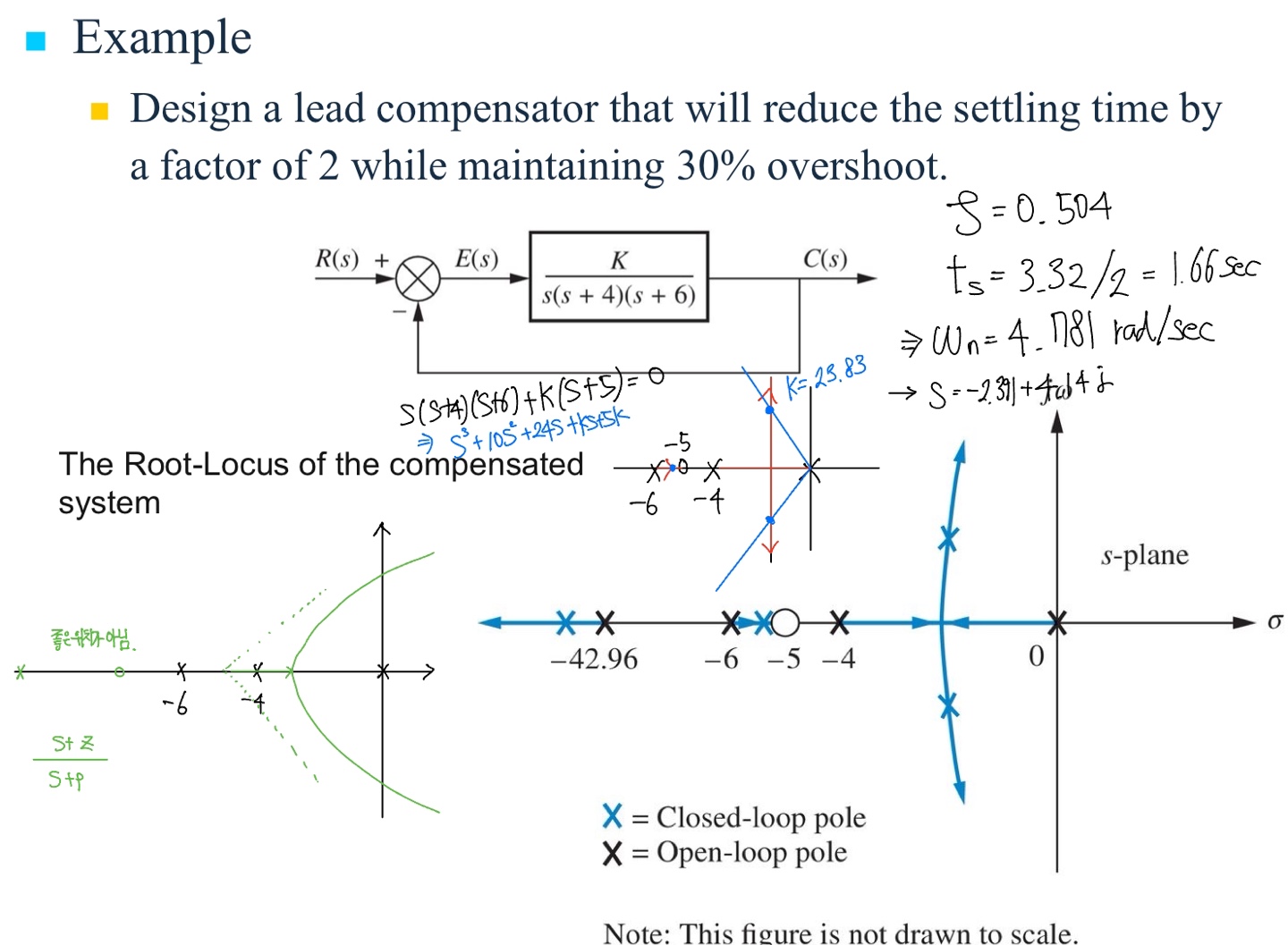
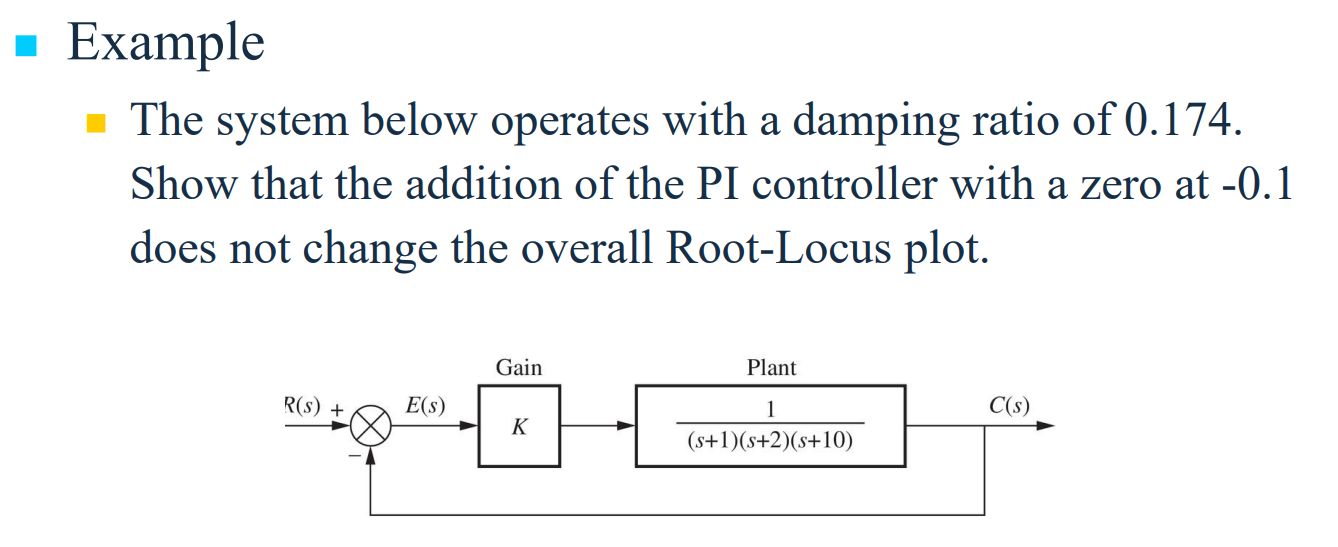
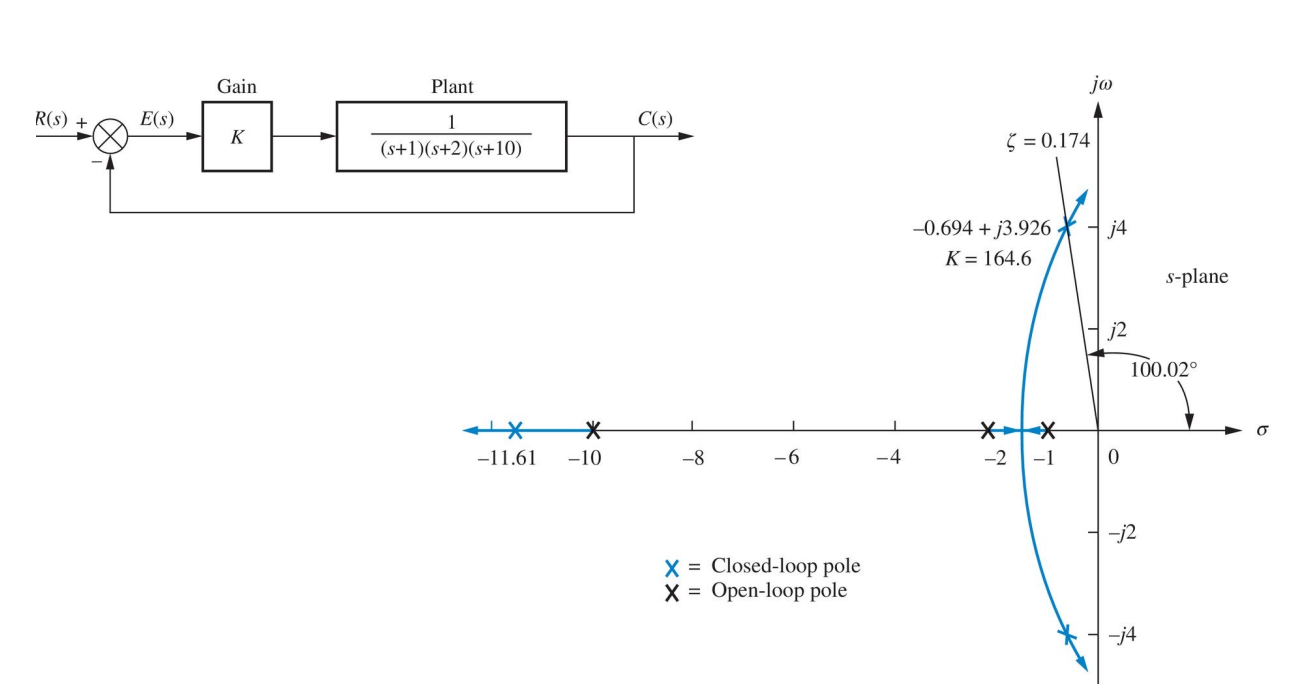
3장으로부터 감쇠비 $\zeta \ge 0.5$와 고유진동수 $\omega_n \cong 1.8/0.3 = 6 \mathrm{rad/s}$가 요구조건을 만족할 것이라고 예상할 수 있다. 어느 정도 여유룰 주기 위해 $\zeta \ge 0.5$와 $\omega_n \ge 7 \mathrm{rad/s}$를 가지고 시도한다. 첫번째로 $D(s)=K\frac{s+2}{s+10}$으로 보상을 시도한다. $K=70$이면, $\zeta=0.56$과 $\omega_n=7.7 \mathrm{rad/s}$가 되므로 초기 추정치는 주어진 사양을 만족한다. $K=70$ 일 때 세번째 극점은 $s=-2.4$에 위치한다. 세번째 극점이 앞섬보상기 영점에 매우 가깝게 있어 오버슈트가 2차 시스템의 경우에 비해 크게 증가되지 않을 것이다. 그러나 다음 그림으로부터 계단응답은 오버슈트 사양을 약간 초과함을 알 수 있다.
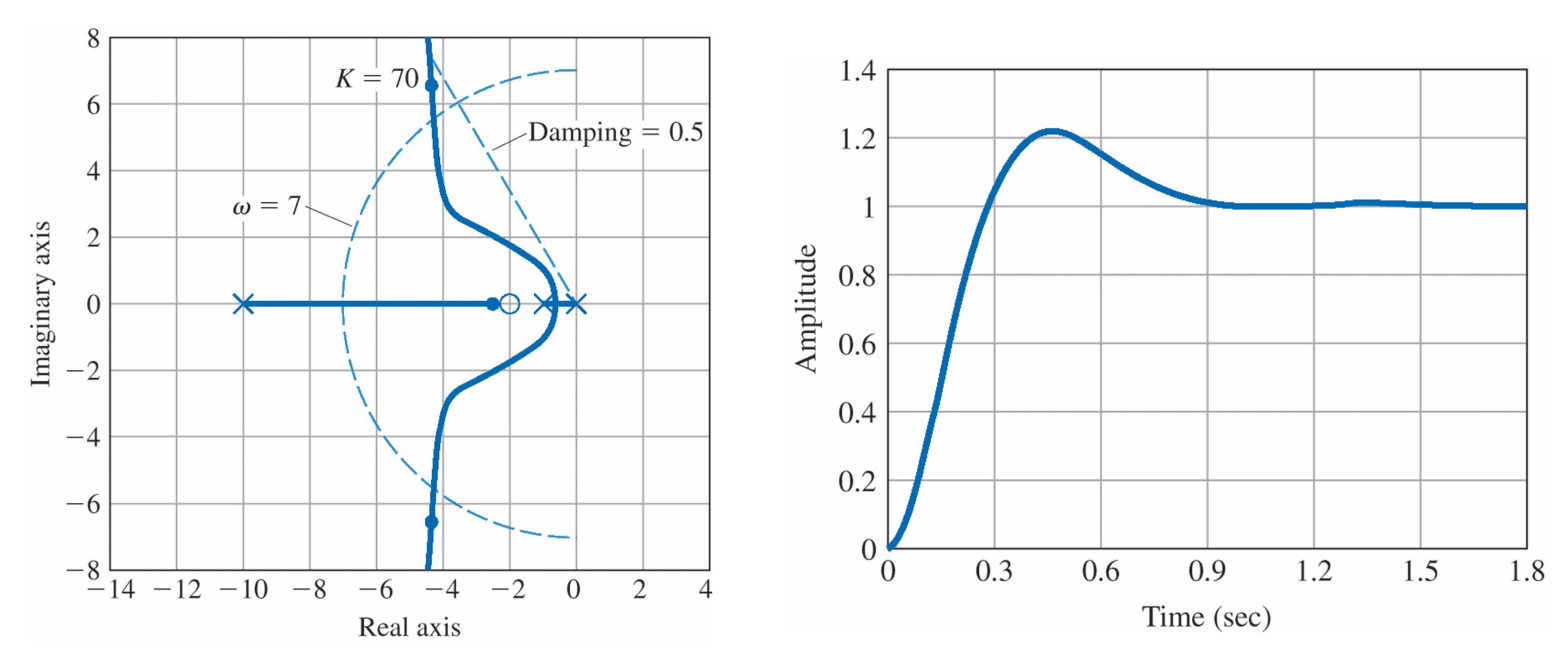
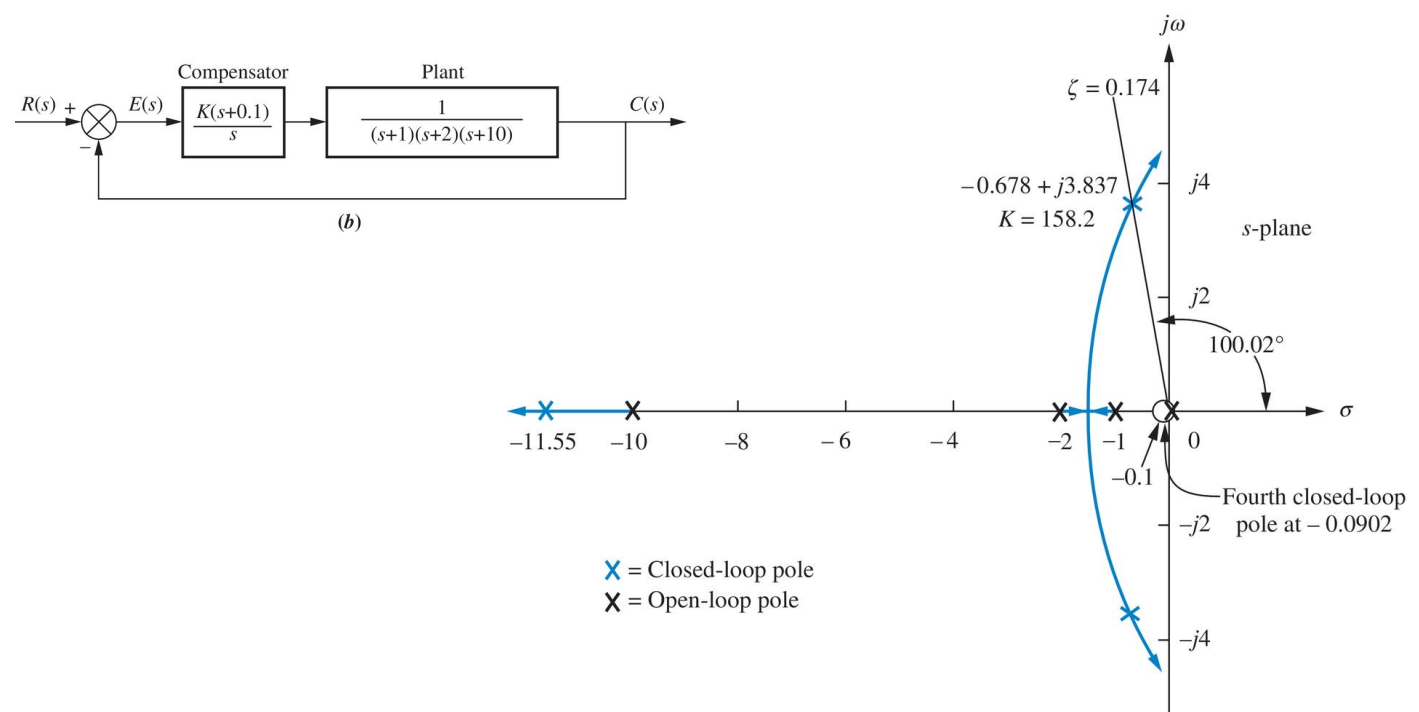
과도응담에서 오버슈트를 줄일 수 있는 향상된 감쇠효과를 얻기 위해 보상기를 조정한다. 일반적으로 $p/z$비율이 대략 25이하로 유지될 경우 $p$를 증가시키는 것이 감쇠를 증가시키는 최선의 방법이다. 명백하게 이 예제에 대해 요구되는 만큼의 감쇠의 증가가 없으므로 $p$를 적절한 값, 예를들어 10에서 13 사이로 증가시키는 것이 합리적인 선택이 될 것이다. 따라서 앞섬보상기는 다음과 같이 된다.
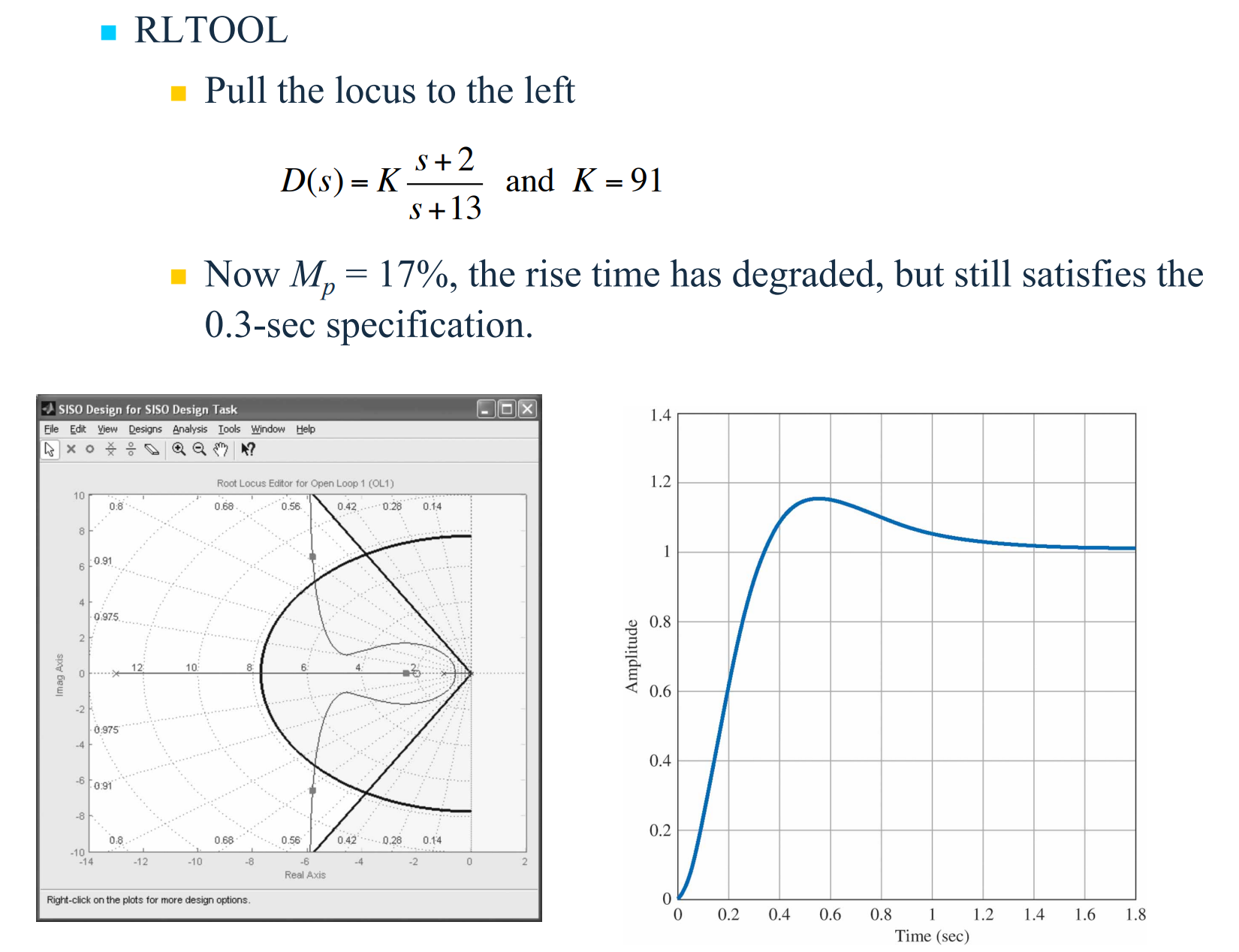
이제부터 예시를 통해 알아본다.
다른 예를 보자.

뒤짐보상을 이용한 설계

동적 응답에 대한 뒤짐보상의 효과는 해당 근궤적을 조사함으로써 알아볼 수 있다. 다음 과정을 통해 속도상수를 구할 수 있다.
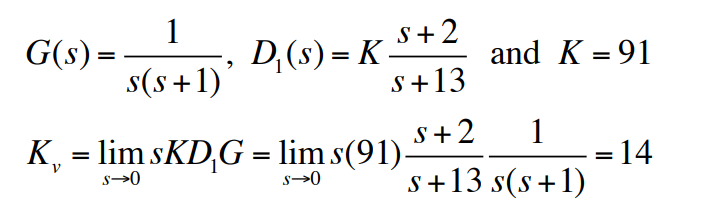
속도오차를 5배 줄일 수 있도록 $K_v = 70 \mathrm{sec}^{-1}$이 요구된다고 가정한다. 이것을 만족시키기 위해 속도상수를 5배 증가시킬 수 있는 $z/p=5$를 작는 뒤짐보상이 필요하다. 이는 $p=-0.01$과 $z=-0.05$에 위치한 극점과 영점에 의해 가능한데, 이 극점과 영점은 $z$와 $p$의 값을 모두 작게 유지하므로 $D(s)$는 $\omega_n = 7\mathrm{rad/s}$ 근처에서 지배적인 동특성을 나타내는 부분에 해당되는 궤적에 거의 영향을 미치지 않게 된다. 그 결과는 다음과 같은 전달함수를 가지는 뒤짐보상이다.
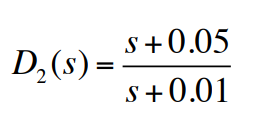
앞섬과 뒤짐 보상의 두 가지를 가지는 근궤적은 다음과 같은데, 왼쪽의 큰 스케일의 그림으로부터 앞섬 보상의 예제와 크게 다르지 않음을 알 수 있다.
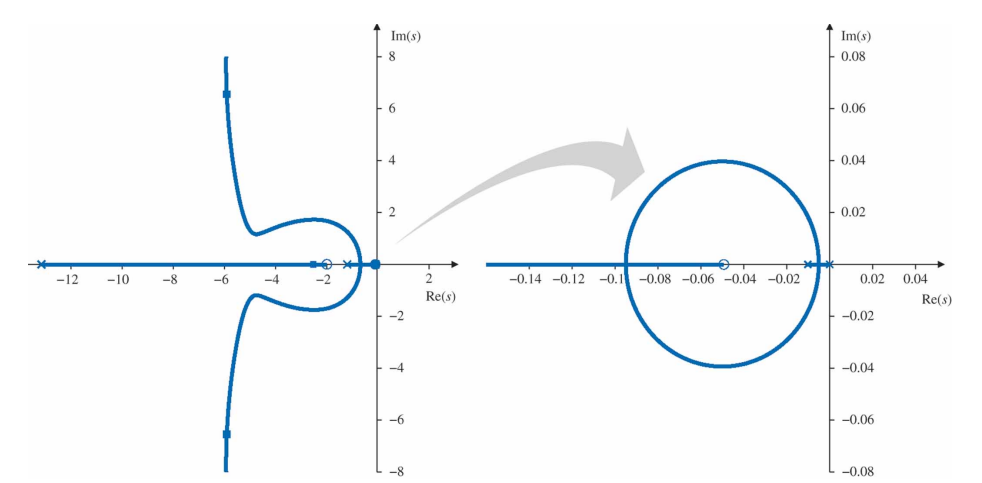
이는 극점과 영점을 매우 작은 값으로 선정한 결과이다. $K=91$일 경우, $-5.8 \pm j6.5$에 지배근(dominant root)가 나타난다. 뒤짐보상의 효과는 원점 근처의 궤적 영역을 위와같이 확대함으로써 확인할 수 있다. 여기서 원형 궤적은 매우 작은 극점과 영점의 결과임을 알 수 있다. 폐루프 근은 뒤짐보상 영점 $-0.05$에 매우 가깝게 남아있다. 이 근은 영점이 전달함수의 극점과 거의 상쇄되기 때문에 아주 작은 크기를 갖고 있어서 매우 느리게 소멸하는 과도응답을 나타낼 것이다. 그러나 소멸이 느리기 때문에 이 항은 정착시간에 커다란 영향을 줄 수 가 없다. 게다가 영점은 외란토크에 대한 계단응답에는 나타나지 않을 것이기 때문에 느린 과도상태는 더욱 명료해질 것이다. 이러한 효과 때문에 뒤짐 극점-영점의 조합은 지배적인 근의 위치에 큰 변화가 없게 가능한 고주파수 영역에 위치하게 하는 것이 중요하다. 다음 예를 보자.
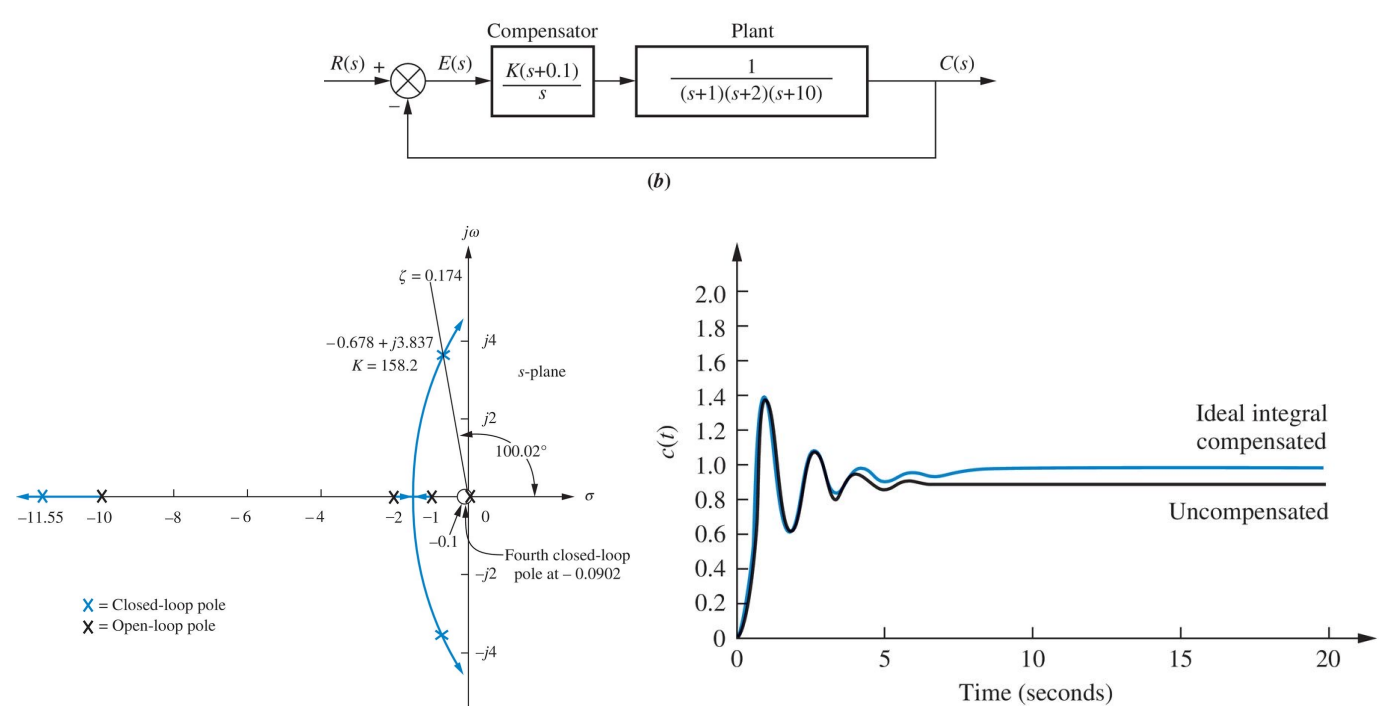
노치보상을 이용한 설계
다음과 같이 앞섬과 뒤짐 보상이 설계되었다고 가정하자.
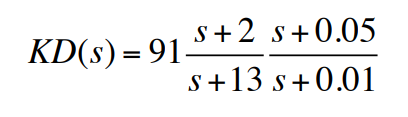
그러나 $\omega_n = 50\mathrm{rad/s}$의 고유진동수에서 예상하지 못했던 비연관된 유연성 때문에 약 $50 \mathrm{rad/s}$에서 상당한 진동이 있는 것이 시험을 통해 확인되었다고 가정한다. 재검토 결과, 유연성의 효과를 포함하는 플랜트 전달함수는 다음과 같이 추정되었다.
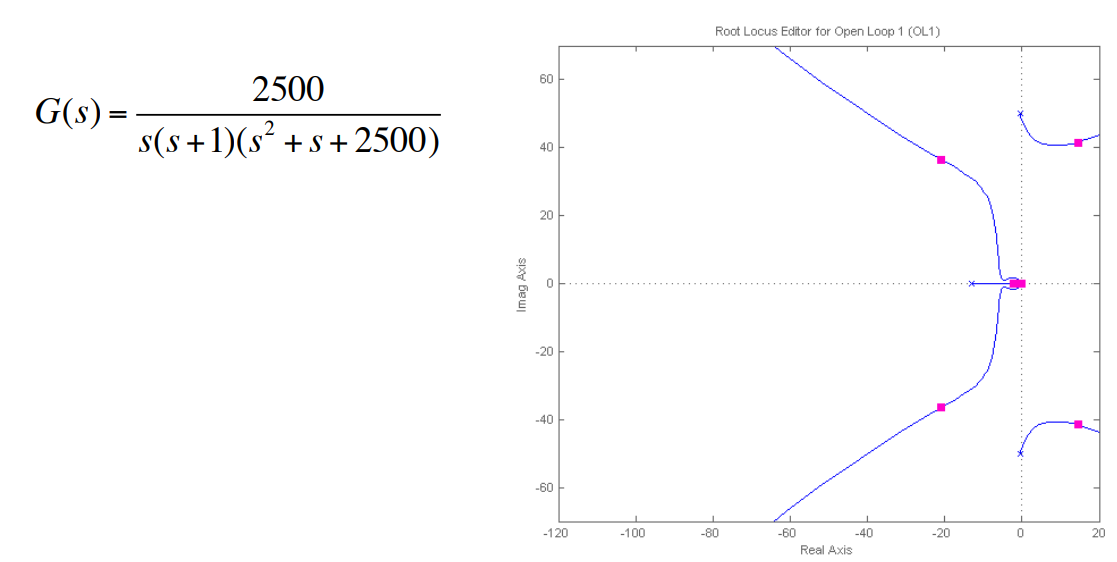
이는 추가적인 뒤짐보상이 제어 에너지가 흘러 들어가는 현상을 크게 감소시키고 진동을 제거할 만큼 충분히 루프게인을 낮출 수 있다. 고주파수에서의 게인 저감을 게인 안정화(gain stabilization)라고 부른다. 게인 안정화 때문에 응답시간이 너무 오래 걸린다면 2차적인 방법으로 공진 극점으로부터의 이탈각을 이동시켜 폐루프의 근이 좌반평면(LHP)으로 움직여 이와 관련된 과도반응이 없어지도록 공진 근처에 영점을 추가하는 것이다. 이 방법을 위상 안정화(phase stabilization)라고 부르며 운동제어에서의 유연성과 유사한 기능을 한다. 위상 안정화의 결과를 노치보상(notch compensation)이라고 부르며 전달함수는 다음과 같다.
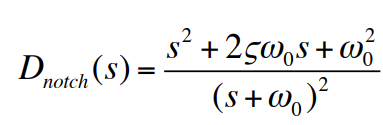
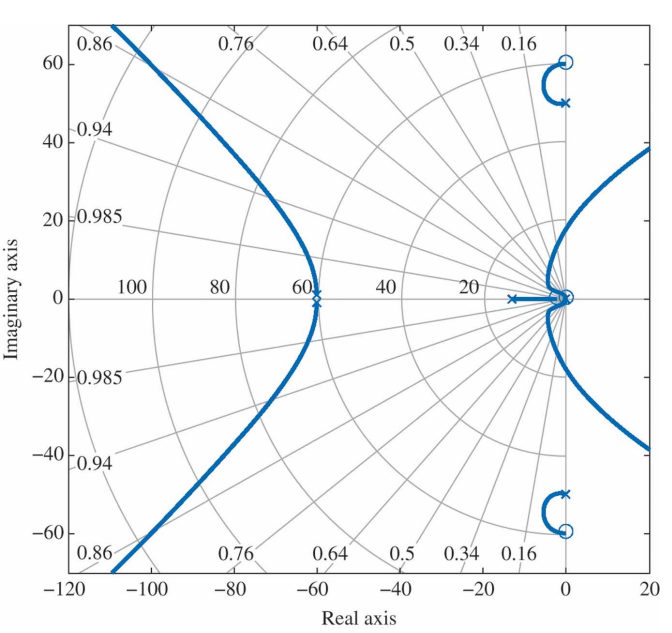
설계에 필요한 결정은 필요한 위상을 얻기 위해서 노치주파수를 유연성의 고유공진주파수보다 높게 위치시킬 것이냐 아니면 낮게 위치시킬 것이냐를 결정하는 것이다. 이탈각을 확인한 결과, 위 예에서 식 $KD(s)=91[\frac{s+2}{s+13}][\frac{s+0.05}{s+0.01}]$에 의해 보상된 플랜트와 주어진 노치에 대해 좌반평면으로 향하는 이탈각을 얻기 위해 공진주파수보다 높게 주파수를 위치시키는 것을 알게 된다. 따라서 다음과 같은 전달함수의 노피보상이 추가된다.
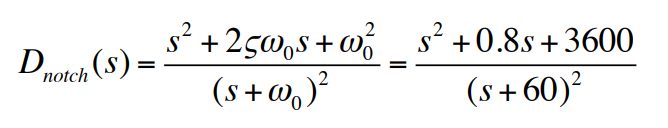
새로운 근궤적은 다음과 같다.
댓글남기기