2장 신경망의 수학적 구성 요소
Updated:
신경망과의 첫 만남
케라스 파이썬 라이브러리를 사용하여 손글씨 숫자 분류를 학습하는 구체적인 신경망 예제를 살펴본다. 지금 풀려는 문제는 흑백 손글씨 숫자 이미지(28 X 28 픽셀)를 10개의 범주(0에서 9까지)로 분류하는 것이다. 머신 러닝 커뮤니티에서 고전으로 취급받는 데이터셋인 MNIST를 사용한다. MNIST 문제를 딥러닝계의 “hello world”라고 생각해도 된다. 다음은 몇 개의 MNIST 샘플이다.

머신 러닝에서 분류 문제의 범주(category)를 클래스(class)라고 한다. 데이터 포인트는 샘플(sample)이라고 하며, 특정 샘플의 클래스는 레이블(label)이라고 한다.
다음 예를 보자. MNIST 데이터셋은 넘파이(Numpy) 배열 형태로 케라스에 이미 포함되어 있다.
from tensorflow.keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
- train_images: 훈련용 이미지 데이터이다.
- train_labels: 각 훈련에 해당하는 레이블(정답)을 담고 있다.
- test_images: 테스트용 이미지 데이터로, 훈련에 사용되지 않은 10000개의 이미지로 구성되어 있으며, 훈련된 모델의 성능을 평가하는 데 사용된다.
- test_labels: 테스트용 이미지에 대한 실제 레이블(정답)이다. 10000개의 이미지 각각에 대한 숫자(0~9)가 저장되어 있다.
train_images와 train_labels가 모델이 학습해야 할 훈련 세트(training set)를 구성한다. 모델은 test_images와 test_labels로 구성된 테스트 세트(test set)에서 테스트될 것이다. 이미지는 넘파이 배열로 인코딩되어 있고 레이블은 0부터 9까지의 숫자 배열이다. 이미지와 레이블은 일대일 관계이다. 훈련 데이터를 살펴보자.

- train_images.shape
- (60000, 28, 28): 28 X 28의 image가 6만개 있다.
- len(train_labels)
- 60000: 60000개의 훈련 이미지 각각에 대해 하나의 레이블이 존재한다.
- train_labels
- 각 이미지가 나타내는 숫자를 0부터 9 사이의 정수로 표현한 배열로, 배열 안에는 각 이미지의 숫자 값이 들어 있다.
- 예를 들어, train_labels[0]는 첫 번째 이미지가 나타내는 숫자를 의미한다.

작업 순서는 다음과 같다. 먼저 훈련 데이터 train_images와 train_labels를 네트워크에 주입한다. 그러면 네트워크는 이미지와 레이블을 연관시킬 수 있도록 학습된다. 마지막으로 test_images에 대한 에측을 네트워크에 요청한다. 그리고 이 예측이 test_labels와 맞는지 확인할 것이다.
이제 신경망을 만들어 본다.
from tensorflow import keras
from tensorflow.keras import layers
model = keras.Sequential([
layers.Dense(512, activation="relu"),
layers.Dense(10, activation="softmax")
])
- keras.Sequential: Sequential 클래스는 신경망 모델을 순차적으로 쌓을 때 사용하는 기본적인 모델 형태이다. 입력 데이터는 각 층을 통과하게 된다.
- layers.Dense(512, activation=”relu”)
- 첫 번째 Dense 레이어(완전 연결층, Fully Connected Layer)로, 512개의 노드를 가진다.
- relu라는 activation 함수가 사용된다.
- 음수를 0으로 만들고 양수는 그대로 두는 방식
- layers.Dense(10, activation=”softmax”)
- 두 번째 Dense 레이어로, 10개의 노드를 가지며, MNIST 데이터셋에서 숫자 0~9를 예측하기 때문에 출력층의 노드수가 10이다.
- softmax라는 activation 함수가 사용된다.
- 출력 값을 확률로 변환하여 각 클래스(0~9) 중 어느 클래스에 속할 가능성이 가장 높은지 모델이 예측할 수 있게 한다.
신경망의 핵심 구성 요소는 층(layer)이다. 어떤 데이터가 들어가면 더 유용한 형태로 출력되며, 조금 더 구체적으로 층은 주어진 문제에 더 의미 있는 표현(representation)을 입력된 데이터로부터 추출한다. 대부분의 딥러닝은 간단한 층을 연결하여 구성되어 있고, 점진적으로 데이터를 정제하는 형태를 띠고 있다. 딥러닝 모델은 데이터 정제 필터(층)가 연속되어 있는 데이터 프로세싱을 위한 여과기와 같다.
위 예에서는 조밀하게 연결된(완전 연결(fully connected)된) 신경망 층인 Dense 층 2개가 연속되어 있다. 두 번째 층은 10개의 확률 점수가 들어 있는 배열(모두 더하면 1)을 반환하는 소프트맥스(softmax) 분류 층이다. 각 점수는 현재 숫자 이미지가 10개의 숫자 클래스 중 하나에 속할 확률이다.
신경망이 훈련 준비를 마치기 위해서 컴파일 단계에 포함될 세 가지가 더 필요하다.
- 옵티마이저(optimizer): 성능을 향상시키기 위해 입력된 데이터를 기반으로 모델을 업데이트하는 메커니즘
- 손실 함수(loss function): 훈련 데이터에서 모델의 성능을 측정하는 방법으로 모델이 옳은 방법으로 학습될 수 있도록 도와준다.
- 훈련과 테스트 과정을 모니터링할 지표: 정확도(정확히 분류된 이미지의 비율)
model.compile(optimizer="rmsprop",
loss="sparse_categorical_crossentropy",
metrics=["accuracy"])
훈련을 시작하기 전에 데이터를 모델에 맞는 크기로 바꾸고 모든 값을 0과 1 사이로 스케일을 조정한다. 저장된 [0, 255] 사이의 값인 훈련 이미지는 (60000, 28, 28) 크기를 가진 배열로 저장되어 있다. 이 데이터를 0과 1 사이의 값을 가지는 float32 타입의 (60000, 28 * 28) 크기인 배열로 바꾼다.
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype("float32") / 255
test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype("float32") / 255
이제 모델을 훈련시킬 준비가 되었다. 케라스에서는 모델의 fit() 메서드를 호출하여 훈련 데이터에 모델을 학습시킨다.
model.fit(train_images, train_labels, epochs=5, batch_size=128)

훈련 데이터에 대한 모델의 손실과 정확도가 출력되고 있다. 훈련 데이터에 대해 0.989의 정확도를 금방 달성한다.
이제 훈련된 모델이 있으므로 이를 사용하여 새로운 숫자 이미지에 대한 클래스 확률을 예측할 수 있다. 새로운 이미지는 테스트 세트처럼 훈련 데이터가 아닌 이미지를 말한다.
test_digits = test_images[0:10]
predictions = model.predict(test_digits)
predictions[0]

출력된 배열의 인덱스 i에 있는 숫자는 숫자 이미지 test_digits[0]이 클래스 i에 속할 확률에 해당한다. 위 테스트에서 숫자는 인덱스 7에서 가장 높은 확률 값을 얻었으므로 모델의 예측 결과는 7이된다.

- test_labels[0]: 테스트 데이터의 레이블과 맞는지 확인한다.
이제 전체 테스트 세트에 대해 평균적인 정확도를 계산해본다.
test_loss, test_acc = model.evaluate(test_images, test_labels)
print(f"테스트 정확도: {test_acc}")

테스트 세트의 정확도는 97.89%로 나왔다. 훈련 세트 정확도보다는 약간 낮다. 훈련 정확도와 테스트 정확도 사이의 차이는 과대적합(overfitting) 때문이다. 이는 머신 러닝 모델이 훈련 데이터보다 새로운 데이터에서 성능이 낮아지는 경향을 말한다.
신경망을 위한 데이터 표현
이전 예제에서 텐서(tensor)라고 부르는 다차원 넘파이 배열에 데이터를 저장하는 것부터 시작했다. 최근 모든 머신 러닝 시스템은 일반적으로 텐서를 기본 데이터 구조로 사용한다. 텐서는 머신 러닝의 기본 구성 요소이다.
핵심적으로 텐서는 데이터를 위한 컨테이너(container)이다. 일반적으로 수치형 데이터를 다루므로 숫자를 위한 컨테이너이다. 텐서는 임의의 차원 개수를 가지는 행렬의 일반화된 모습이다(텐서에서는 차원(dimension)을 종종 축(axis)이라고 부른다).
스칼라(랭크-0 텐서)
하나의 숫자만 담고 있는 텐서를 스칼라(Scalar) 또는 스칼라 텐서, 랭크-0 텐서, 0D 텐서라고 한다. Numpy에서 float32나 float64 타입의 숫자는 스칼라 텐서(배열 스칼라, array scalar)이다. ndim 속성을 사용하면 numpy 배열의 축 개수를 확인할 수 있고 이를 확인하면 스칼라 텐서의 축 개수 ndim == 0이다.

벡터(랭크-1 텐서)
숫자의 배열을 벡터(vector) 또는 랭크-1 텐서나 1D 텐서라고한다. 벡터는 딱 하나의 축을 가진다. Numpy에서 벡터를 나타내면 다음과 같다.

이 벡터는 5개의 원소를 가지고 있으므로 5차원 벡터(5D vector)라고 부른다. 이는 5D 벡터는 하나의 축을 따라 5개의 차원을 가진 것이므로 5개의 축을 가진 5D 텐서와는 다르다.
행렬(랭크-2 텐서)
벡터의 배열은 행렬(matrix) 또는 랭크-2 텐서나 2D 텐서라고한다. 행렬에는 2개의 축(행과 열)이 있다. Numpy에서 행렬을 나타내면 다음과 같다.

랭크-3 텐서와 더 높은 랭크의 텐서
행렬들을 하나의 새로운 배열로 합치면 숫자가 채워진 직육면체 형태로 해석할 수 있는 랭크-3 텐서(3D 텐서)가 만들어진다. Numpy에서 랭크-3 텐서를 나타내면 다음과 같다.

랭크-3 테서들을 하나의 배열로 합치면 랭크-4 텐서를 만드는 식으로 이어진다.
핵심 속성
텐서는 3개의 핵심 속성으로 정의한다.
- 축의 개수(랭크): Numpy나 텐서플로 같은 파이썬 라이브러리에서는 ndim 속성에 저장되어 있다.
- 크기(shape): 텐서의 각 축을 따라 얼마나 많은 차원이 있는지를 나타낸 파이썬의 튜플(tuple)이다.
- 앞 예에서 행렬의 크기는 (3, 5), 랭크-3 텐서의 크기는(3, 3, 5), 벡터의 크기는 (5,), 배열 스칼라는 () 처럼 크기가 없다.
- 데이터 타입(dtype): 텐서에 포함된 데이터의 타입이다.
- 예를 들어 float32, float64, uint8 등
이를 확인하기 위해 MNIST 예제에서 사용했던 데이터를 들여다본다.
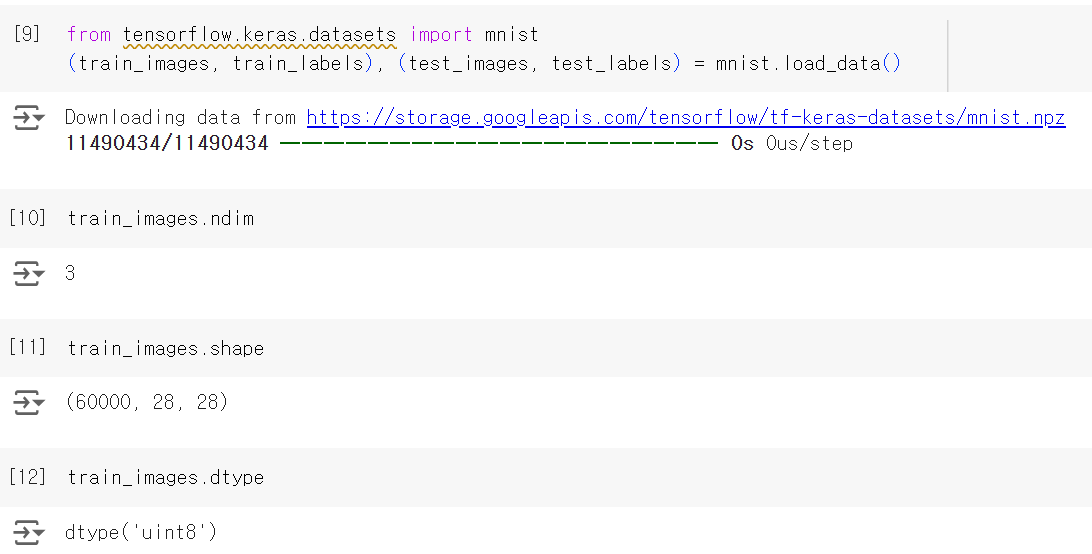
위 배열은 8비트 정수형 랭크-3 텐서, 즉 $28 \times 28$ 크기의 정수 행렬 6만 개가 있는 배열이다. 각 행렬은 하나의 흑백 이미지고, 행렬의 각 원소는 0에서 255 사이의 값을 가진다.
이 랭크-3 텐서에서 다섯 번째 샘플을 Matplotlib 라이브러리를 사용해 확인해본다.
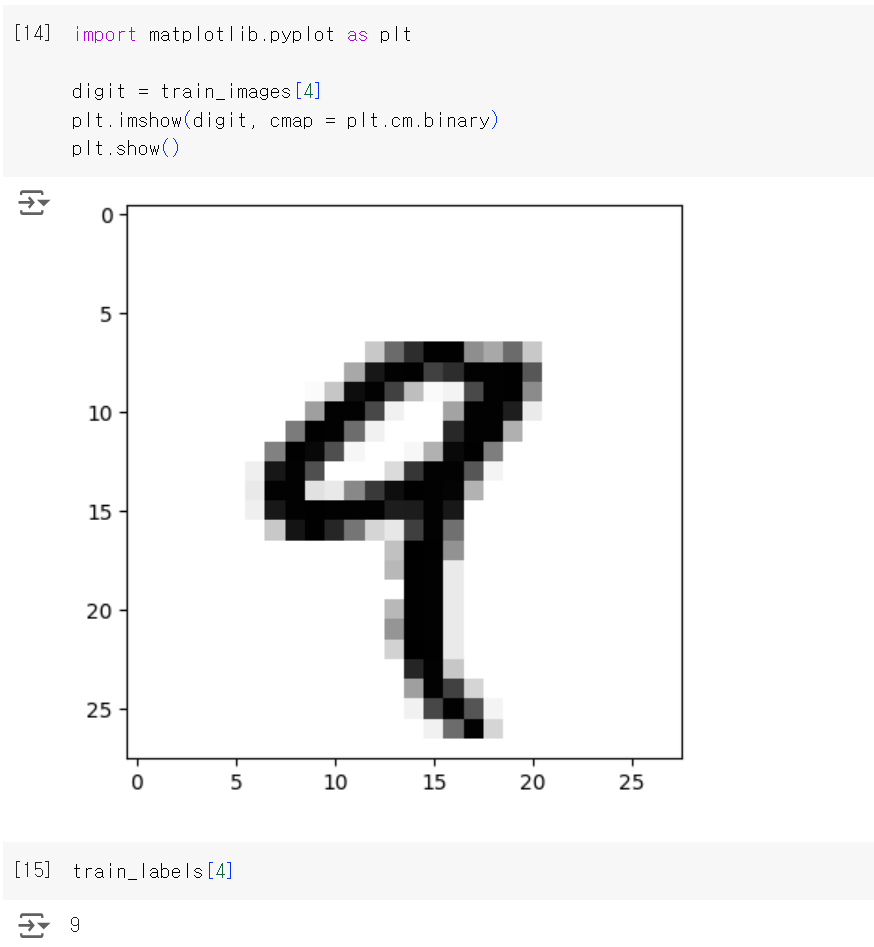
넘파이로 텐서 조작하기
앞 예제와 같이 배열에 있는 특정 원소들을 선택하는 것을 슬라이싱(slicing)이라고 한다. Numpy 배열에서 할 수 있는 슬라이싱 연산을 살펴본다.
다음 예는 11번째에서 101번째까지 숫자를 선택하여 (90, 28, 28) 크기의 배열을 만든다.
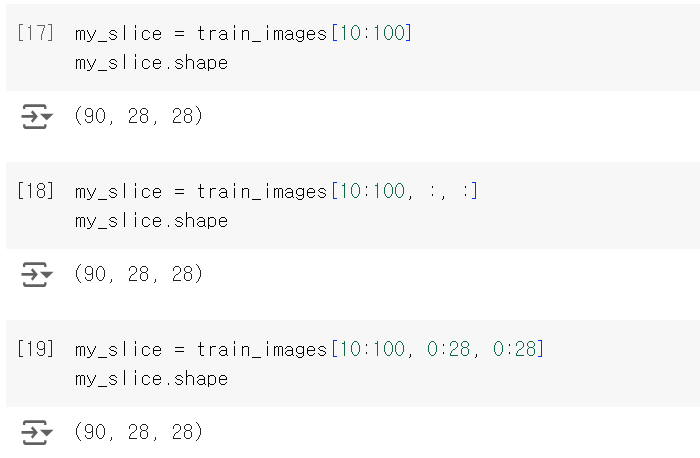
위 3방식은 모두 동일한 예이다. :은 전체 인덱스를 선택한다.
일반적으로 각 배열의 축을 따라 어떤 인덱스 사이도 선택할 수 있다. 예를 들어 이미지의 오른쪽 아래 $14 \times 14$ 픽셀을 선택하려면 my_slice = train_images[:, 14:, 14:]와 같이 하면된다. 또한 파이썬 리스트의 음수 인덱스와 마찬가지로 현재 축의 끝에서 상대적인 위치를 나타내는 음수 인덱스를 사용할 수 있다. 정중앙에 위치한 $14 \times 14$ 픽셀 조각을 이미지에서 잘라내려면 my_slice = train_images[:, 7:-7, 7:-7]과 같이 한다.
배치 데이터
일반적으로 딥러닝에서 사용하는 모든 데이터 텐서의 첫 번째 축(0번 째)은 샘플 축(sample axis)이다. MNIST 예제에서는 숫자 이미지가 샘플이다.
딥러닝 모델은 한 번에 전체 데이터셋을 처리하지 않고 데이터를 작은 배치(batch)로 나눠서 처리한다. 예를들어 MNIST 숫자 데이터에서 크기가 128인 배치 하나는 batch = train_images[:128], 그 다음 배치는 train_images[128:256], n번째 배치는 train_images[128*n: 128*(n+1)]과 같다.
이런 배치 데이터를 다룰 때 첫 번째 축(0번 축)을 배치 축(batch axis) 또는 배치 차원(batch dimension)이라고 부른다.
텐서의 실제 사례
- 벡터 테이터
- 대부분의 경우에 해당
- 하나의 데이터 포인트가 벡터로 인코딩될 수 있으므로 배치 데이터는 랭크-2 텐서로 인코딩될 것이다(즉, 벡터의 배열).
- (samples, features) 크기의 랭크-2 텐서
- 각 샘플은 수치 속성(특성)으로 구성된 벡터
- 예
- 사람의 나이, 성별, 소득으로 구성되 인구 통계 데이터, 각 사람은 3개의 값을 가진 벡터로 구성되고 10만 명이 포한된 전체 데이터셋은 (100000, 3) 크기의 랭크-2 텐서에 저장될 수 있음.
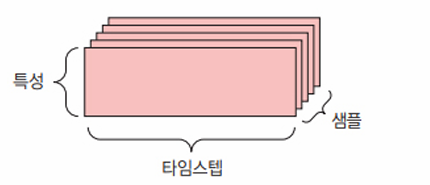
- 시계열 데이터 또는 시퀀스(sequence) 데이터
- 데이터에서 시간이 (또는 연속된 순서가) 중요할 때는 시간 축을 포함하여 랭크-3 텐서로 저장된다.
- (samples, timesteps, features) 크기의 랭크-3 텐서
- 각 샘플은 벡터의 시퀀스(랭크-2 텐서)로 인코딩되므로 배치 데이터는 랭크-3 텐서로 인코딩될 것이다.
- 각 샘플은 특성 벡터의 (길이가 timesteps인) 시퀀스
- 예
- 주식 가격 데이터셋: 1분마다 현재 주식 가격, 지난 1분 동안에 최고 가격과 최소 가격을 저장한다. 1분마다 데이터는 3D 벡터로 인코딩되고 하루 동안의 거래는 (390, 3) 크기의 행렬로 인코딩된다(하루의 거래 시간은 390분). 250일치의 데이터는 (250, 390, 3) 크기의 랭크-3 텐서로 저장될 수 있다.
- 이미지
- 이미지는 전형적으로 높이, 너비, 컬러 채널의 3차원으로 이루어진다. 흑백 이미지는 하나의 컬로 채널만 가지고 있어 랭크-2 텐서로 저장될 수 있지만 관례상 이미지 텐서는 항상 랭크-3 텐서로 저장된다.
- 흑백 이미지의 경우 컬러 채널의 차원 크기는 1이다.
- 채널 마지막(channel-last) 방식인 (samples, height, width, channels) 또는 채널 우선(channel-first) 방식인 (samples, channels, height, width) 크기의 랭크-4 텐서
- 각 샘플은 필셀의 2D 격자고 각 픽셀은 수치 값(채널(channel))의 벡터
- $256 \times 256$크기의 흑백 이미지에 대한 128개의 배치는 (128, 256, 256, 1) 크기의 텐서에 저장될 수 있다.
- 컬러 이미지에 대한 128개의 배치라면 (128, 256, 256, 3) 크기의 텐서에 저장될 수 있다.
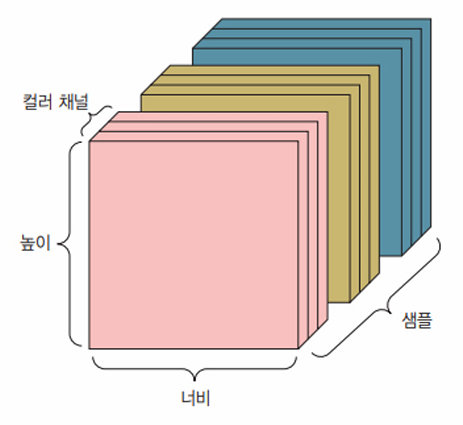
- 이미지는 전형적으로 높이, 너비, 컬러 채널의 3차원으로 이루어진다. 흑백 이미지는 하나의 컬로 채널만 가지고 있어 랭크-2 텐서로 저장될 수 있지만 관례상 이미지 텐서는 항상 랭크-3 텐서로 저장된다.
- 동영상
- 비디오 데이터는 현실에서 랭크-5 텐서가 필요한 몇 안되는 데이터 중 하나이다.
- 하나의 비디오는 프레임의 연속이고 각 프레임은 하나의 컬러 이미지
- 프레임이 (height, width, color_depth)의 랭크-3 텐서로 저장될 수 있기 때문에 프레임의 연속은 (frames, height, width, color_depth)의 랭크-4 텐서로 저장될 수 있다.
- (samples, frames, height, width, channels) 또는 (samples, frames, channels, height, width) 크기의 랭크-5 텐서
- 각 샘플은 이미지의 (길이가 frame인) 시퀀스
- 예
- 60초짜리 $144 \times 256$ 유튜브 비디오 클립은 초당 4프레임으로 샘플링하면 240프레임이 된다. 이런 비디오 클립을 4개 가진 배치는 (4, 240, 144, 256, 3) 크기의 텐서에 저장될 것이다.
신경망의 톱니바퀴: 텐서 연산
컴퓨터 프로그램을 이진수의 입력을 처리하는 몇 개의 이항 연산으로 표현할 수 있는 것처럼, 심층 신경망이 학습한 모든 변환을 수치 데이터 텐서에 적용하는 몇 종류의 텐서 연산(tensor operation) 또는 텐서 함수(tensor function)으로 나타낼 수 있다.
케라스의 층은 keras.layers.Dense(512, activation=”relu”)와 같이 생성했다. 이 층은 행렬을 입력으로 받고 입력 텐서의 새로운 표현인 또 다른 행렬을 반환하는 함수처럼 해석할 수 있다. 구체적으로 보면 이 함수는 W를 행렬, b를 벡터라고 하면 output = relu(dot(W, input) + b)와 같다.
여기에는 3개의 텐서 연산이 있다.
- 입력 텐서와 텐서W 사이의 점곱(dot)
- 점곱으로 만들어진 행렬과 벡터 b사이의 덧셈
- relu 연산
원소별 연산
relu함수와 덧셈은 원소별 연산(element-wise operation)으로 텐서에 있는 각 원소에 독립적으로 적용된다. 이는 고도의 병렬 구현이 가능한 연산이라는 의미이다. 파이썬으로 단순한 원소별 연산을 구현한다면 다음 relu 연산 구현처럼 for 문을 사용할 것이다.
def native_relu(x):
assert len(x.shape) == 2 # x는 랭크-2 Numpy 배열이다.
x = x.copy() # 입력 텐서 자체를 바꾸지 않도록 복사
for i in range(x.shape[0]):
for j in range(x.shape[1]):
x[i, j] = max(x[i, j], 0)
return x
덧셈도 다음과 같이 동일하고 같은 원리로 곱셈, 뺄셈 등을 할 수 있다.
def native_add(x, y):
assert len(x.shape) == 2 # x와 y는 랭크-2 Numpy 배열이다.
assert x.shape == y.shape
x = x.copy() # 입력 텐서 자체를 바꾸지 않도록 복사
for i in range(x.shape[0]):
for j in range(x.shape[1]):
x[i, j] += max(x[i, j], 0)
return x
Numpy 배열을 다룰 때는 최적화된 넘파이 내장 함수로 위 연산들을 다룰 수 있다.
import numpy as np
z = x + y
z = np.maximum(z, 0.)
이는 위 relu 연산을 구현한 for문에 비해 엄청난 연산 속도로 처리한다.
브로드캐스팅
앞에서 구현한 native_add는 동일한 크기의 랭크-2 텐서만 지원하지만, Dense층에서는 랭크-2 텐서와 벡터를 더한것처럼 크기가 다른 두 텐서가 더해질 수 있다.
모호하지 않고 실행 가능하다면 작은 텐서가 큰 텐서의 크기에 맞추어 브로드캐스팅(broadcasting)된다. 브로드캐스팅은 다음과 같이 두 단계로 이루어진다.
- 큰 텐서의 ndim에 맞도록 작은 텐서에 브로드캐스팅 축이라고 부르는 축이 추가된다.
- 작은 텐서가 새 축을 따라서 큰 텐서의 크기에 맞도록 반복된다.
구체적인 예로, x의 크기는 (32, 10)이고 y의 크기는 (10, )이라고 가정하자.
import numpy as np
x = np.random.random((32, 10))
y = np.random.random((10, ))
# y에 비어있는 첫 번째 축을 추가하여 크기를 (1, 10)으로 만든다.
y = np.expand_dims(y, axis=0)
# 이 축이 32번 반복하면 텐서 Y의 크기는 (32, 10)이 된다.
# 여기에서 Y[i,:] = y for i in range(0, 32)이다.
Y = np.concatenate([y] * 32, axis = 0)
# 이제 x와 Y는 크기가 같으므로 더할 수 있다.
def native_add_matrix_and_vector(x, y):
assert len(x.shape) == 2 # x는 랭크-2 넘파이 배열이다.
assert len(y.shape) == 1 # y는 넘파이 벡터이다.
assert x.shape[1] == y.shape[0]
x = x.copy() # 입력 텐서 차제를 바꾸지 않도록 복사
for i in range(x.shape[0]):
for j in range(x.shape[1]):
x[i, j] += y[j]
return x
(a, b, … n, n+1, … m) 크기의 텐서와 (n, n+2, … m) 크기의 텐서 사이에 브로드캐스팅으로 원소별 연산을 적용할 수 있다. 이때 브로드캐스팅은 a부터 n-1 까지의 축에 자동으로 일어난다.
다음은 크기가 다른 두 텐서에 브로드캐스팅으로 원소별 maximum 연산을 적용하는 예이다.
import numpy as np
x = np.random.random((64, 3, 32, 10))
y = np.random.random((32, 10))
z = np.maximum(x, y) # 출력 z의 크기는 x와 동일하게 (64, 3, 32, 10)
텐서 곱셈
텐서 곱셈(tensor product) 또는 점곱(dot product)은 가장 널리 사용되고 유용한 텐서 연산이다. 넘파이에서 텐서 곱셈은 np.dot 함수를 사용하여 수행한다.
x = np.random.random((32,))
y = np.random.random((32,))
z = np.dot(x, y)
2개의 벡터 x와 y의 점곱은 다음과 같이 계산한다. 두 벡터의 점곱은 스칼라가 되므로 원소 개수가 같은 벡터끼리 점곱이 가능하다.
def native_vector_dot(x, y):
assert len(x.shape) == 1
assert len(y.shape) == 1 # x와 y는 넘파이 벡터
assert x.shape[0] == y.shape[0]
z = 0.
for i in range(x.shape[0]):
z += x[i] * y[i]
return z
행렬 x와 벡터 y 사이에서도 점곱이 가능하다. y와 x의 행 사이에서 점곱이 일어나므로 벡터가 반환된다. dot 연산에서는 교환법칙이 성립하지 않는다.
def native_matrix_vector_dot(x, y):
assert len(x.shape) == 2
assert len(y.shape) == 1
assert x.shape[1] == y.shape[0] # x의 두 번째 차원이 y의 첫 번째 차원과 같아야 한다.
z = np.zeros(x.shape[0]) # x의 행과 같은 크기의 0이 채워진 벡터를 만든다.
for i in range(x.shape[0]):
for j in range(y.shape[1]):
z[i] += x[i, j] * y[j]
return z
물론 점곱은 임의의 축 개수를 가진 텐서에 일반화된다. 가장 일반적인 용도는 두 행렬 간의 점곱이다. x.shape[1] == y.shape[0] 일 때 두 행렬 x와 y의 점곱(dot(x,y))이 성립된다.x의 행과 y의 열 사이에 벡터 점곱으로 인해 (x.shape[0], y.shape[1]) 크기의 행렬이 된다.
def native_matrix_dot(x, y):
assert len(x.shape) == 2
assert len(y.shape) == 2
assert x.shape[1] == y.shape[0] # x의 두 번째 차원이 y의 첫 번째 차원과 같아야 한다.
z = np.zeros((x.shape[0], y.shape[1]))
for i in range(x.shape[0]):
for j in range(y.shape[1]):
row_x = x[i, :]
column_y = y[:, j]
z[i, j] = native_vector_dot(row_x, column_y)
return z
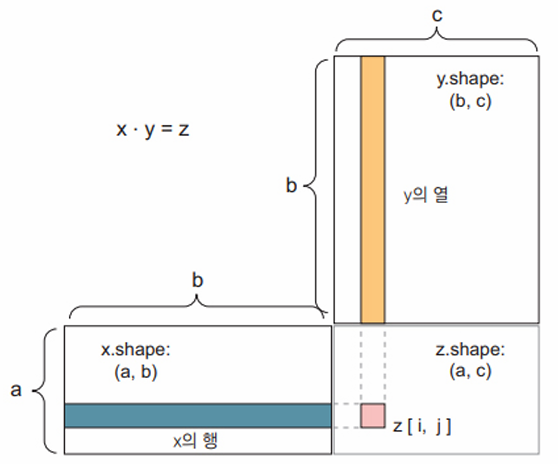
더 일반적으로는 앞서 설명한 2D의 경우처럼 크기를 맞추는 동일한 규칙을 따르면 다음과 같이 고차원 텐서 간의 점곱을 할 수 있다.
- $(a, b, c, d) \cdot (d, ) -> (a, b, c)$
- $(a, b, c, d) \cdot (d, e) -> (a, b, c, e)$
텐서 크기 변환
텐서 크기 변환(tensor reshaping)은 Dense 층에서는 사용되지 않았지만 모델에 주입할 숫자 데이터를 전처리할 때 사용했다.
train_images = train_images.reshape((60000, 28 * 28))
텐서의 크기를 변환한다는 것은 특정 크기에 맞게 열과 행을 재배열한다는 뜻이다. 당연히 크기가 변환된 텐서는 원래 텐서와 원소 개수가 동일한다. 다음 예를 보자.

자주 사용하는 특별한 크기 변환은 전치(transposition)로 행렬의 행과 열을 바꾸는 것을 의미한다. 즉, x[i, :]는 x[:, i]가 된다.

텐서 연산의 기하학적 해석
텐서 연산이 조작하는 텐서의 내용은 어떤 기하학적 공간에 있는 좌표 포인트로 해석될 수 있기 때문에 모든 텐서 연산은 기하학적 해석이 가능하다. 예를 들어 덧셈을 생각해 본다. 벡터 A = [0.5, 1]는 2D 공간에 있다. 일반적으로 다음과 같이 원점에서 포인트를 연결하는 화살표 벡터로 나타낸다.
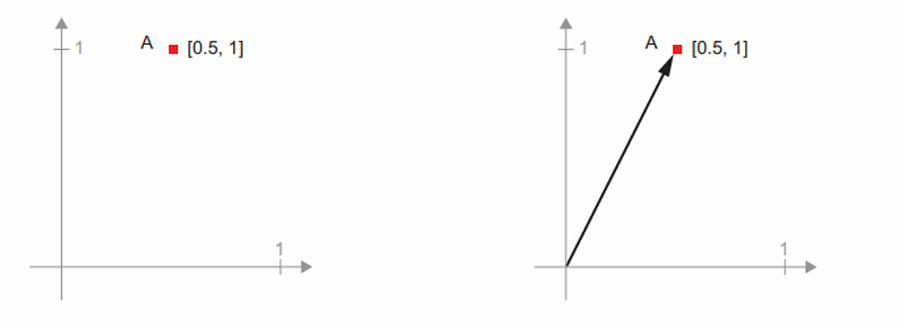
새로운 포인트 B = [1, 0.25]를 이전 벡터에 더해본다.
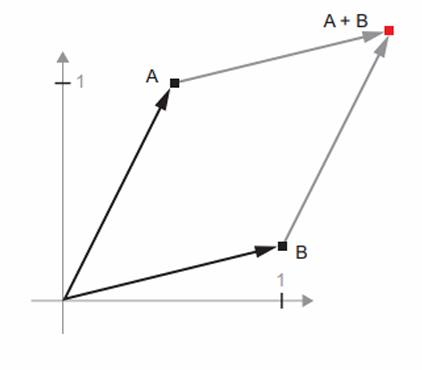
벡터 A에 벡터 B를 더하는 것은 점 A를 새로운 위치로 복사하는 동작이다. 동일한 벡터 덧셈을 평면에 있는 점 집합(하나의 객체)에 적용하면 새로운 위치에서 전체 객체의 복사본을 만들게 된다. 따라서 텐서 덧셈은 객체를 특정 방향으로 특정 양만큼 객체를 왜곡시키지 않고 이동하는 행동을 나타낸다.
일반적으로 이동(translation), 회전(rotation), 크기 변경(scaling), 기울이기(skewing) 등과 같은 기본적인 기하학적 연산은 텐서 연산으로 표현될 수 있다.
- 이동: 한 점에 벡터를 더하면 고정된 방향으로 고정된 양만큼 이 점을 이동시킨다.
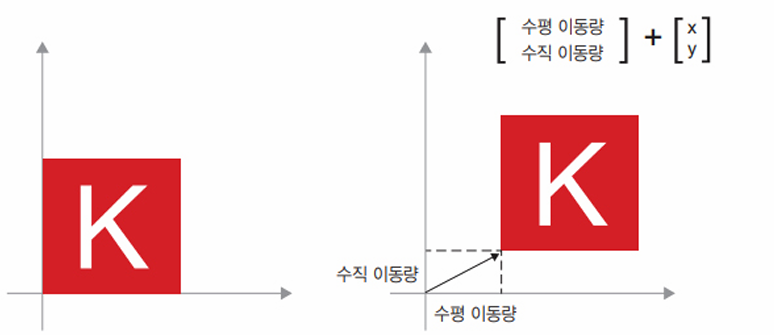
- 회전: 각도 theta만큼 2D 벡터를 반시계 방향 회전한 결과는 $2 \times 2$ 행렬 R = [[cos(theta), -sin(theta)],[sin(theta), cos(theta)]] 와 점곱하여 얻을 수 있다.
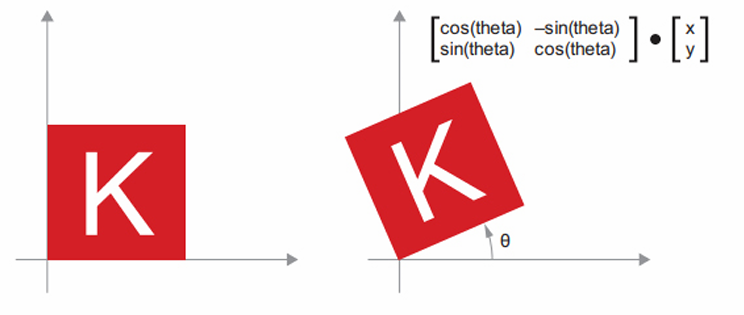
- 크기 변경: $2 \times 2$ 행렬 S = [[horizontal_factor, 0], [0, vertical_factor]] (대각 행렬, diagonal matrix)와 점곱하여 수직과 수평 방향으로 크기를 변경시킨 이미지를 얻을 수 있다.
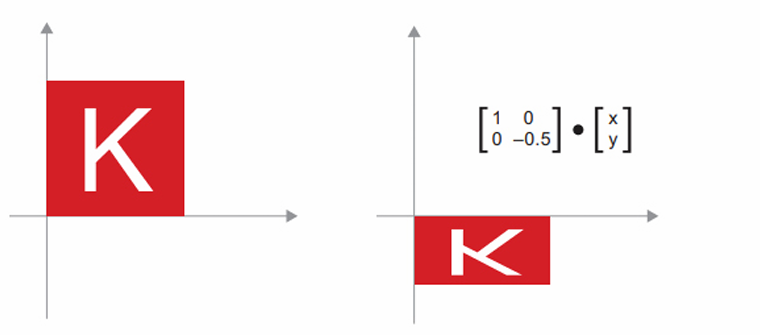
- 선형 변환(linear transform): 임의의 행렬과 점곱하면 선형 변환이 수행된다. 크기 변경과 회전은 정의상 선형 변환에 해당한다.
- 아핀 변환(affine transform): 선형 변환과 이동의 조합이다.
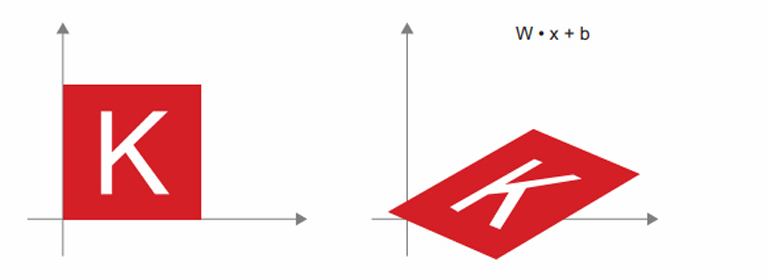
아핀 변환의 중요한 성질 하나는 여러 아핀 변환을 반복해서 적용해도 결국 하나의 아핀 변환이 된다는 것이다. 다음과 같은 2개의 아핀 변환을 생각해보자.
$\mathrm{Affine2}(\mathrm{affine1}(x)) = W2 \cdot (W1 \cdot x + b1) + b2 = (W2 \cdot W1) \cdot x + (W2 \cdot b1 + b2)$
이는 선형 변환 부분이 행렬 $W2 \cdot W1$이고, 이동 부분이 벡터 $W2 \cdot b1 + b2$인 하나의 아핀 변환이다. 결국 활성화 함수 없이 Dense 층으로만 구서된 다층 신경망은 하나의 Dense 층과 같다. 즉, 하나의 선형 모델이 심층 신경망으로 위장한 것과 같고 이것이 relu 같은 활성화 함수가 필요한 이유다.
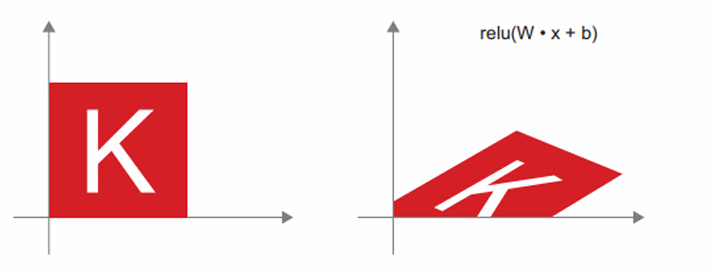
활성화 함수 덕분에 Dense 층을 중첩하여 매우 복잡하고 비선형적인 기하학적 변형을 구현하여 심층 신경망에 매우 풀부한 가설 공간을 제공할 수 있다.
딥러닝의 기하학적 해석
신경망은 전체적으로 텐서 연산의 연결로 구성된 것이고, 모든 텐서 연산은 입력 데이터의 간단한 기하학적 변환이다. 단순한 단계들이 길게 이어져 구현된 신경망을 고차원에서 매우 복잡한 기하학적 변환을 하는 것으로 해석할 수 있다.
하나는 빨간색이고 다른 하나는 파란색인 2개의 색종이가 있다고 가정하고, 두 장을 겹친 다음 뭉쳐서 작은 공으로 만든다고하자. 이때, 종이 공이 입력 데이터이고 색정이는 분류 문제의 데이터 클래스이다. 신경망이 해야 할 일은 종이 공을 펼쳐서 두 클래스가 다시 깔끔하게 분리되는 변환을 찾는것으로 손까락으로 종이 공을 조금씩 펼치는 것처럼 딥러닝을 사용하여 3D 공간에서 간단한 변환들을 연결해서 이를 구현할 수 있다.
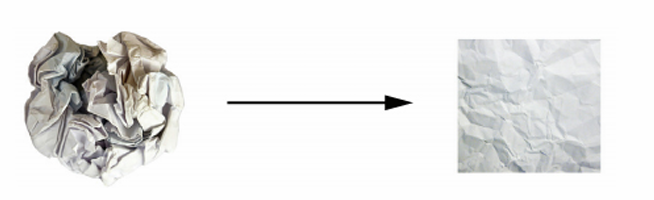
종이 공을 펼치는 것이 머신 러닝이 하는 일, 즉 고차원 공간에서 복잡하고 심하게 꼬여 있는 데이터의 매니폴드에 대한 깔끔한 표현을 찾는 일이다. 딥러닝은 기초적인 연산을 길게 연결하여 복잡한 기하학적 변환을 조금씩 분해하는 방식이 마치 사람이 종이 공을 펼치기 위한 전력과 매우 흡사하기 때문에 딥러닝은 이런 작업에 뛰어나다. 심층 신경망의 각 층은 데이터를 조금씩 풀러 주는 변환을 적용하므로, 이런 층을 깊게 쌓으면 아주 복잡한 분해 과정을 처리할 수 있다.
신경망의 엔진: 그레이디언트 기반 최적화
첫 번째 모델 예제에 있는 각 층은 입력 데이터를 output = relu(dot(W, input) + b)와같이 변환한다. 이 식에서 텐서 W와 b는 층의 속성처럼 볼 수 있고 가충치(weight) 또는 훈련되는 파라미터(trainable parameter)라고 부한다. 이런 가중치에는 훈련 데이터를 모델에 노출시켜서 학습된 정보가 담겨 있다.
초기에는 가중치 행렬이 작은 난수로 채워져 있다(무작위 초기화(random initialization)). 물론 W와 b가 난수일 때 relu(dot(w, input) + b)가 유용한 어떤 표현을 만들 것이라고 기대할 수 없다. 즉, 의미 없는 표현이 만들어진다. 하지만 이는 시작 단계일 뿐이다. 그다음에는 피드백 신호에 기초하여 가중치가 점진적으로 조정될 것이다. 이런 점진적인 조정 또는 훈련(training)이 머신 러닝 학습의 핵심이다.
훈련은 다음과 같은 훈련 반복 루프(training loop) 안에서 일어난다. 손실이 충분히 낮아질 때까지 반복 루프 안에서 아런 단계가 반복된다.
- 훈련 샘플 x와 이에 상응하는 타깃 y_true의 배치를 추출한다.
- x를 사용하여 모델을 실행하고(정방향 패스(forword pass) 단계), 얘측 y_pred를 구한다.
- y_pred와 y_true의 차이를 측정하여 이 배치에 대한 모델의 손실을 계산한다.
- 배치에 대한 손실이 조금 감소되도록 모델의 모든 가중치를 업데이트한다.
결국 훈련 데이터에서 모델의 손실, 즉 예측 y_pred와 타깃 y_true의 오차가 매우 작아질 것이다. 이 모델은 입력에 정확한 타깃을 매핑하는 것을 학습했다. 개별적인 단계로 쪼개어 보면 단순하다.
단계 1은 그냥 입출력 코드이므로 매우 쉽다. 단계 2와 단계 3은 몇 개의 텐서 연산을 적용한것뿐이므로 구현할 수 있다. 어려운 부분은 모델의 가중치를 업데이트하는 단계 4이다. 개별적인 가중치가 없을 때 값이 증가해야 할지 감소해야 할지, 또 얼마큼 업데이트해야 하는지 알아본다.
한 가지 간단한 방법은 모델에 있는 가중치 행렬의 원소를 모두 고정하고 관심 있는 하나만 다른 값을 적용해 보는 것이다. 이 가중치의 초깃값이 0.3이라고 가정하고 배치 데이터를 정방향 패스에 통과시킨 후 모델의 손실이 0.5가 나왔다. 이 가중치 값을 0.35로 변경하고 다시 정방향 패스를 실행했더니 손실이 0.6으로 증가했다. 반대로 0.25로 줄이면 손실이 0.4로 감소했다. 이 경우 가중치를 -0.05만큼 업데이트한 것이 손실을 줄이는 데 기여한 것으로 보인다. 이런 식으로 모델의 모든 가중치를 반복한다.
이런 접근 방식은 모든 가중치 행렬의 원소마다 두 번의 정방향 패스를 계산해야 하므로 엄청나게 비효율적이다. 다행이 더 나은 방법인 경사 하강법(gradient descent)이 있다.
경사 하강법은 현대 신경망을 가능하게 만든 최적화 기술이다. 모델에 사용하는 모든 함수는 입력을 매끄럽고 연속적인 방식으로 변환한다. 예를 들어 $z = x + y$에서 y를 조금 바꾸면 z가 조금만 변경된다. y의 반경 방향을 알고 있다면 z의 변경 방향을 추측할 수 있다. 이를 수학적으로 미분 가능(differentiable)하다고 말한다. 이런 함수를 연결하여 만든 함수도 여전히 미분 가능하다. 이는 배치 데이터에서 모델의 가중치와 모델의 손실을 매필하는 함수에도 적용된다. 즉, 모델의 가중치를 조금 변경하면 손실값이 예측 가능한 방향으로 조금 바뀐다. 그레디언트(gradient)라는 수학 연산을 사용하여 모델 가중치를 여러 방향으로 이동했을 때 손실이 얼마나 변하는지 설명할 수 있다. 이 그레디언트를 계산하면 이를 사용하여 손실이 감소하는 방향으로 가중치를 이동시킬 수 있다.
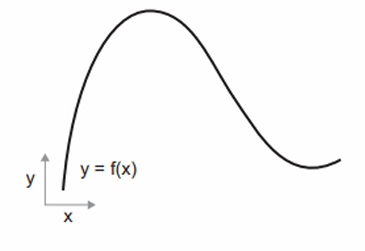
이 함수가 연속적이므로 x를 조금 바꾸면 y가 조금만 변경될 것이다. 다음과 같이 x를 작은 값 epsilon_x만큼 증가시켰을 때 y가 epsilon_y만큼 바뀐다고 말할 수 있다.
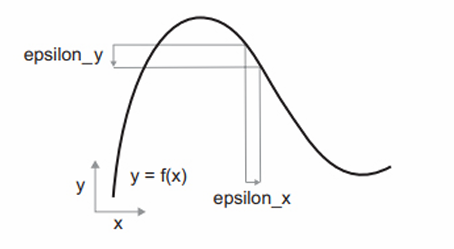
또한, 이 함수가 매끈하므로 epsilon_x가 충분히 작다면 어떤 포인트 p에서 기울기 a의 선형 함수로 f를 근사할 수 있다. 따라서 epsilon_y는 a * epsilon_x가 된다(f(x + epsilon_x) = y + a * epsilon_x). 이 선형적인 근사는 x가 p에 충분히 가까울 때 유효하다.
이 기울기 p에서 f의 도함수(derivative)라고 한다. 이는 a가 음수일 때 p에서 양수 x만큼 조금 이동하면 f(x)가 감소한다는 것을 의미한다. a가 양수일 때는
도한수란?
실수 x를 새로운 실수 y로 매핑하는 연속적이고 매끄러운 함수 f(x) = y를 생각해본다.

이 함수가 연속적이므로 x를 조금 바꾸면 y가 조금만 변경될 것이다. 이것이 연속성의 개념이다. 다음과 같이 x를 작은 값 epsilon_x만큼 증가시켰을 때 y가 epsilon_y만큼 바뀐다고 말할 수 있다.

또한, 이 함수가 매끈하므로 epsilon_x가 충분히 작다면 어떤 포인트 p에서 기울기 a의 선형 함수로 f를 근사할 수 있다. 따라서 epsilon_y는 a * epsilon_x가 된다(f(x + epsilon_x) = y + a * epsilon_x). 이 선형적인 근사는 x가 p에 충분히 가까울 때 유효하다.
이 기울기 p에서 f의 도함수(derivative)라고 한다. 이는 a가 음수일 때 p에서 양수 x만큼 조금 이동하면 f(x)가 감소한다는 것을 의미한다. a가 양수일 때는 p에서 양수 x만큼 조금 이동하면 f(x)가 감소한다는 것을 의미한다. a가 양수일 때는 음수 x만큼 조금 이동하면 f(x)가 감소된다. a의 절댓값(도함수의 크기)은 이런 증가나 감소가 얼마나 빠르게 일어날지 알려준다.
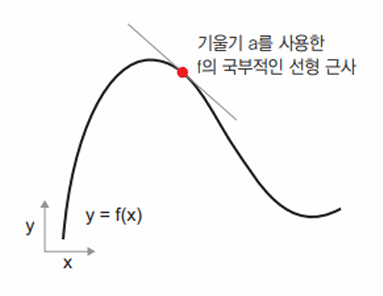
모든 미분 가능한 함수 f(x)에 대해 x값을 f의 국부적인 선형 근사인 그 지점의 기울기로 매핑하는 도함수 f’(x)가 존재한다.
함수를 미분할 수 있다는 것은 f(x)의 값을 최소화하는 x 값을 찾는 작업인 최적화(optimization)에 매우 강력한 도구이다. f(x)를 최소화하기 위해 epsilon_x만큼 x가 업데이트하고 싶을 때 f의 도함수를 알고 있으면 해결된다.
텐서 연산의 도함수: 그레디언트
텐서 연산의 도함수를 그레디언트(gradient)라고 부른다. 그레디언트는 텐서를 입력으로 받는 함수로 도함수의 개념을 일반화한 것이다. 텐서 함수의 그레디언트는 다차원 표면의 곡률(curvature)을 나타낸다. 입력 파라미터가 바뀔 때 함수의 출력이 어떻게 바뀌는지 결정한다.
머신 러닝 기반의 예를 살펴본다.
- 입력 벡터, x(데이터셋에 있는 샘플)
- 행렬, W(모델의 가중치)
- 타깃, y_true(모델이 x에 연관시키기 위해 학습해야 할 값)
- 손실 함수, loss(현재의 예측과 y_true 간의 차이를 측정하기 위해 사용)
W를 사용하여 예측 y_pred를 계산하고, 그다음 예측 y_pred와 타깃 y_true 사이의 손실 또는 차이를 계산한다.
y_pred = dot(W, x) # 모델 가중치 W를 사용하여 x에 대한 예측을 만든다.
loss_value = loss(y_pred, y_true) # 예측이 얼마나 벗어났는지 추정한다.
이제 그레디언트를 사용하여 loss_value가 작아지도록 W를 업데이트해본다. 고정된 입력 x와 y_true가 있을 때 앞의 연산은 모델의 가중치 W 값을 손실 값에 매핑하는 함수로 해석할 수 있다.
loss_value = f(W) # f는 W가 변화할 때 손실 값이 형성하는 곡선(또는 다차원 표면)을 설명
현재의 W값을 W0라 하면, 점 W0에서 f의 도함수는 W와 크기가 같은 텐서 grad(loss_value, W0)이다. 이 텐서의 각 원소 grad(loss_value, W0)[i, j]는 W0[i, j]를 수정했을 때 loss_value가 바뀌는 방향과 크기를 나타낸다. 텐서 grad(loss_value, W0)가 W0에서 함수 f(W) = loss_value의 그레디언트다. 또는 W0 근처에서 W에 대한 loss_value의 그레디언트라고 말한다.
참고로 입력으로 행렬 W를 받는 텐서 연산 grad(f(W), W)는 스칼라 함수 grad_ij(f(W), w_ij)의 조합으로 표현할 수 있다. 이 스칼라 함수는 W의 다른 모든 가중치가 일정하다고 가정할 때 가중치 W[i, j]에 대한 loss_value = f(W)의 도함수를 반환한다. 이때 grad_ij를 W[i, j]에 대한 f의 편도함수(partial derivatie)라고 부른다.
앞에서 하나의 가중치를 가진 함수 f(x)의 도함수는 곡선 f의 기울기로 해석할 수 있다는 것과 비슷하게 grad(loss_value, W0)는 W0에서 loss_value=f(x)가 가장 가파르게 상승하는 방향과 이 방향의 기울기를 나타내는 텐서로 해석할 수 있다. 즉, 편도함수는 f의 특정 방향 기울기를 나타낸다.
따라서 함수 f(x)에 대해서는 도함수의 반대 방향으로 x를 조금 움직이면 f(x)의 값을 감소시킬 수 있는것 처럼, 텐서의 함수 f(W)의 입장에서는 그레디언트의 반대 방향으로 Wㄹㄹ 움직이면 loss_value = f(W)의 값을 줄일 수 있다. 이 말은 f가 가장 가파르게 상승하는 방향의 반대 방향으로 움직이면 곡선의 낮은 위치로 이동하게 된다는 의미이다. grad(loss_value, W0)는 W0에 아주 가까이 있을 때 기울기를 근사한 것이므로 W0에서 너무 크게 벗어나지 않기 위해 스케일링 비율 step이 필요하다.
확률적 경사 하강법
미분 가능한 함수가 주어지면 이론적으로 이 함수의 최솟값을 해석적으로 구할 수 있다(도함수가 0인 지점). 그러므로 도함수가 0이 되는 지점을 모두 찾고 이 중에서 어떤 포인트의 함수 값이 가장 작은지 확인면 최솟값을 구할 수 있다.
신경망에 이를 적용하면 가장 작은 손실 함수의 값을 만드는 가중치의 조합으로 해석적으로 찾는 것을 의미한다. 이는 W에 대한 식 grad(f(W), W)=0를 풀면 해결된다. 이 식은 N개의 변수로 이루어진 다항식으로 N은 모델의 가중치 개수를 의미한다. 하지만 실제 신경망에서는 파라미터의 개수가 수천만 개가 되기 때문에 해석적으로 해결하기는 어렵다.
그 대신 앞에서 본 알고리즘 네 단계를 사용할 수 있다. 랜덤한 배치 데이터에서 현재 손실 값을 토대로 하여 조금씩 파라미터를 수정하는 것이다. 미분 가능한 함수를 가지고 있으므로 그레디어트를 계산하여 단계 4를 효율적으로 구현할 수 있다. 그레디언트의 반대 방향으로 가중치를 업데이트하면 손실이 매번 조금씩 감소할 것이다.
- 훈련 샘플 x와 이에 상응하는 타깃 y_true의 배치를 추출한다.
- x를 사용하여 모델을 실행하고(정방향 패스(forword pass) 단계), 얘측 y_pred를 구한다.
- y_pred와 y_true의 차이를 측정하여 이 배치에 대한 모델의 손실을 계산한다.
- 모델의 파라미터에 대한 손실 함수의 그레디언트를 계산한다(역발향 패스(backward pass)).
- 그레디언트의 반대 방향으로 파라미터를 조금 이동시킨다. 예를 들어 W -= learning_rate * gradient처럼 하면 배치에 대한 손실이 조금 감소할 것이다. 이떄 learning_rate는 학습률(learning rate)로 경사 하강법 과정의 속도를 조절하는 스칼라 값이다.
위에서 본 것이 미니 배치 확률적 경사 하강법(mini-batch stochastic gradient descent, 미니 배치 SGD)이다. 확률적(stochastic)이란 단어는 각 배치 데이터가 무작위로 선택된다는 의미이다. 모델의 파라미터가 하나고 훈련 샘플이 하나일 때 이 과정은 다음과 같다.

위 그림에서 볼 수 있듯이 learning_rate 값을 적절히 고르는 것이 중요하다. 이 값이 너무 작으면 곡선을 따라 내려가는 데 너무 많은 반복이 필요하고 지역 최솟값(local minimum)에 갇힐 수 있다. 반대로 learning_rate가 너무 크면 손실 함수 곡선에서 완전히 임의의 위치로 이동시킬 수 있다.
미니 배치 SGD 알고리즘의 한 가지 변종은 반복마다 하나의 샘플과 하나의 타깃을 뽑는 것으로 이것이 진정한(true) SGD다.
다른 한편으로 극단적인 반대의 경우를 생각해 보면 가용한 모든 데이터를 사용하여 반복을 실행할 수 있는데 이를 배치 경사 하강법이라 한다. 이는 더 정확하게 업데이트되지만 더 많은 비용이 든다. 그래서 극단적인 두 가지 방법의 효율적인 절충안은 적절한 크기의 미니 배치를 사용하는 것이다.
앞 그림은 1D 파라미터 공간에서 경사 하강법을 설명하고 있지만 실제로는 매우 고차원 공간에서 경사 하강법을 사용하게 된다. 신경망에 있는 각각의 가중치 값은 이 공간에서 하나의 독립된 차원이고 수만 또는 수백만 개가 될 수도 있다. 손실 함수의 표면을 좀 더 이해하기 위해 다음과 같이 2D 손실 함수의 표면을 따아 진행하는 경사 하강법을 시각화해 볼 수 있다.
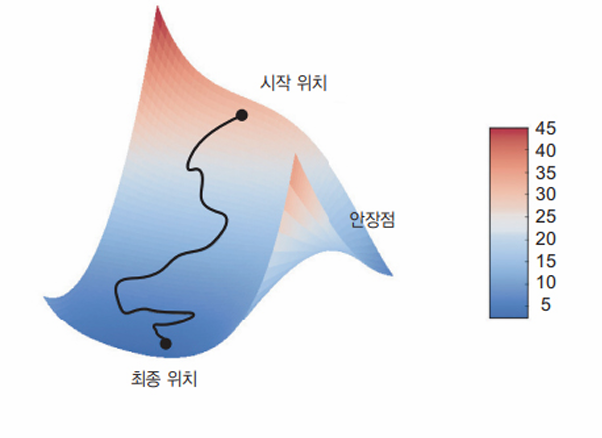
하지만 신경망이 훈련되는 실제 과정을 시각화하기는 어렵고 이는 딥러닝 연구 분야에서 오랫동안 여러 이슈를 일으키는 근원이다.
또한 업데이트할 다음 가중치를 계산할 때 현재 그레디언트 값만 보지 않고 이전에 업데이트된 가주이츨 여러 가지 다른 방식으로 고려하는 SGD 변종이 많이 있다. 이런 변종들은 모두 최적화 방법(optimization method)또는 옵티마이저라고 부른다. 특히 여러 변종에서 사용하는 모멘텀(momentum) 개념은 아주 중요하다. 모멘텀은 SGD에 있는 2개의 문제점인 수렴 속도와 지역 최솟값을 해결하였다. 다음 그림은 모델의 파라미터 하나에 대한 손실 값의 곡선을 보여준다.
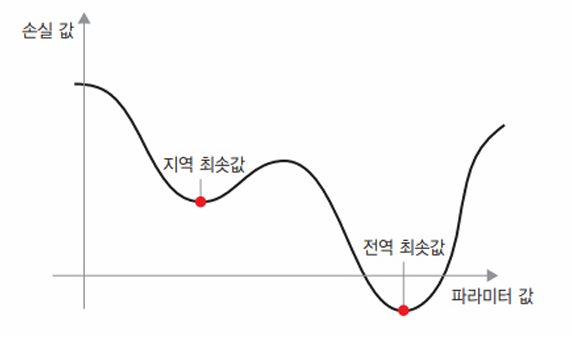
그림에서 볼 수 있듯이 어떤 파라미터 값에서는 지역 최솟값에 도달한다. 그 지점 근처에서는 왼쪽으로 이동해도 손실이 증가하고, 오른쪽으로 이동해도 손실이 증가한다. 대상 파라미터가 작은 학습률을 가진 SGD로 최적화되었다면 최적화 과정이 전역 최솟값으로 향하지 못하고 이 지역 최솟값이 갇히게 될 것이다.
물리학에서 영감을 얻는 모멘텀을 사용하여 이 문제를 피할 수 있다. 여기서 최적화 과정을 손실 곡선 위로 작은 공을 굴리는 것으로 생각해보면, 모멘텀이 충분하면 공이 골짜기에 갇히지 않고 전역 최솟값에 도달할 것이다. 모멘텀은 현재 기울기 값(현재 가속도)뿐만 아니라 (과거 가속도로 인한)현재 속도를 함께 고려하여 각 단계에서 공을 움직인다. 실전에 적용할 때는 현재 그레디언트 값 뿐만 아니라 이전에 업데이트한 파라미터에 기초하여 파라미터 W를 업데이트한다. 다음은 단순한 구현 예이다.
past_velocity = 0.
momentum = 0.1 # 모멘텀 상수
while loss > 0.01: # 최적화 반복 루프
w, loss, gradient = get_current_parameters()
velocity = momentum * past_velocity - learning_rate * gradient
w = w + momentum * velocity - learning_rate * gradient
past_velocity = velocity
update_parameter(w)
도함수 연결: 역전파 알고리즘
2개의 층을 가진 모델의 경우 가중치에 대한 손실의 그레디언트를 구할 때 역전파 알고리즘(Backpropagation algorithm)이 필요한 이유다.
역전파는 간단한 연산의 도함수를 사용해 기초적인 연산을 조합한 복잡한 연산의 그레디엍르를 쉽게 계산하는 방법이다. 결정적으로 신경망은 서로 연결된 많은 텐서 연산으로 구성된다. 이런 연산은 간단하고 해당 도함수가 알려져 있다.
미적분의 연쇄 법칙(chain_rule)을 사용하면 이렇게 연결된 도함수를 구할 수 있다. 두 함수 f와 g가 있고, 구 함수를 연결한 fg가 있다고 가정하면, fg(x) == f(g(x))이다.
def fg(x):
x1 = g(x)
y = f(x1)
return y
연쇄 법칙을 적용하면 grad(y, x) == grad(y, x1) * grad(x1, x)가 된다. 따라서 f와 g의 도함수를 알고 있다면 fg의 도함수를 계산할 수 있다. 신경망의 그레디언트 값을 계산하는 데 이 연쇄 법칙을 적용하는 것이 역전파 알고리즘이다.
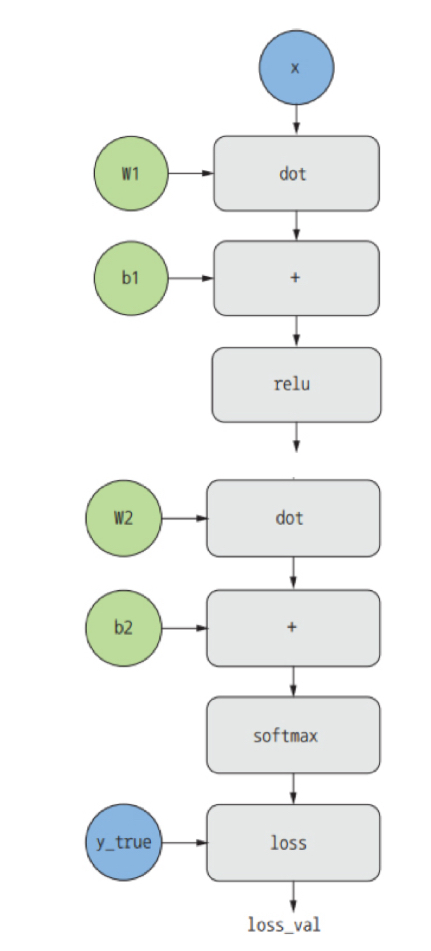
역전파를 계산 그래프(computation graph)관점에서 생각해본다. 계산 그래프는 텐서플로와 일반적인 딥러닝 혁신의 중심에 있는 데이터 구조로 연산의 유향 비순환 그래프(directed acyclic graph)이다. 예를 들어 다음 그림은 이 장에서 첫 번째로 만든 모델의 그래프 표현이다.
계산 그래프를 사용하면 계산을 데이터로 다룰 수 있기 때문에 컴퓨터 과학 분야에서 매우 성공적인 추상화 벙법이다. 계산 가능한 표현은 기계가 인식할 수 있는 데이터 구조로 인코딩되어 다른 프로그램의 입력이나 출력으로 사용될 수 있다.
역전파를 명확하게 설명하기 위해 아주 간단한 계산 그래프를 살펴본다.
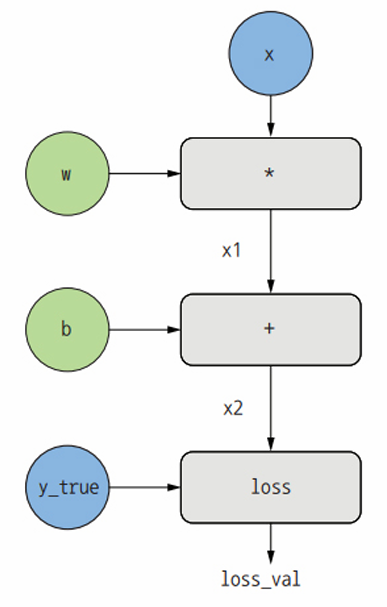
하나의 선형 층만 있고 모든 변수는 스칼라다. 2개의 스칼라 변수 w와 b, 스칼라 입력 x를 받아 몇 개의 연산을 적용하여 출력x2를 만든다. 마지막으로 절댓값 오차 손실 함수 loss_val = abs(y_true - x2)를 적용한다. loss_val을 최소화하도록 w와 b를 업데이트하기 위해 grad(loss_val, b)와 grad(loss_val, w)를 계산한다.
입력 x, 타깃 y_true, w, b에 해당하는 이 그래프의 입력 노드(input node)에 구체적인 값을 설정해본다. 이 값을 loss_val에 도달할 때까지 위에서 아래로 그래프의 모든 노드에 전파한다. 이것이 정방향 패스이다.
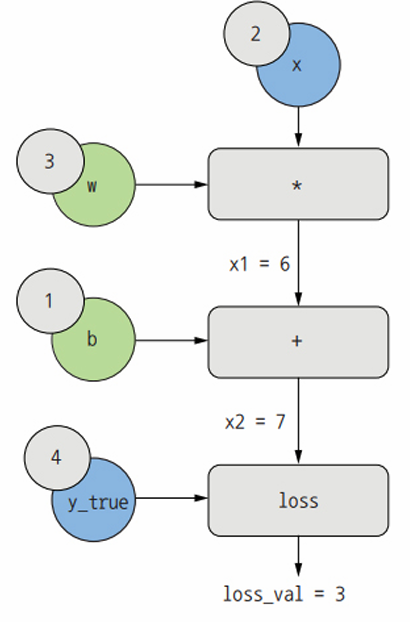
이제 그래프를 뒤집어 본다. A에서 B로 가는 그래프의 모든 에지(edge)에 대해 B에서 A로 가는 반대 edge를 만든다.그리고 A가 바뀔 때 B가 얼마나 변하는지 묻는다. 즉, grad(B, A)는 반대 방향에서 만든 에지에 이 값을 표싷ㄴ다. 이 역방향 그래프가 역방향 패스를 나타낸다.
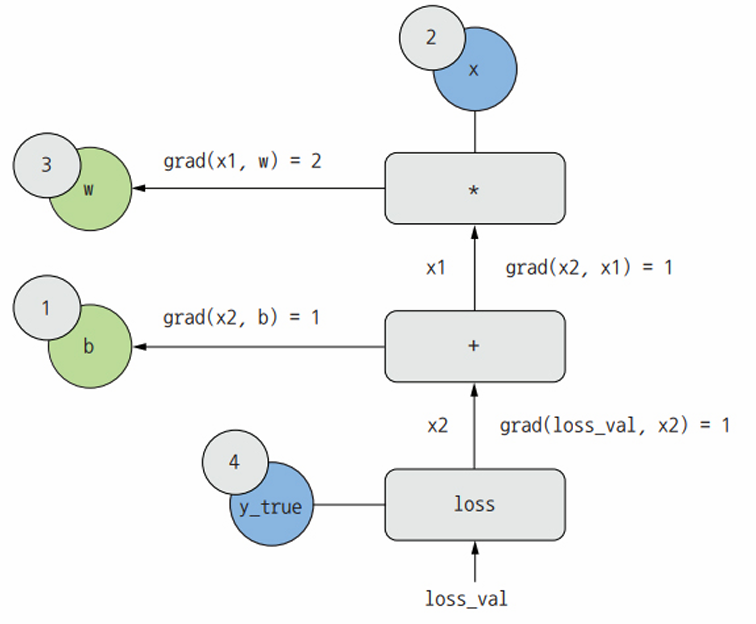
다음과 같은 값을 얻을 수 있다.
- grad(loss_val, x2) = 1
- x2가 epsilon만큼 변할 때 loss_val = abs(4 - x2)가 같은 양만큼 변하기 때문
- grad(x2, x1) = 1
- x1이 epsiolon만틐 변할 때 x2 = x1 + b = x1 + 1이 같은 양만큼 변하기 때문
- grad(x2, b) = 1
- b가 epsilon만큼 변할 때 x2 = x1 + b = 6 + b가 같은 양만큼 변하기 때문
- grad(x1, w) = 2
- w가 epsion만큼 변할 때 x1 = x*w = 2*w는 2*epsion만큼 변하기 때문
연쇄 법칙이 역방향 그래프에 대해 알려 주는 것은 노드가 연결된 경로를 따라 각 edge의 도함수를 곱하면 어떤 노드에 대한 다른 노드의 도함수를 얻을 수 있다는 것이다. 예를 들어, grad(loss_val, w) = grad(loss_val, x2) * grad(x2, x1) * grad(x1, w)이다.
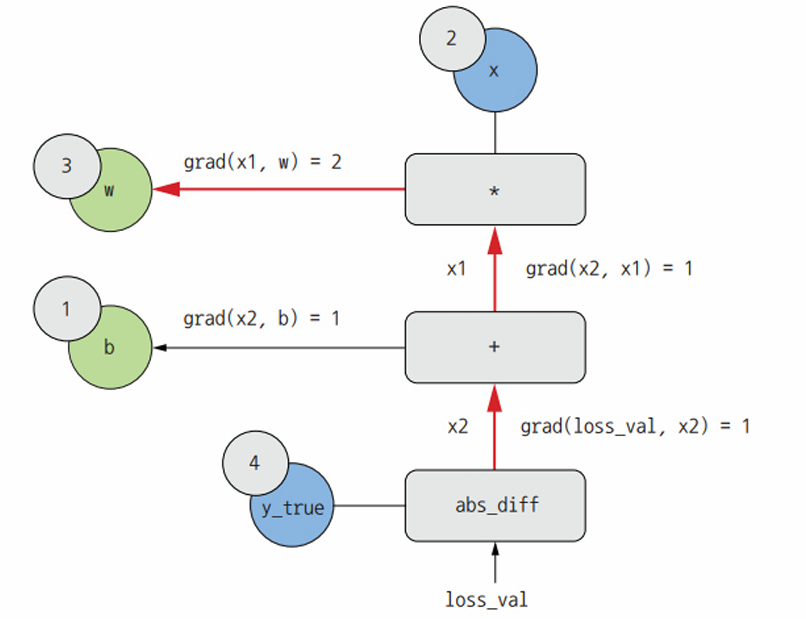
이 그래프에 연쇄 법칙을 적용하여 원하는 값을 구할 수 있다. 역방향 그래프에서 관심 대상인 두 노드 a와 b를 연결하는 경로가 여러 개라면 모든 경로의 도함수를 더해서 grad(a, b)를 얻을 수 있다.
- grad(loss_val, w) = 1 * 1 * 2 = 2
- grad(loss_val, b) = 1 * 1 = 1
위 과정이 역전파로, 역전파는 연쇄 법칙을 계산 그래프에 적용한 것뿐이다. 역전파는 최종 손실 값에서 시작하여 아래층에서 맨 위층까지 거꾸로 거슬러 올라가 각 파라미터가 손실 값에 기여한 정도를 계산한다.
요즘에는 텐서플로와 같이 자동 미분(automatic differentiation)이 가능한 프레임워크를 사용해서 신경망을 구현한다. 자동 미분은 정방향 패스를 작성하는 것 외에 다른 작업 없이 미분 가능한 텐서 연산의 어떤 조합에 대해서도 그레디언트를 계산할 수 있다.
텐서플로의 강력한 자동 미분 기능을 활용할 수 있는 API는 GradientTape이다. 이 API는 파이썬의 with문과 함께 사용하야 해당 코드 블록 안의 모든 텐서 연산을 계산 그래프 형태로 기록한다. 그다음 이 그래프를 사용해서 변수 또는 변수 집합에 대한 어떤 출력의 그레디언트도 계산할 수 있다. tf.Variable은 변경 가능한(mutable) 상태를 담기 위한 특별한 종류의 텐서이다. 예를 들어 신경망의 가중치는 항상 tf.Variable의 인스턴스이다.
import tensorflow as tf
x = tf.Variable(0.) # 초깃값 0으로 스칼라 변수를 생성한다.
with tf.GradientTape() as tape: # GradientTape 블록을 사작한다.
y = 2 * x + 3 # 이 블록 안에서 변수에 텐서 연산을 적용한다.
grad_of_y_wrt_x = tape.gradient(y, x) # tape를 사용해서 변수 x에 대한 출력 y의 그레디언트를 계산한다.
GradientTape를 다차원 텐서와 함께 사용할 수 있다.
x = tf.Variable(tf.zeros((2, 2))) # 크기가 (2,2)고 초깃값이 모두 0인 변수를 생성
with tf.GradientTape() as tape:
y = 2 * x + 3
grad_of_y_wrt_x = tape.gradient(y, x)
# grad_of_y_wrt_x는 x와 크기가 같은 (2,2) 크기의 텐서로
# x = [[0, 0], [0, 0]] 일 때 y = 2*x + 3의 곡률을 나타낸다.
변수 리스트의 그레디언트를 계산할 수도 있다.
W = tf.Variable(tr.random.uniform((2,2)))
b = tf.Variable(tf.zeros((2,)))
x = tf.random.uniform((2,2))
with tf.GradientTape() as tape:
y = tf.matmul(x, W) + b # matmul은 텐서플로의 점곱 함수
grad_of_y_wrt_W_and_b = tape.gradient(y, [W, b])
# grad_of_y_wrt_W_and_b는 2개의 텐서를 담은 리스트
# 각 텐서는 w, b와 크기가 같다.
첫 번째 예제 다시 살펴보기
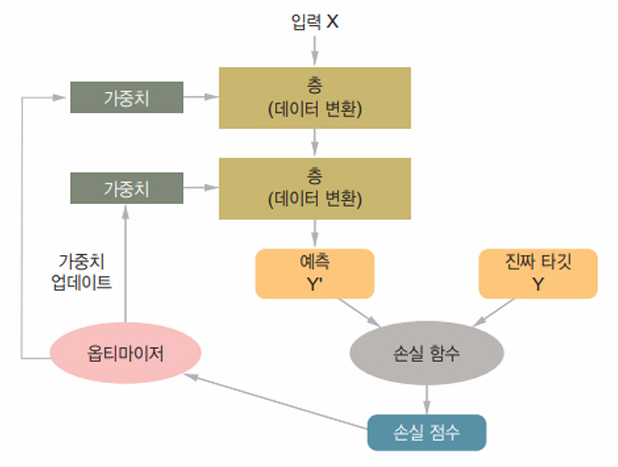
위 블랙박스는 층이 서로 연결되어 모델을 구성하고, 모델은 입력 데이터를 예측으로 매핑한다. 그다음 손실 함수가 이 예측과 타깃을 비교하여 손실 값을 만든다. 즉, 모델의 예측이 기대한 것에 얼마나 잘 맞는지 측정한다. 옵티마이저는 이 손실 값을 사용하여 모델의 가중치를 업데이트한다.
첫 번째 예제로 다시 돌아가 코드를 리뷰해본다. 먼저 입력 데이터이다.
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype("float32") / 255
test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype("float32") / 255
입력 이미지의 데이터 타입은 float32로, 훈련 데이터는 (60000, 784) 크기, 테스트 데이터는 (10000, 784) 크기의 넘파이 배열로 저장된다. 다음은 모델이다.
model = keras.Sequential([
layers.Dense(512, activation="relu"),
layers.Dense(10, activation="softmax")
])
이 모델은 2개의 Dense 층이 연결되어 있고 각 층은 가중치 텐서를 포함하여 입력 데이터에 대한 몇 개의 간단한 텐서 연산을 적용한다. 층의 속성인 가중치 텐서는 모델이 정보를 저장하는 곳이다. 이제 모델을 컴파일 하는 단계이다.
model.compile(optimizer="rmsprop",
loss="sparse_categorical_crossentropy",
metrics=["accuracy"])
sparse_categotical_crossentropy는 손실 함수이다. 가중치 텐서를 학습하기 위한 피드백 신호로 사용되며 훈련하는 동안 최소화된다. 미니 배치 확률적 경사 하강법을 통해 손실이 감소된다. 경사 하강법을 적용하는 구체적인 방식은 첫 번째 매개 변수로 전달된 rmsprop 옵티마이저에 의해 결정된다. 마지막으로 훈련 반복이다.
model.fit(train_images, train_labels, epochs=5, batch_size=128)
fit 메서드를 호출했을 때 다음과 같은 일이 일어난다. 모델이 128개의 샘플의 미니 배치로 훈련 데이터를 다섯 번 반복한다(각 반복을 에포크(epoch)라고 한다). 역전파 알고리즘을 사용하여 각 배치에서 모델이 가중치에 대한 손실의 그레디언트를 계산하다. 그다음 이 배치에서 손실 값을 감소하는 방향으로 가중치를 이동시킨다. 다섯 반의 에포크 동안 모델은 2,345 번의 그레디언트 업데이트를 수해할 것이다(에포크마다 469번).
텐서플로를 사용하여 첫 번째 예제를 밑바닥부터 다시 구현하기
Dense층이 다음과 같은 입력 변환을 구현한다고 배웠다.
- output = activation(dot(W, input) + b)
- W와 b는 모델 파라미터이고 activation은 각 원소에 적용되는 함수이다.
간단한 파이썬 클래스 NaiveDense를 구현하여 2개의 텐서플로 변수 W와 b를 만들고 __call__()메서드에서 앞서 언급한 변환을 적용해본다.
import tensorflow as tf
class NaiveDense:
def __init__(self, input_size, output_size, activation):
self.activation = activation
w_shape = (input_size, output_size) # 랜덤한 값으로 초기화된 행렬 W 생성
w_initial_value = tf.random.uniform(w_shape, minval = 0, maxval = 1e-1)
self.W = tf.Variable(w_initial_value)
b_shape = (output_size,) # 0으로 초기화된 벡터 b를 생성
b_initial_value = tf.zeros(b_shape)
self.b = tf.Variable(b_initial_value)
def __call__(self, inputs): # 정방향 패스를 진행
return self.activation(tf.matmul(inputs, self.W) + self.b)
@property
def weights(self): # 층의 가중치를 추출하기 위한 메서드
return [self.W, self.b]
이제 NativeSequential 클래스를 만들어 층을 연결해본다. 층의 리스트를 받고 __call__() 메서드에서 입력을 사용하여 층을 순서대로 호출한다. 층의 파라미터를 쉽게 구할 수 있도록 weights 속성을 제공한다.
class NaiveSequential:
def __init__(self, layers):
self.layers = layers
def __call__(self, inputs):
x = inputs
for layer in self.layers:
x = layer(x)
return x
@property
def weights(self):
weights = []
for layer in self.layers:
weights += layer.weights
return weights
이제 NativeDense 클래스와 NaiveSequential 클래스를 사용해서 케라스와 유사한 모델을 만들 수 있다.
model = NaiveSequential([
NaiveDense(input_size=28*28, output_size=512, activation=tf.nn.relu),
NaiveDense(input_size=512, output_size=10, activation=tf.nn.softmax)
])
assert len(model.weights) == 4
그다음 MNIST 데이터를 미니 배치로 순회할 방법이 필요하다.
import math
class BatchGenerator:
def __init__(self, images, labels, batch_size=128):
assert len(images) == len(labels)
self.index = 0
self.images = images
self.labels = labels
self.batch_size = batch_size
self.num_batches = math.ceil(len(images)/batch_size)
def next(self):
images = self.images[self.index : self.index + self.batch_size]
labels = self.labels[self.index : self.index + self.batch_size]
self.index += self.batch_size
return images, labels
훈련 스텝 실행하기
이 구현 작업에서 가장 어려운 부분은 훈련 스텝으로 한 배치 데이터에서 모델을 실행하고 가중치를 업데이트 하는 일이다. 이를 위해 다음이 필요하다.
- 배치에 있는 이미지에 대해 모델의 예측을 계산한다.
- 실제 레이블을 사용하여 이 예측의 손실 값을 계산한다.
- 모델 가중치에 대한 손실의 그레디언트를 계산한다.
- 이 그레디언트의 반대 방향으로 가중치를 조금 이동한다.
그레디언트를 계산하기 위해 텐서플로의 GradientTape 객체를 사용한다.
def one_training_step(model, images_batch, labels_batch):
with tf.GradientTape() as tape:
predictions = model(images_batch)
per_sample_losses = tf.keras.losses.sparse_categorical_crossentropy(
labels_batch, predictions)
average_loss = tf.reduce_mean(per_sample_losses) # 정방향 패스 실행
gradients = tape.gradient(average_loss, model.weights) # 가중치에 대한 손실의 그레디언트를 계산
update_weights(gradients, model.weights) # 이 그레디언트를 사용하여 가중치를 업데이트
return average_loss
update_weights 함수에 해당하는 가중치 업데이트 단계의 목적은 이 배치의 손실을 감소시키기 위한 방향으로 가중치를 조금이동하는 것이다. 이동의 크기는 ‘학습률’에 의해 결정된다. 학습률은 일반적으로 작은 값이다. update_weights 함수를 구현하는 가장 간단한 방법은 각 가중치에서 gradient * learning_rate를 빼는 것이다.
learning_rate = 1e-3
def update_weights(gradients, weights):
for g, w in zip(gradients, weights):
w.assign_sub(g * learning_rate) # 텐서플로 변수의 assign_sun 메서드는 -=와 동일
실제로는 이런 가중치 업데이트 단계를 수동으로 구현하는 경우는 거의 없다. 그 대신 다음과 같은 케라스의 Optimizer 인스턴스를 사용한다.
from tensorflow.keras import optimizers
optimizer = optimizers.SGD(learning_rate=1e-3)
def update_weights(gradients, weights):
optimizer.apply_gradients(zip(gradients,weights))
이제 배치 훈련 스탭이 준비되었으니 훈련 에포크 전체를 구현할 수 있다.
전체 훈련 루프
훈련 에포크 하나는 단순히 훈련 데이터의 각 배치에 대한 훈련 스텝을 반복하는 것이다. 전체 훈련 루프(loop)는 단순히 에포크의 반복이다.
def fit(model, images, labels, epochs, batch_size=128):
for epoch_counter in range(epochs):
print(f"에포크 {epoch_counter}")
batch_generator = BatchGenerator(images, labels)
for batch_counter in range(batch_generator.num_batches):
images_batch, labels_batch = batch_generator.next()
loss = one_training_step(model, images_batch, labels_batch)
if batch_counter % 100 == 0:
print(f"{batch_counter}번째 배치 손실: {loss:2f}")
이 함수를 테스트해 본다.
from tensorflow.keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
train_images = train_images.reshape((60000, 28*28))
train_images = train_images.astype("float32") / 255
test_images = test_images.reshape((10000, 28*28))
test_images = test_images.astype("float32") / 255
fit(model, train_images, train_labels, epochs=10, batch_size=128)

모델 평가하기
텍스트 이미지에 대한 예측에 argmax 함수를 적용하고, 예상 레이블과 비교하여 모델을 평가할 수 있다.
import numpy as np
predictions = model(test_images)
predictions = predictions.numpy()
# 텐서플로 텐서의 .numpy() 메서드를 호출하여 넘파이 배열로 변경
predicted_labels = np.argmax(predictions, axis=1)
matches = predicted_labels == test_labels
print(f"정확도: {matches.mean(): 2f}")
이를 실행하면 정확도: 0.811600이 출력된다.
댓글남기기