11장 동적 계획법
Updated:
동적 계획법(Dynamic Programming)은 복잡한 문제를 여러 개의 간단한 문제로 분리하여 부분의 문제들을 해결함으로써 최종적으로 복잡한 문제의 답을 구하는 방법을 뜻한다.
동적 계획법의 핵심 이론
동적 계획법의 원리와 구현 방식은 다음과 같다.
- 큰 문제를 작은 문제로 나눌 수 있어야 한다.
- 작은 문제들이 반복돼 나타나고 사용되며 이 작은 문제들의 결괏값은 항상 같아야 한다.
- 모든 작은 문제들은 한 번만 계산해 DP 테이블에 저장하여 추후 재사용할 때는 이 DP 테이블을 이용한다(메모이제이션 기법, memoization).
- 동적 계획법은 톱-다운 방식(top-down)과 바텀-업 방식(bottom-up)으로 구현할 수 있다.
먼저 동적 계획법으로 풀 수 있는지 확인해야 한다. 피보나치 수열을 예로 들면, 6버째 피보나치 수열은 5번째 피보나치 수열과 4번째 피보나치 수열의 합이다. 즉, 6번째 피보나치 수열을 구하는 문제는 5번째 피보나치 수열과 4번째 피보나치 수열을 구하는 작은 문제로 나눌 수 있고, 수열의 값은 항상 같기 때문에 동적 계획법으로 풀 수 있다.
다음으로 점화식을 세워야 한다. 점화식을 세울 때는 논리적으로 전체 문제를 나누고, 전체 문제와 부분 문제 간의 인과 관계를 파악해야 한다.
메모이제이션은 부분 문제를 풀었을 때 이 문제를 DP 테이블에 저장해 놓고 다음에 같은 문제가 나왔을 때 재계산하지 않고 DP 테이블의 값을 이용하는 것을 말한다. 이러한 방식을 사용하면 불필요한 연산과 탐색이 줄어들어 시간 복잡도 측면에서 많은 이점을 가질 수 있다.
톱-다운 방식웨어서 부터 문제를 파악해 내려오는 방식으로, 주로 재귀 함수 형태로 코드를 구현한다. 코드의 가독성이 좋고, 이해하기 편하다는 장점이 있다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
public static int[] D;
public static int fib(int n) {
// 기존에 계산한 적이 있는 부분 문제는 다시 계산하지 않고 반환
if (D[n] != -1) {
return D[n];
}
// 메모이제이션: 구현 값을 바로 반환하지 않고 테이블에 저장 후 반환하도록 구현
return D[n] = fib(n - 2) + fib(n - 1);
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(bf.readLine());
D = new int[N];
for (int i = 0; i <= N; i++) {
D[i] = -1;
}
D[0] = 0;
D[1] = 1;
fib(N);
System.out.println(D[N]);
}
}
바텀-업 방식은 가장 작은 부분 문제부터 문제를 해결하면서 점점 큰 문제로 확장해 나가는 방식이다. 주로 반복문의 형태로 구현한다.
import java.io.BufferedReader;
import java.io.IOException;
public class Main {
public static int[] D;
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(bf.readLine());
D = new int[N];
for (int i = 0; i <= N; i++) {
D[i] = -1;
}
D[0] = 0;
D[1] = 1;
for (int i = 2; i <= N; i++) {
D[i] = D[i - 1] + D[i - 2];
}
System.out.println(D[N]);
}
}
두 방식 중 좀 더 안전한 방식은 바텀-업이다. 톱-다운 방식은 재귀 함수의 형태로 구현돼있기 때문에 재귀의 깊이가 매우 깊어질 경우 런타임 에러가 방생할 수 있다.
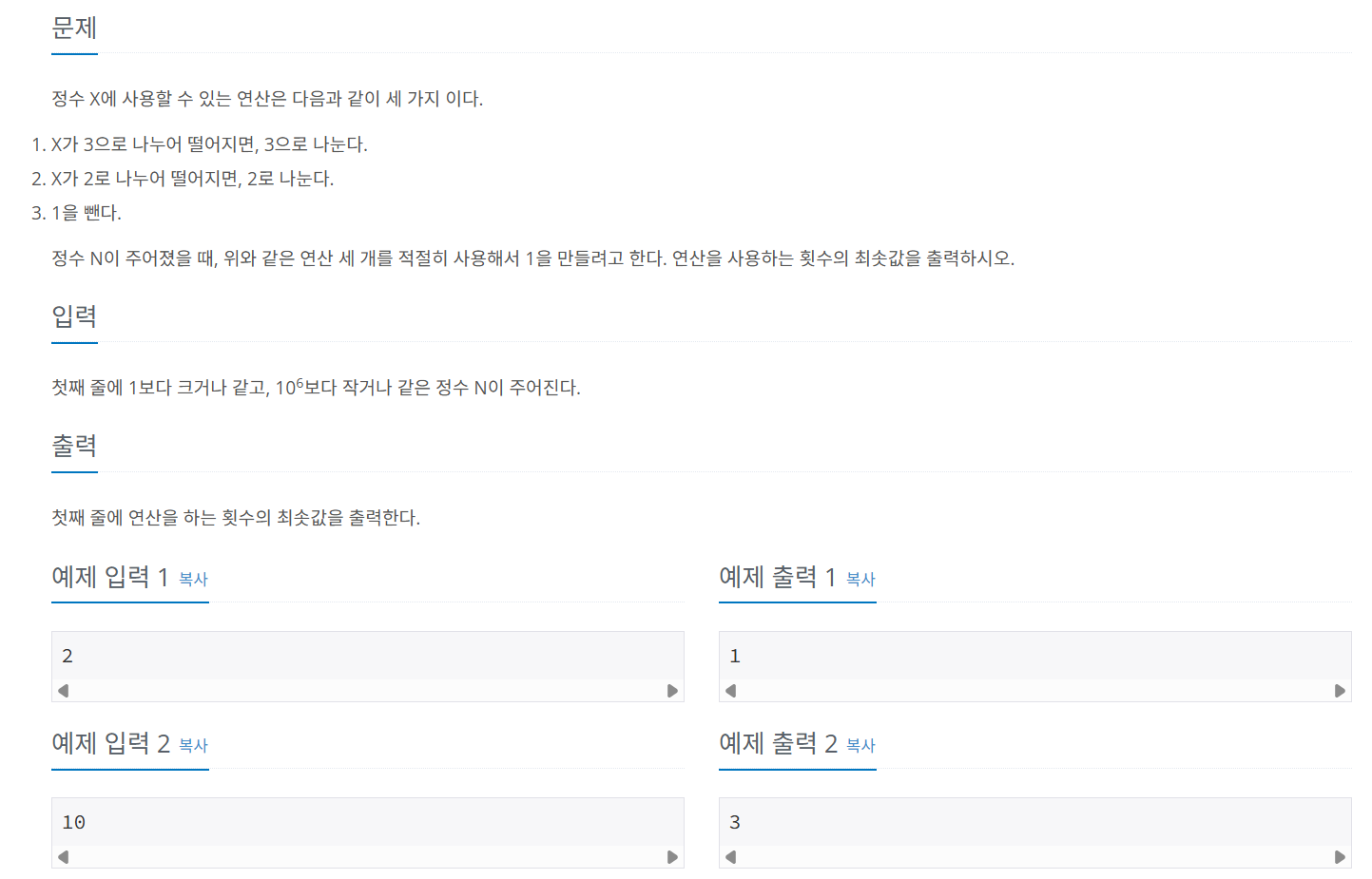
문제 084 정수를 1로 만들기
시간 제한: 0.15초, 난이도: 실버3, 1463번
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(bf.readLine());
int[] D = new int[N + 1];
D[1] = 0;
for (int i = 2; i <= N; i++) {
D[i] = D[i - 1] + 1; // 1을 뺀다.
if (i % 2 == 0) {
D[i] = Math.min(D[i], D[i / 2] + 1);
}
if (i % 3 == 0) {
D[i] = Math.min(D[i], D[i / 3] + 1);
}
}
System.out.println(D[N]);
}
}
문제 085 퇴사 준비하기
시간 제한: 2초, 난이도: 실버3, 14501번
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class P085 {
public static int[] T;
public static int[] P;
public static int[] D;
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(bf.readLine());
T = new int[16];
P = new int[16];
D = new int[17];
for (int i = 1; i < N + 1; i++) {
StringTokenizer st = new StringTokenizer(bf.readLine());
T[i] = Integer.parseInt(st.nextToken());
P[i] = Integer.parseInt(st.nextToken());
}
for (int i = N; i > 0; i--) {
if (i + T[i] > N + 1) {
D[i] = D[i + 1];
} else {
D[i] = Math.max(D[i + 1], P[i] + D[i + T[i]]);
}
}
System.out.println(D[1]);
}
}
i=N 부터 시작해서 Top-Down 방식으로 접근했다. i가 감소할 때, 현재 날짜에 상담한 후 벌 수 있는 가격과 다음날 부터 상담해서 벌 수 있는 금액을 비교한 후 그 중에 최대값을 저장한다. 만약 i + T[i] 가 N + 1 보다 크면 상담을 할 수 없으므로 이때는 전 날의 정보를 저장한다.
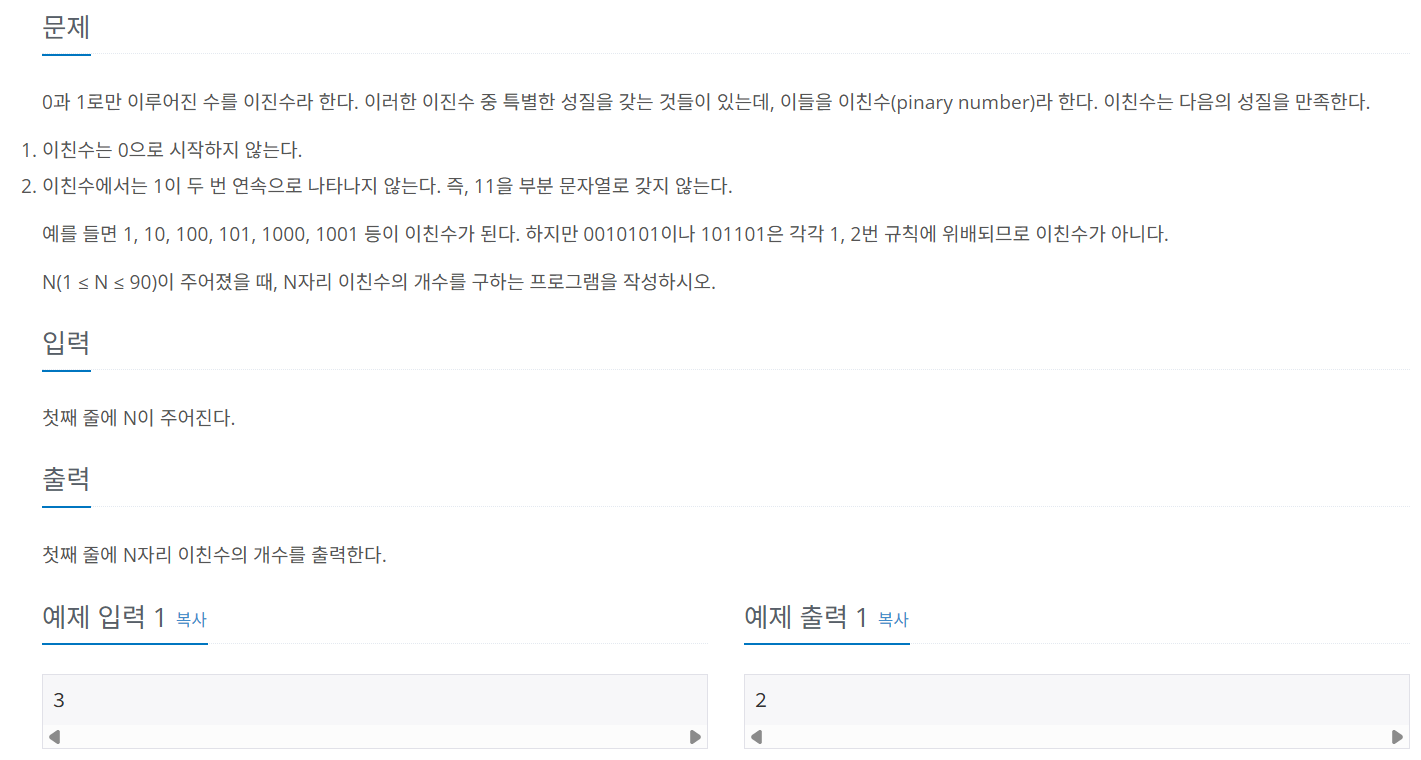
문제 086 이친수 구하기
시간 제한: 2초, 난이도: 실버3, 2193번
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
public static long[][] D;
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(bf.readLine());
D = new long[N + 1][2];
D[1][0] = 0;
D[1][1] = 1;
for (int i = 2; i < N + 1; i++) {
D[i][0] = D[i - 1][1] + D[i - 1][0];
D[i][1] = D[i - 1][0];
}
System.out.println(D[N][1] + D[N][0]);
}
}
배열 D[i][0]은 i길이에서 끝이 0으로 끝나는 이친수의 개수, D[i][1]은 i길이에서 끝이 1로 끝나는 이친수의 개수이다. 이때, 1은 연속해서 올 수 없으므로 D[i + 1][0]은 D[i][0]과 D[i][1]의 합과 같고, D[i + 1][1]은 D[i][0]의 값과 같다.
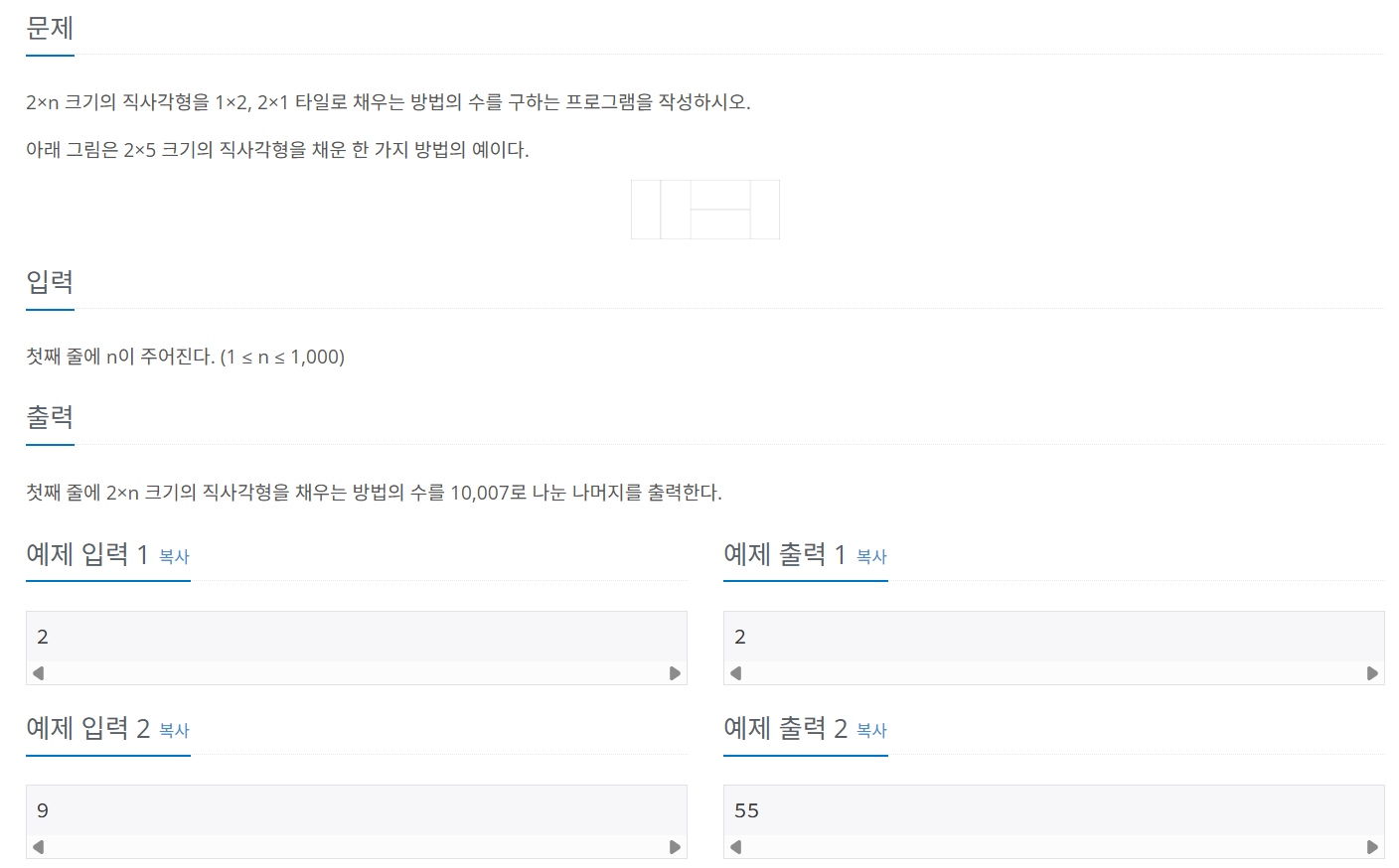
문제 087 2*N 타일 채우기
시간 제한: 1초, 난이도: 실버3, 11726번
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(bf.readLine());
long[] D = new long[1001];
D[1] = 1;
D[2] = 2;
for (int i = 3; i <= N; i++) {
D[i] = (D[i - 1] + D[i - 2]) % 10007;
}
System.out.println(D[N]);
}
}
i번째 타일을 채우는 경우의 수는 i - 1번째 타일에서 1 X 2 타일을 넣으면 되고, 1 - 2번째 타일에서 2 x 1 타일 2개를 넣으면 되기 때문에, D[i] = D[i - 1] + D[i - 2]와 같다.
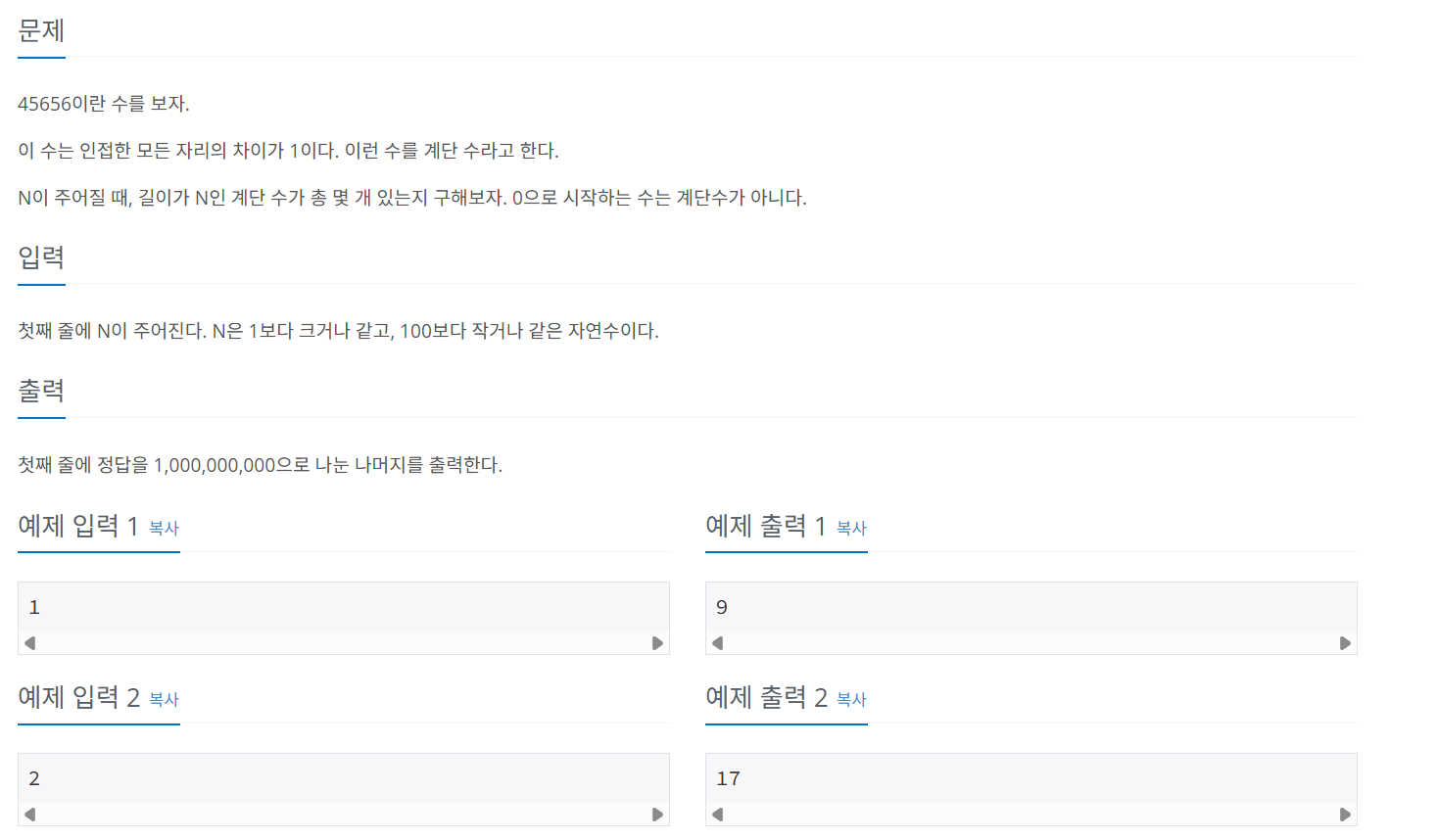
문제 088 계단 수 구하기
시간 제한: 1초, 난이도: 실버1, 10844번
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(bf.readLine());
long[][] D = new long[101][11];
for (int i = 1; i < 11; i++) {
D[1][i] = 1;
}
for (int i = 2; i < N + 1; i++) {
D[i][0] = D[i - 1][1];
D[i][9] = D[i - 1][8];
for (int j = 1; j < 9; j++) {
D[i][j] = (D[i - 1][j - 1] + D[i - 1][j + 1]) % 1000000000;
}
}
long sum = 0;
for (int i = 0; i < 10; i++) {
sum = (sum + D[N][i]) % 1000000000;
}
System.out.println(sum);
}
}
배열 D[N][H] 를 길이가 N인 숫자에서 끝이 H인 숫자의 경우의 수를 의미한다. 그래서 H = 0 이면 D[i][H] = D[i - 1][1] 과 같고, H = 9이면 D[i][H] = D[i - 1][8] 과 같다. 나머지 경우에서는 D[i][H] = D[i - 1][H - 1] + D[i - 1][H + 1] 과 같으므로 위와 같은 반복문을 통해 구현했다.
문제 089 연속된 정수의 합 구하기
시간 제한: 2초, 난이도: 골드5, 13398번
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(bf.readLine());
int[] A = new int[N];
StringTokenizer st = new StringTokenizer(bf.readLine());
for (int i = 0; i < N; i++) {
A[i] = Integer.parseInt(st.nextToken());
}
int[] L = new int[N];
int[] R = new int[N];
L[0] = A[0];
int max = A[0];
for (int i = 1; i < N; i++) {
L[i] = Math.max(L[i - 1] + A[i], A[i]);
// 하나도 제거하지 않았을 때를 기본 최대값으로 저장
max = Math.max(max, L[i]);
}
R[N - 1] = A[N - 1];
for (int i = N - 2; i >= 0; i--) {
R[i] = Math.max(A[i], R[i + 1] + A[i]);
}
// L[i - 1] + R[i + 1] 두 개의 구간 합 배열을 더해주면 i 번째 값을 제거한 효과
for (int i = 1; i < N - 1; i++) {
int temp = L[i - 1] + R[i + 1];
max = Math.max(max, temp);
}
System.out.println(max);
}
}
배열 A에 입력된 값들을 저장하고, 배열 L은 왼쪽부터 더해서 최대값일 때를 저장하고, R은 오른쪽 부터 더해서 최대값일 때를 저장한다. 그리고 마지막으로 i 번째 원소를 제외했을 때 합을 구해서 그것과 전의 최대값을 비교해 제외했을 때와 제외하지 않았을 때의 최대값을 비교해 결과를 출력한다.
문제 090 최장 공통부분 수열 찾기
시간 제한: 1초, 난이도: 골드5, 9252번
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Stack;
public class Main {
public static String A;
public static String B;
public static int[][] D;
public static Stack<Character> LCS = new Stack<>();
public static int maxLen;
public static void LCS(int a, int b) {
if (a == 0 || b == 0) {
return;
}
if (A.charAt(a - 1) == B.charAt(b - 1)) {
LCS.push(A.charAt(a - 1));
LCS(a - 1, b - 1);
} else {
if (D[a - 1][b] > D[a][b - 1]) {
LCS(a - 1, b);
} else {
LCS(a, b - 1);
}
}
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
A = bf.readLine();
B = bf.readLine();
D = new int[A.length() + 1][B.length() + 1];
for (int i = 1; i < A.length() + 1; i++) {
for (int j = 1; j < B.length() + 1; j++) {
if (A.charAt(i - 1) == B.charAt(j - 1)) {
D[i][j] = D[i - 1][j - 1] + 1;
} else {
D[i][j] = Math.max(D[i - 1][j], D[i][j - 1]);
}
}
}
maxLen = D[A.length()][B.length()];
System.out.println(maxLen);
if (maxLen != 0) {
LCS(A.length(), B.length());
int iter = LCS.size();
for (int i = 0; i < iter; i++) {
System.out.print(LCS.pop());
}
}
}
}
먼저 DP에 필요한 배열을 2차원 배열로 만든 다음에 입력된 두 문자열의 각 자리수가 같으면 최장 공통 부분에 들어가므로 D[i][j] = D[i - 1][j - 1] + 1 (대각선 방향)을 해준다. 같지 않으면 D[i - 1][j]와 D[i][j - 1] 중에 큰 값을 가져온다. 그러면 D[A.length() + 1][B.length() + 1]에는 최장 공통 부분의 길이가 들어가게 된다.
이제 D[A.lenhth() + 1][B.length() + 1] 부터 A와 B의 각 자리수가 같으면 대각선 방향으로, 같지 않으면 왼쪽 또는 위쪽 중 큰 방향으로 이동하면서 LCS 함수를 호출한다. 이때 스택에 같은 문자를 넣고 마지막에 스택에 들어있는 모든 문자들을 출력한다.
문제 091 가장 큰 정사각형 찾기
시간 제한: 1초, 난이도: 골드4, 1915번
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static int N;
public static int M;
public static int[][] D;
public static int Min(int a, int b, int c) {
int min = Math.min(a, b);
min = Math.min(min, c);
return min;
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(bf.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
D = new int[N][M];
int max = 0;
for (int i = 0; i < N; i++) {
String input = bf.readLine();
for (int j = 0; j < M; j++) {
D[i][j] = input.charAt(j) - '0';
if (D[i][j] == 1) {
max = 1;
}
}
}
for (int i = 1; i < N; i++) {
for (int j = 1; j < M; j++) {
if (D[i][j] == 1) {
D[i][j] = Min(D[i - 1][j - 1], D[i - 1][j], D[i][j - 1]) + 1;
}
if (max < D[i][j]) {
max = D[i][j];
}
}
}
System.out.println(max * max);
}
}
배열 D[i][j]를 오른쪽 아래 꼭짓점이 [i][j]인 사각형에서 만들 수 있는 정사각형의 최대 길이로 정의하고 이를 이용해 DP로 풀었다.
문제 092 빌딩 순서 구하기
시간 제한: 2초, 난이도: 플래티넘5, 1328번
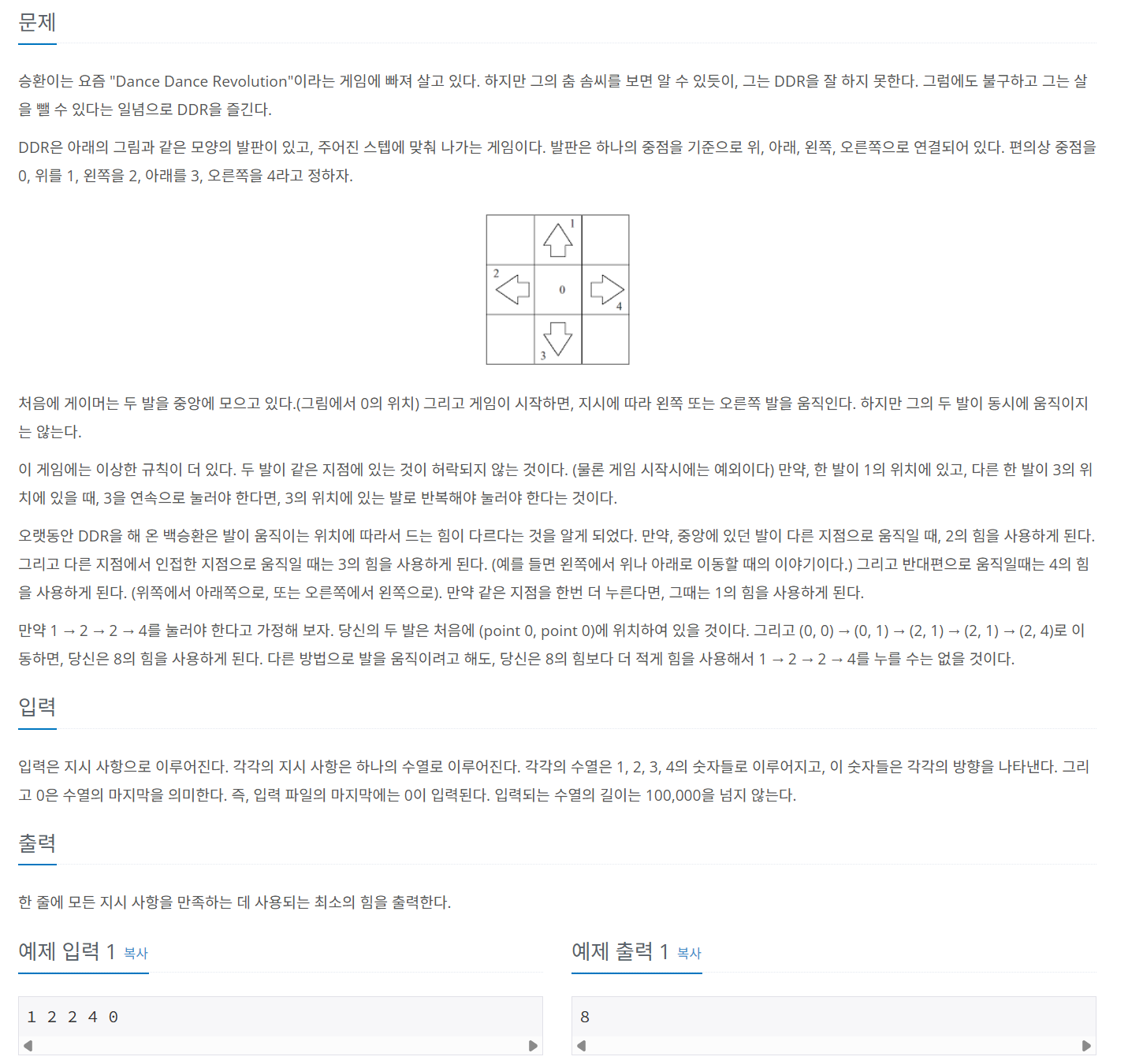
문제 093 DDR을 해보자
시간 제한: 2초, 난이도: 골드3, 2342번
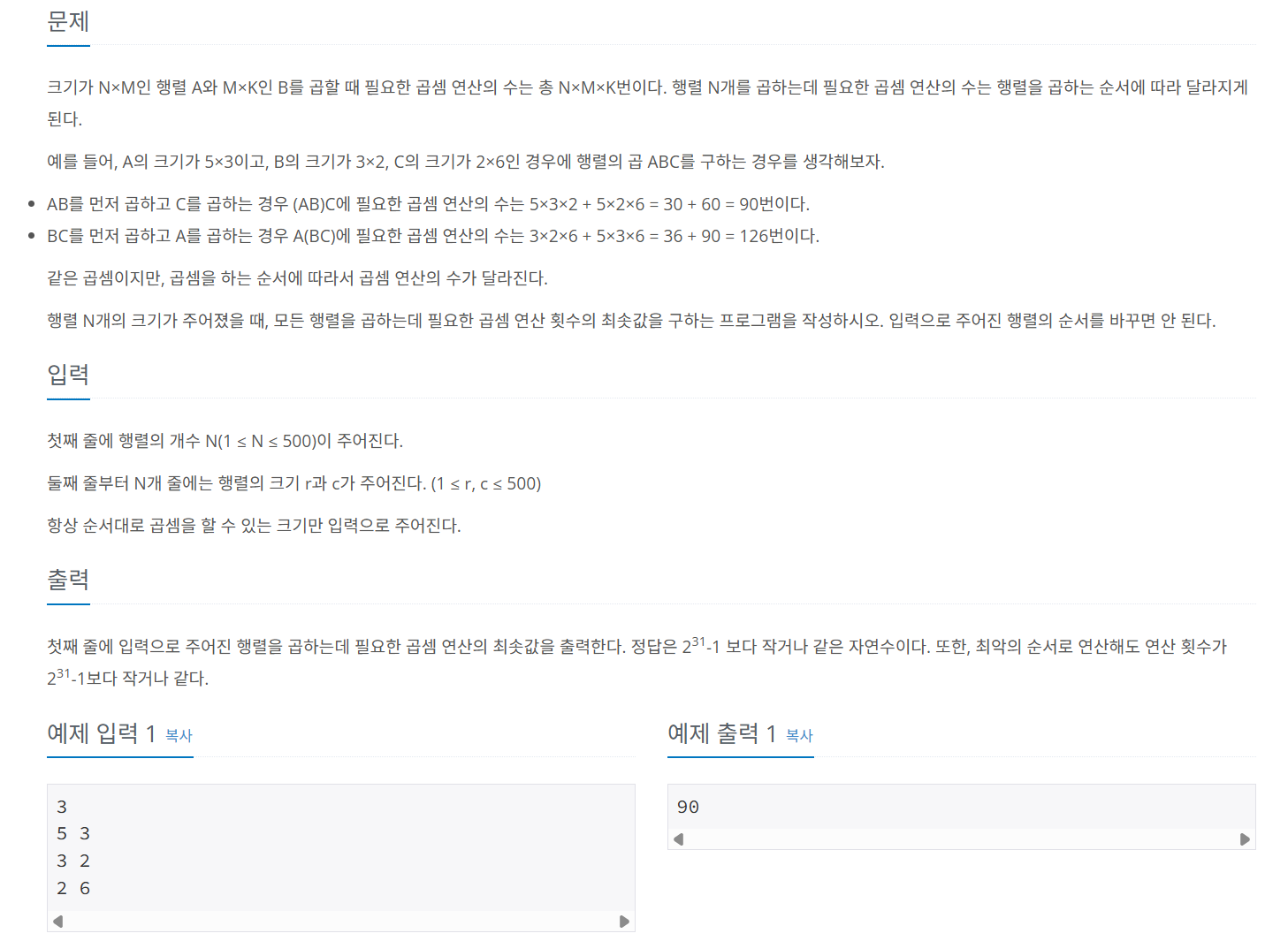
문제 094 행렬 곱 연산 횟수의 최솟값 구하기
시간 제한: 1초, 난이도: 골드3, 11049번
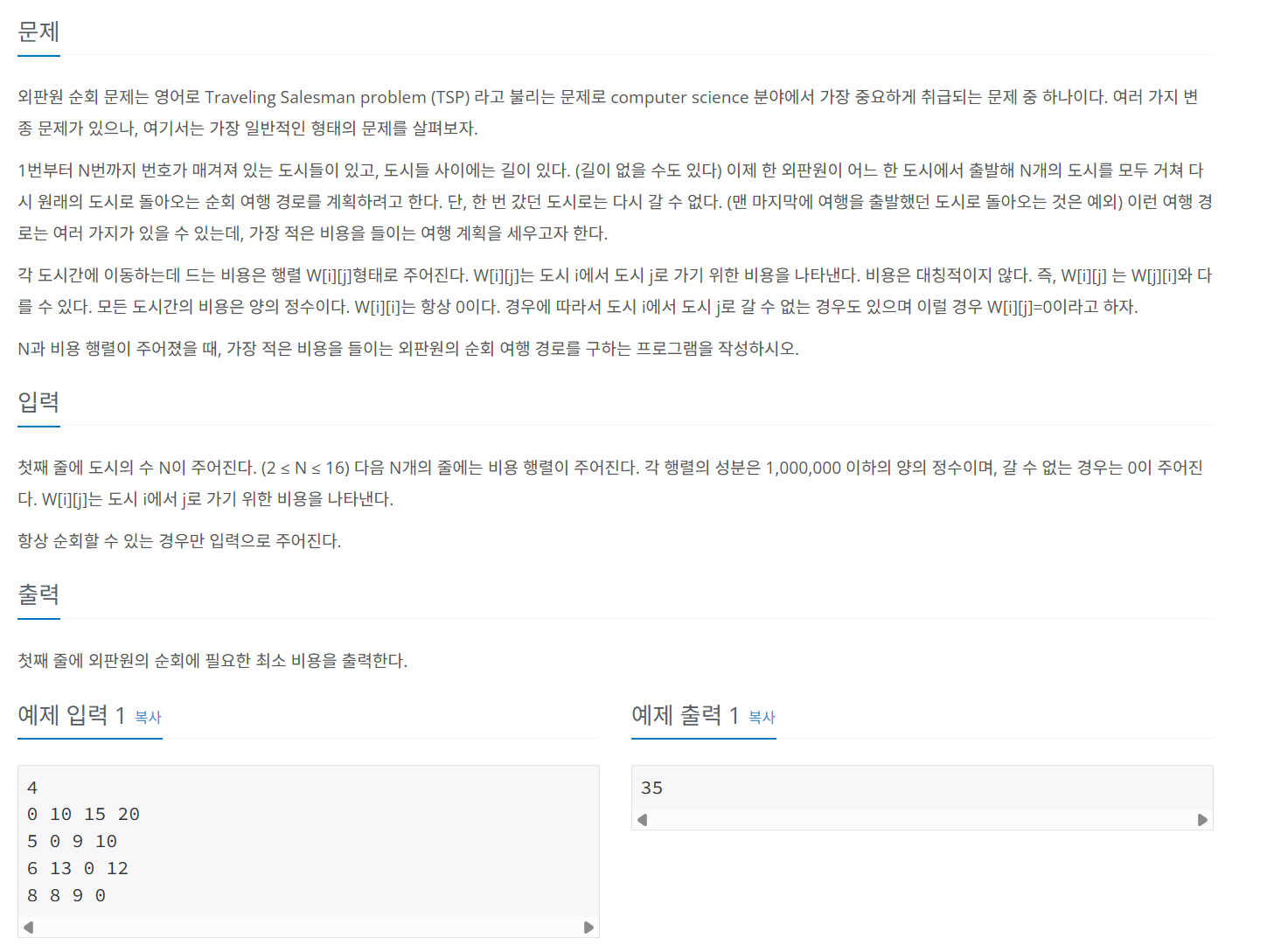
문제 095 외판원의 순회 경로 짜기
시간 제한: 1초, 난이도: 골드1, 2098번
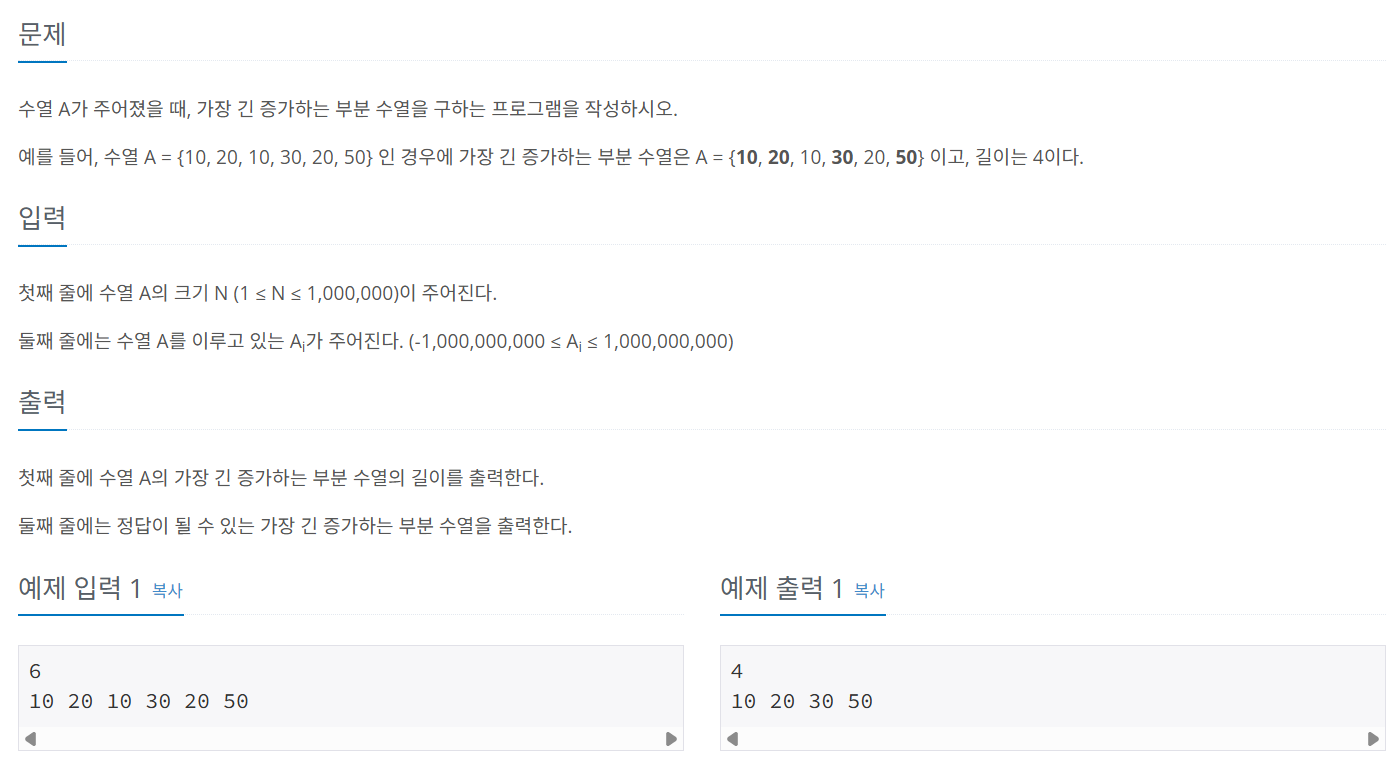
문제 096 가장 길게 증가하는 부분 수열 찾기
시간 제한: 3초, 난이도: 플래티넘5, 14003번
댓글남기기