1장 어떤 알고리즘으로 풀어야 할까?

시간 복잡도 표기법 알아보기

　알고리즘에서 시간 복잡도는 주어진 문제를 해결하기 위한 연산 횟수를 말한다. 일반적으로 C++에서는 1억 번의 연산을 1초의 수행 시간으로 예측할 수 있다.

시간 복잡도 정의하기

　시간 복잡도를 정의하는 3가지 유형은 다음과 같다.

• 빅-오메가($\Omega$(n)): 최선일 때(best case)의 연산 횟수를 나타낸 표기법
• 빅-세타($\Theta$(n)): 보통일 때(average case)의 연산 횟수를 나타낸 표기법
• 빅-오(O(n)): 최악일 때(worst case)의 연산 횟수를 나타낸 표기법

　코딩 테스트에서는 빅-오 표기법을 기준으로 수행 시간을 계산하는 것이 좋다.

시간 복잡도 활용하기

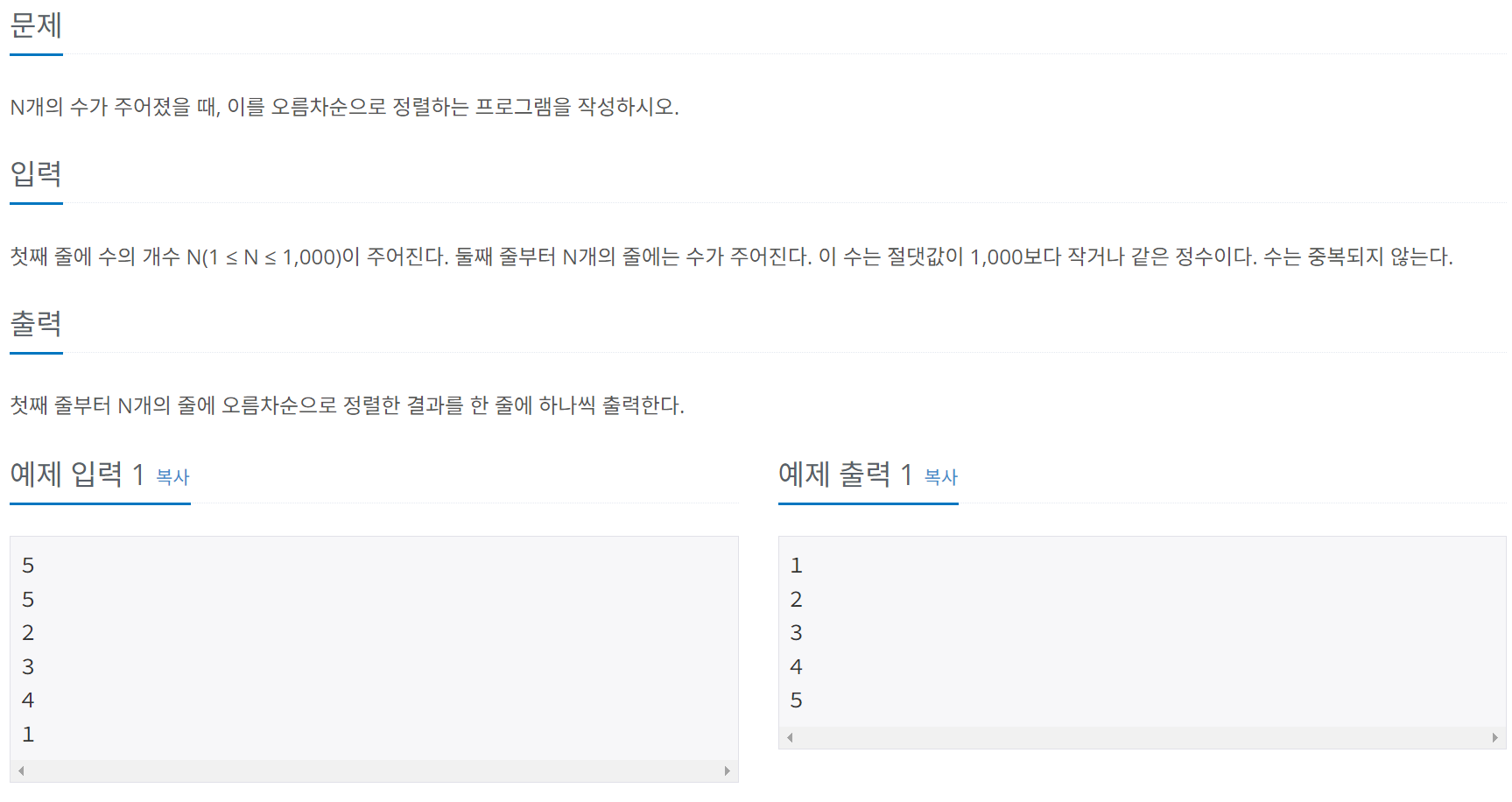
문제 000

시간 제한: 2초, 2750번

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

int main(){
    ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);
    
    int N;
    cin>>N;
    
    vector<int>A(N,0);
    
    for(int i=0; i<N; i++){
        int tmp;
        cin>>tmp;
        A[i]=tmp;
    }
    
    sort(A.begin(),A.end());
    
    for(int i=0; i<N;i++){
        cout<<A[i]<<"\n";
    }
}

　시간제한이 2초이므로 연산 횟수가 2억 번 안에 원하는 답을 구해야 한다. 버블 정렬(O($n^2$))은 약 1조 번의 연산 횟수가 필요하므로 이 문제를 풀기에 적합한 알고리즘이 아니다. 병합 정렬(O(nlogn))은 약 2,000만 번의 연산 횟수로 답을 구할 수 있으므로 문제를 풀기에 적합한 알고리즘이라고 판단할 수 있다.
　이와 같이 시간 복잡도 분석으로 문제에서 사용할 수 있는 알고리즘을 선택할 수 잇고, 이 범위를 바탕으로 문제의 실마리를 찾을 수 있다. 즉, 데이터의 크기(N)를 단서로 사용해야하는 알고리즘을 추측해 볼 수 있다.