10장 조합
Updated:
순열과 조합의 핵심 이론
조합의 점화식은 다음 3가지 단계로 세울 수 있다.
- 특정 문제를 가정하기
- 5개의 데이터에서 3개를 선택하는 조합의 경우의 수를 푸는 문제를 가정한다.
- 모든 부분 문제가 해결된 상황이라고 가정하고 지금 문제 생각하기
- 먼저 5개의 데이터 중에서 4개가 이미 선택 여부가 결정된 데이터라고 가정한다.
- 5번째 데이터의 선택 여부에 따른 경우의 수를 계산한다.
- 5번째 데이터를 포함해 총 3개의 데이터를 선택: 선택이 완료됐다고 가정한 4개의 데이터에서 2개가 선택
- 5번째 데이터를 포함하지 않고 총 3개의 데이터를 선택: 데이터 4개 중 3개가 선택 - 5개 중 3개를 선택하는 경우의 수 점화식: D[5][3] = D[4][2] + D[4][3]
- 특정 문제를 해결한 내용을 바탕으로 일반 점화식 도출하기
- 일반화된 점화식을 이용하면 조합과 관련된 모든 경우의 수를 쉽게 구할 수 있다.
- 조합 점화식: D[i][j] = D[i - 1][j] + D[i - 1][j - 1]
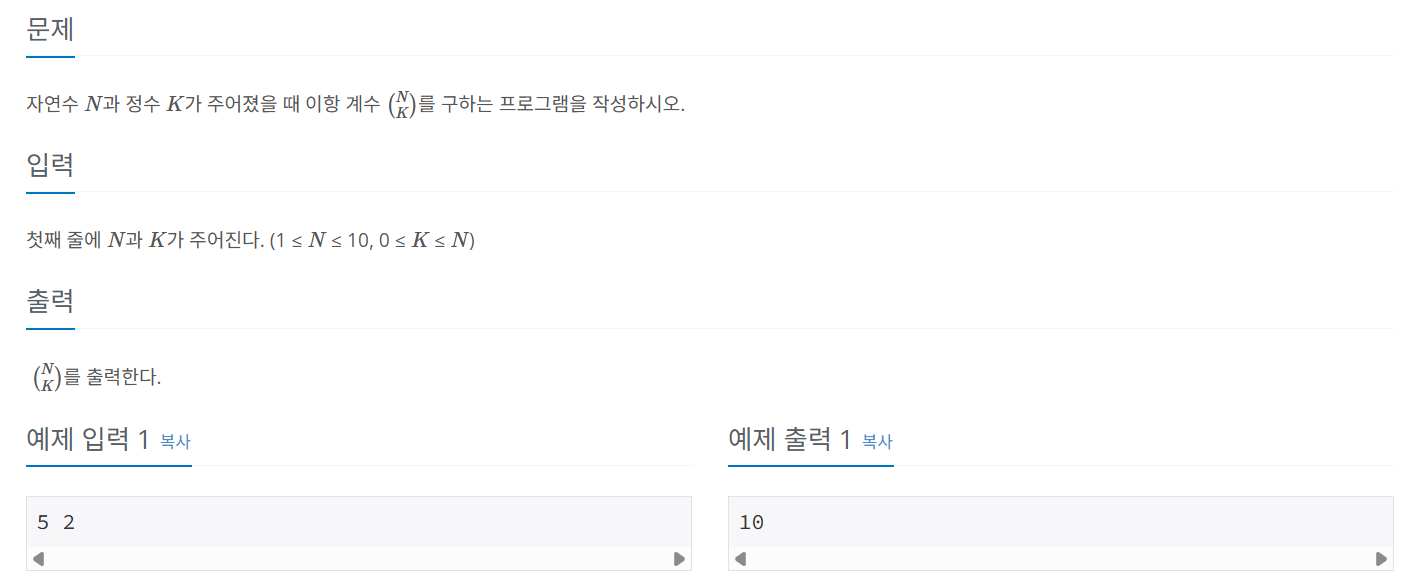
문제 076 이항계수 구하기 1
시간 제한: 1초, 난이도: 브론즈1, 11050번
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(bf.readLine());
int N = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
int[][] D = new int[11][11];
// 배열 초기화
for (int i = 0; i < 11; i++) {
D[i][1] = 1;
D[i][i] = 1;
D[i][0] = 1;
}
for (int i = 1; i < N + 1; i++) {
for (int j = 1; j < i; j++) {
D[i][j] = D[i - 1][j] + D[i - 1][j - 1];
}
}
System.out.println(D[N][K]);
}
}
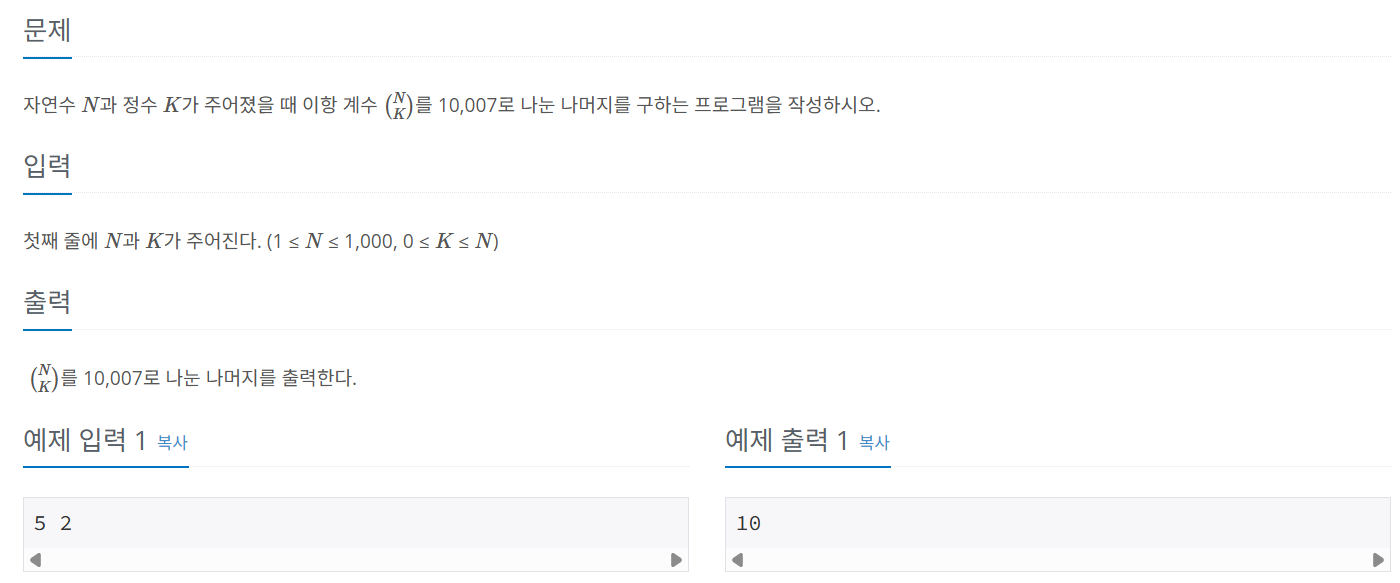
문제 077 이항계수 구하기 2
시간 제한: 1초, 난이도: 실버1, 11051번
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(bf.readLine());
int N = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
int[][] D = new int[1001][1001];
for (int i = 0; i < 1001; i++) {
D[i][i] = 1;
D[i][0] = 1;
D[i][1] = i;
}
for (int i = 2; i < N + 1; i++) {
for (int j = 1; j < i; j++) {
D[i][j] = D[i - 1][j] + D[i - 1][j - 1];
D[i][j] = D[i][j] % 10007;
}
}
System.out.println(D[N][K]);
}
}
모듈러 연산의 특성 (A mod N + B mod N) mod N = (A + B) mod N을 이용해 해결하였다.
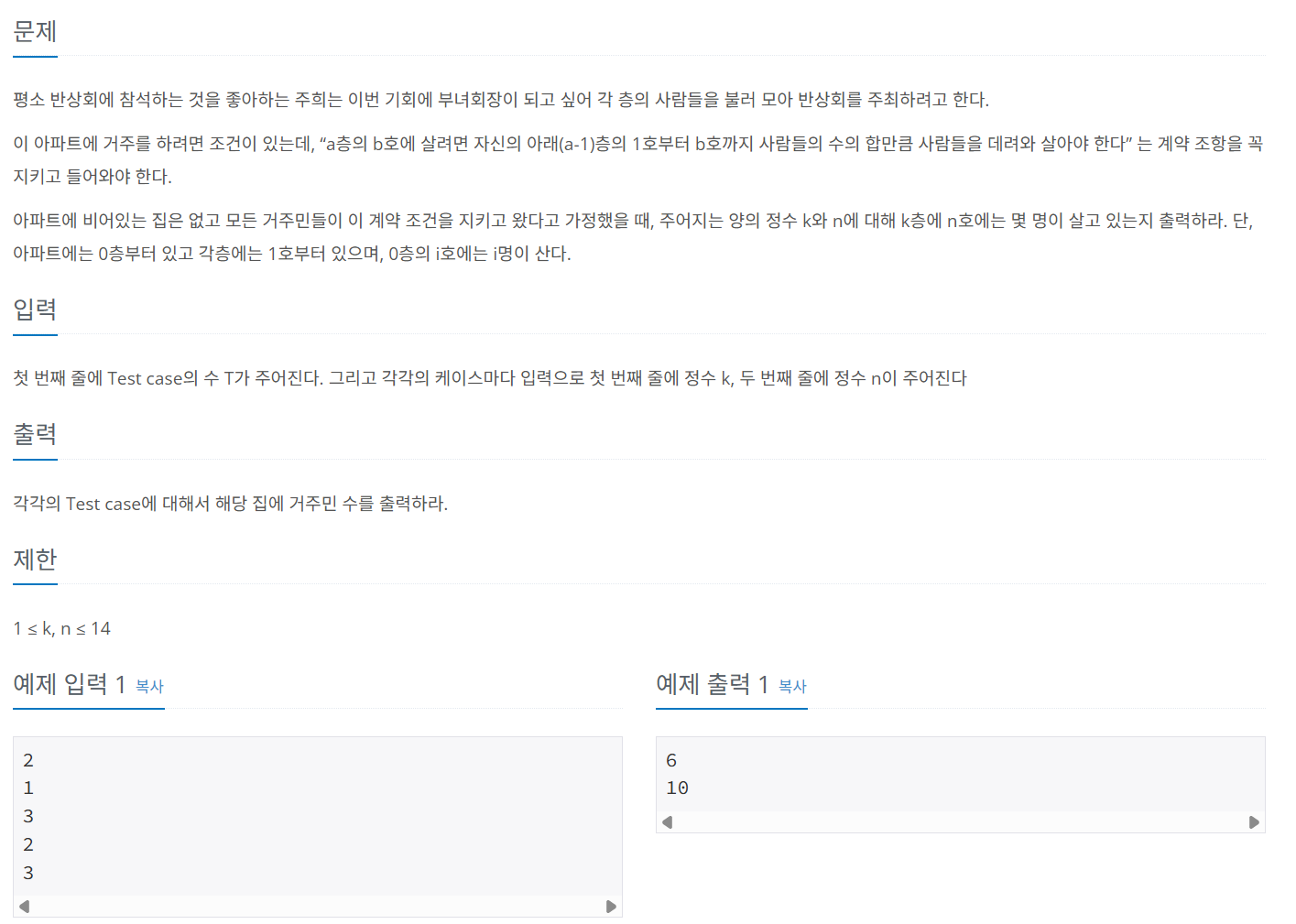
문제 078 부녀회장이 될 테야
시간 제한: 1초, 난이도: 브론즈2, 2775번
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int[][] D = new int[15][15];
// 배열 초기화
D[0][1] = 1;
for (int i = 1; i < 15; i++) {
D[0][i] = i;
D[i][1] = 1;
}
for (int i = 1; i < 15; i++) {
for (int j = 2; j < 15; j++) {
D[i][j] = D[i - 1][j] + D[i][j - 1];
}
}
int T = Integer.parseInt(bf.readLine());
for (int i = 0; i < T; i++) {
int k = Integer.parseInt(bf.readLine());
int n = Integer.parseInt(bf.readLine());
System.out.println(D[k][n]);
}
}
}
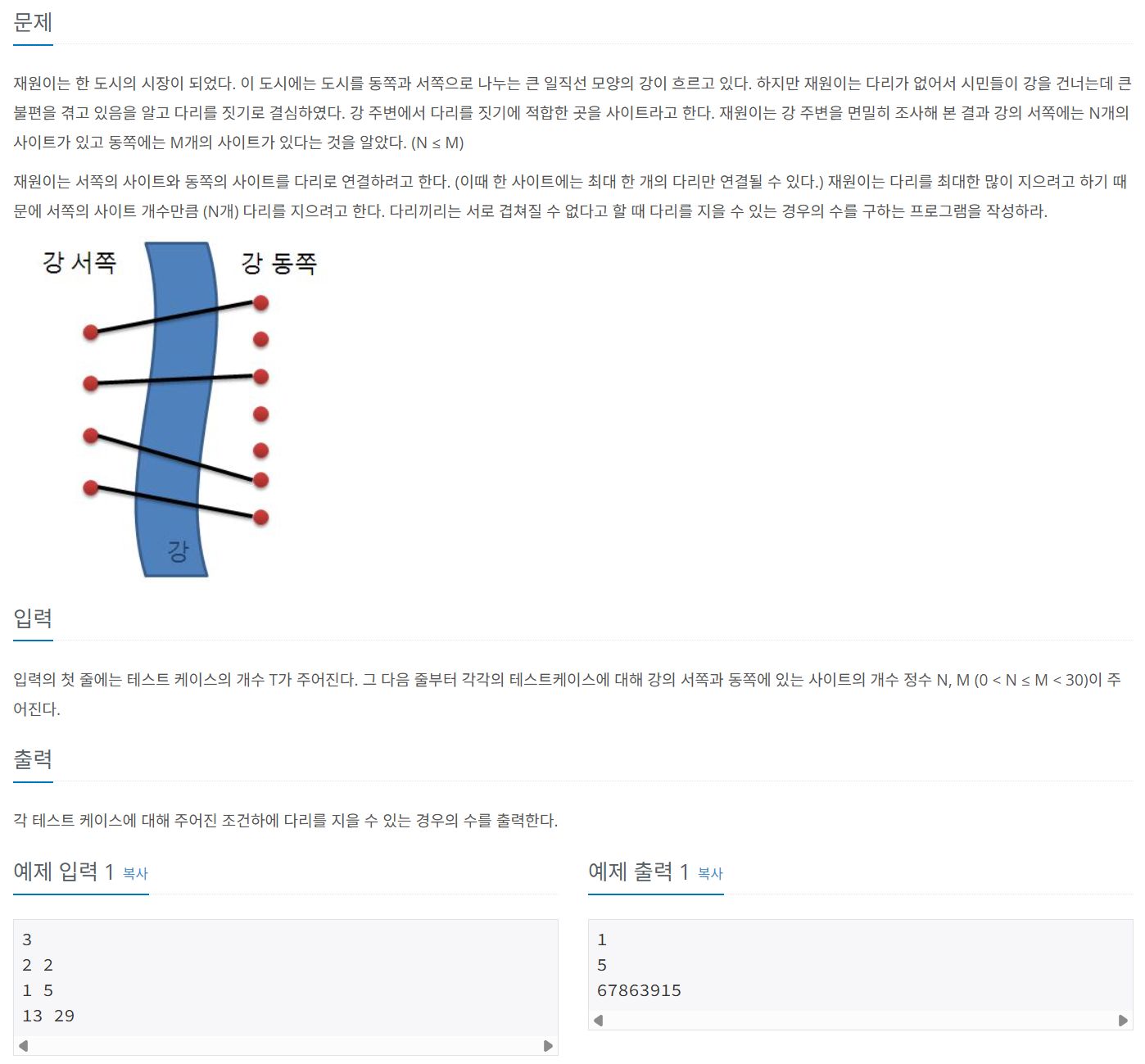
문제 079 다리 놓기
시간 제한: 0.5초, 난이도: 실버5, 1010번
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int[][] D = new int[30][30];
for (int i = 1; i < 30; i++) {
D[1][i] = i;
D[i][i] = 1;
}
for (int i = 2; i < 30; i++) {
for (int j = i; j < 30; j++) {
D[i][j] = D[i][j - 1] + D[i - 1][j - 1];
}
}
int T = Integer.parseInt(bf.readLine());
for (int i = 0; i < T; i++) {
StringTokenizer st = new StringTokenizer(bf.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
System.out.println(D[N][M]);
}
}
}
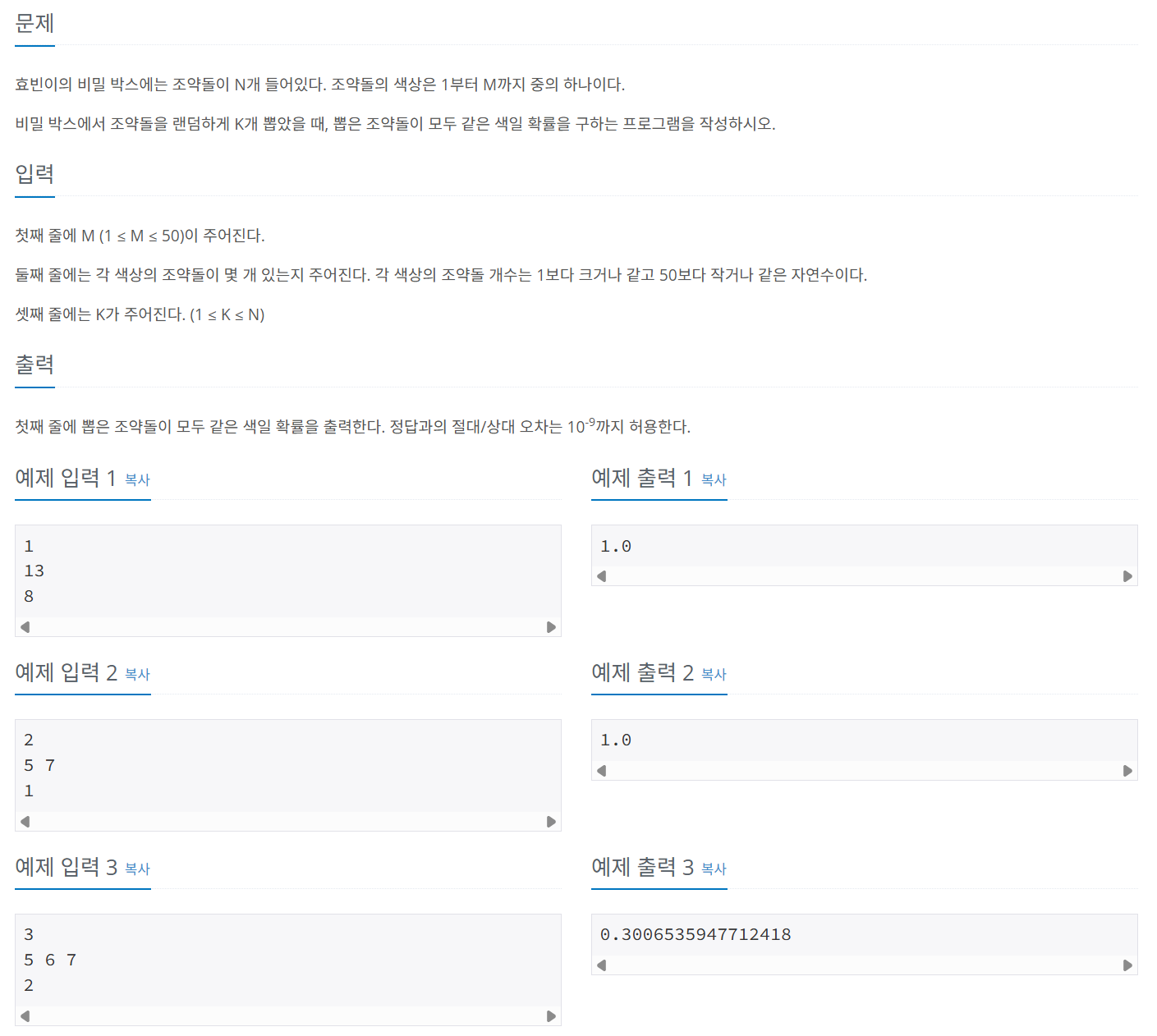
문제 080 조약돌 꺼내기
시간 제한: 2초, 난이도: 실버3, 13251번
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int M = Integer.parseInt(bf.readLine());
int[] D = new int[M];
double[] P = new double[M];
double result = 0.0;
int sum = 0;
StringTokenizer st = new StringTokenizer(bf.readLine());
for (int i = 0; i < M; i++) {
int input = Integer.parseInt(st.nextToken());
D[i] = input;
sum += input;
}
int K = Integer.parseInt(bf.readLine());
for (int i = 0; i < M; i++) {
if (D[i] >= K) {
P[i] = 1.0;
}
for (int j = 0; j < K; j++) {
P[i] = P[i] * ((double) (D[i] - j) / (sum - j));
}
result += P[i];
}
System.out.println(result);
}
}
for문에서 현재 뽑은 확률 * 다음번째 같은것을 뽑을 확률을 이용해 풀었다.
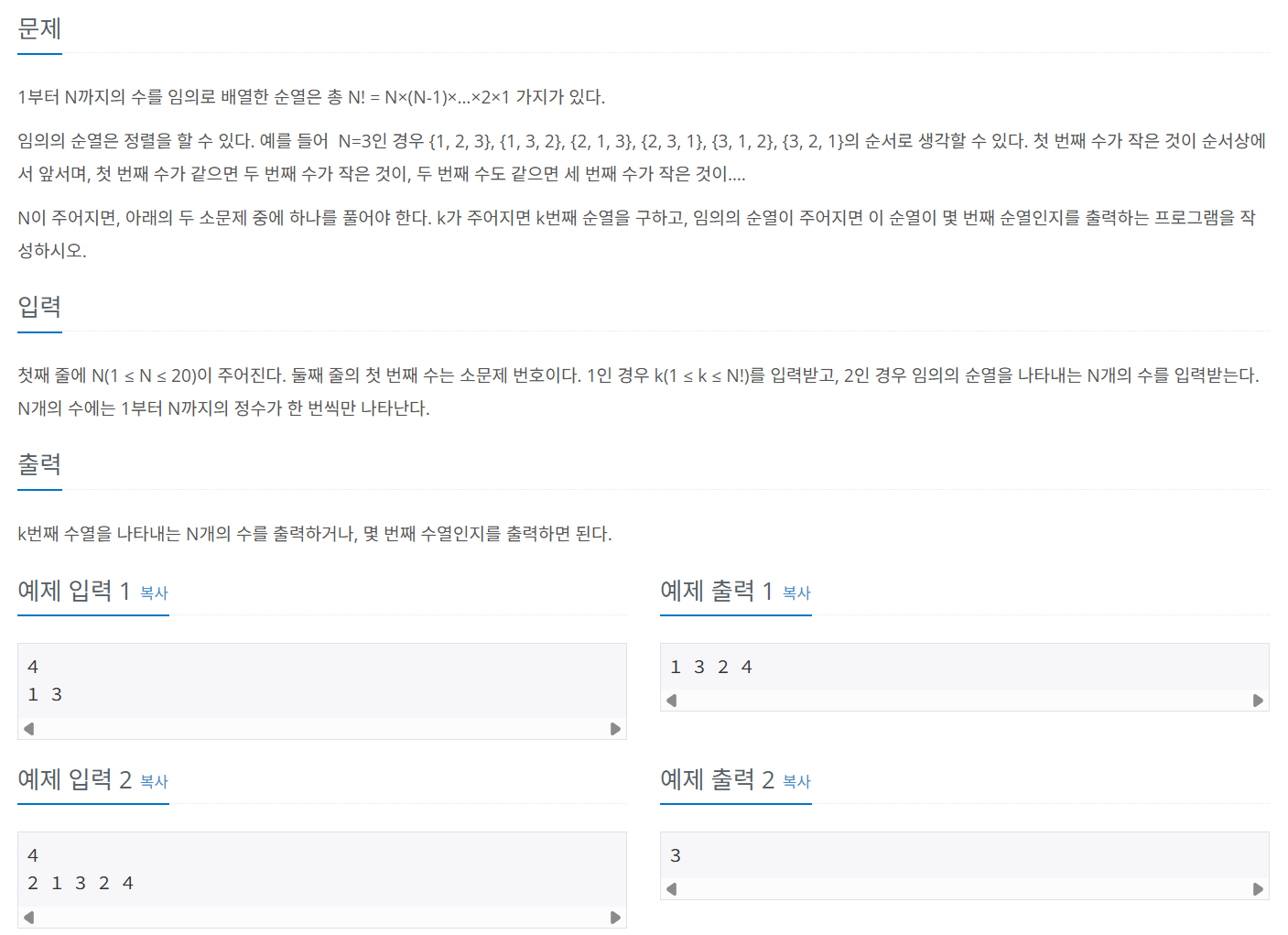
문제 081 순열의 순서 구하기
시간 제한: 2초, 난이도: 골드5, 1722번
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(bf.readLine());
StringTokenizer st = new StringTokenizer(bf.readLine());
int Q = Integer.parseInt(st.nextToken());
boolean[] visited = new boolean[21];
long[] F = new long[21];
int[] S = new int[21];
F[0] = 1; // 0! = 1
for (int i = 1; i < N + 1; i++) {
F[i] = F[i - 1] * i;
}
if (Q == 1) {
long k = Long.parseLong(st.nextToken());
for (int i = 1; i < N + 1; i++) {
int count = 1;
for (int j = 1; j < N + 1; j++) {
if (visited[j]) {
continue;
}
if (k <= count * F[N - i]) {
k = k - (F[N - i] * (count - 1));
S[i] = j;
visited[j] = true;
break;
}
count++;
}
}
for (int i = 1; i < N + 1; i++) {
System.out.print(S[i] + " ");
}
} else {
long k = 1;
for (int i = 1; i <= N; i++) {
S[i] = Integer.parseInt(st.nextToken());
long count = 0;
for (int j = 1; j < S[i]; j++) {
if (!visited[j]) {
count++;
}
}
k = k + F[N - i] * count;
visited[S[i]] = true;
}
System.out.println(k);
}
}
}
고등학교 확률과 통계 문제에서 몇 번째 숫자를 구하시오 같은 문제와 같이 Q = 1일 때 문제를 풀었고, 무슨 숫자가 몇 번째 숫자인지 구하시오를 구하는 문제 같이 Q = 2를 풀었다.
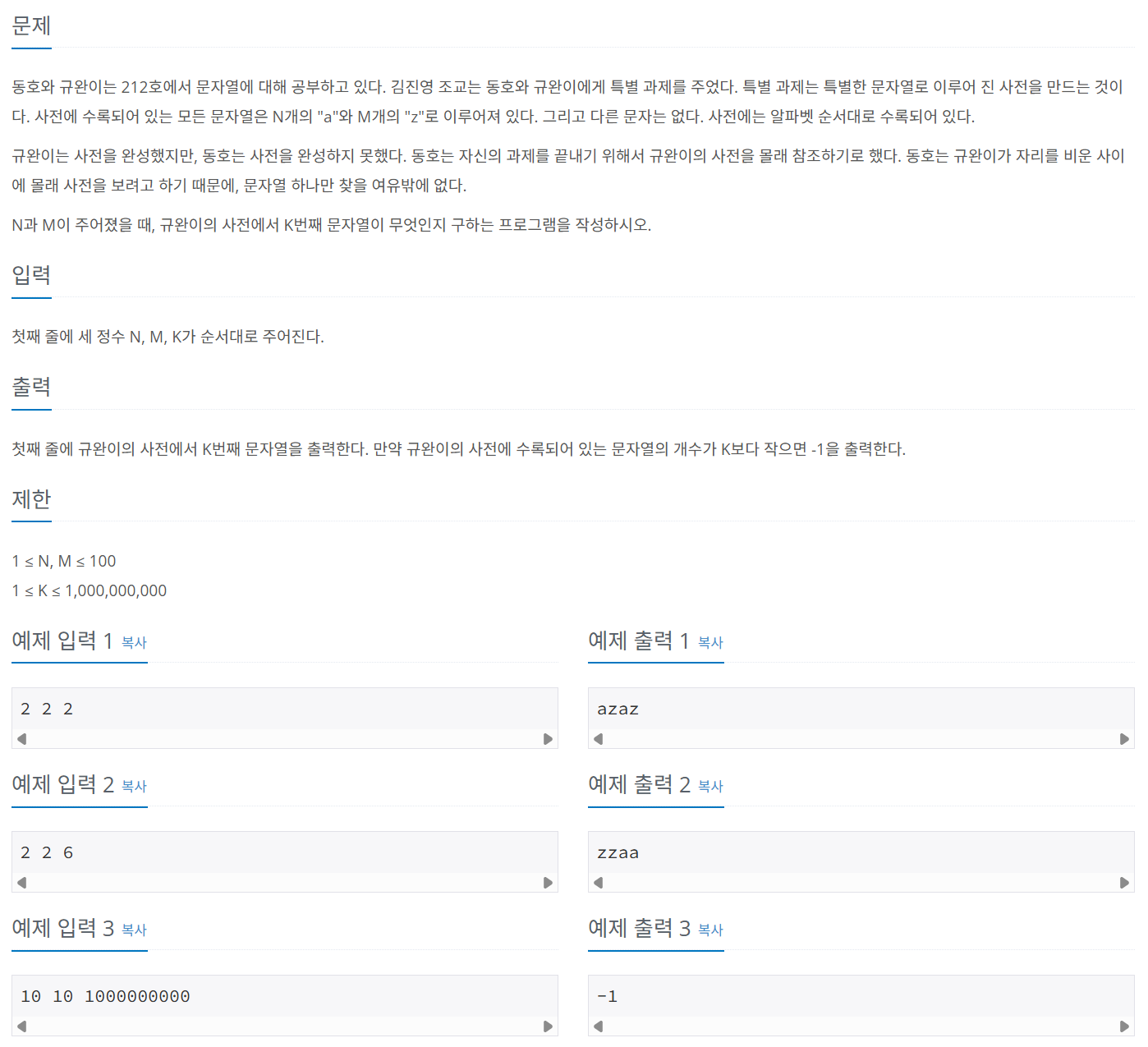
문제 082 사전 찾기
시간 제한: 2초, 난이도: 골드2, 1256번
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(bf.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
/*
(N+M)!/N!*M! = (N+M)!/(N+M-M)!M! => (N+M)C(M)
*/
int[][] D = new int[201][201];
for (int i = 0; i < 201; i++) {
for (int j = 0; j <= i; j++) {
if (j == 0 || j == i) {
D[i][j] = 1;
} else {
D[i][j] = D[i - 1][j - 1] + D[i - 1][j];
if (D[i][j] > 1000000000) {
D[i][j] = 1000000001; // K의 최대값
}
}
}
}
if (D[N + M][M] < K) {
System.out.println(-1);
} else {
while (!(N == 0 && M == 0)) {
if (D[N - 1 + M][M] >= K) {
System.out.print("a");
N--;
} else {
System.out.print("z");
K = K - D[N - 1 + M][M];
M--;
}
}
}
}
}
문자 a N개와, z M개를 나열하는 방법의 수는 N+M개의 문자에서 M개를 선택하는 경우의 수랑 같다는 것을 이용해 풀어다.
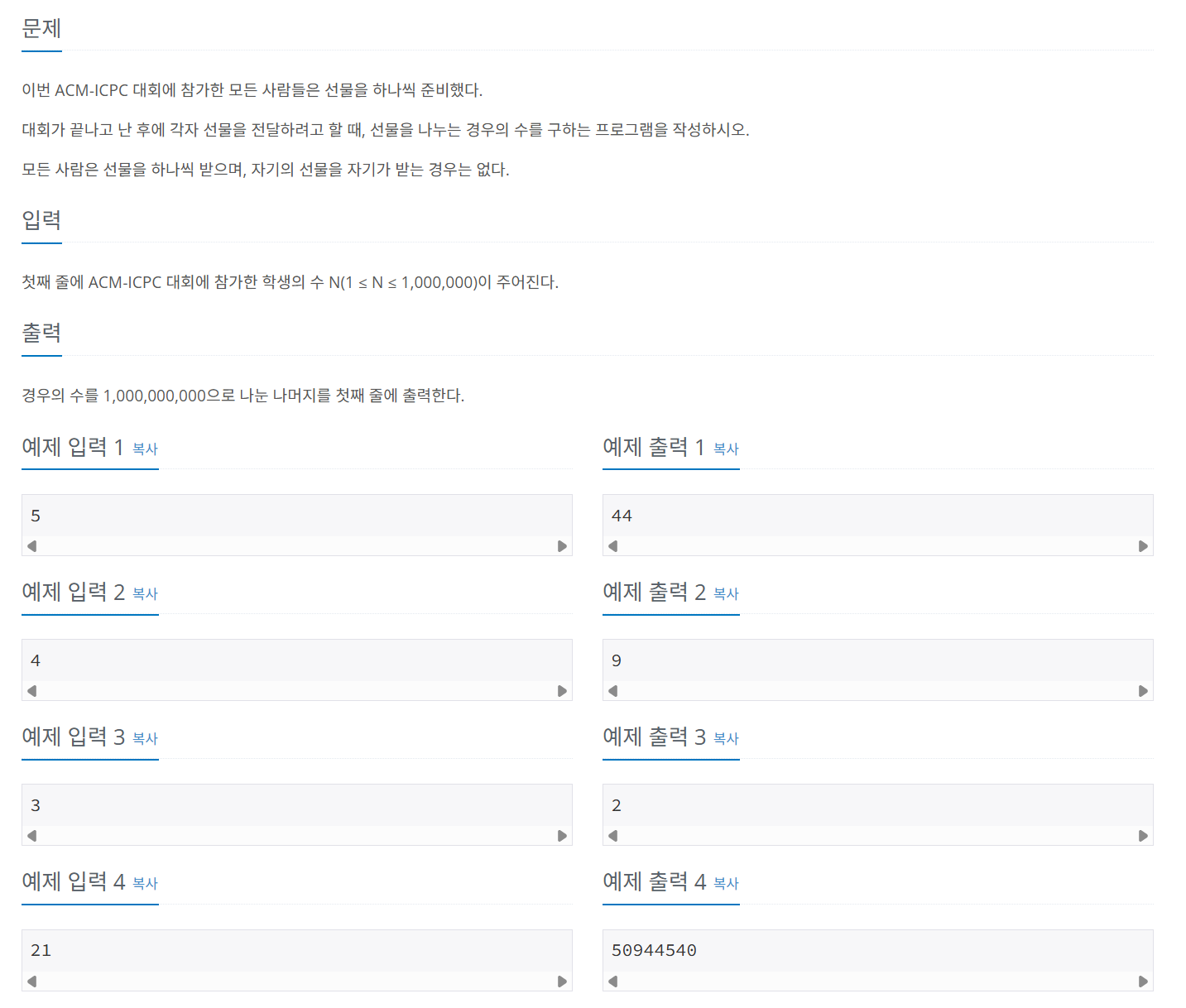
문제 083 선물 전달하기
시간 제한: 2초, 난이도: 골드3, 1947번
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
// D[N] = (N - 1) * (D[N - 1] + D[N - 2])
int N = Integer.parseInt(bf.readLine());
long[] D = new long[1000001];
D[1] = 0;
D[2] = 1;
for (int i = 3; i < N + 1; i++) {
D[i] = (i - 1) * (D[i - 1] + D[i - 2]) % 1000000000;
}
System.out.println(D[N]);
}
}
점화식 D[N] = (N - 1) * (D[N - 1] + D[N - 2])을 사용해 풀었다. 이는 1명이 선물을 줄 1명을 선택했을 때, 그 사람이 첫번째 사람에게 주면 D[N - 2]의 경우의 수와 같고 다른 사람에게 주면 D[N - 1]의 경우의 수와 같기 때문이다.
댓글남기기