3장 자료구조

Updated: October 11, 2023

배열과 리스트 그리고 벡터

기본 자료구조인 배열과 리스트는 비슷한 점도 많지만 다른 점도 많다. 두 자료구조의 특징을 정확하게 이해하고 문제가 요구하는 조건에 따라 적절하게 선택해 사용하는 것이 중요하다.

배열과 리스트의 핵심 이론

배열
배열은 메모리의 연속 공간에 값이 채워져 있는 형태의 자료구조이다. 배열의 값은 인덱스를 통해 참조할 수 있으며, 선언한 자료형의 값만 저장할 수 있다.

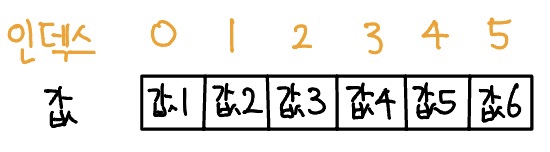
배열의 특징을 정리하면 다음과 같다.

인덱스를 사용하여 값에 바로 접근할 수 있다.
새로운 값을 삽입하거나 특정 인덱스에 있는 값을 삭제하기 어렵다. 값을 삽입하거나 삭제하려면 해당 인덱스 주변에 있는 값을 이동시키는 과정이 필요하다.
배열의 크기는 선언할 때 지정할 수 있으며, 한 번 선언하면 크기를 늘리거나 줄일 수 없다.
구조가 간단하므로 코딩 테스트에서 많이 사용한다.

리스트
리스트는 값과 포인터를 묶은 노드라는 것을 포인터로 연결한 자료구조이다.

리스트의 특징을 정리하면 다음과 같다.

인덱스가 없으므로 값에 접근하려면 Head 포인터부터 순서대로 접근해야 한다. 다시 말해 값에 접근하는 속도가 느리다.
포인터로 연결되어 있으므로 데이터를 삽입하거나 삭제하는 연산 속도가 빠르다.
선언할 때 크기를 별도로 지정하지 않아도 된다. 다시 말해 리스트의 크기는 정해져 있지 않으며, 크기가 변하기 쉬운 데이터를 다룰 때 적절하다.
포인터를 저장할 공간이 필요하므로 배열보다 구조가 복잡하다.

벡터
vector는 C++ 표준 라이브러리에 있는 자료구조 컨테이너 중 하나로, 사용자가 손쉽게 사용하기 위해 정의된 클래스이다. 기존의 배열과 같은 특징을 가지면서 배열의 단점을 보완한 동적 배열의 형태라고 생각하면 된다.
벡터의 특징은 다음과 같다.

동적으로 원소를 추가할 수 있다. 즉, 크기가 자동으로 늘어난다.
맨 마지막 위치에 데이터를 삽입하거나 삭제할 때는 문제가 없지만 중간 데이터의 삽입 삭제는 배열과 같은 메커니즘으로 동작한다.
배열과 마찬가지로 인덱스를 이용하여 각 데이터에 직접 접근할 수 있다.

다음은 벡터의 기본 사용법이다.

// 선언
vector<int> A;                // vector<자료형> 변수이름; 형태로 선언

// 삽입 연산
A.push_back(1);               // 마지막에 1 추가
A.insert(A.begin(), 7);       // 맨 앞에 7을 삽입
A.insert(A.begin() + 2, 10);  // index 2에 위치에 10 삽입

// 값 변경
A[4] = -5;                    // index 4의 값을 -5로 변경

// 삭제 연산
A.pop_back();                 // 마지막 값 삭제
A.erase(A.begin() + 3);       // index 3에 해당하는 값 삭제
A.clear();                    // 모든 값 삭제

// 정보 가져오기
A.size();                     // 데이터 개수
A.front();                    // 처음 값
A.back();                     // 마지막 값
A[3];                         // index 3에 해당하는 값
A.at(5);                      // index 5에 해당하는 값
A.begin();                    // 첫 번째 데이터 위치
A.end();                      // 마지막 데이터 다음 위치

문제 001 숫자의 합 구하기

시간 제한: 1초, 난이도: 브론즈4, 11720번

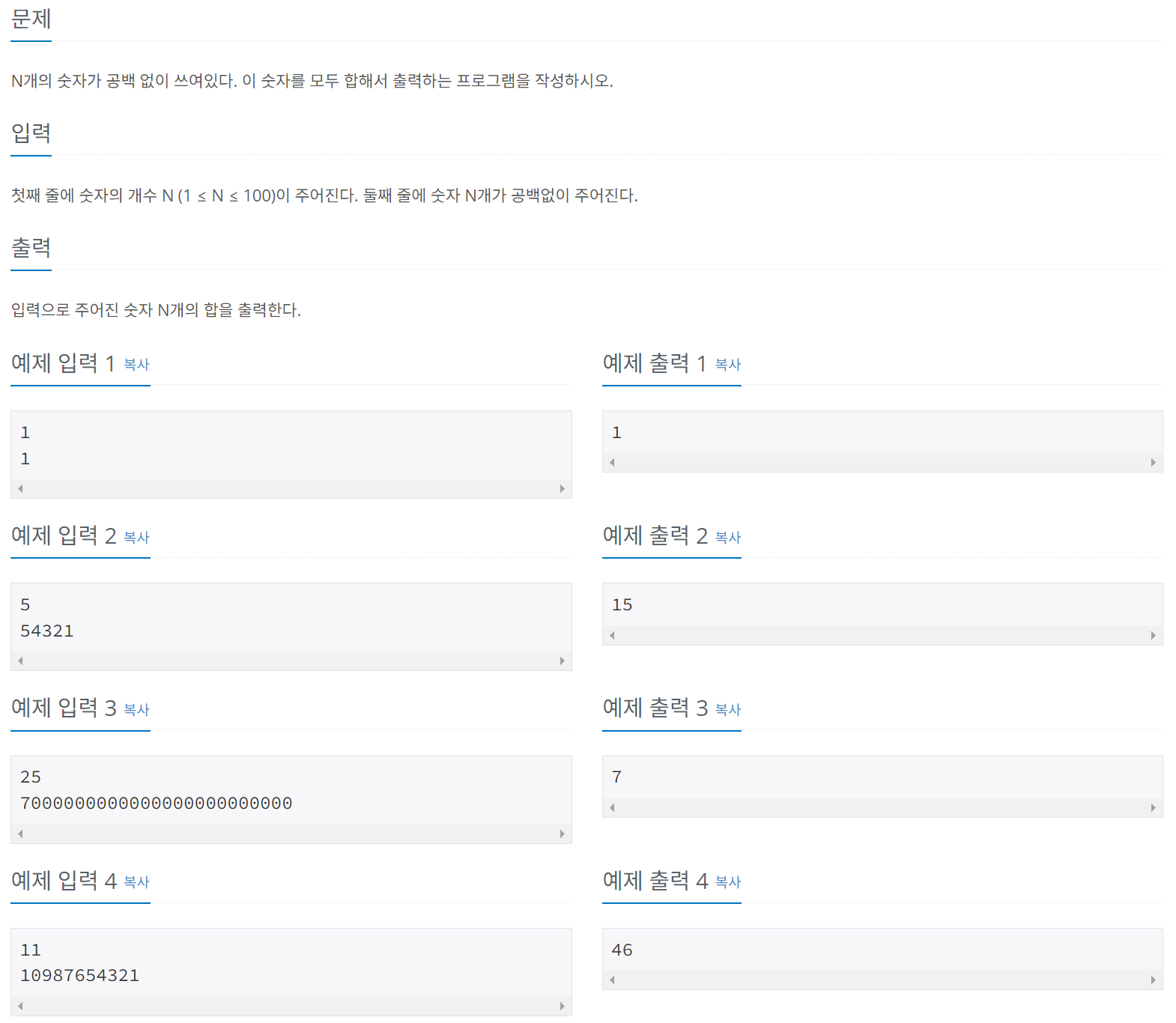
풀이

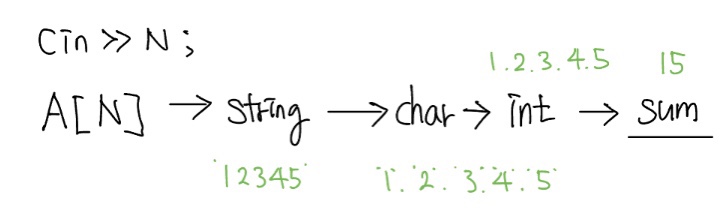
문자열을 숫자형으로 변경하려면 아스키코드를 이해해야 한다. 아스키코드에서 같은 의미의 문자와 숫자의 코드값 차이는 48이다. 예를 들어, 문자 ‘1’은 아스키코드 값이 49이므로, 문자 ‘1’을 숫자 1로 변환하려면 ‘1’ - 48 또는 ‘1’ - ‘0’과 같이 연산하면 된다.

# include <iostream>
using namespace std;

int main() {
	int N;
	string num;

	cin >> N >> num;

	int sum = 0;

	for (int i = 0; i < N; i++) {
		sum += num[i] - '0';
	}
	
	cout << sum;
}

C++ 에서의 형 변환
string형에서 숫자형(int, long, double, float)로 변환

#include <string> // 헤더파일 추가
string sNum = "1234";
string sNum_d = "1234.56";
int inum    = stoi(sNum);
long lnum   = stol(sNum);
double dnum = stod(sNum_d);
float fnum  = stof(sNum_d);

숫자형(int, long, double, float)에서 string형으로 변환

#include <string> // 헤더파일 추가
int inum = 1234;
long lnum = 1234;
double dnum = 1234.56;
float fnum = 1234.56;
string intToString    = to_string(inum);
string longToString   = to_string(lnum);
string doubleToString = to_string(dnum);
string floatToString  = to_string(fnum);

문제 002 평균 구하기

제한시간: 2초, 난이도: 브론즈1, 1546번

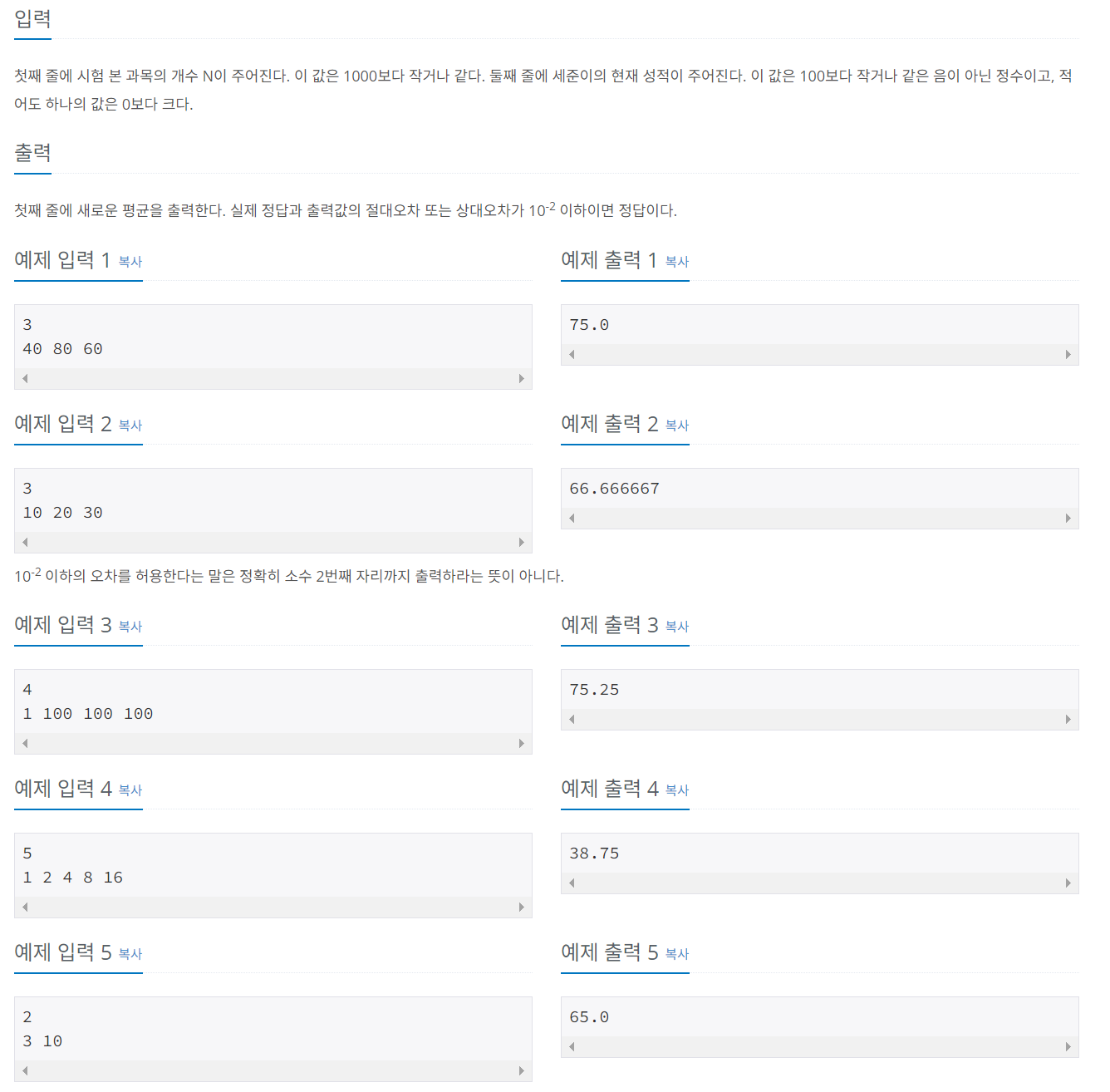
풀이

#include <iostream>
#include <vector>
using namespace std;

int main() {
	int N;
	cin >> N;

	vector<int>score;
	for (int i = 0; i < N; i++)
		cin >> score[i];

	double sum = 0;
	int score_Max = score[0];

	for (int i = 1; i < N; i++) {
		if (score_Max < score[i]) {
			score_Max = score[i];
		}
	}

	for (int i = 0; i < N; i++) {
		sum += score[i];
	}

	sum = sum *100 / score_Max /N;
	cout << sum;
}

위 코드를 실행해보니 다음과 같은 에러가 발생하였다.

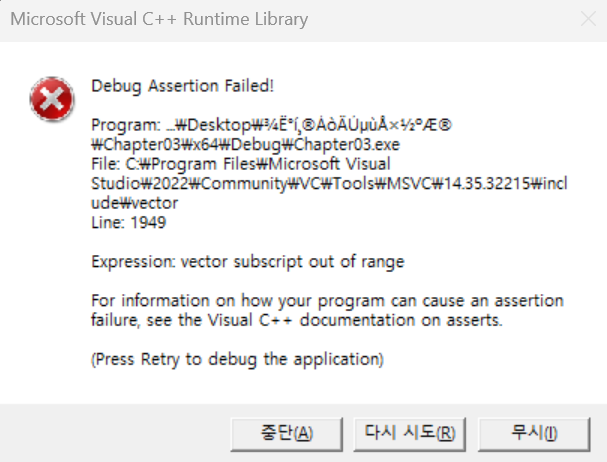
그래서 아래와 같이 “vector$<$int$>$score;”대신 N이 1000보다 작거나 같으므로 “int score[1000];”으로 선언해 주었다.

#include <iostream>
#include <vector>
using namespace std;

int main() {
	int N;
	cin >> N;

	int score[1000];
	for (int i = 0; i < N; i++)
		cin >> score[i];

	double sum = 0;
	int score_Max = score[0];

	for (int i = 1; i < N; i++) {
		if (score_Max < score[i]) {
			score_Max = score[i];
		}
	}

	for (int i = 0; i < N; i++) {
		sum += score[i];
	}

	sum = sum *100 / score_Max /N;
	cout << sum;
}

구간 합

구간 합은 합 배열을 이용하여 시간 복잡도를 더 줄이기 위해 사용하는 특수한 목적의 알고리즘이다.

구간 합의 핵심 이론

구간 합 알고리즘을 활용하려면 먼저 합 배열을 구해야 한다. 배열 A가 있을 때 합 배열 S는 다음과 같이 정의한다.

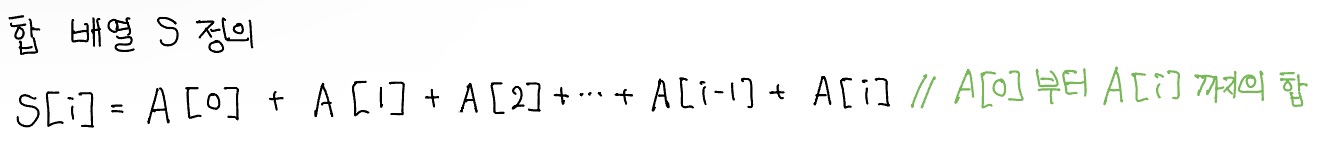
합 배열은 기존의 배열을 전처리한 배열이라 생각하면 된다. 이렇게 합 배열을 미리 구해 놓으면 기존 배열의 일정 범위의 합을 구하는 시간 보잡도가 O(N)에서 O(1)로 감소한다. 다음 그림을 보자.

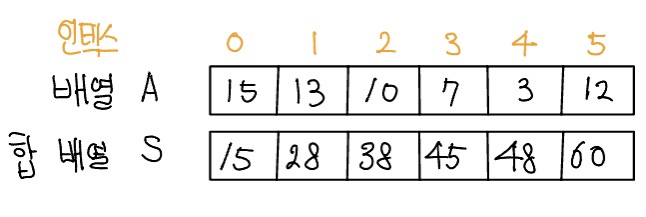
A[i]부터 A[j]까지의 배열 합을 합 배열 없이 구하는 경우, 최악의 경우는 i가 0이고 j가 N인 경우로 시간 복잡도는 O(N)이다. 이런 경우 위에서 알아본 합 배열을 사용하면 O(1) 안에 답을 구할 수 있다. 합 배열은 다음과 같은 간단한 공식으로 만들 수 있다.

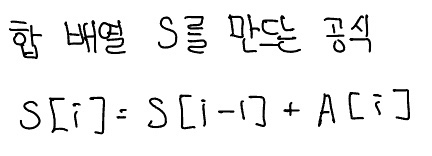
이렇게 합 배열을 이용하여 구간 합 역시 쉽게 구할 수 있다. i에서 j까지 구간 합을 구하는 공식은 다음과 같다.

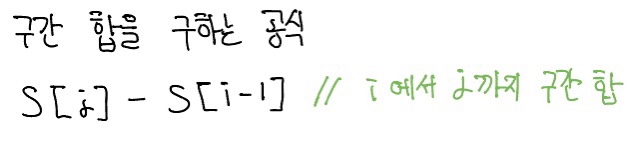
구간 합 공식이 어떻게 나온 것인지 다음 그림 통해 알아보자. 다음 그림은 배열 A의 A[2]부터 A[5]까지의 구간 합을 합 배열을 통해 구하는 과정을 보여 준다.

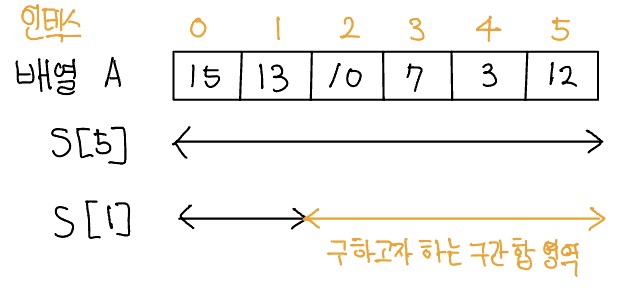
합 배열만 미리 구해 두면 구간 합은 한 번의 계산으로 구할 수 있는 것이다.

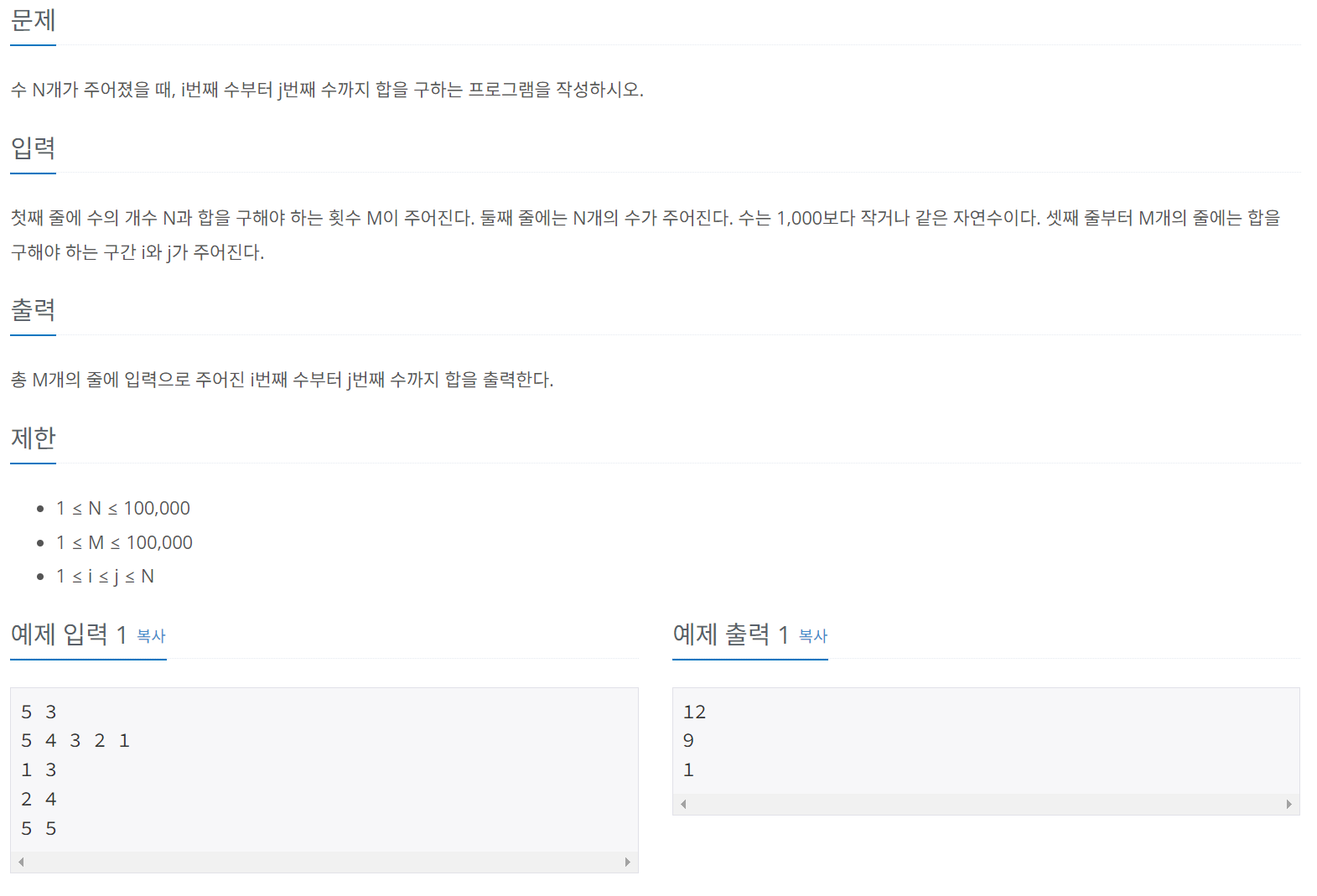
문제 003 구간 합 구하기 1

시간 제한: 0.5초 난이도: 실버3, 11659번

풀이

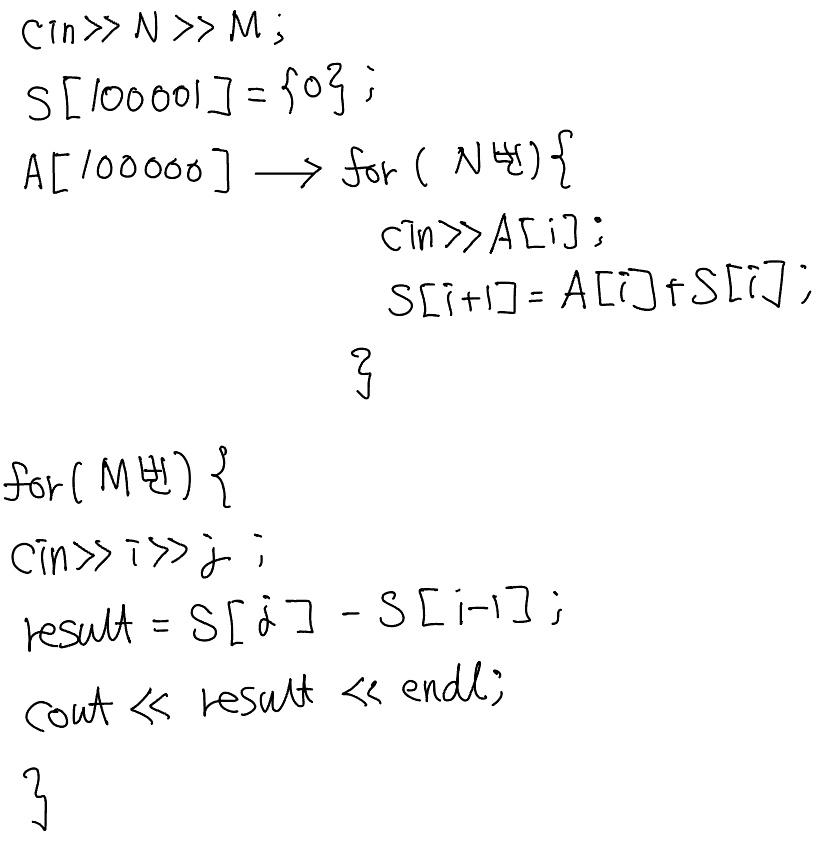
#include<iostream>
using namespace std;

int main() {
	int N, M;
	cin >> N >> M;

	int S[100001] = { 0 };
	int A[100000];
	for (int i = 0; i < N; i++) {
		cin >> A[i];
		S[i + 1] = temp + S[i];
	}

	for (int k = 0; k < M; k++) {
		int i, j;
		cin >> i >> j;
		int result = S[j] - S[i - 1];
		cout << result << endl;
	}
}

이 코드를 실행해 보았더니 시간 초과가 되었다. 그래서 책을 참조해서 코드를 수정해 주었다.

#include<iostream>
using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N, M;
	cin >> N >> M;

	int S[100001] = { };
	for (int i = 0; i < N; i++) {
		int temp;
		cin >> temp;
		S[i + 1] = temp + S[i];
	}

	for (int k = 0; k < M; k++) {
		int i, j;
		cin >> i >> j;
		cout << S[j] - S[i - 1] << "\n";
	}
}

위 코드를 통해서 다음과 같은 것을 알 수 있었다.

ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);

위 코드는 C++에서 시간 단축을 할 수 있게 해주는 코드이다. 이 코드는 자동으로 버퍼를 비워주는 것을 보장한다. 또한 endl보다는 \n이 처리시간이 더 빠르다는 것을 알 수 있었다.

문제 004 구간 합 구하기 2

시간 제한: 1초, 난이도: 실버1, 11660번

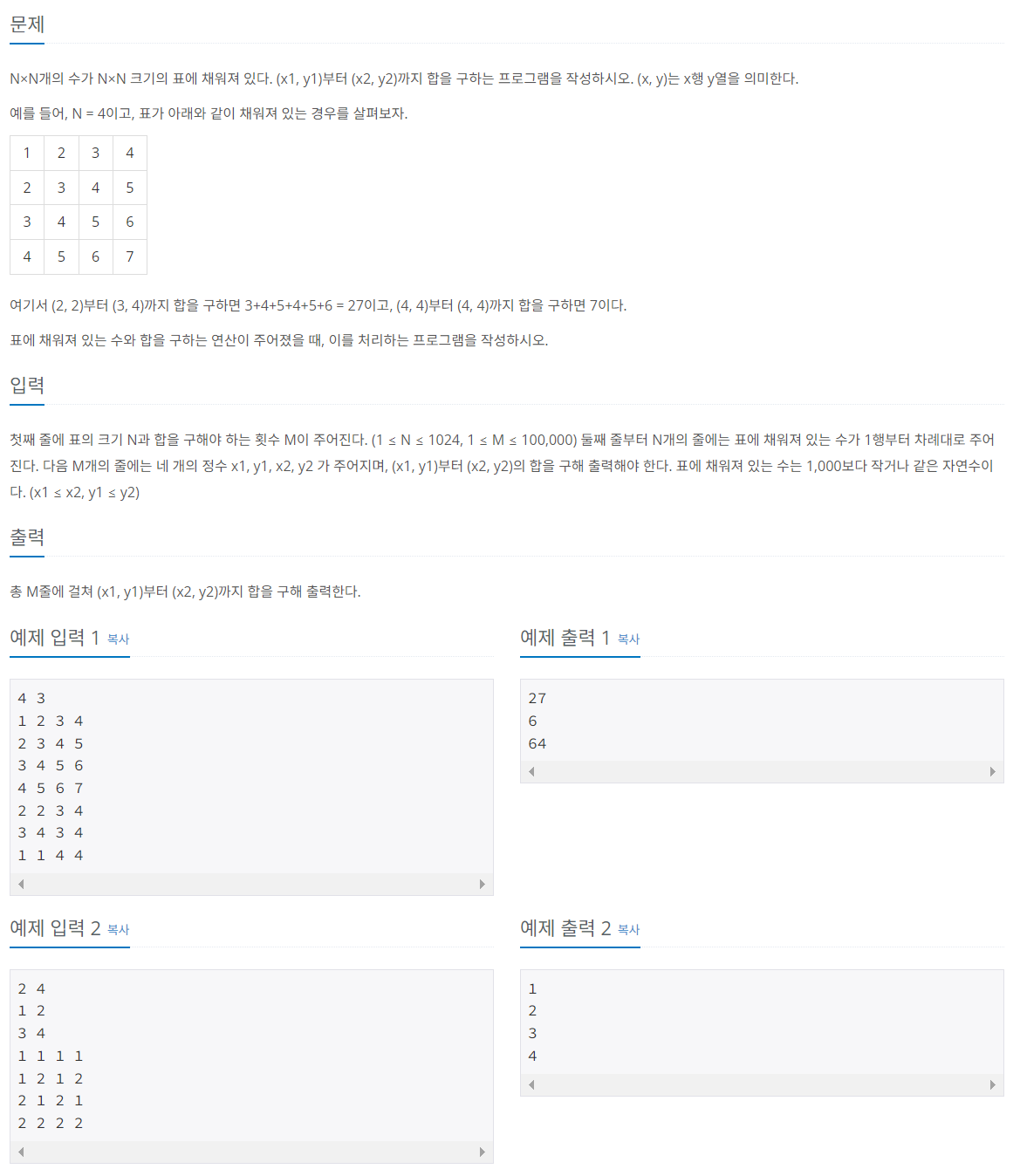
풀이

#include <iostream>
#include <vector>
using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N, M;
	cin >> N >> M;

	vector<vector<int>>A(N + 1, vector<int>(N + 1, 0));
	vector<vector<int>>S(N + 1, vector<int>(N + 1, 0));

	for (int i = 1; i < N + 1; i++) {
		for (int j = 1; j < N + 1; j++) {
			cin >> A[i][j];
			S[i][j] = S[i][j - 1] + S[i - 1][j] - S[i - 1][j - 1] + A[i][j];
		}
	}

	for (int i = 0; i < M; i++) {
		int X1, Y1, X2, Y2;
		cin >> X1 >> Y1 >> X2 >> Y2;
		cout << S[X2][Y2] - S[X2][Y1 - 1] - S[X1 - 1][Y2] + S[X1 - 1][Y1 - 1] << "\n";
	}

}

문제 005 나머지 합 구하기

시간 제한: 1초 난이도: 골드3, 10986번

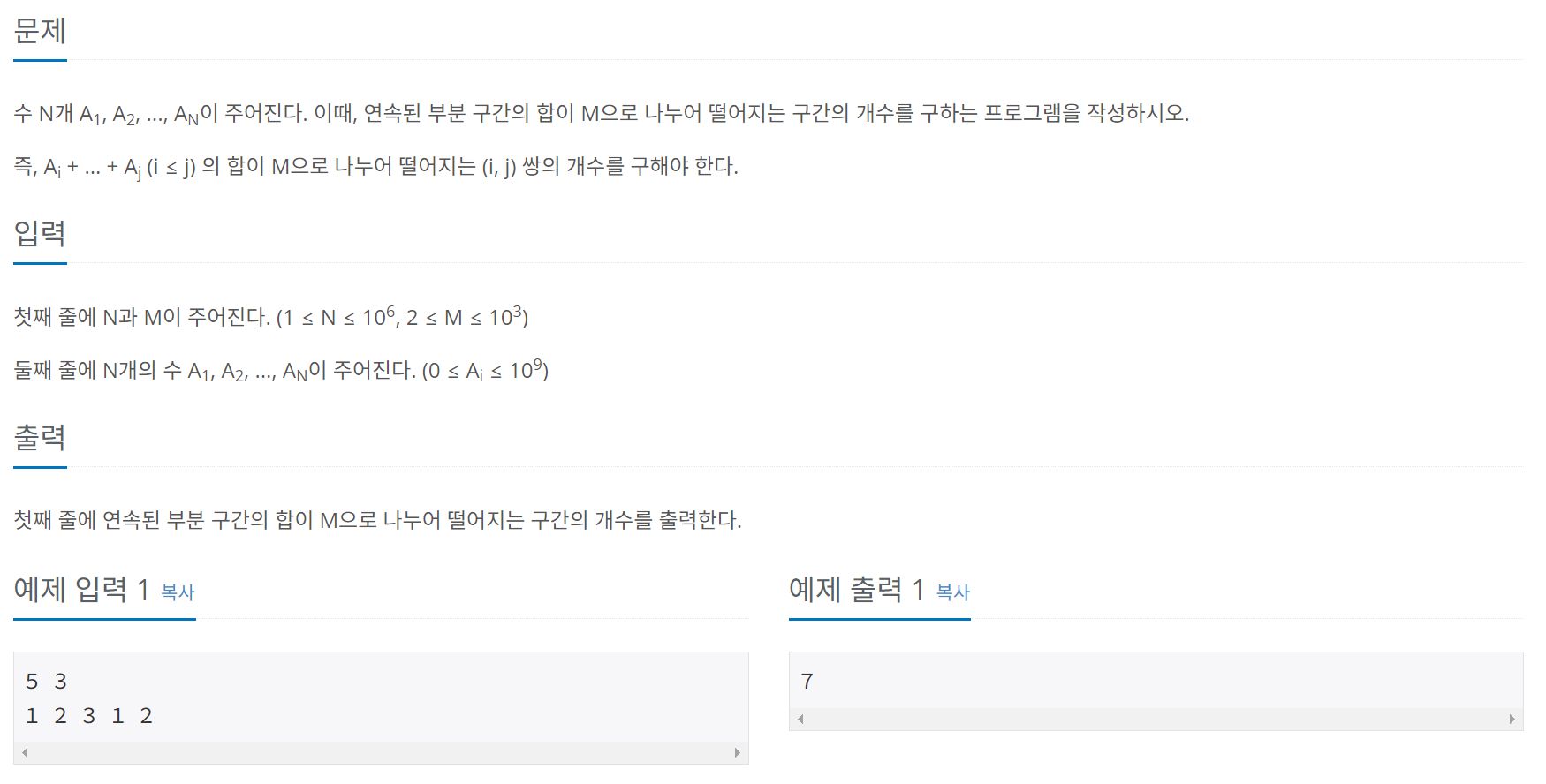
풀이

#include <iostream>
#include <vector>
using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N, M;
	cin >> N >> M;

	vector<int>A(N, 0);
	int a = 0;
	for (int i = 0; i < N; i++) {
		a = a + i + 1;
		cin >> A[i];
	}

	vector<int>S(a, 0);
	int k = 0;
	for (int i = 0; i < N; i++) {
		S[k] = A[i];
		k++;
		
		for (int j = i; j > 0; j--) {
			S[k] = S[k - 1] + A[j - 1];
			k++;
		}
	}

	int ans = 0;
	for (int i = 0; i < a; i++) {
		if (S[i] % M == 0)
			ans++;
	}

	cout << ans;
}

위와 같이 풀었는데 Visual Studio에서는 컴파일이 되었지만 백준에 제출을 할 때는 런타임에러(bad_alloc)가 발생하였다. 이는 int가 이 배열의 용량을 감당할 수 없어서 나온 것으로 보인다. long, long long으로도 해 봤는데 해결 되지가 않아 책을 참조 하였다.
이와 같은 나머지 합 문제 풀이의 핵심 아이디어는 다음과 같다.

$(A + B) \% C$ 는 $((A \% C) + (B \% C)) \% C$ 와 같다. 다시 말해 특정 구간 수들의 나머지 연산을 더해 나머지 연산을 한 값과 이 구간 합의 나머지 연산을 한 값은 동일하다.
구간 합 배열을 이용한 식 $\mathrm{S[j]} - \mathrm{S[i]}$ 는 원본 배열의 i+1부터 j까지의 구간 합이다.
$\mathrm{S[j]} \% \mathrm{M}$ 의 값과 $\mathrm{S[i]} \% \mathrm{M}$ 의 값이 같다면 $(\mathrm{S[j]} - \mathrm{S[i]}) \% M$ 은 $0$ 이다. 즉, 구간 합 배열의 원소를 M으로 나눈 나머지로 업데이트하고 S[j]와 S[i]가 같은, (i, j)쌍을 찾으면 원본 배열에서 i + 1부터 j까지의 구간 합이 M으로 나누어떨어진다는 것을 알 수 있다.

풀이

#include <iostream>
#include <vector>
using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N, M;
	cin >> N >> M;

	vector<long>S(N + 1, 0);
	vector<long>C(M, 0);
	

	for (int i = 1; i <= N; i++) {
		int temp;
		cin >> temp;
		S[i] = temp + S[i - 1];
	}

	long ans = 0;
	for (int i = 1; i <= N; i++) {
		int R = S[i] % M;
		if (R == 0)
			ans++;
		C[R]++;
	}

	for (int i = 0; i < M; i++)
		ans = ans + C[i] * (C[i] - 1) / 2;
	
	cout << ans;
}

투 포인터

투 포인터는 2개의 포인터로 알고리즘의 시간 복잡도를 최적화한다.

문제 006 연속된 자연수의 합 구하기

시간 제한: 2초 난이도: 실버4, 2018번

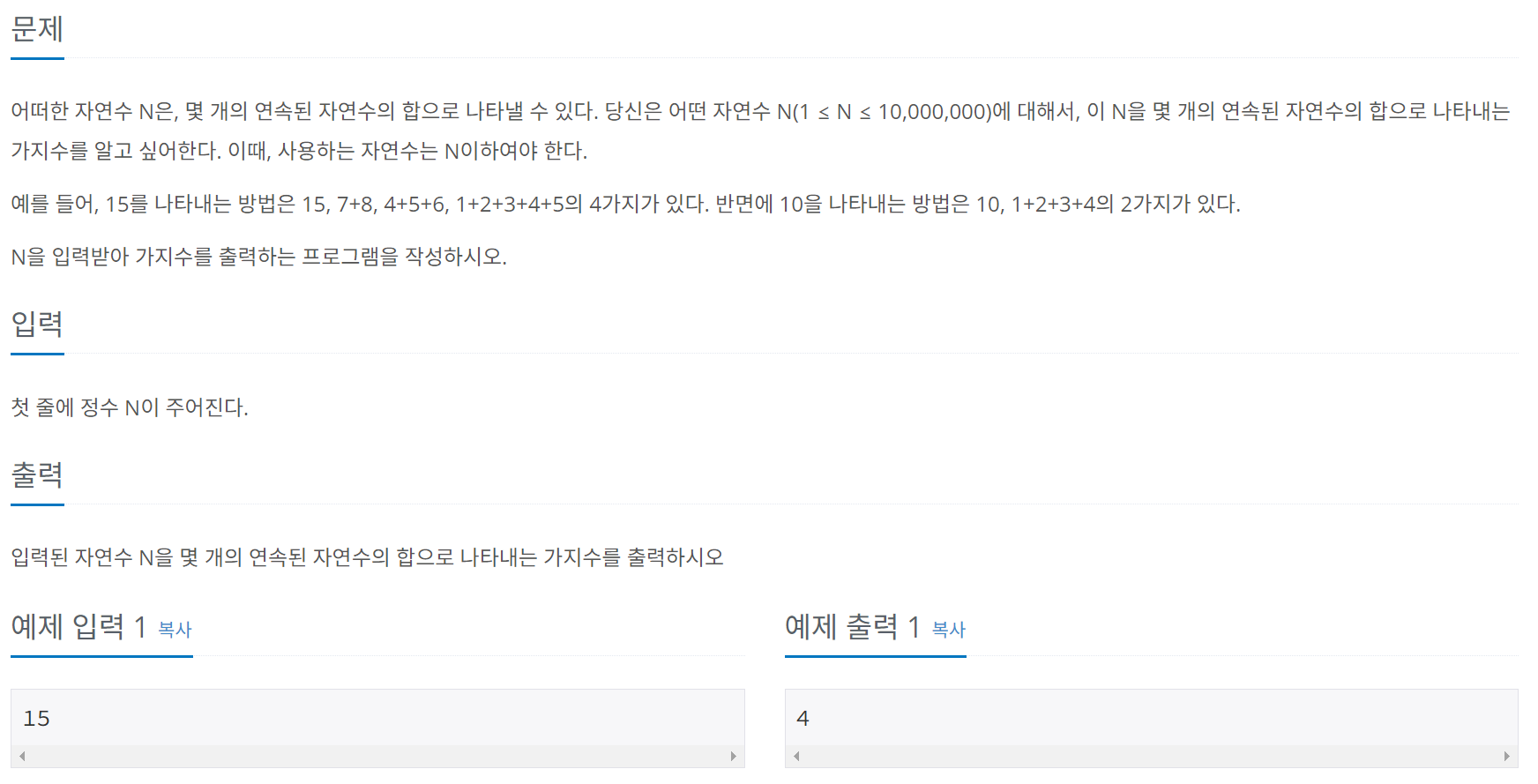
풀이

#include <iostream>
#include <vector>
using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N;
	cin >> N;

	vector<int>A(N, 0);
	for (int i = 0; i < N; i++) {
		A[i] = i + 1;
	}

	int count = 0;
	for (int i = 0; i < N; i++) {
		int sum = 0;
		for (int j = i; j < N; j++) {
			sum = sum + A[j];
			if (sum == N) {
				count++;
				break;
			}
		}
	}
	cout << count;
}

위와 같이 풀었는데 메모리 초과가 나왔다. 이 문제는 시간 복잡도 분석으로 알고리즘의 범위부터 줄여야 한다. 우선 문제에 주어진 시간 제한은 2초이고 N의 최대값은 10,000,000으로 매우 크게 잡혀 있다. 이런 상황에서는 O(n)의 시간 복잡도 알고리즘을 사용해야 한다. 그래서 다음과 같이 풀었다.

#include <iostream>
#include <vector>
using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N;
	cin >> N;

	int count = 1;
	int start_index = 1;
	int end_index = 1;
	int sum = 1;

	while (end_index != N ) {
		if (sum == N) {
			count++;
			end_index++;
			sum = sum + end_index;
		}
		else if (sum < N) {
			end_index++;
			sum = sum + end_index;
		}
		else if (sum > N) {
			sum = sum - start_index;
			start_index++;
		}
	}

	cout << count;
}

문제 007 주몽의 명령

시간 제한: 2초 난이도: 실버4, 1940번

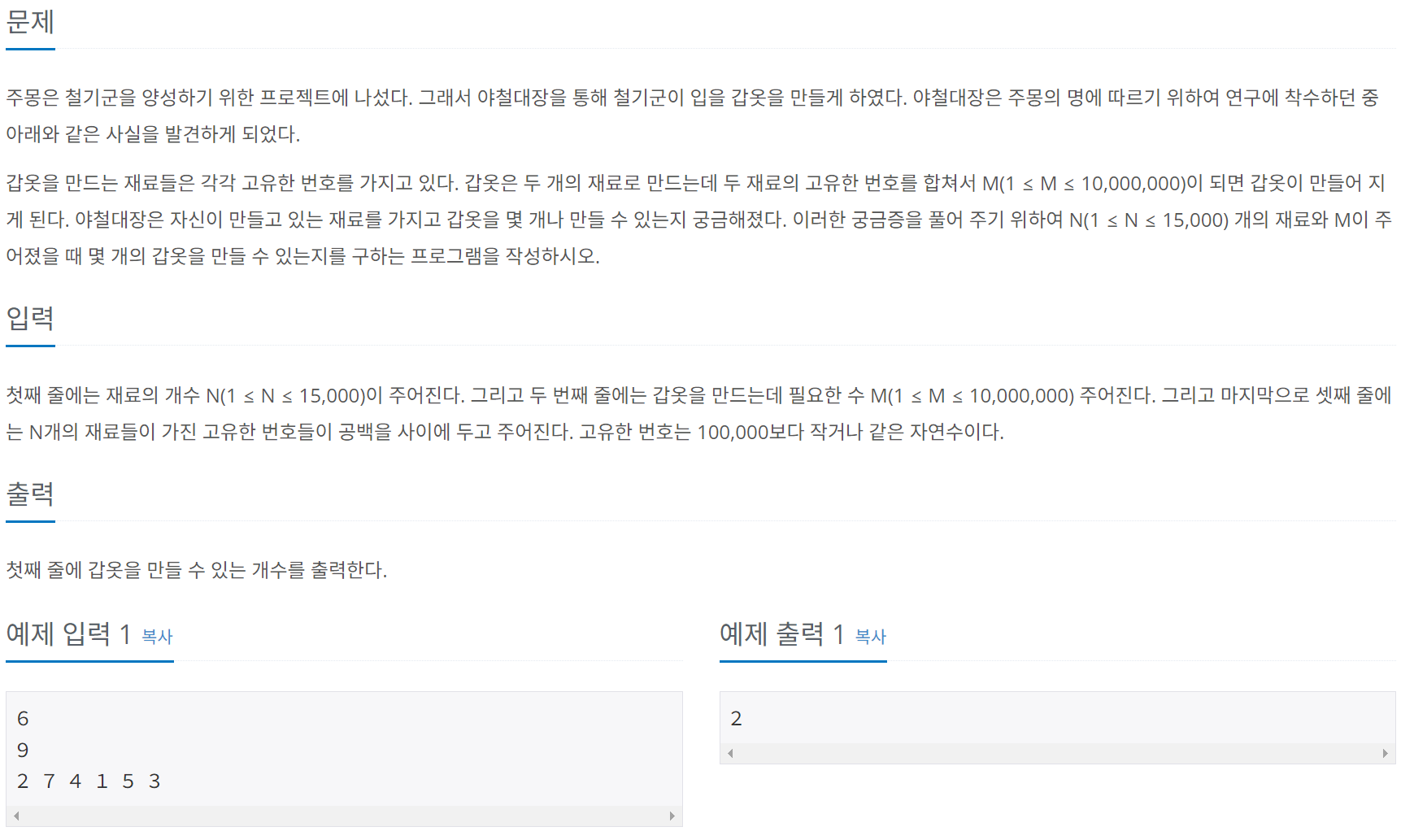
풀이

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N, M;
	cin >> N >> M;

	vector<int>A(N, 0);
	for (int i = 0; i < N; i++) {
		cin >> A[i];
	}
	sort(A.begin(), A.end());

	int start = 0;
	int end = 1;
	int count = 0;

	while (end > start) {
		int sum = A[start] + A[end];
		if (sum == M) {
			count++;
			start++;
			end--;
		}
		else if (sum < M) {
			if (end == N - 1)
				start++;
			else
				end++;
		}
		else if (sum > M) {
			start++;
			end--;
		}
	}

	cout << count;
}

위와 같이 풀었는데 “틀렸습니다”가 나왔다. 위 경우 다음과 같은 경우 올바르게 출력되지 않는다.

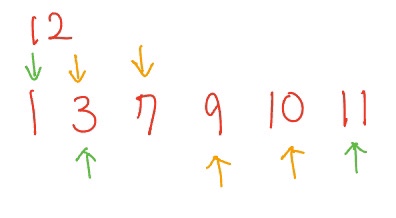
따라서 end를 뒤부터 시작해서 다음처럼 수정하였다.

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N, M;
	cin >> N >> M;

	vector<int>A(N, 0);
	for (int i = 0; i < N; i++) {
		cin >> A[i];
	}
	sort(A.begin(), A.end());

	int start = 0;
	int end = N - 1;
	int count = 0;

	while (end > start) {
		int sum = A[start] + A[end];
		if (sum == M) {
			count++;
			start++;
			end--;
		}
		else if (sum < M) {
				start++;
		}
		else if (sum > M) {
			end--;
		}
	}

	cout << count;
}

문제 008 ‘좋은 수’ 구하기

시간 제한: 2초 난이도: 골드4, 1253번

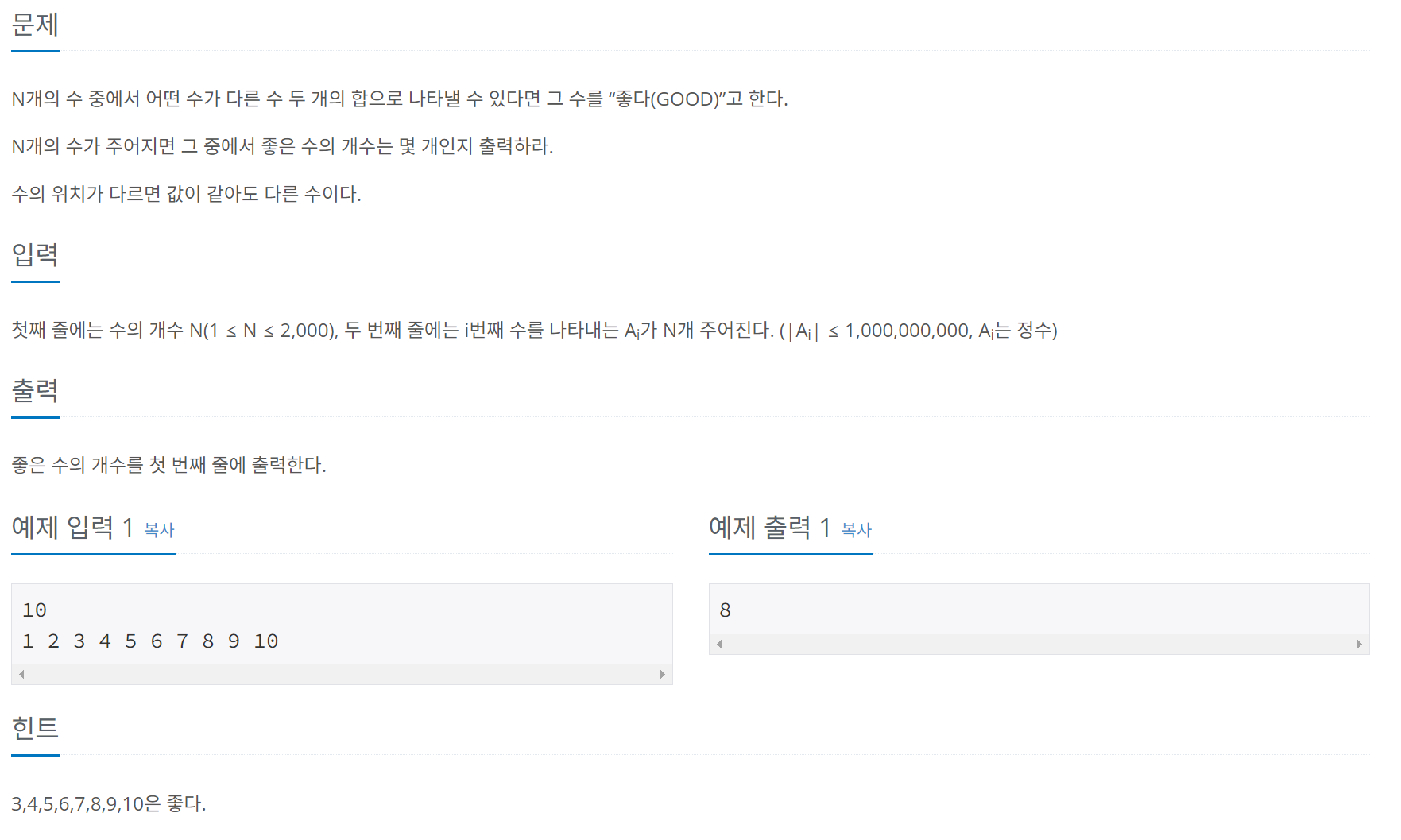
풀이

위 풀이에서는 다음과 같은 상황에서 올바른 값이 출력되지 않는다.

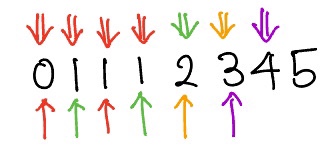
그래서 다음과 같이 수정하였다.

하지만 위 풀이에서도 다음과 같은 상황에서 올바른 값이 출력되지 않는다.

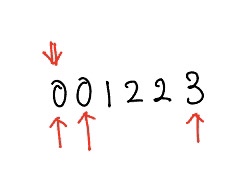
따라서 다음과 같이 수정하였다.

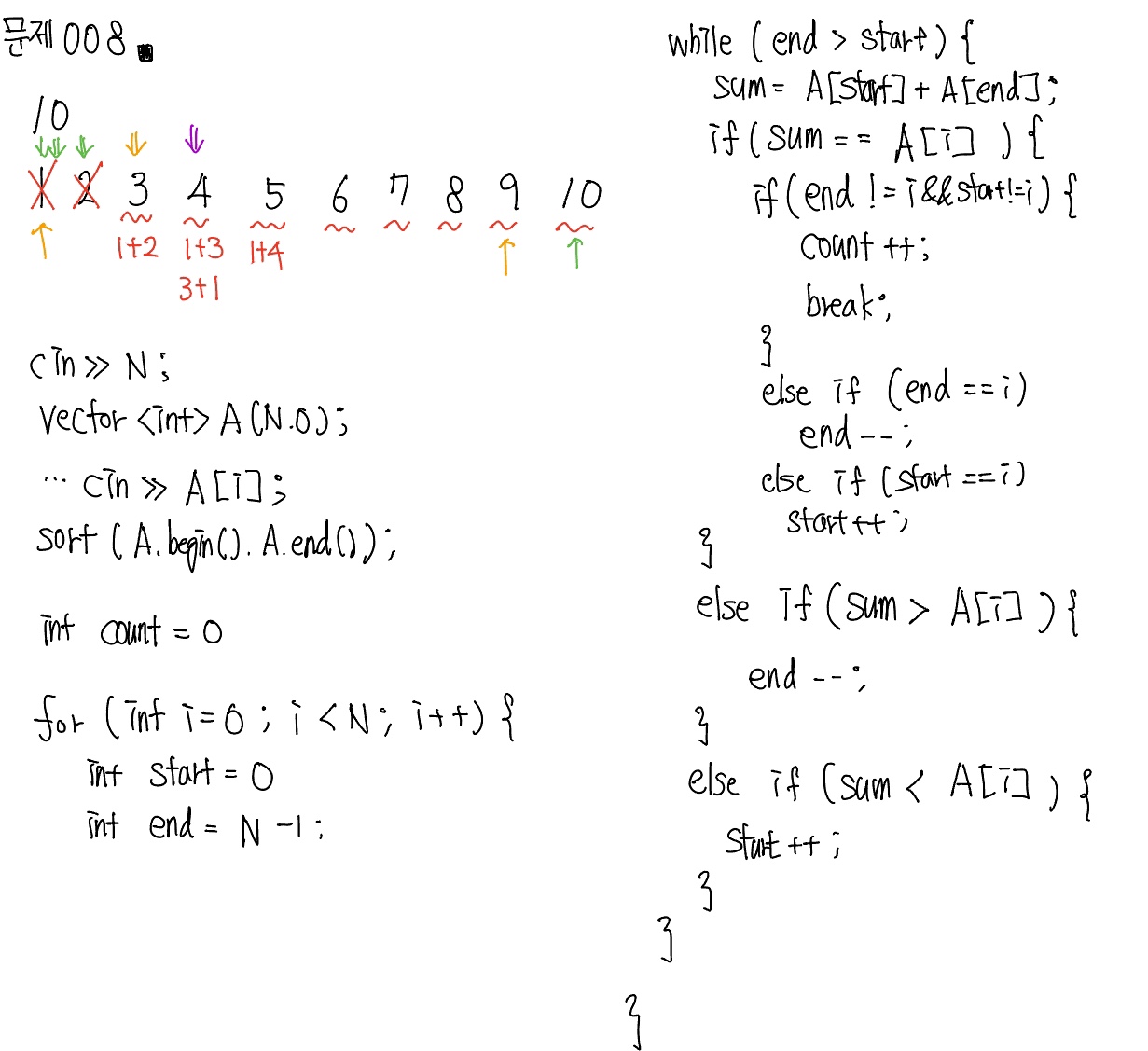
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N;
	cin >> N;

	vector<int>A(N, 0);
	for (int i = 0; i < N; i++) {
		cin >> A[i];
	}
	sort(A.begin(), A.end());

	int count = 0;

	for (int i = 0; i < N; i++) {
		int start = 0;
		int end = N - 1;

		while (end > start) {
			int sum = A[start] + A[end];
			if (sum == A[i]) {
				if (end != i && start != i) {
					count++;
					break;
				}
				else if (end == i)
					end--;
				else if (start == i)
					start++;
			}
			else if (sum < A[i]) {
				start++;
			}
			else if (sum > A[i]) {
				end--;
			}
		}

	}
	cout << count;
}

슬라이딩 윈도우

슬라이딩 윈도우 알고리즘은 2개의 포인터로 범위를 지전한 다음, 범위(window)를 유지한 채로 이동(sliding)하며 문제를 해결한다. 투 포인터 알고리즘과 매우 비슷하고 원리도 간단하다.

문제 009 DNA 비밀번호

시간 제한: 2초 난이도: 실버4, 12891번

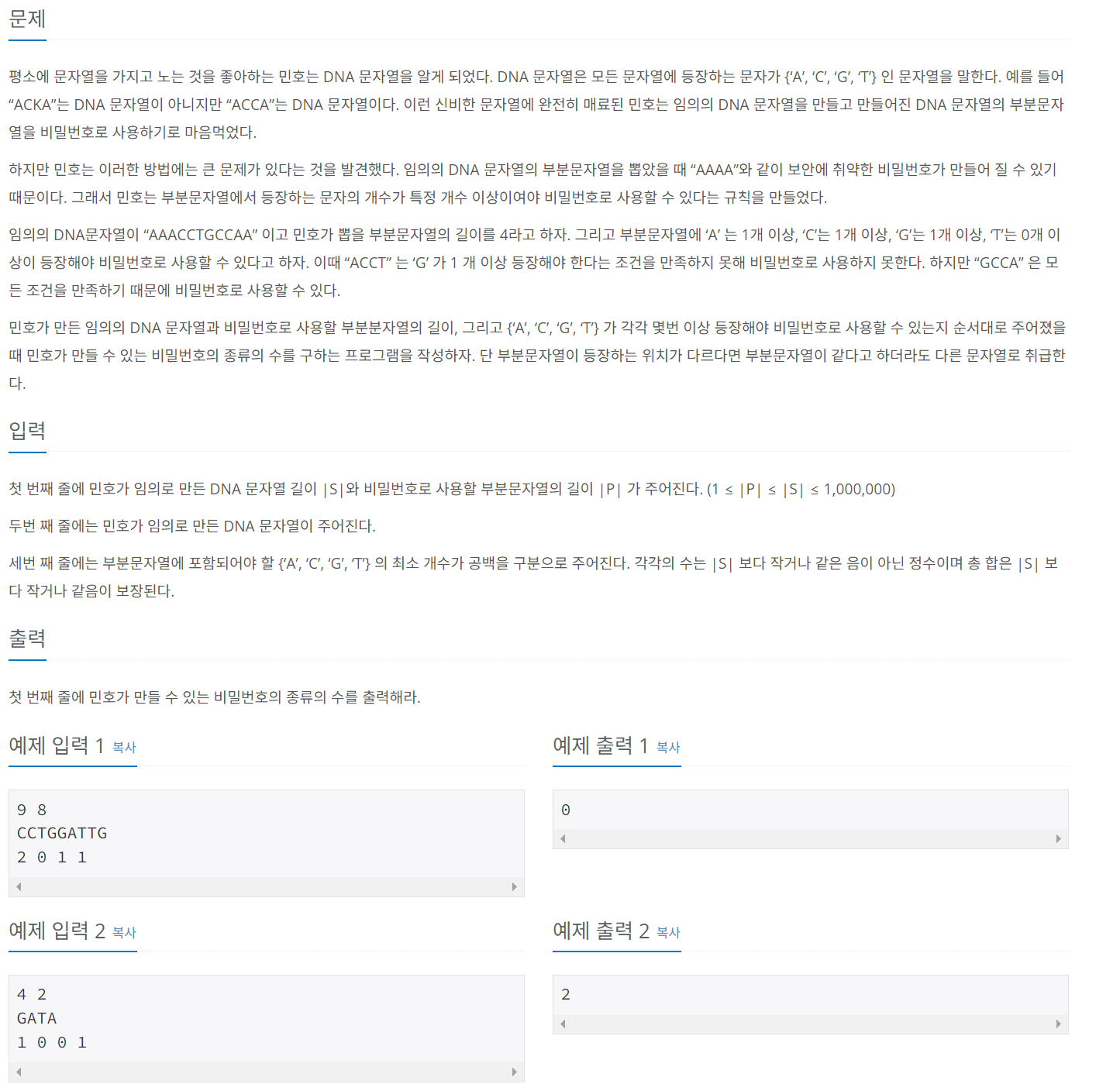
풀이

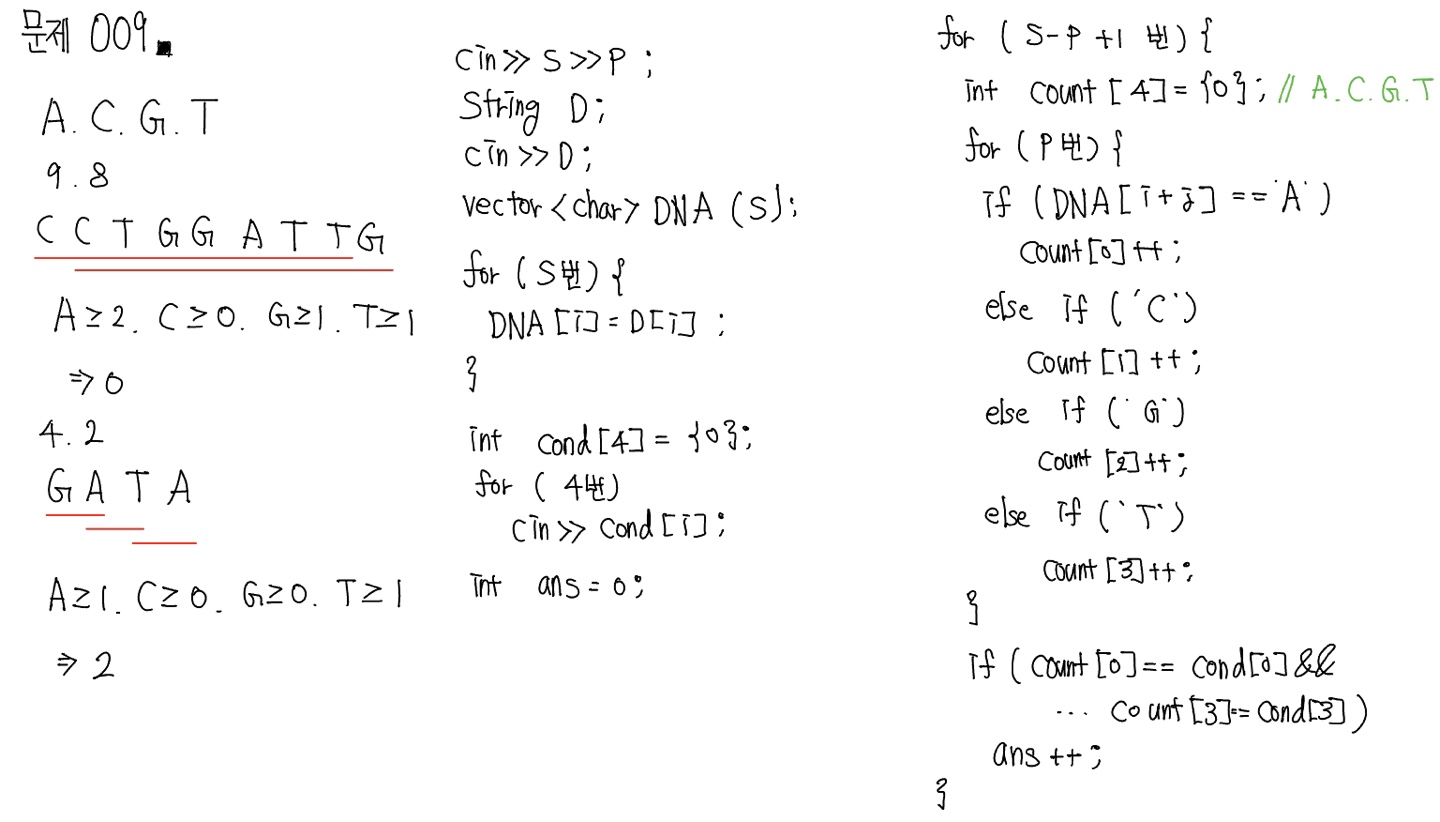
#include <iostream>
#include <vector>
#include <string>
using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int S, P;
	cin >> S >> P;
	string D;
	cin >> D;

	vector<char>DNA(S);
	for (int i = 0; i < S; i++) {
		DNA[i] = D[i];
	}

	int cond[4] = { 0 };
	for (int i = 0; i < 4; i++) {
		cin >> cond[i];
	}

	int ans = 0;

	for (int i = 0; i < S - P + 1; i++) {
		int count[4] = { 0 };
		for (int j = 0; j < P; j++) {
			if (DNA[i + j] == 'A')
				count[0]++;
			else if (DNA[i + j] == 'C')
				count[1]++;
			else if (DNA[i + j] == 'G')
				count[2]++;
			else if (DNA[i + j] == 'T')
				count[3]++;
		}
		if (count[0] == cond[0] && count[1] == cond[1] && count[2] == cond[2] && count[3] == cond[3])
			ans++;
	}

	cout << ans;
}

위와 같이 풀었는데 시간초과가 발생하였다. 이 문제에서 P와 S의 길이가 1,000,000으로 매우 크기 때문에 O(n)의 시간 복잡도 알고리즘으로 문제를 해결해야 한다. 이때 부분 문자열의 길이가 P이므로 슬라이딩 윈도우의 개념을 이용하면 문제를 쉽게 해결할 수 있다. 다음 그림을 보자.

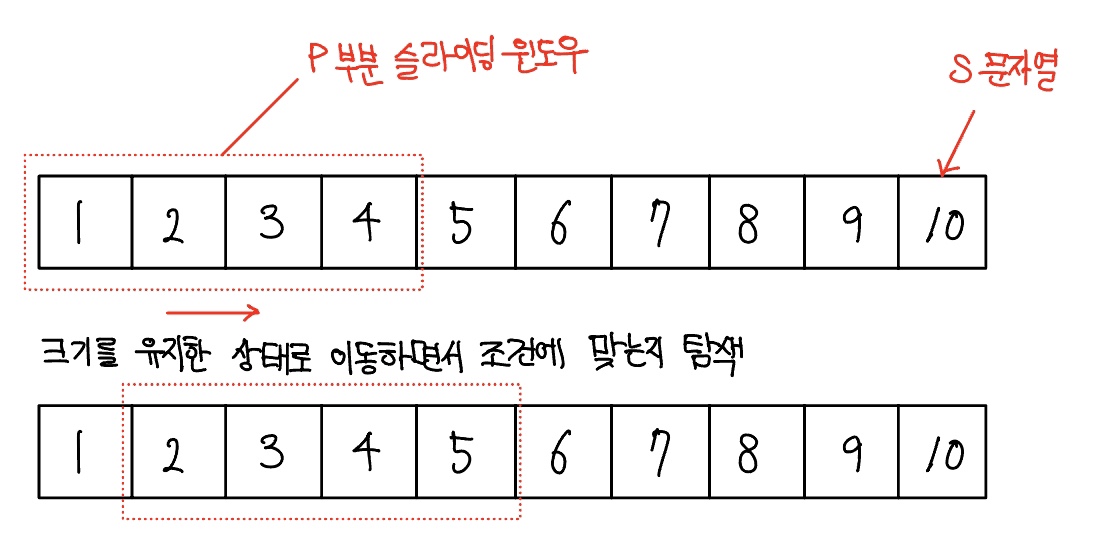
위 그림에서 길이가 P인 윈도우를 지정하여 배열 S의 시작점에 놓는다. 그런 다음 윈도우를 오른쪽으로 밀면서 윈도우에 잡힌 값들이 조건에 맞는지 탐색한다. 배열 S의 길이만큼만 탐색을 진행하면 되므로 O(n)의 시간 복잡도로 문제를 해결할 수 있다. 따라서 다음과 같이 수정하였다.

#include <iostream>
#include <vector>
#include <string>
using namespace std;

int cont[4] = { 0 };
int cond[4] = { 0 };
int check = 0;
void Add(char C);
void Remove(char C);

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int S, P;
	cin >> S >> P;
	string D;
	cin >> D;


	for (int i = 0; i < 4; i++) {
		cin >> cond[i];
		if (cond[i] == 0)
			check++;
	}

	int ans = 0;

	for (int i = 0; i < P; i++) {
		Add(D[i]);
	}
	if (check == 4)
		ans++;

	for (int i = P; i < S; i++) {
		int j = i - P;
		Add(D[i]);
		Remove(D[j]);
		if (check == 4)
			ans++;
	}

	cout << ans;
}

void Add(char c) {
	switch (c) {
	case 'A':
		cont[0]++;
		if (cont[0] == cond[0])
			check++;
		break;
	case 'C':
		cont[1]++;
		if (cont[1] == cond[1])
			check++;
		break;
	case 'G':
		cont[2]++;
		if (cont[2] == cond[2])
			check++;
		break;
	case 'T':
		cont[3]++;
		if (cont[3] == cond[3])
			check++;
		break;
	}
}

void Remove(char c) {
	switch (c) {
	case 'A':
		if (cont[0] == cond[0])
			check--;
		cont[0]--;
		break;
	case 'C':
		if (cont[1] == cond[1])
			check--;
		cont[1]--;
		break;
	case 'G':
		if (cont[2] == cond[2])
			check--;
		cont[2]--;
		break;
	case 'T':
		if (cont[3] == cond[3])
			check--;
		cont[3]--;
		break;
	}
}

문제 010 최소값 찾기 1

시간 제한: 2.4초 난이도: 플래티넘5, 11003번

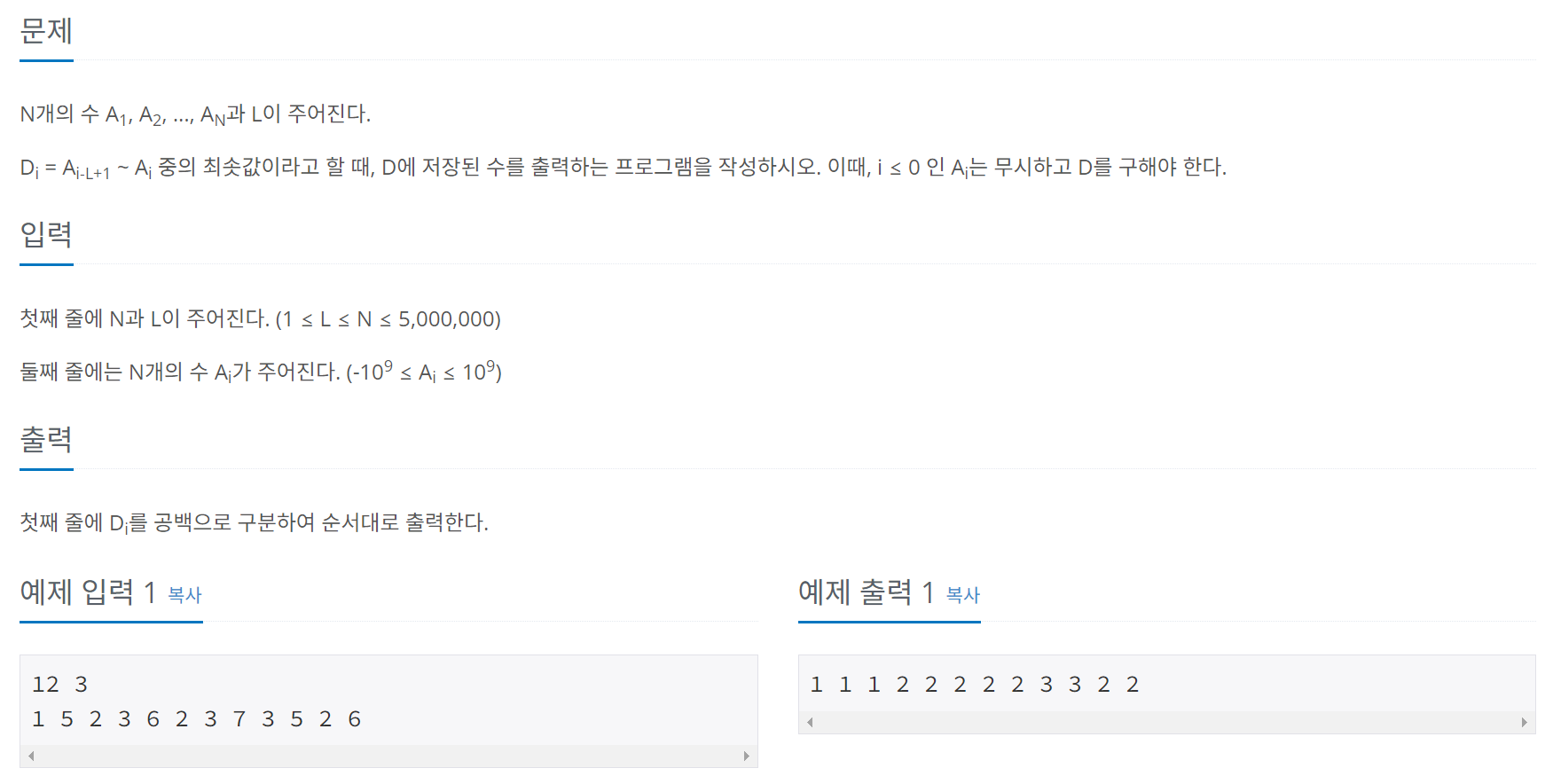
일반적으로 정렬은 O(nlogn)의 시간 복잡도를 가지므로 최대 범위가 5000000인 이 문제에서는 정렬을 사용할 수 없고, O(n)의 시간 복잡도로 해결해야 한다. 슬라이딩 윈도우를 덱(deque)으로 구현하면 정렬 효과를 볼 수 있다. 덱의 구조는 다음과 같다.

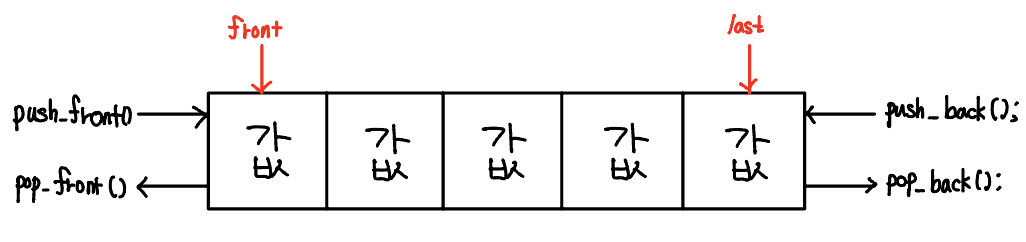
덱은 양 끝에서 데이터를 삽입하거나 삭제할 수 있는 자료구조라고 알 수 있다. 왼쪽에서는 push_front(), pop_front() 함수가 삽입, 삭제 역할을 하고, 오른쪽에서는 push_back(), pop_back() 함수가 삽입, 삭제 역할을 한다.

풀이

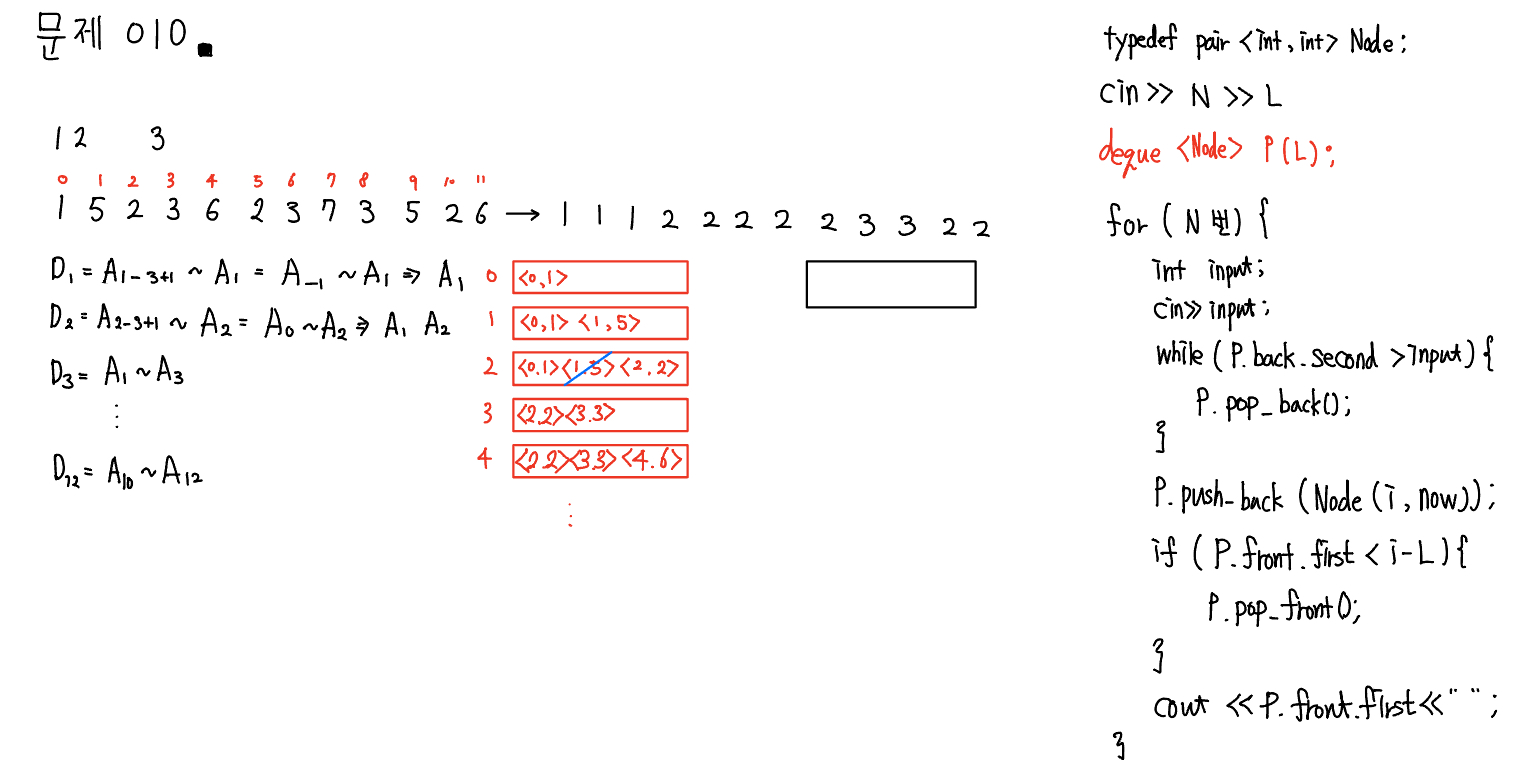
#include <iostream>
#include <deque>
using namespace std;
typedef pair<int, int>Node;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N, L;
	cin >> N >> L;
	deque<Node>P;

	for (int i = 0; i < N; i++) {
		int input;
		cin >> input;

		while (P.size() && P.back().second > input) {
			P.pop_back();
		}
		
		P.push_back(Node(i, input));

		if (P.front().first <= i - L) {
			P.pop_front();
		}
		cout << P.front().second << " ";
	}
}

스택과 큐

스택과 큐의 핵심 이론

스택
스택(stack)은 삽입과 삭제 연산이 후입선출(LIFO: Last-in First-out)로 이루어지는 자료구조이다. 후입선출은 삽입과 삭제가 한 쪽에서만 일어나는 특징이 있다. 다음 그림을 보자.

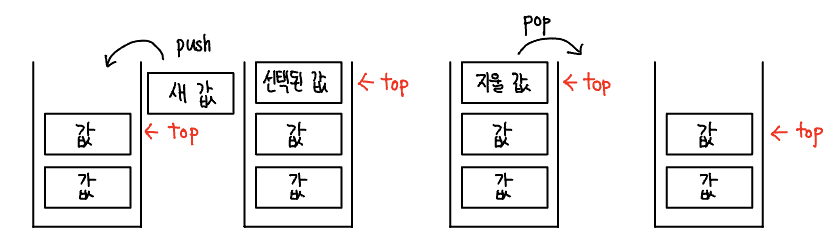
위 그림에서 새 값이 스택에 들어가면 top이 새 값을 가리킨다. 스택에서 값을 빼낼 때 pop은 top이 가리키는 값을 스택에서 빼게 되어 있으므로 결과적으로는 가장 마지막에 넣었던 값이 나오게 된다.

큐
큐(queue)는 삽입과 삭제 연산이 선입선출(FIFO: First-in First-out)로 이루어지는 자료구조이다. 스택과 다르게 먼저 들어온 데이터가 먼저 나간다. 그래서 삽입과 삭제가 양방향에서 이뤄진다.

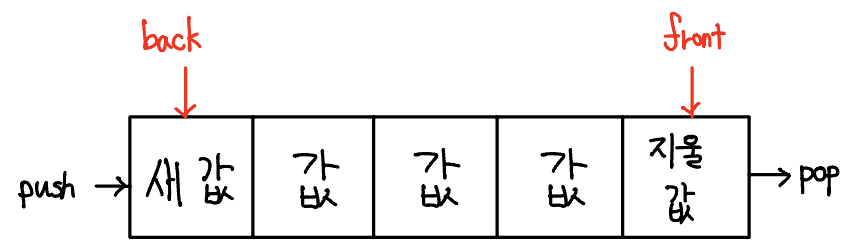
위 그림에서 새 값 추가는 큐의 back에서 이뤄지고, 삭제는 큐의 front에서 이뤄진다.

문제 011 스택으로 수열 만들기

시간 제한: 2초 난이도: 실버3, 1874번

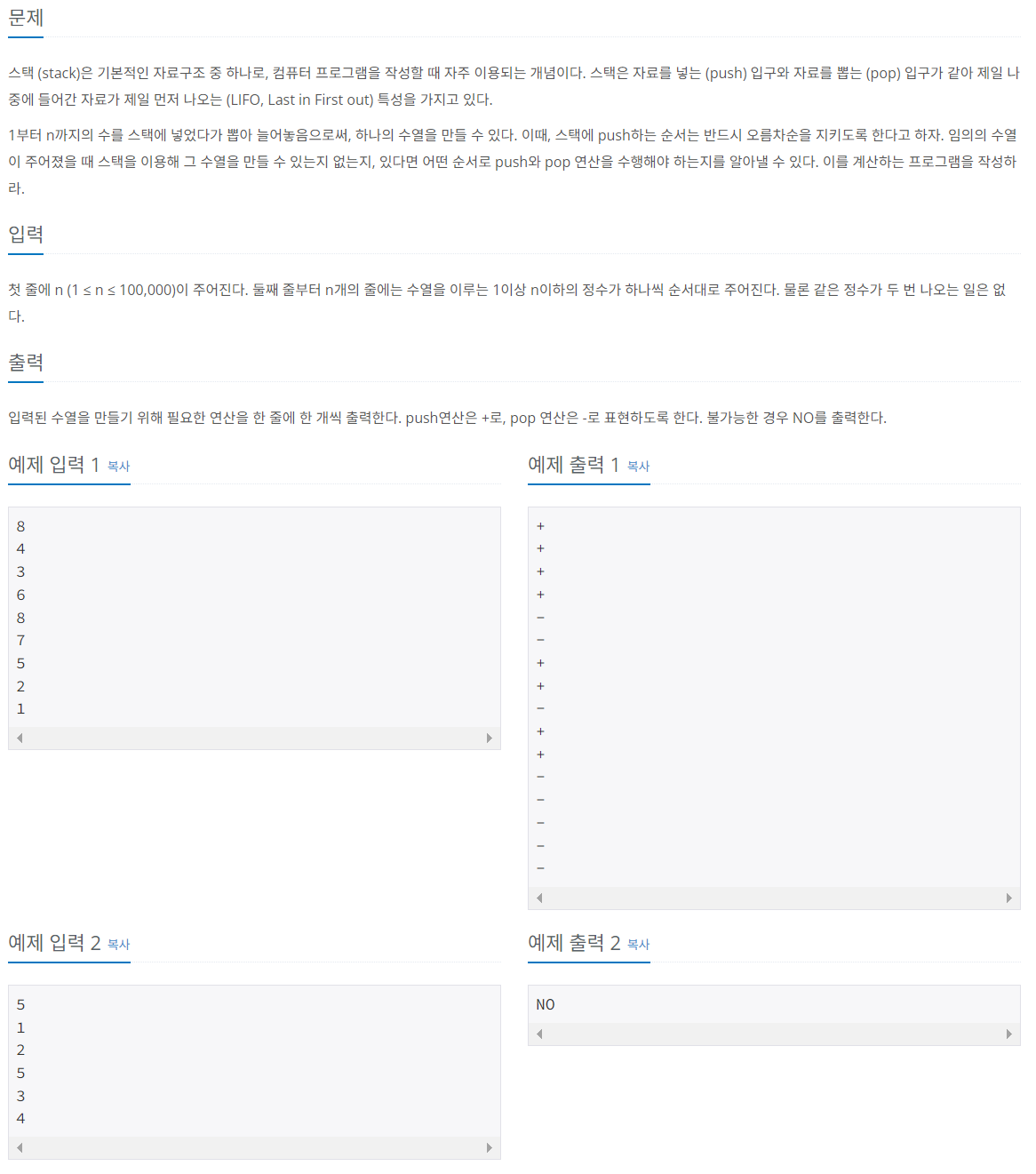
풀이

#include <iostream>
#include <vector>
#include <stack>
using namespace std;

int main() {
    ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

    int n;
	cin >> n;

	vector<int>A(n, 0);
	vector<char>result;

	for (int i = 0; i < n; i++) {
		cin >> A[i];
	}

	stack<int>myStack;
	int k = 1;
	bool r = true;

	for (int i = 0; i < n; i++) {
		int temp = A[i];
		if (k <= temp) {
			while (k <= temp) {
				myStack.push(k);
				k++;
				result.push_back('+');
			}
			myStack.pop();
			result.push_back('-');
		}
		else {
			int pop = myStack.top();
			myStack.pop();
			if (temp < pop) {
				cout << "NO";
				r = false;
				break;
			}
			else {
				result.push_back('-');
			}
		}
	}
	if (r) {
		for (int i = 0; i < result.size(); i++) {
			cout << result[i] << '\n';
		}
	}
}

문제 012 오큰수 구하기

시간 제한: 1초 난이도: 골드4, 17298번

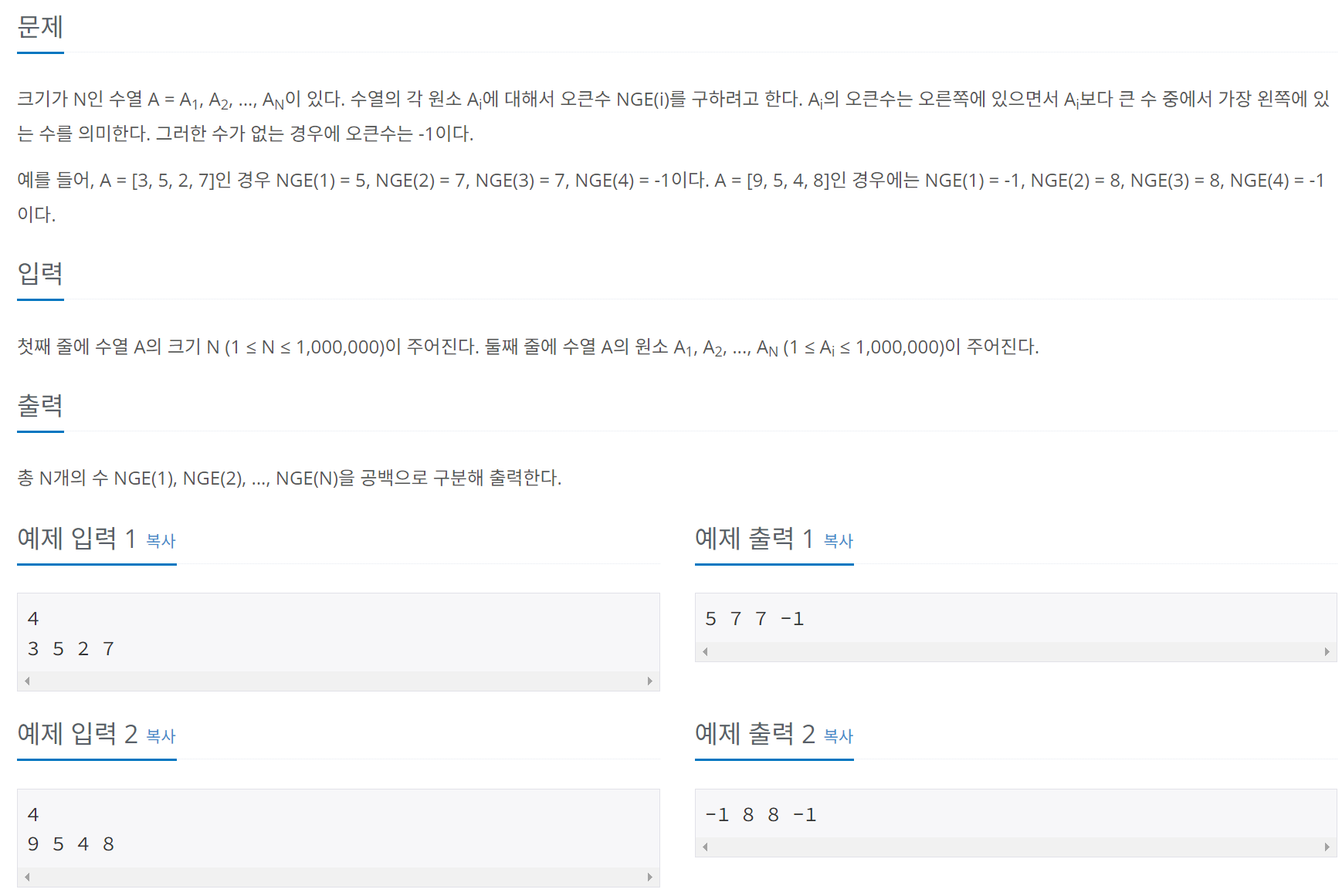
풀이

#include <iostream>
#include <queue>
using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N;
	cin >> N;
	queue<int>myQueue;

	for (int i = 0; i < N; i++) {
		int tmp;
		cin >> tmp;
		myQueue.push(tmp);
	}

	for (int i = 0; i < N; i++) {
		int tmp = myQueue.front();
		myQueue.pop();
		queue<int>tempQueue = myQueue;

		while (tempQueue.size() && tempQueue.front() < tmp) {
			tempQueue.pop();
		}

		if (tempQueue.empty()) {
			cout << "-1 ";
		}
		else
			cout << tempQueue.front() << ' ';
	}

}

위와 같이 큐를 사용해 풀었는데 시간초과가 발생 하였다. 책을 보고 스택을 이용해서 다시 풀어보았다.

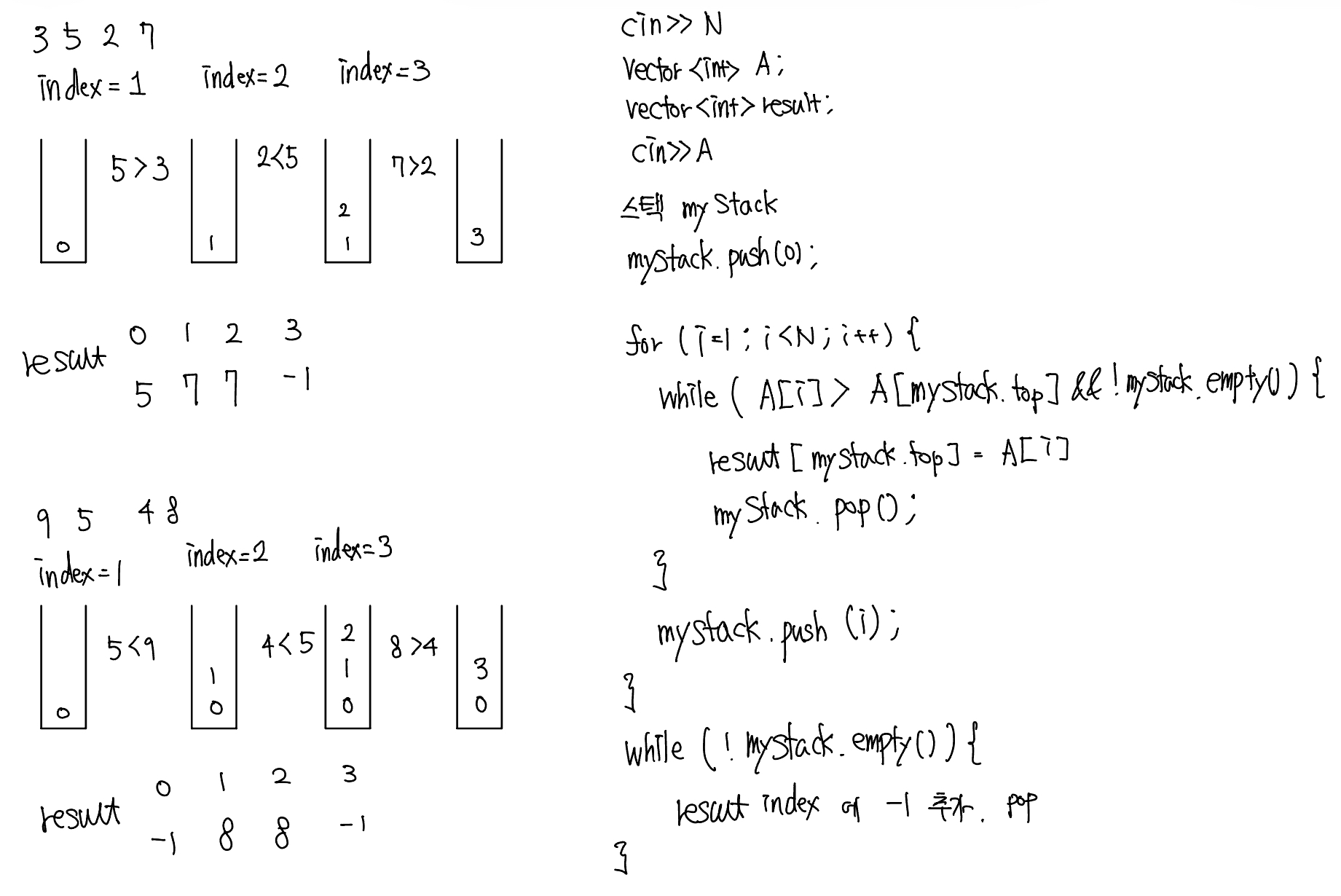
스택을 이용해 index=1 부터 시작하여, A[myStack.top()]와 비교하여, index가 크면 myStack.top()의 인덱스에 index의 값을 저장한다. 이후 index를 myStack에 push한다. 반복문이 끝났는데 myStack이 비어있지 않으면, myStack에 있는 값에 -1을 저장한다.

#include <iostream>
#include <stack>
#include <vector>
using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N;
	cin >> N;
	vector<int>A(N, 0);
	vector<int>result(N, 0);
	for (int i = 0; i < N; i++) {
		cin >> A[i];
	}

	stack<int>myStack;
	myStack.push(0);

	for (int i = 1; i < N; i++) {
		while(!myStack.empty() && A[i] > A[myStack.top()]) {
			result[myStack.top()] = A[i];
			myStack.pop();
		}
		myStack.push(i);
	}

	while (!myStack.empty()) {
		result[myStack.top()] = -1;
		myStack.pop();
	}

	for (int i = 0; i < N; i++) {
		cout << result[i] << ' ';
	}

}

문제 013 카드 게임

시간 제한: 2초 난이도: 실버4, 2164번

풀이

#include <iostream>
#include <queue>
using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);
	
	int N;
	cin >> N;

	queue<int>myQueue;
	for (int i = 0; i < N; i++) {
		myQueue.push(i + 1);
	}

	while (myQueue.size() != 1) {
		myQueue.pop();
		int temp = myQueue.front();
		myQueue.pop();
		myQueue.push(temp);
	}

	cout << myQueue.front();
}

문제 014 절댓값 힙 구현하기

시간 제한: 2초 난이도: 실버1, 11286번

풀이

#include <iostream>
#include <queue>
#include <cmath>
using namespace std;

struct cmp {
	bool operator()(int n1, int n2) {
		if (abs(n1) > abs(n2))
			return true;
		else if (abs(n1) == abs(n2)) {
			if (n1 > n2)
				return true;
			else
				return false;
		}
		return false;
	}
};

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N;
	cin >> N;

	priority_queue<int, vector<int>, cmp>myQueue;

	for (int i = 0; i < N; i++) {
		int temp;
		cin >> temp;

		if (temp != 0) {
			myQueue.push(temp);
		}
		else {
			if (myQueue.size() != 0) {
				cout << myQueue.top() << "\n";
				myQueue.pop();
			}
			else
				cout << '0' << "\n";
		}
	}
}

Twitter Facebook LinkedIn

MyeongWoo