5장 탐색

Updated: February 23, 2024

깊이 우선 탐색

　깊이 우선 탐색(DFS: Depth-First Search)은 그래프 완전 탐색 기법 중 하나이다. 깊이 우선 탐색은 그래프의 시작 노드에서 출발하여 탐색할 한쪽 분기를 정하여 최대 깊이까지 탐색을 마친 후 다른 쪽 분기로 이동하여 다시 탐색을 수행하는 알고리즘이다. 다음은 깊이 우선 탐색의 기능, 특징, 시간 복잡도를 정리한 것이다.

기능	특징	시간 복잡도(노드 수:V, 엣지 수:E)
그래프 완전 탐색	재귀 함수로 구현, 스택 자료구조 이용	O(V+E)

　깊이 우선 탐색은 실제 구현 시 재귀 함수를 이용하므로 스택 오프틀로(Stack Overflow)에 유의해야 한다. 깊이 우선 탐색을 응용하여 풀 수 있는 문제는 단절점 찾기, 단절선 찾기, 사이클 찾기, 위상 정렬 등이 있다.

깊이 우선 탐색의 핵심 이론

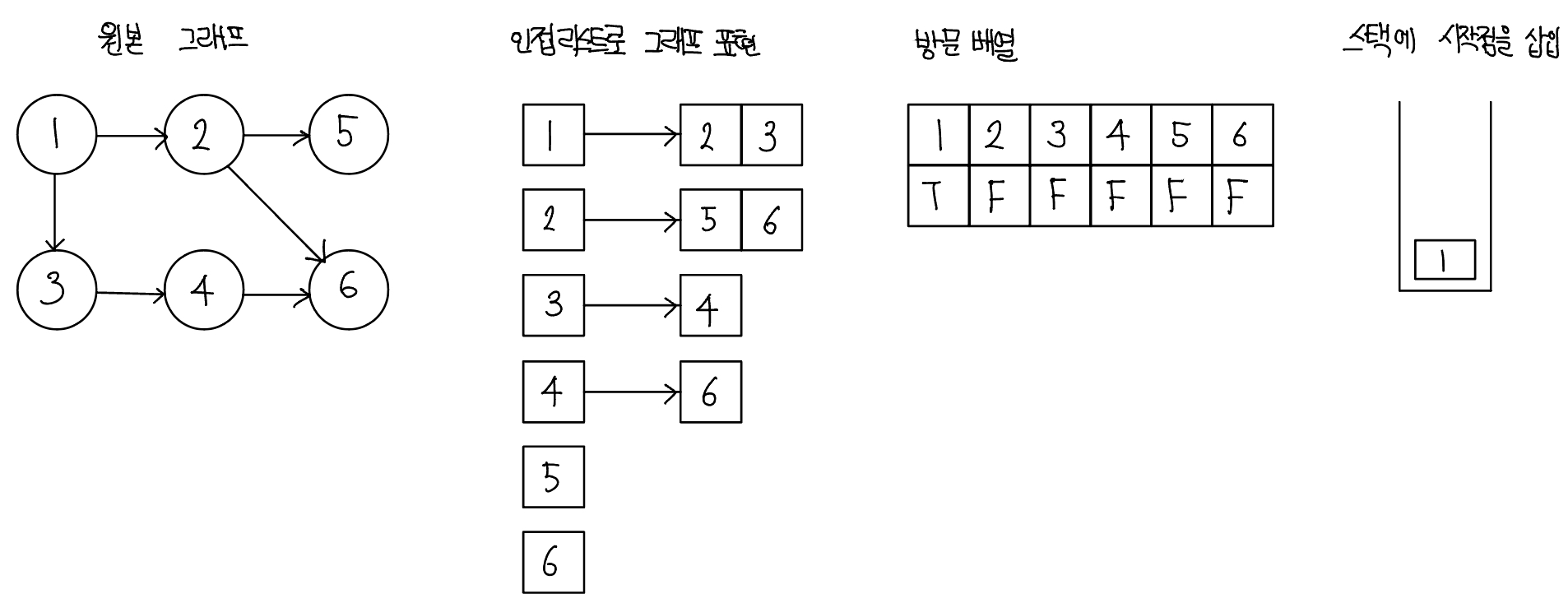
　DFS는 한 번 방문한 노드를 다시 방문하면 안 되므로 노드 방문 여부를 체크할 배열이 필요하며, 그래프는 인접 리스트로 표현한다. 그리고 DFS의 탐색 방식은 후입선출 특성을 가지므로 스택을 사용할 수 있다. 1. DFS를 시작할 노드를 정한 후 사용할 자료구조 초기화하기

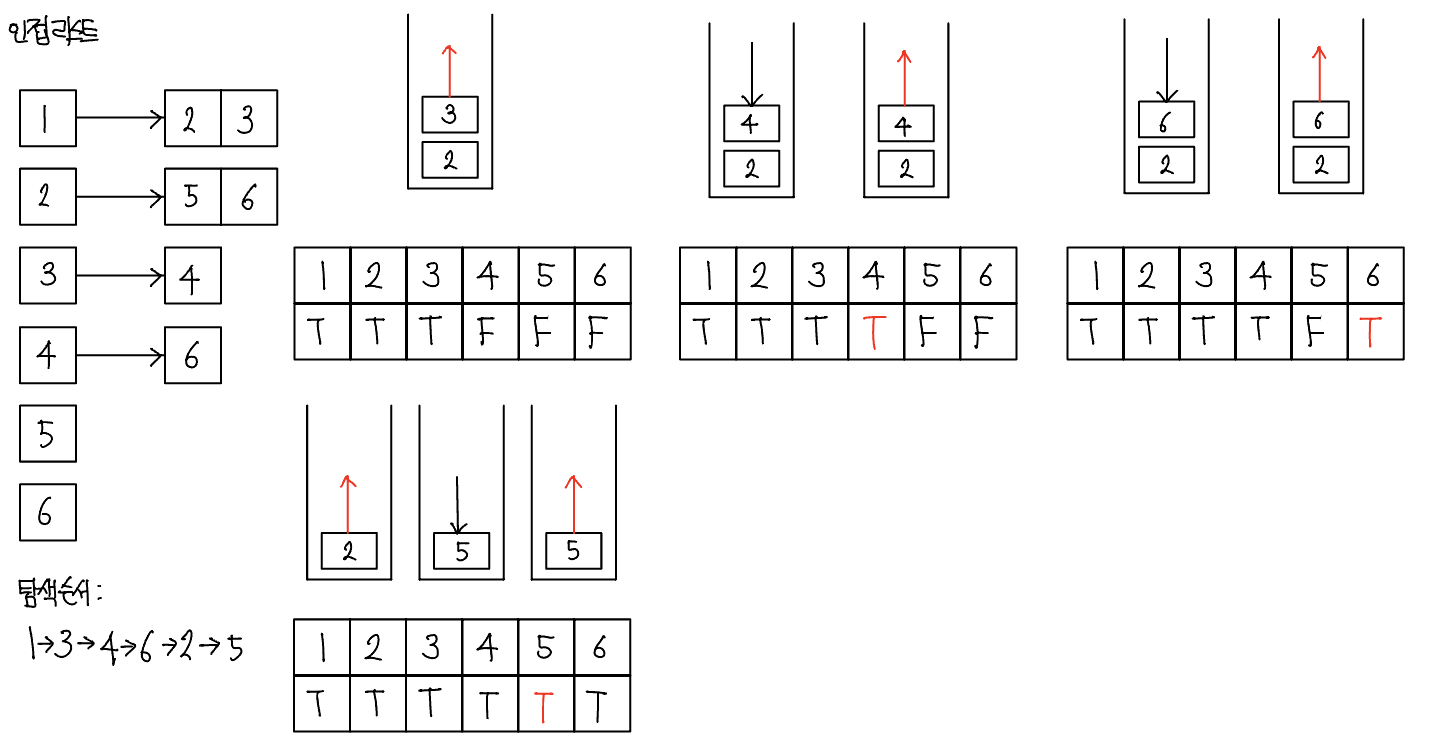
DFS를 위해 필요할 초기 작업은 인접 리스트로 그래프 표현하기, 방문 배열 초기화하기, 시작 노드 스택에 삽입하기이다. 스택에 시작 노드를 1로 삽입할 때 해당 위치의 방문 배열을 채크하면 T, F, F, F, F, F가 된다.

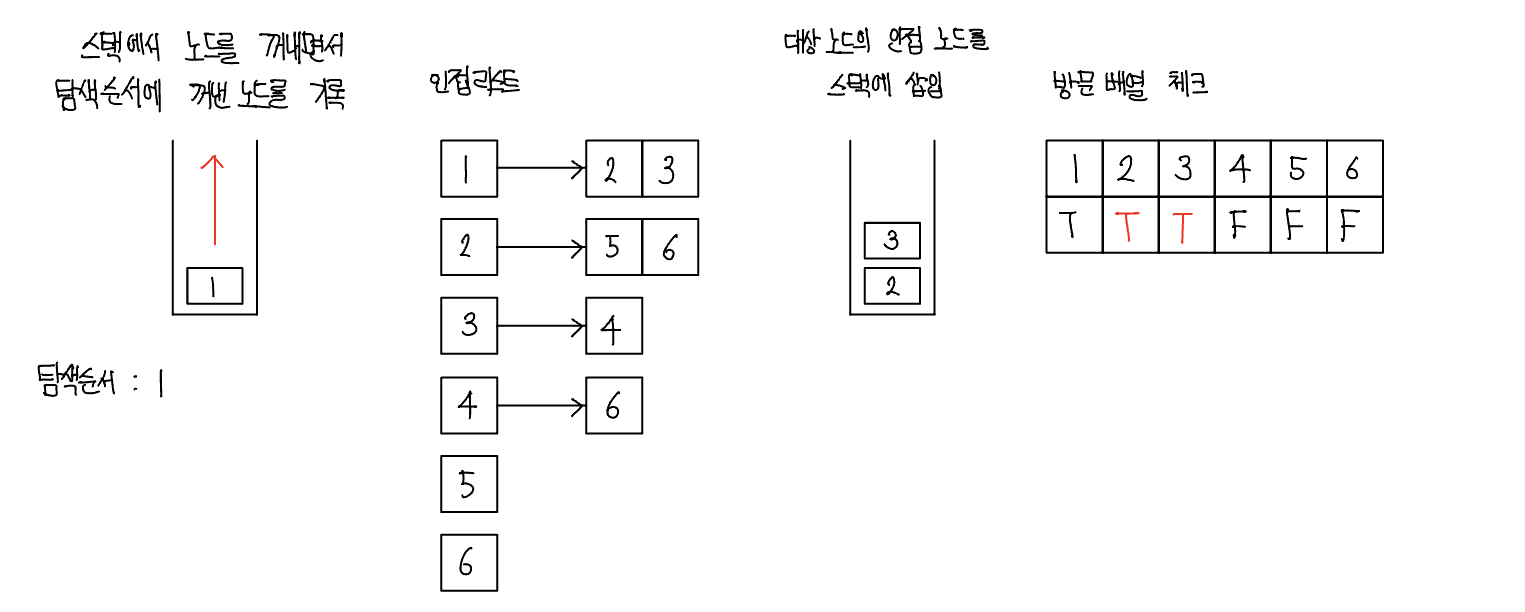
2. 스택에서 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 스택에 삽입하기

이제 pop을 수행하여 노드를 꺼낸다. 꺼낸 노드를 탐색 순서에 기입하고 인접 리스트의 인접 노드를 스택에 삽입하며 방문 배열을 체크한다. 방문 배열은 T, T, T, F, F, F가 된다.

3. 스택 자료구조에 값이 없을 때까지 반복하기

앞선 과정을 스택 자료구조에 값이 없을 때까지 반복한다. 이때 이미 다녀간 노드는 방문 배열을 바탕으로 재삽입하지 않는 것이 핵심이다.

문제 023 연결 요쇼의 개수 구하기

시간 제한: 3초, 난이도: 실버2, 11724번

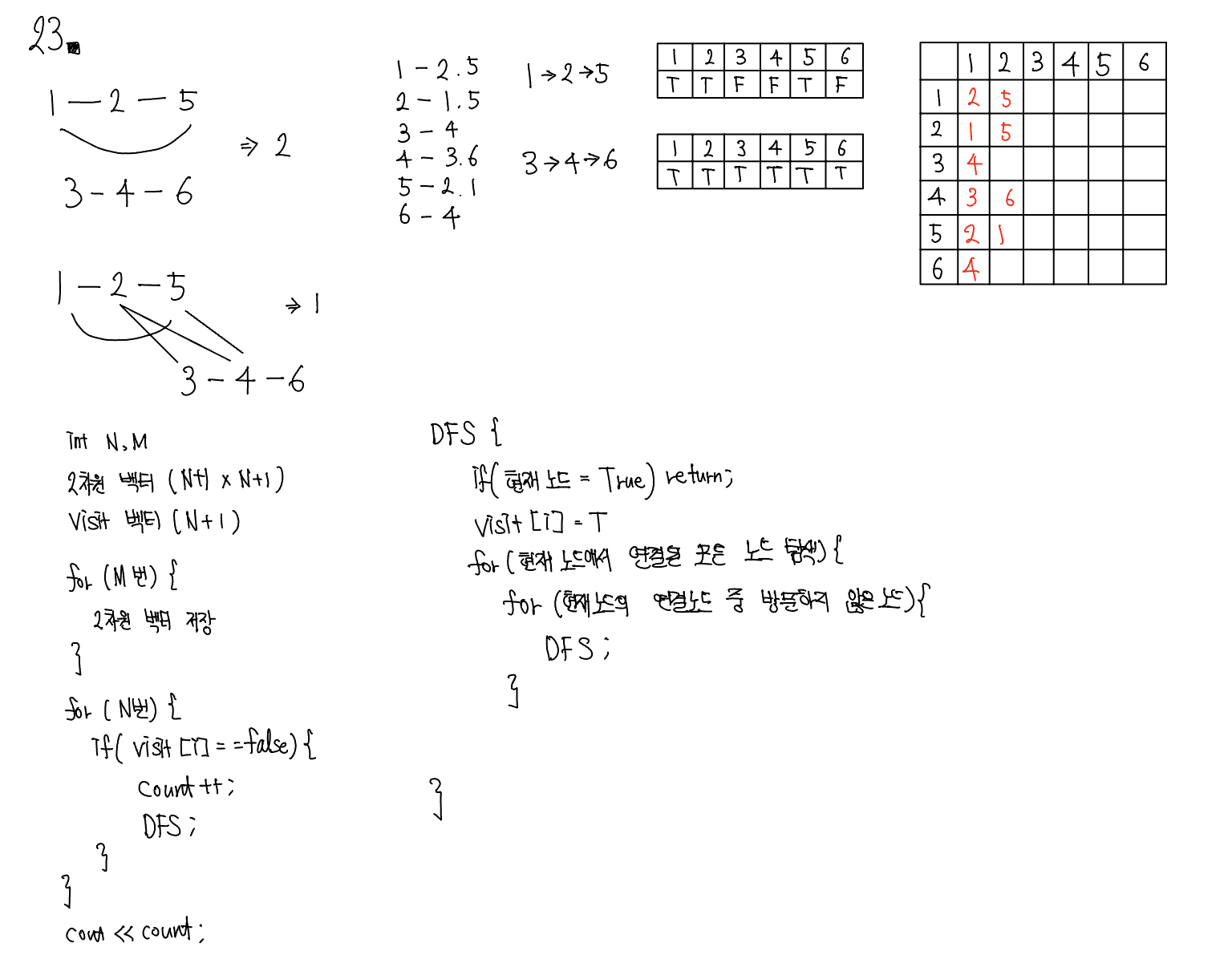
풀이

#include <iostream>
#include <vector>
using namespace std;

vector<vector<int>> A;
vector<bool> V;
void DFS(int v);

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N, M;
	cin >> N >> M;
	A.resize(N + 1);
	V = vector<bool>(N + 1, false);

	for (int i = 0; i < M; i++) {
		int s, e;
		cin >> s >> e;
		A[s].push_back(e);
		A[e].push_back(s);
	}

	int count = 0;

	for (int i = 1; i < N + 1; i++) {
		if (V[i] == false) {
			count++;
			DFS(i);
		}
	}
	cout << count;
}

void DFS(int v) {
	if (V[v]) {
		return;
	}

	V[v] = true;

	/* 범위 기반 for문
	for (int i: A[v]) {
		if (V[i] == false) {
			DFS(i);
		}
	}
	*/

	for (int i = 0; i < A[v].size(); i++) {
		int temp = A[v][i];
		if (V[temp] == false) {
			DFS(temp);
		}
	}
}

그래프에서 vertexs와 edges를 표현하기 위해 2 by 2 Matrix를 만들었고 입력 받은 값들을 넣었다. 또한 특정 vertex를 방문했는지 확인하기 위해 V 배열을 만들었고 만약 해당 vertex를 방문했다면 다음 vertex로 갈 수 있게 알고리즘을 작성하였다.

문제 024 신기한 소수 찾기

시간 제한: 2초, 난이도: 골드5, 2023번

풀이

static int N;
void DFS(int, int);
bool isPrime(int);

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	cin >> N;
	DFS(2, 1);
	DFS(3, 1);
	DFS(5, 1);
	DFS(7, 1);
}

void DFS(int a, int b) {
	if (b == N) {
		if (isPrime(a)) {
			cout << a << "\n";
		}
		return;
	}

	for (int i = 1; i < 10; i = i + 2) {
		if (isPrime(a * 10 + i)) {
			DFS(a * 10 + i, b + 1);
		}
	}
}

bool isPrime(int num) {
	for (int i = 2; i < num; i++) {
		if (num % i == 0) {
			return false;
		}
	}
	return true;
}

문제 025 친구 관계 파악하기

시간 제한: 2초, 난이도: 골드5, 13023번

풀이

#include <iostream>
#include <vector>
using namespace std;

vector<vector <int>> G;
bool visit[2000] = { false };
bool arrive;
void DFS(int now, int depth);

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N, M;
	cin >> N >> M;

	arrive = false;
	G.resize(N);

	for (int i = 0; i < M; i++) {
		int a, b;
		cin >> a >> b;
		G[a].push_back(b);
		G[b].push_back(a);
	}
	
	for (int i = 0; i < N; i++) {
		DFS(i, 1);
		if (arrive) {
			break;
		}
	}

	if (arrive) {
		cout << "1";
	}
	else {
		cout << "0";
	}

}

void DFS(int now, int depth) {
	if (depth == 5 || arrive) {
		arrive = true;
		return;
	}

	visit[now] = true;
	for (int i: G[now]) {
		if (!visit[i]) {
			DFS(i, depth + 1);
		}
	}
	visit[now] = false;
}

너비 우선 탐색

너비 우선 탐색(BFS, Breadth-First Search)도 그래프를 완전 탐색하는 방법 중 하나로, 시작 노드에서 출발해 시작 노드를 기준으로 가까운 노드를 먼저 방문하면서 탐색하는 알고리즘이다.

기능	특징	시간복잡도(노드 수: V, 에지 수: E)
그래프 완전 탐색	FIFO 탐색 Queue 자료구조 이용	O(V + E)

너비 우선 탐색은 선입선출 방식으로 탐색하므로 큐를 이용해 구현한다. 또한 너비 우선 탐색은 탐색 시작 노드와 가까운 노드를 우선하여 탐색하므로 목표 노드에 도착하는 경로가 여러 개일 때 최단 경로를 보장한다. 너비 우선 탐색은 BFS라 부른다.

너비 우선 탐색의 핵심 이론

1. BFS를 시작할 노드를 정한 후 사용할 자료구조 초기화하기 - BFS도 DFS와 마찬가지로 방문했던 노드는 다시 방문하지 않으므로 방문한 노드를 체크하기 위한 배열이 필요하다. 그래프를 인접 리스트로 표현하는 것 역시 DFS와 동일하다. 하나 차이점이 있다면 탐색을 위해 스택이 아닌 큐를 사용한다.

2. 큐에서 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 큐에 삽입하기 - 큐에서 노드를 꺼내면서 인접 노드를 큐에 삽입한다. 이때 방문 배열을 체크하여 이미 방문한 노드는 큐에 삽입하지 않는다. 또한 큐에서 꺼낸 노드는 탐색 순서에 기록한다.

3. 큐 자료구조에 값이 없을 때까지 반복하기 - 큐에 노드가 없을 때까지 앞선 과정을 반복한다. 선입선출 방식으로 탐색하므로 탐색 순서가 DFS와 다르다.

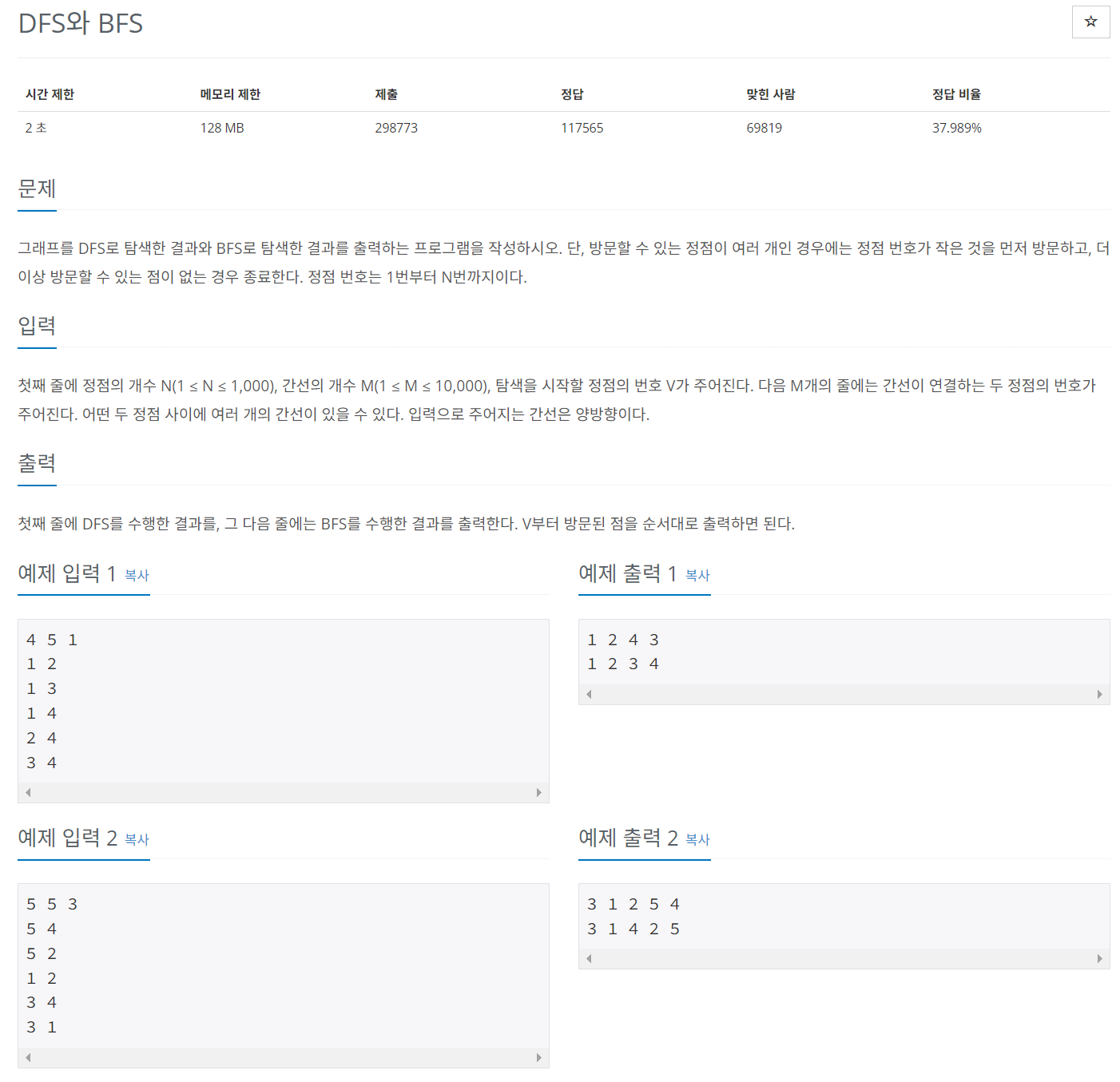
문제 026 DFS와 BFS 프로그램

시간 제한: 2초, 난이도: 실버2, 1260번

import java.io.*;
import java.util.*;

public class Main {

    public static ArrayList<ArrayList<Integer>> graph = new ArrayList<>();
    public static boolean[] visit;// 방문 배열

    public static void DFS(int V) {
        visit[V] = true;
        System.out.print(V + " ");

        for (int node : graph.get(V)) {
            if (!visit[node]) {
                DFS(node);
            }
        }

    }

    public static void BFS(int V) {
        Queue<Integer> qu = new LinkedList<>();

        qu.offer(V);
        visit[V] = true;

        while (!qu.isEmpty()) {
            int node = qu.poll();
            System.out.print(node + " ");
            for (int i = 0; i < graph.get(node).size(); i++) {
                int temp = graph.get(node).get(i);
                if (!visit[temp]) {
                    visit[temp] = true;
                    qu.offer(temp);
                }
            }
        }

    }

    public static void main(String[] args) throws IOException {

        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();
        int M = sc.nextInt();
        int V = sc.nextInt();

        for (int i = 0; i <= N; i++) {
            graph.add(new ArrayList<>());
        }   // 각 노드 별 리스트를 만들어준다.

        for (int i = 0; i < M; i++) {
            int a = sc.nextInt();
            int b = sc.nextInt();

            graph.get(a).add(b);
            graph.get(b).add(a);
        }   // Graph 완성

        for (int i = 1; i <= N; i++) {
            Collections.sort(graph.get(i));
        }

        visit = new boolean[N + 1];

        DFS(V);
        Arrays.fill(visit, Boolean.FALSE);
        System.out.println();
        BFS(V);
    }
}

자바에서는 ArrayList를 사용해 ArrayList<ArrayList<Integer>>와 같이 그래프를 구현하였다. 또한 Queue를 사용할 때 add와 remove 대신에 offer과 poll을 사용하였다. 그리고 DFS를 한 후 Visit 배열을 초기화 하기 위해 Arrays.fill 매소드를 사용해 FALSE로 초기화를 하였다.

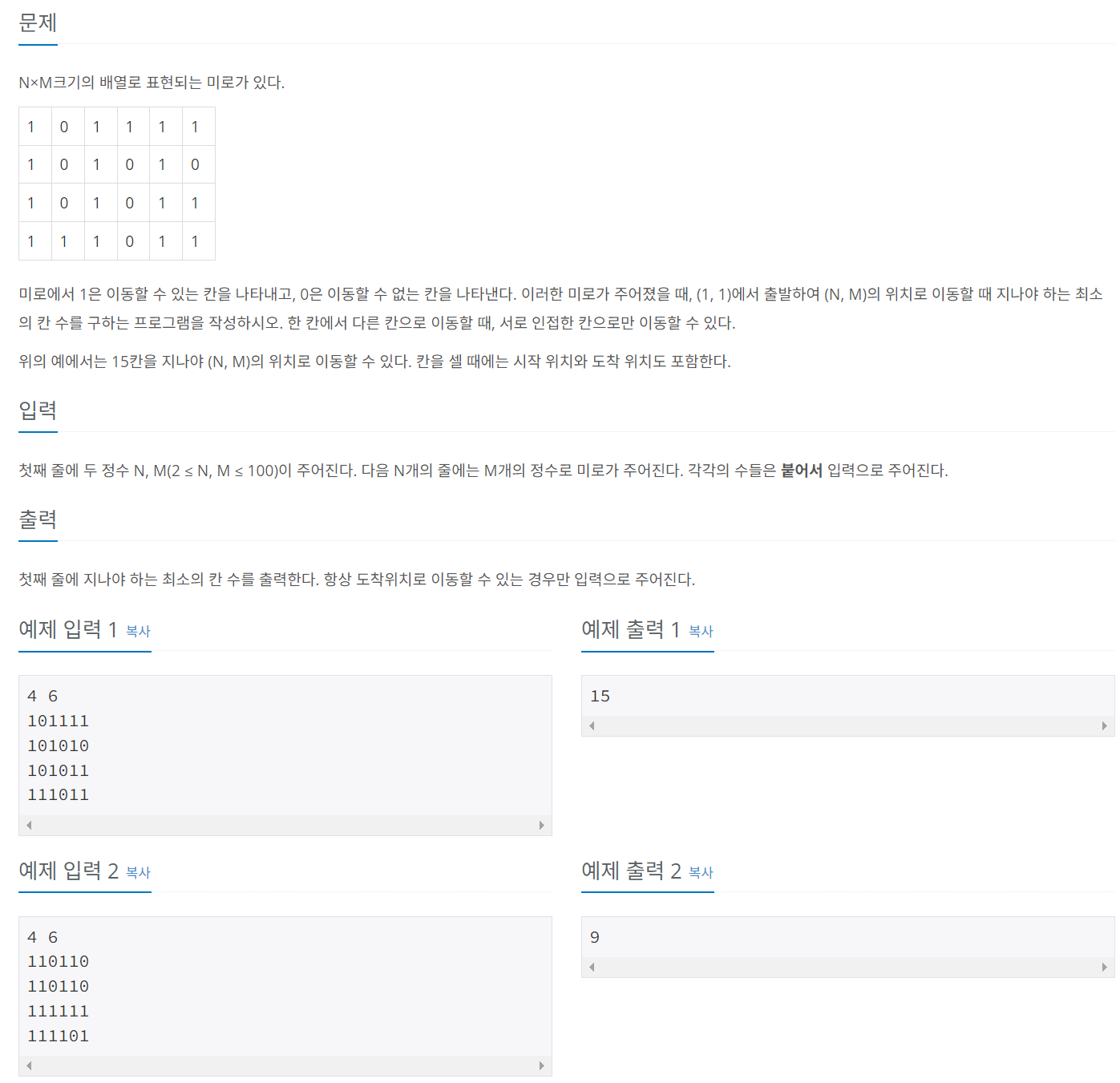
문제 027 미로 탐색하기

시간 제한: 1초, 난이도: 실버1, 2178번

풀이

import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;


public class Main {

    public static int[] x = {-1, 1, 0, 0};
    public static int[] y = {0, 0, -1, 1};
    // 현재 위치에서 4방향을 검사하기 위해 사용하는 배열

    public static class Pair<A, B> {
        private A first;
        private B second;

        Pair(A first, B second) {
            this.first = first;
            this.second = second;
        }
    }

    public static void main(String[] args) {

        Scanner sc = new Scanner(System.in);

        int N = sc.nextInt();
        int M = sc.nextInt();

        int[][] maze = new int[N + 1][M + 1];
        boolean[][] visit = new boolean[N + 1][M + 1];
        Queue<Pair<Integer, Integer>> qu = new LinkedList<>(); // BFS를 위한 Queue

        for (int i = 1; i <= N; i++) {
            String[] StrArr = sc.next().split("");

            for (int j = 1; j <= M; j++) {
                maze[i][j] = Integer.parseInt(StrArr[j - 1]);
            }
        }   // 공백없이 입력 받을 때 나누는 방법

        qu.offer(new Pair(1, 1));
        visit[1][1] = true; // (1,1)에서 시작

        while (!qu.isEmpty()) {
            Pair temp = qu.poll();
            int current_x = (int) temp.first;
            int current_y = (int) temp.second;

            for (int i = 0; i < 4; i++) {
                int next_x = current_x + x[i];
                int next_y = current_y + y[i];

                if (next_x <= N && next_y <= M) {
                    if (!visit[next_x][next_y] && maze[next_x][next_y] != 0) {
                        qu.offer(new Pair(next_x, next_y));
                        visit[next_x][next_y] = true;
                        maze[next_x][next_y] = maze[current_x][current_y] + 1;
                    }
                }

            }
        }

        System.out.println(maze[N][M]);
    }
}

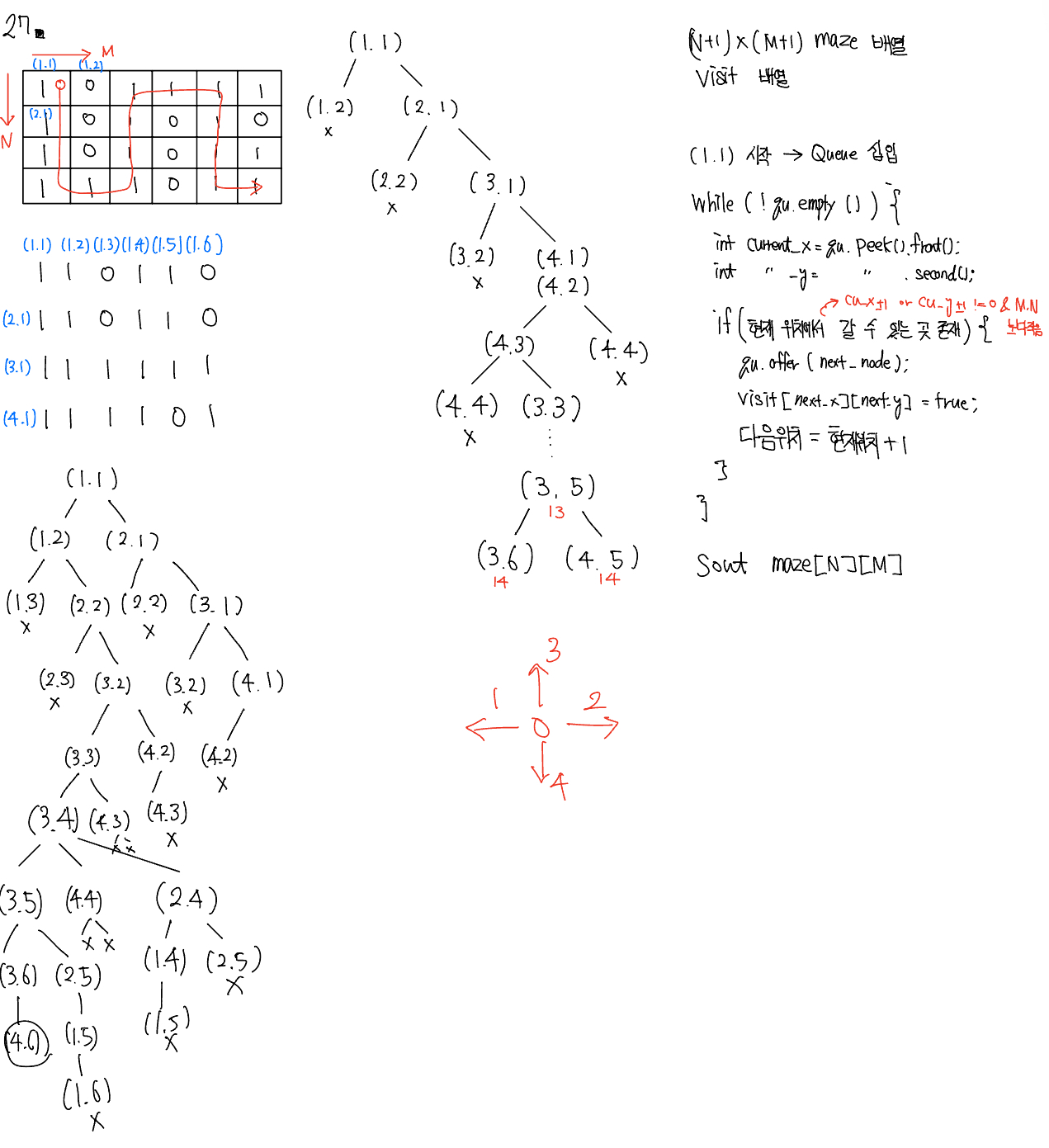
위 풀이에서 Pair를 사용하기 위해서 Pair 클래스를 만들어 사용하였고, 띄어쓰기 없이 입력을 받을경우 각각을 저장하기 위해 split을 사용하였다. 또한 상, 하, 좌, 우를 탐색하기 위해 전역으로 x,y 배열을 선언하였다.

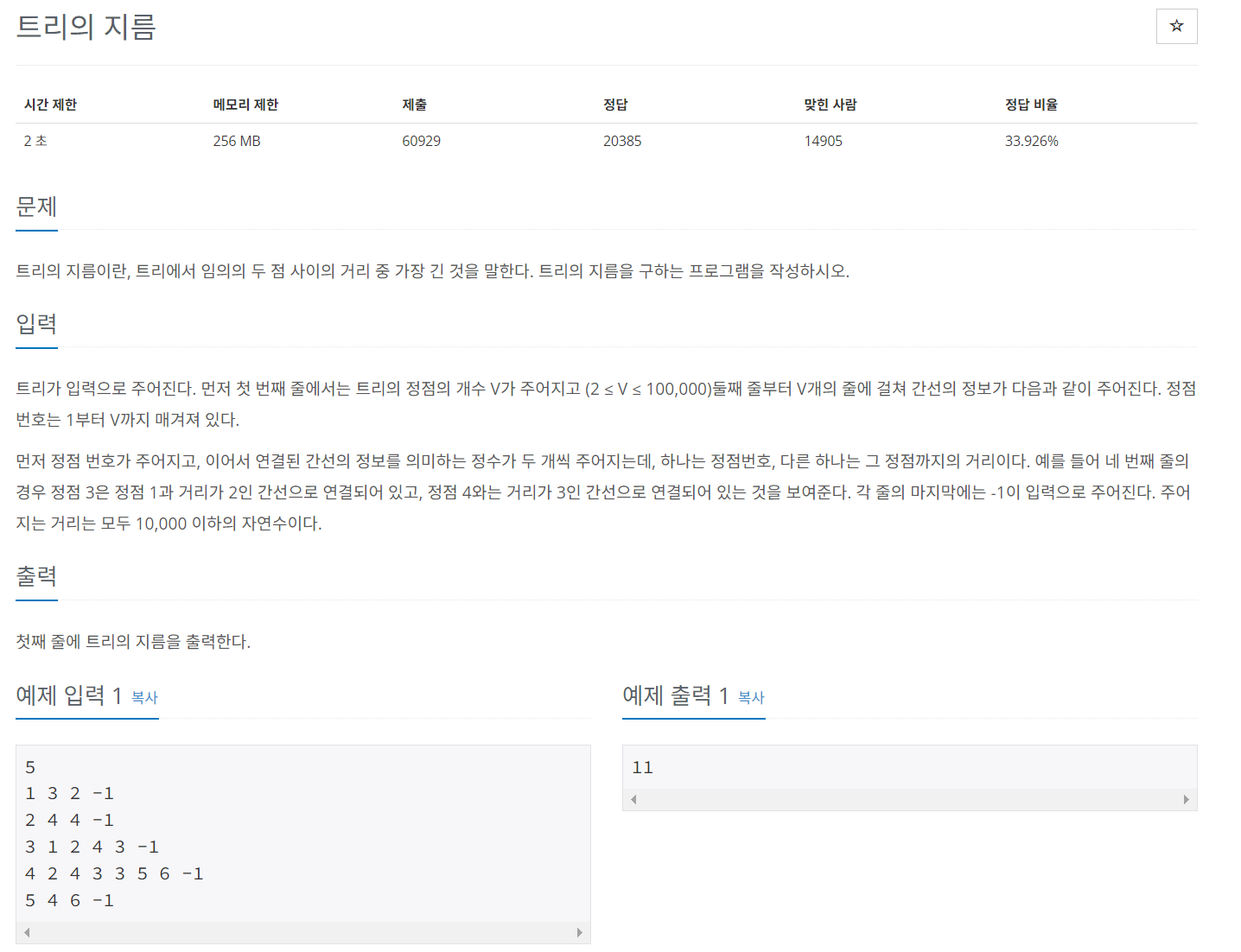
문제 028 트리의 지름 구하기

시간 제한: 2초, 난이도: 골드2, 1167번

import java.util.*;

public class Main {

    static int V;
    public static ArrayList<ArrayList<Integer>> graph = new ArrayList<>();
    public static ArrayList<ArrayList<Integer>> weight = new ArrayList<>();

    static boolean[] visit; // 방문 배열
    static int[] max;   // 지름을 구하기 위한 배열

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        V = sc.nextInt();

        for (int i = 0; i <= V; i++) {
            graph.add(new ArrayList<>());
            weight.add(new ArrayList<>());
        }   // 각 노드 별 리스트를 만들어준다.

        visit = new boolean[V + 1];
        max = new int[V + 1];

        for (int i = 0; i < V; i++) {
            int start = sc.nextInt();
            while (true) {
                int node = sc.nextInt();
                if (node == -1) {
                    break;
                }

                graph.get(start).add(node);

                int tmpweight = sc.nextInt();
                weight.get(start).add(tmpweight);
            }
        }   // 트리 정보 입력

        BFS(2);

        int restart = 1;
        for (int i = 1; i <= V; i++) {
            int tmp = max[i];
            if (tmp > max[restart]) {
                restart = i;
            }
        }

        Arrays.fill(max, 0);
        BFS(restart);
        restart = 1;
        for (int i = 1; i <= V; i++) {
            int tmp = max[i];
            if (tmp > max[restart]) {
                restart = i;
            }
        }
        System.out.println(max[restart]);

    }

    public static void BFS(int start) {
        Arrays.fill(visit, false);

        Queue<Integer> qu = new LinkedList<>();
        qu.offer(start);

        while (!qu.isEmpty()) {
            int node = qu.poll();
            visit[node] = true;
            for (int i = 0; i < graph.get(node).size(); i++) {
                int nextNode = graph.get(node).get(i);
                if (!visit[nextNode]) {
                    qu.offer(nextNode);
                    max[nextNode] = max[node] + weight.get(node).get(i);
                }
            }
        }


    }
}

트리의 지름은 어느 한 시작점에서 가장 먼곳의 정점을 찾고, 그 정점으로부터 가장 멀리 있는 정점까지의 거리를 구하는 것이다. 처음에는 V X V 배열을 만들어서 하였으나, 메모리를 초과하여 위와 같이 ArrayList<ArrayList<Integer>>로 구현을 하였다.

이진 탐색

이진 탐색(Binary Search)은 데이터가 정렬된 상태에서 원하는 값을 찾아내는 알고리즘이다. 대상 데이터의 중앙값과 찾고자 하는 값을 비교해 데이터의 크기를 절반씩 줄이면서 대상을 찾는다. 이진 탐색의 시간 복잡도는 O(log N)이다.

이진 탐색의 핵심 이론

이진 탐색은 오름차순으로 정렬된 데이터에서 다음 4가지 과정을 반복한다.

현재 데이터셋의 중앙값(median)을 선택한다.
중앙값 > 타깃 데이터(target data)일 때 중앙값 기준으로 왼쪽 데이터셋을 선택한다.
중앙값 < 타깃 데이터일 때 중앙값 기준으로 오른쪽 데이터셋을 선택한다.
위 1~3 과저을 반복하다가 중앙값 == 타깃 데이터일 때 탐색을 종료한다.

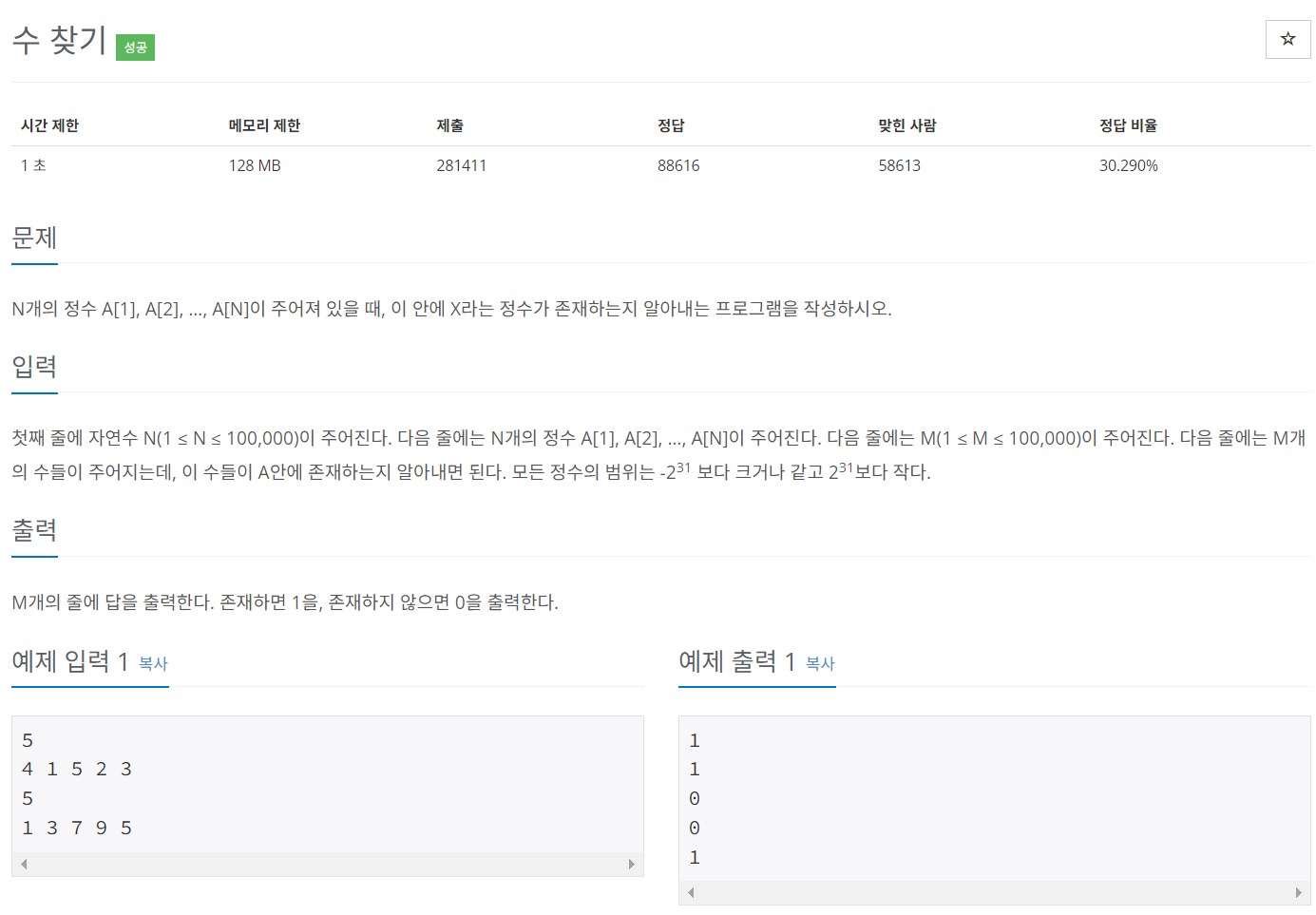
문제 029 원하는 정수 찾기

시간 제한: 1초, 난이도: 실버4, 1920번

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N;
	cin >> N;
	vector<int>A(N, 0);
	for (int i = 0; i < N; i++) {
		cin >> A[i];
	}
	sort(A.begin(), A.end());

	int M;
	cin >> M;
	vector<int>B(M, 0);
	for (int i = 0; i < M; i++) {
		cin >> B[i];
	}
	vector<int>result(M, 0);

	for (int i = 0; i < M; i++) {
		int tmp = B[i];
		bool exe = binary_search(A.begin(), A.end(), tmp);

		if (exe == true) {
			result[i] = 1;
		}
	}

	for (int i = 0; i < M; i++) {
		cout << result[i] << "\n";
	}
}

백준 Class 문제를 풀 때 풀었던 문제이다.

문제 030 블루레이 만들기

시간 제한: 2초, 난이도: 실버1, 2343번

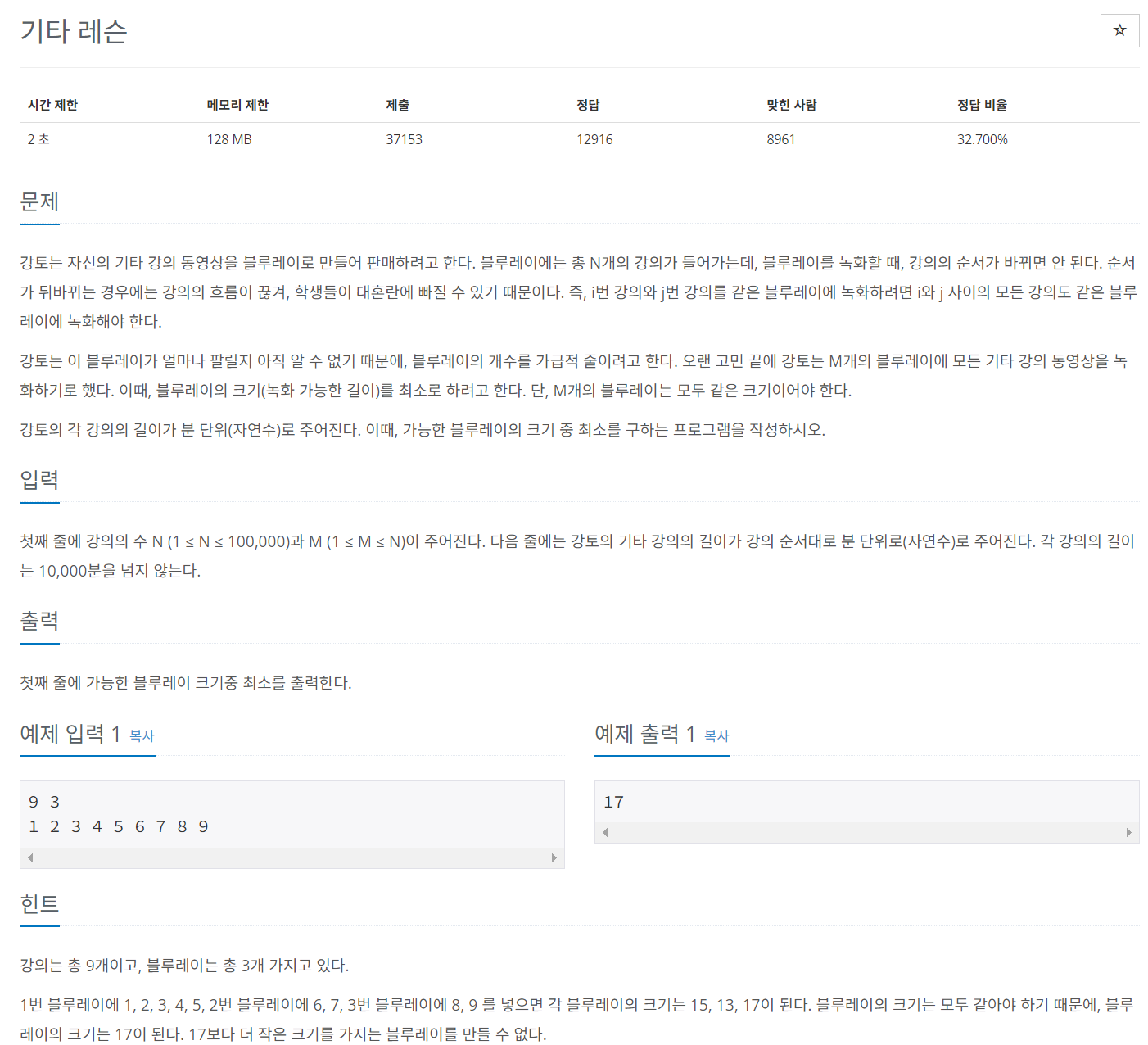
풀이

import java.rmi.dgc.VMID;
import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();
        int M = sc.nextInt();

        // Binary Search를 하기 위한 파라미터
        int min = 0;
        int max = 0;

        int[] arr =new int[N];
        for (int i = 0; i < N; i++) {
            arr[i] = sc.nextInt();
            max = max + arr[i];
            if (arr[i] > min) {
                min = arr[i];
            }
        }

        while (min <= max) {
            int count = 0;
            int mid = (min + max) / 2;
            int sum = 0;

            for (int i = 0; i < N; i++) {
                if (sum + arr[i] <= mid) {
                    sum += arr[i];
                }   // sum + arr[i]가 mid값을 넘지 않으면 더하기
                else {
                    count++;
                    sum = arr[i];
                }
            }

            if (sum != 0) {
                count++;
            }	// for문 나오면서 마지막 sum의 경우 count가 되지 않으므로 만약 sum이 0이 아니면 count++

            if (count > M) {
                min = mid + 1;
            } else {
                max = mid - 1;
            }
        }

        System.out.println(min);
    }
}

문제 031 배열에서 K번째 수 찾기

시간 제한: 2초, 난이도: 골드1, 1300번

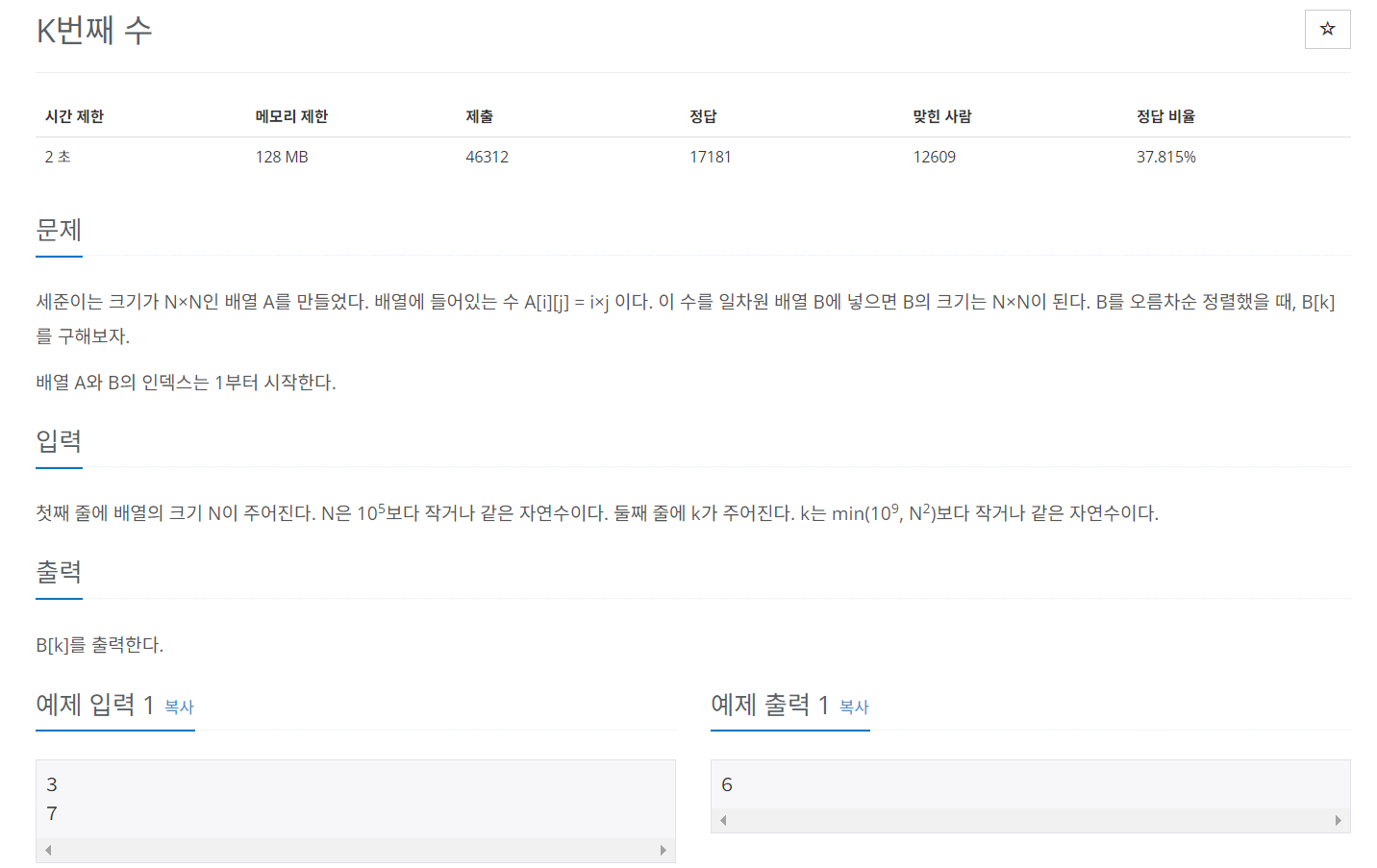
풀이

import java.io.*;

public class Main {

    public static void main(String[] args) throws IOException {
        BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        long N = Integer.parseInt(bf.readLine());
        long K = Integer.parseInt(bf.readLine());

        long start = 1;
        long end = K;
        long ans = 0;

        while (start <= end) {
            long next = 0;
            long mid = (start + end) / 2;
            for (int i = 1; i <= N; i++) {
                long tmp = mid / i;
                if (tmp > N) {
                    tmp = N;
                }

                next += tmp;
            }

            if (next < K) {
                start = mid + 1;
            } else {
                ans = mid;
                end = mid - 1;
            }

        }

        System.out.println(ans);
    }
}

위 풀이를 정리하면 중앙값보다 작은 수의 개수가 k보다 작으면 시작 인덱스를 중앙값 + 1, 중앙값보다 작은 수의 개수가 k보다 크거나 같으면 종료 인덱스를 중앙값 - 1로 하면서 정답을 중앙값으로 업데이트하며 시작 인덱스가 종료 인덱스보다 커질 때까지 Binary Search를 진행한다.

Twitter Facebook LinkedIn

MyeongWoo