7장 정수론
Updated:
소수 구하기
소수(Prime Number)는 자신보다 작은 2개의 자연수를 곱해 만들 수 없는 1보다 큰 자연수를 말한다. 이와 같은 의미로 1과 자기 자신 외에 약수가 존재하지 않는 수를 말한다.
소수 구하기의 핵심 이론
소수를 구하는 대표적인 판별법으로는 에라토스테네스의 채를 들 수 있다. 에라토스테네스의 채 원리는 다음과 같다.
- 구하고자 하는 소수의 범위만큼 1차원 배열을 생성한다.
- 2부터 시작하고 현재 숫자가 지원진 상태가 아닌 겨우 현재 선택된 배수에 해당하는 수를 배열에서 끝까지 탐색하면서 지운다. 이때 처음으로 선택된 숫자는 지우지 않는다.
- 배열의 끝까지 2를 반복한 후 배열에 남은 모든 수를 출력한다.
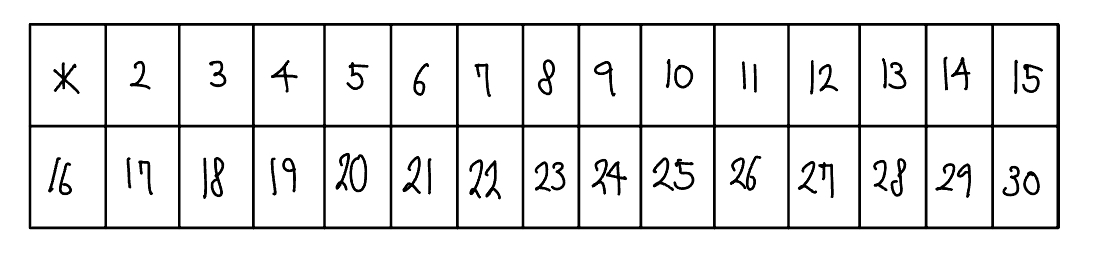
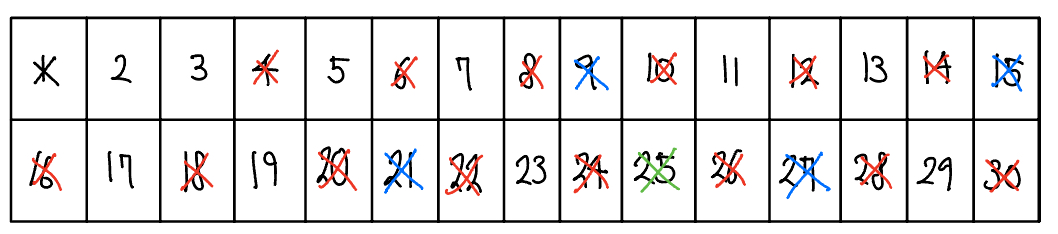
1부터 30까지의 수 중 소수를 구하는 예를 보자. 먼저 주어진 범위까지 배열을 생성한다. 1은 소수가 아니므로 삭제하고, 배열은 2부터 시작한다.
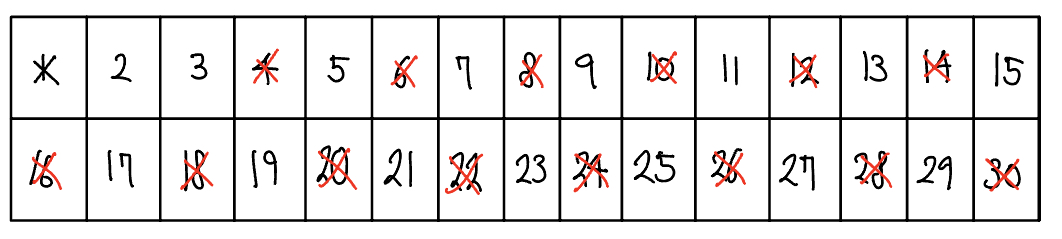
선택한 수의 배수를 모두 삭제한다. 현재의 경우 2의 배수를 모두 삭제한다.
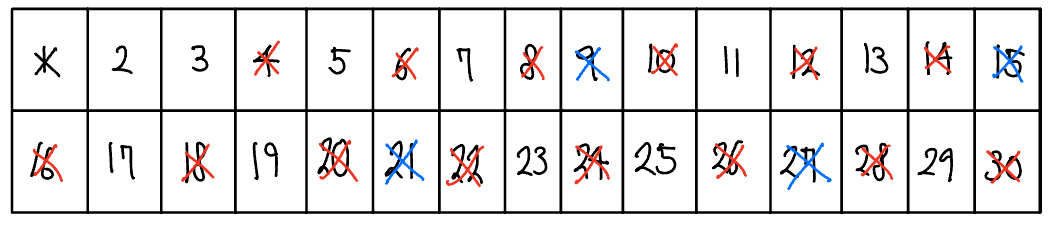
다음 지워지지 않은 수를 선택한다. 즉, 3을 선택하고 선택한 수의 모든 배수를 삭제한다.
앞의 과정을 배열의 끝까지 반복한다.
삭제되지 않은 수를 모두 출력한다.
즉, 1부터 30까지의 수 중 소수는 2, 3, 5, 7, 11, 13, 17, 19, 23, 29이다.
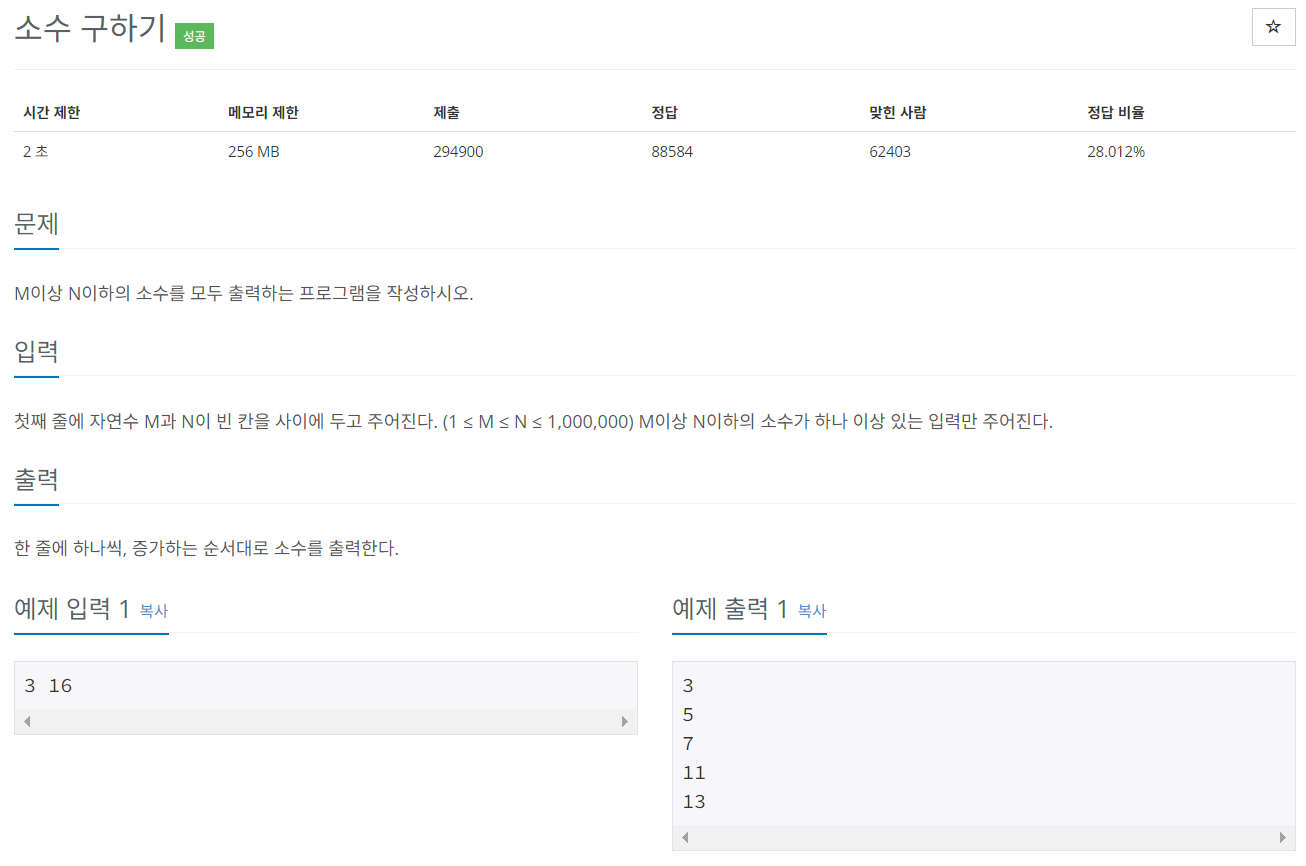
문제 037 소수 구하기
시간 제한: 2초, 난이도: 실버3, 1929번
import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main{
public static boolean[] arr;
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
String s = bf.readLine();
StringTokenizer st = new StringTokenizer(s);
int M = Integer.parseInt(st.nextToken());
int N = Integer.parseInt(st.nextToken());
arr = new boolean[N + 1];
Prime();
for (int i = M; i <= N; i++) {
if (!arr[i]) {
bw.write(i + "\n");
}
}
bw.flush();
bw.close();
}
public static void Prime() {
arr[0] = true;
arr[1] = true;
for (int i = 2; i <= Math.sqrt(arr.length); i++) {
if (arr[i]) {
continue;
}
for (int j = i * i; j < arr.length; j += i) {
arr[j] = true;
}
}
}
}
백준 Class2 문제를 풀 때 풀었던 문제이다.
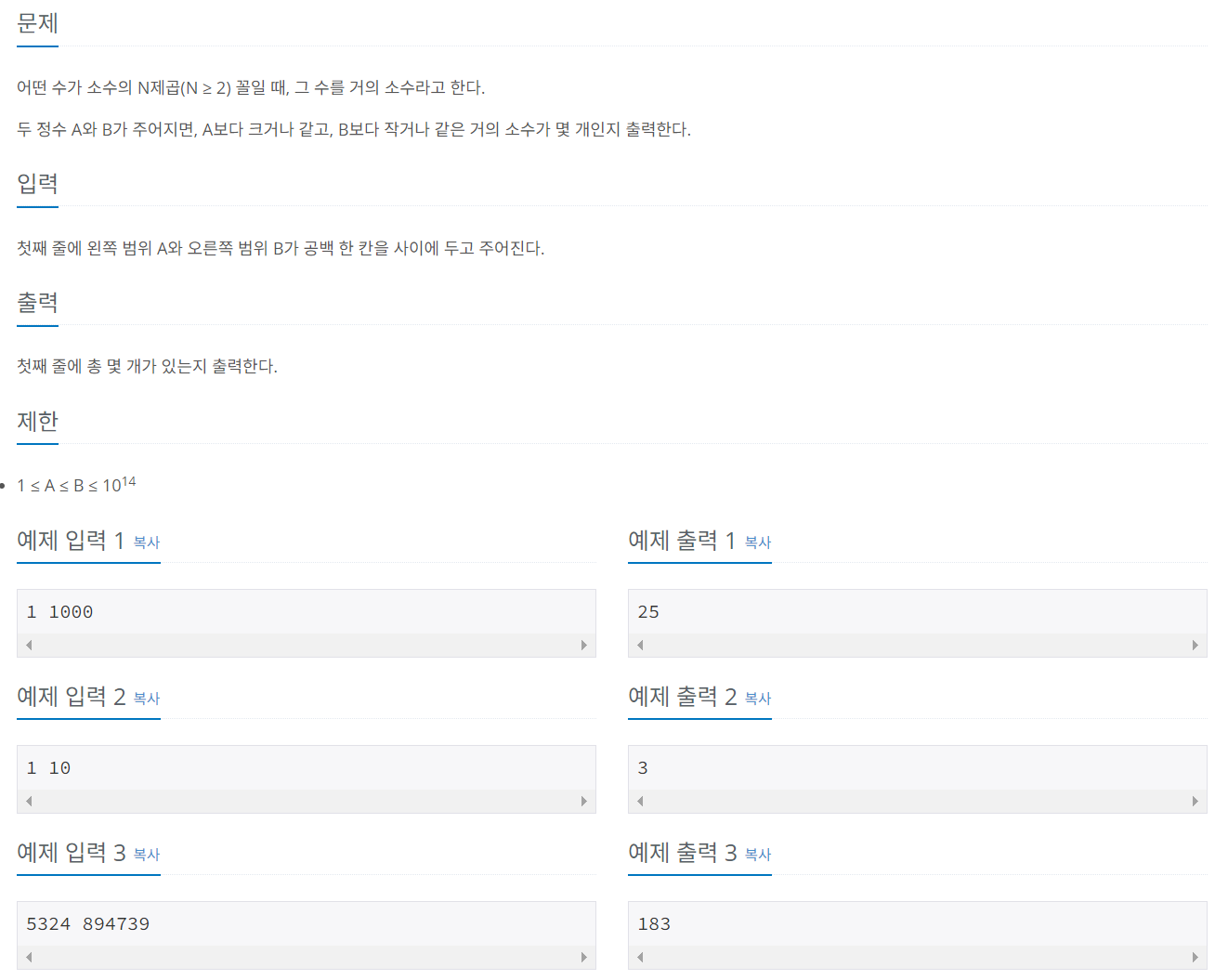
문제 038 거의 소수 구하기
시간 제한: 2초, 난이도: 골드5, 1456번
import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
public static Boolean[] arr;
// 에라토스테네스의 채
public static void isPrime(int a) {
arr[0] = false;
arr[1] = false;
for (int i = 2; i <= Math.sqrt(a); i++) {
if (arr[i]) {
for (int j = i + i; j <= a; j += i) {
arr[j] = false;
}
}
}
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(bf.readLine());
long A = Long.parseLong(st.nextToken());
long B = Long.parseLong(st.nextToken());
int rootB = (int) Math.sqrt(B);
arr = new Boolean[rootB + 1];
Arrays.fill(arr, true);
isPrime(rootB);
int count = 0;
for (int i = 0; i <= rootB; i++) {
if (arr[i]) {
long temp = i;
while (temp <= (double) B / i) {
if (temp >= (double) A / i) {
count++;
}
temp = temp * i;
}
}
}
bw.write(count + "\n");
bw.flush();
bw.close();
}
}
에라토스테네스의 채를 사용해 소수가 아닌 숫자들을 분류한 뒤, 이 소수 중 N제곱이 범위 안에 있으면 count하는 알고리즘이다. 하지만, temp = temp * i가 만약 long의 범위를 넘어갈 수 있기 때문에 위 while문에서 i로 나누어, temp의 제곱부터 count해야하지만, temp부터 count를 하는 알고리즘으로 만들었다.
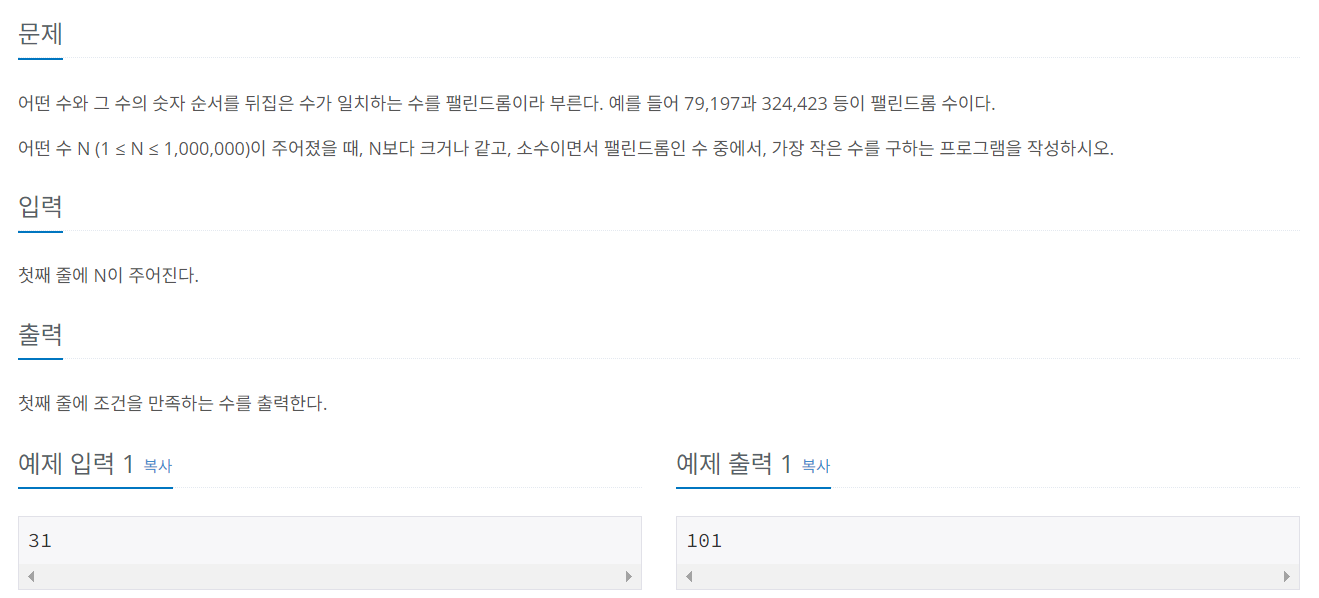
문제 039 소수 & 팰린드롬 수 중에서 최솟값 찾기
시간 제한: 2초, 난이도: 실버1, 1747번
import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
public static boolean[] number = new boolean[1005001];
public static void Eratosthenes() {
Arrays.fill(number, true);
number[0] = false;
number[1] = false;
for (int i = 2; i < Math.sqrt(1005000); i++) {
if (number[i]) {
for (int j = i + i; j < 1005001; j += i) {
number[j] = false;
}
}
}
}
public static boolean Pal(int a) {
String aNumber = String.valueOf(a);
String[] LR = aNumber.split("");
boolean result = true;
for (int i = aNumber.length() - 1; i >=0 ; i--) {
if (!LR[aNumber.length() - i - 1].equals(LR[i])) {
result = false;
break;
}
}
return result;
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(bf.readLine());
Eratosthenes();
int result = 0;
for (int i = N; i <= 1005000; i++) {
if (Pal(i) && number[i]) {
result = i;
break;
}
}
bw.write(result + "\n");
bw.flush();
bw.close();
}
}
소수와 팰린드롬 수를 만족하는 구간을 1부터 1000000까지로 했지만, N = 1000000 일 떄, 0이 출력이 되어서 1000000보다 큰 소수이면서 팰린드롬수를 만족하는 것이 1003001이므로, 이 구간을 늘려서 다시 풀어주었다.
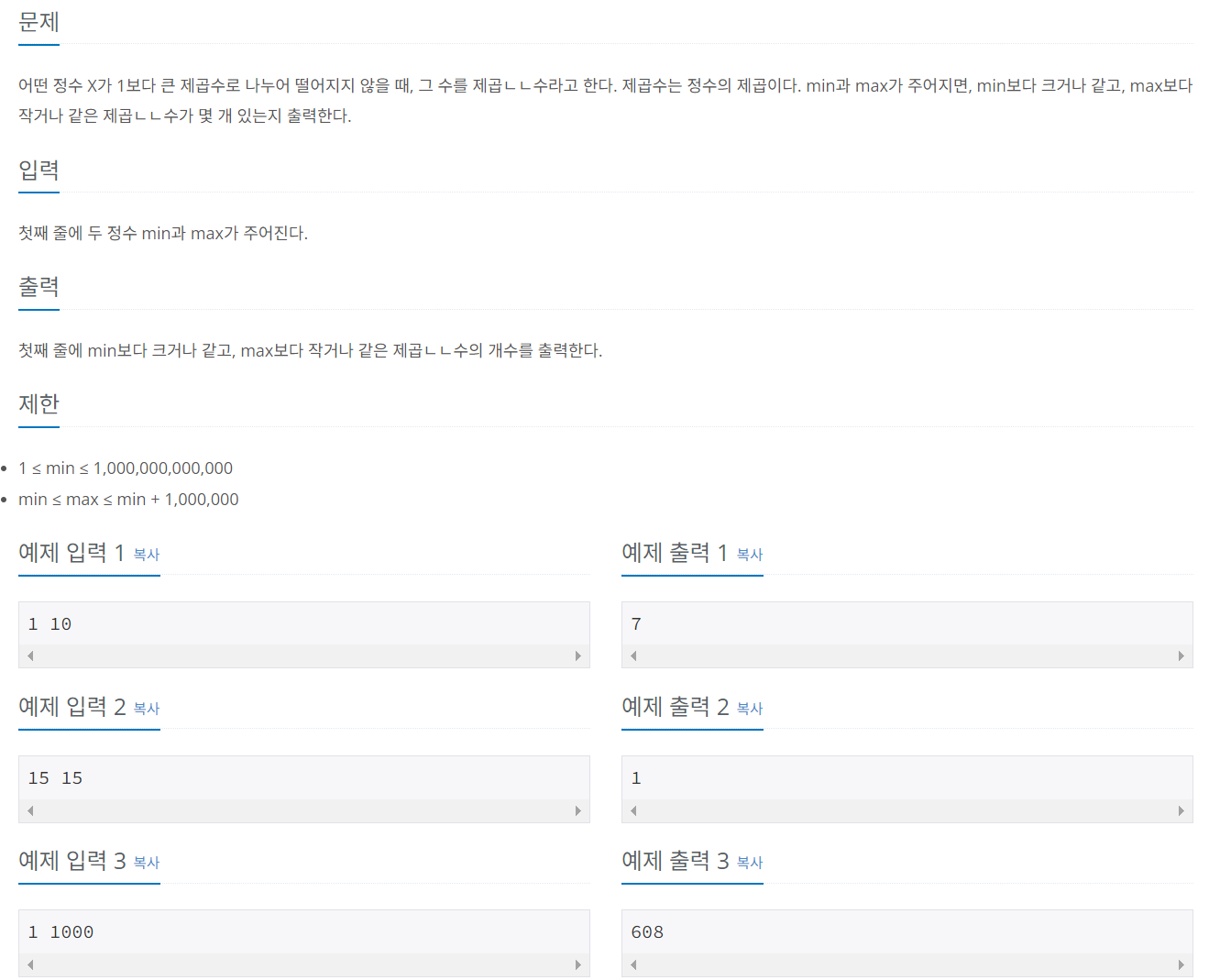
문제 040 제곱이 아닌 수 찾기
시간 제한: 2초, 난이도: 골드1, 1016번
풀이
import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(bf.readLine());
long min = Long.parseLong(st.nextToken());
long max = Long.parseLong(st.nextToken());
boolean[] number = new boolean[(int) (max - min + 1)];
for (long i = 2; i <= Math.sqrt(max); i++) {
long pow = i * i;
long temp = min / pow;
if (min % pow != 0) {
temp++;
}
for (long j = temp; j * pow <= max; j++) {
number[(int) (j * pow - min)] = true;
}
}
int result = 0;
for (int i = 0; i < max - min + 1; i++) {
if (!number[i]) {
result++;
}
}
bw.write(result + "\n");
bw.flush();
bw.close();
}
}
에라토스테네스의 채의 원리를 이용해 해당 문제를 접근하였다. 처음 시도할 때는 에라토스테네스의 채 처럼 boolean배열을 max까지 만들어 하였지만 이는 boundary를 초과하는 행동이여서 위 풀이와 같이 min부터 max까지의 boolean 배열을 만든 후 ““j*pow - min”“과 같은 연산을 해서 해당 배열의 index가 원하는 숫자와 match되게 하였다.
오일러 피
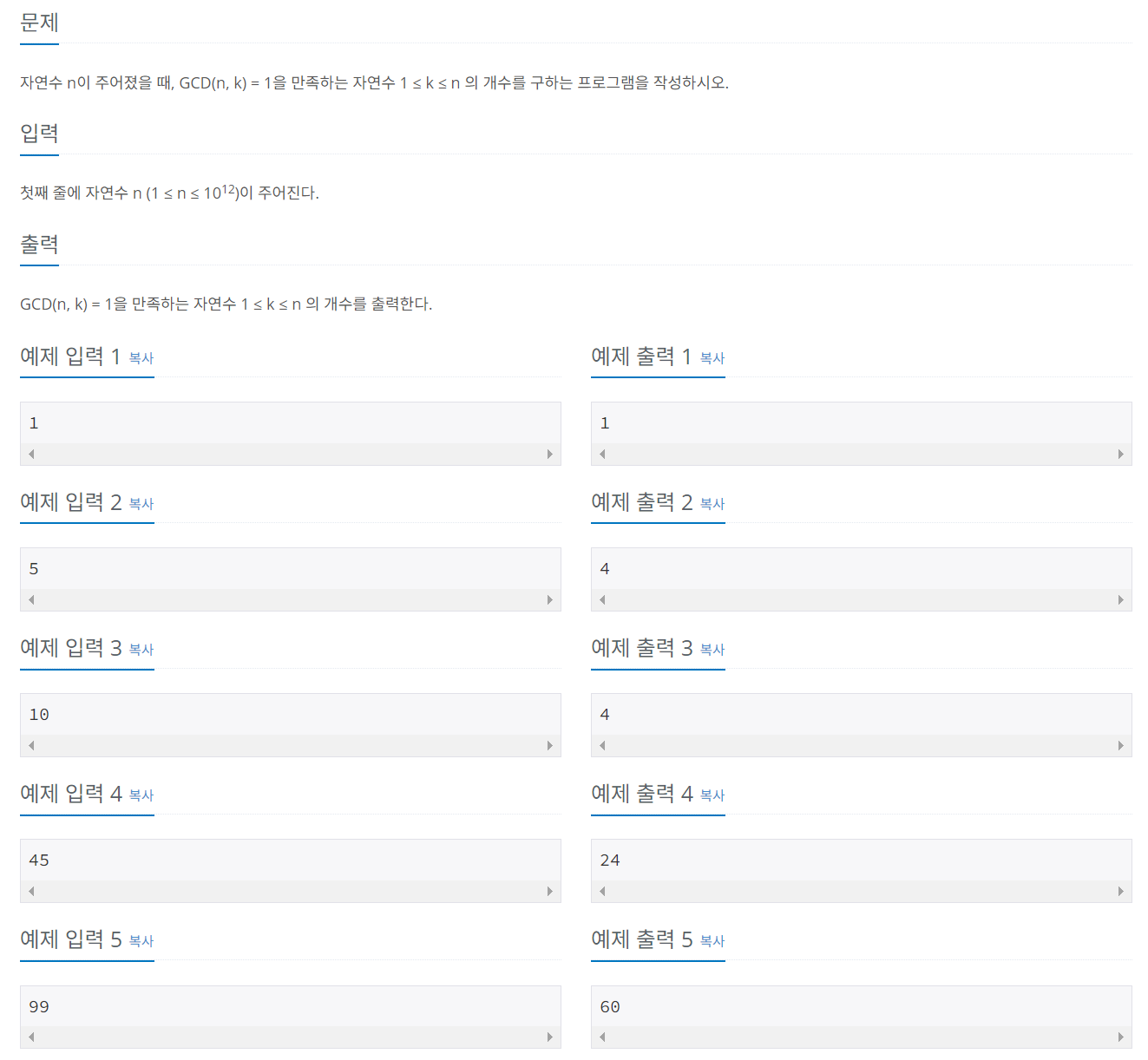
오일러 피 함수 P(N)의 정의는 1부터 N까지 범위에서 N과 서로소인 자연수의 개수를 뜻한다.
오일러 피의 핵심 이론
오일러 피 함수의 원리는 에라토스테네스의 채와 비슷하다.
- 구하고자 하는 오일러 피의 범위만큼 배열을 자기 자신의 인덱스값으로 초기화한다.
- 2부터 시작해 현재 배열의 값과 인덱스가 같으면(= 소수일 때), 현재 선택된 숫자(K)의 배수에 해당하는 수를 배열에 끝까지 탐색하며 $P[i] = P[i] - P[i]/K$ 연산을 수행한다. (i는 K의 배수)
- 배열의 끝까지 2를 반복하여 오일러 피 함수를 완성한다.
다음 예를 통해 오일러 피 함수를 좀 더 자세히 알아본다.
- 구하고자 하는 범위까지 배열을 생성한 후 2를 선택한다.
- 2의 모든 배수마다 $P[i] = P[i] - P[i]/2$ 연산을 수행해 값을 갱신한다.
- 소수 구하기에서 배수를 지우는 부분만 $P[i] = P[i] - P[i]/K$로 변경하면 오일러 피 함수를 간단히 구현할 수 있다. 탐색을 계속 진행하면서 $N = f(N)$인 곳(소수)을 찾아 값을 갱신한다.
- 배열이 끝날 때까지 반복한다.
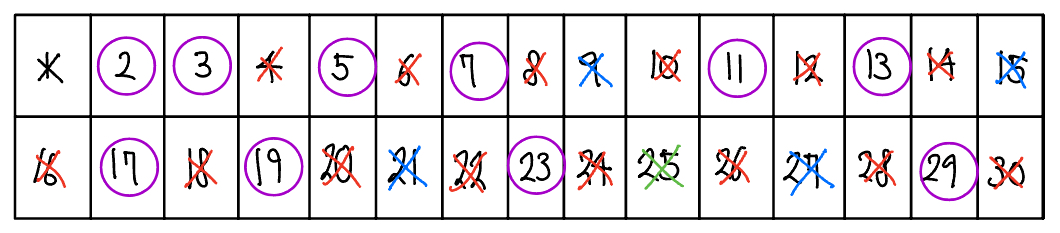
1 부터 15까지 범위에서 15와 서로소인 자연수의 개수는 8개이다.
문제 041 오일러 피 함수 구현하기
시간 제한: 1초, 난이도: 골드1, 11689번
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
long n = Long.parseLong(bf.readLine());
long result = n;
for (long i = 2; i <= Math.sqrt(n); i++) {
if (n % i == 0) {
result = result - result / i;
while (n % i == 0) {
n = n / i;
}
}
}
if (n > 1) {
result = result - result / n;
}
bw.write(result + "\n");
bw.flush();
bw.close();
}
}
위는 오일러 피의 원리를 이용해 구현하였다. 이전 오일러 피의 원리를 보는 과정에서 N의 소인수로 $N = N - N / K$ 연산을 진행하여 N의 소인수가 모두 이 연산을 완료하면 그 떄의 N이 위 문제의 결과가 되므로 에라토스테네스의 채처럼 소수만 필요로 하므로, N의 제곱근까지 이를 진행하고, 만일 n의 소인수가 남아있다면, 마지막 연산을 통해 이를 진행해 결과가 옳게 출력되게 하였다.
유클리드 호제법
유클리드 호제법(euclidean-algorithm)은 두 수의 최대 공약수를 구하는 알고리즘이다. 일반적으로 최대 공약수를 구하는 방법은 소인수 분해를 이용한 공통된 소수의 곱으로 표현할 수 있지만 유클리드 호제법은 좀 더 간단한 방법을 제시한다.
유클리드 호제법의 핵심 이론
유클리드 호제법을 수행하려면 먼저 MOD 연산을 이해야 한다. MOD 연산은 두 값을 나눈 나머지를 구하는 연산으로, 예를들어 10 MOD 4 = 2이다. MOD 연산을 이용해 유클리드 호제법을 구현할 수 있다. 참고로 최대 공약수를 구하는 연산은 일반적으로 gcd로 정의한다.
- 큰 수를 작은 수로 나누는 MOD 연산을 수행한다.
- 앞 단계에서의 작은 수와 MOD 연산 결괏값(나머지)으로 MOD 연산을 수행한다.
- 단계 2를 반복하다가 나머지가 0이 되는 순간의 작은 수를 최대 공약수로 선택한다.
270과 192의 최대 공약수를 유클리드 호제법으로 찾아보자.
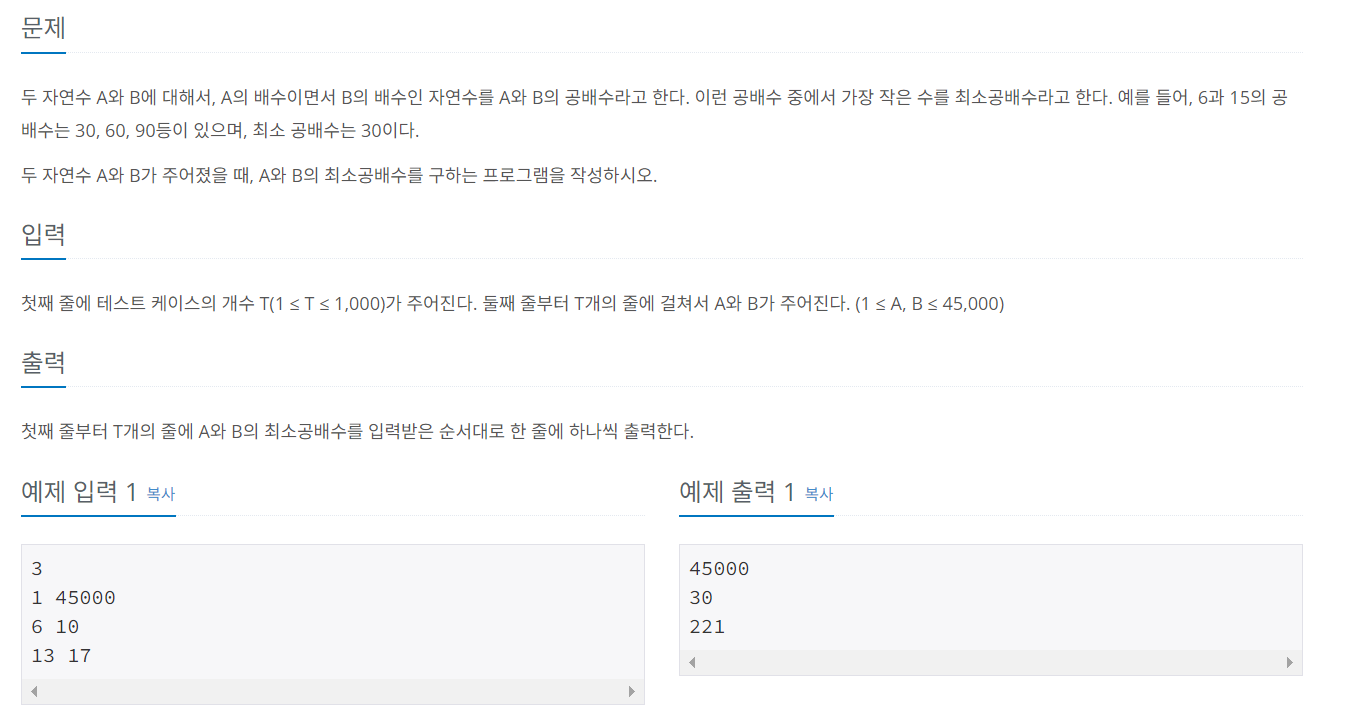
문제 042 최소 공배수 구하기
시간 제한: 1초, 난이도: 브론즈1, 1934번
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static void LCM(int a, int b) {
int a_temp = a;
int b_temp = b;
int temp = a_temp % b_temp;
while (temp != 0) {
a_temp = b_temp;
b_temp = temp;
temp = a_temp % b_temp;
}
int r = a / b_temp * b / b_temp * b_temp;
System.out.println(r);
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int T = Integer.parseInt(bf.readLine());
for (int i = 0; i < T; i++) {
StringTokenizer st = new StringTokenizer(bf.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
LCM(a, b);
}
}
}
유클리드 호제법을 이용해 gcd를 구한 후 이 gcd와 a, b를 gcd로 나눈 몫과 곱해 최소 공배수를 구한다.
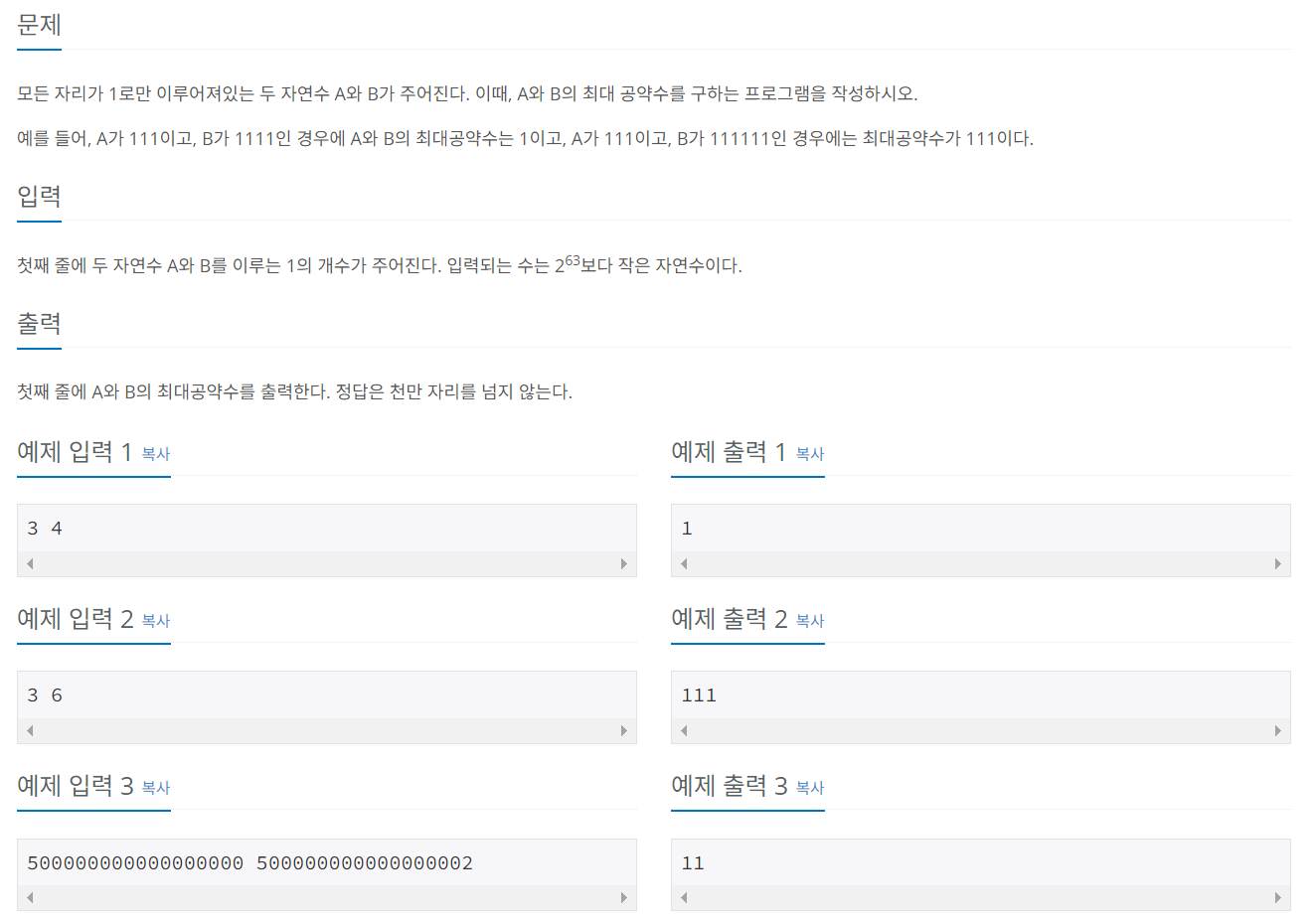
문제 043 최대 공약수 구하기
시간 제한: 2초, 난이도: 실버1, 1850번
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
public static void GCD(long a, long b) throws IOException {
if (a < b) {
long temp = a;
a = b;
b = temp;
}
long remain = a % b;
while (remain != 0) {
a = b;
b = remain;
remain = a % b;
}
for (int i = 0; i < b; i++) {
bw.write(1 + "");
}
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(bf.readLine());
long A = Long.parseLong(st.nextToken());
long B = Long.parseLong(st.nextToken());
GCD(A, B);
bw.flush();
bw.close();
}
}
유클리드 호제법을 이용해 최대 공약수를 구한 후 그 갯수만큼 1을 출력하였다.
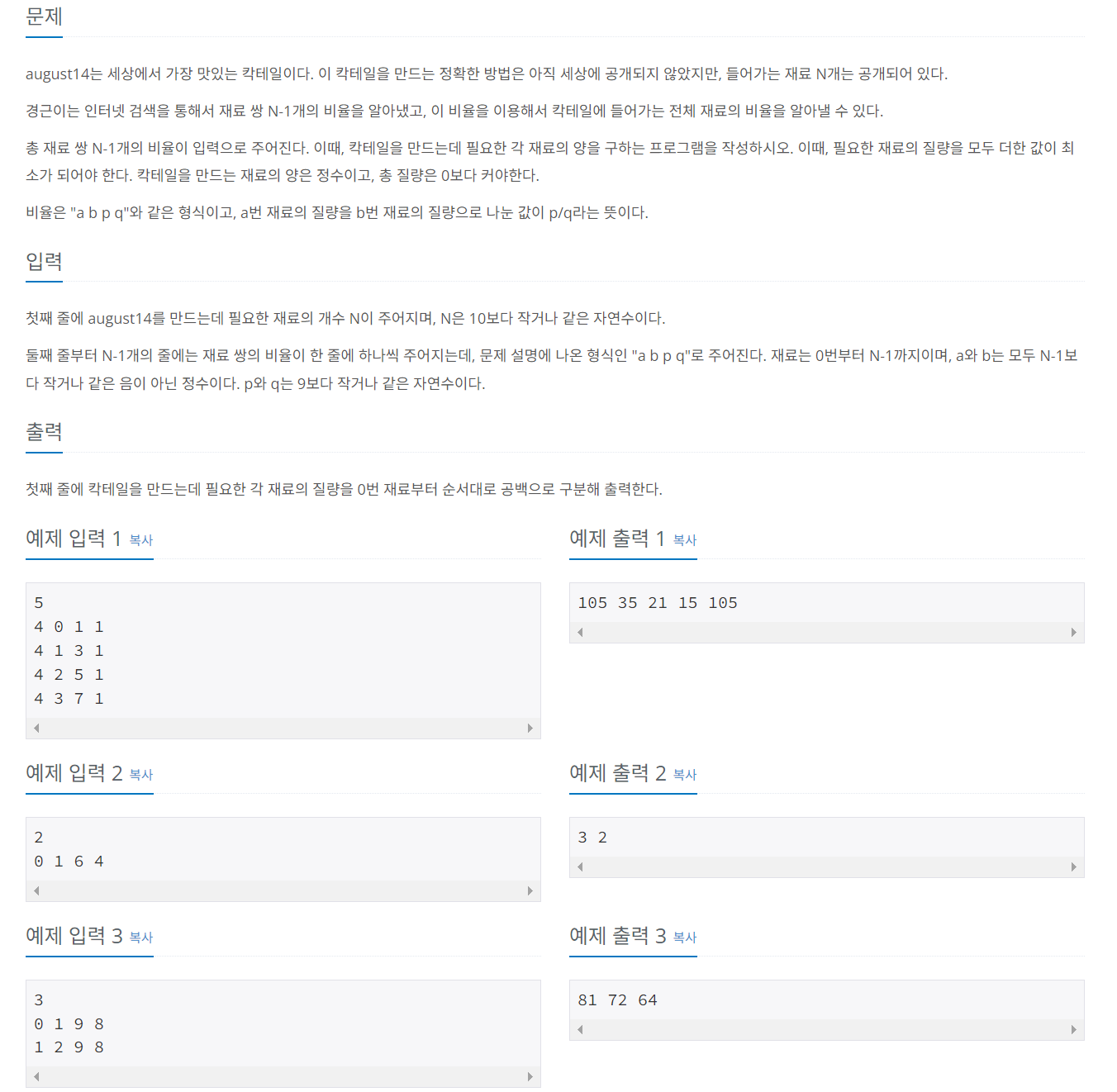
문제 044 칵테일 만들기
시간 제한: 2초, 난이도: 골드2, 1033번
풀이
import java.io.*;
import java.util.ArrayList;
import java.util.StringTokenizer;
public class Main {
public static ArrayList<cNode>[] arr;
public static boolean visit[];
public static long num[];
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(bf.readLine());
arr = new ArrayList[N];
for (int i = 0; i < N; i++) {
arr[i] = new ArrayList<>();
}
num = new long[N];
visit = new boolean[N];
long LCM = 1;
for (int i = 0; i < N - 1; i++) {
StringTokenizer st = new StringTokenizer(bf.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int p = Integer.parseInt(st.nextToken());
int q = Integer.parseInt(st.nextToken());
arr[a].add(new cNode(b, p, q));
arr[b].add(new cNode(a, q, p));
LCM *= (p * q / GCD(p, q));
}
num[0] = LCM;
DFS(0);
long gcd = num[0];
for (int i = 1; i < N; i++) {
gcd = GCD(gcd, num[i]);
}
for (int i = 0; i < N; i++) {
bw.write(num[i] / gcd + " ");
}
bw.flush();
bw.close();
}
public static class cNode {
int node;
int p;
int q;
public cNode(int node, int p, int q) {
this.node = node;
this.p = p;
this.q = q;
}
}
public static long GCD(long a, long b) {
if (b == 0) {
return a;
} else {
return GCD(b, a % b);
}
}
public static void DFS(int node) {
visit[node] = true;
for (cNode adjNode : arr[node]) {
int next = adjNode.node;
if (!visit[next]) {
num[next] = num[node] * adjNode.q / adjNode.p;
DFS(next);
}
}
}
}
확장 유클리드 호제법
유클리드 호제법의 목적이 두 수의 최대 공약수를 구하는 것이라면 확장 유클리드 호제법의 목적은 방정식의 해를 구하는 것이다.
확장 유클리드 호제법의 핵심 이론
확장 유클리드 호제법에서 해를 구하고자 하는 방정식은 $ax + by = c (a, b, c, x, y\mathrm{는 정수})$과 같다. 이때 방정식은 c % gcd(a, b) = 0인 경우에만 정수해를 가진다. 이는 $ax + by = c$가 정수해를 갖게 하는 c의 최솟값이 gcd(a, b)라는 것을 의미한다. 이는 재귀 함수를 이용해 구현한다.
$5x + 9y = 2$일 때 이 식을 만족하는 정수 $x, y$를 구해보자.
- 우선 $5x + 9y$가 정수해를 갖게 하는 $c$의 최솟값이 gcd(5, 9)라는 것을 적용하여 식을 다시 놓는다. gcd(5, 9) = 1이므로 $5x + 9y = 1$로 식을 다시 놓고 다음 단계를 진행한다.
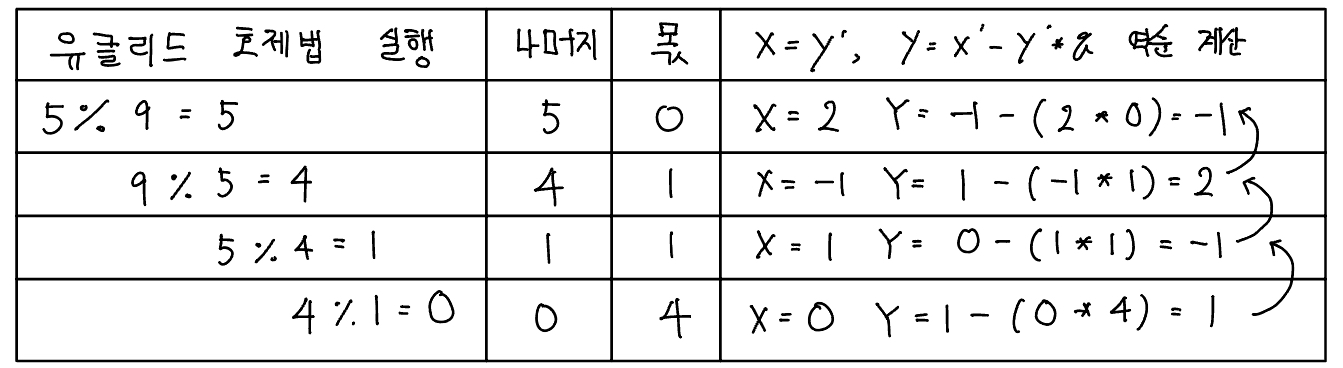
- a, b로 유클리드 호제법을 반복 실행하며 몫, 나머지를 저장한다. 반복은 나머지가 0이 되면 중단한다.
- 반복으로 구한 나머지와 몫을 이용하여 거꾸로 올라가며 $x = y^\prime$, $y = x^\prime - y^\prime * q$를 계산한다. $x^\prime$은 이전 $x$, $y^\prime$은 이전 $y$를 의미하고, $q$는 현재 보고 있는 몫을 의미한다. 이때 처음 시작하는 $x$, $y$는 이전 $x$와 이전 $y$가 없으므로 각각 1, 0으로 지정하여 역계산을 진행한다.
- 이렇게 재귀 방식으로 알아낸 최종 $x$, $y$는 $ax + by = \mathrm{gcd}(a, b)$를 만족한다. 그리고 c / gcd(a, b) = K를 가정하면 최초 방정식의 해는 $Kx$, $Ky$로 간단히 구할 수 있다. 과정 3에서 찾은 $x$는 2, $y$는 -1이고 K값을 구하면 2(c값)/1(최대 공약수) = 2가 되므로 2의 값을 기존의 $x$, $y$ 값에 각각 곱한다. 이에 따라 최초 방정식의 해는 4, -2가 된다.
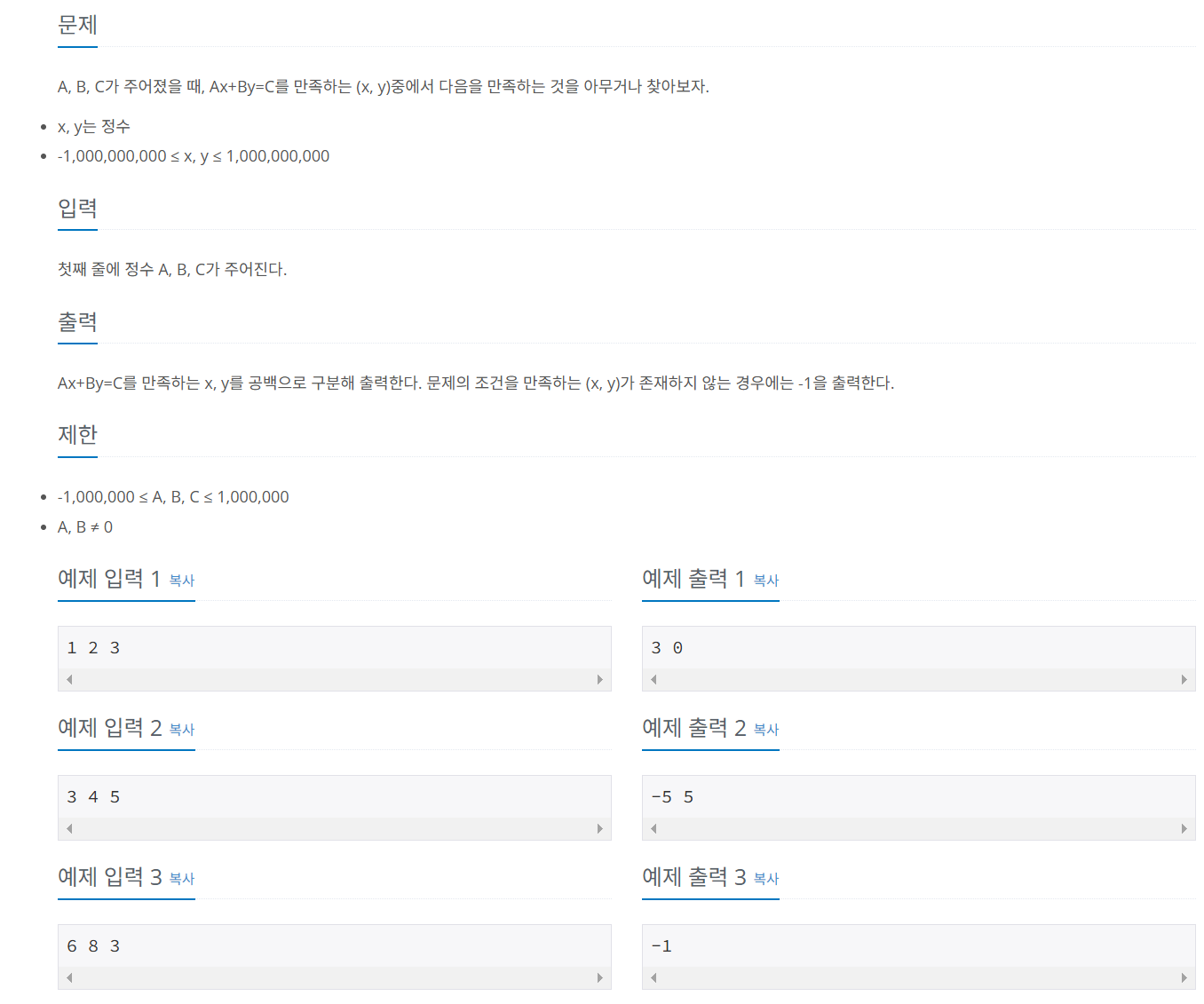
문제 045 Ax + By = C
시간 제한: 1초, 난이도: 골드1, 21566번
풀이
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static int X = 1;
public static int Y = 0;
public static int GCD(int A, int B) {
if (B > A) {
int temp = A;
A = B;
B = temp;
} // A를 큰 수로
int temp = A % B;
while (temp != 0) {
A = B;
B = temp;
temp = A % B;
}
return B;
}
public static void Root(int A, int B) {
int root = A / B;
int remain = A % B;
if (remain != 0) {
Root(B, remain);
}
int XPre = X;
int YPre = Y;
X = YPre;
Y = XPre - (YPre * root);
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(bf.readLine());
int A = Integer.parseInt(st.nextToken());
int B = Integer.parseInt(st.nextToken());
int C = Integer.parseInt(st.nextToken());
if (C % GCD(A, B) != 0) {
bw.write("-1");
} else {
int K = C / GCD(A, B);
Root(A, B);
X = K * X;
Y = K * Y;
bw.write(X + " " + Y);
}
bw.flush();
bw.close();
}
}









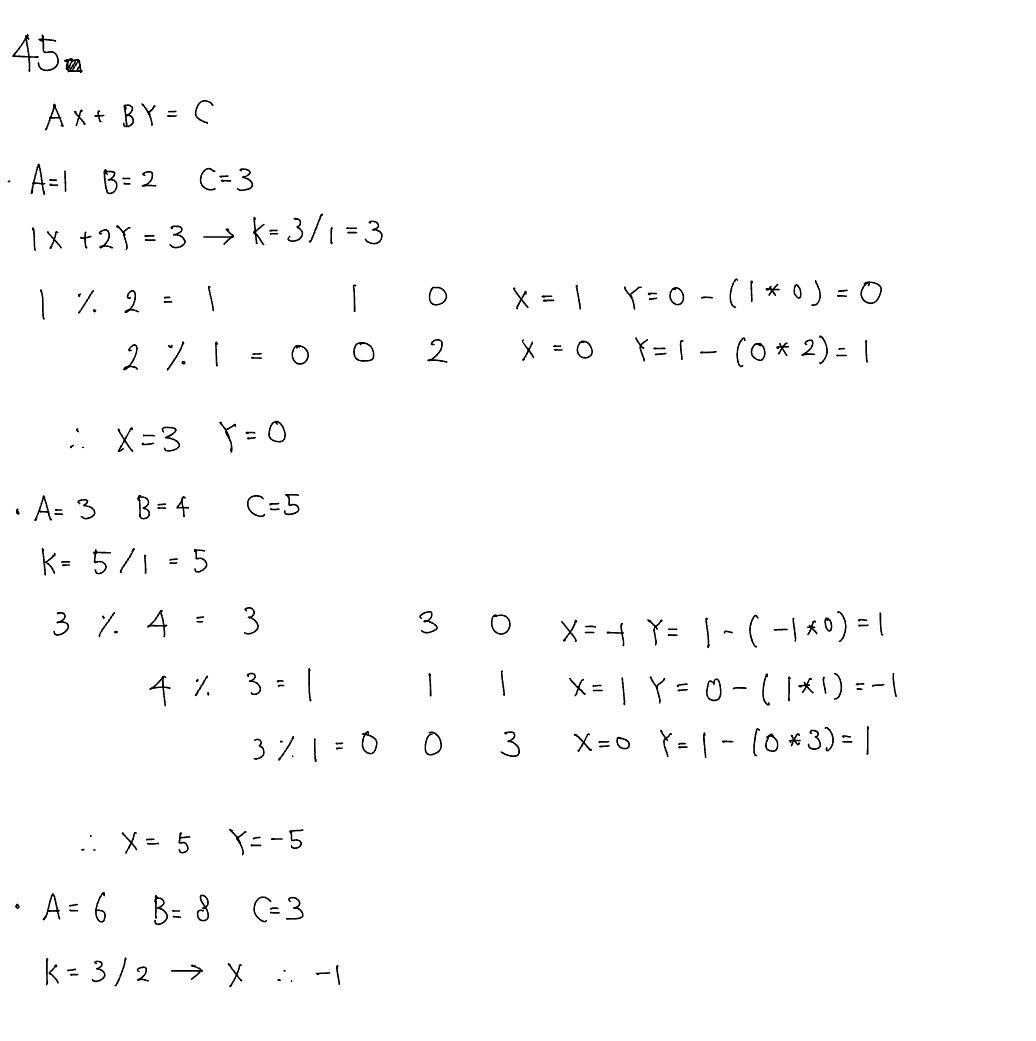
댓글남기기