8장 그래프
Updated:
그래프의 표현
그래프를 구현하는 3가지 방법을 알아본다.
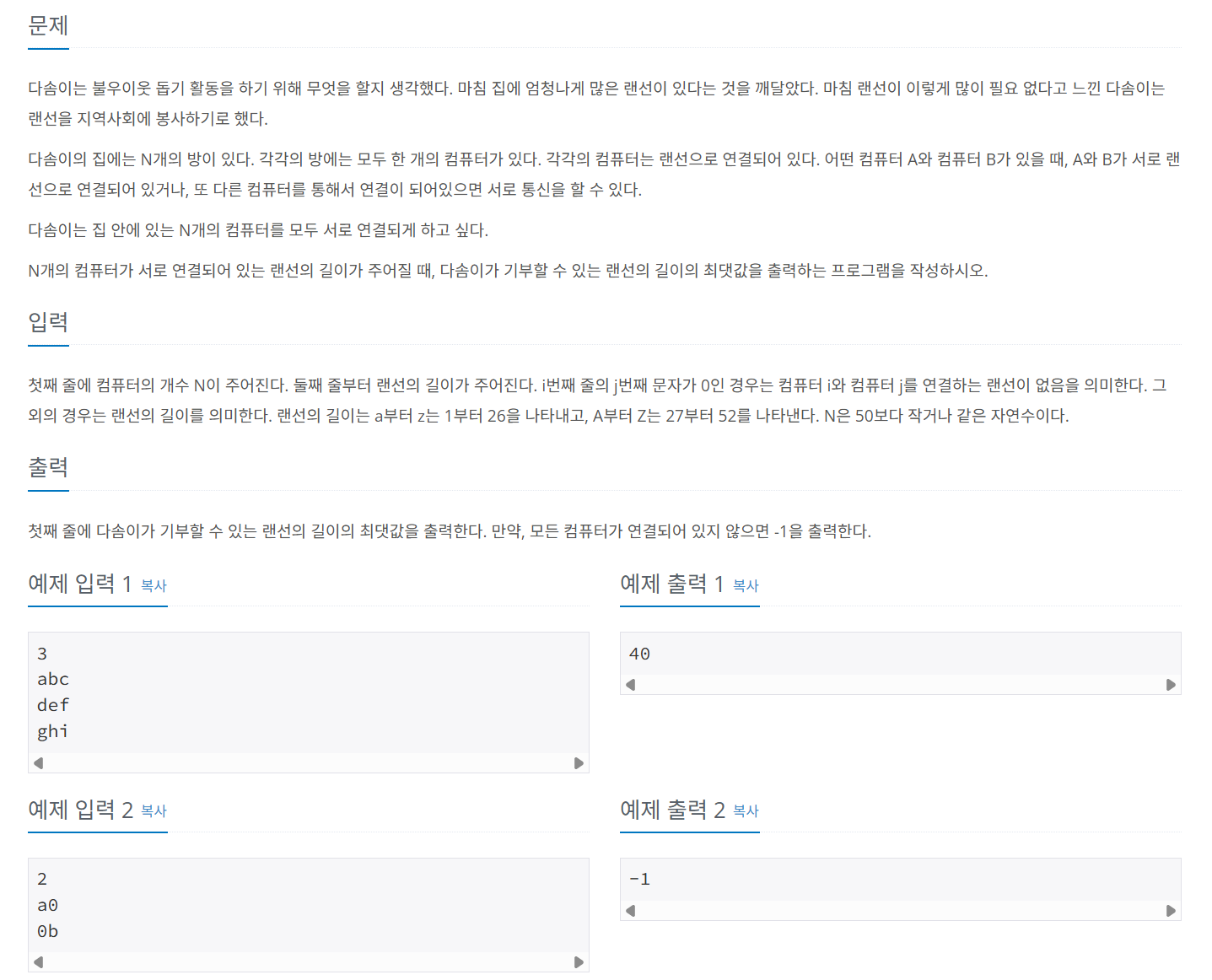
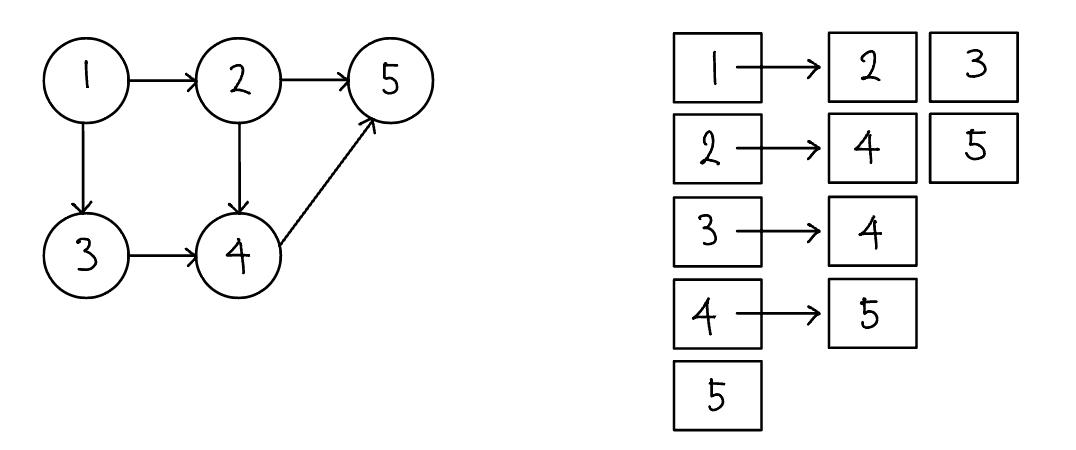
에지 리스트
에지 리스트(Edge list)는 에지를 중심으로 그래프를 표현한다. Edge list는 배열에 출발 노드, 도착 노드를 저장하여 Edge를 표현한다. 또는 출발 노드, 도착 노드, 가중치를 저장하여 가중치가 있는 Edge를 표현한다.
에지 리스트로 가중치 없는 그래프 표현하기
가중치가 없는 그래프는 출발 노드와 도착 노드만 표현하므로 배열의 열은 2개면 충분하다. 이처럼 방향이 있는 그래프는 순서에 맞게 노드를 배열에 저장하는 방식으로 표현한다. 그리고 노드를 배열에 저장하여 Edge를 표현하므로 에지 리스트라 한다.
에지 리스트로 가중치 있는 그래프 표현하기
가중치가 있는 그래프는 열을 3개로 늘려 3번째 열에 가중치를 저장하면 된다. 위 그림처럼 에지 리스트는 구현하기 쉽다. 하지만 특정 노드와 관련된 에지를 탐색하기는 쉽지 않다. 에지 리스트는 노드 사이의 최단 거리를 구하는 벨만-포드나 최소 신장 트리를 찾는 크루스칼 알고리즘에 사용하며, 노드 중심 알고리즘에는 잘 사용하지 않는다.
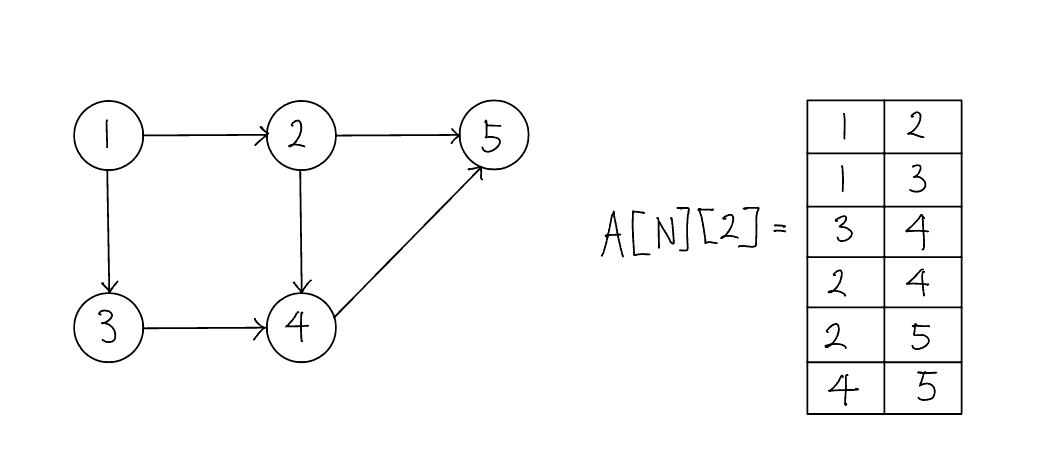
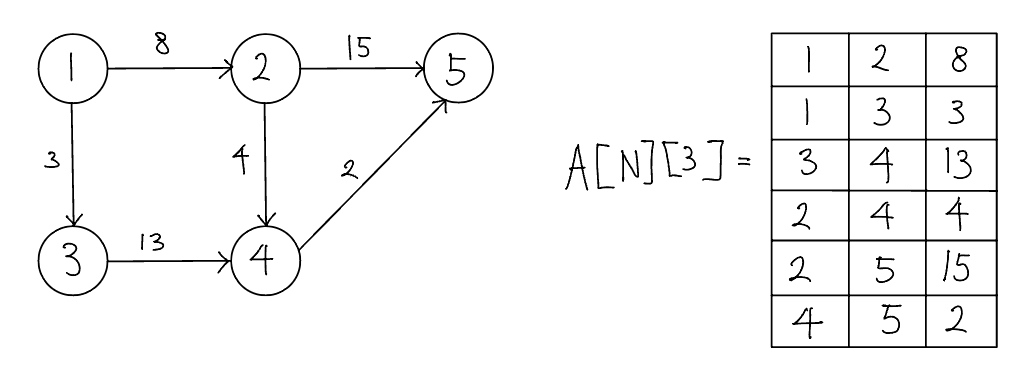
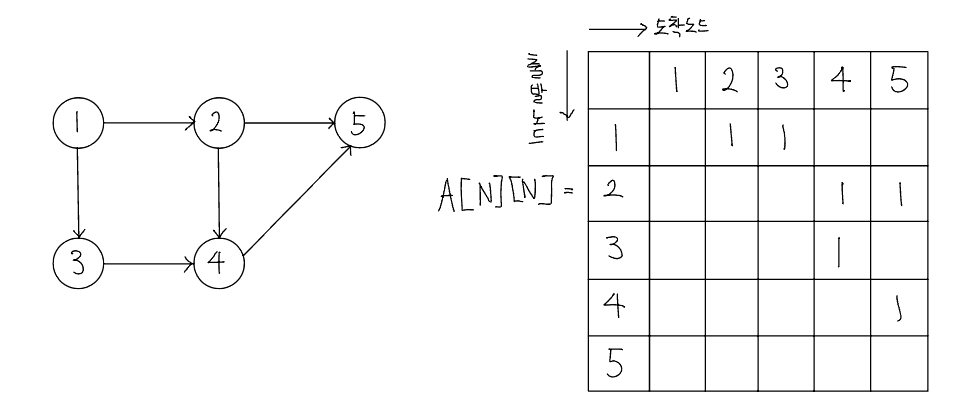
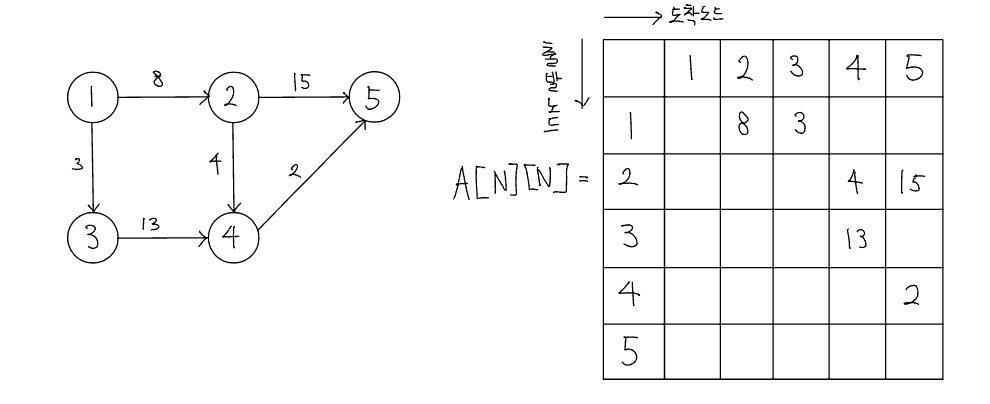
인접 행렬
인접 행렬(Adjacency Matric)은 2차원 배열을 자료구조로 이용하여 그래프를 표현한다. 인접 행렬은 에지 리스트와 다르게 노드 중심으로 그래프를 표현한다. 다음은 노드가 5개인 그래프를 $5 \times 5$ 인접 행렬로 표현한 것이다.
인접 행렬로 가중치 없는 그래프 표현하기
인접 행렬로 가중치 있는 그래프 표현하기
이처럼 인접 행렬을 이용한 그래프 구현은 쉽다. 두 노드를 연결하는 에지의 여부와 가중치값은 배열에 직접 접근하면 바로 확인할 수 있는 것도 장점이다. 하지만 노드와 관련되어 있는 에지를 탐색하려면 N번 접근해야 하므로 시간 복잡도가 인접 리스트에 비해 느리고 노드 개수에 비해 에지가 적을 때는 공간 효울성이 떨아진다.
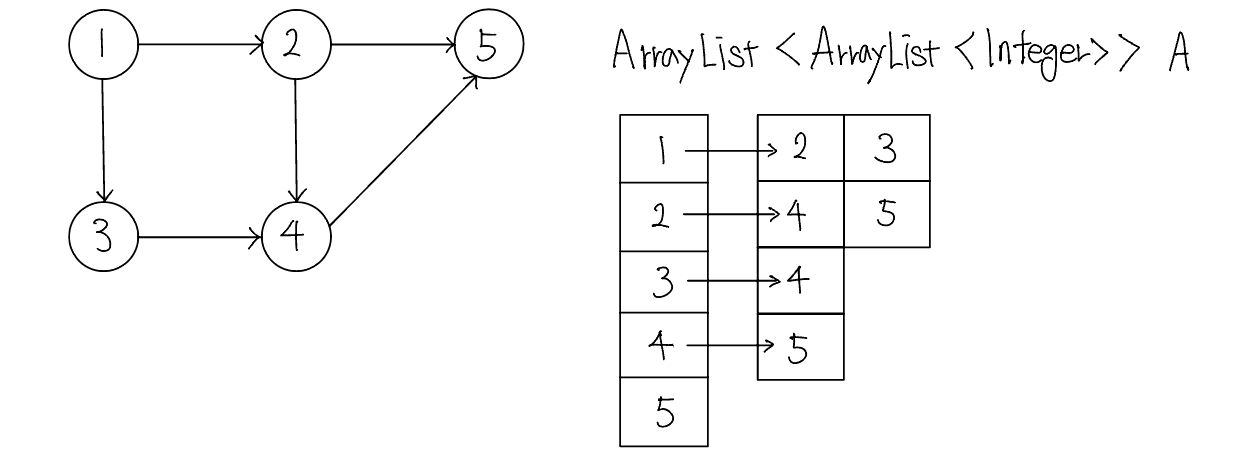
인접 리스트
인접 리스트(Adjacency list)는 2차원 ArrayList로 그래프를 표현한다.
인접 리스트로 가중치 없는 그래프 표현하기
위는 인접 리스트로 가중치 없는 그래프를 표현한 것이다. ArrayList로 인접 리스트를 선언해 준뒤, 인접 리스트로 선언된 그래프에 ArrayList를 넣어주면서 초기화 해준다.
ArrayList<ArrayList<Integer>> graph = new ArrayList<>();
for(int i=0; i <=n; i++) {
graph.add(new ArrayList<>());
}
이후 A.get(a).add(b)를 해주며 노드와 데이터를 추가한다.
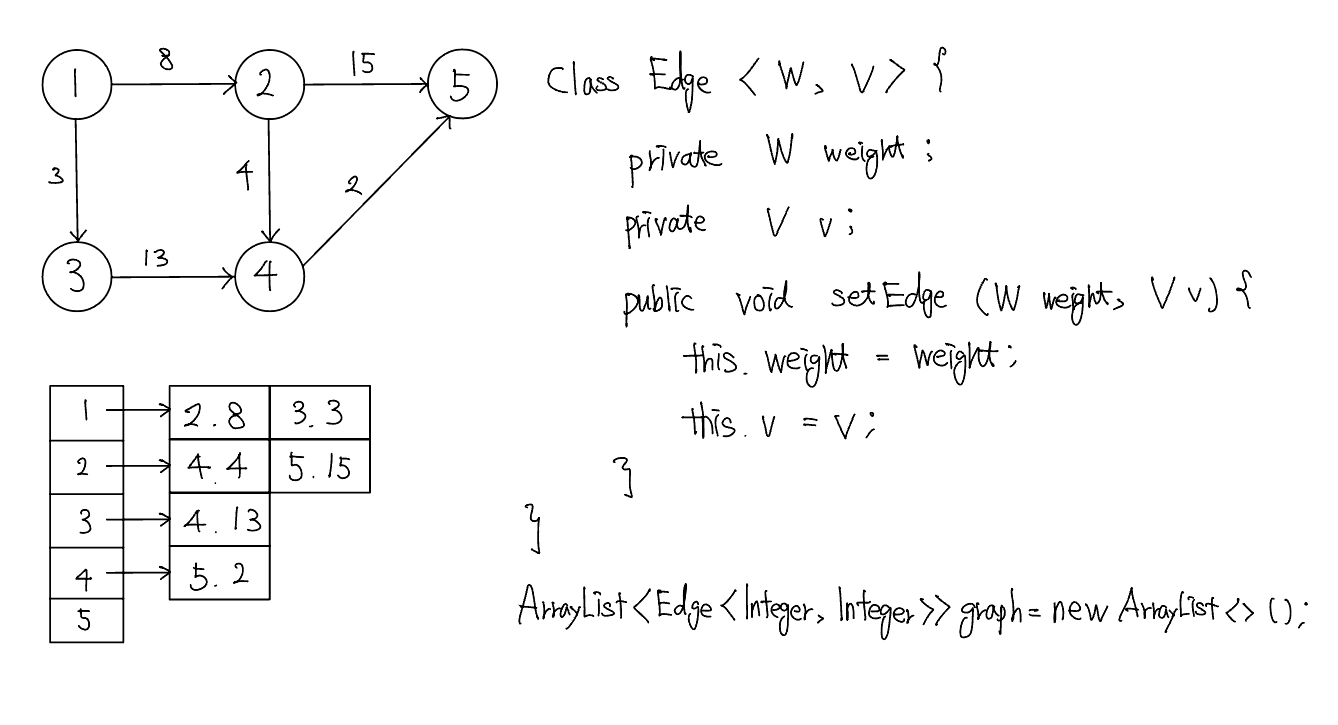
인접 리스트로 가중치 없는 그래프 표현하기
가중치가 있는 경우 Edge 클래스를 선언하여 표연할 수 있다.
인접 리스트를 이용한 그래프 구현은 다른 방법에 비해 복잡한 편이다. 하지만 노드와 연결된 에지를 탐색하는 시간은 매우 뛰어나며, 노드 개수가 커도 공간 효율이 좋아 메모리 초과 에러도 발생하지 않는다.
문제 046 특정 거리의 도시 찾기
시간 제한: 2초, 난이도: 실버2, 18352번
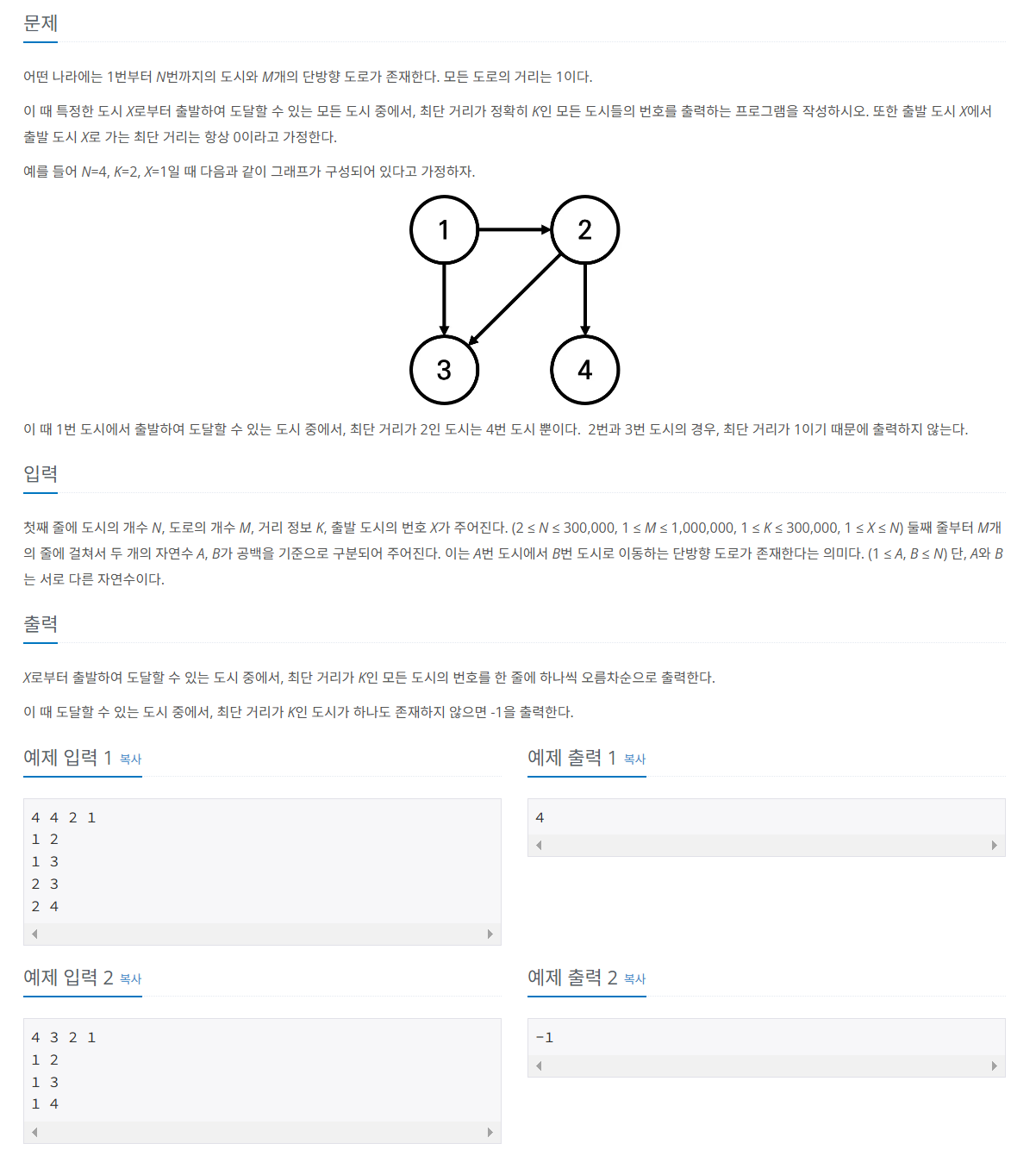
import java.io.*;
import java.util.*;
public class Main {
public static ArrayList<ArrayList<Integer>> Graph;
public static boolean[] Visit;
public static int[] min;
public static void BFS(int a) {
Queue<Integer> qu = new LinkedList<>();
qu.offer(a);
Visit[a] = true;
min[a] = 0;
while (!qu.isEmpty()) {
int node = qu.poll();
for (int i = 0; i < Graph.get(node).size(); i++) {
int temp = Graph.get(node).get(i);
if (!Visit[temp]) {
Visit[temp] = true;
min[temp] = min[node] + 1;
qu.offer(temp);
}
}
}
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(bf.readLine());
int N = Integer.parseInt(st.nextToken()); // 도시의 개수
int M = Integer.parseInt(st.nextToken()); // 도로의 개수
int K = Integer.parseInt(st.nextToken()); // 거리 정보
int X = Integer.parseInt(st.nextToken()); // 출발 도시
Graph = new ArrayList<>();
for (int i = 0; i <= N; i++) {
Graph.add(new ArrayList<>());
}
Visit = new boolean[N + 1];
min = new int[N + 1]; // 최단 거리를 담아두기 위한 배열
for (int i = 0; i < M; i++) {
StringTokenizer st2 = new StringTokenizer(bf.readLine());
int A = Integer.parseInt(st2.nextToken());
int B = Integer.parseInt(st2.nextToken());
Graph.get(A).add(B);
}
BFS(X);
int count = 0;
for (int i = 1; i <= N; i++) {
if (min[i] == K) {
count++;
bw.write(i + "\n");
}
}
if (count == 0) {
bw.write("-1");
}
bw.flush();
bw.close();
}
}
BFS를 하면서 최단 거리를 담는 배열에 이전 node 값에 +1을 해서 넣어주었다.
문제 047 효율적으로 해킹하기
시간 제한: 5초, 난이도: 실버1, 1325번
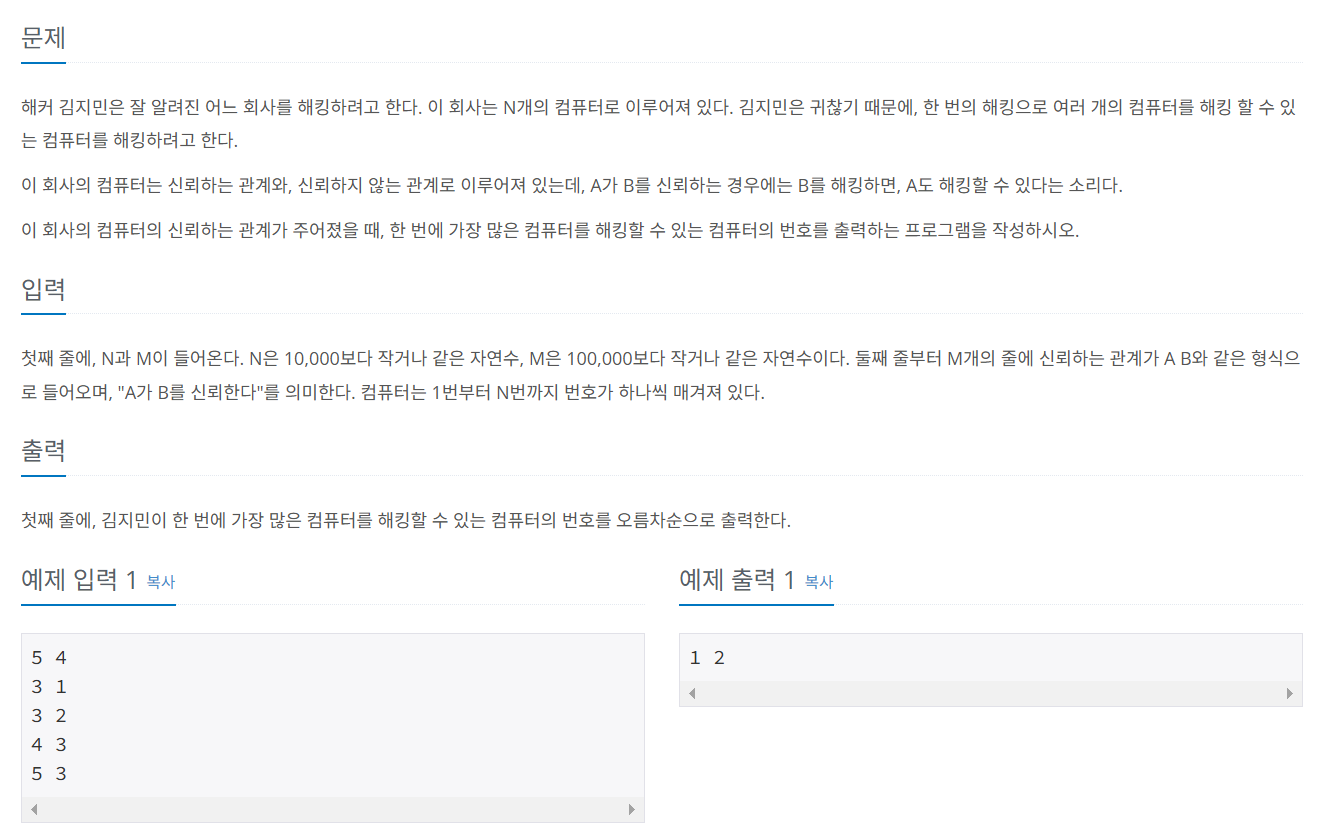
import java.io.*;
import java.util.*;
public class Main {
public static ArrayList<ArrayList<Integer>> company = new ArrayList<>();
public static int[] count;
public static boolean[] visit;
public static void BFS(int a) {
Queue<Integer> qu = new LinkedList<>();
qu.add(a);
visit[a] = true;
while (!qu.isEmpty()) {
int temp = qu.poll();
for (int i : company.get(temp)) {
if (!visit[i]) {
visit[i] = true;
count[a]++;
qu.add(i);
}
}
}
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(bf.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
count = new int[N + 1];
for (int i = 0; i < N + 1; i++) {
company.add(new ArrayList<>());
}
for (int i = 0; i < M; i++) {
st = new StringTokenizer(bf.readLine());
int A = Integer.parseInt(st.nextToken());
int B = Integer.parseInt(st.nextToken());
company.get(B).add(A);
}
int maxCount = 0;
for (int i = 1; i <= N; i++) {
visit = new boolean[N + 1];
BFS(i);
if (count[i] > maxCount) {
maxCount = count[i];
}
}
// count 배열에서 최대값
for (int i = 1; i <= N; i++) {
if (count[i] == maxCount) {
bw.write(i + " ");
}
}
bw.flush();
bw.close();
}
}
DFS를 해서 풀었더니 시간초과가 발생해서 BFS로 풀었다.
문제 048 이분 그래프 판별하기
시간 제한: 2초, 난이도: 골드4, 1707번
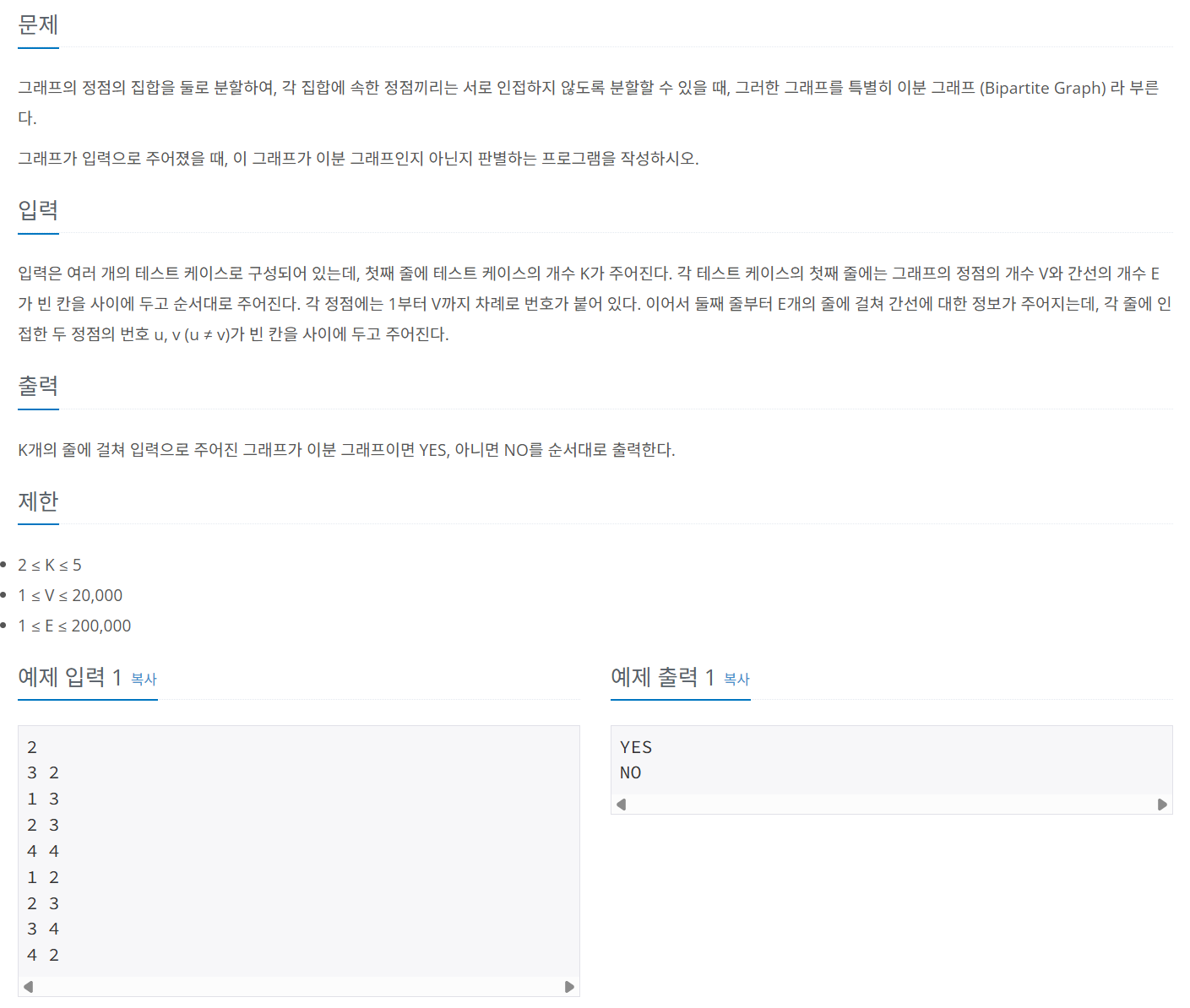
import java.io.*;
import java.util.ArrayList;
import java.util.StringTokenizer;
public class Main {
public static BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
public static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
public static ArrayList<ArrayList<Integer>> Graph;
public static int[] Visit;
public static boolean IsBiGraph;
public static int V;
public static int E;
public static void DFS(int a) {
for (int i = 0; i < Graph.get(a).size(); i++) {
int temp = Graph.get(a).get(i);
if (Visit[temp] == 0) {
if (Visit[a] == 2) {
Visit[temp] = 3;
DFS(temp);
} else {
Visit[temp] = 2;
DFS(temp);
}
} else if (Visit[temp] == Visit[a]) {
IsBiGraph = false;
}
}
}
public static void BiGraph() throws IOException {
StringTokenizer st = new StringTokenizer(bf.readLine());
Graph = new ArrayList<>();
V = Integer.parseInt(st.nextToken());
E = Integer.parseInt(st.nextToken());
IsBiGraph = true;
for (int i = 0; i <= V; i++) {
Graph.add(new ArrayList<>());
}
for (int i = 0; i < E; i++) {
st = new StringTokenizer(bf.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
Graph.get(a).add(b);
Graph.get(b).add(a);
}
Visit = new int[V + 1];
for (int i = 1; i <= V; i++) {
if (Visit[i] == 0) {
Visit[i] = 2;
DFS(i);
if (!IsBiGraph) {
break;
}
}
}
if (IsBiGraph) {
bw.write("YES\n");
} else {
bw.write("NO\n");
}
}
public static void main(String[] args) throws IOException {
int K = Integer.parseInt(bf.readLine());
for (int i = 0; i < K; i++) {
BiGraph();
}
bw.flush();
bw.close();
}
}
이분 그래프인지 찾는 문제는 그래프를 두 가지 색으로 같은 색이 인접하지 않게 색칠할 수 있는가를 물어보는 것이다. 따라서 위와 같이 DFS를 수행하면서 색을 칠해 본다. 또한 모든 그래프가 연결되지 않을 수도 있기 때문에 방문하지 않은 정점에 대해서 다시 DFS를 수행한다.
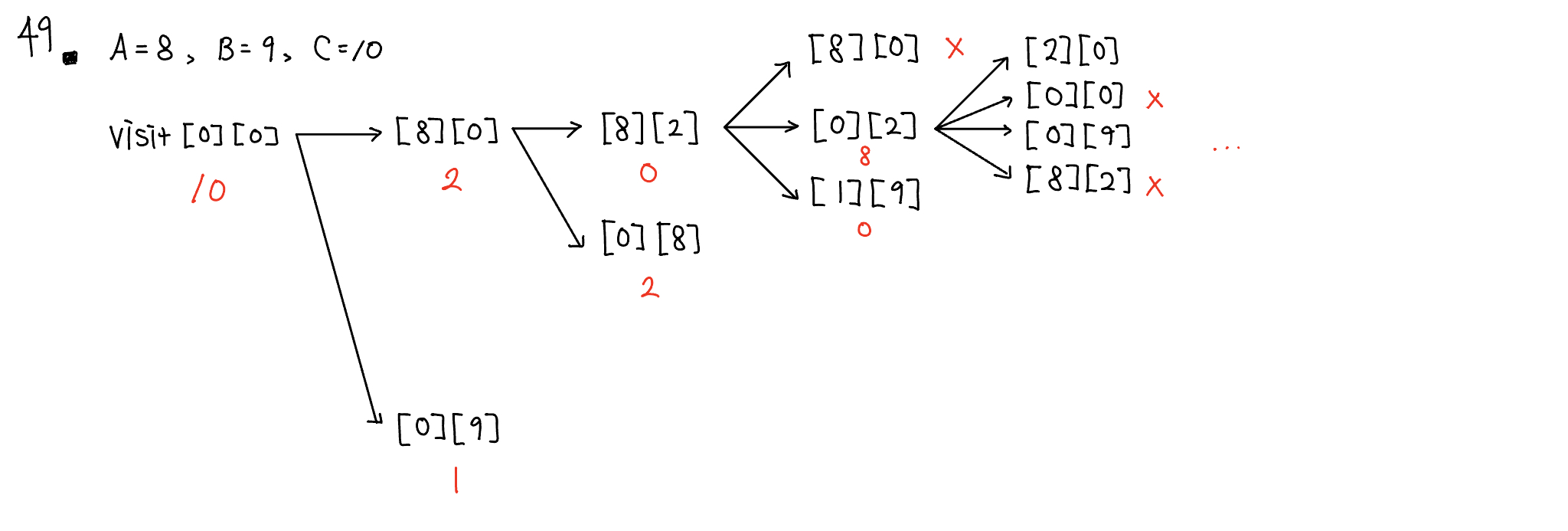
문제 049 물의 양 구하기
시간 제한: 1초, 난이도: 골드4, 2251번
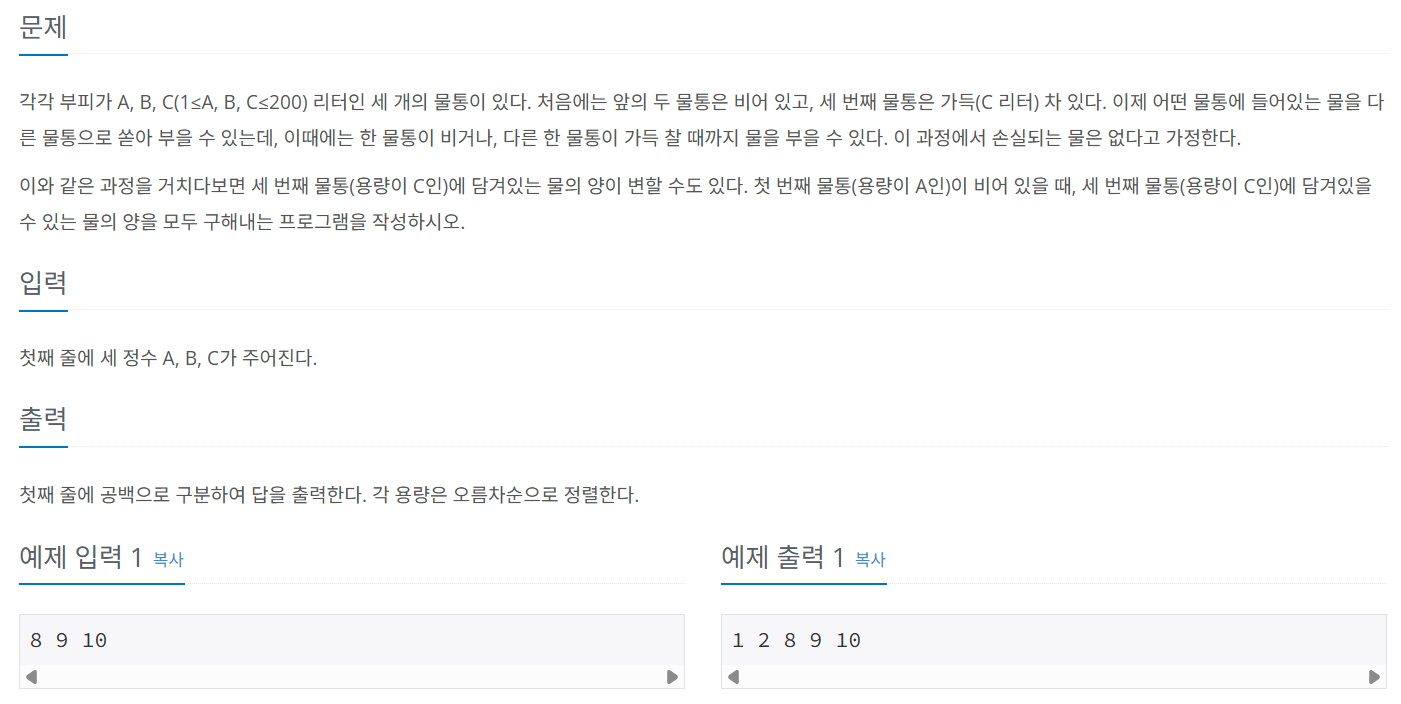
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static int A, B, C;
public static boolean Visit[][];
public static boolean result[];
public static void DFS(int a, int b) {
if (Visit[a][b]) {
return;
}
Visit[a][b] = true;
int c = C - (a + b); // 물통 C에 있는 물의 양
if (a == 0) { // 물통 A가 비어있을 때
result[c] = true;
}
if (a > 0) {
if (a + b > B) { // A to B
DFS(a + b - B, B);
} else {
DFS(0, a + b);
}
DFS(0, b); // A to C
}
if (b > 0) {
if (a + b > A) {
DFS(A, a + b - A);
} else {
DFS(a + b, 0);
}
DFS(a, 0);
}
if (c > 0) {
if (a + c > A) {
DFS(A, b);
} else {
DFS(a + c, b);
}
if (b + c > B) {
DFS(a, B);
} else {
DFS(a, b + c);
}
}
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(bf.readLine());
A = Integer.parseInt(st.nextToken());
B = Integer.parseInt(st.nextToken());
C = Integer.parseInt(st.nextToken());
Visit = new boolean[A + 1][B + 1];
result = new boolean[C + 1];
DFS(0, 0);
for (int i = 0; i < C + 1; i++) {
if (result[i]) {
bw.write(i + " ");
}
}
bw.flush();
bw.close();
}
}
DFS로 문제를 접근하였다. A에 있는 물을 B와 C로, B에 있는 물을 A와 C로, C에 있는 물을 A와 B로 옮기는 순서로 DFS를 진행하고, 만약 물통 A가 비어있다면 결과 배열을 true로 바꿨다.
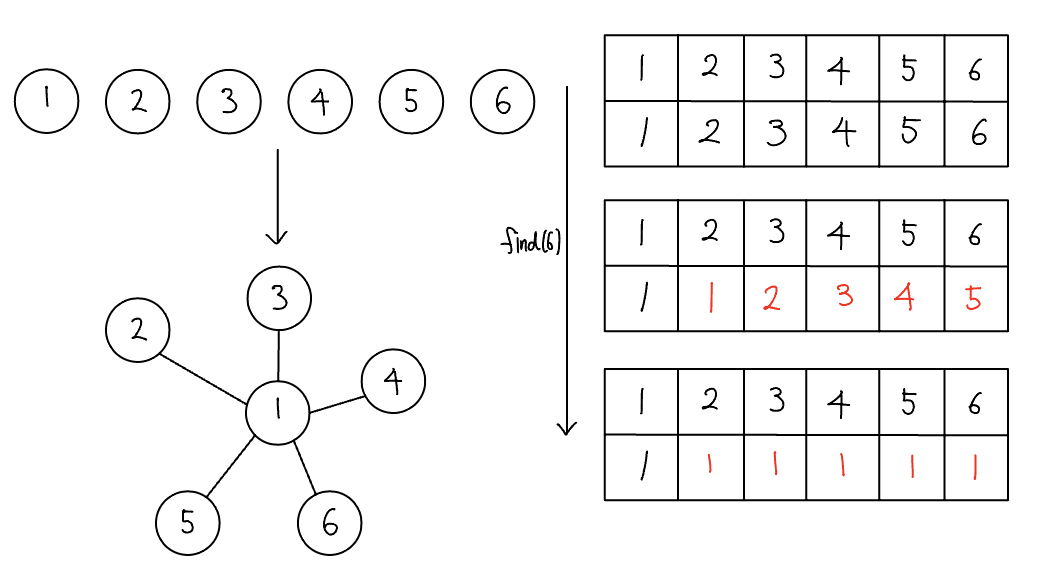
유니온 파인드
유니온 파인트(union-find)는 일반적으로 여러 노드가 있을 때 특정 2개의 노드를 연결해 1개의 집합으로 묶는 union 연산과 두 노드가 같은 집합에 속해 있는지를 확인하는 find 연산으로 구성된 알고리즘이다.
유니온 파인드의 핵심 이론
유니온 파인드는 union, find 연산을 완벽히 이해하는 것이 핵심이다. 두 연산은 다음과 같다.
- union 연산: 각 노드가 속한 집합을 1개로 합치는 연산이다. 노드 a, b가 $a \in A, b \in B$일 때 union(a, b)는 $A \cup B$를 말한다.
- find 연산: 특정 노드 a에 관해 a가 속한 집합의 대표 노드를 반환하는 연산이다. 노드 a가 $a \in A$일 때, find(a)는 A 집합의 대표 노드를 반환한다.
유니온 파인드 알고리즘 구현 방법을 알아본다.
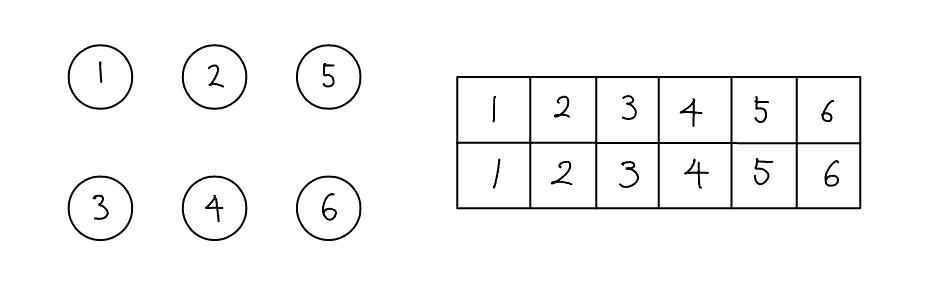
- 유니온 파인드를 표현하는 일반적인 방법은 1차원 배열을 이용하는 것이다. 처음에는 노드가 연결되어 있지 않으므로 각 노드가 대표 노드가 된다. 각 노드가 모두 대표 노드이므로 배열은 자신의 인덱스값으로 초기화한다.
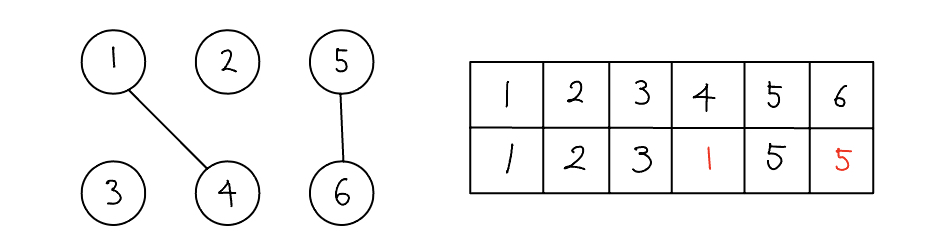
- 2개의 노드를 선택해 각각의 대표 노드를 찾아 연결하는 union 연산을 수행한다. 배열을 보면 1, 4와 5, 6을 union 연산으로 연결한다. 배열[4]는 1로, 배열[6]은 5로 업데이트한다. 이후 union(4, 6)으로 4와 6을 연결한다. 이때 4와 6은 대표 노드가 아니므로 find 연산을 이용해 각 노드의 대표 노드를 찾아 올라간 다음 그 대표 노드를 연결한다.
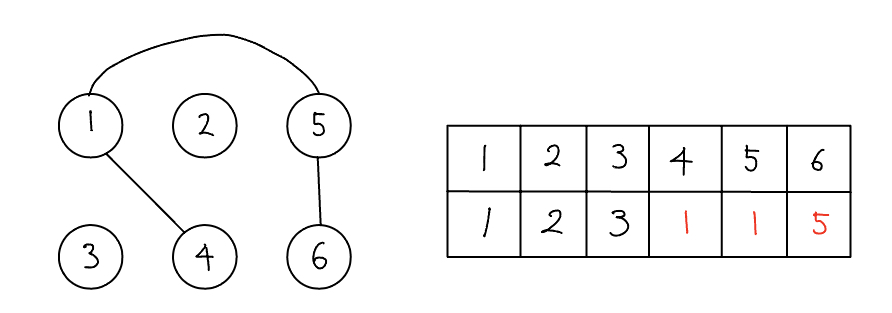
- 1, 4의 연결을 예로 들면 1은 대표 노드, 4는 자식 노드로 union 연산을 하므로 배열[4]의 대표 노드를 1로 설정한 것이다.
- 위 과정 이후, 배열은 그림과 같이 [1, 2, 3, 1, 1, 5]가 된다.
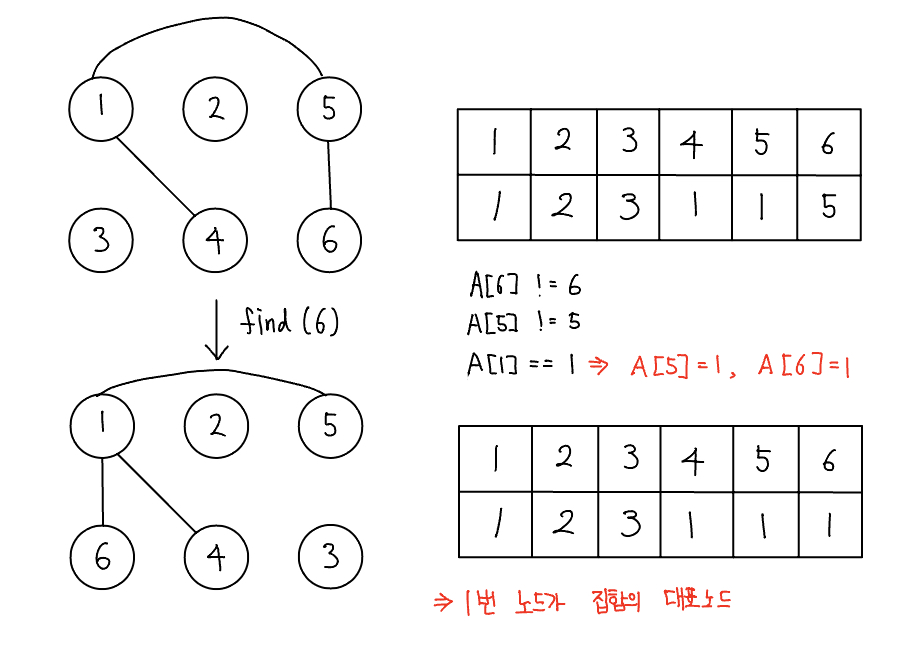
- find 연산은 자식이 속한 집합의 대표 노드를 찾는 연산이다. find 연산은 단순히 대표 노드를 찾는 역할만 하는 것이 아니라 그래프를 정돈하고 시간 복잡도를 줄인다.
- find 연산의 작동 원리
- 대상 노드 배열에 index 값과 value 값이 동일한지 확인한다.
- 동일하지 않으면 value 값이 가리키는 index 위치로 이동한다.
- 이동 위치의 index 값과 value 값이 같을 때까지 위 두 과정을 반복한다. 반복이므로 이 부분은 재귀 함수로 구현한다.
- 대표 노드에 도달하면 재귀 함수를 빠져나오면서 거치는 모든 노드값을 대표 노드값으로 변경한다.
- find 연산의 작동 원리
- find 연산은 잘 생각하면 시간 복잡도가 줄어드는 효과를 얻게 된다. 연산을 할 때 거치는 노드들이 대표 노드와 바로 연결되는 현태로 변경되는 것을 알 수 있다. 이렇게 되면 추후 노드와 관련된 find 연산 속도가 O(1)로 변경된다.
- 한 번의 find 연산을 이용해 모든 노드가 루트 노드에 직접 연결되는 형태로 변경되는 것을 볼 수 있다. 이러한 형태로 변경되면 이후 find 연산이 진행될 때 경로 압축의 효과가 나타난다. 예를 들어 이후 find(4) 연산을 수행하면 한 번의 이동으로 바로 대표 노드를 찾을 수 있다.
문제 050 집합 표현하기
시간 제한: 2초, 난이도: 골드5, 1717번
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static int[] arr;
public static void union(int a, int b) {
a = find(a);
b = find(b);
if (a != b) {
arr[b] = a;
}
}
public static int find(int a) {
if (a == arr[a]) {
return a;
} else {
return arr[a] = find(arr[a]);
}
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(bf.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
arr = new int[n + 1];
for (int i = 0; i < n + 1; i++) {
arr[i] = i;
}
for (int i = 0; i < m; i++) {
st = new StringTokenizer(bf.readLine());
int k = Integer.parseInt(st.nextToken());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
if (k == 0) {
union(a, b);
} else {
if (find(a) == find(b)) {
System.out.println("YES");
} else {
System.out.println("NO");
}
}
}
}
}
유니온 파인드의 이론과 같이 구현하였다.
문제 051 여행 계획 짜기
시간 제한: 2초, 난이도: 골드4, 1976번
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static int[] arr;
public static void union(int a, int b) {
a = find(a);
b = find(b);
if (a != b) {
arr[b] = a;
}
}
public static int find(int a) {
if (a == arr[a]) {
return a;
} else {
return arr[a] = find(arr[a]);
}
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(bf.readLine());
int M = Integer.parseInt(bf.readLine());
arr = new int[N + 1];
for (int i = 1; i < N + 1; i++) {
arr[i] = i;
}
for (int i = 1; i < N + 1; i++) {
StringTokenizer st = new StringTokenizer(bf.readLine());
for (int j = 1; j < N + 1; j++) {
int a = Integer.parseInt(st.nextToken());
if (a == 1) {
union(i, j);
}
}
}
StringTokenizer st = new StringTokenizer(bf.readLine());
int connect = find(Integer.parseInt(st.nextToken()));
boolean result = true;
for (int i = 1; i < M; i++) {
if (connect != find(Integer.parseInt(st.nextToken()))) {
result = false;
break;
}
}
if (result) {
System.out.println("YES");
} else {
System.out.println("NO");
}
}
}
유니온 파인드의 이론과 같이 구현했다.
문제 052 거짓말쟁이가 되긴 싫어
시간 제한: 2초, 난이도: 골드4, 1043번
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.StringTokenizer;
public class Main {
public static int[] arr;
public static ArrayList<ArrayList<Integer>> Graph;
public static void union(int a, int b) {
a = find(a);
b = find(b);
if (a != b) {
arr[b] = a;
}
}
public static int find(int a) {
if (a == arr[a]) {
return a;
} else {
return arr[a] = find(arr[a]);
}
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(bf.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
Graph = new ArrayList<>();
arr = new int[N + 1];
for (int i = 0; i < N + 1; i++) {
arr[i] = i;
}
st = new StringTokenizer(bf.readLine());
int iter = Integer.parseInt(st.nextToken());
ArrayList<Integer> trueP = new ArrayList<>();
for (int i = 0; i < iter; i++) {
int temp = Integer.parseInt(st.nextToken());
trueP.add(temp);
}
for (int i = 0; i < M; i++) {
Graph.add(new ArrayList<>());
}
for (int i = 0; i < M; i++) {
st = new StringTokenizer(bf.readLine());
int tempIter = Integer.parseInt(st.nextToken());
for (int j = 0; j < tempIter; j++) {
int temp = Integer.parseInt(st.nextToken());
Graph.get(i).add(temp);
}
for (int j = 0; j < tempIter - 1; j++) {
int temp1 = Graph.get(i).get(j);
int temp2 = Graph.get(i).get(j + 1);
union(temp1, temp2);
}
}
int count = 0;
for (int i = 0; i < M; i++) {
boolean truePerson = true;
int temp = Graph.get(i).get(0);
for (int j = 0; j < iter; j++) {
if (find(temp) == find(trueP.get(j))) {
truePerson = false;
break;
}
}
if (truePerson) {
count++;
}
}
System.out.println(count);
}
}
유니온 파인드 이론대로 함수를 구현했고 진실을 알고있는 사람을 ArrayList로 구현해 추가하면서 Graph에 진실을 알고 있는 사람과 find 연산으로 비교하면서 count를 증가시킨다.
위상 정렬
위상 정렬(topology sort)은 사이클이 없는 방향 그래프에서 노드 순서를 찾는 알고리즘이다. 위상 정렬에서는 항상 유일한 값으로 정렬되지 않는다. 또한 사이클이 존재하면 노드 간의 순서를 명확하게 정의할 수 없으므로 위상 정렬을 적용할 수 없다.
위상 정렬의 핵심 이론
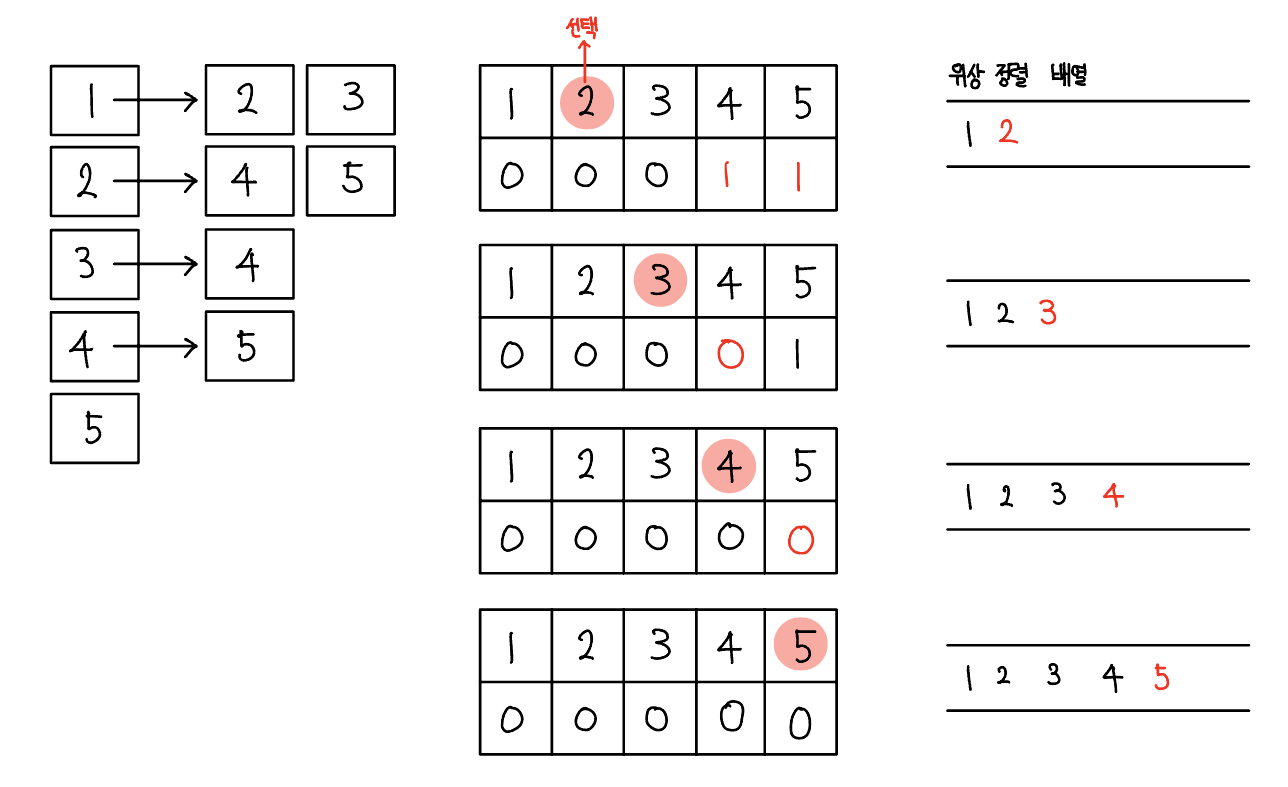
위상 정렬은 다음과 같은 단계로 진행된다.
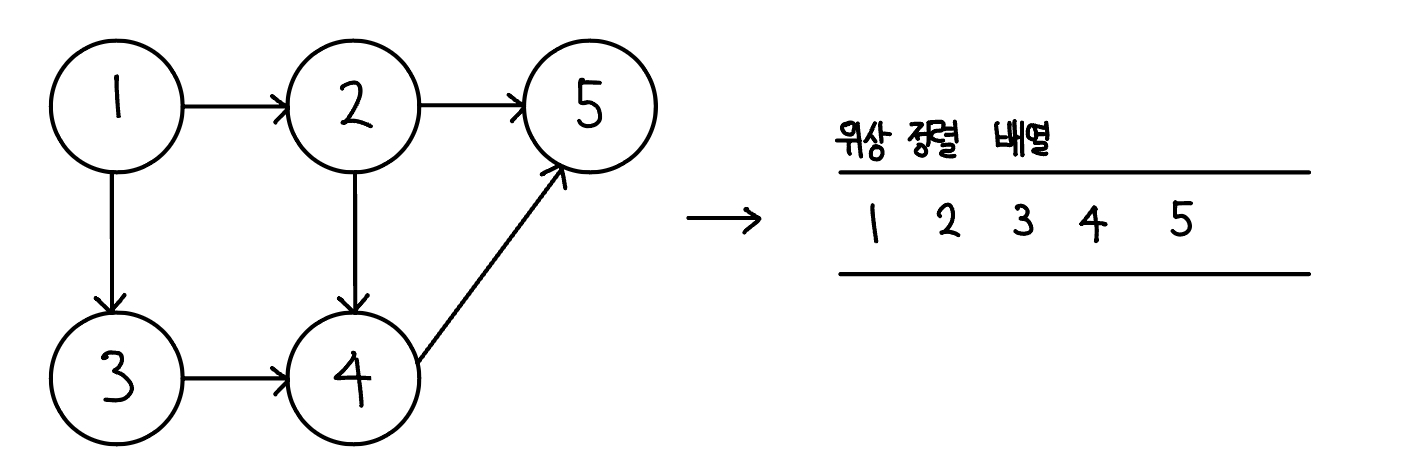
- 진입 차수(in-degree)는 자기 자신을 가리키는 Edge의 개수이다. 다음을 보면 이차원 ArratList로 그래프를 표현했다. 그래프는 사이클이 없는 상태이다.
- 진입 차수 배열 D를 다음과 같이 업데이트한다. 1에서 2, 3을 가리키고 있으므로 D[2], D[3]을 각각 1만큼 증가시킨다. 인접 리스트에 기반을 둔 진입 차수 배열은 다음과 같이 만들 수 있다.
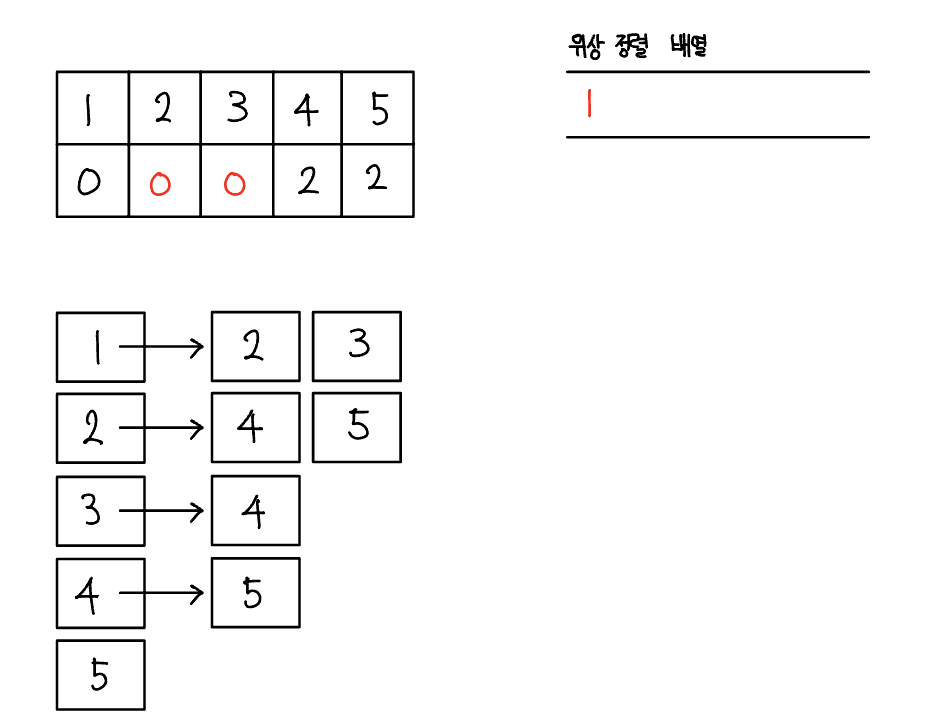
- 진입 차수 배열에서 진입 차수가 0인 노드를 선택하고 선택된 노드를 정렬 배열에 저장한다. 그 후 인접 리스트에서 선택된 노드가 가리키는 노드들의 진입 차수를 1씩 뺀다.
- 위 그림의 경우 진입 차수가 0인 노드 1을 선택하여 2, 3의 진입 차수를 1씩 빼 D[2], D[3]을 0으로 만든 것이다. 계속해서 다음 노드 2를 선택하여 반복한다. 이 과정은 모든 노드가 정렬될 때까지 반복한다. 여기서 진입 차수가 0인 노드 3을 먼저 선택했다면 3이 우선 위상 정렬 배열에 들어갈 것이다. 이 때문에 위상 정렬이 늘 같은 정렬 결과를 보장하지 않는다.
위상 정렬 배열 결과는 다음과 같다.
문제 053 줄 세우기기
시간 제한: 2초, 난이도: 골드3, 2252번
import java.io.*;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
public static ArrayList<ArrayList<Integer>> Graph;
public static int[] Students;
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(bf.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
Queue<Integer> qu = new LinkedList<>();
Students = new int[N + 1];
Graph = new ArrayList<>();
for (int i = 0; i < N + 1; i++) {
Graph.add(new ArrayList<>());
}
for (int i = 0; i < M; i++) {
st = new StringTokenizer(bf.readLine());
int A = Integer.parseInt(st.nextToken());
int B = Integer.parseInt(st.nextToken());
Graph.get(A).add(B);
Students[B]++;
}
for (int i = 1; i < N + 1; i++) {
if (Students[i] == 0) {
qu.add(i);
}
}
while (!qu.isEmpty()) {
int std = qu.poll();
bw.write(std + " ");
for (int i = 0; i < Graph.get(std).size(); i++) {
int temp = Graph.get(std).get(i);
Students[temp]--;
if (Students[temp] == 0) {
qu.add(temp);
}
}
}
bw.flush();
bw.close();
}
}
위상 정렬의 정의대로 구현하였다.
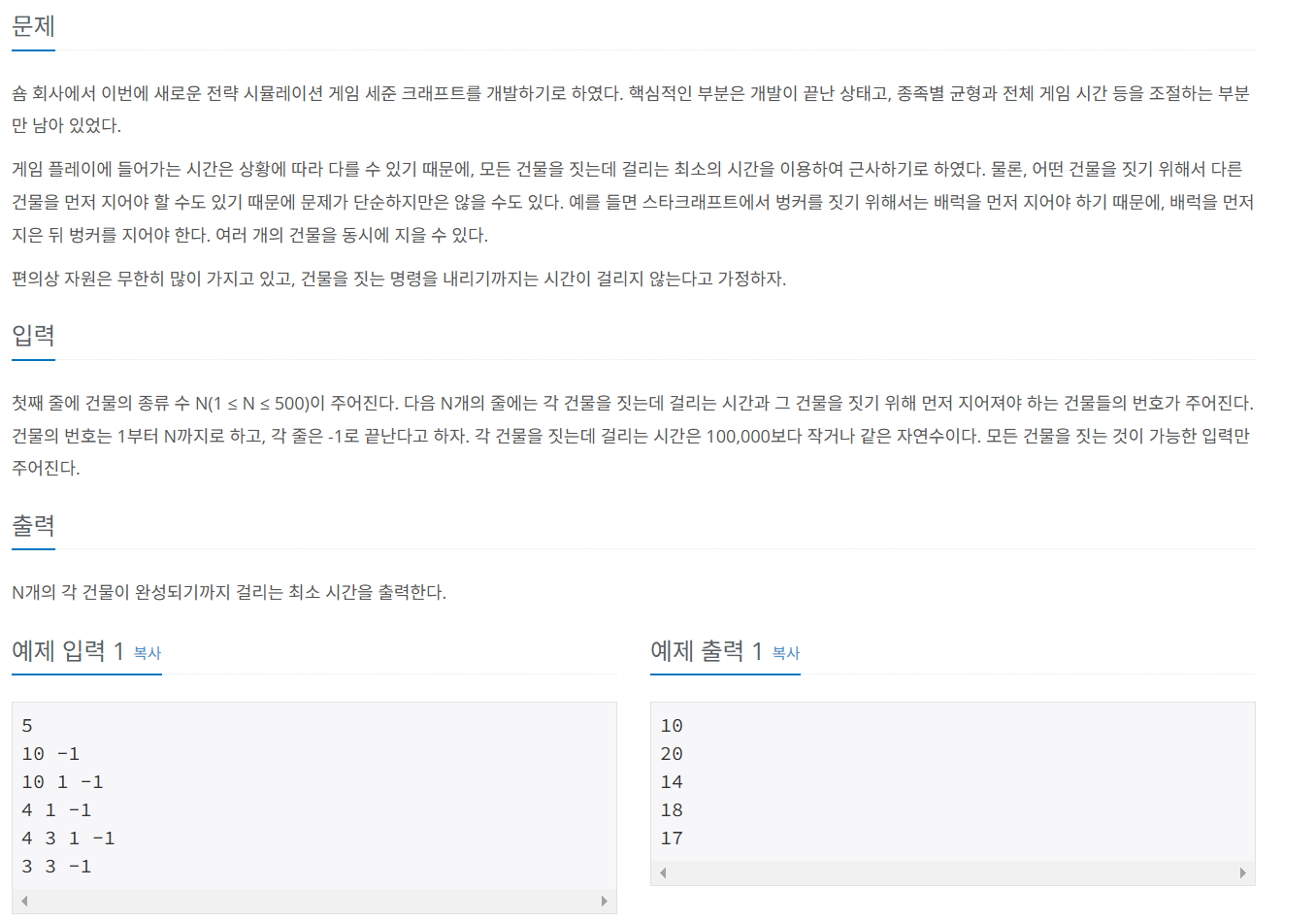
문제 054 게임 개발하기기
시간 제한: 2초, 난이도: 골드3, 1516번
import java.io.*;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(bf.readLine());
ArrayList<ArrayList<Integer>> Building = new ArrayList<>();
for (int i = 0; i < N + 1; i++) {
Building.add(new ArrayList<>());
}
int[] D = new int[N + 1];
int[] Time = new int[N + 1];
int[] Result = new int[N + 1];
for (int i = 1; i < N + 1; i++) {
StringTokenizer st = new StringTokenizer(bf.readLine());
int a = Integer.parseInt(st.nextToken());
Time[i] = a;
while (true) {
int next = Integer.parseInt(st.nextToken());
if (next == -1) {
break;
}
Building.get(next).add(i);
D[i]++;
}
}
Queue<Integer> qu = new LinkedList<>();
for (int i = 1; i < N + 1; i++) {
if (D[i] == 0) {
qu.add(i);
}
}
while (!qu.isEmpty()) {
int next = qu.poll();
for (int i = 0; i < Building.get(next).size(); i++) {
int temp = Building.get(next).get(i);
D[temp]--;
Result[temp] = Math.max(Result[temp], Result[next] + Time[next]);
if (D[temp] == 0) {
qu.add(temp);
}
}
}
for (int i = 1; i < N + 1; i++) {
Result[i] = Result[i] + Time[i];
bw.write(Result[i] + "\n");
}
bw.flush();
bw.close();
}
}
위상 정렬 정의대로 문제에 접근을 하였고, Result 배열에는 현재 건물에 저장된 최대 시간과 이전 건물에 저장된 최대 시간 + 현재 건물의 생성 시간 중 최대값을 저장 한 뒤, 출력 하기 전에 현재 건물의 생성 시간을 더해서 출력해 주었다.
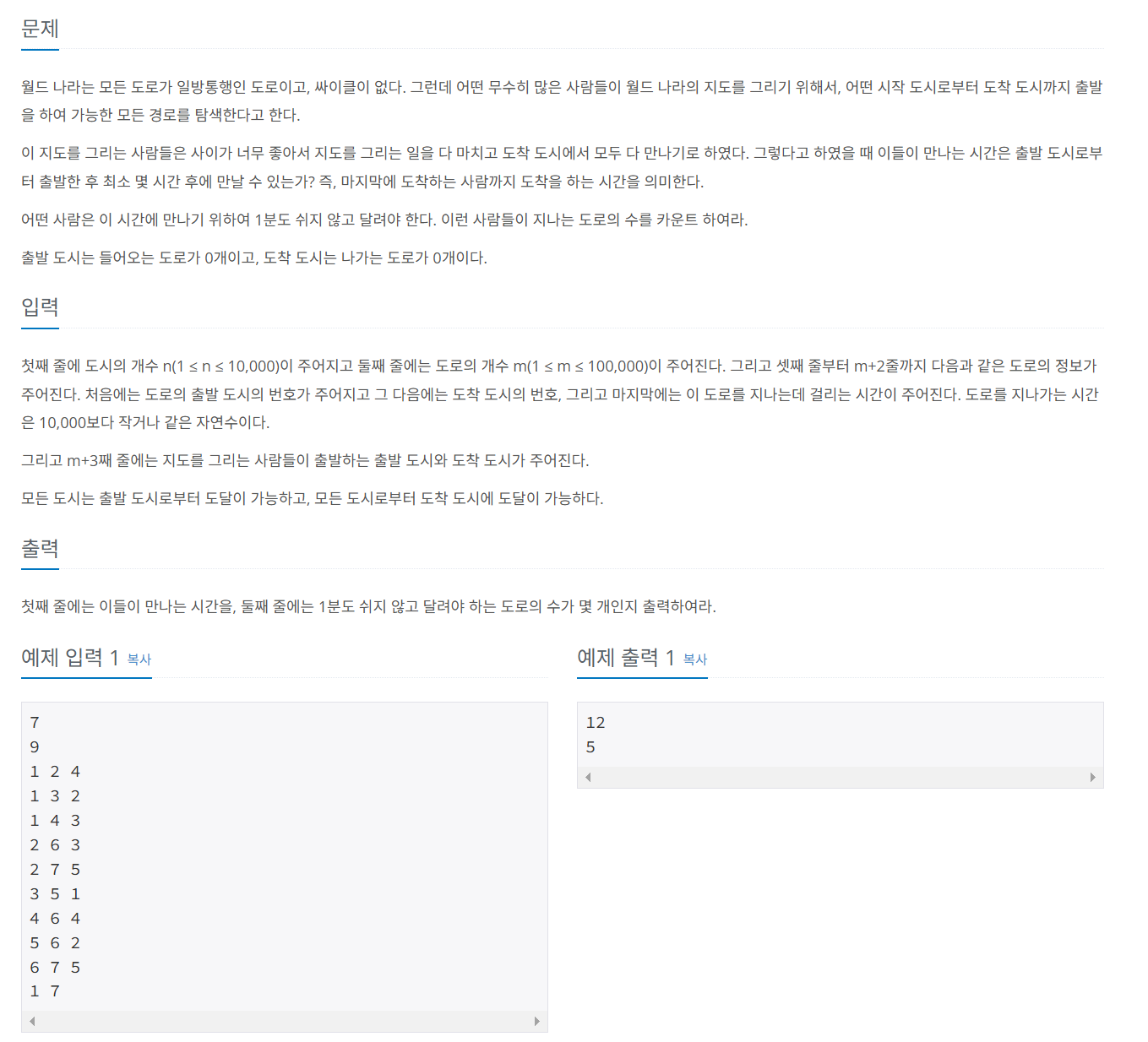
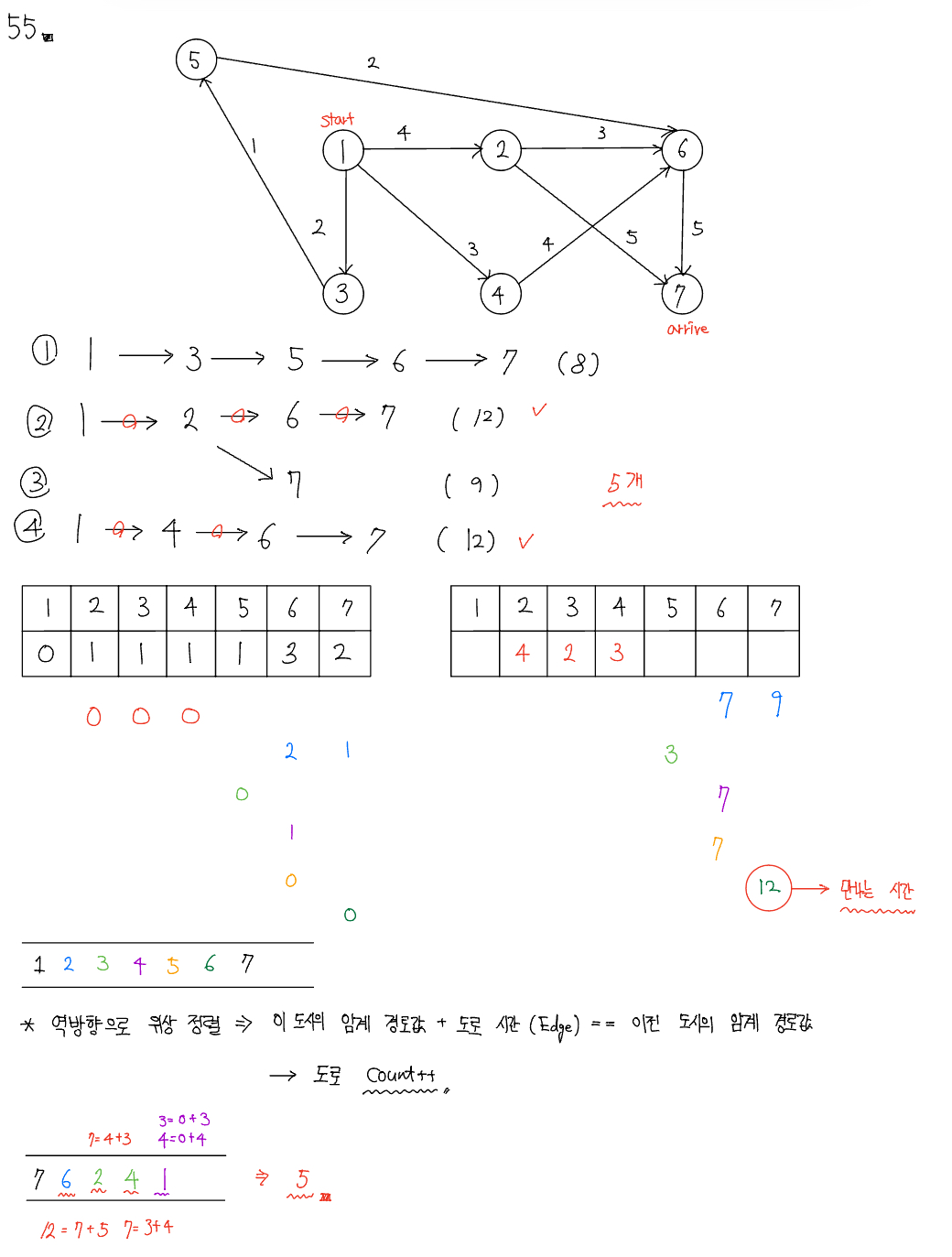
문제 055 임계 경로 구하기기
시간 제한: 2초, 난이도: 플래티넘5, 1948번
풀이
import java.io.*;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int n = Integer.parseInt(bf.readLine());
int m = Integer.parseInt(bf.readLine());
int[] D = new int[n + 1];
int[] Time = new int[n + 1];
ArrayList<ArrayList<Node>> TMap = new ArrayList<>();
ArrayList<ArrayList<Node>> ReTMap = new ArrayList<>();
for (int i = 0; i < n + 1; i++) {
TMap.add(new ArrayList<>());
ReTMap.add(new ArrayList<>());
}
for (int i = 0; i < m; i++) {
StringTokenizer st = new StringTokenizer(bf.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
int time = Integer.parseInt(st.nextToken());
TMap.get(start).add(new Node(end, time));
ReTMap.get(end).add(new Node(start, time));
D[end]++;
}
StringTokenizer st = new StringTokenizer(bf.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
Queue<Integer> qu = new LinkedList<>();
qu.add(start);
while (!qu.isEmpty()) {
int now = qu.poll();
for (int i = 0; i < TMap.get(now).size(); i++) {
Node next = TMap.get(now).get(i);
D[next.destination]--;
Time[next.destination] = Math.max(Time[next.destination], Time[now] + next.time);
if (D[next.destination] == 0) {
qu.add(next.destination);
}
}
}
qu.add(end); // 역방향 위상정렬렬
int count = 0;
boolean[] Visit = new boolean[n + 1];
Visit[end] = true;
while (!qu.isEmpty()) {
int now = qu.poll();
for (int i = 0; i < ReTMap.get(now).size(); i++) {
Node next = ReTMap.get(now).get(i);
if (Time[next.destination] + next.time == Time[now]) {
count++;
if (Visit[next.destination] == false) {
Visit[next.destination] = true;
qu.add(next.destination);
}
}
}
}
bw.write(Time[end] + "\n");
bw.write(count + "");
bw.flush();
bw.close();
}
public static class Node {
int destination;
int time;
public Node(int destination, int time) {
this.destination = destination;
this.time = time;
}
}
}
만나는 시간만 구하면 54번처럼 위상정렬을 하면 되지만, 도로의 수를 출력해야 하므로 이런 경우에는 역방향으로 위상정렬을 시도해야한다. 그래서 원래 그래프를 뒤집은 ReTMap ArrayList를 선언해 주었고, 역방향으로 위상정렬을 할 때 다음 도시의 임계 경로값 + 도로 시간 == 현재 도시의 임계 경로값일 때 1분도 쉬지 않고 달려야 하는 도시로 카운팅을 진행하였다.
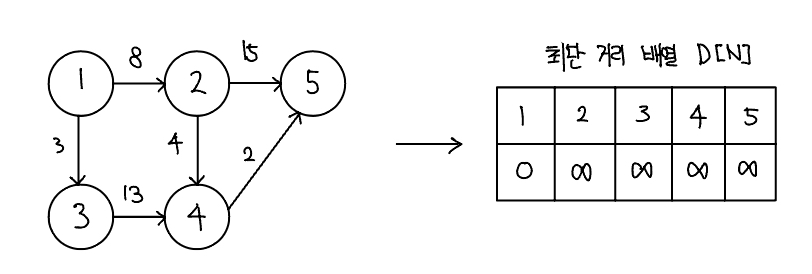
다익스트라
다익스트라(dijkstra) 알고리즘은 그래프에서 최단 거리를 구하는 알고리즘으로, 주요 특징은 Edge는 모두 양수이고 시간 복잡도는 노드 수를 V, 에지 수를 E라고 하면 O(ElogV)이다.
다익스트라 알고리즘의 핵심 이론
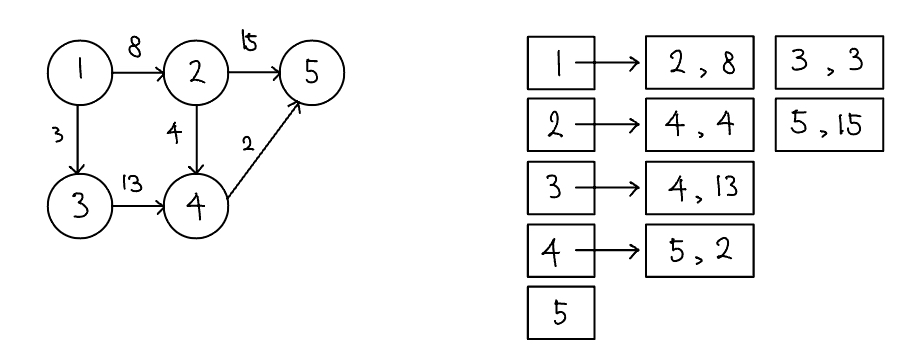
- 인접 리스트로 그래프 구현하기
- 먼저 다음과 같이 주어진 그래프를 인접 리스트로 구현한다.
- 최단 거리 배열 초기화하기
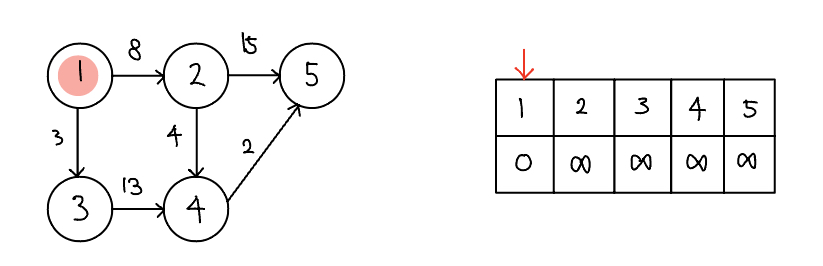
- 최단 거리 배열을 만들고, 출발 노드는 0, 이외의 노드는 무한으로 초기화한다.
- 값이 가장 작은 노드 고르기
- 최단 거리 배열에서 현재 값이 가장 작은 노드를 고른다. 여기서는 값이 0인 출발 노드에서 시작하면 된다.
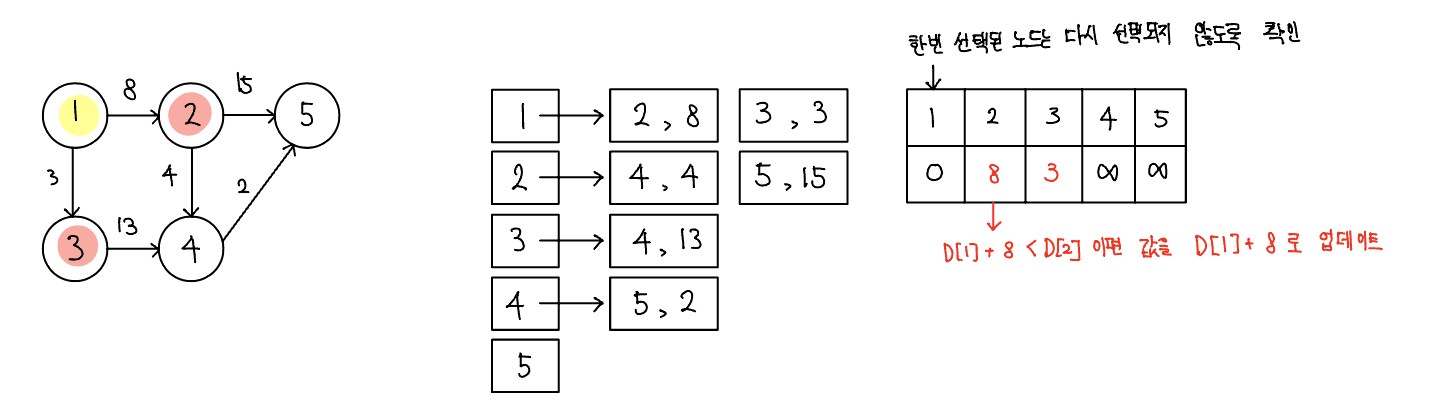
- 최단 거리 배열 업데이트하기
- 선택된 노드에 연결된 에지의 값을 바탕으로 다른 노드의 값을 업데이트한다. 1단계에서 저장한 인접 리스트를 이용해 현재 노드의 에지를 탐색하고 업데이트하면 된다. 연결 노드의 최단 거리는 선택 노드의 최단 거리 배열의 값 + 에지 가중치와 연결 노드의 최단 거리 배열의 값 중 더 작은 값으로 업데이트한다.
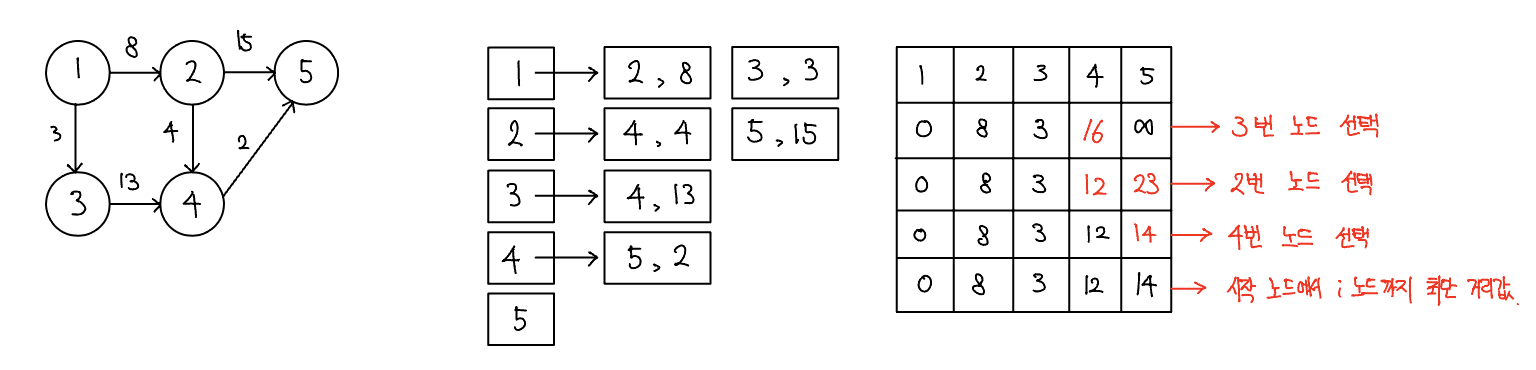
- 과정 3-4를 반복해 최단 거리 배열 완성하기
- 모든 노드가 처리될 때까지 과정 3~4를 반복한다. 과정 4에서 선택 노드가 될 때마다 다시 선택되지 않도록 방문 배열을 만들어 처리하고, 모든 노드가 선택될 때까지 반복하면 최단 거리 배열이 완성된다.
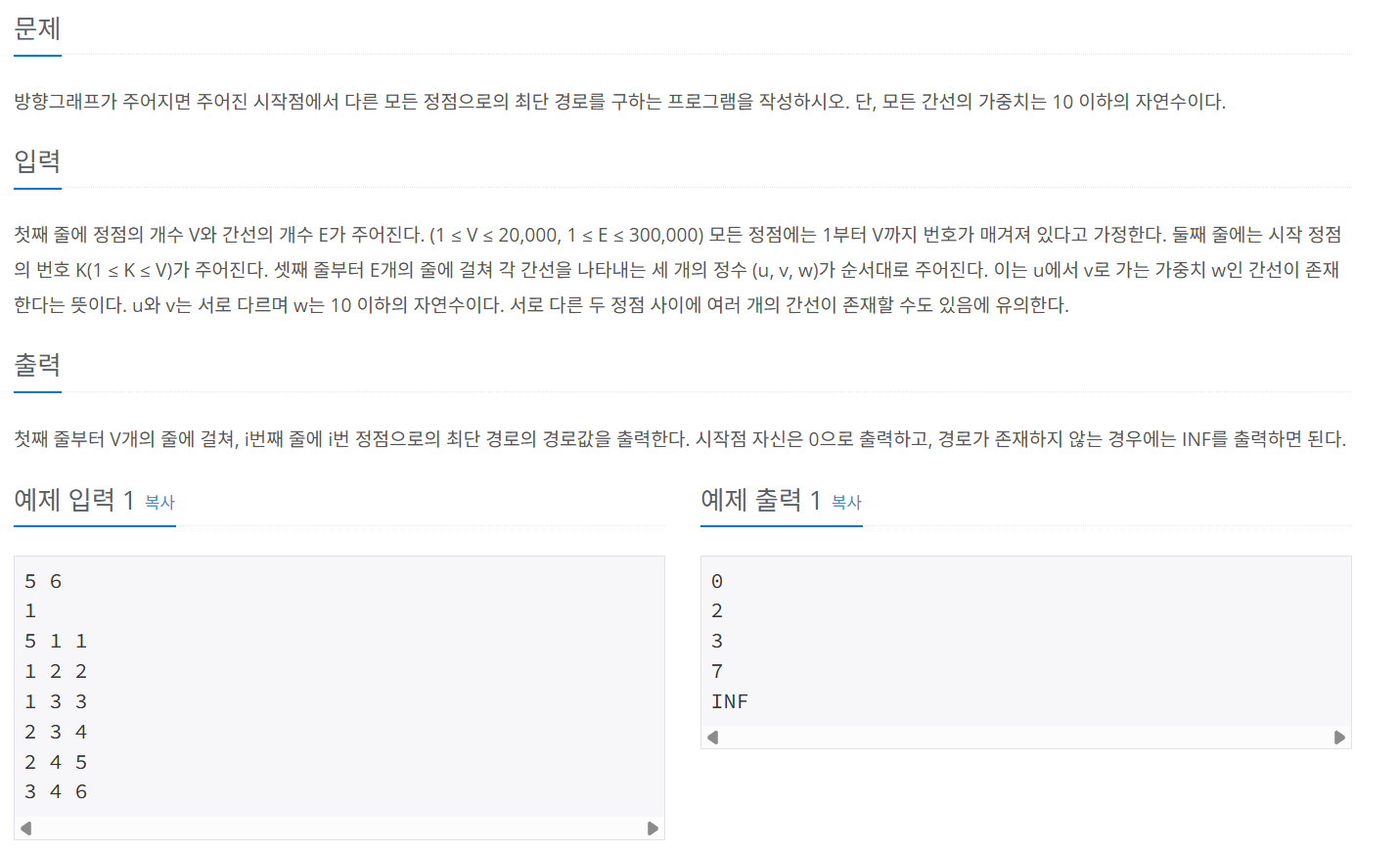
문제 056 최단 경로 구하기
시간 제한: 1초, 난이도: 골드5, 1753번
import java.io.*;
import java.util.*;
public class Main {
public static ArrayList<ArrayList<Node>> Graph;
public static int[] D;
public static boolean[] Visit;
public static int INF = 2147483647;
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(bf.readLine());
int V = Integer.parseInt(st.nextToken());
int E = Integer.parseInt(st.nextToken());
D = new int[V + 1];
Visit = new boolean[V + 1];
Graph = new ArrayList<>();
for (int i = 0; i < V + 1; i++) {
Graph.add(new ArrayList<>());
}
int K = Integer.parseInt(bf.readLine());
for (int i = 1; i < V + 1; i++) {
if (i == K) {
D[i] = 0;
} else {
D[i] = INF;
}
}
for (int i = 0; i < E; i++) {
st = new StringTokenizer(bf.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
int w = Integer.parseInt(st.nextToken());
Graph.get(u).add(new Node(v, w));
}
PriorityQueue<Node> pq = new PriorityQueue<>();
pq.add(new Node(K, 0));
while (!pq.isEmpty()) {
Node now = pq.poll();
Visit[now.v] = true;
for (int i = 0; i < Graph.get(now.v).size(); i++) {
Node next = Graph.get(now.v).get(i);
int nextNode = next.v;
int nextWeight = next.w;
if (Visit[nextNode]) {
continue;
}
if (D[now.v] + nextWeight < D[nextNode]) {
D[nextNode] = D[now.v] + nextWeight;
pq.add(new Node(nextNode, D[nextNode]));
}
}
}
for (int i = 1; i < V + 1; i++) {
if (D[i] != INF) {
bw.write(D[i] + "\n");
} else {
bw.write("INF" + "\n");
}
}
bw.flush();
bw.close();
}
public static class Node implements Comparable<Node> {
int v;
int w;
public Node(int v, int w) {
this.v = v;
this.w = w;
}
@Override
public int compareTo(Node o) {
return w - o.w;
}
}
}
Dijkstra를 구현하기 위해서 Priority Queue를 이용을 하였고, 80%대에서 틀렸습니다가 나왔는데 이는 INF가 충분히 크지 않아서 INF를 Interger Max로 지정했다.
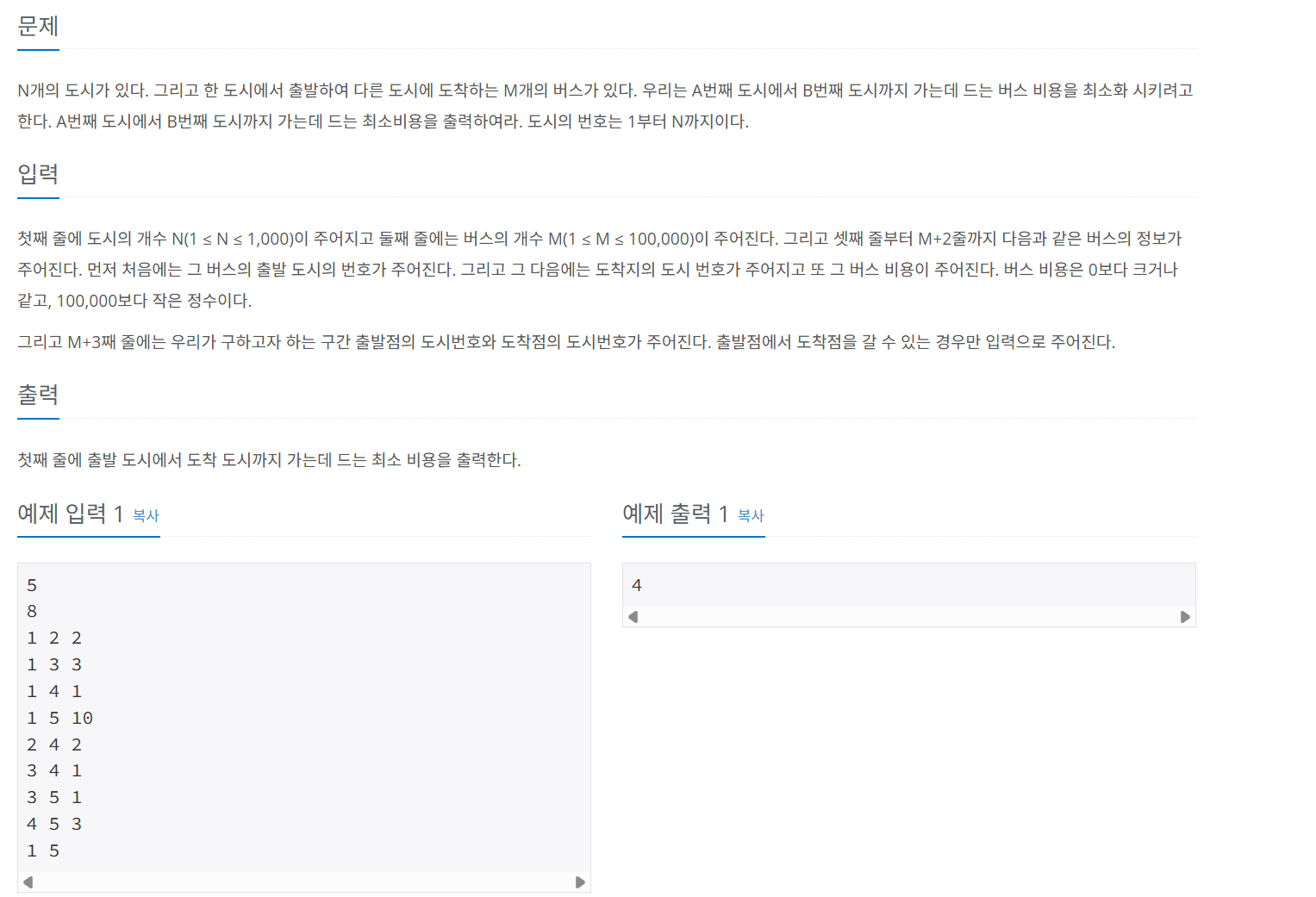
문제 057 최소 비용 구하기
시간 제한: 0.5초, 난이도: 골드5, 1916번
import java.io.*;
import java.util.ArrayList;
import java.util.BitSet;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class Main {
public static ArrayList<ArrayList<Node>> City;
public static int[] D;
public static boolean[] Visit;
public static int INF = 2147483647;
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(bf.readLine());
int M = Integer.parseInt(bf.readLine());
D = new int[N + 1];
Visit = new boolean[N + 1];
City = new ArrayList<>();
for (int i = 0; i < N + 1; i++) {
City.add(new ArrayList<>());
}
for (int i = 0; i < M; i++) {
StringTokenizer st = new StringTokenizer(bf.readLine());
int start = Integer.parseInt(st.nextToken());
int arrive = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
City.get(start).add(new Node(arrive, weight));
}
StringTokenizer st = new StringTokenizer(bf.readLine());
int start = Integer.parseInt(st.nextToken());
int arrival = Integer.parseInt(st.nextToken());
for (int i = 0; i < N + 1; i++) {
if (i == start) {
D[i] = 0;
} else {
D[i] = INF;
}
}
PriorityQueue<Node> pq = new PriorityQueue<>();
pq.add(new Node(start, 0));
while (!pq.isEmpty()) {
Node now = pq.poll();
if (Visit[now.v]) {
continue;
}
Visit[now.v] = true;
for (int i = 0; i < City.get(now.v).size(); i++) {
Node next = City.get(now.v).get(i);
int nextNode = next.v;
int nextWeight = next.weight;
if (D[now.v] + nextWeight < D[nextNode]) {
D[nextNode] = D[now.v] + nextWeight;
pq.add(new Node(nextNode, D[nextNode]));
}
}
}
bw.write(D[arrival] + "\n");
bw.flush();
bw.close();
}
public static class Node implements Comparable<Node> {
int v;
int weight;
public Node(int v, int weight) {
this.v = v;
this.weight = weight;
}
@Override
public int compareTo(Node o) {
return weight - o.weight;
}
}
}
56번과 같이 Priority queue를 이용해 Dijkstra 알고리즘을 구현했고 배열 D에서 도착지의 인덱스 값을 출력하였다.
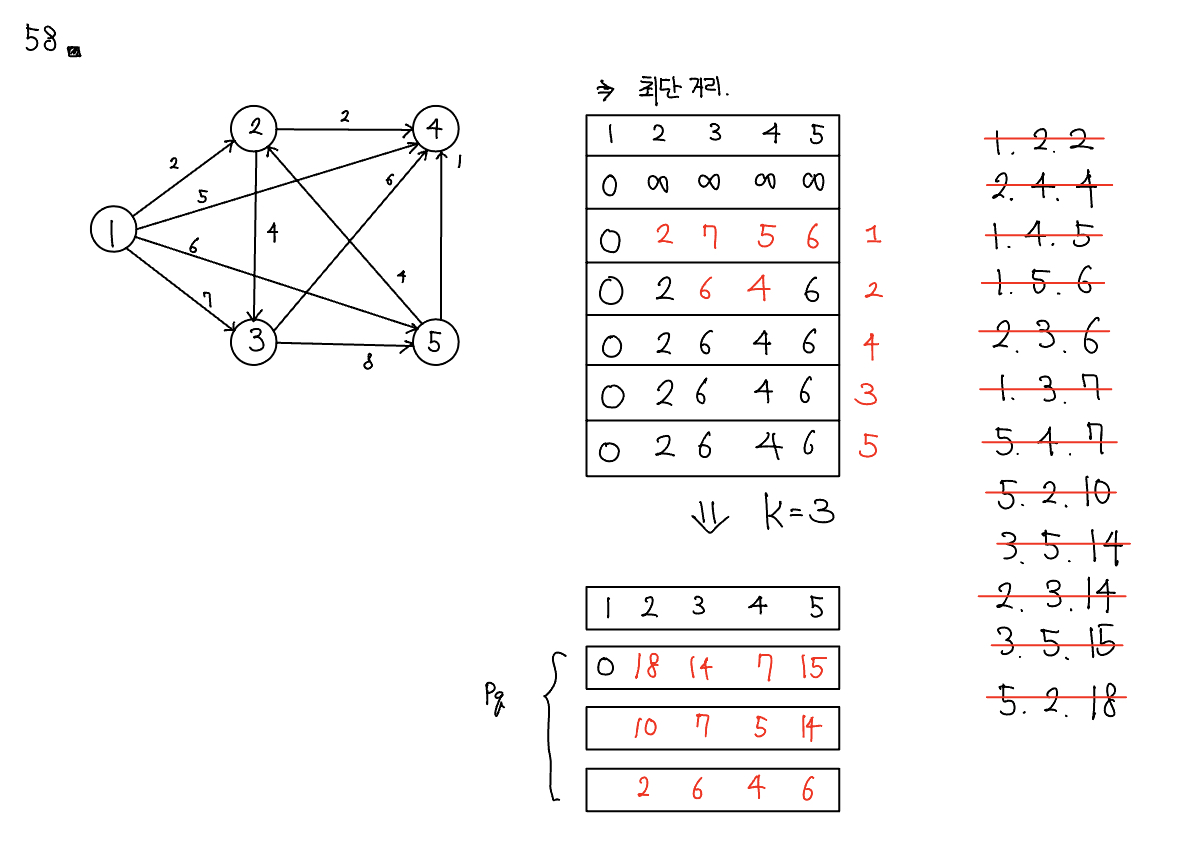
문제 058 K번째 최단 경로 찾기
시간 제한: 2초, 난이도: 플레티넘4, 1854번
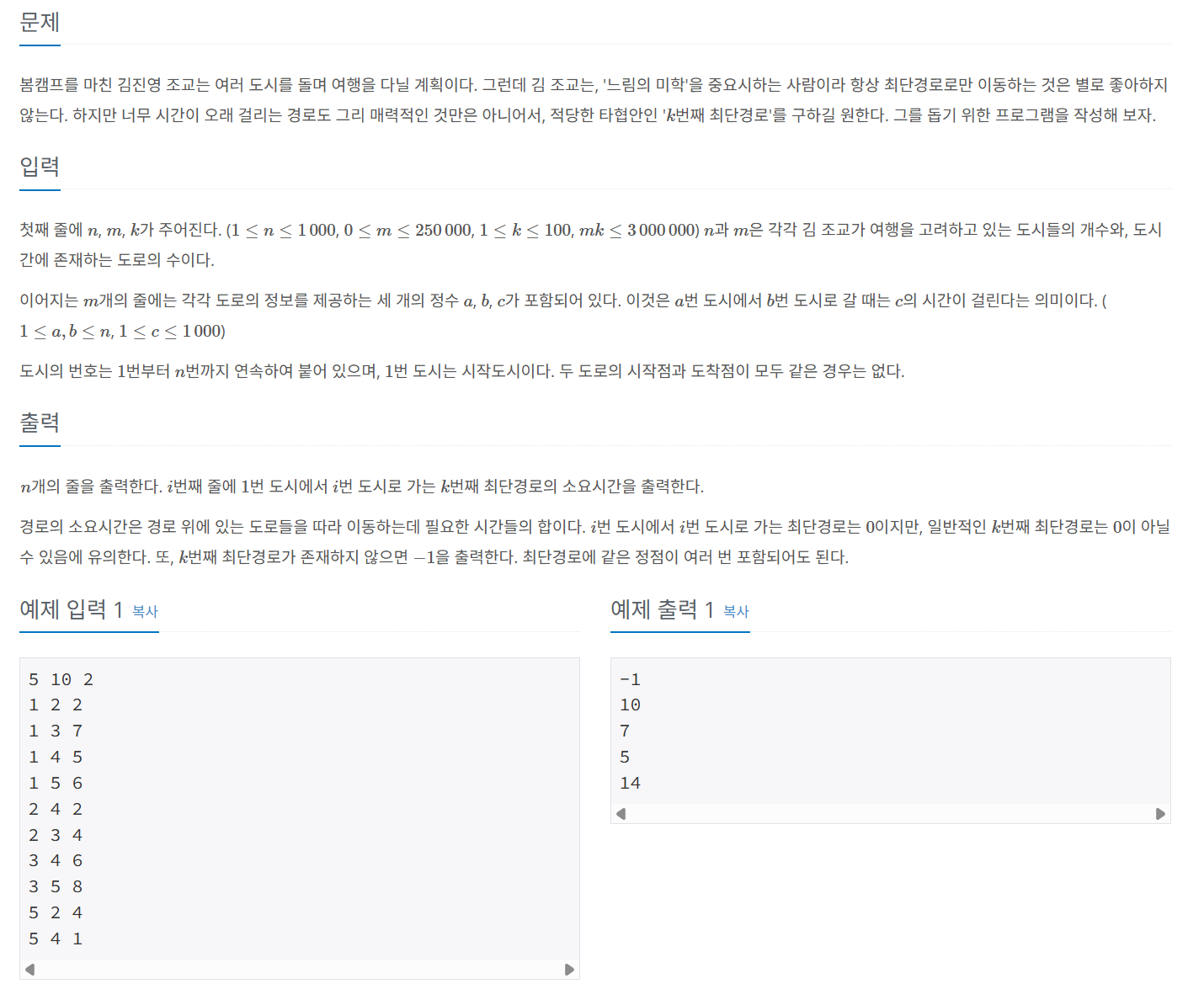
풀이
import java.io.*;
import java.util.ArrayList;
import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class Main {
public static ArrayList<ArrayList<Node>> Graph;
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(bf.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
Graph = new ArrayList<>();
for (int i = 0; i < n + 1; i++) {
Graph.add(new ArrayList<>());
}
for (int i = 0; i < m; i++) {
st = new StringTokenizer(bf.readLine());
int start = Integer.parseInt(st.nextToken());
int arrive = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
Graph.get(start).add(new Node(arrive, weight));
}
PriorityQueue<Integer>[] dPq = new PriorityQueue[n + 1]; // D배열을 Pq로 선언
Comparator<Integer> cp = new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o1 < o2 ? 1 : -1;
}
};
for (int i = 0; i < n + 1; i++) {
dPq[i] = new PriorityQueue<>(k, cp);
}
PriorityQueue<Node> pq = new PriorityQueue<>(); // Dijkstra와 동일하게 Pq 선언
pq.add(new Node(1, 0));
dPq[1].add(0);
while (!pq.isEmpty()) {
Node now = pq.poll();
int nowNode = now.arrival;
int nowWeight = now.weight;
for (int i = 0; i < Graph.get(nowNode).size(); i++) {
Node next = Graph.get(nowNode).get(i);
int nextNode = next.arrival;
int nextWeight = next.weight;
if (dPq[nextNode].size() < k) {
dPq[nextNode].add(nowWeight + nextWeight);
pq.add(new Node(nextNode, nowWeight + nextWeight));
} else if (dPq[nextNode].peek() > nowWeight + nextWeight) {
dPq[nextNode].poll();
dPq[nextNode].add(nowWeight + nextWeight);
pq.add(new Node(nextNode, nowWeight + nextWeight));
}
}
}
for (int i = 1; i < n + 1; i++) {
if (dPq[i].size() == k) {
bw.write(dPq[i].peek() + "\n");
} else {
bw.write("-1\n");
}
}
bw.flush();
bw.close();
}
public static class Node implements Comparable<Node> {
int arrival;
int weight;
public Node(int arrival, int weight) {
this.arrival = arrival;
this.weight = weight;
}
@Override
public int compareTo(Node o) {
return weight - o.weight;
}
}
}
기존 Dijkstra처럼 풀면 최단 거리만을 구할 수 있다. 하지만 k번째 최단 거리를 구하기 위해서는 기존 int 배열로 선언했던 D배열을 prioirty queue로 선언을 해주고 이미 방문했던 노드도 재방문 할 수 있게 Visit 배열을 사용하면 안된다. 또한 prioirty queue로 선언한 dPq 배열에서 다음 노드의 배열의 사이즈가 k보다 작으면 가중치를 넣고 이를 pq에 넣어주고 만약 다음 노드의 배열의 사이즈가 k이면, nowWeight + nextWeight가 dPq[nextNode].peek()가 이보다 작으면, dPq[nextNode]의 peek값을 제거하고 이를 넣어준다. 이렇게 한 뒤 마지막에 dPq의 peek값을 출력한다.
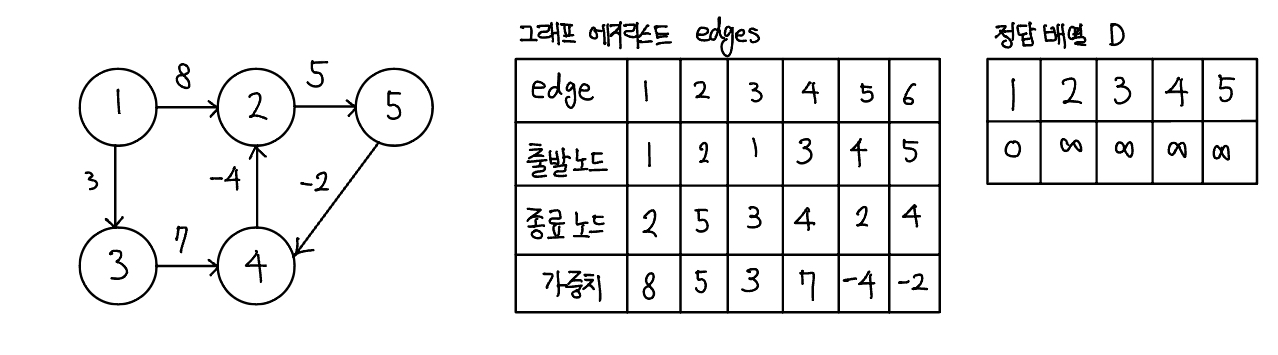
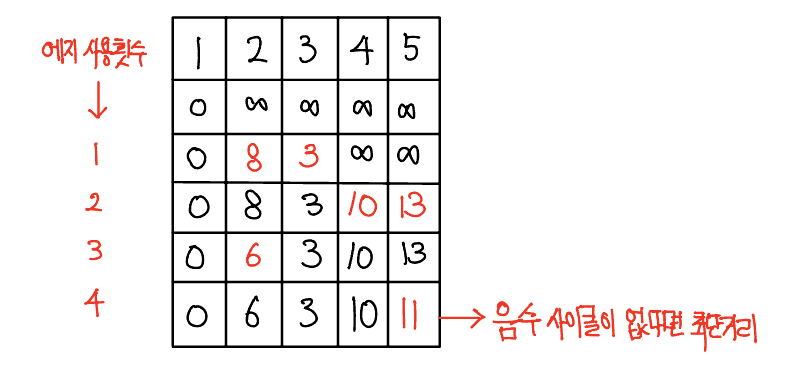
벨만-포드
벨만-포드(bellman-ford-moore) 알고리즘은 그래프에서 최단 거리를 구하는 알고리즘으로, 주요 특징은 특정 출발 노드에서 다른 모든 노드까지의 최단 경로 탐색을 하며 음수 가중치 Edge가 있어도 수행할 수 있고, 전체 그래프에서 음수 사이클의 존재 여부를 판단할 수 있다. 시간 복잡도는 노드 수를 V, 에지 수를 E라고 하면 O(VE)이다.
벨만-포드의 핵심 이론
벤만-포드 알고리즘은 다음 3다지 단계의 원리로 동작한다.
- 에지 리스트로 그래프를 구현하고 최단 경로 배열 초기화 하기
- 벨만-포드 알고리즘은 에지를 중심으로 동작하므로 그래프를 에지 리스트로 구현한다. 또한 최단 경로 배열을 출발 노드는 0, 나머지 노드는 무한대로 초기화한다.
- 모든 에지를 확인해 정답 배열 업데이트하기
- 최단 거리 배열에서 업데이트 반복 횟수는 노드 개수 -1 이다. 노드 개수가 N이고, 음수 사이클이 없을 때 특정 두 노드의 최단 거리를 구성할 수 있는 에지의 최대 개수는 N - 1이기 때문이다.
- 모든 에지 E = (s, e, w)에서 다음 조건을 만족하면 업데이트를 실행한다.
- D[s] != INF이며 D[e] > D[s] + w일 때 D[e] = D[s] + w로 배열의 값을 업데이트한다.
- 업데이트 반복 횟수가 K번이라면 해당 시점에 정답 배열의 값은 시작점에서 K개의 에지를 사용했을 때 각 노드에 대한 최단 거리이다.
- 음수 사이클이 없을 때 N - 1번 에지 사용 횟수를 반복하면 출발 노드와 모든 노드 간의 최단 거리를 알려 주는 정답 배열이 완성된다.
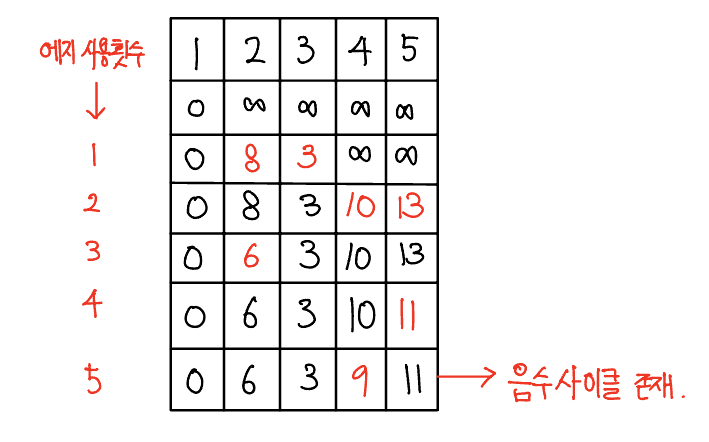
- 음수 사이클 유무 확인하기기
- 음수 사이클 유무를 확인하기 위해 모든 에지를 한 번씩 다시 사용해 업데이트되는 노드가 발생하는지 확인한다. 만약 업데이트되는 노드가 있다면 음수 사이클이 있다는 뜻이 되고, 2단계에서 도출한 정답 배열이 무의미하고 최단 거리를 찾을 수 없는 그래프라는 뜻이 된다.
- 음수 사이클이 존재하면 이 사이클을 무한하게 돌수록 가중치가 계속 감소하므로 최단 거리를 구할 수 없다.
문제 059 타임머신으로 빨리 가기
시간 제한: 1초, 난이도: 골드4, 11657번
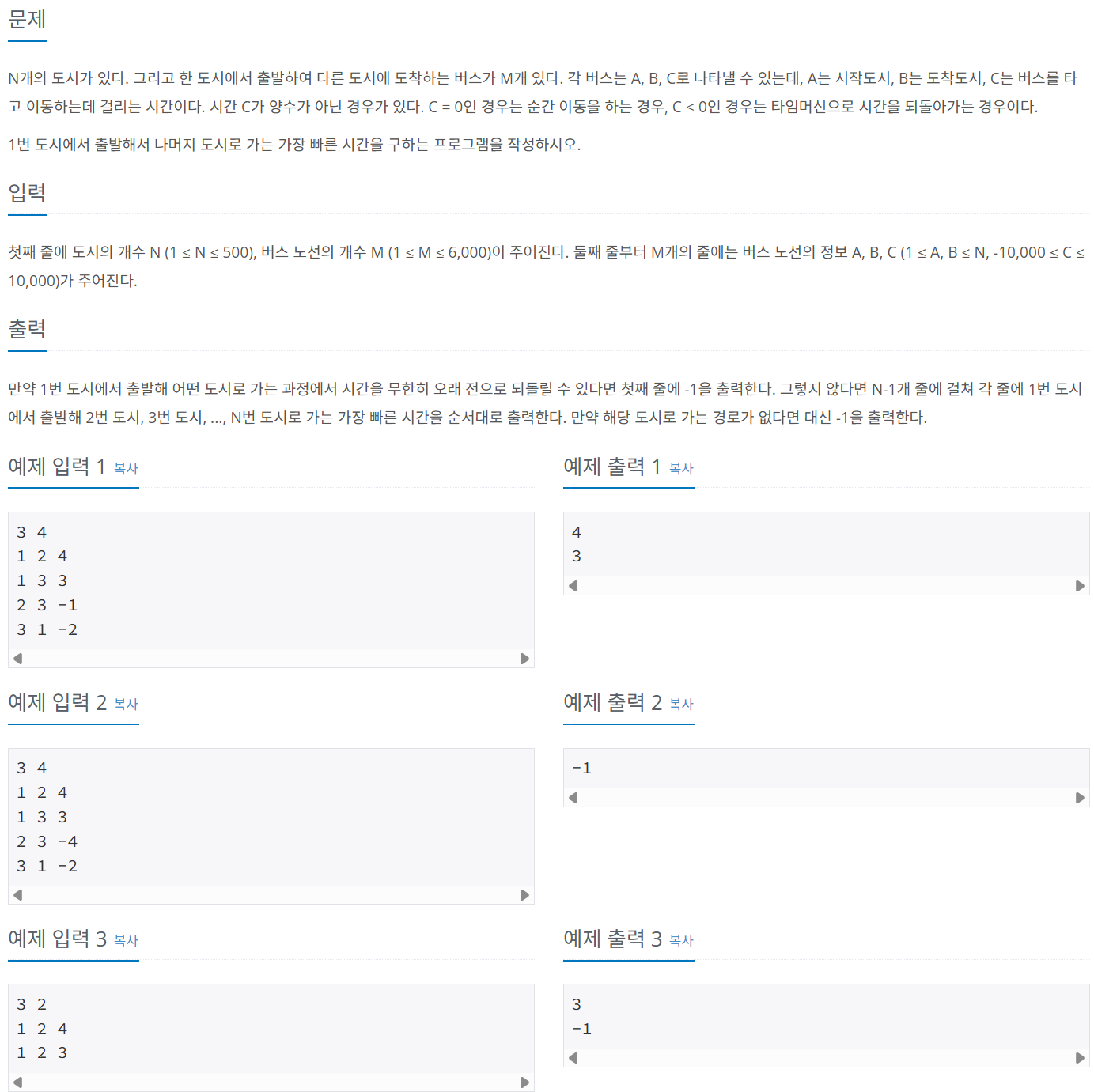
import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
public static Edge edges[];
public static long D[];
public static int INF = Integer.MAX_VALUE;
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(bf.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
edges = new Edge[M + 1];
D = new long[N + 1];
Arrays.fill(D, INF);
D[1] = 0;
for (int i = 1; i < M + 1; i++) {
st = new StringTokenizer(bf.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
edges[i] = new Edge(start, end, weight);
}
for (int i = 0; i < N; i++) {
for (int j = 1; j < M + 1; j++) {
int start = edges[j].start;
int end = edges[j].end;
int weight = edges[j].weight;
if (D[start] != INF && D[end] > D[start] + weight) {
D[end] = D[start] + weight;
}
}
}
boolean update = false;
for (int j = 1; j < M + 1; j++) {
int start = edges[j].start;
int end = edges[j].end;
int weight = edges[j].weight;
if (D[start] != INF && D[end] > D[start] + weight) {
update = true;
break;
}
}
if (update) {
bw.write(-1 + "\n");
} else {
for (int i = 2; i < N + 1; i++) {
if (D[i] != INF) {
bw.write(D[i] + "\n");
} else {
bw.write(-1 + "\n");
}
}
}
bw.flush();
bw.close();
}
public static class Edge {
int start;
int end;
int weight;
public Edge(int start, int end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
}
}
벨만-포드 알고리즘 그대로 구현했다. INF를 처음에 Long.MAX_VALUE로 했더니 출력초과가 발생해서 Integer.MAX_VALUE로 했더니 맞았다.
문제 060 세일즈맨의 고민
시간 제한: 2초, 난이도: 플래티넘5, 1219번
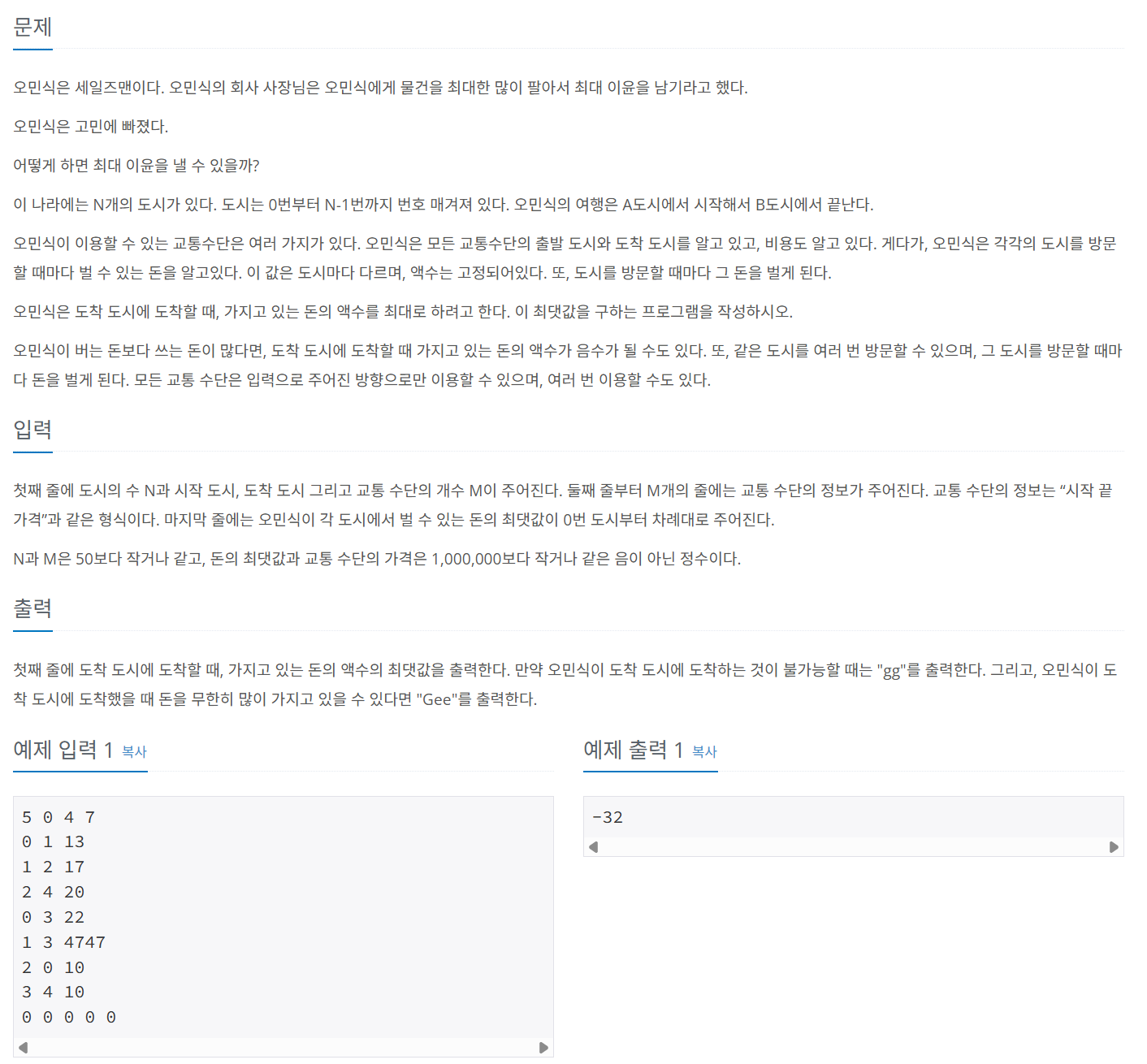
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static Edge[] Graph;
public static long[] D;
public static int[] CityMoney;
public static long MIN = Long.MIN_VALUE;
public static long MAX = Long.MAX_VALUE;
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(bf.readLine());
int N = Integer.parseInt(st.nextToken());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
Graph = new Edge[M];
D = new long[N];
CityMoney = new int[N];
for (int i = 0; i < M; i++) {
st = new StringTokenizer(bf.readLine());
int s = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
int w = Integer.parseInt(st.nextToken());
Graph[i] = new Edge(s, e, w);
}
st = new StringTokenizer(bf.readLine());
for (int i = 0; i < N; i++) {
CityMoney[i] = Integer.parseInt(st.nextToken());
if (i == start) {
D[i] = 0;
} else {
D[i] = MIN;
}
}
D[start] = CityMoney[start];
for (int i = 0; i < N + 50; i++) {
for (int j = 0; j < M; j++) {
int s = Graph[j].s;
int e = Graph[j].e;
int w = Graph[j].w;
if (D[s] == MIN) {
continue;
} else if (D[s] == MAX) {
D[e] = MAX;
} else if (D[e] < D[s] + CityMoney[e] - w) {
D[e] = D[s] + CityMoney[e] - w;
if (i > N - 1) {
D[e] = MAX;
}
}
}
}
if (D[end] == MIN) {
bw.write("gg\n");
} else if (D[end] == MAX) {
bw.write("Gee\n");
} else {
bw.write(D[end] + "\n");
}
bw.flush();
bw.close();
}
public static class Edge {
int s;
int e;
int w;
public Edge(int s, int e, int w) {
this.s = s;
this.e = e;
this.w = w;
}
}
}
벨만-포드 알고리즘은 최단 거리를 구하는 알고리즘이지만, 이 문제에서는 최대값을 구하여야 하므로 이를 반대로 생각해야하고, 기존의 음수 사이클을 양수 사이클로 생각하면 된다. 그래서 처음 시작하는 도시의 D[start]값을 CityMoney[start]값으로 초기 설정해 주고 나머지 배열 D의 값들은 Long.MIN_VALUE로 초기화를 한다. 이후 D[e]값이 MIN이면 continue, D[s] == MAX면 D[e] = MAX로 마지막으로 기존과 반대로 D[e] < D[s] - w + CityMoney[e]일 때 D[e]값을 갱신해준다. 또한 N의 최대값은 50이므로 기존 N - 1 사이클 이후에 갱신되면 음수 사이클인 것처럼 N + 50 번의 반복문 속에서 N - 1 이후에 값이 갱신되면 양수 사이클로 판단을 해 Gee를 출력하게 한다.
플로이드-위셜
플로이드-위셜(floyd-warshall) 알고리즘은 그래프에서 최단 거리를 구하는 알고리즘으로, 주요 특징은 음수 가중치 에지가 있어도 수행할 수 있고 동적 계획법의 원리를 이용해 알고리즘에 접근한다. 노드 수가 V이면 시간 복잡도는 O($V^3$)이다.
플로이드-위셜의 핵심 이론
플로이드-위셜 알고리즘을 도출하는 가장 핵심적인 원리는 A 노드에서 B 노드까지 최단 경로를 구했다고 가정했을 때 최단 경로 위에 K 노드가 존재한다면 그것을 이루는 부분 경로 역시 최단 경로라는 것이다.
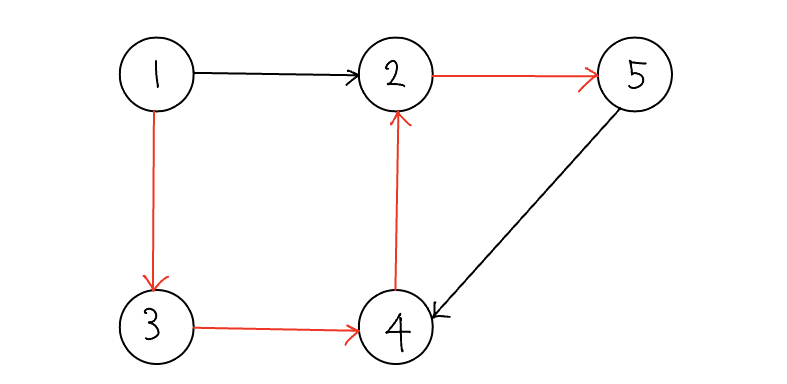
색칠된 Edge 경로가 1에서 5로 가는 최단 경로라면 1에서 4로 가는 최단 경로와 4에서 5로가는 최단 경로 역시 색칠된 Edge로 이뤄질 수밖에 없다. 즉, 전체 경로의 최단 경로는 부분 경로의 조합으로 이뤄진다는 의미가 된다. 이 원리로 다음과 같은 점화식을 도출할 수 있다.
D[S][E] = min(D[S][E], D[S][K] + D[K][E])
위 내용을 바탕으로 플로이드-위셜 알고리즘 구현 방법을 알아본다.
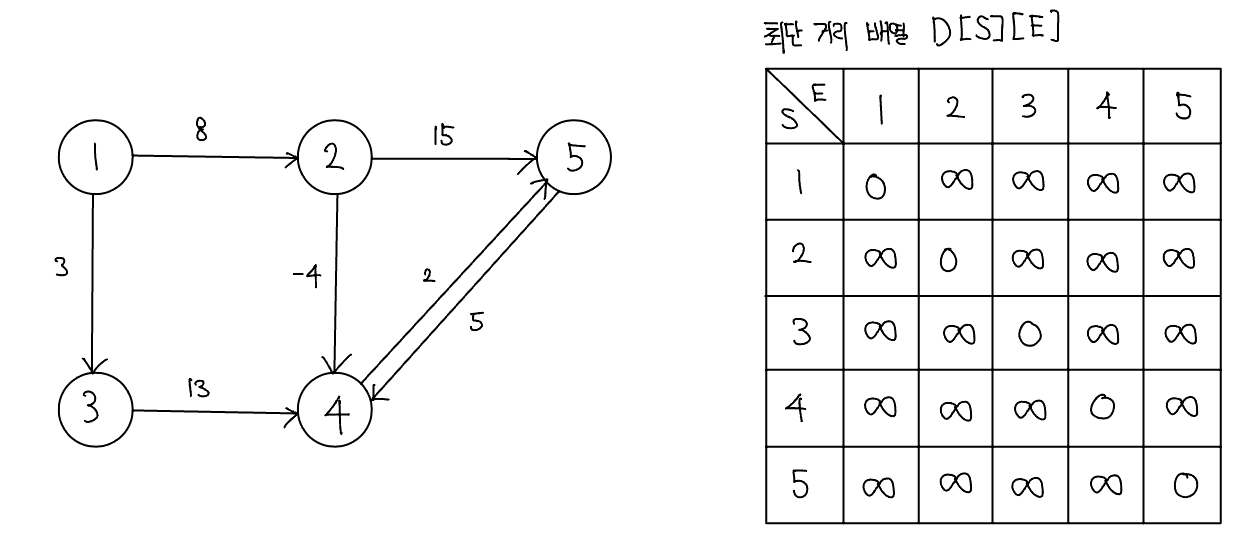
- 배열을 선언하고 초기화하기
- D[S][E]는 노드 S에서 노드 E까지의 최단 거리를 저장하는 배열이 정의한다. S와 E의 값이 같은 칸은 0, 다른 칸은 $\infty$로 초기화한다.
- 최단 거리 배열에 그래프 데이터 저장하기
- 출발 노드는 S, 도착 노드는 E, 이 Edge의 가중치는 W라고 했을 때 D[S][E] = W로 Edge의 정보를 배열에 입력한다. 이로써 플로이드-위셜 알고리즘은 그래프를 인접 행렬로 표현한다는 것을 알 수 있다.
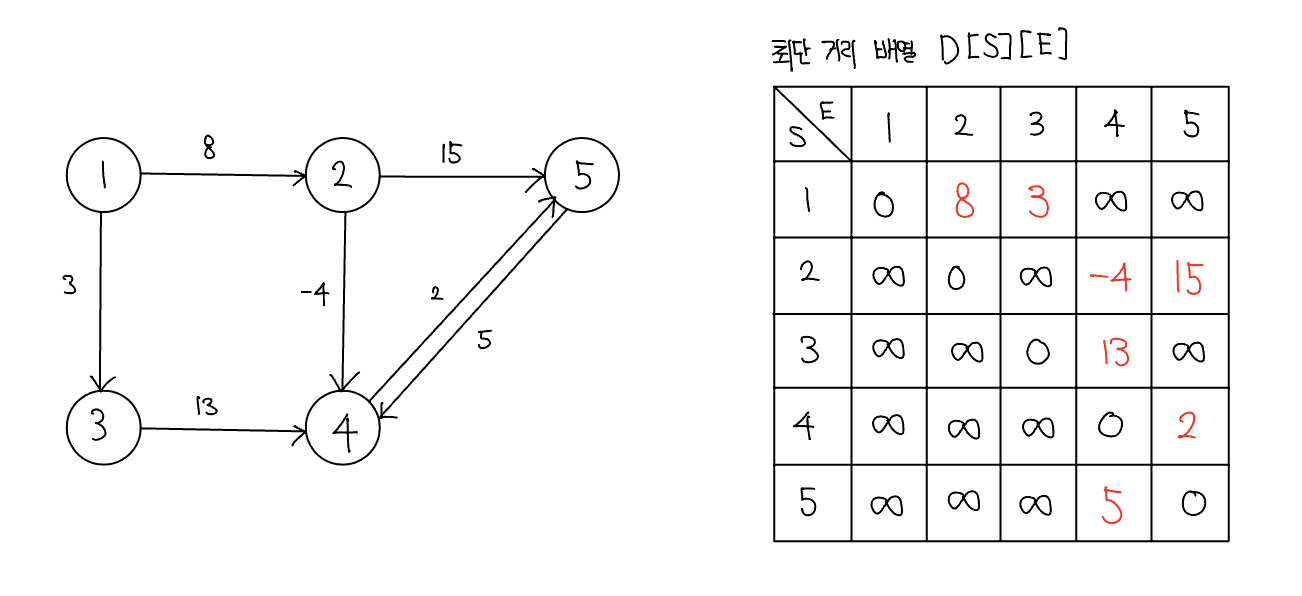
- 점화식으로 배열 업데이트하기
- 기존에 구했던 점화식을 3중 for문의 형태로 반복하면서 배열의 값을 업데이트한다.
for 경유지 K에 관해 (1 ~ N) // N: 노드 개수
for 출발 노드 S에 관해 (1 ~ N)
for 도착 노드 E에 관해 (1 ~ N)
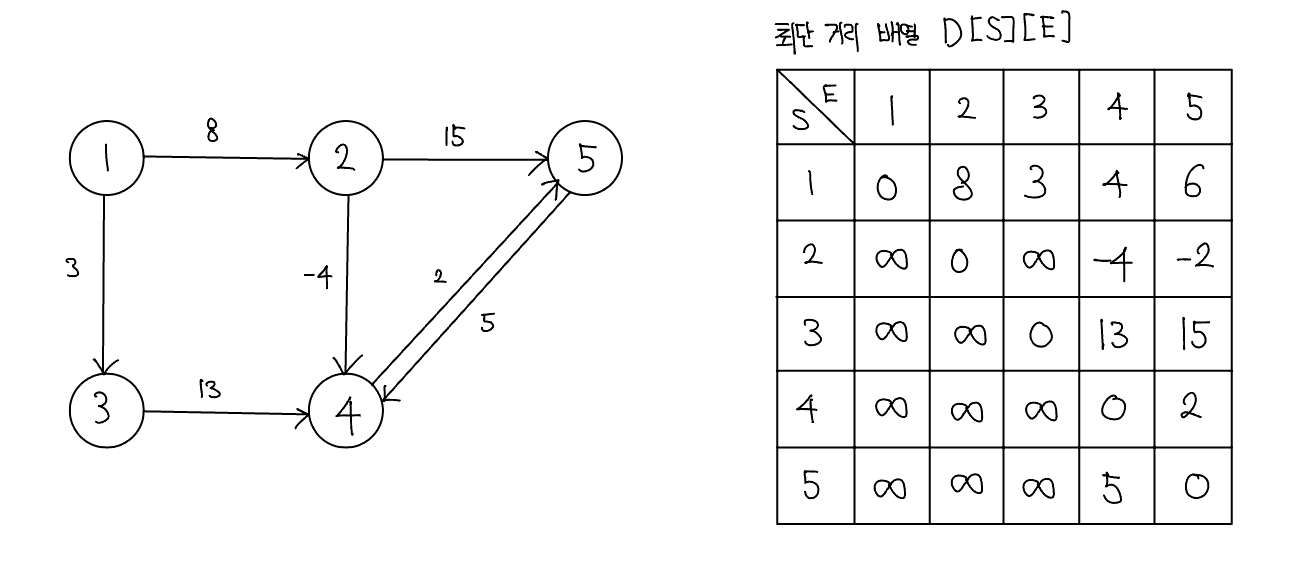
D[S][E] = min(D[s][E], D[S][K] + D[K][E])
완성된 배열은 모든 노드 간의 최단 거리를 알려준다.
문제 061 가장 빠른 버스 노선 구하기
시간 제한: 1초, 난이도: 골드4, 11404번
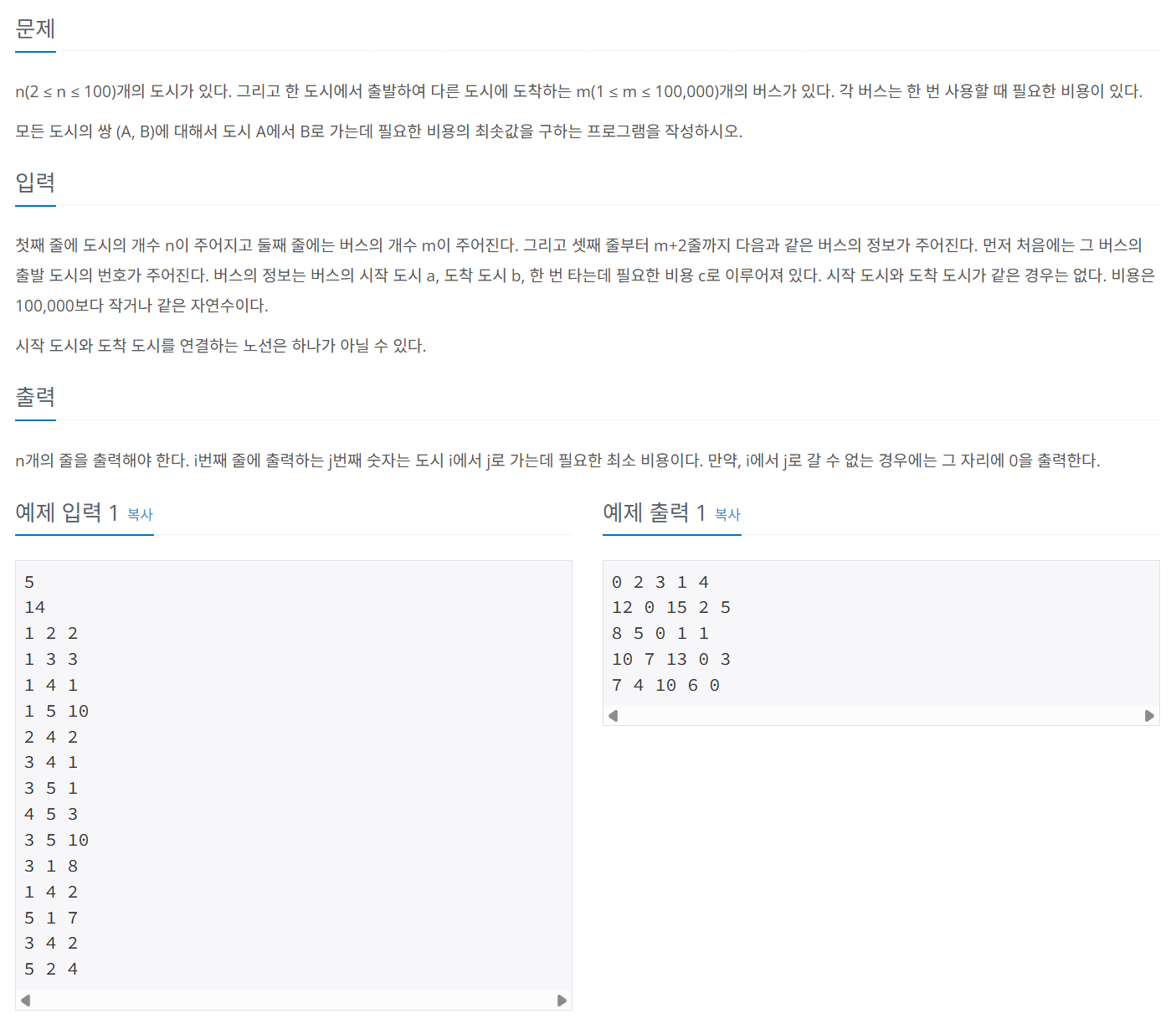
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static long[][] D;
public static int INF = Integer.MAX_VALUE;
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int n = Integer.parseInt(bf.readLine());
int m = Integer.parseInt(bf.readLine());
D = new long[n + 1][n + 1];
for (int i = 0; i < n + 1; i++) {
for (int j = 0; j < n + 1; j++) {
if (i == j) {
D[i][j] = 0;
} else {
D[i][j] = INF;
}
}
} // 배열 초기화
for (int i = 0; i < m; i++) {
StringTokenizer st = new StringTokenizer(bf.readLine());
int start = Integer.parseInt(st.nextToken());
int arrive = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
if (D[start][arrive] > weight) {
D[start][arrive] = weight;
}
} // 최단 거리 배열에 그래프 데이터 저장하기
for (int i = 1; i < n + 1; i++) {
for (int j = 1; j < n + 1; j++) {
for (int k = 1; k < n + 1; k++) {
D[j][k] = Math.min(D[j][k], D[j][i] + D[i][k]);
}
}
} // 플로이드-위셜 점화식 사용
for (int i = 1; i < n + 1; i++) {
for (int j = 1; j < n + 1; j++) {
if (D[i][j] == INF) {
bw.write(0 + " ");
} else {
bw.write(D[i][j] + " ");
}
}
bw.write("\n");
}
bw.flush();
bw.close();
}
}
플로이드-위셜의 정의대로 풀었다.
문제 062 경로 찾기
시간 제한: 1초, 난이도: 실버1, 11403번
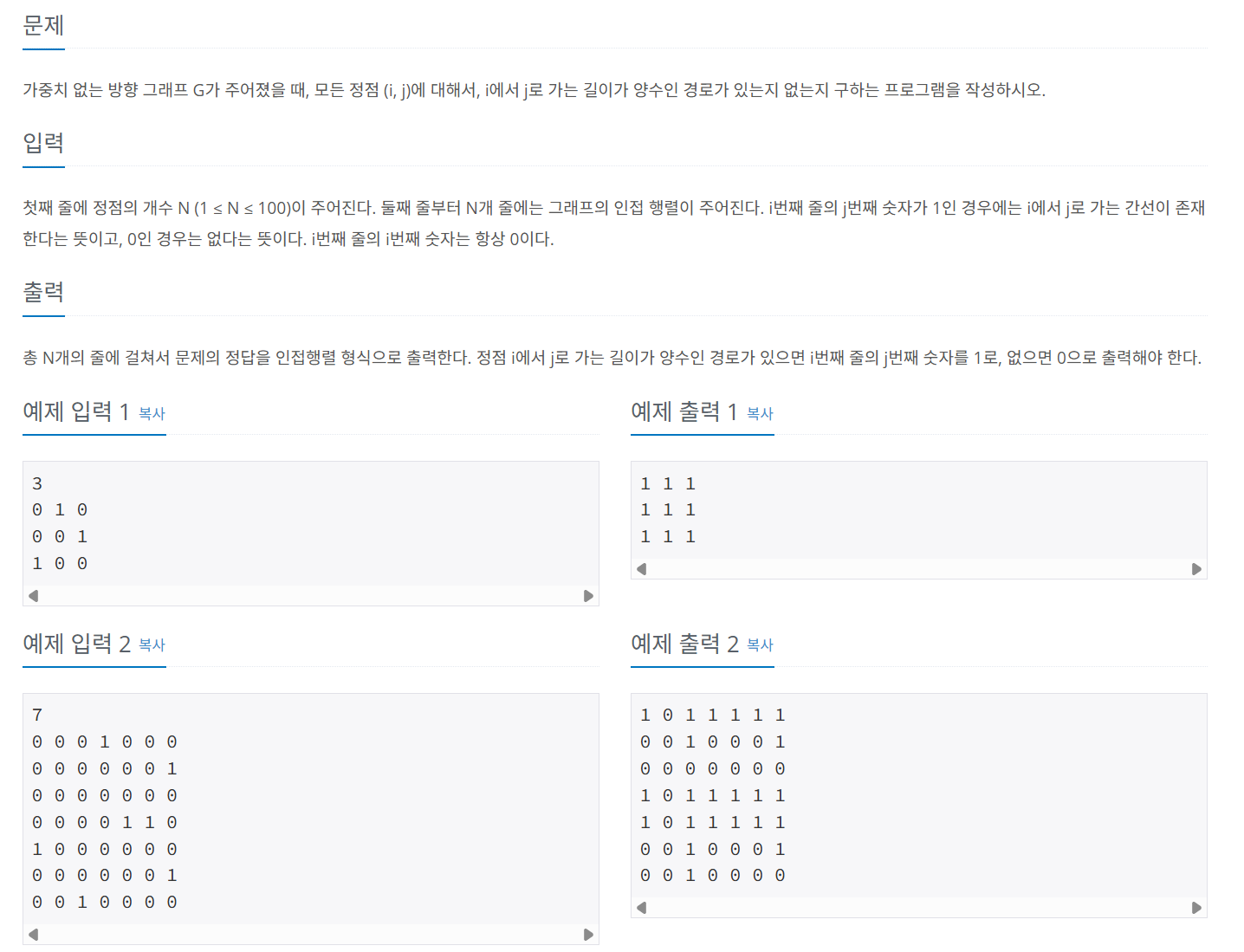
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static int N;
public static int[][] graph;
public static void next(int a, boolean[] visit) {
for (int i = 0; i <= N; i++) {
if (graph[a][i] == 1 && !visit[i]) {
visit[i] = true;
next(i, visit);
}
}
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
N = Integer.parseInt(bf.readLine());
graph = new int[N + 1][N + 1];
for (int i = 1; i <= N; i++) {
StringTokenizer st = new StringTokenizer(bf.readLine());
for (int j = 1; j <= N; j++) {
graph[i][j] = Integer.parseInt(st.nextToken());
}
}
for (int i = 1; i <= N; i++) {
boolean[] visit = new boolean[N + 1];
for (int j = 1; j <= N; j++) {
if (graph[i][j] == 1 && !visit[j]) {
visit[j] = true;
next(j, visit);
}
}
for (int j = 1; j <= N; j++) {
if (visit[j]) {
bw.write("1 ");
} else {
bw.write("0 ");
}
}
bw.write("\n");
}
bw.flush();
bw.close();
}
}
기존에 풀었던 방식대로 풀었던 문제이다.
문제 063 케빈 베이컨의 6단계 법칙
시간 제한: 2초, 난이도: 실버1, 1389번
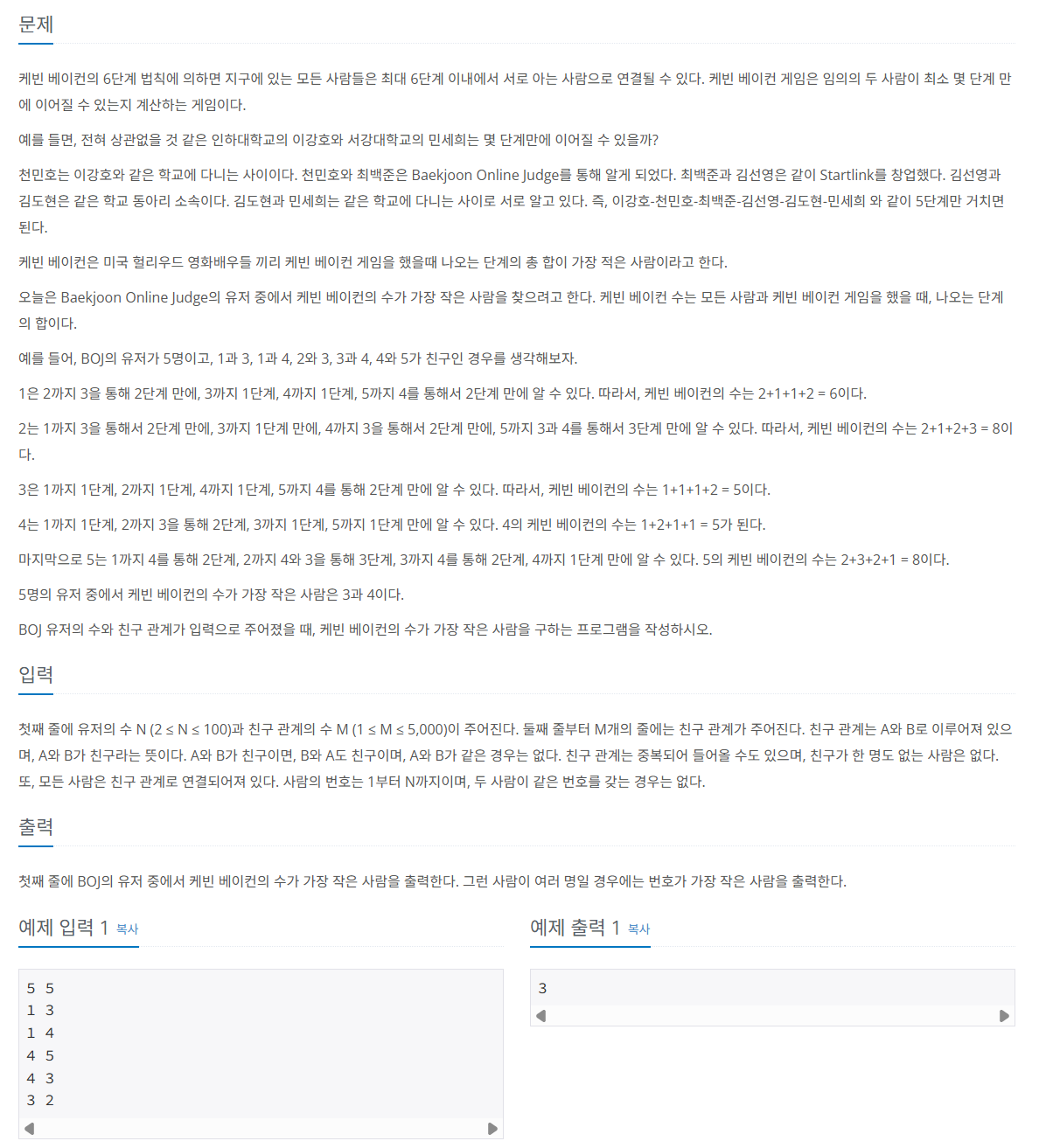
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static int[][] D;
public static int INF = 10000000;
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(bf.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
D = new int[N + 1][N + 1];
for (int i = 1; i < N + 1; i++) {
for (int j = 1; j < N + 1; j++) {
if (i != j) {
D[i][j] = INF;
} else {
D[i][j] = 0;
}
}
}
for (int i = 0; i < M; i++) {
st = new StringTokenizer(bf.readLine());
int A = Integer.parseInt(st.nextToken());
int B = Integer.parseInt(st.nextToken());
D[A][B] = 1;
D[B][A] = 1;
}
for (int i = 1; i < N + 1; i++) {
for (int j = 1; j < N + 1; j++) {
for (int k = 1; k < N + 1; k++) {
D[j][k] = Math.min(D[j][k], D[j][i] + D[i][k]);
}
}
}
int answer = 0;
int sum = INF;
for (int i = 1; i < N + 1; i++) {
int tempSum = 0;
for (int j = 1; j < N + 1; j++) {
if (D[i][j] != INF) {
tempSum += D[i][j];
}
}
if (tempSum < sum) {
sum = tempSum;
answer = i;
}
}
bw.write(answer + "\n");
bw.flush();
bw.close();
}
}
최소 신장 트리
최소 신장 트리(Minimum spanning tree)는 그래프에서 모든 노드를 연결할 때 사용된 에지들의 가중치의 합을 최소로 하는 트리이다. 주요 특징은 다음과 같다.
- 사이클이 포함되면 가중치의 합이 최소가 될 수 없으므로 사이클을 포함하지 않는다.
- N개으 노드가 있으면 최소 신장 트리를 구성하는 애지의 개수는 N - 1 개다.
최소 신장 트리의 핵심 이론
- 에지 리스트로 그래프를 구현하고 유니온 파인드 배열 초기화하기
- 최소 신장 트리는 데이터를 노드가 아닌 에지 중심으로 저장하므로 인접 리스트가 아닌 에지 리스트의 형태로 저장한다. 이 리스트는 일반적으로 노드 변수 2개와 가중치 변수로 구성된다. 사이클 처리를 위한 유니온 파인드 배열도 함깨 초기화한다. 배열의 인덱스를 해당 자리의 값으로 초기화하면 된다.
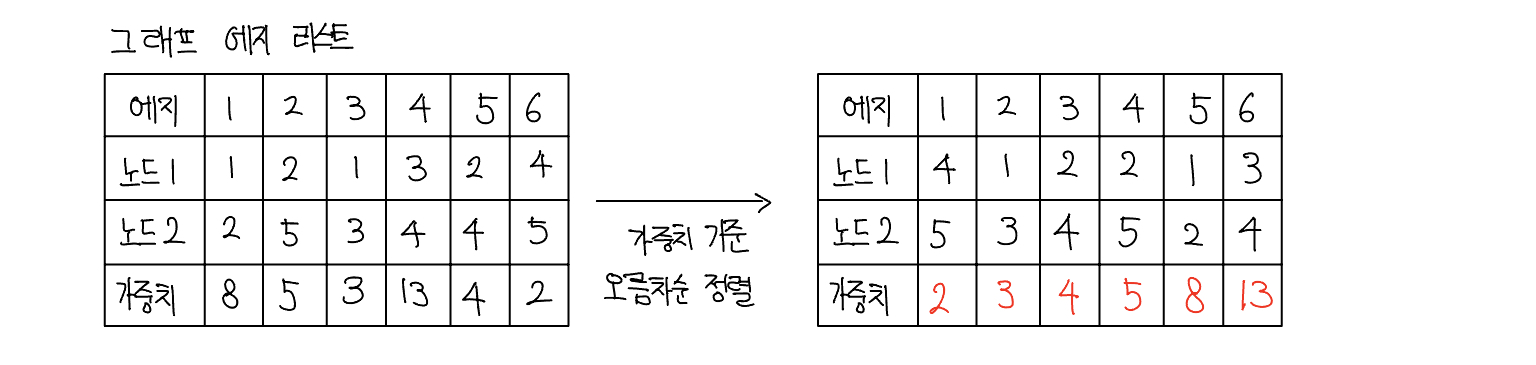
- 그래프 데이터를 가중치 기준으로 정렬하기
- 에지 리스트에 담긴 그래프 데이터를 가중치 기준으로 오름차순 정렬한다.
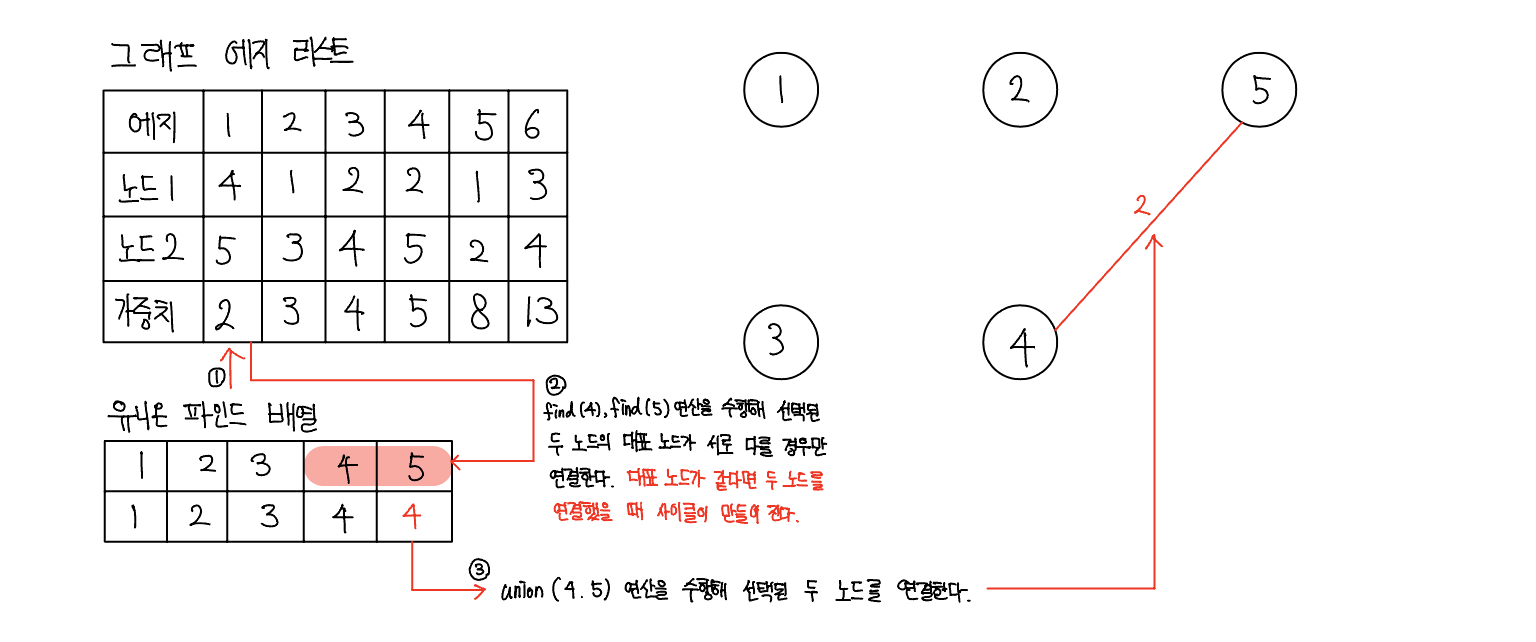
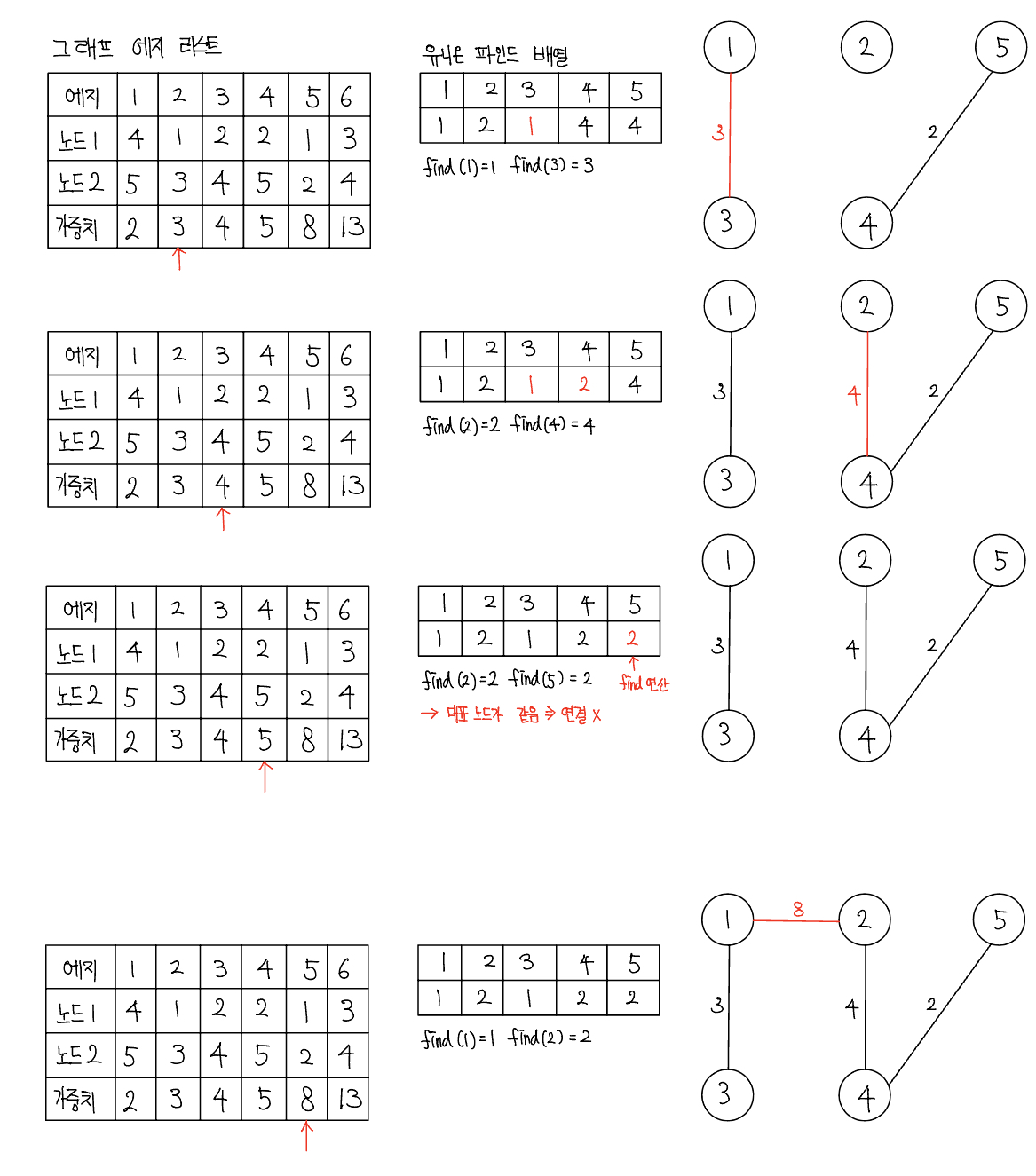
- 가중치가 낮은 에지부터 연결 시도하기
- 가중치가 낮은 에지부터 순서대로 선택해 연결을 시도한다. 이때 바로 연결하지 않고 이 에지를 연결했을 때 그래프에 사이클 형성 여부를 find 연산을 이용해 확인한 후 사이클이 형성되지 않을 때만 union 연산을 이용해 두 노드를 연결한다.
- 과정 3 반복하기
- 전체 노드의 개수가 N개이면 연결할 에지의 개수가 N - 1이 될 때까지 과정 3을 반복한다.
- 총 에지 비용 출력하기
- 에지의 개수가 N - 1이 되면 알고리즘을 종료하고, 완성된 최소 신장 트리의 총 에지 비용을 출력한다.
최소 신장 트리는 다른 그래프 알고리즘과 달리, 에지 리스트의 형태를 이용해 데이터를 담는다는 특징이 있다. 그 이유는 에지를 기준으로 하는 알고리즘이기 때문이다. 또한 사이클이 존재하면 안 되는 특징을 지니고 있기 때문에 사이클 판별 알고리즘인 유니온 파인드 알고리즘을 내부에 구현해야 한다.
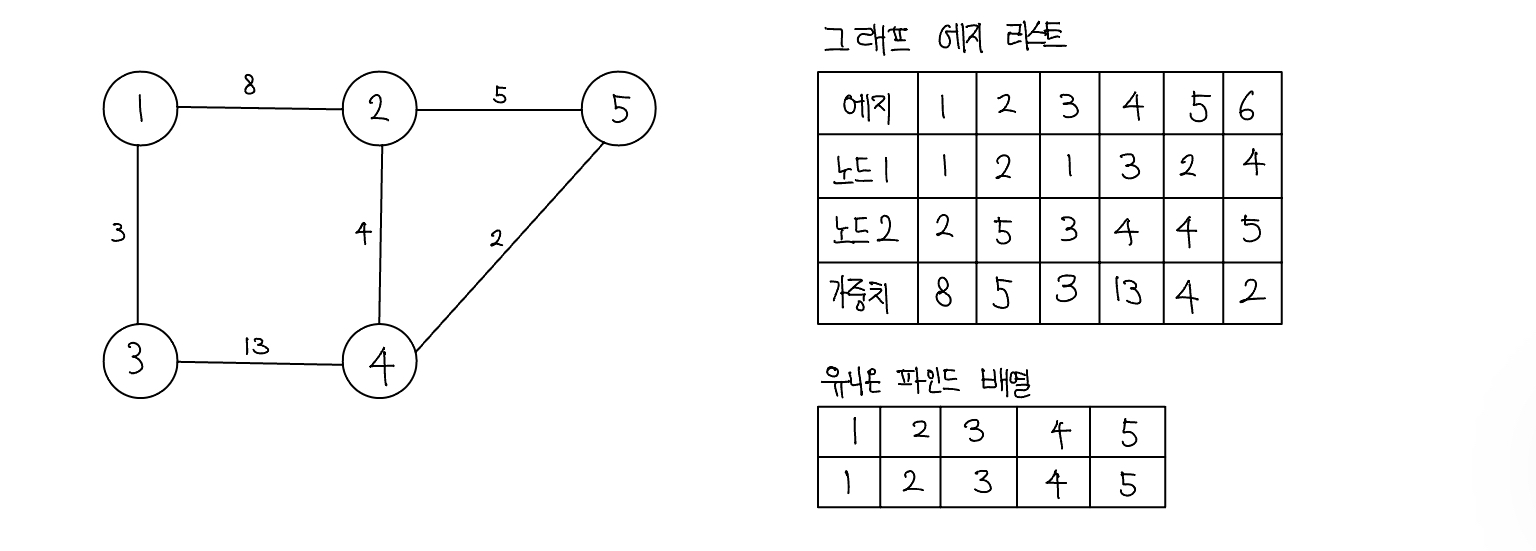
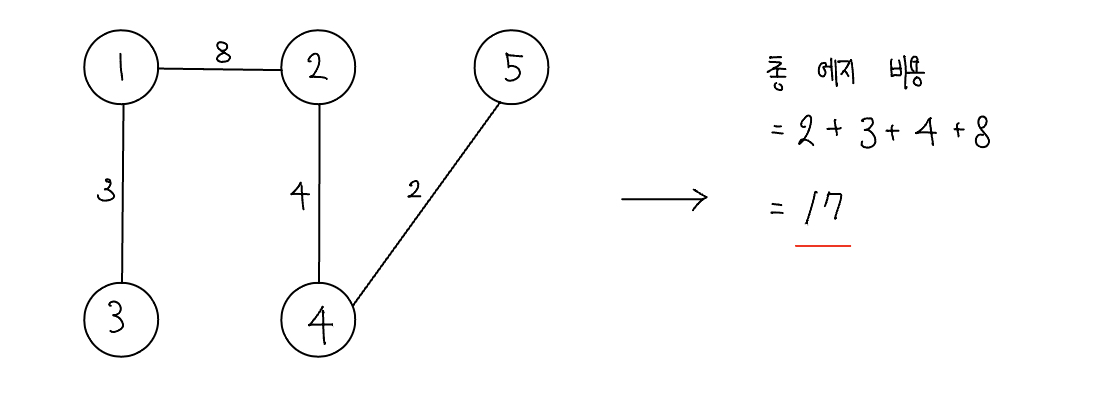
문제 064 최소 신장 트리 구하기
시간 제한: 2초, 난이도: 골드4, 1197번
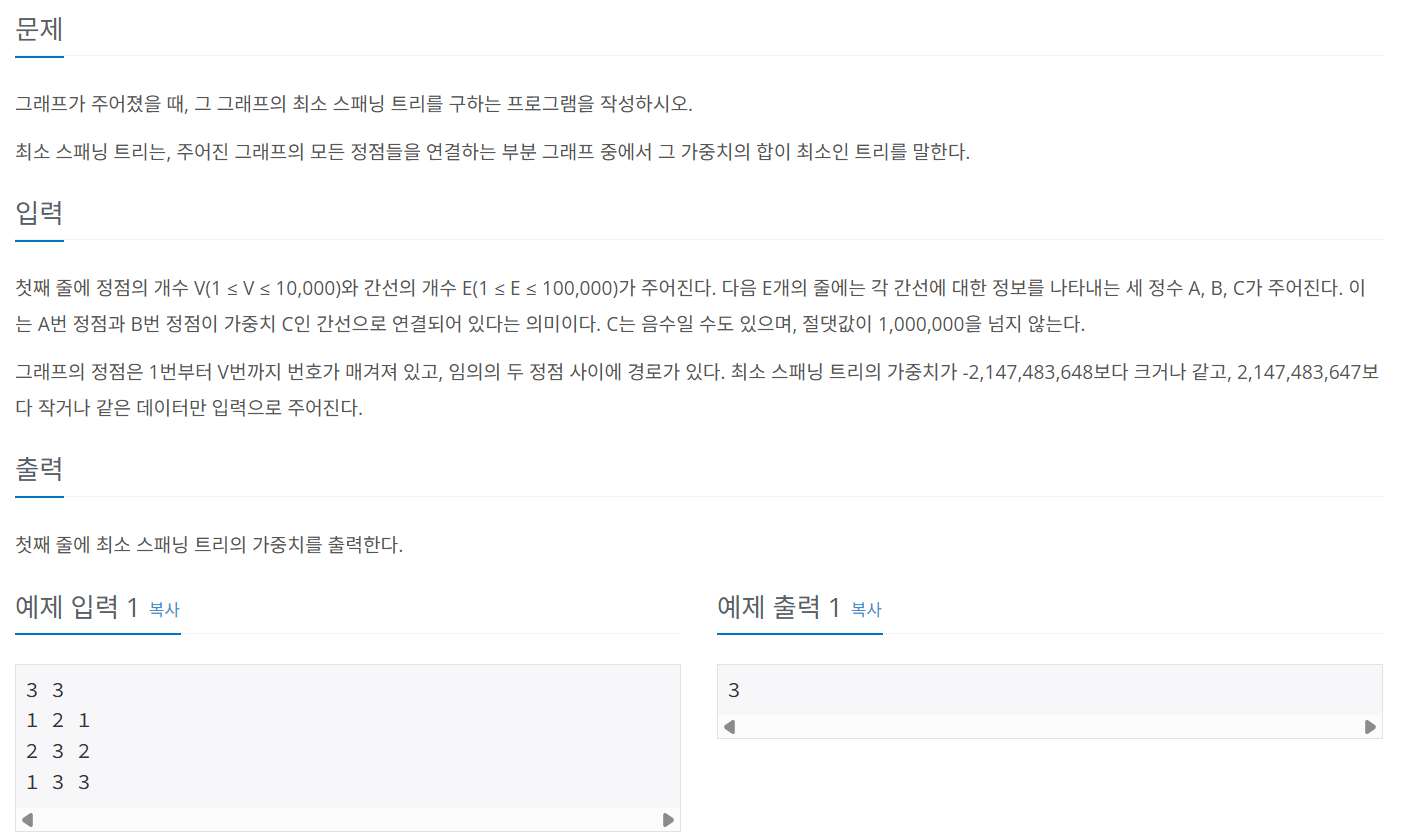
import java.io.*;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class Main {
public static PriorityQueue<Edge> pq;
public static int[] arr;
public static void union(int a, int b) {
a = find(a);
b = find(b);
if (a != b) {
arr[b] = a;
}
}
public static int find(int a) {
if (a == arr[a]) {
return a;
} else {
return arr[a] = find(arr[a]);
}
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(bf.readLine());
int V = Integer.parseInt(st.nextToken());
int E = Integer.parseInt(st.nextToken());
pq = new PriorityQueue<>();
arr = new int[V + 1];
for (int i = 1; i < V + 1; i++) {
arr[i] = i;
}
for (int i = 0; i < E; i++) {
st = new StringTokenizer(bf.readLine());
int A = Integer.parseInt(st.nextToken());
int B = Integer.parseInt(st.nextToken());
int C = Integer.parseInt(st.nextToken());
pq.add(new Edge(A, B, C));
}
int sum = 0;
int sumCount = 0;
while (sumCount < V - 1) {
Edge current = pq.poll();
int s = current.start;
int e = current.arrive;
int w = current.weight;
if (find(s) != find(e)) {
union(s, e);
sum += w;
sumCount++;
}
}
bw.write(sum + "\n");
bw.flush();
bw.close();
}
public static class Edge implements Comparable<Edge> {
int start;
int arrive;
int weight;
public Edge(int start, int arrive, int weight) {
this.start = start;
this.arrive = arrive;
this.weight = weight;
}
@Override
public int compareTo(Edge o) {
return weight - o.weight;
}
}
}
최소 신장 트리의 정의대로 구현하였다.
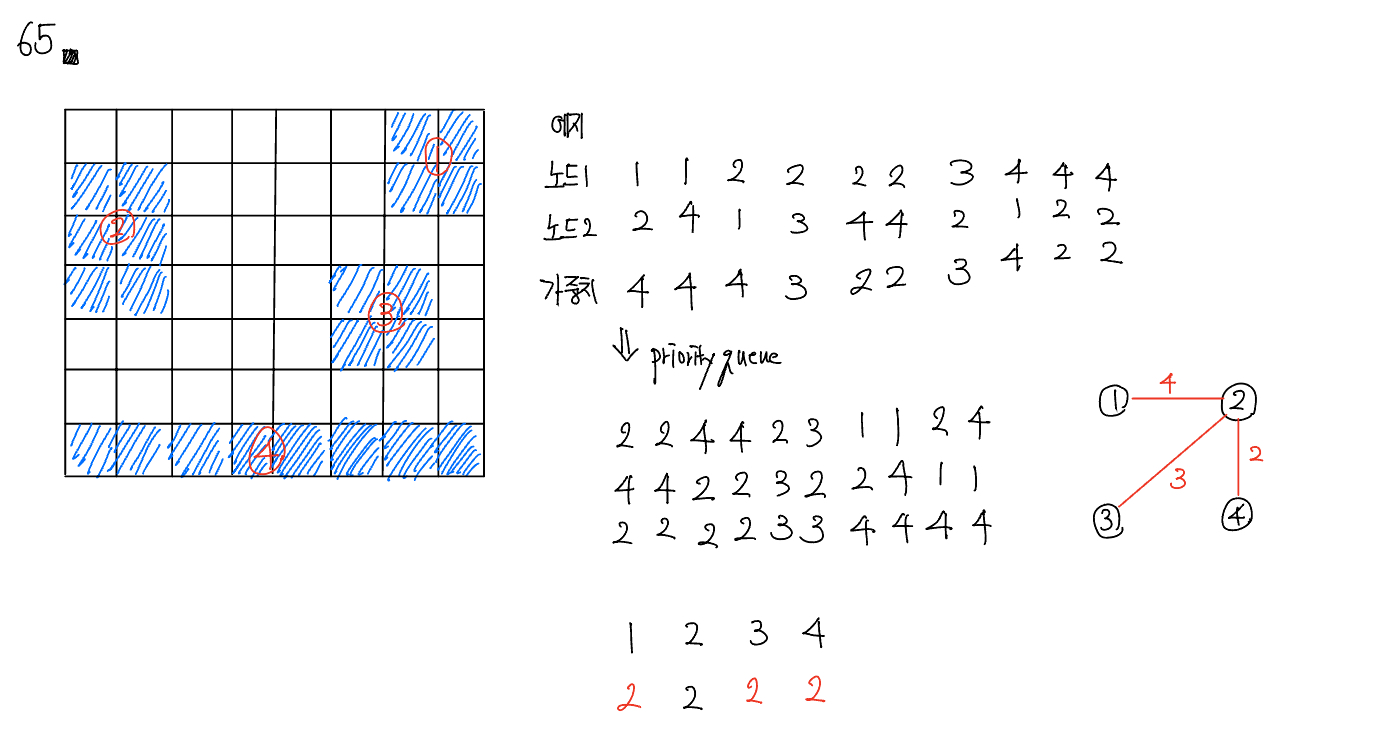
문제 065 다리 만들기
시간 제한: 1초, 난이도: 골드1, 17472번

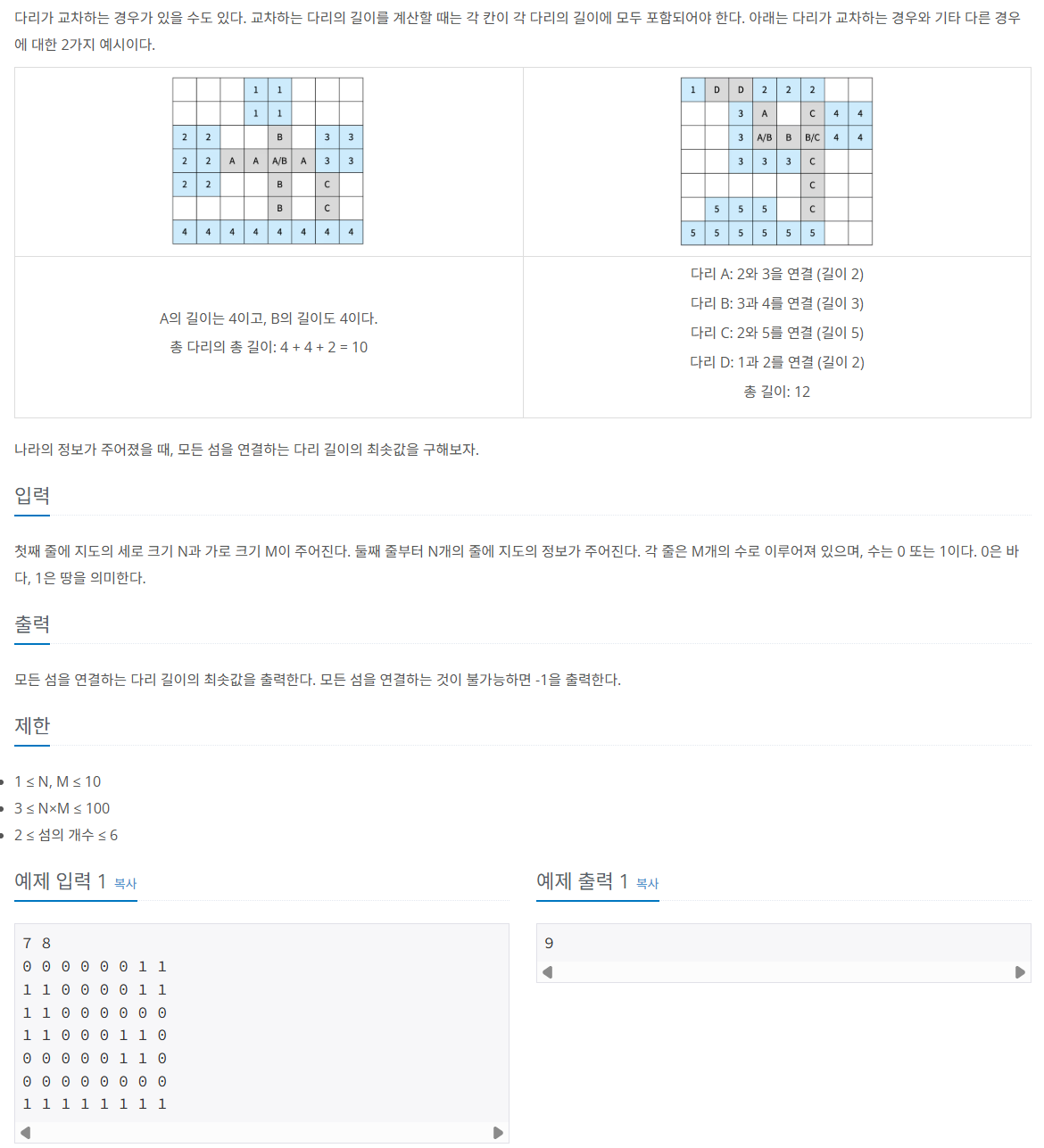
풀이
import java.io.*;
import java.util.*;
public class Main {
public static int N;
public static int M;
public static int INum; // 섬 번호
public static int[][] Sea;
public static ArrayList<ArrayList<Position>> Island; // 섬 정보 저장
public static boolean[][] Visit; // BFS를 위한 Visit 배열
public static PriorityQueue<Edge> pq;
public static void BFS(int a, int b) {
Queue<Position> qu = new LinkedList<>();
Island.get(INum).add(new Position(a, b));
qu.add(new Position(a, b));
Visit[a][b] = true;
Sea[a][b] = INum;
while (!qu.isEmpty()) {
Position cur = qu.poll();
int curX = cur.x; // 세로축
int curY = cur.y; // 가로축
if (curX > 0 && Sea[curX - 1][curY] == 1 && !Visit[curX - 1][curY]) {
Sea[curX - 1][curY] = INum;
Visit[curX - 1][curY] = true;
Island.get(INum).add(new Position(curX - 1, curY));
qu.add(new Position(curX - 1, curY));
} // 상
if (curX < N - 1 && Sea[curX + 1][curY] == 1 && !Visit[curX + 1][curY]) {
Sea[curX + 1][curY] = INum;
Visit[curX + 1][curY] = true;
Island.get(INum).add(new Position(curX + 1, curY));
qu.add(new Position(curX + 1, curY));
}
if (curY > 0 && Sea[curX][curY - 1] == 1 && !Visit[curX][curY - 1]) {
Sea[curX][curY - 1] = INum;
Visit[curX][curY - 1] = true;
Island.get(INum).add(new Position(curX, curY - 1));
qu.add(new Position(curX, curY - 1));
}
if (curY < M - 1 && Sea[curX][curY + 1] == 1 && !Visit[curX][curY + 1]) {
Sea[curX][curY + 1] = INum;
Visit[curX][curY + 1] = true;
Island.get(INum).add(new Position(curX, curY + 1));
qu.add(new Position(curX, curY + 1));
}
}
}
public static int[] arr; // 유니온 파인드를 위한 배열
public static void union(int a, int b) {
a = find(a);
b = find(b);
if (a != b) {
arr[b] = a;
}
}
public static int find(int a) {
if (arr[a] == a) {
return a;
} else {
return arr[a] = find(arr[a]);
}
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(bf.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
Sea = new int[N][M];
Visit = new boolean[N][M];
INum = 1;
pq = new PriorityQueue<>(); // 최소 신장 트리를 위한 PQ
for (int i = 0; i < N; i++) {
st = new StringTokenizer(bf.readLine());
for (int j = 0; j < M; j++) {
Sea[i][j] = Integer.parseInt(st.nextToken());
}
} // 섬 정보 저장
Island = new ArrayList<>();
for (int i = 0; i < 7; i++) {
Island.add(new ArrayList<>());
} // 섬의 개수는 최대 6개 이므로 7까지 add
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
if (Sea[i][j] == 1 && !Visit[i][j]) {
BFS(i, j);
INum++;
}
}
}
int[] D1 = new int[]{-1, 0, 1, 0};
int[] D2 = new int[]{0, -1, 0, 1};
for (int i = 1; i < INum; i++) {
for (int j = 0; j < Island.get(i).size(); j++) {
Position current = Island.get(i).get(j);
int currentX = current.x;
int currentY = current.y;
// 4방향 탐색
for (int k = 0; k < 4; k++) {
int temp1 = D1[k]; // 상하
int temp2 = D2[k]; // 좌우
int Bridge = 0;
while (currentX + temp1 >= 0 && currentX + temp1 < N && currentY + temp2 >= 0 && currentY + temp2 < M) {
if (Sea[currentX + temp1][currentY + temp2] == INum) {
break;
}
if (Sea[currentX + temp1][currentY + temp2] != 0) {
if (Bridge > 1) {
pq.add(new Edge(i, Sea[currentX+temp1][currentY+temp2], Bridge));
}
break;
} else {
Bridge++;
}
if (temp1 < 0) {
temp1--;
} else if (temp1 > 0) {
temp1++;
} else if (temp2 < 0) {
temp2--;
} else if (temp2 > 0) {
temp2++;
}
}
}
}
} // 최소 신장 트리를 위한 PQ 생성
// 최소 신장 트리 알고리즘 사용
arr = new int[INum];
for (int i = 1; i < INum; i++) {
arr[i] = i;
}
int answer = 0;
int connectedIsland = 0;
while (!pq.isEmpty()) {
Edge current = pq.poll();
if (find(current.start) != find(current.end)) {
union(current.start, current.end);
answer += current.weight;
connectedIsland++;
}
}
if (connectedIsland == INum - 2) {
bw.write(answer + "\n");
} else {
bw.write(-1 + "\n");
}
bw.flush();
bw.close();
}
public static class Position {
int x;
int y;
public Position(int x, int y) {
this.x = x;
this.y = y;
}
}
public static class Edge implements Comparable<Edge> {
int start;
int end;
int weight;
public Edge(int start, int end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
@Override
public int compareTo(Edge o) {
return weight - o.weight;
}
}
}
먼저 BFS를 통해 바다에 있는 섬의 구역을 나누고 섬의 정보를 한 배열에 담는다. 이후 섬의 정보가 들어있는 배열에서 상하좌우를 탐색하는데 해당 섬과 같은 섬이면 섬 배열의 다음 인덱스로 넘어가고 바다이면 다리의 길이를 늘리고, 다른 섬에 도착하면 다리의 길이가 1보다 크면 최소 신장 트리를 위한 Priority Queue에 담는다. 이후 이 Priority Queue와 유니온 파인드 알고리즘을 사용해 최소 신장 트리 알고리즘을 이용해 다리 길이의 최소값을 출력한다. 만약 연결된 섬의 수가 INum - 2와 같지 않으면 모든 섬이 연결되지 않았으므로 -1을 출력한다.
문제 066 불우이웃돕기
시간 제한: 2초, 난이도: 골드3, 1414번
import java.io.*;
import java.util.PriorityQueue;
public class Main {
public static int[] arr;
public static PriorityQueue<Edge> pq;
public static void union(int a, int b) {
a = find(a);
b = find(b);
if (a != b) {
arr[b] = a;
}
}
public static int find(int a) {
if (arr[a] == a) {
return a;
} else {
return arr[a] = find(arr[a]);
}
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(bf.readLine());
arr = new int[N];
pq = new PriorityQueue<>();
// A의 아스키 코드 65, a의 아스키코드 97
// 아스키 코드가 97보다 작으면 38을 빼고 97보다 크면 96을 뺀다.
int AllLineLength = 0;
for (int i = 0; i < N; i++) {
String inputString = bf.readLine();
char[] charArr = inputString.toCharArray();
for (int j = 0; j < N; j++) {
int length = charArr[j];
if (length == 48) {
continue;
} else if (length < 97) {
length = length - 38;
} else {
length = length - 96;
}
pq.add(new Edge(i, j, length));
AllLineLength += length;
}
}
int connectedLength = 0;
int connectedComputer = 0;
for (int i = 0; i < N; i++) {
arr[i] = i;
}
while (!pq.isEmpty()) {
Edge now = pq.poll();
if (find(now.start) != find(now.end)) {
union(now.start, now.end);
connectedComputer++;
connectedLength += now.weight;
}
}
if (connectedComputer == N - 1) {
int answer = AllLineLength - connectedLength;
bw.write(answer + "\n");
} else {
bw.write(-1 + "\n");
}
bw.flush();
bw.close();
}
public static class Edge implements Comparable<Edge> {
int start;
int end;
int weight;
public Edge(int start, int end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
@Override
public int compareTo(Edge o) {
return weight - o.weight;
}
}
}
최소 신장 트리의 정의대로 구현했다.
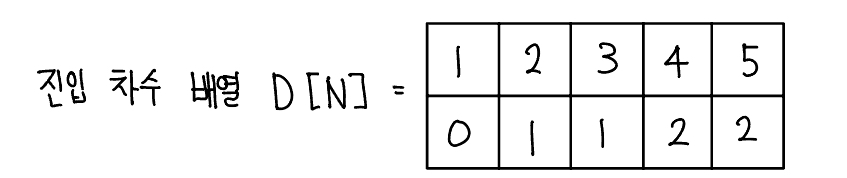
댓글남기기