9장 트리
Updated:
트리 알아보기
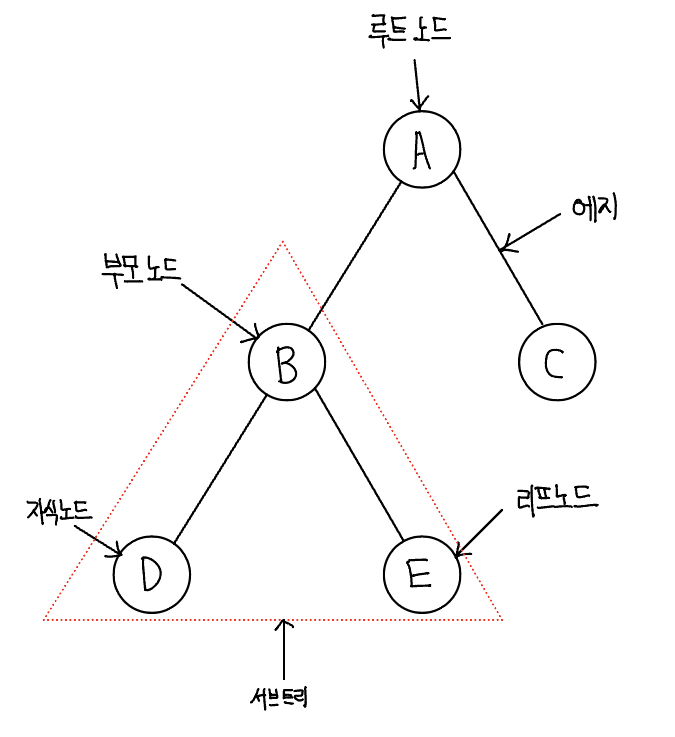
트리(tree)는 노드와 에지로 연결된 그래프의 특수한 형태로, 주요 특징은 다음과 같다.
- 순환 구조(cycle)를 지니고 있지 않고, 1개의 루트 노드가 존재한다.
- 루트 노드를 제외한 노드는 단 1개의 부모 노드를 갖는다.
- 트리의 부분 트리(subtree) 역시 트리의 모든 특징을 따른다.
트리의 핵심 이론
- 노드: 데이터의 index와 value를 표현하는 요소
- 에지: 노드와 노드의 연결 관계를나타내는 선
- 루트 노드: 트리에서 가장 상위에 존재하는 노드
- 부모 노드: 두 노드 사이의 관계에서 상위 노드에 해당하는 노드
- 자식 노드: 두 노드 사이의 관계에서 하위 노드에 해당하는 노드
- 리프 노드: 트리에서 가장 하위에 존재하는 노드(자식 노드가 없는 노드)
- 서브 트리: 전체 트리에 속한 작은 트리
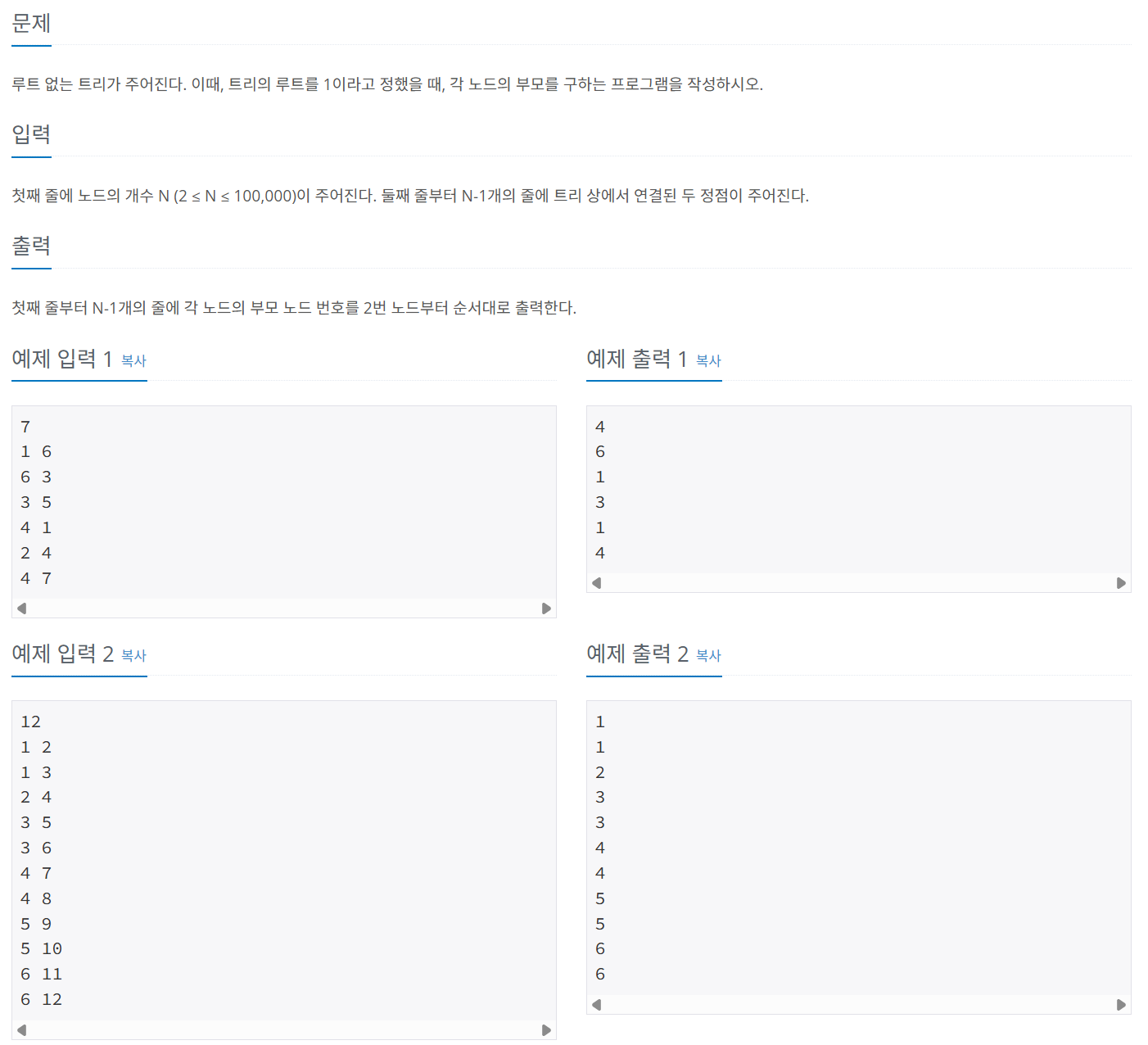
문제 067 트리의 부모 찾기
시간 제한: 1초, 난이도: 실버2, 11725번
import java.io.*;
import java.util.ArrayList;
import java.util.StringTokenizer;
public class Main {
public static ArrayList<ArrayList<Integer>> Tree;
public static boolean Visit[];
public static int parent[];
public static void DFS(int a) {
if (Visit[a]) {
return;
}
Visit[a] = true;
for (int i = 0; i < Tree.get(a).size(); i++) {
int next = Tree.get(a).get(i);
if (!Visit[next]) {
parent[next] = a;
DFS(next);
}
}
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
Tree = new ArrayList<>();
int N = Integer.parseInt(bf.readLine());
for (int i = 0; i <= N; i++) {
Tree.add(new ArrayList<>());
}
Visit = new boolean[N + 1];
parent = new int[N + 1];
for (int i = 1; i < N; i++) {
StringTokenizer st = new StringTokenizer(bf.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
Tree.get(a).add(b);
Tree.get(b).add(a);
}
DFS(1);
for (int i = 2; i < N + 1; i++) {
bw.write(parent[i] + "\n");
}
bw.flush();
bw.close();
}
}
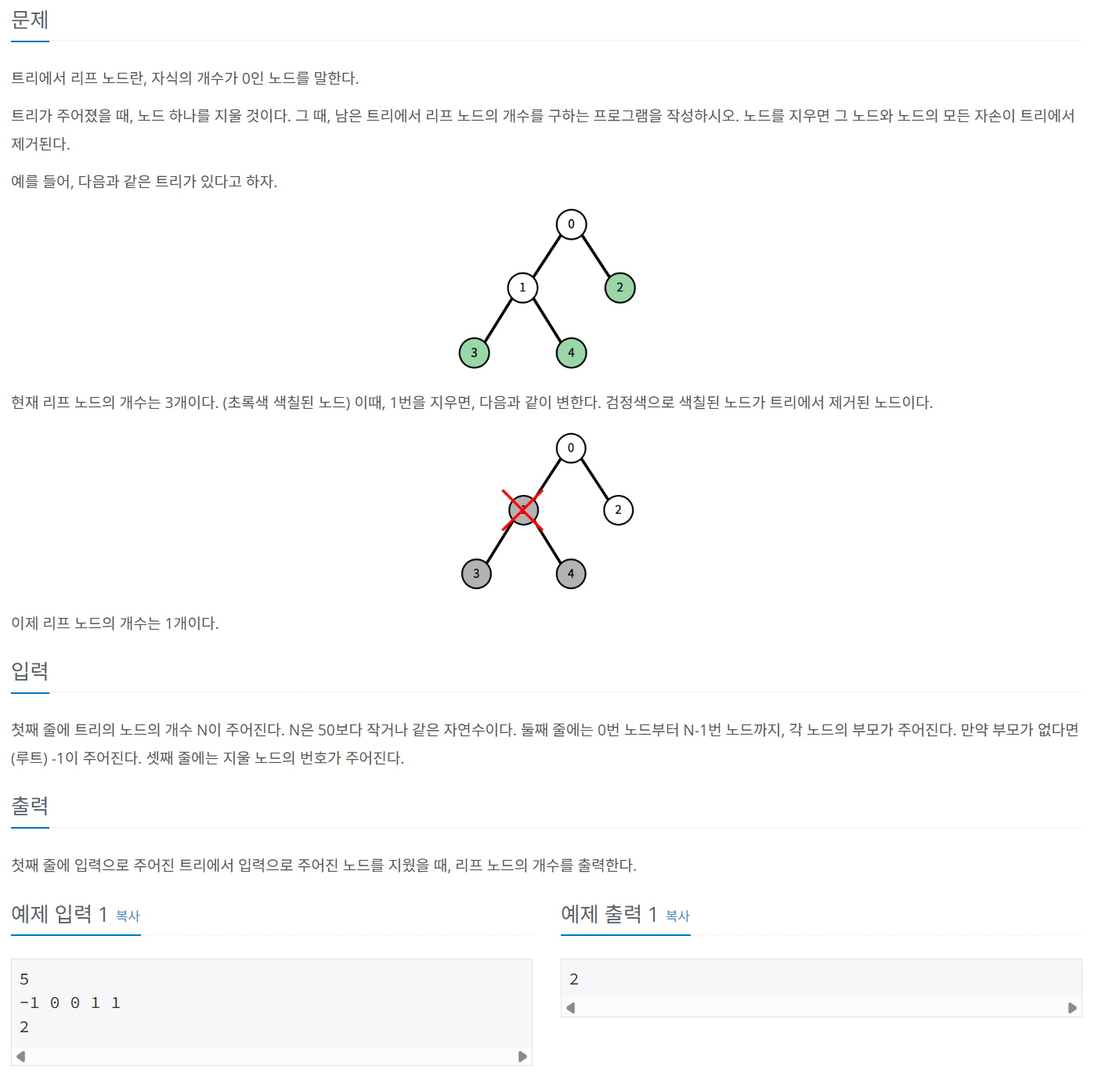
문제 068 리프 노드의 개수 구하기
시간 제한: 2초, 난이도: 골드5, 1068번
import java.io.*;
import java.util.ArrayList;
import java.util.StringTokenizer;
public class Main {
public static ArrayList<ArrayList<Integer>> Tree;
public static boolean[] Visit;
public static int count = 0;
public static void DFS(int a) {
if (Tree.get(a).size() == 0) {
count++;
}
for (int i = 0; i < Tree.get(a).size(); i++) {
int nextNode = Tree.get(a).get(i);
if (!Visit[nextNode]) {
Visit[nextNode] = true;
DFS(nextNode);
}
}
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(bf.readLine());
Visit = new boolean[N];
Tree = new ArrayList<>();
for (int i = 0; i < N; i++) {
Tree.add(new ArrayList<>());
}
StringTokenizer st = new StringTokenizer(bf.readLine());
int root = 0;
for (int i = 0; i < N; i++) {
int parent = Integer.parseInt(st.nextToken());
if (parent != -1) {
Tree.get(parent).add(i);
} else {
root = i;
}
}
int del = Integer.parseInt(bf.readLine());
if (del == root) {
for (int i = 0; i < Tree.get(root).size(); i++) {
Tree.get(root).remove(i);
}
bw.write(0 + "\n");
} else {
for (int i = 0; i < N; i++) {
for (int j = 0; j < Tree.get(i).size(); j++) {
if (Tree.get(i).get(j) == del) {
Tree.get(i).remove(j);
}
}
}
DFS(root);
bw.write(count + "\n");
}
bw.flush();
bw.close();
}
}
트라이
트라이(trie)는 문자열 검색을 빠르게 실행할 수 있도록 설계한 트라 형태의 자료구조이다.
트라이의 핵심 이론
트라이는 일반적으로 단어들을 사전의 형태로 생성한 후 트리의 부모 자식 노드 관계를 이용해 검색을 수행한다. 트라이 자료구조의 특징은 다음과 같다.
- N진 트리: 문자 종류의 개수에 따라 N이 결정된다. 예를 들어 알파벳은 26개의 문자로 이뤄져 있으므로 26진 트리로 구성된다.
- 루트 노드는 항상 빈 문자열을 뜩하는 공백 상태를 유지한다.
다음은 영단어 apple, air, apply를 순서대로 트라이 자료구조에 삽입하는 모습니다.
- 먼저 루트 노드는 공백을 유지하고 apply의 각 알파벳에 해당하는 노드를 생성한다.
- 그다음으로 air를 삽입할 때는 루트 노드에서부터 검색한다. a노드는 공백상태가 아니므로 이동하고, i와 r은 공백 상태이므로 신규 노드를 생성한다.
- apply를 삽입할 때도 검색 노드가 공백 상태이면 신규 노드를 생성하고, 아니면 이동하는 원리로 트라이 자료구조를 구현한다.
문제 069 문자열 찾기
시간 제한: 2초, 난이도: 실버4, 14425번

import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static Node root;
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(bf.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
root = new Node();
while (N > 0) {
String text = bf.readLine();
Node now = root;
for (int i = 0; i < text.length(); i++) {
char a = text.charAt(i);
// 입력은 소문자로만 이루어져 있고 index를 나타내기 위해 'a'를 뺌
if (now.next[a - 'a'] == null) {
now.next[a - 'a'] = new Node();
}
now = now.next[a - 'a'];
if (i == text.length() - 1) {
now.isEnd = true;
}
}
N--;
}
int count = 0;
while (M > 0) {
String text = bf.readLine();
Node now = root;
for (int i = 0; i < text.length(); i++) {
char a = text.charAt(i);
if (now.next[a - 'a'] == null) {
break;
} // now의 next가 존재하지 않으면 break
now = now.next[a - 'a'];
if (i == text.length() - 1 && now.isEnd) {
count++;
}
}
M--;
}
bw.write(count + "\n");
bw.flush();
bw.close();
}
public static class Node {
Node[] next = new Node[26]; // 알파벳 26개
boolean isEnd; // 문자열의 마지막인지 표시
}
}
트라이 자료구조를 활용하기 위해서는 26진 트리를 만들어야 하기 때문에 크기가 26인 Node를 만들어 주고 문자열의 마지막에 도달하면 리프 노드라고 표시해야한다. 또한 now노드를 유지하기 위해 for문을 사용하지 않고 while문을 사용해 반복문을 진행한다.
이진 트리
이진 트리(binary tree)는 각 노드의 자식 노드(차수)의 개수가 2 이하로 구성된 트리를 말한다. 트리 영역에서 가장 많이 사용되는 형태이다.
이진 트리의 핵심 이론
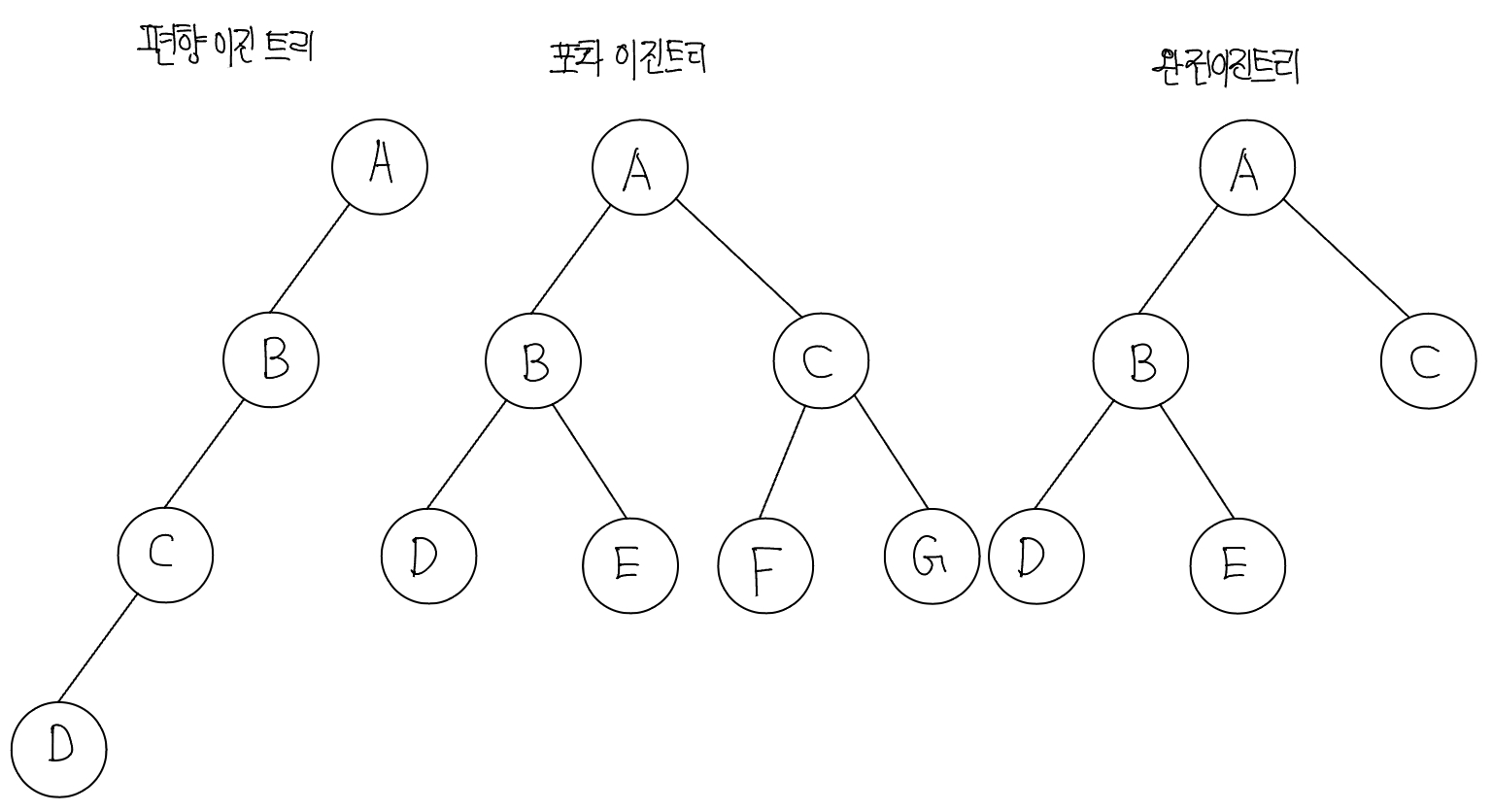
이진 트리의 종류는 다음과 같다.
- 편향 이진 트리: 노드들이 한쪽으로 편향돼 생성된 이진 트리
- 포화 이진 트리: 트리의 높이가 모두 일정하며 리프 노드가 꽉 찬 이진 트리
- 완전 이진 트리: 마지막 레벨을 제외하고 완전하게 노드들이 채워져 있고, 마지막 레벨은 왼쪽부터 채워진 트리
데이터를 트리 자료구조에 저장할 때 편향 이진 트리의 형태로 저장하면 탐색 속도가 저하되고 공간이 많이 낭비되는 단점이 있으므로 일반적으로 완전 이진 트리를 사용한다.
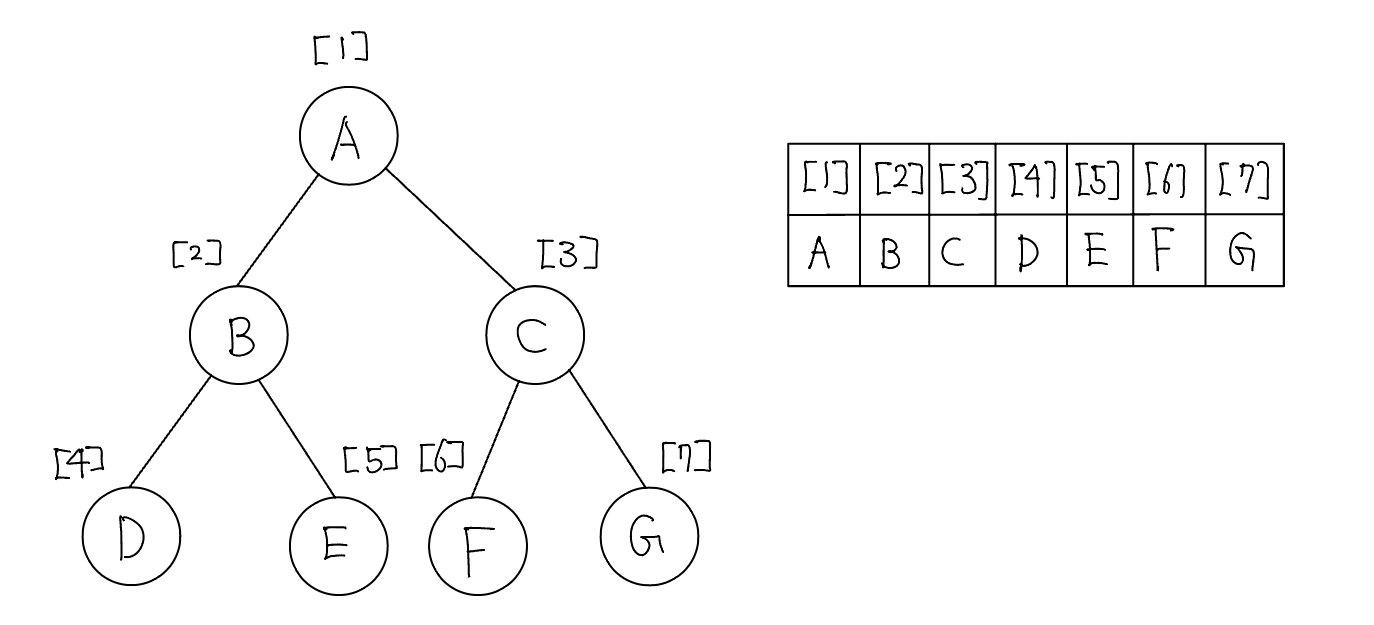
가장 직관적이면서 편리한 트리 자료구조 형태는 배열이다.
이진 트리는 위와 같이 1차원 배열의 형태로 표현할 수 있다. 노드 개수를 N개라고 할때 1차원 배열의 형태로 표현된 트리의 노드와 배열의 인덱스 간의 상관관계는 다음과 같다.
- 이동 목표 노드: 루트 노드
- 인덱스 연산: index = 1
- 이동 목표 노드: 부모 노드
- 인덱스 연산: index = index / 2
- 제약 조건: 현재 노드가 루트 노드가 아님
- 이동 목표 노드: 왼쪽 자식 노드
- 인덱스 연산: index = index * 2
- 제약 조건: index * 2 <= N
- 이동 목표 노드: 오른쪽 자식 노드
- 인덱스 연산: index = index * 2 + 1
- 제약 조건: index * 2 + 1 <= N
위 인덱스 연산 방식은 향후 세그먼트 트리(segment tree)나 LCA(lowest common ancestor)알고리즘에서도 기본이 되는 연산이다.
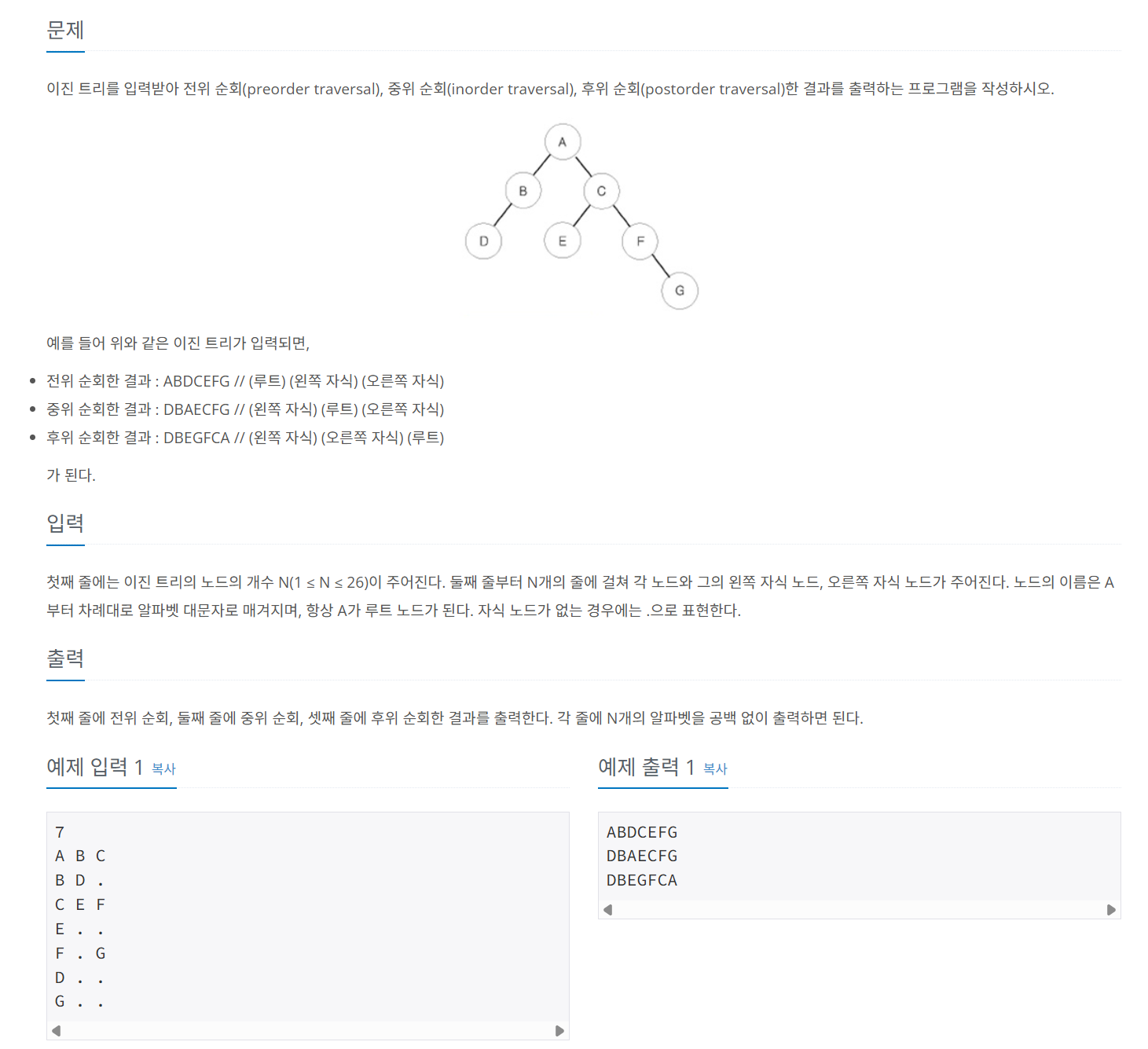
문제 070 트리 순회하기
시간 제한: 2초, 난이도: 실버1, 1991번
import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
public static BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
public static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
public static int N;
public static int[][] Tree;
public static void PreOrder(int a) throws IOException { // 전위 순회
if (a == -1) {
return;
}
bw.write(((char) (a + 'A')) + "");
PreOrder(Tree[a][0]);
PreOrder(Tree[a][1]);
}
public static void InOrder(int a) throws IOException { // 중위 순회
if (a == -1) {
return;
}
InOrder(Tree[a][0]);
bw.write(((char) (a + 'A')) + "");
InOrder(Tree[a][1]);
}
public static void PostOrder(int a) throws IOException { // 후위 순회
if (a == -1) {
return;
}
PostOrder(Tree[a][0]);
PostOrder(Tree[a][1]);
bw.write(((char) (a + 'A')) + "");
}
public static void main(String[] args) throws IOException {
N = Integer.parseInt(bf.readLine());
Tree = new int[N][2]; // 인덱스 0부터 A, 1행은 Right, 2행은 Left
for (int i = 0; i < N; i++) {
StringTokenizer st = new StringTokenizer(bf.readLine());
char CNode = st.nextToken().charAt(0);
char LNode = st.nextToken().charAt(0);
char RNode = st.nextToken().charAt(0);
int CN = CNode - 'A';
if (LNode == '.') {
Tree[CN][0] = -1;
} else {
Tree[CN][0] = LNode - 'A';
}
if (RNode == '.') {
Tree[CN][1] = -1;
} else {
Tree[CN][1] = RNode - 'A';
}
}
PreOrder(0);
bw.write("\n" + "");
InOrder(0);
bw.write("\n" + "");
PostOrder(0);
bw.flush();
bw.close();
}
}
이진 트리를 2차원 배열로 나타내서 알고리즘을 구현하였다. 배열은 index를 나타내기 위해서 char 자료형을 사용하였고, 2차원 베열에서 1행은 왼쪽 노드, 2행은 오른쪽 노드를 나타낸다.
세그먼트 트리
주어진 데이터의 구간 합과 데이터 업데이트를 빠르게 수행하기 위해 고안해 낸 자료구조의 형태가 바로 세스먼트 트리이다. 더 큰 범위는 ‘인덱스 트리’라고 부른다.
세그먼트 트리의 핵심 이론
세그먼트 트리의 종류는 구간 합, 최대$\cdot$최소 구하기로 나눌 수 있고, 구현 단계는 트리 초기화하기, 질의값 구하기(구간 합 또는 최대$\cdot$최소), 데이터 업데이트하기로 나눌 수 있다.
1. 트리 초기화 하기
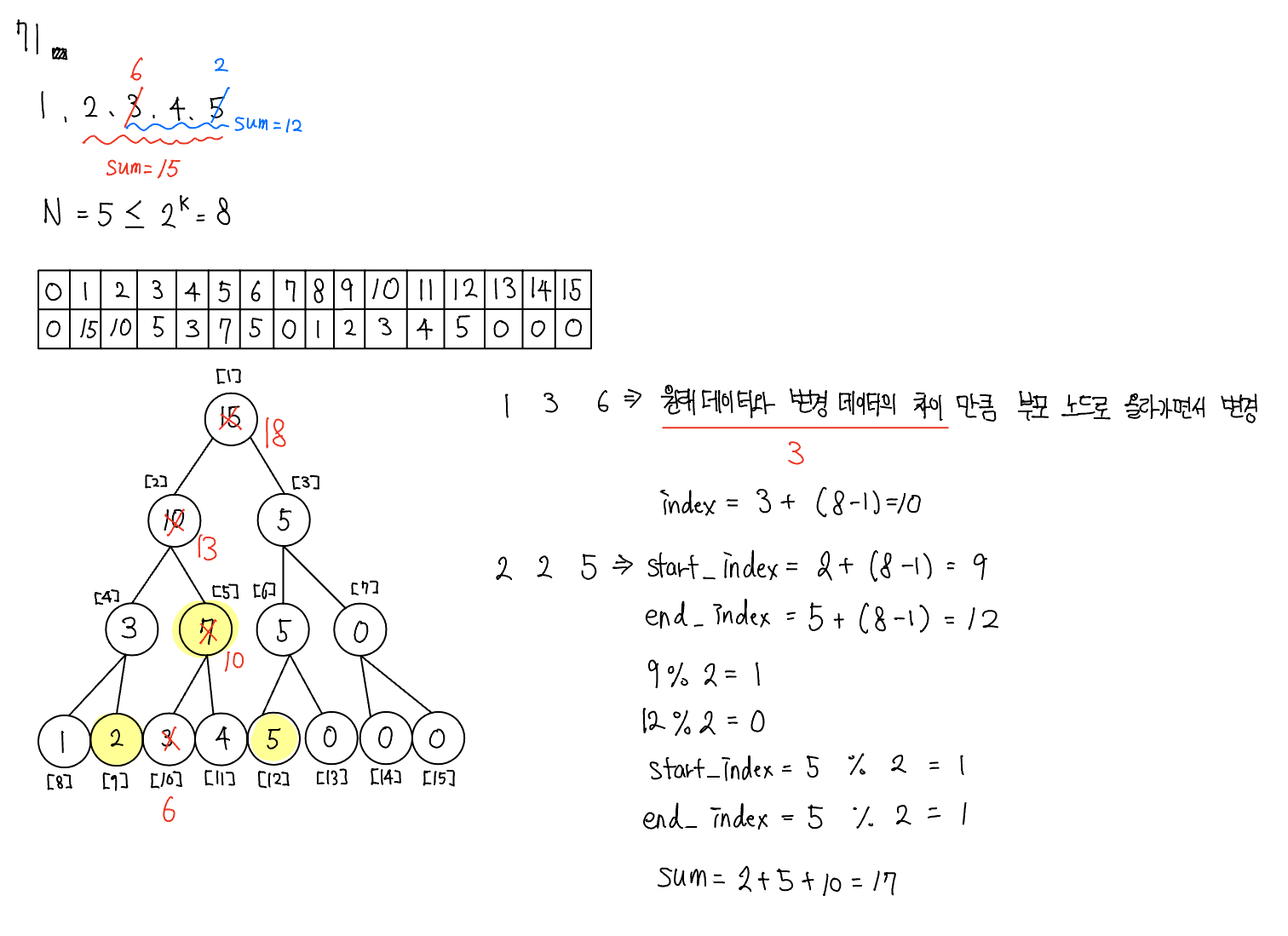
- 리프 토드의 개수가 데이터의 개수(N) 이상이 되도록 트리 배열을 만든다. 트리 배열의 크기를 구하는 방법은 $2^k \geq N$을 만족하는 k의 최솟값을 구한 후 $2^k * 2$를 트리 배열의 크기로 정의하면 된다. 예를 들어 샘플 데이터 {5, 8, 4, 3, 7, 2, 1, 6}이 있다면 N = 8이므로 $2^3 \geq 8$이므로 배열의 크기를 $2^3 * 2 = 16$으로 정의한다.
- 리프 노드에 원본 데이터를 입력한다. 이때 리프 노드의 시작 위치를 트리 배열의 인덱스로 구해야 하는데, 구하는 방식은 $2^k$를 시작 인덱스로 취하면 된다. 예를 들어 k의 값이 3이면 start_index = 8이 된다.
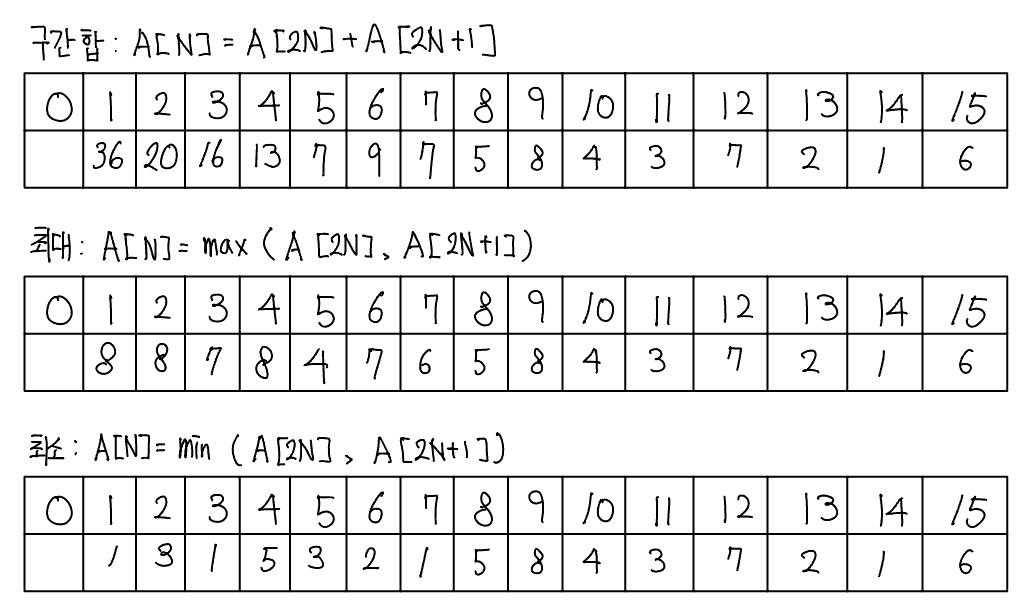
- 리프 노드를 제외한 나머지 노드의 값을 채운다($2^k - 1$부터 1번 쪽으로 채운다). 채워야 하는 인덱스가 N이라고 가정하면 자신의 자식 노드를 이용해 해당 값을 채울 수 있다. 자식 노드의 인덱스는 이진 트리 형식이기 때문에 2N, 2N + 1이 된다. 케이스 별로 적절하게 계산한다.
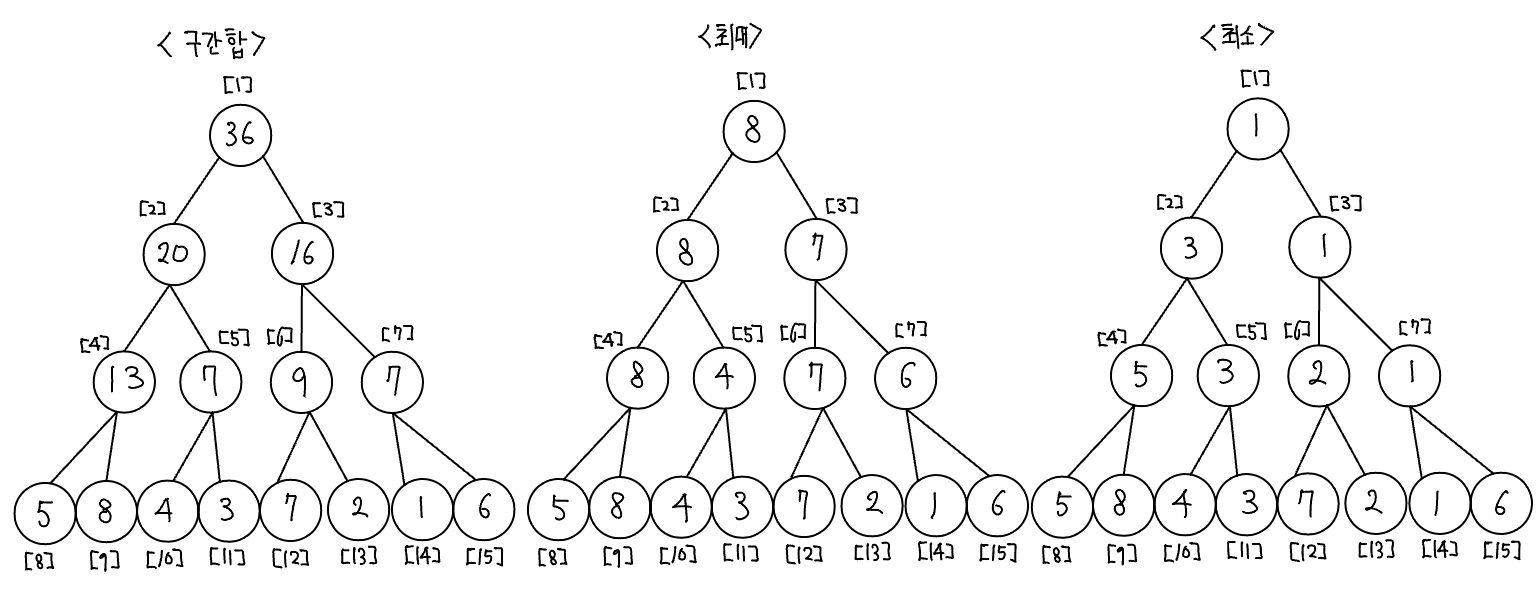
- 위 세그먼트 트리 배열을 실제 트리 모양으로 구조화 하면 다음과 같다.
- 이렇게 세그먼트 트리를 구성해 놓으면 그 이후 질의와 관련된 결괏값이나 데이터 업데이트 요구 사항에 관해 좀 더 빠른 시간 복잡도 안에서 해결할 수 있다.
2. 질의값 구하기 - 주어진 질의 인덱스를 세그먼트 트리의 리프 노드에 해당하는 인덱스로 변경한다. 기존 샘플을 기준으로 한 인덱스값과 세그먼트 트리 배열에서의 인덱스값이 다르기 때문에 인덱스를 변경해야 한다. 인덱스 변경 방법은 세그먼트 트리 index = 주어진 질의 index + $2^k - 1$과 같다.
- 질의에서의 시작 인덱스와 종료 인덱스에 관해 부모 노드로 이동하면서 주어진 질의에 해당하는 값을 다음과 같이 구현한다.
- start_index % 2 == 1일 때 해당 노드를 선택한다.
- end_index % 2 == 0일 때 해당 노드를 선택한다.
- start_index depth 변경: start_index = (start_index + 1) / 2 연산을 한다.
- end_index depth 변경: end_index = (end_index - 1) / 2 연산을 한다.
- 1~4 과정을 반복하다가 end_index < start_index가 되면 종료한다.
- 1~2에서 해당 노드를 선택했다는 것은 해당 노드의 부모가 나타내는 범위가 질의 범위를 넘어가기 때문에 해당 노드를 질의값에 영향을 미치는 독립 노드로 선택하고, 해당 노드의 부모 노드는 대상 범위에서 제외한다는 뜻이다.
- 부모 노드를 대상 범위에서 제거하는 방범은 바로 3~4에서 질의 범위에 해당하는 부모 노드로 이동하기 위해 인덱스 연산을 index/2가 아닌 (index + 1) / 2, (index - 1) / 2로 수행하는 것이다.
- 질의에 해당하는 노드를 선택하는 방법은 구간 합, 최대값 구하기, 최솟값 구하기 모두 동일하고 선택된 노드들에 관해 마지막에 연산하는 방식만 다르다.
- 구간합: 선택된 노드를 모두 더한다.
- 최댓값 구하기: 선택된 노드 중 MAX값을 선택해 출력한다.
- 최솟값 구하기: 선택된 노드 중 MIN값을 선택해 출력한다.
3. 데이터 업데이트하기
- 업데이트 방식은 자신의 부모 노드로 이동하면서 업데이트한다는 것은 동일하지만, 어떤 값으로 업데이트할 것인지에 관해서는 트리 타입별로 조금 다르다.
- 부모 노드로 이동하는 방식은 index = index / 2로 변경하면 된다.
- 구간합: 원래 데이터와 변경 데이터의 차이만큼 부모 노드로 올라가면서 변경한다.
- 최댓값 찾기: 변경 데이터와 자신과 같은 부모를 지니고 있는 다른 자식 노드와 비교해 더 큰 값으로 업데이트한다. 업데이터가 일어나지 않으면 종료한다.
- 최솟값 찾기: 변경 데이터와 자신과 같은 부모를 지니고 있는 다른 자식 노드와 비교해 더 작은 값으로 업데이트한다. 업데이트가 일어나지 않으면 종료한다.
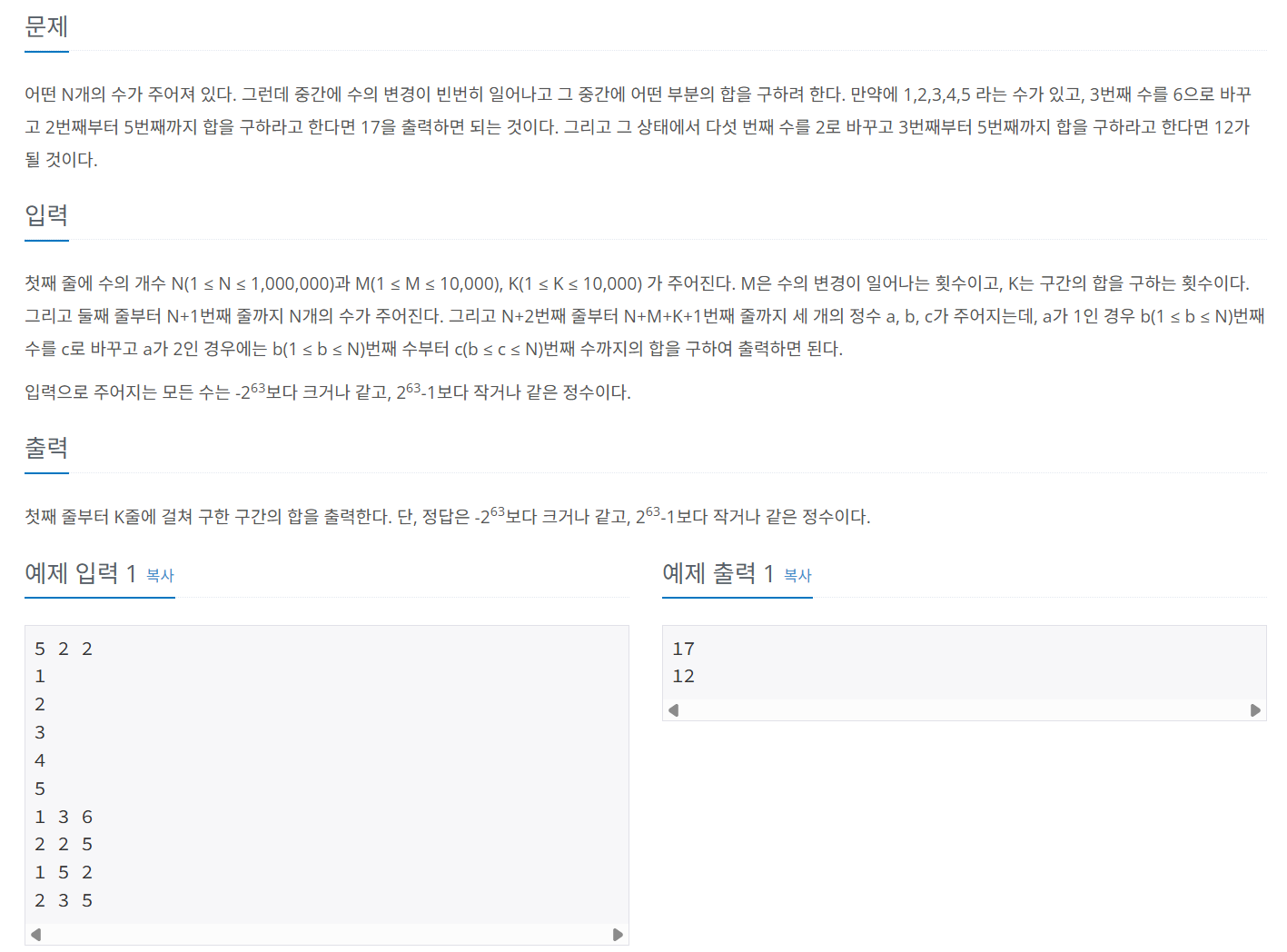
문제 071 구간 합 구하기3
시간 제한: 2초, 난이도: 골드1, 2042번
풀이
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
public static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
public static long[] Tree;
public static int k;
public static void AddData(int N) throws IOException {
int index = (int) Math.pow(2, k);
for (int i = 0; i < N; i++) {
long data = Long.parseLong(bf.readLine());
Tree[index] = data;
index++;
}
}
public static void ChangeData(int changeIndex, long data) {
int index = (int) (changeIndex + (Math.pow(2, k) - 1));
long diff = data - Tree[(int) ((Math.pow(2, k) - 1) + changeIndex)];
while (index > 0) {
Tree[index] += diff;
index = index / 2;
}
}
public static void SumData(int startIndex, int endIndex) throws IOException {
startIndex = (int) (startIndex + (Math.pow(2, k) - 1));
endIndex = (int) (endIndex + (Math.pow(2, k) - 1));
long sum = 0;
while (startIndex <= endIndex) {
if (startIndex % 2 == 1) {
sum += Tree[startIndex];
}
if (endIndex % 2 == 0) {
sum += Tree[endIndex];
}
startIndex = (startIndex + 1) / 2;
endIndex = (endIndex - 1) / 2;
}
bw.write(sum + "\n");
}
public static void main(String[] args) throws IOException {
StringTokenizer st = new StringTokenizer(bf.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
// k값 구하기
k = 0;
while (Math.pow(2, k) < N) {
k++;
}
Tree = new long[(int) Math.pow(2, k) * 2];
// 기존 데이터 채우기
AddData(N);
// 세그먼트 트리 채우기
for (int i = (int) (Math.pow(2, k) - 1); i > 0; i--) {
Tree[i] = Tree[2 * i] + Tree[2 * i + 1];
}
for (int i = 0; i < M + K; i++) {
st = new StringTokenizer(bf.readLine());
int a = Integer.parseInt(st.nextToken());
if (a == 1) {
int b = Integer.parseInt(st.nextToken());
long c = Long.parseLong(st.nextToken());
ChangeData(b, c);
} else if (a == 2) {
int b = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
SumData(b, c);
}
}
bw.flush();
bw.close();
}
}
세그먼트 트리의 구간합 이론을 이용해 풀었다. 해당 문제에서 입력되는 숫자가 long 범위이므로 이를 주의해서 풀어야 한다.
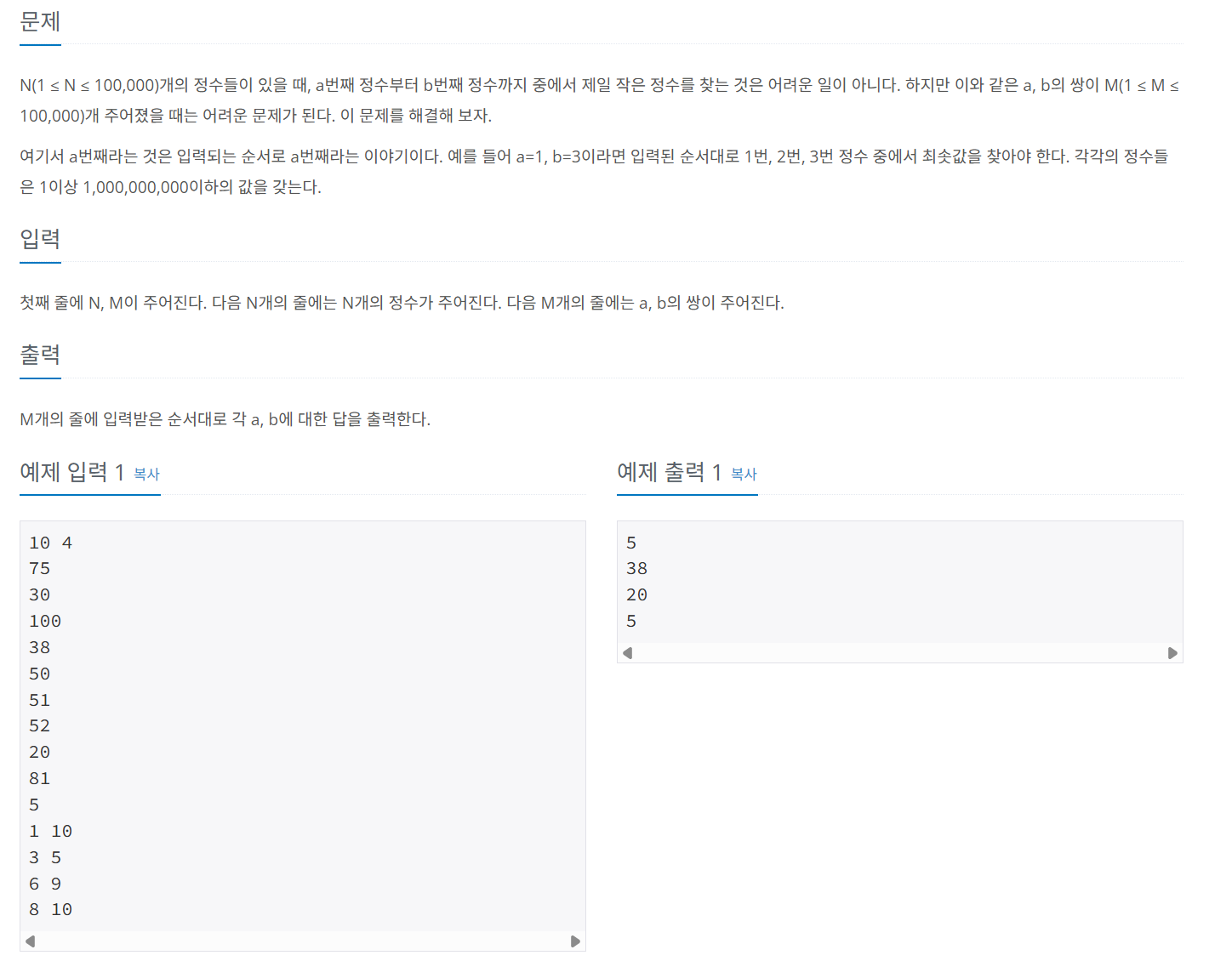
문제 072 최솟값 찾기2
시간 제한: 1초, 난이도: 골드1, 10868번
풀이
import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
public static int[] Tree;
public static int k;
public static int Min(int startIndex, int endIndex) {
startIndex = (int) (startIndex + (Math.pow(2, k) - 1));
endIndex = (int) (endIndex + (Math.pow(2, k) - 1));
int min = 1000000000;
while (startIndex <= endIndex) {
if (startIndex % 2 == 1) {
if (Tree[startIndex] < min) {
min = Tree[startIndex];
}
}
if (endIndex % 2 == 0) {
if (Tree[endIndex] < min) {
min = Tree[endIndex];
}
}
startIndex = (startIndex + 1) / 2;
endIndex = (endIndex - 1) / 2;
}
return min;
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(bf.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
k = 0;
while (Math.pow(2, k) < N) {
k++;
}
Tree = new int[(int) Math.pow(2, k + 1)];
Arrays.fill(Tree, 1000000000);
int index = (int) Math.pow(2, k);
for (int i = 0; i < N; i++) {
int input = Integer.parseInt(bf.readLine());
Tree[index] = input;
index++;
}
for (int i = (int) (Math.pow(2, k) - 1); i > 0; i--) {
Tree[i] = Math.min(Tree[2 * i], Tree[2 * i + 1]);
}
for (int i = 0; i < M; i++) {
st = new StringTokenizer(bf.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int min = Min(a, b);
bw.write(min + "\n");
}
bw.flush();
bw.close();
}
}
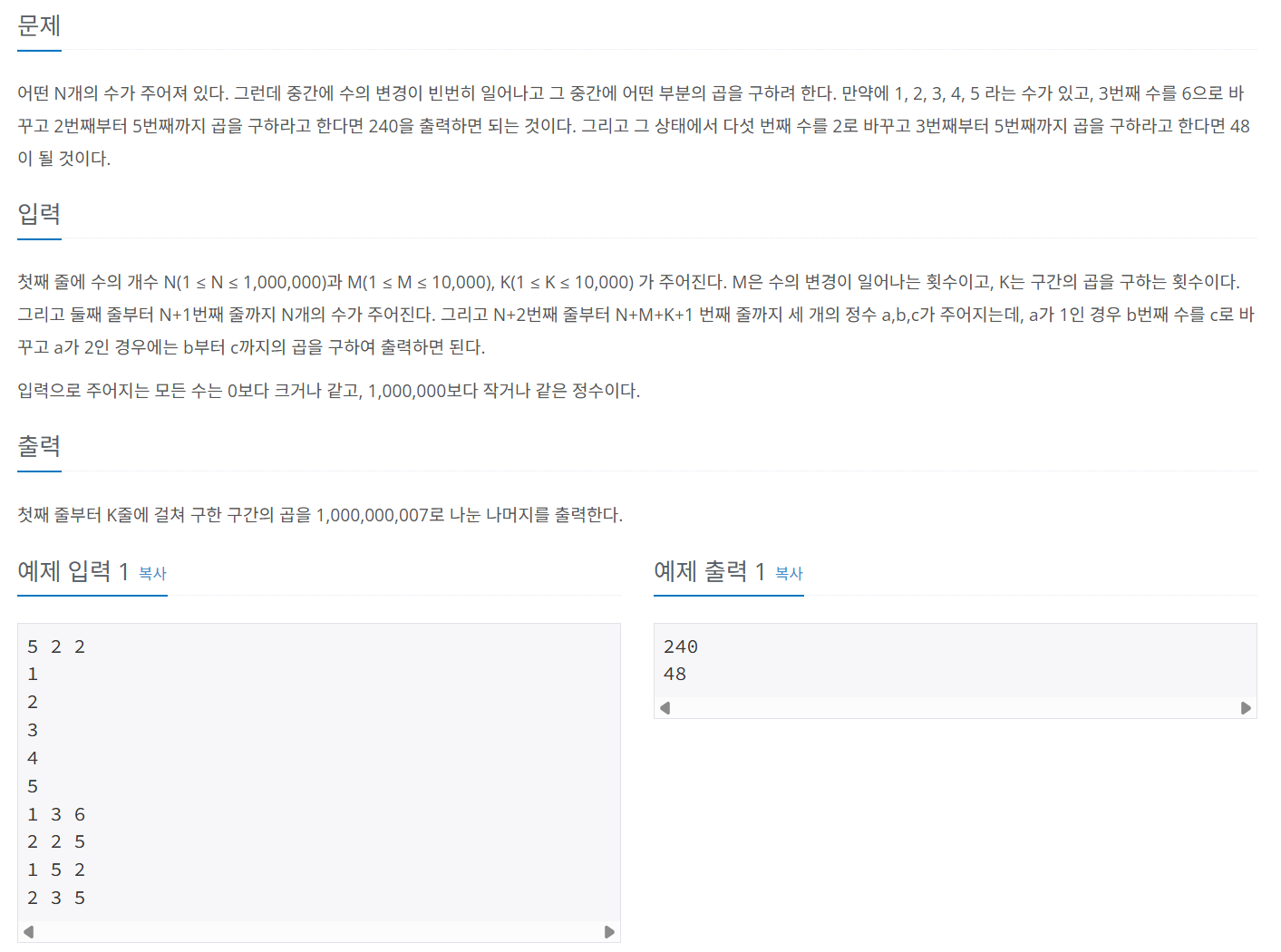
문제 073 구간 곱 구하기
시간 제한: 1초, 난이도: 골드1, 11505번
import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
public static long[] Tree;
public static int k;
public static long Mod(long a, long b) {
long result = ((a % 1000000007) * (b % 1000000007)) % 1000000007;
return result;
}
public static void ChangeTree(int index, int value) {
index = (int) (index + (Math.pow(2, k) - 1));
Tree[index] = value;
while (index > 1) {
index = index / 2;
Tree[index] = Mod(Tree[index * 2], Tree[index * 2 + 1]);
}
}
public static long MulTree(int startIndex, int endIndex) {
startIndex = (int) (startIndex + (Math.pow(2, k) - 1));
endIndex = (int) (endIndex + (Math.pow(2, k) - 1));
long mul = 1;
while (startIndex <= endIndex) {
if (startIndex % 2 == 1) {
mul = Mod(mul, Tree[startIndex]);
}
if (endIndex % 2 == 0) {
mul = Mod(mul, Tree[endIndex]);
}
startIndex = (startIndex + 1) / 2;
endIndex = (endIndex - 1) / 2;
}
return mul;
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(bf.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
k = 0;
while (Math.pow(2, k) < N) {
k++;
}
Tree = new long[(int) Math.pow(2, k + 1)];
Arrays.fill(Tree, 1); // 구간 곱이기 때문에 1로 초기화
int index = (int) Math.pow(2, k);
for (int i = 0; i < N; i++) {
Tree[index] = Integer.parseInt(bf.readLine());
index++;
}
for (int i = (int) (Math.pow(2, k) - 1); i > 0; i--) {
Tree[i] = Mod(Tree[2 * i], Tree[2 * i + 1]);
}
for (int i = 0; i < M + K; i++) {
st = new StringTokenizer(bf.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
if (a == 1) {
ChangeTree(b, c);
} else if (a == 2) {
long answer = MulTree(b, c);
bw.write(answer + "\n");
}
}
bw.flush();
bw.close();
}
}
구간 합을 응용해서 이 로직을 곱으로 바꿔서 구현하였다. 또한 MOD 연산을 사용하였고, 곱을 하면 범위 문제가 있으므로 자료형을 long으로 설정해서 구현했다.
최소 공통 조상
트리 그래프에서 임의의 두 노드를 선택했을 때 두 노드가 각각 자신을 포함해 거슬러 올라가면서 부모 노드를 탐색할 때 처음 공통으로 만나게 되는 부모 노드를 최소 공통 조상(LCA, Lowest common ancestor)이라고 한다.
최소 공통 조상의 핵심 이론
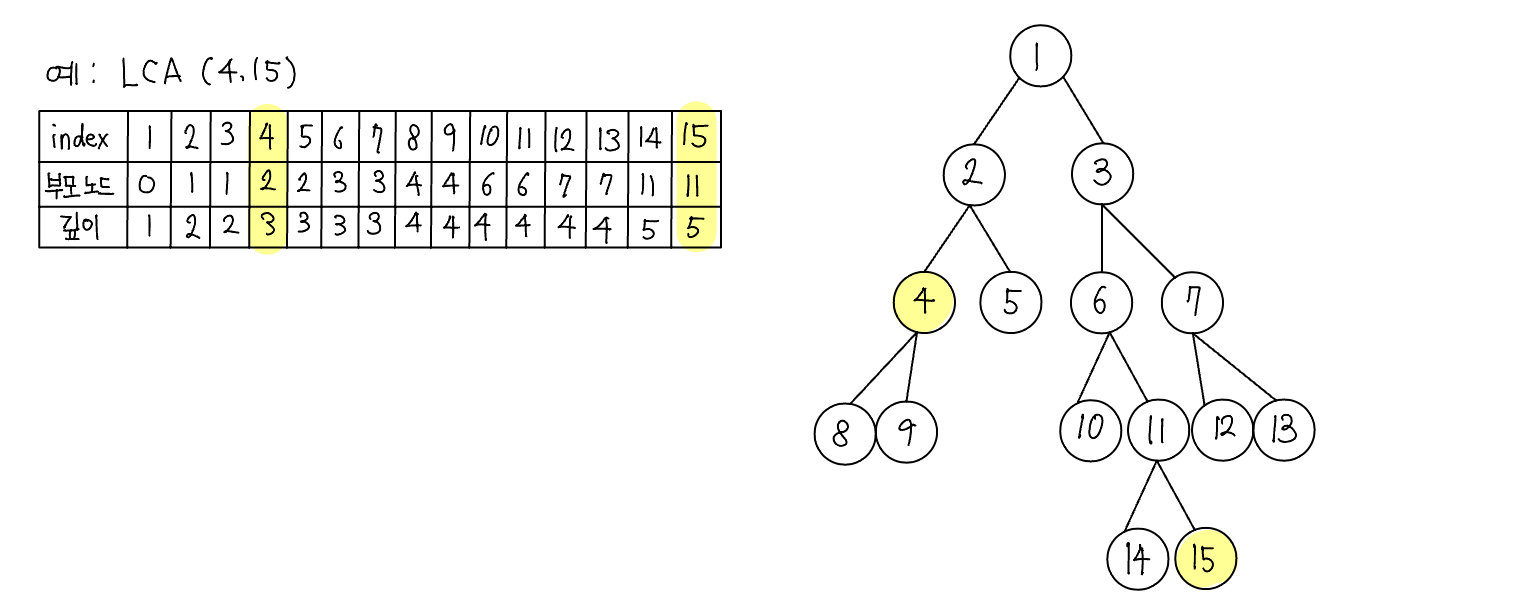
먼저 트리의 높이가 크지 않을 때 최소 공통 조상을 구하는 방법을 알아본다. 루트 노드에서 탐색을 시작해 각 노드의 부모 노드와 깊이를 저장한다.
- 선택된 두 노드의 깊이가 다른 경우, 더 깊은 노드의 노드를 부모 노드로 1개씩 올려 주면서 같은 깊이로 맞춘다. 이때 두 노드가 같으면 해당 노드가 최소 공통 조상이므로 탐색을 종료한다.
- 깊이가 같은 상태에서는 동시에 부모 노드로 올라가면서 두 노드가 같은 노드가 될 때까지 반복한다. 이때 처음 만나는 노드가 최소 공통 조상이 된다.
다음은 최소 공통 조상을 빠르게 구하는 방법이다. 이 방법의 핵심은 서로의 깊이를 맞춰 주거나 같아지는 노드를 찾을 때 기존에 한 단계식 올려 주는 방식에서 $2^k$씩 올라가 비교하는 방식이다. 따라서 기존에 자신의 부모 노드만 저장해 놓던 방식에서 $2^k$번째 위치의 부모 노드까지 저장해 둬야 한다.
- 부모 노드 저장 배열 만들기
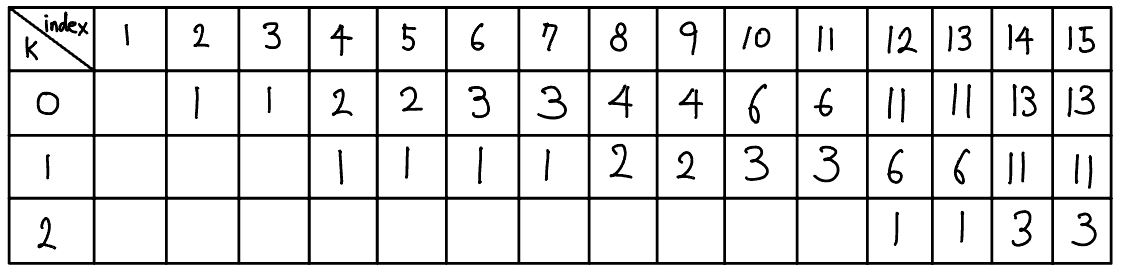
- 부모 노드 배열의 정의: P[K][N] = N번 노드의 $2^K$ 번째 부모의 노드 번호
- 부모 노드 배열의 점화식: P[K][N] = P[K - 1][P[K - 1][N]]
- K = 4라고 가정하면 N의 16번째 부모 노드는 N의 여덟 번째($2^{k - 1}$) 부모 노드의 어떫 번째 부모 노드라는 의미
- K는 ‘트리의 깊이 > $2^k$’를 만족하는 최대값, 위 트리에서 최대 깊이는 5이기 때문에 K = 2 이므로 모든 노드는 $2^3$ 번째 부모 노드를 지닌 경우가 없음
- P[2][14] = P[1][P[1][14]] = P[1][11] = 3
- 선택된 두 노드의 깊이 맞추기
- P 배열을 이용해 기존에 한 단계씩 맞췄던 깊이를 $2^k$ 단위로 넘어가면서 맞춘다.
- 노드 2와 노드 15의 깊이를 맞춘다고 하면, 노드 2의 깊이는 2, 노드 15의 깊이는 6으로 두 노드의 깊이 차이는 4이다. 깊이를 맞추기 위해 더 깊이 있는 노드 15의 4번째 부모 노드를 P배열을 이용해 찾는다. K = 2이고, P[2][15] = 3이므로 노드 3으로 이동하면 노드 2와 높이를 맞추게 된다.
- 만약 높이 차이가 20이라고 가정하면 $2^ \leq 20$을 만족하면서 K가 최대가 되는 만큼 이동하면서 높이 차이가 0이 될 때까지 반복한다.
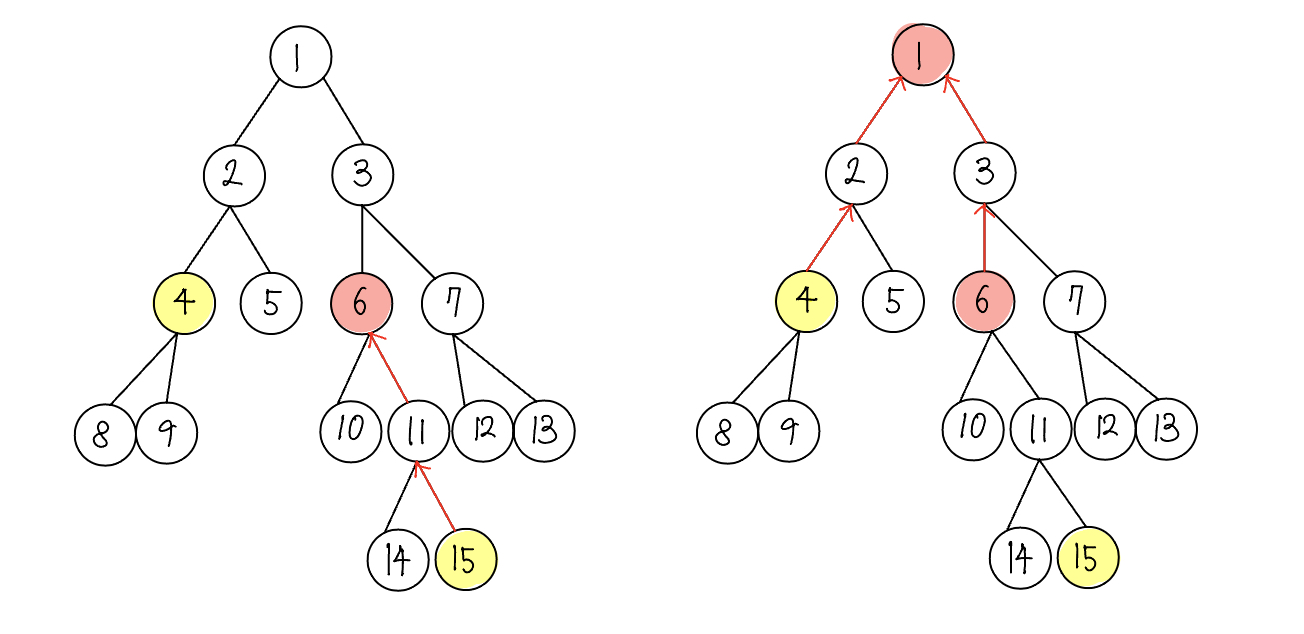
- 최소 공통 조상 찾기
- 공통 조상을 찾는 작업 역시 한 단계씩이 아닌 $2^k$ 단위로 점프하면서 맞춘다.
- K값을 1씩 감소하면서 P 배열을 이용해 최초로 두 노드의 부모가 달라지는 값을 찾는다.
- P[2][14] = 3 == P[2][15]
- P[1][14] = 10 != P[1][15] = 11
- 최초로 달라지는 K에 대한 두 노드의 부모 노드를 찾아 이동한다(노드 10, 노드 11). 이를 K가 0이 될 때까지 반복한다.
- 반복문이 종료된 후 이동한 2개의 노드가 같은 노드라면 해당 노드가, 다른 노드라면 바로 위의 노드가 최소 공통 조사이 된다.
- 여기에서는 노드 10, 11이 다른 노드이기 때문에 바로 위 노드를 뜻하는 P[0][11] 또는 P[0][11], 즉 노드 6이 최소 공통 조상이 된다(LCA(14, 15) = 6).
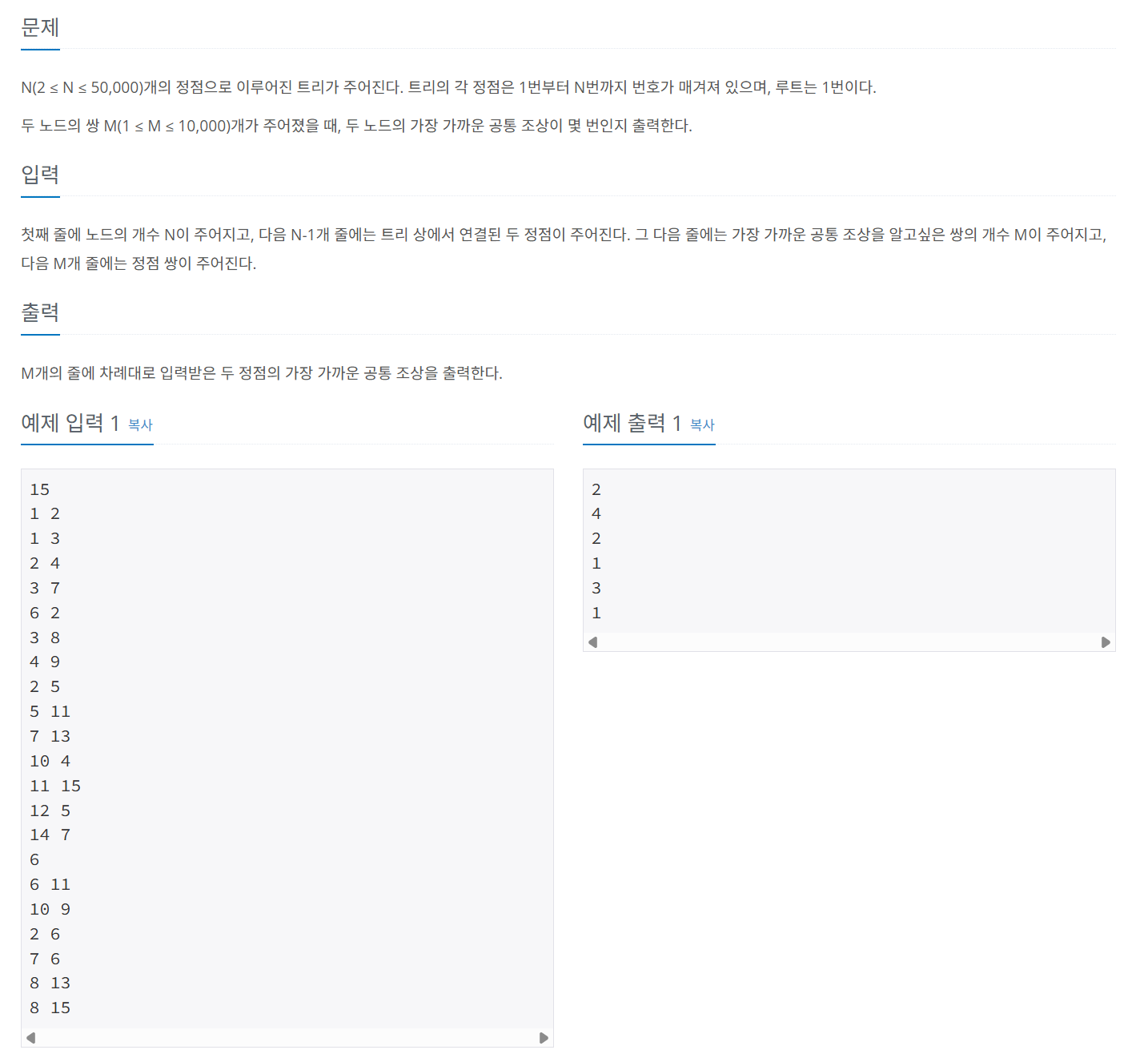
문제 074 최소 공통 조상 구하기 1
시간 제한: 3초, 난이도: 골드3, 11437번
import java.io.*;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
public static ArrayList<ArrayList<Integer>> tree = new ArrayList<>();
public static int[] depth;
public static int[] parent;
public static boolean[] visited;
public static void BFS(int index) {
Queue<Integer> qu = new LinkedList<>();
qu.add(index);
visited[index] = true;
int level = 1;
int currentSize = 1;
int count = 0;
while (!qu.isEmpty()) {
int current = qu.poll();
for (int next : tree.get(current)) {
if (!visited[next]) {
visited[next] = true;
qu.add(next);
parent[next] = current;
depth[next] = level;
}
}
count++;
if (count == currentSize) {
count = 0;
currentSize = qu.size();
level++;
}
}
}
public static int LCA(int A, int B) {
// 깊이 동일하기 하기
if (depth[A] < depth[B]) {
int temp = A;
A = B;
B = temp;
}
while (depth[A] != depth[B]) {
A = parent[A];
}
// 깊이가 같아졌으므로 동시에 부모 노드 찾기
while (A != B) {
A = parent[A];
B = parent[B];
}
return A;
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(bf.readLine());
for (int i = 0; i <= N; i++) {
tree.add(new ArrayList<>());
}
for (int i = 0; i < N - 1; i++) {
StringTokenizer st = new StringTokenizer(bf.readLine());
int A = Integer.parseInt(st.nextToken());
int B = Integer.parseInt(st.nextToken());
tree.get(A).add(B);
tree.get(B).add(A);
}
depth = new int[N + 1];
parent = new int[N + 1];
visited = new boolean[N + 1];
BFS(1);
int M = Integer.parseInt(bf.readLine());
for (int i = 0; i < M; i++) {
StringTokenizer st = new StringTokenizer(bf.readLine());
int A = Integer.parseInt(st.nextToken());
int B = Integer.parseInt(st.nextToken());
System.out.println(LCA(A, B));
}
}
}
일반적인 방법으로 최소 공통 조상을 찾았다.
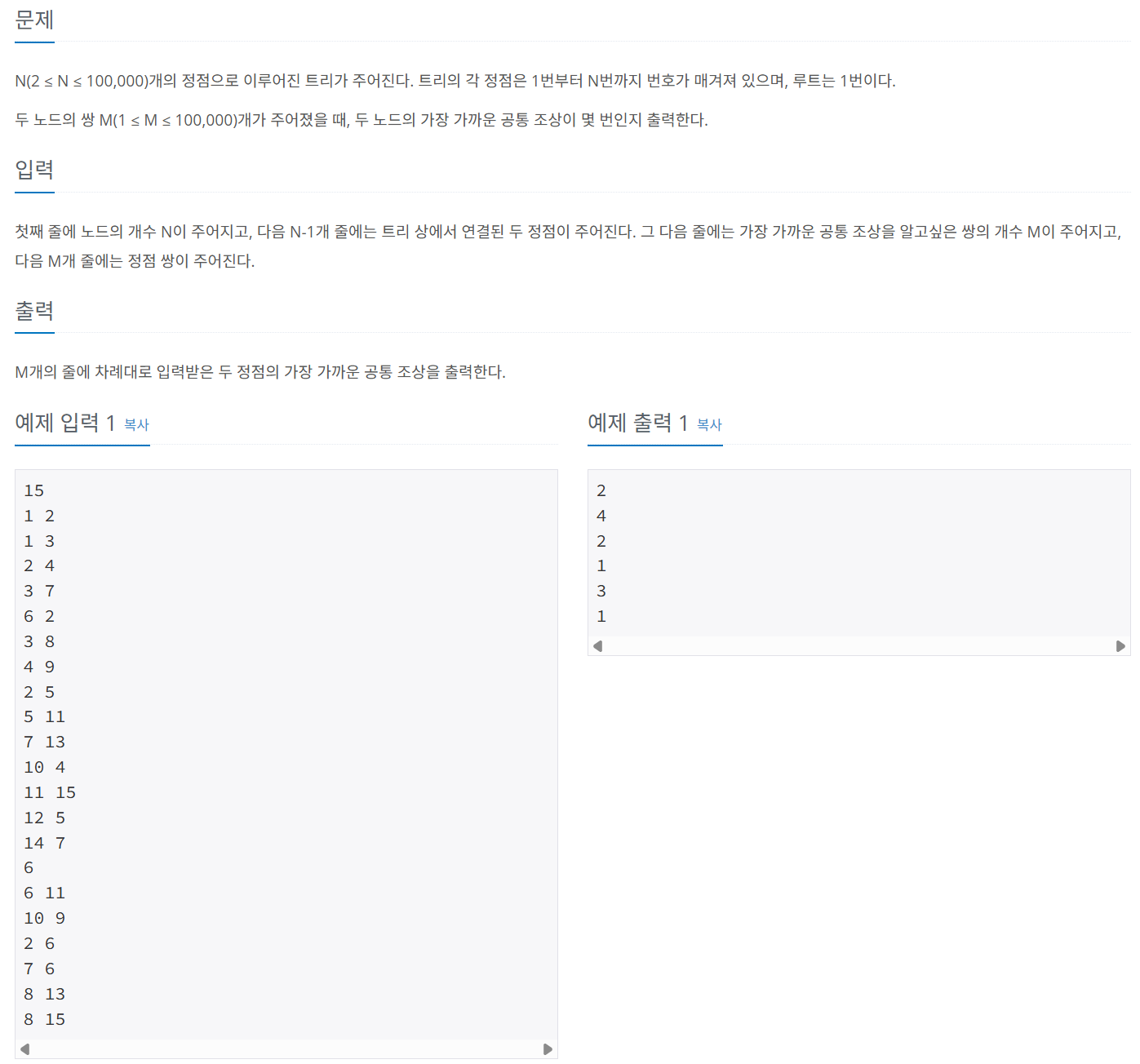
문제 075 최소 공통 조상 구하기 2
시간 제한: 1.5초, 난이도: 플래티넘5, 11438번
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
public static ArrayList<ArrayList<Integer>> tree = new ArrayList<>();
public static boolean[] visit;
public static int[] depth;
public static int[][] parent;
public static int kMax;
public static void BFS(int node) {
Queue<Integer> qu = new LinkedList<>();
qu.add(node);
visit[node] = true;
int level = 1;
int currentSize = 1;
int count = 0;
while (!qu.isEmpty()) {
int currentNode = qu.poll();
for (int nextNode : tree.get(currentNode)) {
if (!visit[nextNode]) {
qu.add(nextNode);
visit[nextNode] = true;
parent[0][nextNode] = currentNode;
depth[nextNode] = level;
}
}
count++;
if (count == currentSize) {
count = 0;
currentSize = qu.size();
level++;
}
}
}
public static int LCA(int a, int b) {
if (depth[a] > depth[b]) {
int temp = a;
a = b;
b = temp;
}
// depth 맞추기
for (int k = kMax; k >= 0; k--) {
if (Math.pow(2, k) <= depth[b] - depth[a]) {
if (depth[a] <= depth[parent[k][b]]) {
b = parent[k][b];
}
}
}
// 최소 공통 조상 찾기
for (int k = kMax; k >= 0 && a != b; k--) {
if (parent[k][a] != parent[k][b]) {
a = parent[k][a];
b = parent[k][b];
}
}
int result = a;
if (a != b) {
result = parent[0][result];
}
return result;
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(bf.readLine());
for (int i = 1; i <= N + 1; i++) {
tree.add(new ArrayList<>());
}
visit = new boolean[N + 1];
depth = new int[N + 1];
for (int i = 0; i < N - 1; i++) {
StringTokenizer st = new StringTokenizer(bf.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
tree.get(a).add(b);
tree.get(b).add(a);
}
// K의 최대값 구하기
int temp = 1;
kMax = 0;
while (temp < N) {
temp *= 2;
kMax++;
}
parent = new int[kMax + 1][N + 1];
BFS(1);
// P[K][N] = P[K - 1][P[k - 1][N]]
for (int k = 1; k <= kMax; k++) {
for (int n = 1; n <= N; n++) {
parent[k][n] = parent[k - 1][parent[k - 1][n]];
}
}
int M = Integer.parseInt(bf.readLine());
for (int i = 0; i < M; i++) {
StringTokenizer st = new StringTokenizer(bf.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
System.out.println(LCA(a, b));
}
}
}
최소 공통 조상을 빠르게 구하는 방법으로 구현하였다.



댓글남기기