19장 스키마 정제와 정규형

스키마 정제의 소계

　스키마 정제가 해결하고자 하는 문제점들의 개요와 해결하기 위한 분해에 기반한 정제 방식에 대해 알아본다. 근복적으로는 정보를 중복해서 저장한다는 사실이 이러한 문제점들의 주요 원인이다. 그러나 분해가 중복성을 없앨 수 있지만, 분해가 그 자체의 문제점을 야기할 수 있으므로 주의가 필요하다.

중복성으로 야기되는 문제점들

　동일한 정보를 데이터베이스 내의 여러 곳에 반복해서 저장하게 되면 다음과 같은 여러 문제점들이 야기될 수 있다.

• 중복 저장(Redundant Storage): 어떤 정보가 반복적으로 저장된다.
• 갱신 이상(Update Anomaly): 만약 반복되어 저장된 데이터 중 한 사본만을 갱신하는 경우, 모든 사본이 함께 갱신되지 않으면 데이터간의 불일치가 발생된다.
• 삽입 이상(Insertion Anomaly): 어떤 새로운 정보를 저장하기 위해 이와 관련이 없는 다른 정보도 함께 저장하여야 한다.
• 삭제 이상(Deletion Anomaly): 만약 어떤 정보를 삭제하는 경우, 이와 관련이 없는 다른 정보도 함께 상실될 수가 있다.

　다음과 같은 Hourly_Emps 개체 집합 생각해보자.

Hourly_Emps(ssn, name, lot, rating, hourly_wages, hourly_worked)

　위 릴레이션을 SNLRWH로 표현할 수 있다. 위의 Hourly_Emps 릴레이션에서 키가 ssn이고(S$\rightarrow$SNLRWH), hourly-wage 애트리뷰트는 rating 애트리뷰트에 의해 결정된다고 가정하자(R $\rightarrow$ W). 즉, 이러한 조건은 어떤 rating 값이 주어지면, 이에 대응하는 hourly_wages 값은 반드시 하나만 존재한다는 사실을 의미하는 것이다. 무결성 제약 조건은 다음 예와 같이 Hourly_Emps 릴레이션 내에서 중복성이 생길 수 있음을 보여준다.

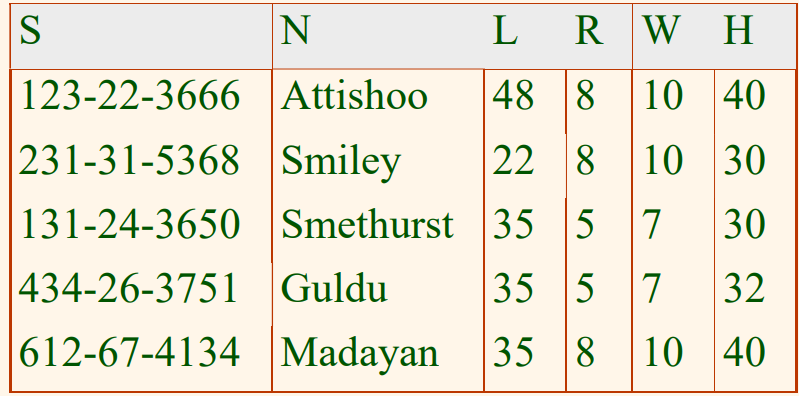
　만약 두 개의 투플에 대해 rating 열에서 같은 값이 나타나면, 이러한 무결성 제약조건에 따르면 hourly_wages 열에도 같은 값이 나타나야 한다. 이러한 중복성을 다음과 같은 부정적인 결과들을 야기할 수 있다.

• 중복 저장: rating 값 8은 hourly_wages 값 10과 대응하는데, 이 연관성이 세 번 반복된다.
• 갱신 이상: 만약 첫 번째 투플의 hourly_wages의 값은 갱신되고 두 번째 투플에서는 갱신되지 않을 수 있다.
• 삽입 이상: 한 직원의 rating 값에 대응하는 시간당 임금을 모르면, 그 직원의 투플을 삽입할 수 없다.
• 삭제 이상: 어떤 특정 rating 값을 가지고 있는 모든 투플들을 삭제하면(예를 들어, Smethurst와 Guldu 투플들), 그 rating 값과 hourly_wages 값과의 연관성을 상실한다.

분해

　직관적으로, 중복성은 애트리뷰트들을 부자연스럽게 연관지어서 생성된 릴레이션 스키마에서 발생할 수 있다. 함수 종속 관계를 이용하면 이러한 상황을 식별해 낼 수 있고, 또한 스키마를 정제할 필요성이 있는가를 파악할 수 있다. 이와 관련된 핵심적인 아이디어는 하나의 릴레이션을 여러 개의 더 작은 릴레이션들로 대체함으로써 중복성으로 야기되는 많은 문제점들이 처리될 수 있다는 점이다.
　릴레이션 스키마 R의 분해(decomposition of a relation schama R)는 이 스키마를 두 개이상의 릴레이션 스키마로 대치하는 것인데, 이 릴레이션들의 각 스키마는 R의 애트리뷰트의 부분 집합을 가지고 있고, 이들 전체는 R의 모든 애트리뷰트들을 포함해야 한다.(replacing ABCD with, say, AB and BCD, or ACD and ABD)
　앞의 예의 Hourly_Emps 릴레이션을 다음과 같이 두 개의 릴레이션으로 분해한다.

Hourly_Emps2(ssn, name, lot, rating, hourly_worked), Wages(rating, hourly_wages)

Hourly_Emps2

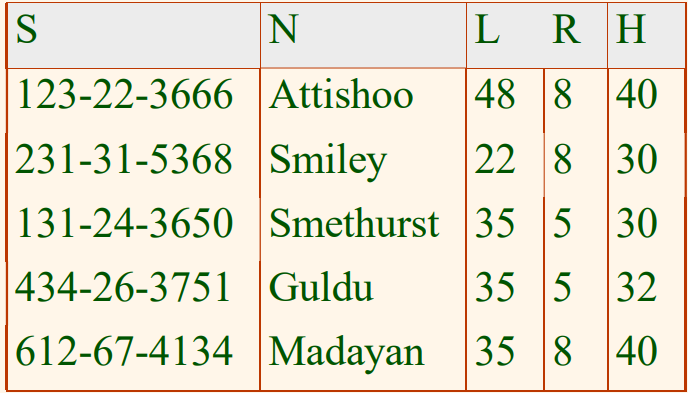
Wages

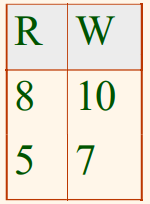
　위를 보면 어떠한 rating 값에 대해서도 이에 해당되는 투플을 Wages 릴레이션에 단지 추가함으로서 hourly_wages 값을 쉽게 기록할 수 있음을 알 수 있다. 즉, Hourly_Emp2 릴레이션의 현재 인스턴스에서 그 rating 값에 해당하는 직원 투플이 없더라도 무방하다. 그리고 어떤 rating 값에 해당하는 hourly_wages의 값을 갱신하고자 한다면, 단지 Wages에 속한 투플 하나만 갱신하면 된다. 처음 Hourly_Emp에서 여러 개의 투플들을 모두 한꺼번에 갱신해야 했던 것보다는 효율적이고, 또한 일관성을 위반할 수 있는 가능성도 없어지게 된다.

분해와 관련된 문제점들

　릴레이션 스키마를 분해할 때 주의하지 않으면 자칫 중복성 문제보다 더 심각한 문제들을 발생시킬 수 있다. 따라서 다음과 같은 두 가지 질문들을 항상 반복적으로 고려하여야 한다.

• 릴레이션을 분해 할 필요가 있는가?
• 분해하고 난 후 발생할 수 있는 문제점들은 무엇인가?

　첫 번째 질문에는 릴레이션에 대해 몇 가지 정규형(normal form)들이 제안되어 있다. 만약 어떤 릴레이션 스키마가 어느 한 정규형에 속한다면 우리는 앞에서 언급한 특정 유형의 문제점들이 발생하지 않는다는 점을 알 수 있다. 따라서 주어진 릴레이션 스키마가 어느 정규형에 속하는지를 알면, 더 분해할 필요가 있는지 아닌지를 결정하는 데에 도움이 된다. 이렇게 해서 만약 그 릴레이션 스키마를 더 분해해야 되겠다고 결정하고나면, 어떻게 분해하는지에 대한 방법을 선택하여야 한다.
　두 번째 질문의 경우에는, 분해와 관련된 두 가지 중요한 성질들을 고려하여야 한다. 무손실 조인(lossless-join) 성질은 분해된 각 작은 릴레이션의 인스턴스로부터 분해되기 전의 원래의 릴레이션 인스턴스를 항상 복구할 수 있도록 하여 준다. 종속성 유지(dependency preservation) 성질은 분해된 작은 릴레이션 각각에 있는 어떤 제약조건들을 검증해 주기만하면 원래 릴레이션에 주어진 어떠한 제약조건들도 그대로 검증될 수 있도록 하여 준다. 즉, 원래의 릴레이션에 대한 제약조건이 위배되었는가를 검증하기 위하여 분해시킨 릴레이션들을 조인할 필요가 없다.

함수 종속성

　함수 종속성(Functional dependency:FD)은 일종의 무결성 제약조건(IC)으로서, 키의 개념을 일반화한 것이다. 어떤 릴레이션 스키마를 R이라 하고 X와 Y를 R에 속한 애트리뷰트들의 집합이라 하면, 이제 R의 어떤 인스턴스 r에 속한 모든 투플쌍 t1과 t2에 대해서 다음의 조건을 만족할 때, r은 FD X$\rightarrow$Y를 만족한다고 한다.

만약 t1.X=t2.X 이면 t1.Y=t2.Y 이다.

　FD X$\rightarrow$Y는 결국 임의의 두 개의 투플에 대해서 만약 X 애트리뷰트들의 값이 일치한다면, Y 애트리뷰트들의 값도 역시 일치해야 된다는 것을 의미한다.

FD에 대한 추론

　어떤 릴레이션 스키마 R에 대해 FD들이 주어졌을 때, 새로운 FD들을 추가적으로 얻어낼 수 있다. 다음 예제를 보자.

Workers(ssn, name, lot, did, since)

　위의 릴레이션에서 ssn$\rightarrow$did와 did$\rightarrow$lot가 성립한다고 가정하면, 이 사실을 이용하여 ssn$\rightarrow$lot도 성립할 수 있다. 첫 번째 FD를 참조하면, 만약 임의의 두 개의 투플들이 같은 ssn값을 갖는다고 하면, 이 투플들 역시 did 값을 갖게 된다. 두 번째 FD를 참조하면, 만약 임의의 두 개의 투플들이 같은 did 값을 갖는다고 하면, 이 투플들 역시 같은 lot 값을 갖게 된다. 이 두 가지 FD로 부터 ssn$\rightarrow$lot도 역시 성립한다는 것을 알 수 있다.
　어떤 릴레이션 스키마에 정의된 FD들의 집합을 F라 표기하면 이때 만약 어떤 FD f가 F의 모든 종속성들을 만족하는 각각의 모든 릴레이션 인스턴스들에 의해 만족된다면, FD f가 F에의해 내포(imply) 혹은 추론(infer)된다고 정의한다. 즉, F의 모든 FD들이 유지될 때마다, f도 역시 유지된다. 여기서 f가 F의 모든 종속성들을 만족하는 어떤 일부 인스턴스들에 대해서 유지된다고 하는 것은 불충분하며, f는 반드시 F의 모든 종속성들을 만족하는 각각의 모든 인스턴스에 대해서 유지된다.

FD 집합에 대한 폐포

　FD들의 집합 F에 의해 추론되는 모든 FD들의 집합을 F의 폐포(closure)라고 하며, 이를 $\mathrm{F}^+$로 표기한다. F의 $\mathrm{F}^+$를 구할 수 있는 방법은 암스트롱의 공리(Armstrong`s Axioms)라고 하는 다음 세가지 법칙들을 반복해서 적용하면 FD들의 집합 F에 의해 내포되는 모든 FD들을 추론해 낼 수 있다. 이를 위해 X, Y, Z를 각각 릴레이션 스키마 R에 정의된 애트리뷰트의 집합이라고 하자.

• 재귀: 만약 X$\supseteq$Y이면 X$\rightarrow$Y이다.
• 부가: 만약 X$\rightarrow$Y이면 XZ$\rightarrow$YZ이다.
• 이행: 만약 X$\rightarrow$Y이고 Y$\rightarrow$Z이면 X$\rightarrow$Z이다.

　암스트롱의 공리는 정당(sound)하고 완전(complete)하다.
　$F^+$에 대한 추론을 계산하기 위해 다음과 같은 법칙들을 추가적으로 알아두는 것이 편리하다.

• 결합(Union): 만약 X$\rightarrow$Y이고, X$\rightarrow$Z이면, X$\rightarrow$YZ이다.
• 분해(Decomposition): 만약 X$\rightarrow$YZ이면, X$\rightarrow$Y이고 X$\rightarrow$Z이다.

　다음과 같은 릴레이션의 예를보자.

Contracts(contractid, supplierid, projectid, deptid, partid, qty, value)

　Constracts 릴레이션 스키마를 CSJDPQV로 나타낸다. 여기서 이 스키마에 속한 투플의 의미는 다음과 같이 해석될 수 있다. 어떤 공급자(S, supplierid)가 부품(P, partid)을 Q 수량(qty)만큼, 어떤 부서 D(deptid)가 수행하는 프로젝트 J(projectid)에게 공급하기로 한 계약번호가 C(contractid)인 계약을 체결하였으며, 이 계약의 금액 V는 가격 애트리뷰트 value와 같다.
　위의 Contracts 릴레이션에서 다음의 FD들이 성립된다고 가정하자.

• 계약번호 C는 키이다. C$\rightarrow$CSJDPQV
• 한 프로젝트에서 하나의 부품을 구매하는 것은 단 하나의 계약을 통해서만 이루어진다. JP$\rightarrow$C
• 각 부서는 각 공급자로부터 최대 하나의 부품만 구매할 수 있다. SD$\rightarrow$P

　이렇게 주어진 FD들의 집합에 대한 폐포에는 다음과 같은 FD들이 추가적으로 추론될 수 있다.

• J$\rightarrow$C와 C$\rightarrow$CSJDPQV로부터, 이행 법칙에 의해. JP$\rightarrow$CSJDPQV가 추론된다.
• SD$\rightarrow$P로부터, 부가 법칙에 의해, SDJ$\rightarrow$JP가 추론된다.
• SDJ$\rightarrow$JP와 JP$\rightarrow$CSJDPQV로부터, 이행 법칙에 의해, SDJ$\rightarrow$CSJDPQV가 추론된다.
  • 참조로 여기에서 조심해야 할 사항은 좌측과 우측으로부터 J를 각각 소거해서 SD$\rightarrow$CSDPQV로 만들 수 있는 것인데 이는 성립이 되지 않는다.

　이와 유사하게 부가 법칙 혹은 분해 규칙을 이용하면 이 릴레이션에서 성립될 수 있는 FD들을 추가적으로 더 추론해 낼 수 있다. 예를 들면, C$\rightarrow$CSJDPQV에 분해 법칙을 적용하면 다음의 FD들을 추론할 수 있다.

• C$\rightarrow$C, C$\rightarrow$S, C$\rightarrow$J, C$\rightarrow$D, 등등

　만약 어떤 X$\rightarrow$Y와 같은 함수 종속성이 주어졌을 떄, 이 종속성이 FD들의 집합인 F의 폐포에 속하는지의 여부를 검사하고 싶다면, $F^+$를 모두 구할 필요 없이 이를 효율적으로 검사하는 방법이 있다.(Computing the closure of a set of FDs can be expensive. (Size of closure is exponential in # attrs))
　이 경우에는 우선 F에 대하여 애트리뷰트 폐포(attribute closure) $X^+$를 구현하면 되는데, 이것은 암스트롱의 공리를 사용해서 X$\rightarrow$A라고 추론될 수 있는 모든 애트리뷰트 A의 집합을 말한다. 즉, $X^+$는 X에 의해 결정되는 모든 애트리뷰트들의 집합을 의미한다. 다음 예제를 보자.

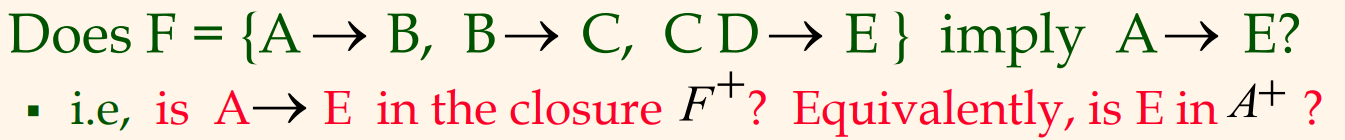
　풀이는 다음과 같다.

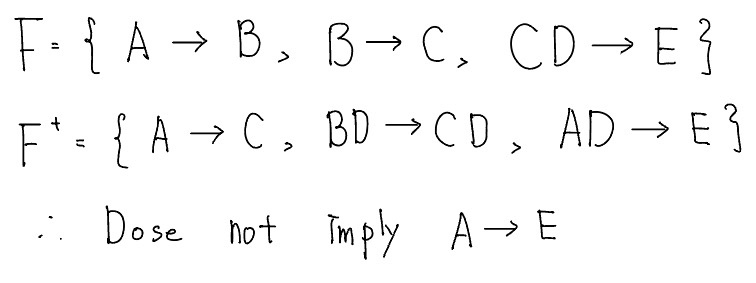
정규형

　어떤 릴레이션 스키마가 주어졌을 때, 우리는 이 스키마가 좋은 설계인지, 혹은 그렇지 않으면 여러 개의 더 작은 릴레이션들로 분해하여야 되는지를 판단할 필요가 있다. 이러한 판단을 하기 위해서는 좋은 설계가 어떤 것인지 판단할 수 있는 기준이 필요한데, 이는 현재 주어진 스키마로부터 발생할 수 있는 문제점들이 무엇인지를 이해하는 것으로 출발한다. 이러한 기준을 제공하기 위해서 몇 개의 유용한 정규형(normal form)들이 제안되었다. 만약 주어진 릴레이션 스키마가 이들 정규형 중 어느 하나에 속한다는 것을 알게 되면 우리는 어떤 유형의 문제점들은 발생하지 않는다는 것을 알 수 있다.
　FD에 기반한 정규형들은 제1정규형(first normal form: 1NF), 제2정규형(second normal form: 2NF), 제3정규형(third normal form: 3NF), 보이스-코드 정규형(Boyce-Code normal form: BCNF)의 네가지가 있다. 이들 정규형들은 점차적으로 뒤의 정규형으로 갈수록 제약 조건들이 많아지게 됨을 알 수 있다. 즉 BCNF에 속하는 모든 릴레이션들은 역시 3NF에 속하고, 3NF에 속하는 모든 릴레이션들은 역시 2NF에 속하고, 2NF에 속하는 모든 릴레이션들은 역시 1NF에 속한다는 사실이다. 여기서 가장 기본적인 정규형인 제1정규형은 다음과 같은 제약 조건을 갖고 있다. 어떤 릴레이션에서 모든 각 애트리뷰트에 원자 값(atomic value)만 반드시 허용이 되는 경우(즉, 리스트 혹은 집합 값들과 같이 여러 개의 값들이 허용이 안되는 경우), 이 릴레이션을 제1정규형이라 한다.
　정규형을 배우는 데 있어 FD들이 어떠한 역할을 하는지를 이해하는 것이 중요하다. 예를 들어, ABC라는 애트리뷰트들로 구성된 릴레이션 스키마 R을 생각해 보자. 여기서 어떠한 IC(integrity constraint, 무결성 제약조건)들도 전혀 주어지지 않았다고 가정하면, R의 투플들이 어떠한 값을 갖든지 이는 정당한 인스턴스가 될 것이며, 중복 또한 발생할 가능성이 없을 것이다. 반면에 A$\rightarrow$B와 같은 FD가 주어졌다고 생각해 보면, 이때 A에 대해 동일한 값을 갖는 투플들이 여러 개 있다면 이들 투플들 역시 B에 대해서도 역시 동일한 값을 가져야 할 것이다. 따라서 이러한 FD 정보로부터 중복이 발생할 가능성이 있다는 것을 예측할 수 있다. 그리고 좀 더 자세한 IC들이 많이 주어지게 되면, 이들로부터 좀 더 포착하기 어려운 중복 가능성을 탐지해 낼 수 있을 것이다.

보이스-코드 정규형

　어떤 릴레이션 스키마를 R이라 하고, R에 속하는 애트리뷰트들의 부분집합을 X라 하고, R에 속하는 어떤 애트리뷰트를 A라 하면, 이때 R에 주어진 함수 종속성들의 집합 F에 속하는 모든 FD X$\rightarrow$A에 대해, 다음 조건들 중 하나만 만족하는 경우, R을 보이스-코드 정규형이라 한다.

• A $\in$ X (called a trivial FD)
• X는 수퍼키이다. (X contains a key for R)

　어떤 FD들의 집합 F가 주어졌을 때 이에 해당하는 R이 BCNF에 속하는가를 알기 위해서는, 이 정의에 따라 폐쇄 $F^+$에 속하는 각 종속성 X$\rightarrow$A를 모두 살펴 보아야 한다. 그러나 위의 정의에 의하면 F에 속하는 각 FD의 좌측에 키가 포함되어 있는지를 검사하는 것만으로도 충분하다. 다음 예를 보자.

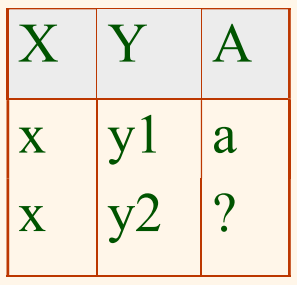
　위의 그림은 세 개의 애트리뷰트들 X, Y, A로 구성된 릴레이션에서 두 개의 투플들을 갖는 어떤 인스턴스의 예를 나타내고 있다. 여기서 이 두 개의 투플들이 애트리뷰트 X에 대해 동일한 값을 갖고 있다. 이 인스턴스가 FD X$\rightarrow$A를 만족한다고 가정하면 두 번째 투플의 애트리뷰트 A의 값이 a의 값을 갖는다는 것을 쉽게 알 수 있다. 그러나 이러한 상황은 중복성의 한 예이다. 따라서 이러한 상황은 BCNF에 속하는 릴레이션에서 발생할 수 없다. 만약 이 릴레이션이 BCNF을 만족한다면 A와 X는 서로 다른 애트리뷰트이므로, X는 키가 되어야 한다. 즉, 만약 X가 키라고 한다면, $y_1 = y_2$가 되고, 따라서 두 개의 투플들은 모든 애트리뷰트에 대해 서로 동일한 값을 갖게 된다. 한 릴레이션에서 동일한 두 개의 투플은 허용이 안되므로, 위와 같이 동일한 투플들이 두 번 나타나는 상황을 발생할 수 없다.

제3정규형

　어떤 릴레이션 스키마를 R이라 하고, R에 속하는 애트리뷰트들의 부분집합을 X, R에 속하는 어떤 애트리뷰트를 A라 할 때, R에 주어진 함수 종속성들의 집합 F에 속하는 모든 FD X$\rightarrow$A에 대해, 다음의 조건들 중 하나만 만족하는 경우, R을 제3정규형이라 한다.

• A $\in$ X (called a trivial FD)
• X는 수펴키이다. (X contains a key for R)
• A는 R의 어떤 키의 일부이다. (A is part of some key for R)

　3NF의 정의는 BCNF와 유사한데 다른 점은 세번째 조건이다. 따라서 모든 BCNF 릴레이션은 3NF에도 속하게 된다. 세 번째 조건은 한 릴레이션에서 키는 다른 모든 애트리뷰트들을 유일하게 결정하는 애트리뷰트들의 최소 집합임을 표현한다. 여기서 A는 반드시 키를 구성하는 애트리뷰트 이어야 한다. 여기서 유의할 점은 A가 수퍼키의 일부인 조건만으로는 불충분한데, 이렇게 되면 어떤 애트리뷰트라도 이 조건을 만족할 수 있기 때문이다. 한 릴레이션 스키마에서 모든 키들을 찾아내는 문제는 NP-complete라는 매우 어려운 문제로 알려져 있고, 따라서 어떤 릴레이션 스키마가 3NF에 속하는가를 알아내는 문제도 마찬가지이다.
　어떤 함수 종속성 X$\rightarrow$A가 3NF를 위반하는 경우는 다음 두 가지이다.

• X는 어떤 키 K의 진부분 집합이다.
  • 이러한 종속성을 부분 종속성(partial dependency)이라고도 한다.
  • 이 경우에는 (X, A)쌍에 대한 여러 개의 투플들을 중복해서 저장하게된다.
  • SBDC(선원, 배, 예약날짜, 계산할 신용카드) 애트리뷰트들로 구성된 Reserves 릴레이션을 참조하면, 이 릴레이션에서 유일한 키는 SBD이고, FD S$\rightarrow$C가 존재한다. 이 릴레이션을 살펴보면 한 선원에 대한 신용카드 번호가 그 선원이 해 놓은 예약의 수만큼 중복되어 저장되게 된다는 사실을 알 수 있다.
• X가 어떤 키의 진부분 집합도 아니다.
  • 이러한 종속성은 결국 K$\rightarrow$X$\rightarrow$A라고 하는 형태의 연쇄적인 종속성을 의미하기 때문에, 이를 이행 종속성(transitive dependency)이라고도 한다.
  • 이러한 형태의 종속성에서 발생하는 문제점은 만약 어떤 X 값과 어떤 K 값을 연관시키기 위해서는, 반드시 어떤 A 값과 어떤 X 값을 역시 연관시켜 주어야 한다는 점이다.
  • SNLRWH(ssn, name, lot, rating, hourly_wages, hourly_worked)의 애트리뷰트들로 구성된 Hourly_Emps 릴레이션을 참조하면, 이 릴레이션에서 유일한 키는 S이고, FD S$\rightarrow$W가 존재한다. 따라서 S$\rightarrow$R$\rightarrow$W라는 연쇄적인 관계가 발생하게 된다.(S는 키이므로 자연스럽게 S$\rightarrow$R가 성립한다.)
  • 따라서 이러한 사실로부터 삽입 이상이 발생할 수 있다. 즉, 어떤 직원 S가 등급 R을 갖고 있다는 사실을 이 릴레이션에 삽입을 원한다고 하면, 그 직원에 해당되는 등급 R에 대한 시간당 임금 W를 알지 않는 한, 이 사실을 이 릴레이션에 기록할 수 없다는 것을 알 수 있다.
  • 여기서 이와 유사하게 삭제 이상, 갱신 이상도 역시 발생하게 된다.

　3NF를 사용하는 이유는 다소 인위적인 것으로 생각할 수 있다. 즉, 키 애트리뷰트들을 포함하는 어떤 종속성들에 대해서는 예외 조항을 둠으로써, 주어진 모든 릴레이션 스키마들을 3NF 릴레이션들로 항상 분해할 수 있음을 보장받는다. 그러나 이러한 보장이 BCNF 릴레이션에는 성립되지 않는다. 따라서 3NF의 정의는 BCNF의 제약 조건을 완화시킴으로서 이러한 보장을 가능하도록 한다.
　3NF에서는 BCNF와 달리 어떤 중복성이 발생할 수 있다. 즉, 만약 종속성 X$\rightarrow$A가 존재하고 X가 수퍼키가 아니라면, 설령 A가 키의 일부이기 때문에 이 릴레이션이 3NF에 속한다고 하더라고, 부분 종속성 및 이행 종속성에 따른 문제들이 여전히 존재하게 된다. SBDC의 애트리뷰트들로 구성된 Reserves 릴레이션을 다시 살펴보자.

• 각 선원은 예약을 지불하기 위해 반드시 하나의 신용 카드만을 사용한다는 제약이 있다고 가정하면, FD S$\rightarrow$C로 표현될 수 있다.
  • 여기서 S는 키가 아니고, 또한 C는 어떠한 키의 일부도 될 수 없다.
  • 즉, 이 릴레이션의 유일한 키는 SBD이다.
  • 따라서 이 릴레이션은 3NF을 만족하지 않으며, (S, C)쌍들이 중복이 되어 저장되게 된다.
• 만약 각 신용카드가 그 소유주를 유일하게 결정한다는 사실을 알게된다면, FD C$\rightarrow$S를 얻게 되며, 이로부터 CBD도 역시 이 릴레이션의 키가 된다.
  • 따라서 종속성 S$\rightarrow$C는 3NF를 위반하지 않으므로, Reserves 릴레이션은 3NF을 만족하게 된다.
  • 그러나 이러한 사실에도 불구하고, 동일한 값들을 갖는 모든 투플들에 대해서, 동일한 (S, C)쌍들이 중복이 되어 저장되게 된다.

　제2정규형을 부분 종속서이 허용이 되지 않는 정규형으로 정의한다. 따라서 만약 어떤 릴레이션이 3NF를 만족한다면, 역시 2NF도 만족하게 된다.

분해의 성질

　분해는 중복성을 제거하기 위해 사용되는 작업이다. 어떤 릴레이션 스키마를 분해할 때, 분해가 다른 새로운 문제점들을 발생시키지 않도록 검증하는 것이 중요하다. 여기서 검증해야 할 사항은 다음과 같다.

• 분해된 릴레이션들로부터 원래의 릴레이션에 있던 정보를 정확히 복구할 수 있냐는 점
• 분해된 릴레이션들에 대해 무결성 제약 조건들이 효율적으로 검증할 수 있냐 하는 점

무손실 조인 분해

　R을 어떤 릴레이션 스키마라고 하고, F을 R에 정의된 FD들의 집합이라고 하면, R을 애트리뷰트들의 집합 X와 Y로 각각 구성된 두 개의 스키마로 분해하였을 때, F에 속하는 종속성들을 만족하는 R의 모든 인스턴스 r에 대해 $\pi_X(r) \bowtie \pi_Y(r) = r$이 성립하면, 이러한 분해를 무손실-조인 분해(lossless-join decomposition)로 정의한다. 즉, 이 정의에 의하면, 분해된 두 개의 릴레이션들로부터 원래의 릴레이션을 항상 복구할 수 있음을 의미한다.
　위의 정의를 R을 두 개 이상의 릴레이션으로 분해하는 경우에 대해서도 쉽게 확장할 수 있다. 여기서 $r\subseteq \pi_X(r) \bowtie \pi_Y(r)$이 항상 성립한다는 것을 쉽게 알 수 있다. 그러나 일반적으로 이에 대한 역은 성립하지 않는다. 만약 어떤 릴레이션에대해 프로젝션 연산들을 수행한 후, 그 프로젝션 연산들의 결과인 릴레이션들을 자연 조인을 이용하여 다시 합치게 되면, 원래 릴레이션에는 없었던 새로운 투플들이 생길 수 있다. 다음 예를 보자.

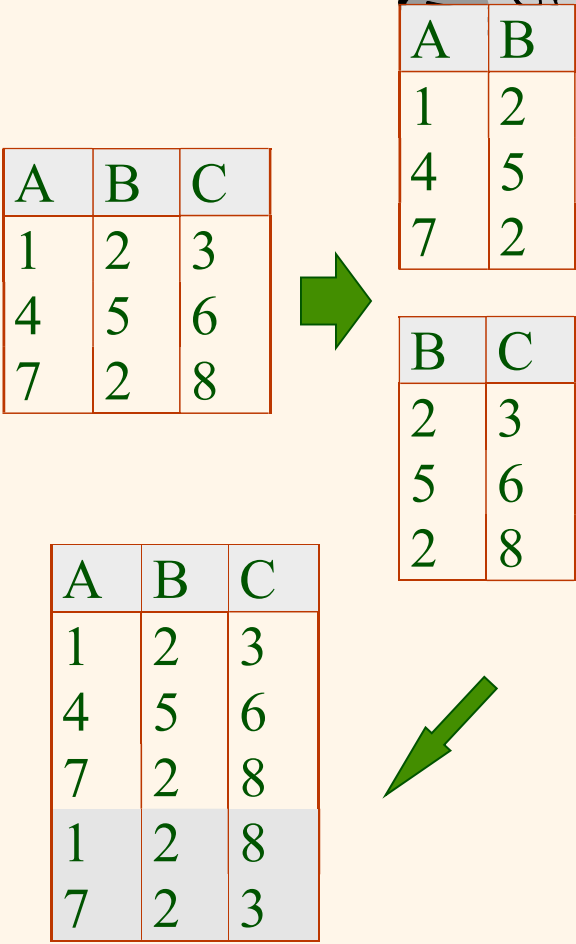
　위에서 인스턴스를 $\pi_{AB}$와 $\pi_{BC}$로 각각 분해한다고 했을 경우, 원래의 정보를 복구할 수가 없다. 즉, $\pi_{AB}$와 $\pi_{BC}$를 다시 자연 조인 했을 경우, 원래의 인스턴스에는 없었던 (1, 2, 8), (7, 2, 3)의 두 개의 투플들이 추가로 생긴다. 이는 원래의 인스톤스에는 없었던 정보가 새로이 생성된 것으로, 이를 일종의 정보의 손실이라 간주할 수 있다. 따라서 이 경우와 같이 분해하는 것을 손실(lossy) 분해인 것이다.
　중복성을 소거하기 위해 사용되는 어떠한 분해든지, 그 분해는 반드시 무손실이어야 한다. R을 어떤 릴레이션이라하고, F를 R에 정의된 FD들의 집합이라고 하면, R을 애트리뷰트들의 집합 $\mathrm{R_1}$과 $\mathrm{R_2}$로 구성된 두 개의 릴레이션으로 분해했을 떄, $F^+$가 다음 조건을 만족하면 이 분해는 무손실 조인이며, 이에 대한 역도 성립한다.

• $\mathrm{R_1} \cap \mathrm{R_2} \rightarrow \mathrm{R_1}$
• $\mathrm{R_1} \cap \mathrm{R_2} \rightarrow \mathrm{R_2}$

　위의 정리에 의하면 $\mathrm{R_1}$과 $\mathrm{R_2}$에 공통적으로 속한 애트리뷰트들은 반드시 $\mathrm{R_1}$ 혹은 $\mathrm{R_2}$에 속한 키를 포함하여야 한다. Hourly_Emps 릴레이션을 다시 한번 참조하면, 이 릴레이션은 SNLRWH의 애트리뷰트들로 구성되고, FD R$\rightarrow$W가 3NF를 위반하고 있다. 이러한 위반 사항을 해결하기 위해서는 이 릴레이션을 SNLRH와 RW로 분해하면 된다. 여기서 애트리뷰트 R이 분해된 두 개의 릴레이션에 각각 공통적으로 속하고, 또한 R$\rightarrow$W가 만족되므로, 이 분해는 무손실-조인이다.
　위의 예를 통해, 만약 어떤 릴레이션 R에 FD X$\rightarrow$Y가 존재하고, X$\cap$Y가 공집합이면, R을 R-Y와 XY로 분해하면, 이 분해는 무손실 조인이다. 여기서 X는 R-Y와 XY에서 모두 나타나고, XY에 대해 키가 된다.

종속성 유지 분해

　CSJDPQV의 애트리뷰트들로 구성된 Contracts 릴레이션을 참조하면, 이 릴레이션에 C$\rightarrow$CSJDPQV, JP$\rightarrow$C, SD$\rightarrow$P의 FD들이 존재한다. 여기서 SD는 키가 아니므로 종속성 SD$\rightarrow$P는 BCNF를 위배하게 된다는 사실을 알 수 있다. 이를 해결하기 위해서 Contracts 릴레이션을 CSJDQV와 SDP라는 두 개의 릴레이션으로 분해할 수 있는데, 이 분해는 무손실 조인 분해임을 쉽게 확인할 수 있다. 그러나 이 시점에서 한 가지 문제가 발생한다. 예를 들어, 무결성 제약 조건인 JP$\rightarrow$C가 Contracts 릴레이션에서 만족되는지를 검증하고 싶다고 하면, 새로운 하나의 투플이 이 릴레이션에 삽입될 때 이 삽입된 투플과 JP 값은 동일하지만 C값은 다른 투플들이 이 릴레이션에 존재하지 않는지를 검증함으로써 쉽게 해결할 수 있다. 그러나 일단 Contracts 릴레이션을 CSJDQV와 SDP로 분해하고 난 후의 경우를 생각해보면, CSJDQV에 하나의 새로운 투플이 삽입될 때마다, 두 개의 릴레이션을 조인을 하고 난 후 이 제약 조건이 만족되는지를 매번 검증해야 한다. 따라서 이러한 분해를 종속성을 유지하는 분해가 아니라고 말할 수 있다.
　직관적으로 종속성 유지 분해(Dependency Preserving Decomposition)란 새로운 투플을 삽입하거나 혹은 어떤 투플을 수정하고자할 떄, 단지 단일 릴레이션에 속한 인스턴스들 자체만 조사하면, 모든 FD들이 만족되는지를 검증해 줄 수 있다는 것을 의미한다.
　어떤 릴레이션 스키마 R이 애트리뷰트들의 집합인 X와 Y로 구성된 두 개의 스키마로 분해되고, 이 R에 정의된 FD들의 집합을 F라고 하면, X에 대한 F의 프로젝션을 X에 속하는 애트리뷰트들만을 포함하는 폐포 $F^+$에 속하는 FD들의 집합으로 정의된다. 여기서 편의상 X에 대한 F의 프로젝션을 Fx로 표기한다. 이제 $F^+$에 속하는 어떤 종속성 U$\rightarrow$V가 Fx에 속하기 위해서는, U와 V에 속하는 모든 애트리뷰트들이 X에 속해야한다.
　FD들의 집합인 F를 갖는 릴레이션 스키마 R을 애트리뷰트들의 집합인 X와 Y로 구성된 두 개의 스키마로 분해될 때, 이 분해가 $(F_x \cup F_Y)^+ = F^+$를 만족할 경우, 이러한 분해를 종속성 유지 분해하고 한다. 즉 Fx와 Fy에 속하는 종속성들을 각각 얻은 후, 이들을 합집합한 결과의 폐포를 계산할 경우, F의 폐포에 속하는 모든 종속성들을 얻게 된다. 따라서 Fx와 Fy에 속한 종속성들만을 테스트 하면 $F^+$에 속한 모든 FD들도 역시 만족된다는 것을 보장할 수 있다. 여기서 Fx를 검증하기 위해서는 단지 릴레이션 X만 조사하면 된다. 또한 이와 유사하게 Fy를 검증하기 위해서는 단지 릴레이션 Y만 존재하면 된다.
　F의 프로젝션을 계산하는 과정에서 폐포 $F^+$를 왜 고려해야 되는 이유를 알기 위해 다음 예제를 살펴본다. 애트리뷰트 ABC로 구성된 릴레이션 R이 AB와 BC로 각각 구성된 두 개의 릴레이션으로 분해했다고 가정한다. R에 대한 FD들의 집합 F에는 A$\rightarrow$B, B$\rightarrow$C, C$\rightarrow$A가 포함되어 있다고 하면, 이들 종속성들 중에서, A$\rightarrow$B는 $F_{AB}$에 포함되어 있으며, B$\rightarrow$C는 $F_{BC}$에 포함되어 있음을 알 수 있다.여기서 C$\rightarrow$A는 직관적으로 보면 이 종속성은 $F_{AB}$와 $F_{BC}$에 열거된 종속성들에 이해 유도가 되지 않음을 알 수 있다.
F의 폐포는 F자체에 있는 모든 종속성들외에 A$\rightarrow$B, B$\rightarrow$C, C$\rightarrow$A를 포함하고 있다. 결과적으로 $F_{AB}$는 역시 B$\rightarrow$A를 포함하며 $F_{BC}$는 C$\rightarrow$B를 포함하고 있다. 따라서 $F_{AB} \cup F_{BC}$는 A$\rightarrow$B, B$\rightarrow$C, B$\rightarrow$A, C$\rightarrow$B를 포함하게 된다. 이제 $F_{AB}$와 $F_{BC}$에 속한 종속성들의 폐포에는 C$\rightarrow$A도 포함하게 된다. 따라서 위의 분해는 종속성 C$\rightarrow$A를 그대로 유지할 수 있다.
　무손실 조인을 만족하지는 않지만, 종속성 유지는 만족하는 분해의 예제도 있다. 간단한 예로, 릴레이션 ABC에서 FD A$\rightarrow$B가 존재하는데, 이 릴레이션을 AB와 BC로 분해한 경우이다.

정규화

　어떤 릴레이션 스키마가 BCNF에 속하지 않는다면, 이를 여러 개의 BCNF 릴레이션 스키마들로 무손실 조인을 유지하면서 분해하는 것은 항상 가능하지만, 불행히도 종속성 유지를 유지하면서 분해하는 방법은 가능하지 않다. 그러나 여러 개의 3NF 릴레이션 스키마들로 종속성 유지와 무손실 조인을 모두 유지하며서 분해하는 것은 항상 가능하다.

BCNF로의 분해

　함수 종속성들의 집합 F를 갖는 릴레이션 스키마 R을 여러 개의 BCNF 릴레이션 스키마들로 분해하는 알고리즘은 다음과 같다.

• R이 BCNF에 속하지 않는다고 하고, X$\subset$R이며, A는 R에 속한 단일 애트리뷰트이며, X$\rightarrow$A는 BCNF를 위해하는 FD라 하면, R을 R-A와 XA로 분해한다.
  • X$\rightarrow$A가 BCNF를 위배하기 때문에, 이 종속성은 분명히 당연한 종속성(trivial dependency)은 아니다.
  • 더욱이 A는 단일 애트리뷰트이므로, A는 X에 속하지 않으며, 즉, X$\cap$A는 공집합이다.
  • 따라서 이 분해는 무손실 조인을 유지한다.
• 만약 R-A혹은 XA가 BCNF에 속하지 않으면, 위의 방법을 순환적으로 적용해서 이 릴레이션들을 계속 분해한다.

　애트리뷰트들 CSJDPQV로 구성되고, 키가 C인 Contracts 릴레이션을 참조하면, 여기서 JP$\rightarrow$C와 SD$\rightarrow$P들의 종속성들이 주어졌다한다. 만약 SD$\rightarrow$P를 선택하여 분해를 하게되면, 두 개의 스키마 SDP와 CSJDQV를 얻는다. 여기서 SDP는 BCNF에 속한다. 그런데 “각 프로젝트에 대해 단 하나의 공급자만 있어야 한다”는 제약조건이 있다고 가정하면(J$\rightarrow$S), 이 제약조건에서 스키마 CSJDQV는 BCNF를 위반하게 된다. 따라서 이 스키마를 JS와 CJDQV로 다시 분해하게 된다. C$\rightarrow$JDQV는 CJDQV에서 만족한다. 그러므로 SDP, JS, CJDQV는 모두 BCNF에 속하게 되고, 이 스키마들을 조인하게 되면 CSJDPQV의 정보가 그대로 복구된다.
　위의 분해 과정의 단계들을 다음과 같이 트리 형태로 나타낼 수 있다. 이 트리에서 루트 노드는 원래의 릴레이션 CSJDPQV이고, 단말 노드들은 분해 알고리즘을 적용해서 생성된 BCNF 릴레이션들이다.(즉, SDP, JS, CSDQV)

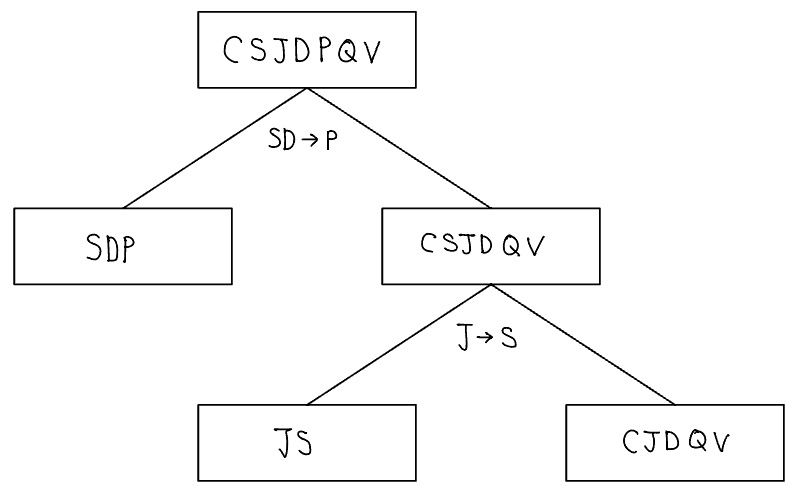
BCNF의 중복성에 대한 재고찰
　CSJDQV를 SDP, JS, CJDQV로 분해하는 것은 종속성 유지를 만족하지 않는다. 직관적으로 보면 종속성 JP$\rightarrow$C를 검증하려면 반드시 조인을 해 주어야 한다는 것을 알 수 있다. 이러한 문제를 해결하는 하나의 방법은 애트리뷰트 CJP를 갖는 릴레이션을 하나 더 추가하여 만드는 것이다. 사실 이러한 해결책은 종속성 검증을 좀 더 효율적으로 하기 위해 일부 정보들을 중복해서 저장하는 것이 된다.

BCNF를 분해하는 다른 방법
　어떤 종속성들이 BCNF를 위배한다고 하면 이 종속성들 중에서 어떤 종속성을 다음 분해 단계의 기준으로 선택하느냐에 따라, 그 결과로 얻는 BCNF 릴레이션들의 모임이 서로 다를 수가 있게 된다. 이를 위해 Contracts 릴레이션을 참조한다. 이 릴레이션을 SDJ, JS, CJDQV로 분해하였다. 이제 이와 다른 방법으로, FD J$\rightarrow$S를 하게 되면, 원래 릴레이션 CSJDPQV이 JS와 CJDPQV로 분해된다. CJDPQV에서 만족되는 유일한 종속성은 JP$\rightarrow$C와 키 종속성 C$\rightarrow$CJDPQV 뿐이다. 여기서 JP는 키이므로 CJDPQV는 BCNF에 속한다. 따라서 스키마 JS와 CJDPQV는 Contracts 릴레이션을 BCNF 릴레이션들로 무손실 조인 분해한 것을 나타낸다.
　여기에서 종속성 이론이 설계 단계에서 중복성이 언제 발생하게 되는지를 알려주고, 또한 이 문제를 해결하기 위해 분해를 어떨게 해야 하는지에 대한 실마리를 제공해 주기는 하지만, 실제로 여러 가지 가능한 분해들 중 어느 것이 좋은지를 구별해 주지는 못한다는 점이다. 따라서 데이터베이스 설계자들은 이런 여러 분해 대안들을 잘 살펴보고 해당되는 응용의 의미에 기반하여 이 중에서 하나를 선정하여야 한다.

BCNF와 종속성 유지
　종속성을 유지하면서 BCNF로 분해할수 없는 경우가 종종 있다. 예를 들어, 릴레이션 스키마 SBD를 참조하면, 이 스키마는 “선원 S가 어떤 날짜 D에 배 B를 예약한다”는 것으로 해석할 수 있다. 이때 여기서 종속성 SB$\rightarrow$D(즉, 각 선원은 최대 하루만 배를 예약할 수 있다.)와 D$\rightarrow$B(하루에 많아야 한 척의 배만 예약받을 수 있다.)가 주어졌다고 가정하면, 이때 B는 키가 아니기 때문에 SBD는 BCNF에 속하지 않는다. 그러나 만약 이 스키마를 분해하려고 시도한다면, 종속성 SB$\rightarrow$D를 그대로 유지할 수 없게 된다.

3NF로의 분해

　BCNF로 무손실 조인 분해하는 방식은, 3NF로 무손실 조인 분해하는 방식에 역시 그대로 적용될 수 있다. 그러나 이 방식은 반드시 종속성 유지를 보장하는 것은 아니다.

FD들의 집합에 대한 최소 커버
　FD들의 집합 F에 대한 최소 커버(minimal cover)는 다음 조건을 만족하는 FD들의 집합 G로 정의된다.

• G에 속하는 모든 종속성들은 X$\rightarrow$A의 형태이고, 이때 A는 단일 애트리뷰트이다.
• 폐쇄 $F^+$는 폐쇄 $G^+$와 동등하다.
• 만약 G의 종속성들을 몇 개 삭제하거나, 혹은 G의 어떤 종속성에 있는 애트리뷰트들을 몇 개 삭제한 후, G로부터 얻게 되는 종속성들의 집합 H에 대해서, $G^+ \neq H^+$이다.

　직관적으로 말하면, FD들의 집합 F에 대한 최소 커버는 다음의 두 가지 관점에서 최소가되는 종속성들의 집합과 동등하다.

• 모든 종속성은 가능한 한 그 크기가 작아야 한다.
  • 죄측에는 애트리뷰트가 반드시 있어야 하고, 우측은 단일 애트리뷰트가 있어랴 한다.
• 최소 커버에 속하는 모든 종속서들은 $F^+$와 동등한 폐포를 구하기 위해 필요하다.

　예를 들어, F가 다음의 종속성들의 집합으로 주어졌다고 하자.

A$\rightarrow$B, ABCD$\rightarrow$E, EF$\rightarrow$G, EF$\rightarrow$H, ACDF$\rightarrow$EG

　우선 ACDF$\rightarrow$EG를 ACDF$\rightarrow$E, ACDF$\rightarrow$G로 작성하여 우측은 모두 단일 애트리뷰트만 있도록 한다. 다음에는 ACDF$\rightarrow$G를 살펴보면, 이 종속성은FD A$\rightarrow$B, ABCD$\rightarrow$E, EF$\rightarrow$G로 부터 유도된다. 따라서 이 종속성은 중복이므로 이를 소거할 수 있다. 마찬가지로 ACDF$\rightarrow$E도 소거할 수 있다. ABCD$\rightarrow$E를 살펴보면, 여기서 A$\rightarrow$B가 성립하기 때문에, 이 ABCD$\rightarrow$E를 ACD$\rightarrow$E로 대체할 수 있다. 따라서 F에 대한 최소 커버는 다음과 같다.

A$\rightarrow$B, ACD$\rightarrow$E, EF$\rightarrow$G, EF$\rightarrow$H

　위 예로부터 어떤 FD들의 집합 F에 대한 최소 커버를 얻는 다음과 같은 일반적인 알고리즘을 얻을 수 있다.

• FD들을 표준 형태로 전환한다.
  • 우측에 반드시 단일 애트리뷰트만 있는 FD들로만 되도록 표준 형태 G를 구한다.(이를 위해 분해 규칙을 이용)
• 각 FD의 좌측을 최소화한다.
  • G에 속하는 각 FD에 대해서, 죄측의 각 애트리뷰트를 검사한다. 만약 이 애트리뷰트를 삭제해도, $F^+$와 동등한지 검사한다.
  • 만약 동등성이 유지되면, 이 애트리뷰트를 삭제한다.
• 중복되는 FD들을 식별하여 이들을 삭제한다.
  • G에 남아있는 FD들을 일일히 검사한다. 만약 이 FD를 삭제해도, $F^+$와 동등한지 검사한다.
  • 만약 동등성이 유지되면, 이 FD를 삭제한다.

　위의 과정들을 수행해가면서 FD들을 어떠한 순서로 선택하는가에 따라서, 서로 다른 최소 커버들이 생성될 수 있다. 즉 주어진 FD들의 집합에 대해 여러 개의 최소 커버들이 존재할 수 있다. 여기서 알수 있는 사실은, 중복되는 FD들을 식별하여 이들을 삭제하기 이전에, 반드시 FD의 좌변을 먼저 최소화해야 한다는 순서가 매우 중요하다. 만약 이 두 순서가 역으로 수행된다면, 최종적으로 생성되는 FD들의 집합에 일부 중복된 FD들이 여전히 남아 있게 된다(즉, 최소 커버가 아니게 된다).

3NF의 종속성 유지 분해
　무손실 조인과 종속성 유지를 만족하면서 3NF 릴레이션들로 분해하는 방법은 다음과 같다. R을 최소 커버인 FD들의 집합 F를 갖는 릴레이션이라 하고, $R-1, R_2, \dot, R_n$을 R의 무손실 조인 분해라고 하면, $1 \le i \le n$인 모든 i에 대해, 각 $R_i$를 3NF에 속하는 릴레이션이라고 하고, $F_i$를 F를 각 $R_i$의 애트리뷰트들에 대해 프로젝션한 결과라고 하자. 이제 다음 과정을 차례로 수행한다.

• F에 속하면서 종속성이 유지가 되지 않는 종속성들의 집합 N을 식별한다. 즉 이들은 $F_i$들의 합집합의 폐포에 포함되지 못하는 종속성들이다.
• N에 속한 각 FD X$\rightarrow$A에 대하여, 릴레이션 스키마 XA를 생성하고, 이 스키마를 R의 분해에 추가한다.

　여기서 알수있는 사실은, 만약 원래의 스키마 R을 스키마 $R_i$들과 이 과정에서 추가적으로 생성되는 XA 형태의 스키마들로 대체하면, F에 속하는 종속성들이 모두 유지된다는 점이다. 이러한 스키마 $R_i$들은 3NF에 속하게 되고, XA형태의 스키마들 역시 모두 3NF에 속한다.
　애트리뷰트 CSJDPQV로 구성되고, 종속성들 JP$\rightarrow$C, SD$\rightarrow$P, J$\rightarrow$S를 갖는 Contracts 릴레이션을 참조하면, 만약 SDP와 CSJDQV로 분해한다면, SDP는 BCNF에 속하지만, CSJDQV는 3NF애 속하지 않는다. 따라서 이 스키마를 JS와 CJDQV로 분해한다. 결과적으로 SDP, JS, CJDQV는 모두 3NF에 속하며(사실은 BCNF에도 속함), 이 분해는 역시 무손실 조인이다. 여기서 종속성 JP$\rightarrow$C는 유지되지 않는다. 이 문제는 릴레이션 스키마 CJP를 추가함으로써 해결할 수 있다.

데이터베이스 설계에서의 스키마 정제

　ER 설계를 마친 후에 스키마 정제 과정을 반드시 적용할 필요성이 있을까에대해 살펴본다.

개체에 속하는 애트리뷰트들의 식별

　다음 예제는 FD들을 잘 살펴보게 되면 릴레이션들의 기반이 되는 개체와 관계들을 좀 더 잘 이해할 수 있음을 알 수 있다. 특히 이 예제는 ER 설계 과정에서 애트리뷰트들을 ‘잘못된’ 개체 집합과 쉽게 연관시킬 수 있음을 보여준다. 다음은 Works_In 관계 집합과 유사한데, 단지 차이점은 ‘각 직원은 최대 하나의 부서에서만 근무한다’는 키 제약조건을 추가로 설정한 관계 집합이다.

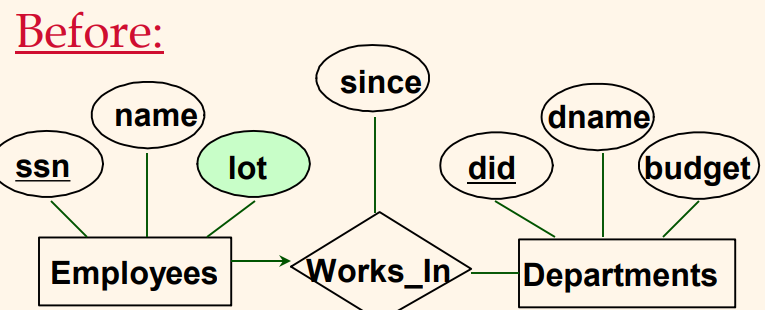
　이러한 키 제약조건을 이용하면 위의 ER 다이어그램을 다음과 같은 두 개의 릴레이션으로 변환할 수 있다.

Workers(ssn, name, lot, did, since), Departments(did, dname, budget)

　여기서 Employees 개체 집합과 Works_In 관계 집합을 합쳐서 단일 릴레이션 Workers로 사상되었다.
　이제 직원들의 주차 공간을 그들의 소속 부서에 따라 할당하게 되어, 어떤 부서에 속한 모든 직원들에게는 동일한 주차 공간을 배정한다고 하자. 이러한 제약조건은 위의 ER 다이어그램으로는 표현할 방법이 없다. 이를 함수 종속성으로 표현하면 FD did$\rightarrow$lot과 같다. 이 종속성에서 발생하는 중복성은 Workers 릴레이션을 다음과 같이 두 개의 릴레이션으로 분해하면 소거된다.

Workers2(ssn, name, did, since), Dept_Lots(did, lot)

　위의 설계가 더 좋은 것이라고 권장한다. 한 부서에 대한 주차 공간을 변경하고 싶으면 두번째 릴레이션의 투플 하나만 갱신하면 된다(즉, 갱신 이상이 발생하지 않는다.). 어떤 부서에 소속된 직원들이 하나도 없는 경우라도, 널 값을 사용하지 않고도, 그 부서에 해당되는 주차공간을 연관시킬 수 있다(즉, 삭제 이상이 발생하지 않는다.). 또한 주차공간을 배정 받지 못한 부서라도 첫 번째 릴레이션에 투플을 삽입함으로써 그 부서에 소속된 직원을 추가할 수 있다(즉, 삽입 이상이 발생하지 않는다.).
　Departments와 Dept_Lots 릴레이션을 살펴보면 둘 다 동일한 키를 갖으며, 따라서 동일한 키 값을 갖는 Departments 투플과 Dept_Lots 투플은 결국 동일한 개체를 묘사한다는 사실을 알 수 있다. 이러한 사실을 ER 다이어그램에 반영시키면 다음과 같다.

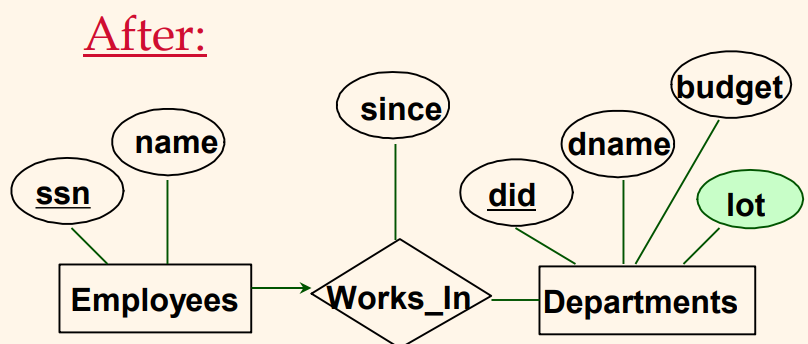
　이 다이어그램을 릴레이션들로 변환하면 다음과 같다.

Workers2(ssn, name, did, since), Departments(did, dname, budget, lot)

　직관적으로는 주차 공간을 직원들에게 연관시키는 것이 당연할 것 같은데, 이 예제에서의 제약조건들은 주차 공간을 실제로는 부서들에 연관시키고 있음을 알려주고 있다. 이처럼 ER 모델링은 주관적인 과정이므로 이러한 사실을 쉽게 간과할 수 있다. 그러나 정규화라는 엄격한 과정을 거치면 이러한 일이 발생하지 않는다.