4장 관계대수와 관계해석
Updated:
질의어(query language)는 데이터베이스에 들어 있는 데이터에 대한 질문, 즉 질의(query)를 하기 위한 특수 언어이다. 관계대수(relational algebra)에서 질의들은 여러 연산자들을 이용해서 구성되며, 각 질의는 원하는 해답을 계산하기 위한 단계적 절차를 기술한다. 즉, 질의들은 조작적인 방법으로 명시된다. 관계해석(relational calculus)에서 질의는 해답이 계산되는 방법을 명시하지 않고 원하는 답을 기술한다. 이러한 비 절차적인 질의 스타일을 선억적(declarative)이라고 한다.
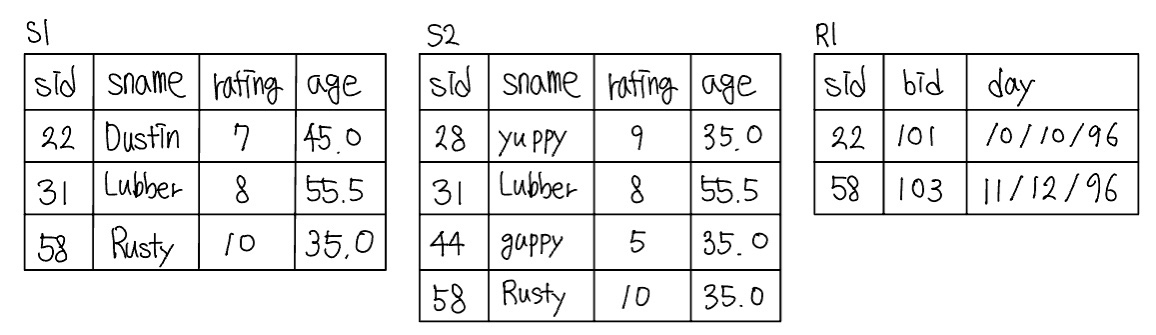
한 질의의 입력과 출력의 형태는 릴레이션이다. 질의는 각 입력 릴레이션의 인스턴스를 이용하여 계산되며 출력 릴레이션의 인스턴스를 산출한다. 다음의 스키마를 이용하여 다양한 샘플 질의들을 소개한다.

키 필드들에는 밑줄을 긋고, 각 필드의 도메인은 필드 이름 다음에 열거한다. 따라서 sid는 Sailors의 키이고, bid는 Boats의 키이며, Reserves에서는 세 필드 모두가 키를 형성한다.
관계대수
관계대수식(relational algebra expression)은 한 릴레이션, 단일 식에 적용되는 단항(unary) 대수 연산자, 또는 두 개의 식에 적용되는 이항(binary) 대수 연산자로 순환적으로 정의된다. 여기에서는 관계대수의 기본 연산자들과 몇 가지 추가적인 연산자들을 기술한다.
기본 연산자(Basic operations)
- 셀렉션( Selection, $\sigma$ ): 릴레이션으로부터 행들을 선택하기 위한 연산자
- 프로젝션( Projection, $\pi$ ): 릴레이션으로부터 열들을 선택하기 위한 연산자
- 크로스 프로덕트( Cross-product, $\times$ ): R$\times$S는 그 스키마가 R의 모든 필드 다은에 S의 모든 필드들을 순서대로 포함하는 릴레이션 인스턴스를 반환한다.
- 차집합( Set-difference, $-$ ): R-S는 R에는 속하고 S에는 속하지 않는 투플들로 구성된 릴레이션 인스턴스를 반환한다.
- 합집합( union, $\cup$ ): R$\cup$S는 R이나 S에 나타나는 모든 투플들을 포함하는 릴레이션 인스턴스를 반환한다.
추가적인 연산자
- 교집합(intersection), 조인(join), 디비전(division), 이름바꾸기(renaming)
프로젝션
프로젝션 연산자 $\pi$는 한 릴레이션으로부터 열들을 추출한다. 예를 들어, $\pi$를 사용하여 모든 뱃사람의 이름과 등급을 구할 수 있다.
위 식은 다음 그림과 같은 릴레이션을 결과로 산출한다.

아래 첨자 sname, rating은 유지될 필드들을 명시하고, 나머지 필드들은 모두 제거된다. 뱃사람들의 나이만 구한다고 하자.
위 식은 다음과 같은 릴레이션을 결과로 산출한다.

세 명의 뱃사함이 나이가 35세이지만, 이 프로젝션의 결과에는 age=35.0인 단일 투플이 나타나는 것이다. 이것은 릴레이션이 투플들의 집합이라는 정의에 따른 결과이다.
셀렉션
셀렉션 연산자 $\sigma$는 한 릴레이션으로부터 행들을 추출한다. 예를 들어, $\sigma$연산자를 사용하여 경험이 많은 뱃사람에 해당하는 투플들을 검색할 수 있다.
위 식은 다음과 같은 릴레이션을 결과로 산출한다.
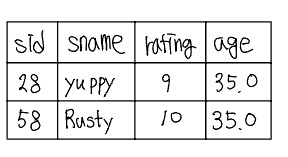
프로젝션과 셀렉션을 조합하여 등급이 아주 높은 뱃사람들의 이름과 등급을 계산할 수 있다.
위 식은 다음과 같은 릴레이션을 결과로 산출한다.
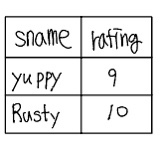
셀렉션 연산자는 셀렉션 조건을 통해 유지할 투플들을 명시한다. 일반적으로, 이 셀렉션 조건은 애트리뷰트 op 상수 또는 애트리뷰트1 op 애트리뷰트2 라는 형태의 항들을 불리언으로 조합한 것이다. 여기서 op는 비교 연산자 $<, >=, =, \neq$ $, >=, >$ 중의 하나이다.
합집합, 교집합, 차집합
- 합집합(union: $\cup$): R $\cup$ S는 R이나 S에 나타나는 모든 투플들을 포함하는 릴레이션 인스턴스를 반환한다.
- 교집합(intersection: $\cap$): R $\cap$ S는 R과 S에 모두 속하는 투플들을 포함하는 릴레이션 인스턴스를 반환한다.
- 차집합(set-difference: $-$): R $-$ S는 R에는 속하고 S에는 속하지 않는 투플들로 구성된 릴레이션 인스턴스를 반환한다.
위 연산의 모든 릴레이션 인스턴스 R, S는 서로 합병가능(union-compatible)해야하고 결과의 스키마는 R의 스키마와 동일하다.
위 식들은 다음과 같은 릴레이션을 결과로 산출한다.
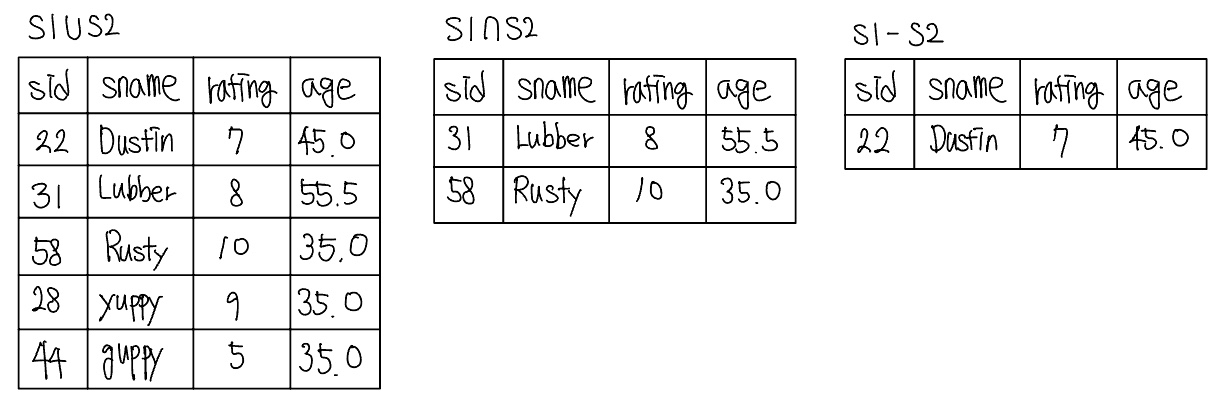
크로스 프로덕트
크로스 프로덕트 R $\times$ S는 그 스키마가 R의 모든 필드 다음에 S의 모든 필드들을 순서대로 포함하는 릴레이션 인스턴스를 반환한다. 크로스 프로덕트는 카티션 프로덕트(Cartesian product)라고도 한다.
R $\times$ S의 필드들은 R과 S의 대응하는 필드로부터 이름을 상속하는 관례를 사용한다. R과 S는 동일한 이름을 갖는 하나 이상의 필드들을 포함할 가능성도 있다 이 경우에 이름 충돌(naming conflict)이 발생한다. 이러한 필드들은 R $\times$ S에서 이름이 만들어지지 않고 그 위치로만 언급한다.
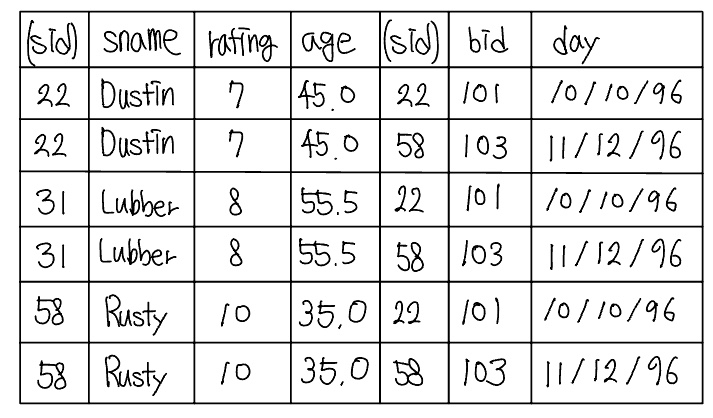
위 그림에서 sid는 상속된 필드이름이 아니라는 것을 강조하기 위해 괄호 안에 들어 있다.
이름바꾸기
이름 출돌이 발생하는 경우 릴레이션 인스턴스의 필드에 이름을 명시적으로 부여할 수 있도록 하는 것이 편리하다. 이런 목적을 위해 개명(renaming) 연산자 $\rho$가 있다. 예를 들어, $\rho$(C(1 $\rightarrow$ sid 1, 5 $\rightarrow$ sid 2), S1 $\times$ R1)는 다음과 같은 스키마를 가진다. C(sid 1: integer, sname: string, rating: integer, age: real, sid 2: integer, bid: integer, day: dates).
조인
조인(join) 연산은 관계대수에서 가장 유용한 연산 중의 하나로서, 두 개 이상의 릴레이션들로부터 정보를 조합하기 위해 가장 일반적으로 사용되는 방법이다. 조인은 크로스 프로덕트를 한 후에 셀렉션과 프로젝션을 하는 것으로 정의될 수 있지만, 실제로 순수한 크로스 프로덕트보다 훨씬 더 자주 사용된다.
조건 조인
조건 조인(condition join)의 가장 일반적인 형태는 조건조인 c와 한 쌍의 릴레이션 인스턴스를 매개변수로 받아들여 하나의 릴레이션 인스턴스를 반환하는 것이다. 이 연산은 다음과 같이 정의된다.
따라서 $\bowtie$는 크로스 프로덕트 후에 셀렉션을 하는 것으로 정의된다.
예를 들어, S1 $\bowtie_{S1.sid < R1.sid}$ R1의 결과는 다음과 같다.
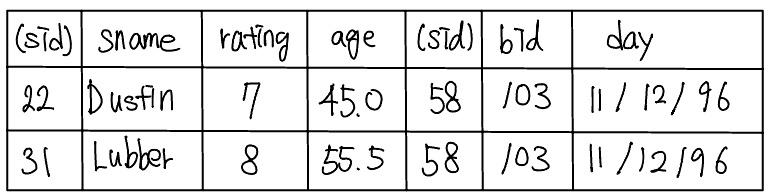
동등 조인
조인 연산 R $\bowtie$ S의 특수한 경우 중에서 가장 흔한 형테는 조인 조건이 R.name1 $=$ S.name2의 형태의 등식들 만으로 구성되는 것이다.
이렇게 등식으로만 구성되는 조인 조건의 경우, 조인 연산은 S.name2가 제거되는 추가적인 프로젝션을 수행함으로써 정제된다. 이러한 정제 작업을 수행하는 조인 연산을 동등 조인(equijoin)이라고 한다.
S1 $\bowtie_{R.sid = S.sid}$ R1의 결과는 다음과 같다. sid 필드는 오직 한번만 결과에 나타난다.

자연 조인
조인 연산 R $\bowtie$ S의 좀 더 특수한 경우는 동증조건이 R과 S에서 동일한 이름을 가지고 있는 모든 필드에 대해 명시되는 동등조인이다. 이 경우에는, 조인 조건을 생략할 수 있다. 이 특수한 경우를 자연 조인(natural join)이라고 하는데, 이 연산은 그 결과가 동일한 이름을 가진 두 필드를 갖지 않도록 보장되는 좋은 설질을 가지고 있다.
동등 조인식 S1 $\bowtie_{R.sid=S.sid}$ R1은 실제로는 자연조인이기 때문에 단순히 S1 $\bowtie$ R1으로 표기될 수 있다. 만일 두 릴레이션이 공통되는 애트리뷰트를 가지고 있지 않다면, S1 $\bowtie$ R1은 크로스 프로덕트가 된다.
디비전
디비전(division) 연산자는 “모든 배를 예약한 뱃사람의 이름을 구하시오.”와 같은 특정한 종류의 질의를 표현할 때 유용하다. 예를 통해 디비전을 알아보자. 두 릴레이션 인스턴스 A와 B를 생각해보자. A에는 정확하게 두 필드 x와 y가 있고, B에는 하나의 필드 y가 있으며 A에 있는 y와 도메인이 같다. 디비전 연산 A$/$B는 B에 있는 모든 y값에 대해서 A에 투플 $<$x, y$>$가 존재하는 모든 x값들의 집합으로 정의된다. 디비전의 예는 다음과 같다.
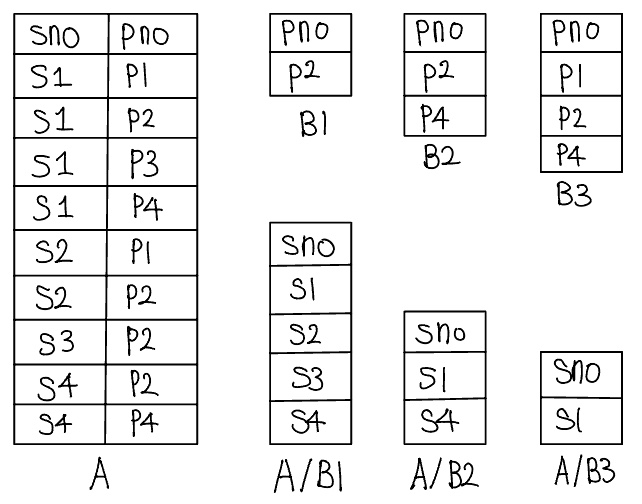
A/B를 기본 대수 연산자로 풀어 표현해 보자. 기본적인 아이디어는 A에서 자격이 없는 모든 x값들을 계산하는 것이다. A에 있는 각 x 값과 B에 속한 y 값을 접합하여, A에 속하지 않는 투플 $<$x, y$>$를 얻으면 그 x값은 자격이 없게 된다(disqualified). 다음의 대수식을 사용하여 자격이 없는 투플들을 계산할 수 있다.
그러므로, A$/$B는 다음과 같이 정의할 수 있다.
대수 질의의 예제들
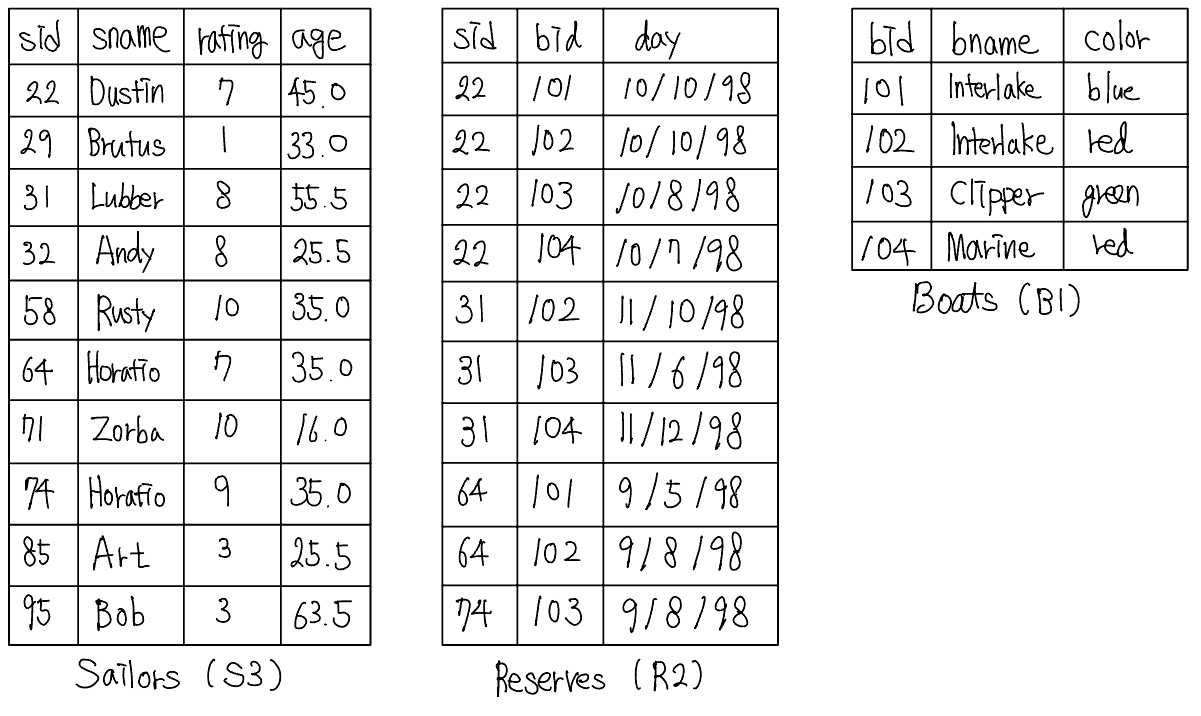
Q1. 배 103을 예약한 뱃사람의 이름을 구하시오.
Sol1) $\pi_{sname}$($\sigma_{bid=103}$(Reserves $\bowtie$ Sailors))
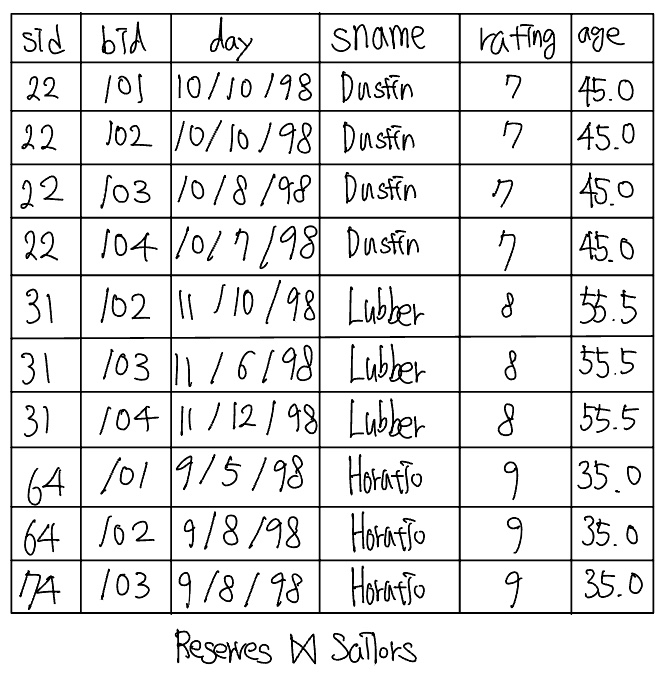
Sol2) $\rho$(Temp1, $\sigma_{bid=103}$(Reserves$\bowtie$Sailors)), $\rho$(Temp2, Temp1 $\bowtie$ Sailors), $\pi_{sname}$(Temp2)
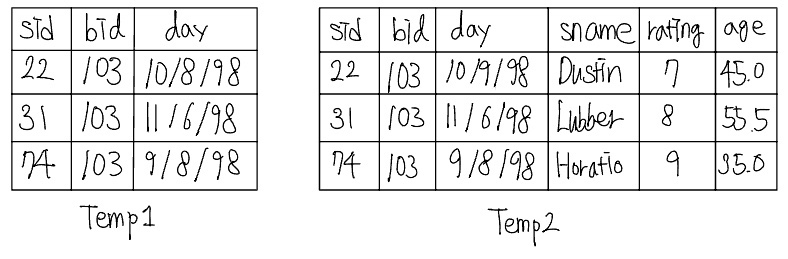
Sol3) $\pi_{sname}$(($\sigma_{bid=103}$Reserves) $\bowtie$ Sailors)
이 예제는 관계 DBMS에서 관계대수가 상당한 역할을 하는 것을 보여준다. DBMS는 SQL 질의를 관계대수로 변환하고, 그 다음에 같은 답을 산출하면서 계산비용은 더 적게 드는 다른 대수식들을 찾는다. 위 답 중에서 최적화기는 Sol3 가 중간 결과의 릴레이션 크기가 더 작기 때문에 계산비용도 더 적게 들 것이다.
Q2. 적색 배를 예약한 뱃사람의 이름을 구하시오.
Sol1) $\pi_{sname}$(($\sigma_{color=’red’}$Boats)$\bowtie$Reserves $\bowtie$ Sailors)
Sol2) $\pi_{sname}$($\pi_{sid}$(($\pi_{bid}\sigma_{color=’red’}$Boats) $\bowtie$ Reserves) $\bowtie$ Sailors)
위 답 중에서 Sol2 는 필드 수가 더 적은 중간 릴레이션들을 생성한다. 그러므로 관계 질의 최적화기는 Sol1 이 주어지면 Sol2 를 찾아내고자 할 것이다.
Q3. Lubber가 예약한 배의 색을 구하시오.
Sol) $\pi_{color}$(($\sigma_{sname=’Lubber’}$Sailors) $\bowtie$ Reserves $\bowtie$ Boats)
Q4. 적어도 한 척의 배를 예약한 뱃사람의 이름을 구하시오.
Sol) $\pi_{sname}$(Sailors $\bowtie$ Reserves)
Q5. 적색 배나 녹색 배를 예약한 뱃사람의 이름을 구하시오.
Sol1) $\rho$ (Tempboats, ($\sigma_{color=’red’}$Boats) $\cup$ ($\sigma_{color=’green’}Boats$)), $\pi_{sname}$(Tempboats $\bowtie$ Reserves $\bowtie$ Sailors)
Sol2) $\rho$ (Tempboats, ($\sigma_{color=’red’ \vee color=’green’}$Boats)), $\pi_{sname}$(Tempboats $\bowtie$ Reserves $\bowtie$ Sailors)
Sol2 에서 $\vee$는 or의 의미이고 $\wedge$는 and의 의미이다.
Q6. 적색 배와 녹색 배를 예약한 뱃사람의 이름을 구하시오.
이를 계산하기 위해 Q5의 답에서 $\cup$을 $\cap$으로 단순히 교체하면 되는 것으로 생각하기 쉽다.
$\rho$ (Tempboats2, ($\sigma_{color=’red’}$Boats) $\cap$ ($\sigma_{color=’green’}Boats$)), $\pi_{sname}$(Tempboats2 $\bowtie$ Reserves $\bowtie$ Sailors)
위 방법은 적색이면서 녹색인 배를 예약한 뱃사람을 구하게 된다. 올바른 접근 방식은 적색 배를 예약한 뱃사람을 구하고 녹색 배를 예약한 뱃사람을 구한 뒤, 이들 두 집합에 대해 교집합을 취하는 것이다.
Sol) $\rho$(Tempred, $\pi_{sid}$(($\sigma_{color=’red’}$Boats) $\bowtie$ Reserves)), $\rho$(Tempgreen, $\pi_{sid}$(($\sigma_{color=’green’}$Boats) $\bowtie$ Reserves)), $\pi_{sname}$((Tempred $cap$ Tempgreen) $\bowtie$ Sailors)
위 답은 적색 배 또는 녹색 배를 예약한 뱃사람들을 구하기 위해 쉽게 수정될 수 있다. 단순히 $\cap$ 를 $\cup$ 로 대체한다.
$\rho$(Tempred, $\pi_{sid}$(($\sigma_{color=’red’}$Boats) $\bowtie$ Reserves)), $\rho$(Tempgreen, $\pi_{sid}$(($\sigma_{color=’green’}$Boats) $\bowtie$ Reserves)), $\pi_{sname}$((Tempred $cup$ Tempgreen) $\bowtie$ Sailors)
이 문제에서 다음과 같은 시도를 생각해보자.
$\rho$(Tempred, $\pi_{sname}$(($\sigma_{color=’red’Boats}$) $\bowtie$ Reserves $\bowtie$ Sailors)), $\rho$(Tempgreen, $\pi_{sname}$(($\sigma_{color=’green’Boats}$) $\bowtie$ Reserves $\bowtie$ Sailors)), Tempred $\cap$ Tempgreen
위 식은 미묘한 이유로 정확한 결과를 얻지 못한다. 예제 인스턴스의 Horatio 처럼, 같은 이름을 가진 서로 다른 두 뱃사람이 적색 배와 녹색 배를 각각 예약할 수 있다. 이 경우에, Horatio라는 사람은 어느 누구도 적색 배와 녹색 배를 모두 예약하지 않았지만 그 결과에는 이름 Horatio가 포함되게 된다. 이러한 오류의 원인은 이 식에서 sname이 뱃사람을 구볗하기 위해 사용되고 있으나, sname은 키가 아니라는 점이다.
Q7. 적어도 두 척의 베를 예약한 뱃새람의 이름을 구하시오.
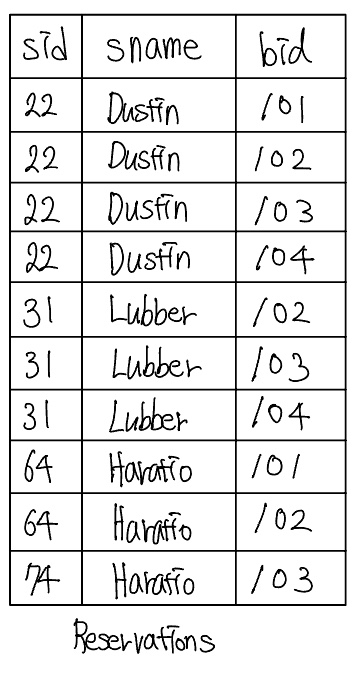
Sol) $\rho$ (Reservations, $\pi_{sid, sname, bid}$(Sailors $\bowtie$ Reserves)), $\rho$(Reservationpairs(1 $\rightarrow$ sid1, 2 $\rightarrow$ sname1, 3 $\rightarrow$ bid1, 4 $\rightarrow$ sid2, 5 $\rightarrow$ sname2, 6 $\rightarrow$ bid2), Reservations $\times$ Reservations), $\pi_{sname1}\sigma_{(sid1=sid2)\wedge(bid1 \neq bid2)}$ Reservations
Q8. 나이가 20세를 초과하고 적색 배를 예약하지 않은 뱃사람의 sid를 구하시오.
Sol) $\pi_{sid}$($\sigma_{age>20}$Sailors) $-$ $\pi_{sid}$(($\sigma_{color=’red’}$Boats) $\bowtie$ Reserves $\bowtie$ Sailors)
Q9. 모든 배를 예약한 뱃사람들의 이름을 구하시오.
‘모든’이란 단어의 사용은 디비전 연산을 적용할 수 있을 것이라는 좋은 암시가 된다.
Sol) $\rho$(Tempsids, ($\pi_{sid,bid}$Reserves)$/$($\pi_{bid}$Boats)), $\pi_{sname}$(Tempsids $\bowtie$ Sailors)
Q10. Interlake라고 하는 배를 모두 예약한 뱃사람들의 이름을 구하시오.
Sol) $\rho$(Tempsids, ($\pi_{sid,bid}$Reserves)$/$($\pi_{bid}$($\sigma_{bname=’Interlake’}$Boats))), $\pi_{sname}$(Tempsids $\bowtie$ Sailors)
댓글남기기