10장 스프링
Updated:
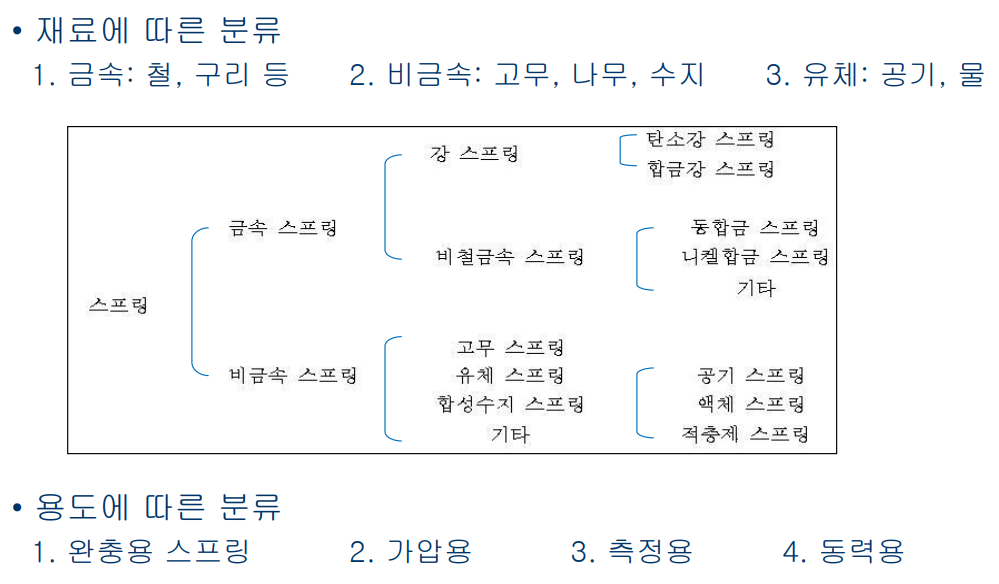
스프링의 종류는 다음과 같다.
나선형 스프링(helical spring)의 응력
다음 그림의 (a)에서는 원형 단면 와이어로 만든 헬리컬 압축스프링(helical compression spring)에 축방향 힘 $F$가 작용하고 있는 것을 보여준다. 여기서 D는 코일의 평균지름(mean coil diameter)이며, $d$는 와이어의 지름(wire diameter)이다.
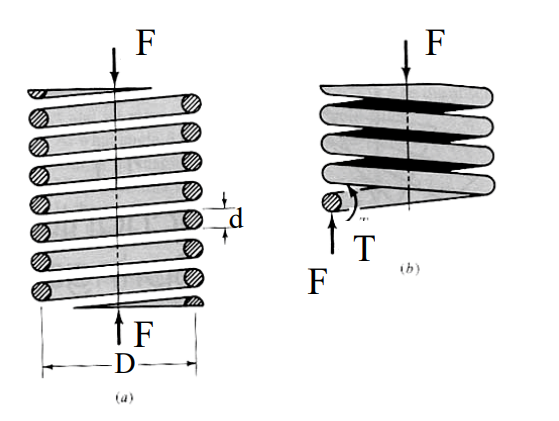
스프링을 임의의 위치에서 절단하여 그 부분을 제거하고, 제거된 부분의 효과를 순수한 내부 반작용으로 대체하였다고 하면, (b)에서 나타낸 바와 같이, 잘린 부분에는 평행상태에서 직접적인 전단력 $F$와 비틀림 모멘트 $T = FD / 2$가 작용할 것이다.
와이어에 작용하는 최대응력은 직접적인 전단응력과 비틀림 전단응력을 중첩하여 구할 수 있다. 그 결과는 스프링의 가장 안쪽 부분에서 다음과 같다.

사각형 단면의 와이어는 공간적 제한으로 불가피한 경우를 제외하고는 바람직하지 못하다. 특수한 단면 형상의 와이어로 만든 스프링은 원형 단면만큼 대량생산되지 않는다. 따라서 특수단면 와이어 스프링은 지속적인 개발이 이루어지지 않아 원형단면을 가진 와이어 스프링보다 취약할 수 있다. 공간이 매우 제한되어 있다면 원형단면 와이어 스프링을 포개어 사용하는 것을 먼저 고려하여야 한다. 이렇게 하면 특수한 단면을 가진 스프링을 사용하는 것보다 강도뿐만 아니라 경제적인 장점도 갖게 된다.
곡률효과
위 식에서 $\tau_{max}$는 와이어가 직선일 경우를 기초로 한 것이다. 그러나 와이어의 곡률이 존재하면 스프링의 안쪽에 작용하는 응력을 증가시키는 반면, 바깥쪽의 응력은 약간 감소시킨다. 이러한 곡률 응력은 피로와 관련하여 근본적인 중요성을 갖는데, 그 이유는 하중의 크기가 국부적인 항복을 발생시키기에는 매우 작기 때문이다.
곡률 계수(curvature factor)를 찾으려면 간접적인 방법이 필요하다. 위 식에서 $K_s$를 곡률과 직접적인 전단을 함께 보정하는 또 다른 계수 $K$로 대체한다고 하면, 이 계수는 다음 두 가지 식에 의해 주어진다.

최대전단응력을 예측하기 위해 다음 식이 사용된다.
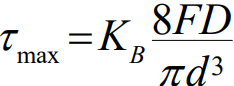
압축코일 스프링의 길이 변화
변형과 힘 사이의 관계는 Castigliano`s theorem을 사용하면 매우 쉽게 구할 수 있다. 헬리컬 스프링의 전체 변형에너지(strain energy)는 비틀림과 전단의 두 가지 요소로 구성되어 있다.

여기서 $N = N_a =$ 유효감김수이다. 그리고 Castigliano`s theorem을 사용하면 전체 처짐 $y$와 스프링 상수 $k$를 구할 수 있다.
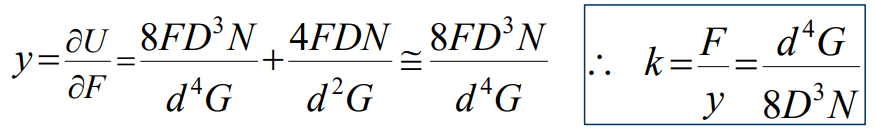
압축스프링
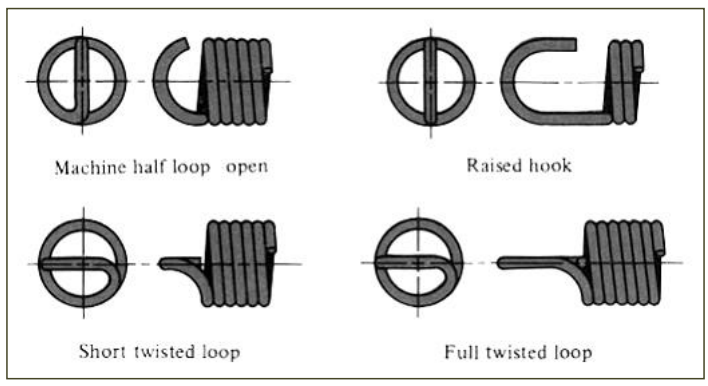
압축스프링(compression spring)에 일반적으로 사용되는 네 가지 종류의 끝부분은 다음과 같다.

중요한 용도로 쓰이는 스프링은 반드시 직사각형으로 만들고 연산작업을 하여야 하중의 전달을 양호하게 할 수 있다.
다음 표에서는 스프링 끝부분의 종류가 코일의 개수와 스프링의 길이에 어떻게 영향을 주는가를 보여준다.
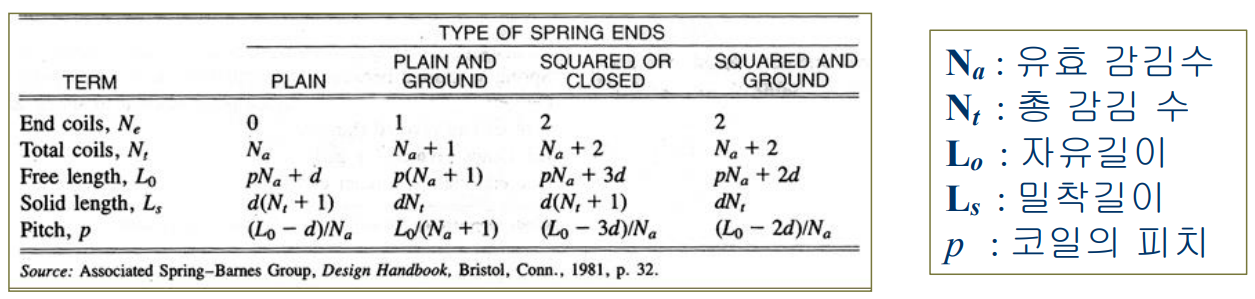
프리 세팅(set removal, presetting)은 유용한 잔류응력을 만들기 위해 압축스프링의 제작에 사용되는 공정이다.

안정성의 고려
하중이 과도하게 커지면 기둥은 좌굴된다. 마찬가지로 압축 코일스프링도 처짐(또는 휨)이 과도하게 커지면 좌굴된다. 임계 처짐은 다음과 같은 식으로 주어진다.
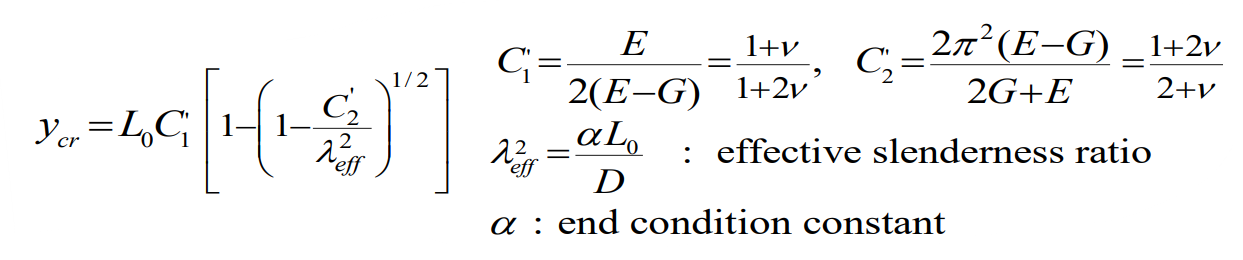
다음은 일반적인 끝부분 상태에 대한 $\alpha$값이 주어져 있다.

절대적 안정상태는 다음과 같다.
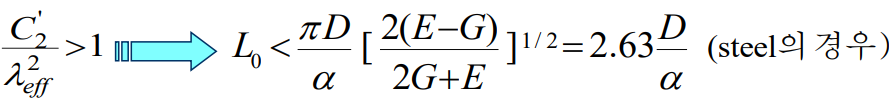
스프링 재료
스프링은 요구되는 재료의 치수, 스프링 상수 및 특성에 따라 열간 또는 냉간 가공공정을 거쳐 제작된다. 스프링을 감을 때에는 굽힘에 의해 잔류응력이 유도되는데, 이것의 방향은 코일스프링 내의 비틀림 작용응력의 방향에 수직이다. 스프링을 감은 후에 연성 열처리(mild thermal treatment)를 하여 잔류응력을 제거하는 것은 스프링 제작 시에 일반적으로 사용되는 공정이다.
가장 일반적으로 사용되는 강에 대한 설명은 다음과 같다.

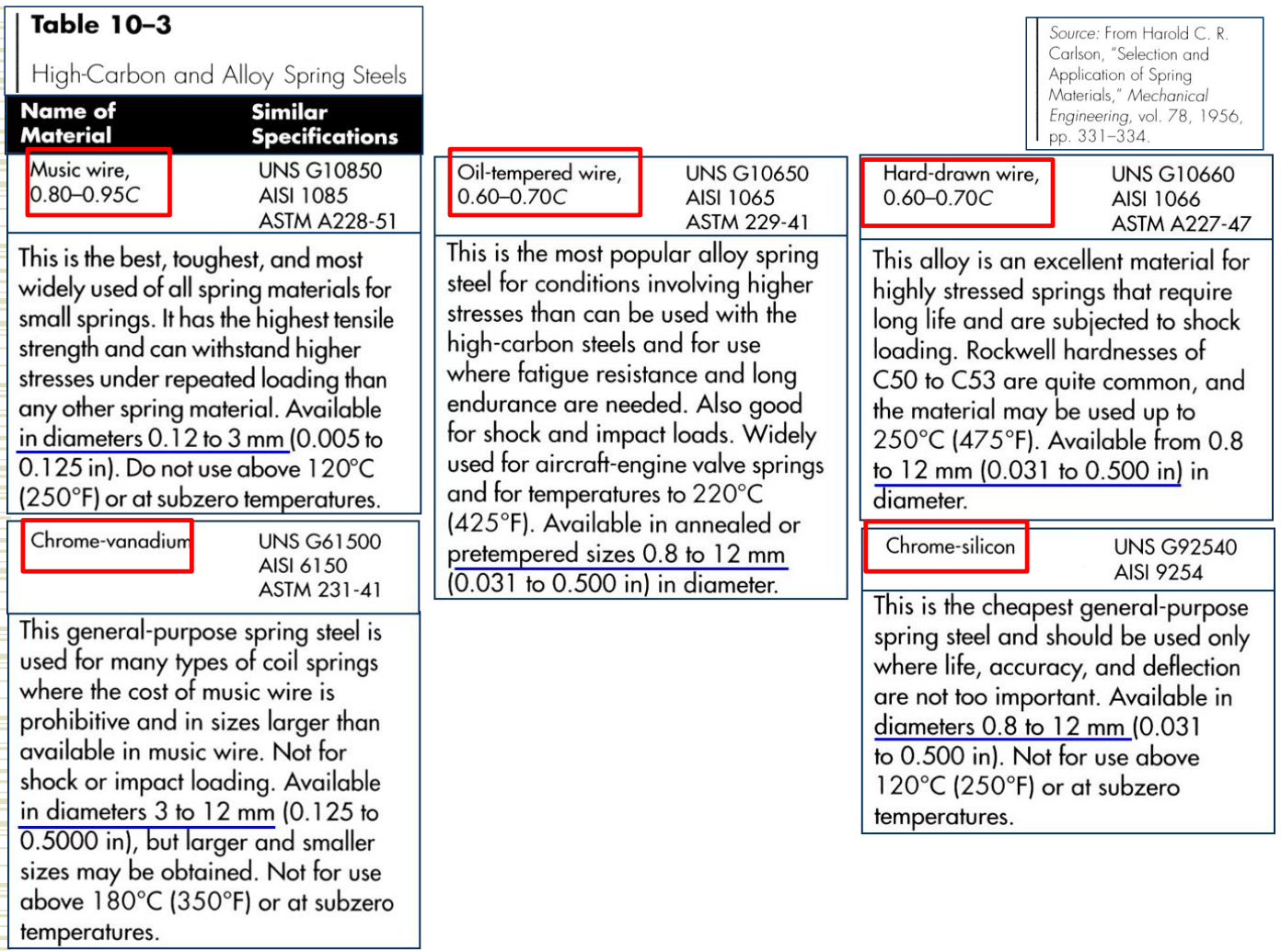
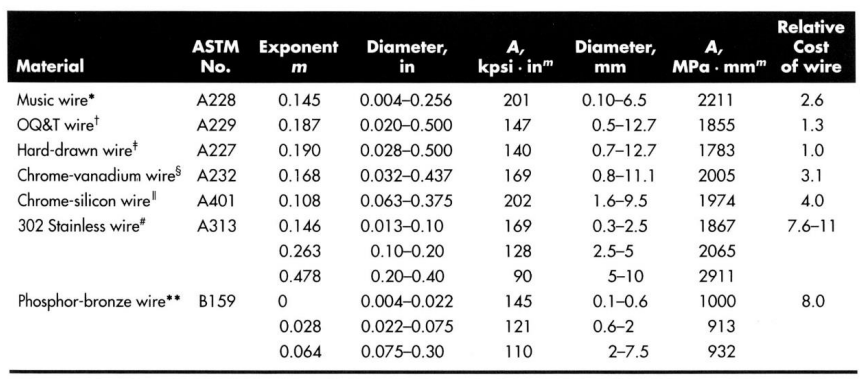
스프링 재료는 그 인장강도를 측정하여 비교할 수 있다. 이 값은 와이어의 치수에 따라서 상당히 달라지므로 와이어의 치수가 알려지기 전까지는 명기할 수 없다. 물론 재료와 그 가공방법도 인장강도에 영향을 준다. 인장강도와 와이어의 지름 사이의 관계에 대한 그래프를 log-log 스케일로 나타내면 몇몇 재료에서는 거의 직선으로 표현된다. 이 직선은 다음과 같은 식으로 나타낼 수 있다.
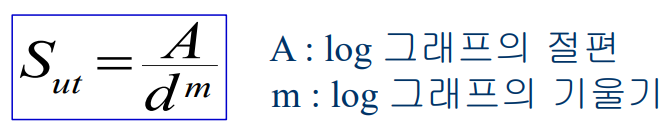
그 직선의 $A$와 $m$이 알려져 있으면 인장강도의 최솟값을 추정할 수 있다.
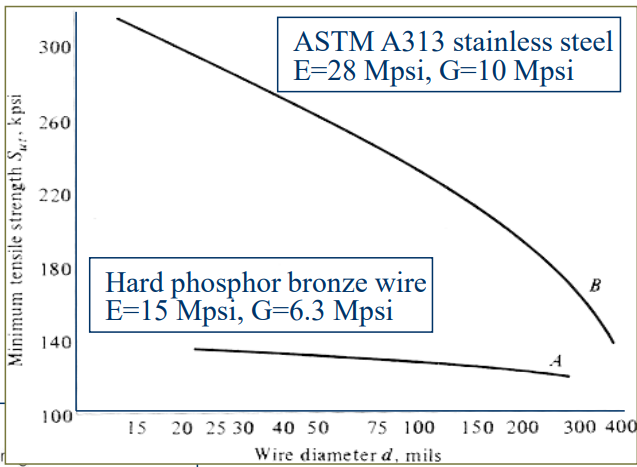
다음 표에는 이 상수들을 알려준다.
스프링을 설계하고 성능을 분석하기 위해서는 비틀림 항복강도가 필요하지만, 스프링 재료는 보통 인장강도만을 시험한다. 그 이유는 그렇게 하는 것이 쉽고 경제적이기 때문이다. 비틀림 항복강도에 대한 매우 대략적인 추정은 인장 항복강도가 인장강도의 $60 \sim 90 \%$라는 가정으로부터 얻을 수 있다. 변형에너지 이론(distortion-energy theory)을 적용하면 비틀림 항복강도($S_{xy} = 0.577S_y$)를 얻을 수 있다. 강에 대해서는 다음과 같은 결과를 얻는다.

최대 허용 비틀림 응력(suggested by Joerres)는 다음과 같다.
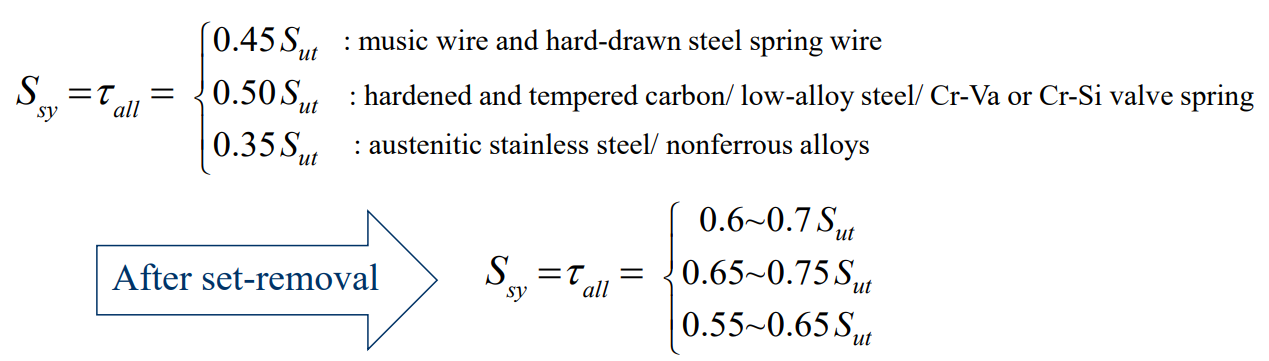
Samonov는 허용응력에 대해 논의하면서 고인장 스프링강에 대해 다음과 같은 식을 제시하였다.
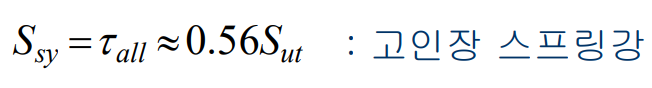
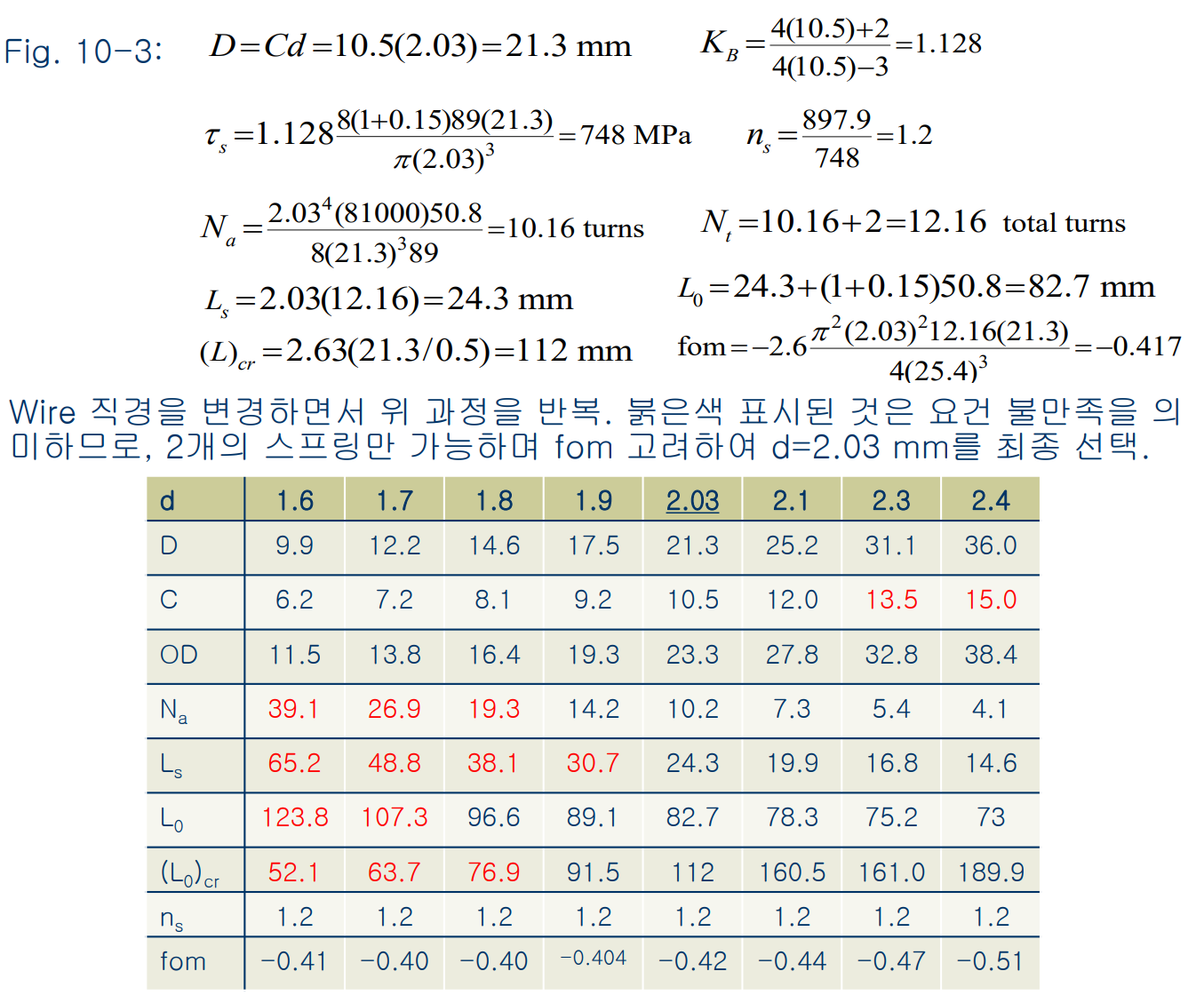
다음 예제를 보자

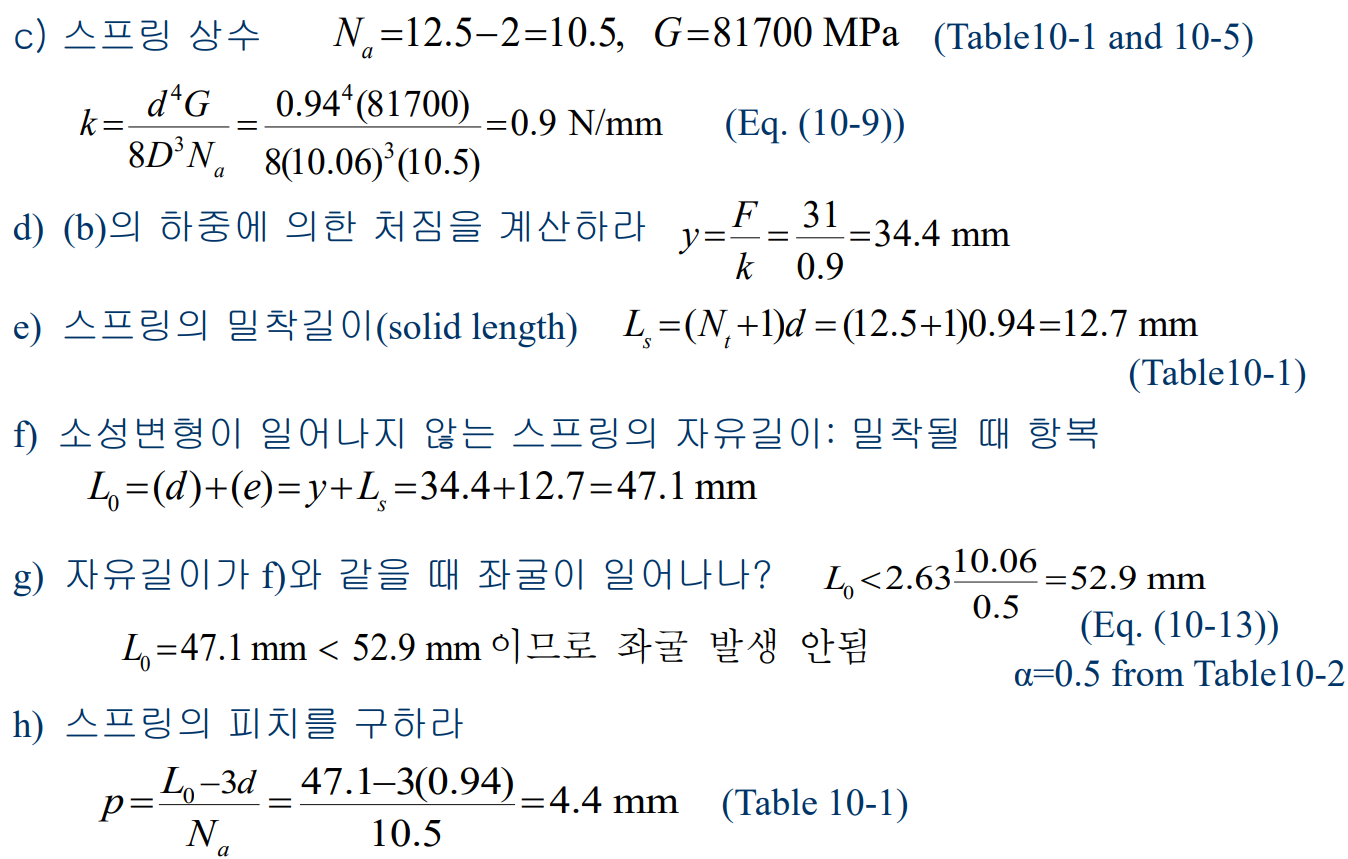
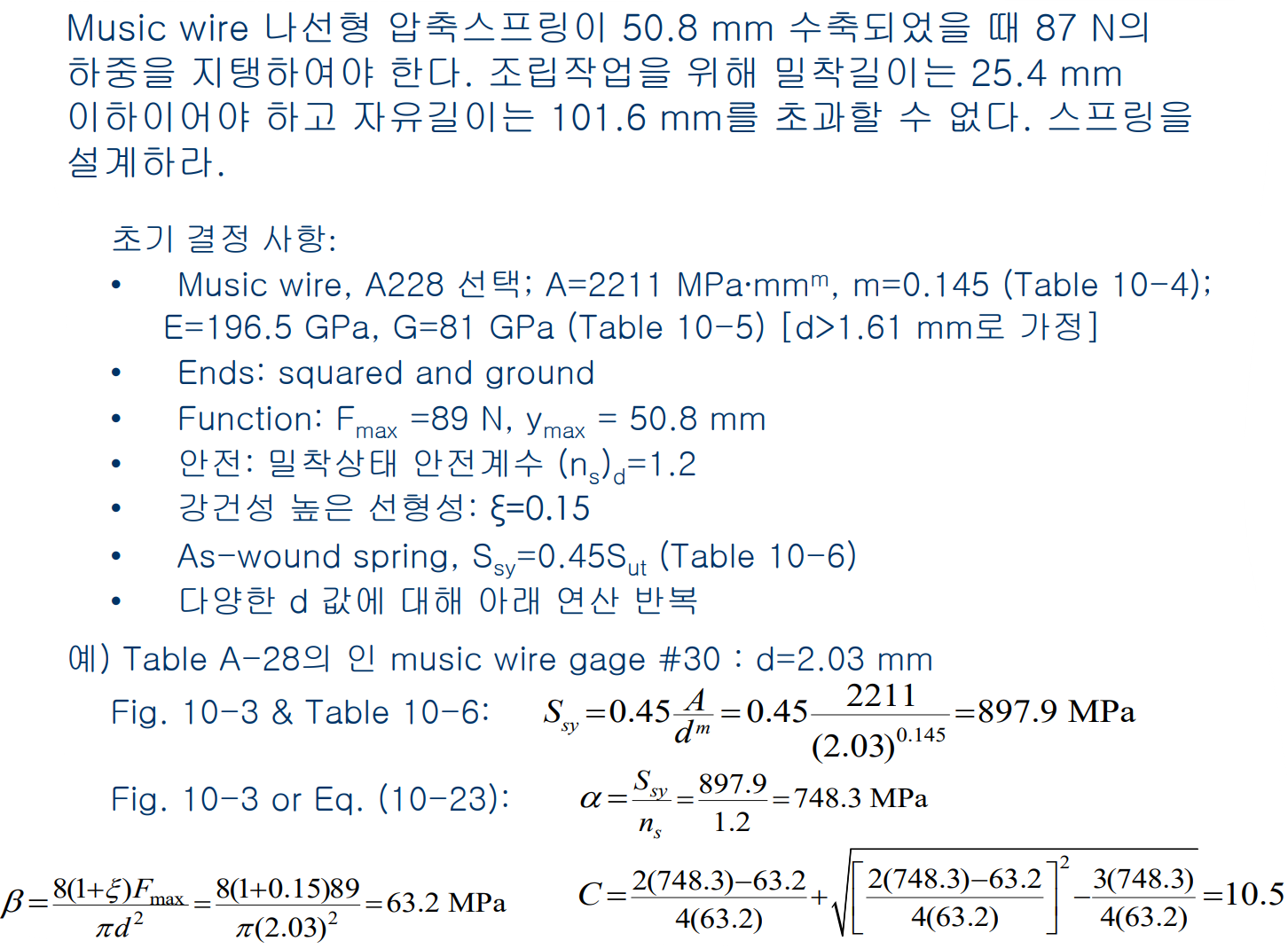
나선형 압축스프링의 설계 - 정하중
스프링을 설계시 권장되는 조건은 다음과 같다.

최대 작동력은 $F_{\mathrm{max}} \leq \frac{7}{8} F_s$로 제한되어야 한다. 이에 대해 Fractional overrun to closure $\xi$을 다음과 같이 정의할 수 있다.
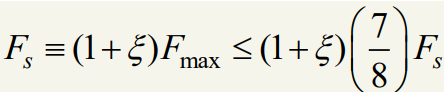
설계전략

다음 예제를 보자
헬리컬 스프링의 임계 진동수
스프링 서지(spring surge)는 스프링을 따라 파동이 왕복하며 전파하는 현상이다. 스프링의 병진 진동에 대한 식은 다음과 같은 파동에 관한 식이다.

2개의 편평하고 평행한 사이에 위치하고 있는 스프링에 대한 조화(harmonic) 고유진동수는 radian per second 단위로 다음과 같이 주어진다.
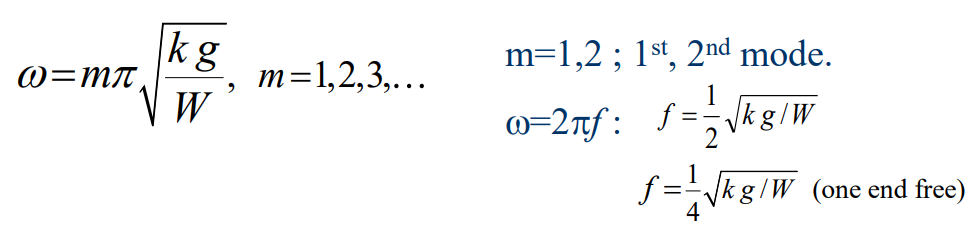
헬리컬 스프링의 유효부분의 무게는 다음과 같다.
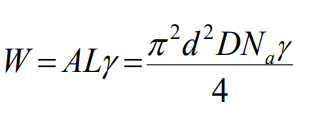
여기서 $\gamma$는 비중이다.
조화파(harmonics)를 동반하는 공진을 방지하기 위해서는, 기본 임계 진동수가 스프링에 가해지는 힘이나 운동의 진동수보다 $15 \sim 20$배 정도 커야 한다. 진동수가 충분히 크지 않을 경우에는 $k$를 증가하거나, $W$를 감소하도록 스프링을 재설계하여야 한다.
압축스프링에서 작용하는 피로하중
스프링은 거의 항상 피로하중에 노출되어 있다. 즉, 무한 수명에 맞춰 설계되어야 한다.
스프링강의 비틀림 내구한도에 대한 가장 양호한 데이터는 Zimmerli가 보고한 것이다. 그는 스프링 치수, 재료, 인장 강도는 10mm 미만의 치수를 갖는 스프링강의 내구한도(무한수명의 경우에만)에는 전혀 영향을 미치지 않는다는 것을 발견하였다. 교번 및 평균 응력은 직경이 10mm 미만의 모든 스프링에 대해 다음 조건을 적용할 수 있다.
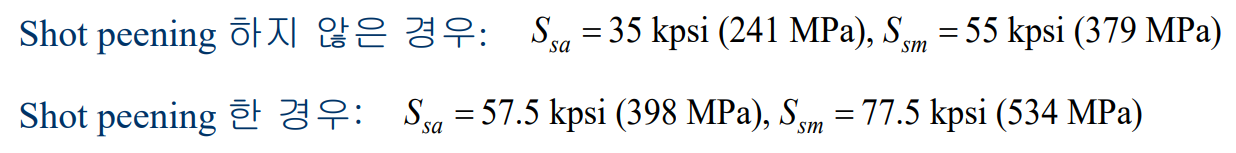
다음 예를 보자.

스프링에 노치가 없으며 표면이 매우 부드러운 경우 파손 기준은 비틀림 피로에 대한 Sines 파손 기준이라 알려져 있다.
이 실험에서 비틀림 파열 계수 $S_{su}$는 다음과 같다.
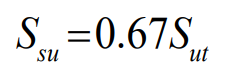
가장 불리한 상태인 예하중이 존재하지 않는 상태, 즉 $\tau_{\mathrm{min}} = 0$인 경우 교번하중 형태의 피로하중과 전단응력 진폭과 편균 전단응력은 다음과 같이 정의된다.
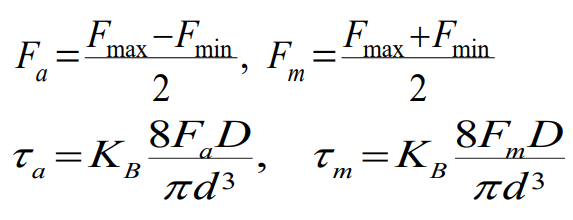
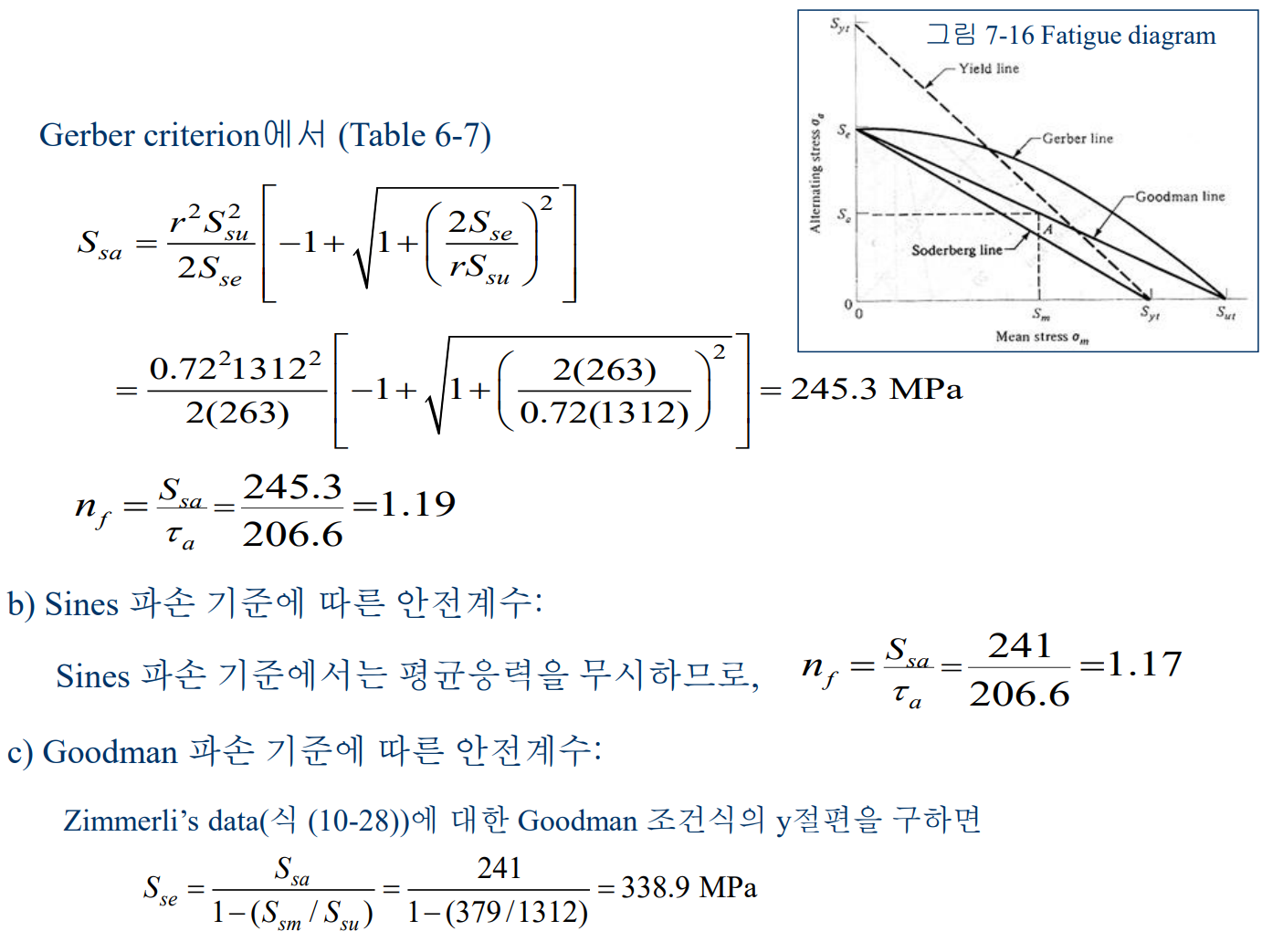
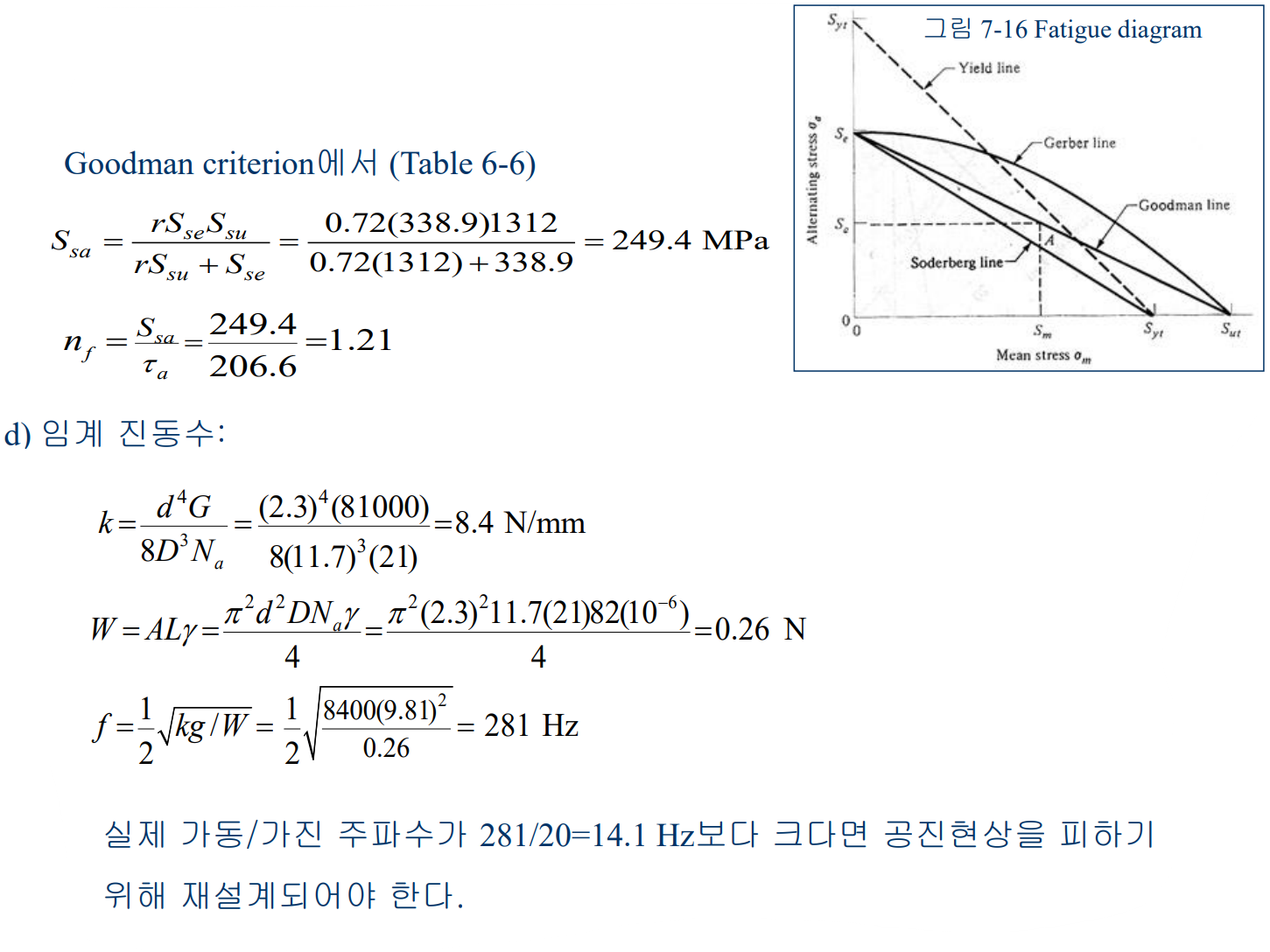
다음 예제를 보자.

인장 스프링
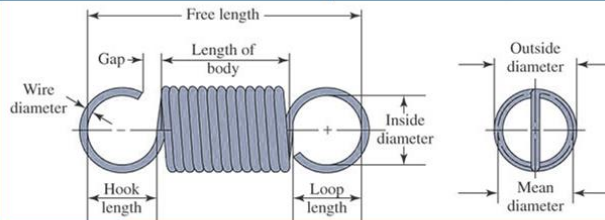
인장 스프링은 인장하중을 전달하는 점에서 압축스프링과 다르다. 또한 인장스프링은 지지점으로부터 스프링의 몸체로 하중을 전달하는 어떤 수단이 필요하며, 스프링몸체는 초기 인장부하가 주어진 상태로 감겨 있다. 하중전달은 나사플러그나 회전고리를 통해 이루어진다. 이것들은 모두 최종적으로 제품의 가격을 상승시키므로, 보통 다음과 같은 방법 중 한 가지를 사용한다.
다음 그림을 보자.
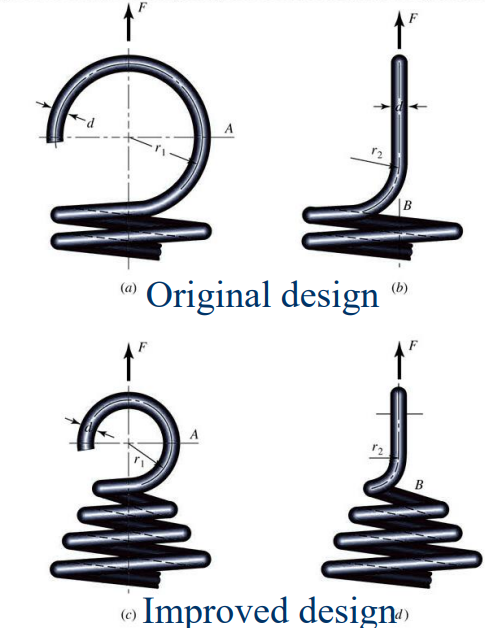
A점에서의 최대 인장응력과 B점에서의 최대 비틀림 응력은 다음과 같다.

인장스프링은 서로 접촉하고 있는 코일로 만들어지므로 밀착 감김(close-wound)이라고 부른다. 스프링 제작자들은 자유길이를 더욱 정확하게 유지하기 위해 밀착 감김 스프링에 어느 정도 초기 인장 만들기를 선호한다. 관련된 하중-변형 곡선은 다음과 같다.
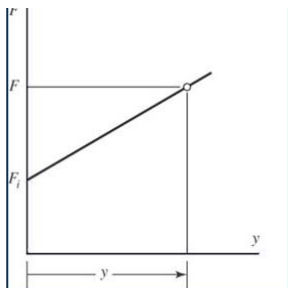
여기서 $y$는 자유길이 $L_0$를 초과하는 인장이며, $F_i$는 스프링이 변형되기 전에 극복해야되는 스프링 내의 초기 인장이다. 하중-변형 관계는 $F=F_i + ky$이다.
여기서 $k$는 스프링 상수이다. 자유길이 $L_0$는 다음과 같이 표현된다.
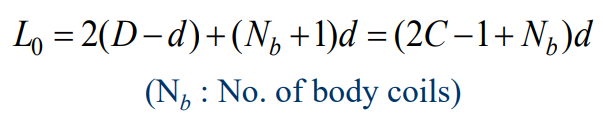
여기서 $D$는 평균 코일지름, $N_b$는 몸체 코일의 수, 그리고 $C$는 스프링 지수이다. 다음 그림의 보통 비틀림 루프에서는 스프링 상수 $k$를 결정할 때 루프의 처짐을 고려한다.
헬리컬 유효 감김수 $N_a$와 동등한 수를 다음과 같이 정의한다.

여기서 $G$와 $E$는 각각 전단 탄성 계수와 인장 탄성 계수이다.
나선형 비틀림 스프링
헬리컬 코일 스프링의 끝부분이 비틀림에 노출되어 있으면, 그 스프링을 비틀림 스프링(torsion spring)이라 부른다. 이 스프링은 헬리컬 코일 인장스프링과 마찬가지로 보통 밀착 감김이지만, 초기 인장은 무시할 만하다. 다음과 같이 단일몸체와 이중몸체의 두 가지 종류가 있다.
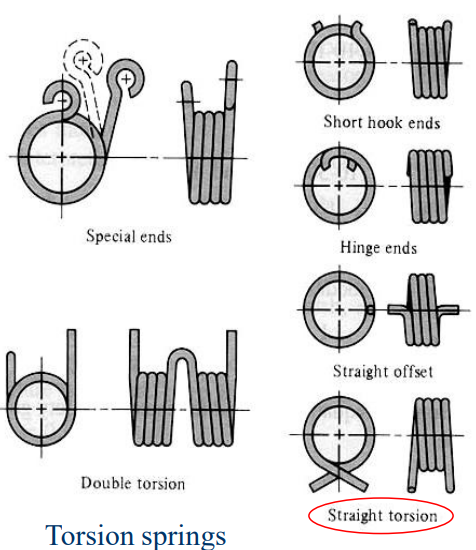
특징은 다음과 같다.

끝부분 위치
비틀림 스프링을 규정할 때에 끝부분은 서로 상대적으로 위치가 규정되어 있어야 한다. 다른 끝에 대한 한쪽 끝의 초기 무부하 상태의 위치를 표현하는 가장 단순한 벙법은 다음과 같이 코일 몸체에 존재하는 부분감김수 $N_p = \beta / 360^{\circ}$를 정의하는 각도 $\beta$를 사용하는 것이다. 스프링 제작자는 끝부분 사잇각 $\alpha$를 자주 사용한다.
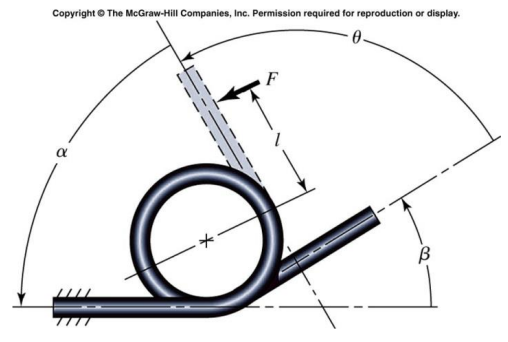
몸체의 감김수 $N_b$는 자유 스프링 몸체의 감김수를 센 것이다. 몸체의 감김수는 초기위치각 $\beta$와 다음과 같은 관계를 갖고 있다.
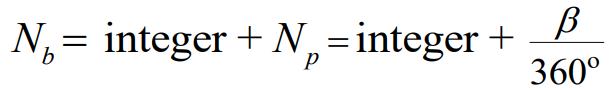
여기서 $N_p$는 부분 감김수를 나타낸다.
굽힘응력
굽힘응력은 다음과 같은 형태로 나태난 굽은 보 이론으로부터 구할 수 있다.
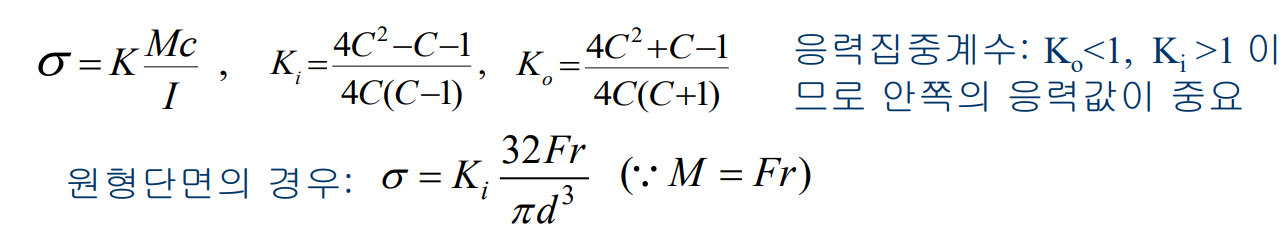
처짐과 스프링 상수


정적 강도
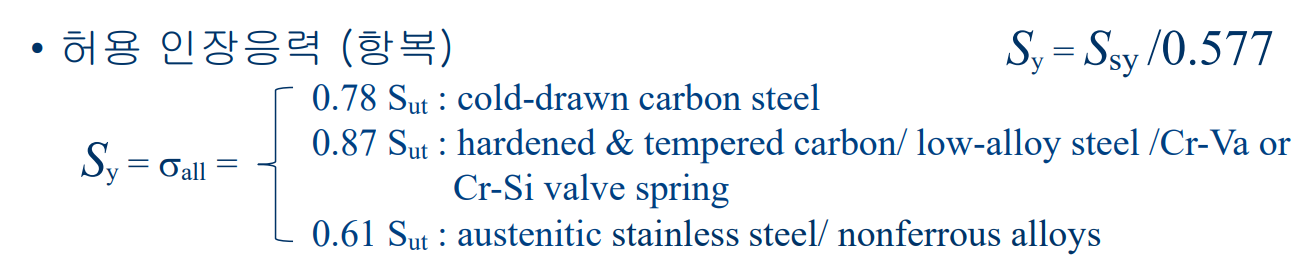
피로 강도
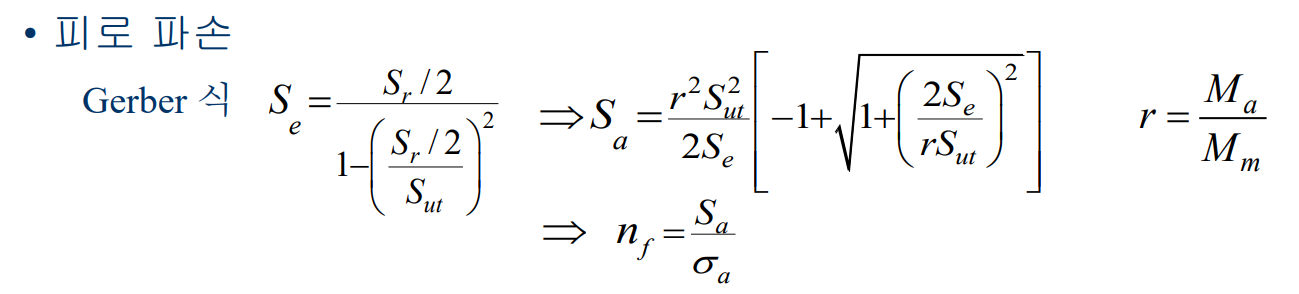
다음 예제를 보자.


접시 스프링
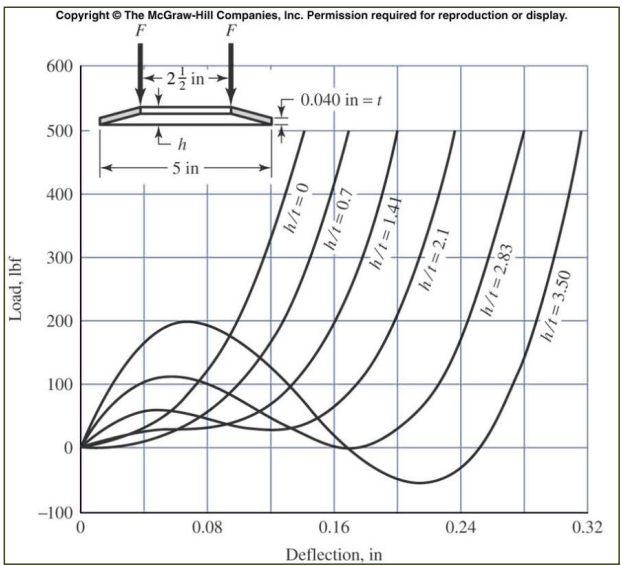
위 그림에 포함된 그림은 보통 접시 스프링(Belleville spring)이라 불리는 원뿔디스크 스프링의 단면을 보여주고 있다.
접시 스프링의 특성은 다음과 같다.

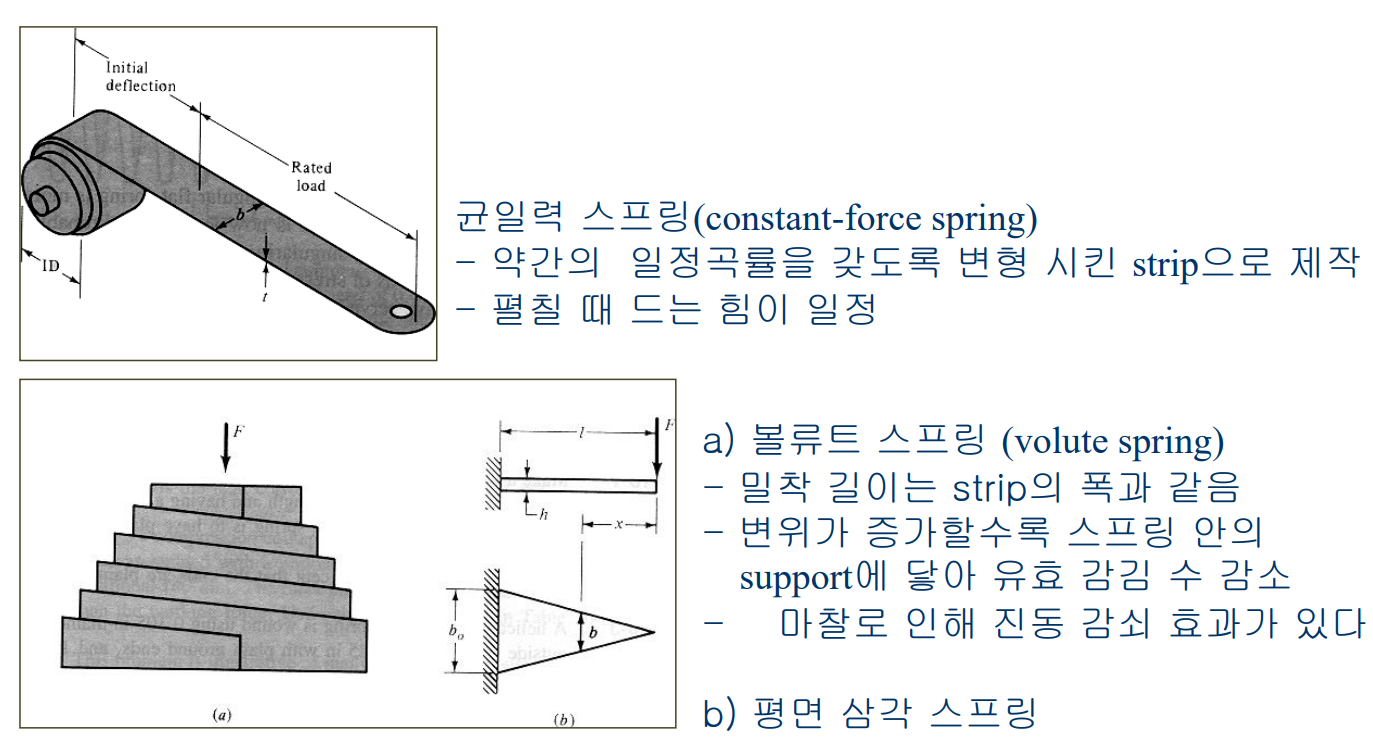
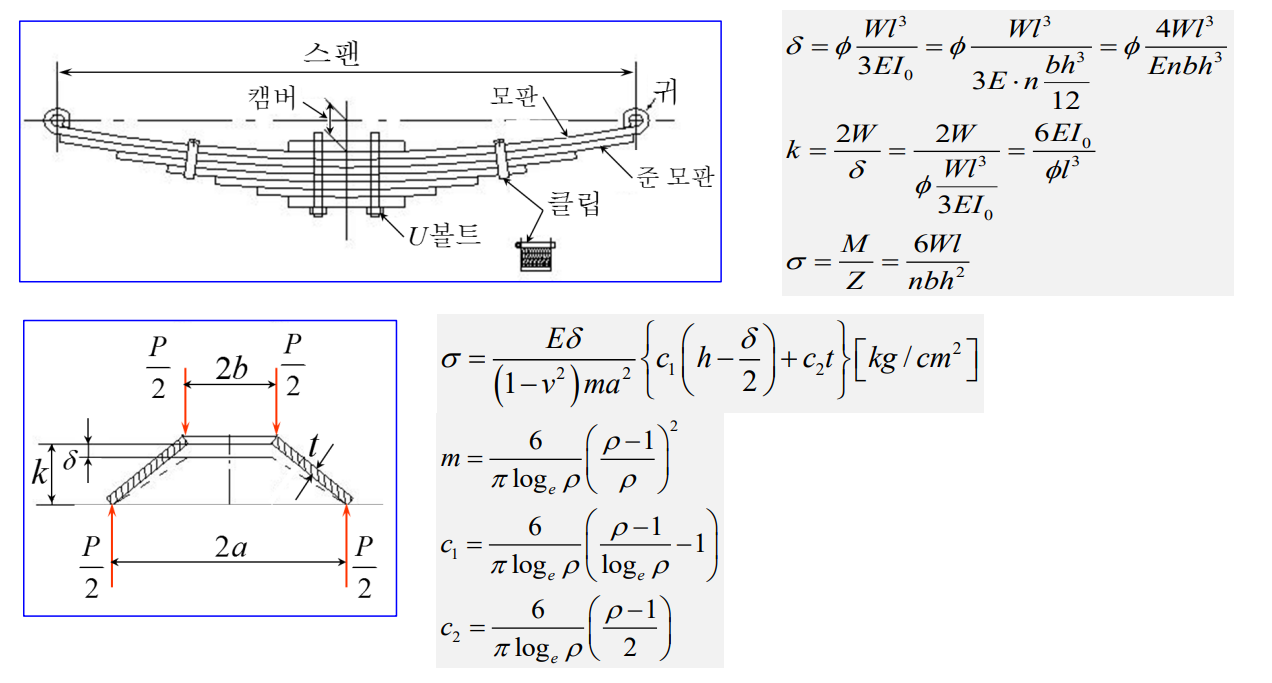
기타 스프링
댓글남기기