2장 재료

재료강도와 강성

표준 인장시험

　응력-변형률선도(stress-strain diagram)를 그리는 방법에는 두 가지가 있다.

공칭 응력-변형률선도
　하중 $P$를 시편의 원래 단면적 $A_0$로 나눔으로써 공칭응력(nominal stress) 또는 공학응력(engineering stress)을 구할 수 있다. 이러한 계산은 시편의 단면적 전체와 표점거리 전체에 걸쳐서 응력이 일정하다고 가정한 것이다.

$\sigma = \frac{P}{A_0}$

　마찬가지로, 공칭변형률(nominal strain) 또는 공학변형률(engineering strain)은 스트레인 게이지로부터 바로 읽거나, 시편의 표점거리의 변화량을 원래의 표점거리 $L_0$로 나누어 구할 수 있다. 여기서 변형률은 표점 사이의 영역 전체에 걸쳐서 일정하다고 가정한다.

$\epsilon = \frac{l - l_0}{L_0}$

　종축을 응력으로 하고 횡축을 변형률로 하여, 응력과 변형률을 그래프로 그리면 공칭 응력-변형률선도(conventional stress-strain diagram)가 된다.

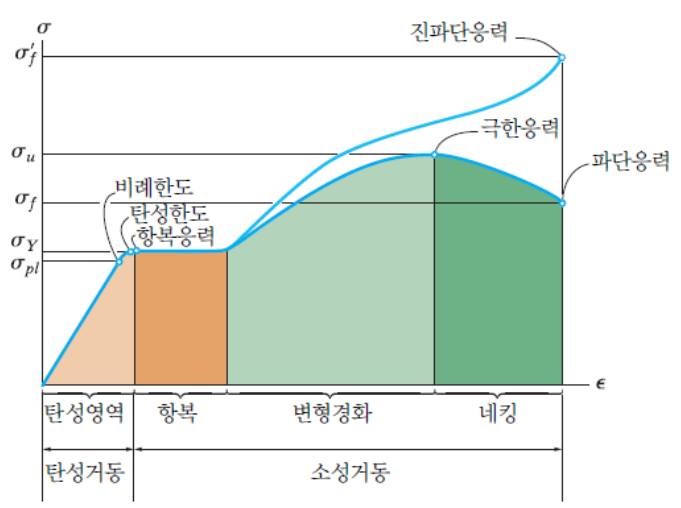
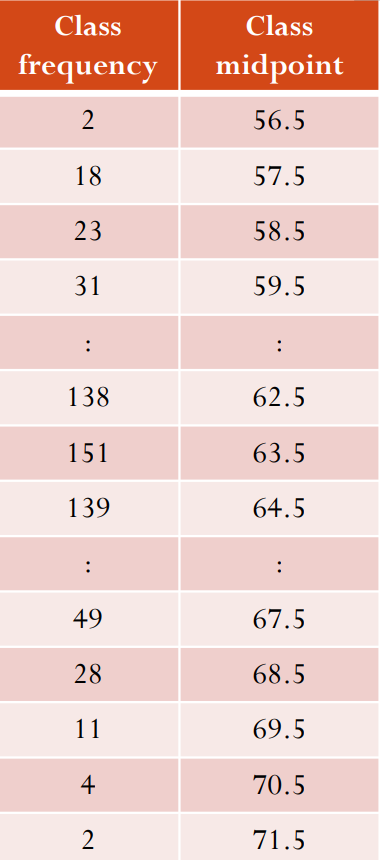
　탄성거동은 변형률이 위 그림의 밝은 주황색 영역에 있을 때 나타난다. 이 영역의 대부분에 걸쳐 응력-변형률선도는 직선이고, 따라서 이 영역에서 응력과 변형률은 비례한다. 다른 표현으로는, 이 영역의 재료거동을 선형탄성(linearly elasric) 이라고 한다. 이러한 선형 관계가 끝나는 가장 큰 응력 값을 비례한도(proportional limit)라 하고 $\sigma_{pl}$로 표시한다. 응력이 비례한도를 약간 넘어서면, 재료가 아직은 탄성적으로 거동하지만 선도가 휘어지고 평평해진다. 이러한 현상은 응력이 탄성한도(elastic limit)에 이르기까지 계속된다. 이 점에 이를 때까지는, 하중을 제거하면 시편이 원래이 상태로 돌아간다.
　탄성범위 내에서 인장시편에 대한 Hooke의 법칙은 다음 식처럼 표현된다.

$\sigma = E\epsilon$

　여기서 상수 $E$는 Young 계수또는 탄성 계수이다.
　탄성한도를 넘어서 응력을 더 증가시키면 재료는 이에 견디지 못하고 영구적으로 변형하게 된다. 이러한 거동을 항복(yielding)이라 하는데, 이는 위 그림의 어두운 주황색 영역에 해당된다. 항복을 초래하는 응력을 항복응력(yield stress)또는 항복점(yield point)이라 하고 $\sigma_Y$로 표시하며, 이 때 발생하는 변형을 소성변형(plastic deformation)이라 한다. 위 그림에서 일단 항복점에 도달하고 나면 하중이 전혀 증가하지 않아도 시편은 계속 늘어난다. 재료가 이와 같이 평평한 선도 상에 있을 때, 재료는 완전소성(perfectly plastic)상태라고 한다.
　항복이 끝나면 시편이 더 큰 하중을 지탱할 수 있게 되는데, 이때 선도는 계속 상승하다가 점점 평평해져서 최대 응력값인 극한응력(ultimate stress, 인장강도, tensile strength) $\sigma_u$에 도달하게 된다. 이와 같이 항복 후 응력-변형률선도가 상승하는 현상을 변형경화(strain hardening)라 한다.
　인장시험 전체에 걸쳐서 시편의 길이가 늘어남에 따라 그 단면적은 감소하는데, 극한응력에 이를 떄까지는 시편의 단면적 감소가 표점거리 전체에 결쳐서 대체로 균일하다. 그러나 극한응력에 이르렀을 때부터 시편의 단면적은 국부적인 영역에서만 감소하기 시작한다. 결과적으로, 시편이 더 늘어남에 따라 “목(neck)”이 생긴다. 네킹(necking)에 따른 응력-변형률성도는 위 그림의 어두운 녹색 역역에 해당된다. 여기서 응력-변형률선도는 아래도 휘어지고, 이는 시편이 파단응력(fracture stress) $\sigma_f$를 받아 끊어질 때까지 계속된다.

진 응력-변형률선도
　응력과 변형률을 계산할 때, 하중이 측정되는 순간에 측정한 시편의 실제 단면적과 길이를 사용할 수도 있다. 이렇게 측정되는 응력과 변형률값을 진응력(true stress) 및 진변형률(true strain)이라 하고, 이 값들로 표시한 응력-변형률선도를 진 응력-변형률선도(true stress-strain diagram)라 한다. 변형률이 작을 때는 공칭 $\sigma$-$\epsilon$ 선도와 진 $\sigma$-$\epsilon$ 선도가 거의 동일하다. 이 두 선도의 차이는 변형률이 상당히 커지는 변형경화 영역에서부터 나타나기 시작하여, 네킹영역에서는 그 차이가 커진다. 네킹영역의 진 $\sigma$-$\epsilon$ 선도를 보면, 진응력은 계속 증가하여 진파단응력$\sigma^{\prime}_f$에 이르는 것을 알 수 있다.
　진응력과 진변형률은 다음과 같이 구할 수 있다.

$\epsilon = \int^{l}_{l_0} \frac{dl}{l} = \ln \frac{l}{l_0}$, 　$\sigma = \frac{P}{A}$

　위 와 같이 표준 인장시험을 통해 재료의 여러 특성 값을 획득할 수 있다.

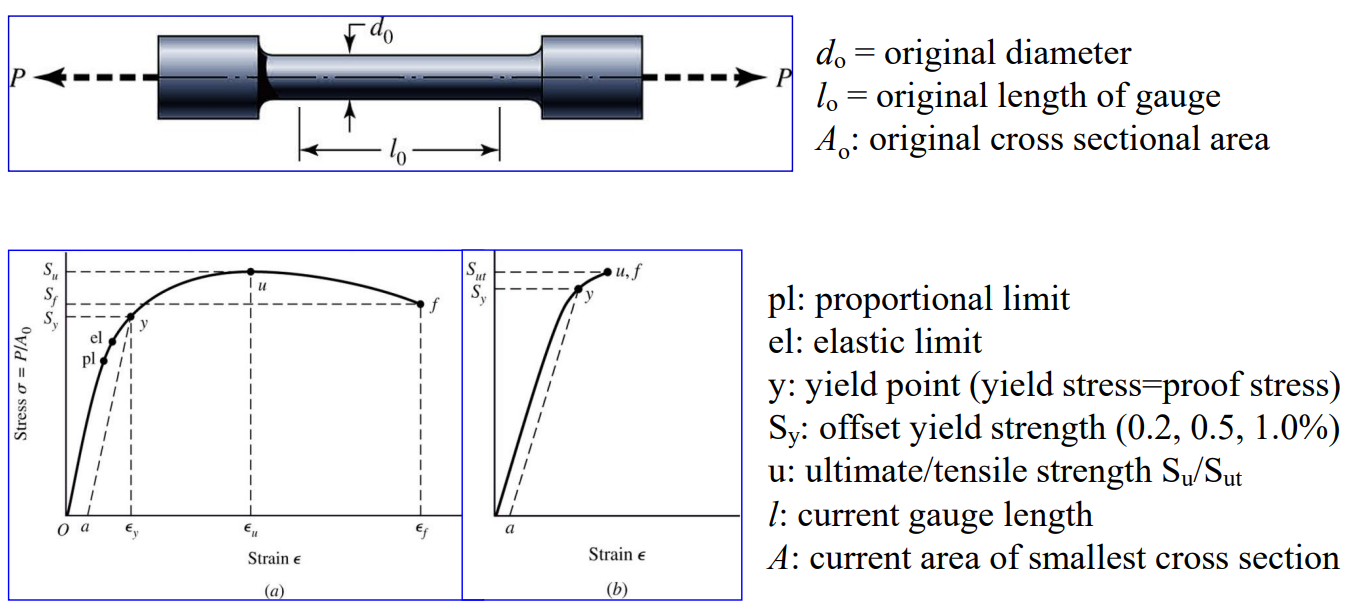
　공칭 응력-변형률성도에서 파단응력$S_f$는 극한응력$S_u$보다 작음을 알 수 있고 진 응력-변형률선도에서 파단응력$\sigma_f$는 극한응력$\sigma_u$보다 큼을 알 수 있다.

압축시험

연성재료와 취성재료의 응력-변형률 거동 　재료는 응력-변형률 거동의 특성에 따라 연성재료와 취성재료로 분류된다.
　파단되기 전에 큰 변형률을 받을 수 있는 재료를 연성재료(ductile material)라 한다. 연성재료들은 충격이나 에너지를 많이 흡수할 수 있고 과하중이 작용할 때 파괴에 앞서 큰 변형을 보여주기 때문에, 엔지니어들은 설계에 있어 연성재료를 많이 선택한다.
　파단 전에 항복 현상이 전혀 또는 거의 일어나지 않는 재료를 취성재료(brittle materials)라 한다. 다음은 취성재료의 한 예이다.

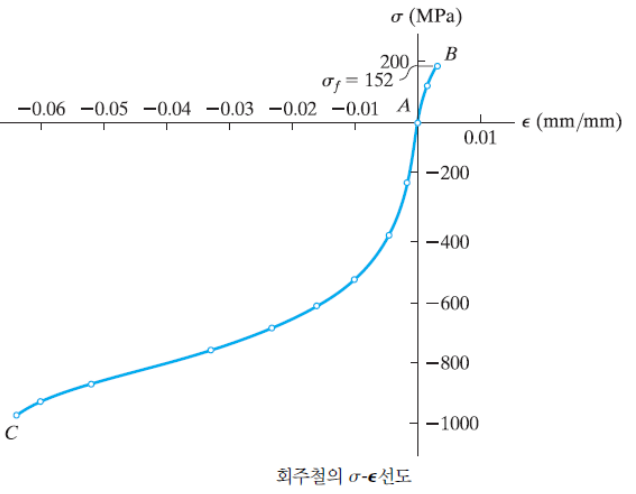
　회주철과 같은 취성재료는 인장 하중에 비해 압축 하중에 훨씬 더 잘 견딜 수 있다. 압축력이 경우 시편 내의 균열 등이 닫혀지고, 하중이 증가함에 따라 변형률이 커지면서 재료가 옆으로 볼록하게 나오고 좌굴 발생에 유의해야 한다. 취성재료의 압축 시험에서는 극한인장강도($S_{ut}$)는 극한압축강도($S_{uc}$)와 같지 않지만 연성재료는 거의 같다.

비틀림시험

　비틀림시험은 토크-비틀림각 커브로부터 여러 특성 값을 구한다. 탄성범위 내에서 다음을 만족한다.

$\theta = \frac{Tl_0}{GJ}$($G$: 전단탄성계수),　$\tau_{max} = \frac{Tr}{J} = \frac{Gr}{l_0}\theta$

　항복이 발생한 후 다음을 만족한다.

$S_{sy} = \frac{T_yr}{J}$, 　$S_{su} = \frac{T_ur}{J}$

　위 식에서 $S_{sy}$는 Torsional yield strength를 의미하고 $T_y$는 항복점에서의 토크, $S_{su}$는 Modulus of rupture, $T_u$는 선도에서 토크의 최대 값을 의미한다.

물성치의 통계적 성질

　다음 예를보자.

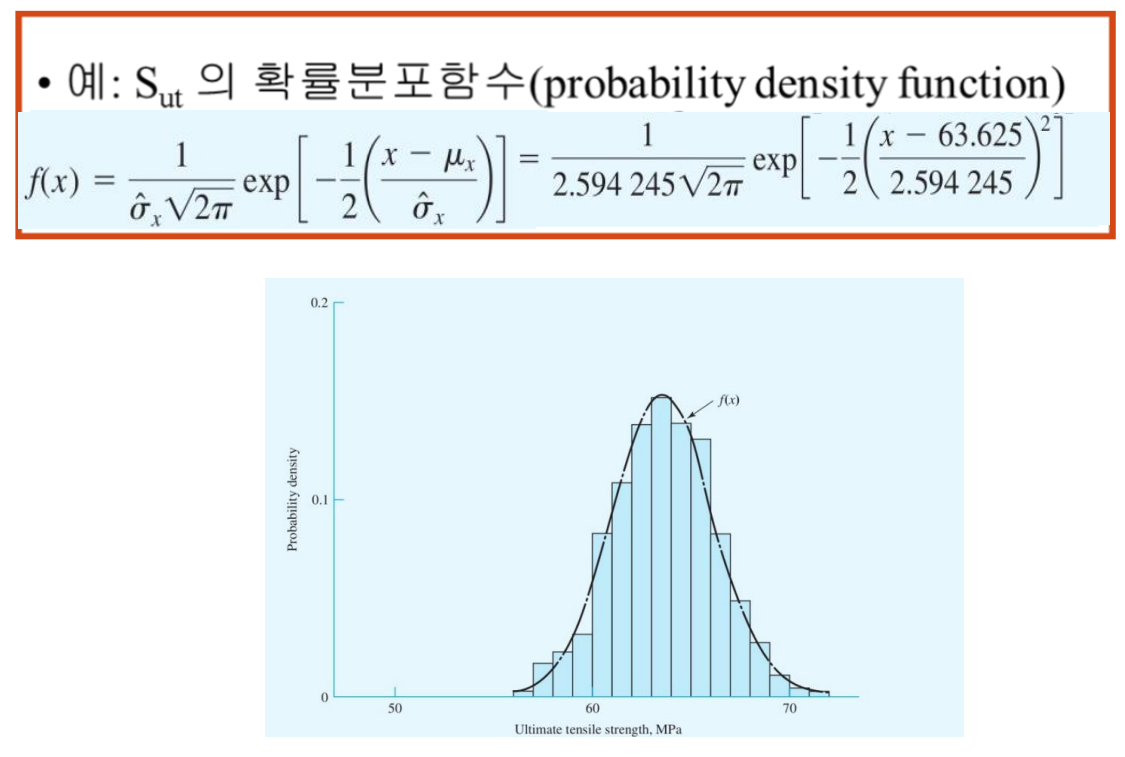
　재료성질 표를 보면 보통 평균값이나 $99^{th}$ percentile의 값을 사용한다. 재료성질 시험을 요청할 때, 분포의 확률적 특성을 알기 충분하도록 데이터를 요구해야 한다.

강도와 냉간 가공(strength and cold work)

　냉간 가공은 재료의 재결정온도 아래에서 소성변형을 일으키는 가공법이다($\leftrightarrow$ 열간 가공(hot working)). 냉간 또는 열간 가공애 따라 재료성질의 변화가 다르다.
　변형률경화(strain-hardening)은 하중이 제거된 상태의 재료는 연성이 저하($\epsilon_f$)되는 성질이다.

　연성의 척도(%RA, reduction in area)는 다음과 같다.

$R = \frac{A_0 - A_f}{A_0} = 1 - \frac{A_f}{A_0}$

　냉간가공도(cold-work factor) $W$는 다음과 같다.

$W = \frac{A_0 - A^{\prime}_i}{A_0} \approx \frac{A_0 - A_i}{A_0}$($A^{\prime}_i$: unloading 후 단면적), $A^{\prime}_i = A_0(1-W)$

　냉간가공 후 피로강도 및 탄성영역 증가 효과에 의해 새로운 강도값을 구할 수 있다.

u점 보다 좌측($\epsilon_i \le \epsilon_u$): $S^{\prime}_y = \frac{P_i}{A^{\prime}_i} = \sigma_o \epsilon^m_i$(elastic strain 무시), $S^{\prime}_u = \frac{P_u}{A^{\prime}_i} = \frac{S_uA_o}{A_o(1-W)} = \frac{S_u}{1-W}$

($\because A^{\prime}_i < A_o, P_u=S_uA_o$)

u점 보다 우측($\epsilon_i > \epsilon_u$) : $S^{\prime}_u \approx S^{\prime}_y \approx \sigma_o\epsilon^m_i$

　다음 예제를 보자.

경도

　경도는 재료가 뾰족한 도구의 누름에 저항하는 정도이다. 경도는 다음과 같이 구할 수 있다.

Steels: $S_u = \begin{cases} 0.5H_B　\mbox{kpsi} \\ 3.4H_B　\mbox{MPa} \end{cases}$ for $200 \le H_B \le 45$

Cast irons: $S_u = \begin{cases} 0.23H_B - 12.5　\mbox{kpsi} \\ 1.58H_B - 86　\mbox{MPa} \end{cases}$

　경도와 강도는 제한된 영역에서 선형적인 상관성이 있다.

　다음 예제를 보자.

충격 성질(impact properties)

　외력이 가해지는 시간이 구조물의 최저고유진동수의 주기의 1/3보다 짧으면 충격하중(impact load), 길면 정하중(static load)이라 한다.

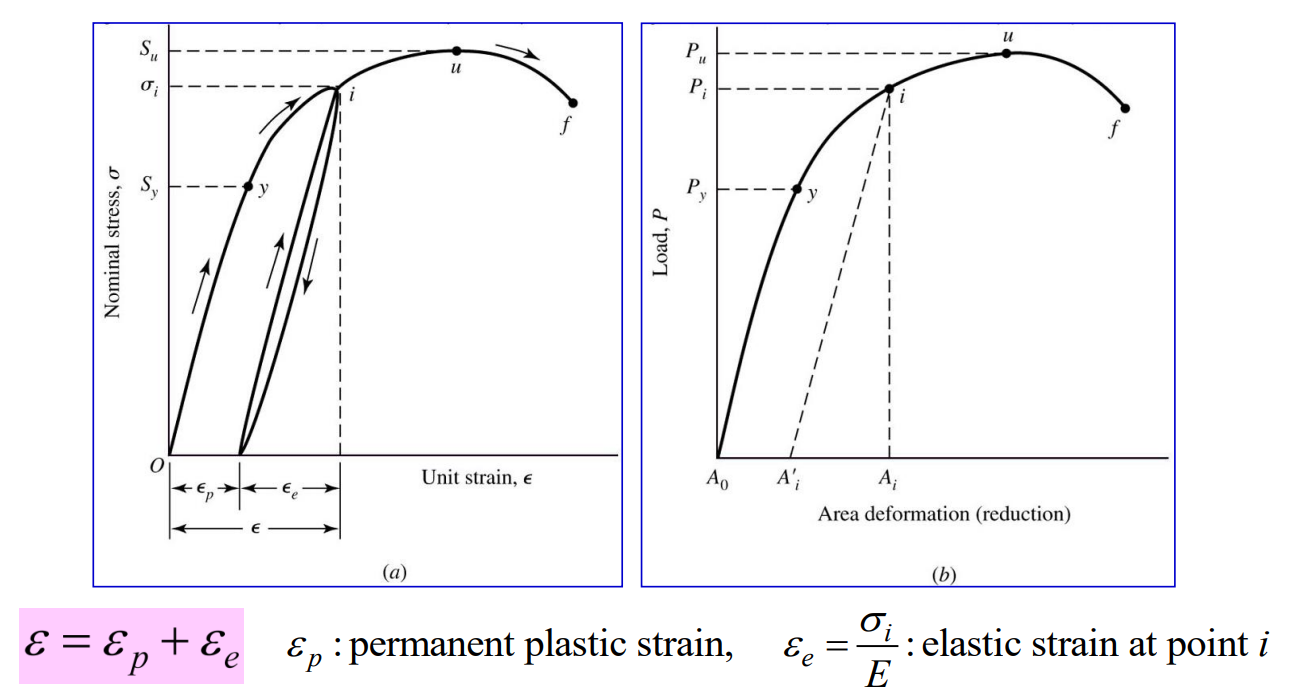
온도효과(temperature effects)

　강도(strength), 연성(ductility, 탄성한계를 넘는 힘을 가함으로써 물체가 파괴되지 않고 늘어나는 성질), 취성(brittleness, 물체가 연성을 갖지 않고 파괴되는 성질)는 사용 온도에 영향을 받는다. 온도 증가에 따라 강도가 감소하고 연성이 증가하여 고온에서는 creep(적은 일정하중에도 시간에 따라 변형 증가)이 쉽게 발생한다. transient temperature(천이온도: 연성에서 취성으로(또는 그반대) 갈때의 온도) 미만에서는 취성파괴가 발생한다. 열처리, 용접 중의 가열/클램핑에 의해서도 재료 성질이 변화한다.