열시스템디자인 학기말 프로젝트
Updated:
배경 및 설계목표
탄소포집저장(CSS: Carbon Capture and Storage)은 지구온난화 및 기후변화의 주범인 이산화탄소를 처리하여 탄소중립을 실현하기 위한 공정이다. 화석연료의 연소를 통해 발생한 과다한 이산화탄소는 다양한 방법으로 포집된 후, 채굴된 유전 또는 가스전의 지하공간에 주입하여 영구 저장된다. 저장공간이 포집장소에 가까운 경우, 기체를 압축하여 배관(pipeline)을 통한 직접 주입이 가능하다. 그러나 많은 경우에 저장공간까지 장거리 수송이 필요하며, 이산화탄소를 높은 밀도로 수송하기 위해 저온의 액체로 액화해야 한다. 특히 에너지 자원을 대부분 수입에 의존하는 우리나라의 경우, 지하 저장공간이 거의 없는 실정이며, 포집된 이산화탄소를 저온의 액체로 액화아여 선박을 통해 해외로 수송해야 한다.
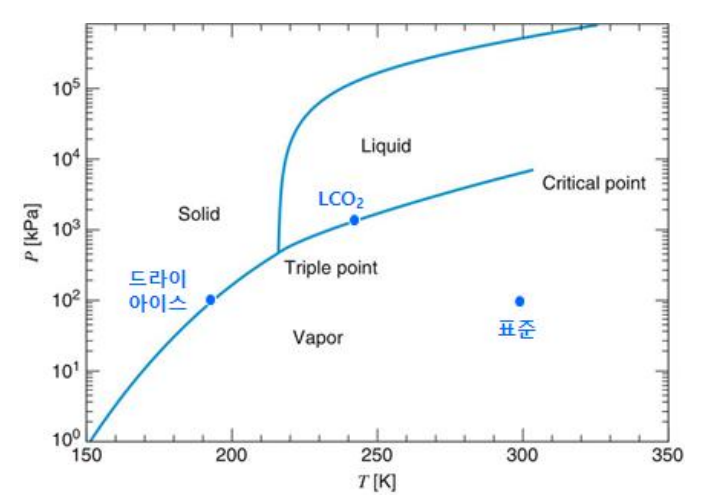
이산화탄소는 삼중점(triple point) 압력이 대기 압력보다 높고, 임계점(critical point) 온도가 실온에 가깝다. 따라서 대기압에서 기체를 냉각하면 바로 고체(드라이아이스)로 동결되며, 액체는 삼중점 이상의 높은 압력과 상온 이하의 낮은 온도에서만 존재한다. 일반적으로 수송을 위한 $\mathrm{LCO}_2$ 의 저장 조건은 “높은 온도”와 “낮은 압력”이 유리하지만, 상경계인 ($-55^{\circ}\mathrm{C}$ , $0.68\mathrm{MPa}$) ~ ($-25^{\circ}\mathrm{C}$ , $1.68\mathrm{MPa}$)을 기준으로 포화 액체 또는 (필요시) 과냉(압축) 액체 상태로 결정된다.
열역학 관점에서 볼 때, 냉동 사이클(Refrigeration Cycle)은 에너지만 출입하는 밀폐(closed) 시스템이지만, 액화 사이클(Liquefaction Cycle)은 기체가 들어와 액체가 나가는 개방(open) 시스템이다.
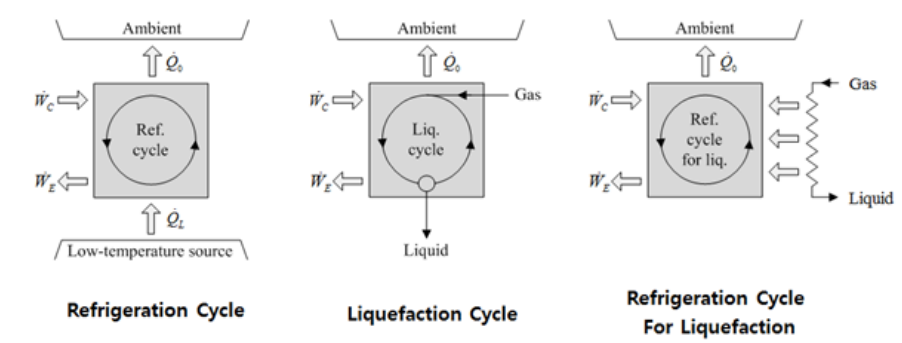
보통의 액화 사이클에서는 액화되는 기체 자체가 압축과 팽창하는 작업유체이지만, 액화용 냉동 사이클은 별도 작업유체(냉매)를 사용하여 액체보다 낮은 온도의 냉동사이클이 상온의 기체 유동을 냉각하여 저온의 액체로 배출하는 구성을 갖고 있다. 두 액화 시스템은 서로 장단점이 존재하는데, CCS용 이산화탄소 액화의 경우, 낮은 운전 압력과 기체 순도의 가변성에서 유리한 냉동용 액화 사이클을 우선적으로 고려한다.
30 Ton/day 급 이산화탄소 액화 플랜트에 적용할 냉동사이클 및 주요 부품이 설계를 목표로 프로젝트를 수행한다. 이를 위해 다음을 수행하고, 그 결과를 구체적이며 정량적으로 제시해야 한다.
- 장거리 선박 수송에 적합한 $\mathrm{LCO}_2$ 의 온도 및 압력 조건 설정
- 주어진 액화에 필요한 열역학적 최소 소비동력 게산
- 냉매 선정 및 2단 압축/팽창 증기압축 냉동사이클의 열역학 설계
- 냉매-$\mathrm{CO}_2$ 열교환기(증발기)의 상세 설계
- 설계한 액화 시스템의 열역학적 평가 및 개선 방향
설계사양 및 제한조건
주위 및 액화 조건
주위 및 액화 조건

냉매 조건
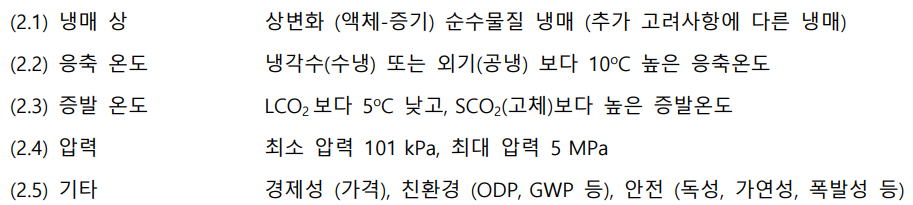
(응축 온도 > 응축 및 후냉각 온도)
냉동 사이클 및 압축 조건

냉매-$\mathrm{CO}_2$ 열교환기 조건

장거리 선박 수송에 적합한 $\mathrm{LCO}_2$의 온도 및 압력 조건 설정
이산화탄소의 액화 방법 및 액화 장치(출원번호: 10-2007-7003795)
<6>에서 액체 이산화탄소를 이송하는 것이 아무 문제가 없거나 비용이 전혀 들지 않는 방법은 아니다. 상기 액체 이산화탄소가 냉각되지 않는다면, 그 것을 액체 상태로 유지하기 위하여 필요한 압력이 높게 되고($60 \sim 80 \mathrm{bar}$), 이는 상기 가압된 저장용기의 필요한 벽 두께를 두껍게 만들며, 그러한 대용량의 냉각되지 않는 액체 이산화탄소를 이송하는 것을 아주 고비용이 되게 한다. 주위 온도 이하에서 액체 이산화탄소를 이송하는 것은 필요한 압력 및 저장용기의 벽 두께를 감소시키지만, 냉각이 필요하므로 비용이 많이 들고, 이산화탄소가 고체 상태를 가지므로 고체 이산화탄소가 형성될 위험이 있다. 고체 이산화탄소가 형성되면, 펌핑하여 이산화탄소를 이송하기가 어렵게 되고, 파이프 또는 밸브의 막힘(blockage)으로 인해 잠제적으로 위험하다.
<7>에서 일반적으로 대규모의 이산화탄소를 이송하기 위하여, 최적 온도는 $-55 \sim -45^{\circ}\mathrm{C}$이 바람직하고, 압력은 $5.5 \sim 7.5 \mathrm{bar}$ ($550 \sim 750 \mathrm{kPa}$)이 바람직하다. 이는 이산화탄소의 상평형도에서 온도, 압력으로 삼중점의 바로 위인 위치이다. 이산화탄소의 삼중점은 $5.2\mathrm{bar}$ 및 $-56.6^{\circ}\mathrm{C}$이다. 보다 낮은 온도와 압력은 드라이아이스를 생성시킬 위험을 높이고, 더 높은 압력은 보다 고가의 저장용기를 필요로 하며, 더 낮은 압력은 기체 또는 고체를 형성시킬 위험을 높인다.
주어진 액화에 필요한 열역학적 최소 소비동력 계산
조건(1.3)의 기체 이산화탄소를 설정된(온도, 압력)의 액체로 액화하는데 필요한 이론적 최소 동력을 게산하라. 열역학 제 1법칙과 제 2법칙을 연립하여 구하는데, 엔트로피 생성이 전혀 없는 이상적인 가역 시스템에 해당하며, 조건 (1.1)의 외기(공냉식) 또는 조건 (1.2)의 냉각수(수냉식)를 흡열원(heat sink)으로 간주한다. 이론적 최소 동력은 설계한 액화시스템을 열역학적으로 평가하는 기준이 된다.
냉매 선정 및 2단 압축/팽창 증기압축 냉동사이클의 열역학 설계
이 액화 시스템에는 $-30^{\circ}\mathrm{C}$ 또는 그 이하의 저온 냉동이 필요하므로, R-134a를 냉매로 사용하기 어렵다. 또한 냉동온도가 낮아질수록 냉매의 압력비가 높아지기 때문에 표준 증기압축 냉동사이클을 적용하기 쉽지 않다. 따라서 이 프로젝트에는 다음과 같이 두 대의 압축기가 직렬로 배치된 2단 압축/팽창 냉동사이클을 적용하며(참고자료 4), 이 냉동사이클에 적합한 냉매를 선정해야 한다.
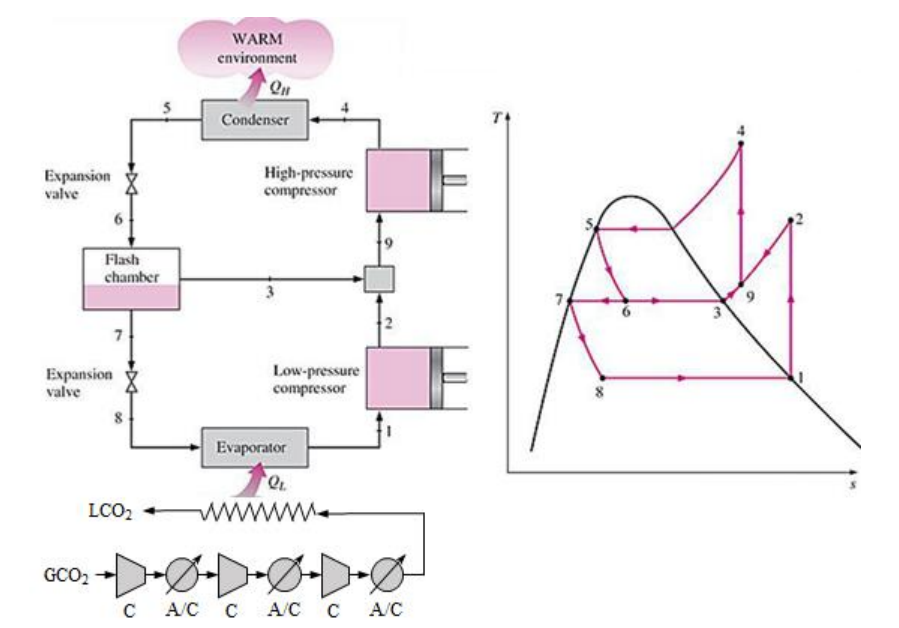
위 그림에서 $\mathrm{GCO}_2$를 압축(C), 냉각(A/C) 과정을 거처 고압의 $\mathrm{GCO}_2$를 만드는데 이 과정은 다음과 같다.
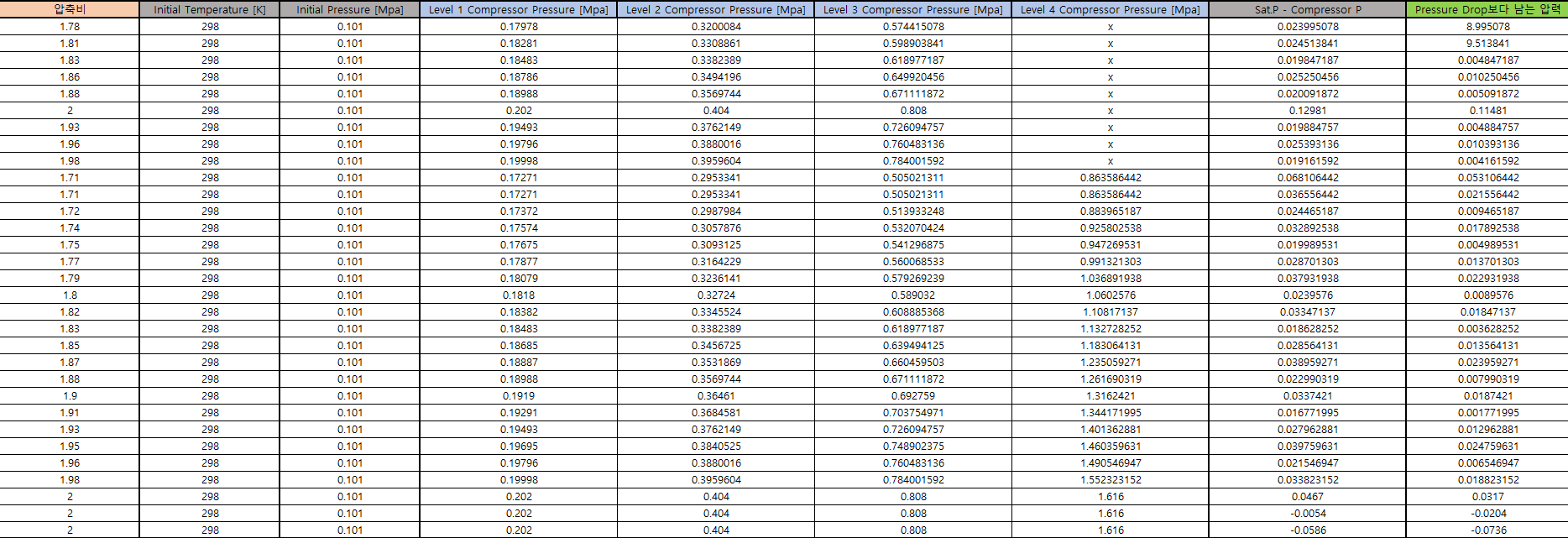
먼저 $1.6 \sim 2.0$의 압축비로 압축을 했을때, 3번째 압축했을 때와 4번째 압축했을때 포화상태 압력에 도달하는 것을 알 수 있다. 왼쪽이 3~4번 압축했을 때 각 온도의 포화상태의 압력이 되는 최대 압축비이다. 따라서 이 압력비로 공냉(냉각 이후 $308\mathrm{K}$)과 수냉(냉각 이후 $303\mathrm{K}$)일 때 각 상태의 엔탈피 차와 유량($0.347\mathrm{kg/s}$)을 곱해 압축과 냉각을 했을 때 들어가는 일을 구할 수 있다. 이 과정에서 FOM(Figure of Merit, 성능 지수)이라는 대안에 비해 장치, 시스템 또는 방법의 성능을 특화하는데 사용되는 수량(quantity)을 사용할 수 있는데, $\mathrm{FOM} = \frac{\mathrm{W_{min}}}{\mathrm{W_R} + \mathrm{W_{CO_2}}}$ 로 정의된다. 따라서 이 과정에서 우리는 $\mathrm{W_{CO_2}}$ 를 알 수 있다.
참고자료4, Multipressure Systems
Introduction
단순 증기 압축 시스템은 two-pressure 시스템이다. two-pressure 보다 많은 시스템은 multistage(다단식의, 단계적인)를, 즉 일을 최소화 하는 compound compression(다단 압축기) 또는 냉매를 주는(?) multi evaporator system, 발생시킨다.
냉매-$\mathrm{CO_2}$ 열교환기(증발기)의 상세 설계
이 액화 시스템의 핵심은 부품은 이산화탄소가 냉매와 열교환하여 액화되는 열교환기이며, 여기에 대한 상세설계가 필요하다. 이 열교환기는 냉동 사이클의 증발에 해당하며, 다양한 종류의 산업용 열교환기가 적용가능한데, 다음과 같은 단위 제원의 판-핀 열교환기(plate-fin heat exchanger)를 선정한다.
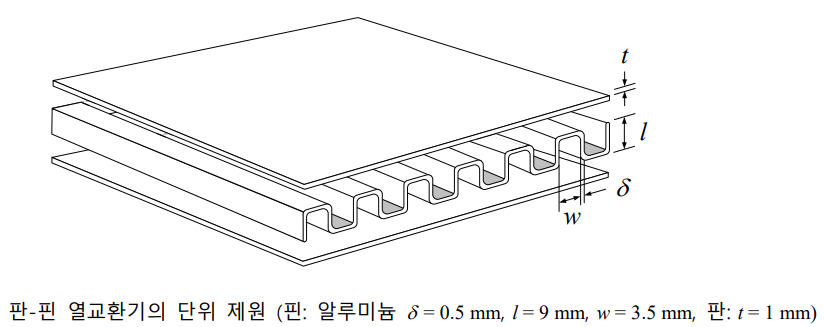
열교환기를 단순한 직육면체 형상으로 간주하고, 그 크기를 결정하라. 즉, 유동 수직방향의 단면적 $W$(폭) $\times$ $H$(높이), 그리고 수평 유동방향 길이 $L$(m)을 각각 결정하라. 각 유동의 수력직경, Re 수, Nu 수, 핀효율, 총합 열전달계수 등을 구하고, 구간별 LMTD 방법 또는 유용도-NTU 방법을 적용하여 필요한 열교환 면적을 계산하는 단계를 거처야 한다.
조건(4.2)$\sim$(4.4)에 판의 개수와 길이를 결정하라. $\mathrm{CO_2}$의 액화 과정은 입구의 과열 증기가 포화 증기로 냉각되는 과정과 포화 증기가 액체로 응축되는 과정으로 구성되며, 냉매의 증발 과정은 포화상태에서 열을 흡수하여 등온과정으로 간주된다. 이 설계에는 내부 유동과 외부 유동에 대한 각각의 대류 열전달계수를 포함한 총합 열전달계수가 필요하며, 구간별 LMTD 방법 또는 유용도-NTU 방법 등을 적용하여 열교환기의 기하학적 사양을 제시해야 한다. 두 유체의 온도 분포를 그래프로 나타내서, 최소 온도차 조건이 만족됨을 반드시 보여야 한다.
#include <iostream>
#include <cmath>
using namespace std;
class Properties {
public:
double Temperature;
double Pressure;
double Densiy;
double Enthalpy;
double C_p;
double Therm_Cond;
double Viscosity;
double Prandtl;
};
// 열교환기 사이즈
const double w = 0.0035; // [m]
const double l = 0.009; // [m]
const double delta = 0.0005; // [m]
const double t = 0.001; // [m]
const double k_al = 220; //[W/m*K]
// 물성치 계산 함수
double Re(double m, double vis, double D); // 질량유량, 점도, N의 개수 입력
double f(double Re); // 마찰계수
double Nu_cond(double f,double Re, double Pr); // 내부 난류유동 Nu, 마찰계수, Re, Pr 입력
double h_cond(double Nu, double k, double D); // 대류 열전달계수, Nu, k 입력
double E(double Q, double rho_L, double rho_G, double Bo);
int main() {
// 질량 유량 [kg/s]
const double m_dot_CO2 = 0.347;
const double m_dot_R1270 = 0.3533;
/*-------------------------------------------------------------------------------------------------------------------------------*/
//CO2i Properties
Properties CO2i;
CO2i.Temperature = 303; //[K] 303K
CO2i.Pressure = 1.2905799; //[MPa] 1.252MPa
CO2i.Densiy = 23.303; //[kg/m^3]
CO2i.Enthalpy = 499130; //[J/kg*K]
CO2i.C_p = 942.32; //[J/kg*K]
CO2i.Therm_Cond = 17.739 * pow(10, -3); // [W/m*K]
CO2i.Viscosity = 15.291 * pow(10, - 6); // [N*s/m^2]
CO2i.Prandtl = 0.81232;
//GCO2 Properties
Properties GCO2;
GCO2.Temperature = 239; //[K]
GCO2.Pressure = 1.2387; //[MPa] 1.2387MPa
GCO2.Densiy = 32.157; //[kg/m^3]
GCO2.Enthalpy = 436350; //[J/kg*K]
GCO2.C_p = 1092.2; //[J/kg*K]
GCO2.Therm_Cond = 13.443 * pow(10, -3); // [W/m*K]
GCO2.Viscosity = 12.067 * pow(10, -6); // [N*s/m^2]
GCO2.Prandtl = 0.98042;
//LCO2 Properties
Properties LCO2;
LCO2.Temperature = 239; //[K]
LCO2.Pressure = 1.2387; //[MPa] 1.2387MPa
LCO2.Densiy = 1093; //[kg/m^3]
LCO2.Enthalpy = 124790; //[J/kg*K]
LCO2.C_p = 2044.5; //[J/kg*K]
LCO2.Therm_Cond = 149.68 * pow(10, -3); // [W/m*K]
LCO2.Viscosity = 175.29 * pow(10, -6); // [N*s/m^2]
LCO2.Prandtl = 2.3944;
//R1270_8 Properties x=0.0617, x8=0.1958
Properties R1270_8;
R1270_8.Temperature = 236;//236.35; //[K]
R1270_8.Pressure; //[MPa]
R1270_8.Densiy; //[kg/m^3]
R1270_8.Enthalpy = 188450;//[J/kg]
R1270_8.C_p; //[J/kg*K]
R1270_8.Therm_Cond;// [W/m*K]
R1270_8.Viscosity;// [N*s/m^2]
R1270_8.Prandtl;
//R1270_1 Properties x=1
Properties R1270_1; // 0.14662MPa
R1270_1.Temperature = 234;//236.35; //[K]
R1270_1.Pressure = 0.14662; //[MPa]
R1270_1.Densiy = 3.3268; //[kg/m^3]
R1270_1.Enthalpy = 538100;//[J/kg]
R1270_1.C_p = 1379.7; //[J/kg*K]
R1270_1.Therm_Cond = 11.540 * pow(10, -3);// [W/m*K]
R1270_1.Viscosity = 6.6091 * pow(10, -6);// [N*s/m^2]
R1270_1.Prandtl = 0.79017;
//LR1270 Properties x=0
Properties LR1270;
LR1270.Temperature = 235;//236.35; //[K]
LR1270.Pressure = 0.14662; //[MPa]
LR1270.Densiy = 599.44; //[kg/m^3]
LR1270.Enthalpy = 108830;//[J/kg]
LR1270.C_p = 2222.7; //[J/kg*K]
LR1270.Therm_Cond = 132.61 * pow(10, -3);// [W/m*K]
LR1270.Viscosity = 176.01 * pow(10, -6);// [N*s/m^2]
LR1270.Prandtl = 2.9500;
Properties mCO2; // 유용도-NTU에 사용할 평균 물성치
mCO2.Temperature = (CO2i.Temperature + GCO2.Temperature) / 2; //[K]
mCO2.Pressure = (CO2i.Pressure + GCO2.Pressure) / 2; //[MPa]
mCO2.Densiy = (CO2i.Densiy + GCO2.Densiy) / 2; //[kg/m^3]
mCO2.Enthalpy = (CO2i.Enthalpy + GCO2.Enthalpy) / 2; //[J/kg*K]
mCO2.C_p = (CO2i.C_p + GCO2.C_p) / 2; //[J/kg*K]
mCO2.Therm_Cond = (CO2i.Therm_Cond + GCO2.Therm_Cond) / 2; // [W/m*K]
mCO2.Viscosity = (CO2i.Viscosity + GCO2.Viscosity) / 2; // [N*s/m^2]
mCO2.Prandtl = (CO2i.Prandtl + GCO2.Prandtl) / 2;
/*-----------------------------------------------------------------------------------------------------------------*/
printf("N_c N_r CO2 포화기체 과정 Re CO2 포화기체 Re CO2 포화 액체 Re N[개] L[m] W[m] H[m] V[m^3]\n");
for (int i = 2; i < 50; i++) {
for (int j = 2; j < 50; j++) {
/*--------------------------------------------------------------------------------------------------------------------------------------------------------------*/
// cout << endl << "CASE1: RCRC...RC" << endl;
int N_c = 1 + i; // W 영향
int N_r = 1 + j; // H 영향
double W, H;
W = (N_c + 1) * delta + N_c * w;
H = (N_r + 1) * t + N_r * l;
// 수력 직경 [m]
double D = (4 * (l * w * N_c)) / (l * (N_c + 1) + w * N_c);
int N = N_r * N_c; // 전체 관의 개수
double case1_m_dot_CO2 = m_dot_CO2 / (N_r / 2);
double case1_m_dot_R1270 = m_dot_R1270 / (N_r / 2);
// epsilon - NTU
double C_co2 = case1_m_dot_CO2 * mCO2.C_p; // [kg/s] * [J/kg*K] = [W/K]
double epsilon = (CO2i.Temperature - GCO2.Temperature) / (CO2i.Temperature - R1270_8.Temperature);
double NTU = -log(1 - epsilon);
double UA = C_co2 * NTU;
// 대류열전달계수
double Re_mco2 = Re(case1_m_dot_CO2, mCO2.Viscosity, D);
double f_mco2 = f(Re_mco2);
double Nu_mco2 = Nu_cond(f_mco2, Re_mco2, mCO2.Prandtl);
double h_mco2 = h_cond(Nu_mco2, mCO2.Therm_Cond, D); // [W/m^2*K]
// 핀효율
double ml = l * sqrt(h_mco2 / (2 * k_al * t));
double eta_f = tanh(ml) / ml;
// 열교환 모델 UA
double UA_R_temp = h_mco2 * (w * N_c + eta_f * N_c * l);
double L_1 = UA / UA_R_temp;
// 냉매 중간 영역 엔탈피, 건도
double i_x = R1270_1.Enthalpy - m_dot_CO2 / m_dot_R1270 * (CO2i.Enthalpy - GCO2.Enthalpy); // [kJ/kg]
double Quality_x = (i_x - LR1270.Enthalpy) / (R1270_1.Enthalpy - LR1270.Enthalpy);
// 1에서 냉매 열전달 계수
double Re_R_1 = Re(case1_m_dot_R1270, R1270_1.Viscosity, D);
double f_R_1 = f(Re_R_1);
double Nu_R_1 = Nu_cond(f_R_1, Re_R_1, R1270_1.Prandtl);
double h_R_1 = h_cond(Nu_R_1, R1270_1.Therm_Cond, D);
// x에서 냉매 비등 열전달 계수 - R1270
double q_TP = case1_m_dot_R1270 * (i_x - R1270_8.Enthalpy); // 8상태에서 x로 갈때 q
double Bo_TP = q_TP / (case1_m_dot_R1270 * (R1270_1.Enthalpy - LR1270.Enthalpy));
double E_TP_x = E(Quality_x, LR1270.Densiy, R1270_1.Densiy, Bo_TP);
double m_dot_flux_R = case1_m_dot_R1270 / (N_c * w * l);
double h_TP_x_tmp1 = (m_dot_flux_R * (1 - Quality_x) * D) / LR1270.Viscosity;
double h_TP_x_tmp2 = (LR1270.C_p * LR1270.Viscosity) / LR1270.Therm_Cond;
double h_TP_x_tmp = 0.023 * (LR1270.Therm_Cond / D) * pow(h_TP_x_tmp1, 0.8) * pow(h_TP_x_tmp2, 0.4);
double h_TP_x = E_TP_x * h_TP_x_tmp;
/*
// 8에서 냉매 비등 열전달 계수 -R1270
double Quality_8 = 0.0617; // 8에서의 건도
double E_TP_8 = E(Quality_8, LR1270.Densiy, R1270_1.Densiy, Bo_TP);
double h_TP_8_tmp1 = (m_dot_flux_R * (1 - Quality_8) * D) / LR1270.Viscosity;
double h_TP_8_tmp2 = (LR1270.C_p * LR1270.Viscosity) / LR1270.Therm_Cond;
double h_TP_8_tmp = 0.023 * (LR1270.Therm_Cond / D) * pow(h_TP_8_tmp1, 0.8) * pow(h_TP_8_tmp2, 0.4);
double h_TP_8 = E_TP_8 * h_TP_8_tmp;
*/
/*---------------------------------------heatflux---------------------------------------------------------------------*/
double q_TP_2 = case1_m_dot_R1270 * (i_x - R1270_8.Enthalpy);
// 응축 Nu-conds
double h_fg = GCO2.Enthalpy - LCO2.Enthalpy; // [kJ/kg*k]
double h_fg_prime = h_fg + 0.375 * LCO2.C_p * (LCO2.Temperature - R1270_8.Temperature); // [kJ/kg*k]
double Nu_conds_tmp1 = (LCO2.Densiy * 9.81 * (LCO2.Densiy - GCO2.Densiy) * h_fg_prime * pow(D, 3)) / (LCO2.Viscosity * LCO2.Therm_Cond * (LCO2.Temperature - R1270_8.Temperature));
double Nu_conds = 0.555 * pow(Nu_conds_tmp1, 0.25);
double h_conds = h_cond(Nu_conds, LCO2.Therm_Cond, D); // [W/m^2*K]
double q_conds = case1_m_dot_CO2 * (GCO2.Enthalpy - LCO2.Enthalpy); // [kW]
double UA_conds = q_conds / 5; // q_conds / delta T
// 응축 부분 핀효율
double ml_conds = l * sqrt(h_conds / (2 * k_al * t));
double eta_f_conds = tanh(ml_conds) / ml_conds;
// cout << endl << endl << "i_x " << eta_f_conds <<" " << h_conds << endl << endl;
// double UA_conds_temp = w * h_conds * N_c + (N_c - 1) * eta_f_conds * h_conds * l;
// double UA_conds_temp = h_mco2 * (w * N_c + eta_f * N_c * l);
double UA_conds_temp = h_conds * (w * N_c + eta_f * N_c * l);
double L_2 = UA_conds / UA_conds_temp;
double L = L_1 + L_2;
// 8에서 냉매 비등 열전달 계수 -R1270
double Quality_8 = 0.0617; // 8에서의 건도
// case1_m_dot_R1270 = case1_m_dot_R1270 / (W * l);
q_TP = (case1_m_dot_R1270 * (i_x - R1270_8.Enthalpy)) / (W * L);
Bo_TP = q_TP / (case1_m_dot_R1270 * (R1270_1.Enthalpy - LR1270.Enthalpy));
double E_TP_8 = E(Quality_8, LR1270.Densiy, R1270_1.Densiy, Bo_TP);
double h_TP_8_tmp1 = (m_dot_flux_R * (1 - Quality_8) * D) / LR1270.Viscosity;
double h_TP_8_tmp2 = (LR1270.C_p * LR1270.Viscosity) / LR1270.Therm_Cond;
double h_TP_8_tmp = 0.023 * (LR1270.Therm_Cond / D) * pow(h_TP_8_tmp1, 0.8) * pow(h_TP_8_tmp2, 0.4);
double h_TP_8 = E_TP_8 * h_TP_8_tmp;
/*--------------------------------------------------------------------------------------------------------------------------------------------------------------*/
// 냉매 열전달 계수 - R1270
/*--------------------------------------------------------------------------------------------------------------------------------------------------------------*/
double V = W * H * (L_1 + L_2);
double q_conv = (k_al * (N_c * w * t) * 5) / (L_1 + L_2);
if ((L_1 + L_2) < 3 && H - 0.005 < W && W < H + 0.005 && W - 0.005 < H && H < W + 0.005) {
printf("%5d %5d ", N_c, N_r);
printf("%20.0f %16.0f %17.0f ", Re_mco2 / N_c, Re(case1_m_dot_CO2, GCO2.Viscosity, D) / N_c, Re(case1_m_dot_CO2, LCO2.Viscosity, D) / N_c);
printf("%5d %12.4f %12.4f %12.4f %6.4f", N, L_1 + L_2, W, H, W * H * (L_1 + L_2));
cout << " " << "CASE1" << " " << q_conv << endl;
}
/*-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------*/
// RCRCRC...R로 끝날때
// cout << "CASE2: RCRC...RCR" << endl;
int case2_N_r = N_r + 1;
N = case2_N_r * N_c; // 전체 관의 개수
W = (N_c + 1) * delta + N_c * w;
H = (case2_N_r + 1) * t + case2_N_r * l;
D = (4 * (l * w * N_c)) / (l * (N_c + 1) + w * N_c);
double case2_m_dot_CO2 = m_dot_CO2 / (case2_N_r / 2 + 1);
double case2_m_dot_R1270 = m_dot_R1270 / (case2_N_r / 2);
// epsilon - NTU
C_co2 = case2_m_dot_CO2 * mCO2.C_p; // [kg/s] * [J/kg*K] = [W/K]
epsilon = (CO2i.Temperature - GCO2.Temperature) / (CO2i.Temperature - R1270_8.Temperature);
NTU = -log(1 - epsilon);
UA = C_co2 * NTU;
// 대류열전달계수
Re_mco2 = Re(case2_m_dot_CO2, mCO2.Viscosity, D);
f_mco2 = f(Re_mco2);
Nu_mco2 = Nu_cond(f_mco2, Re_mco2, mCO2.Prandtl);
h_mco2 = h_cond(Nu_mco2, mCO2.Therm_Cond, D); // [W/m^2*K]
// 핀효율
ml = l * sqrt(h_mco2 / (2 * k_al * t));
eta_f = tanh(ml) / ml;
// 열교환 모델 UA
UA_R_temp = h_mco2 * (w * N_c + eta_f * N_c * l);//w * h_mco2 * N_c + (N_c - 1) * eta_f * h_mco2 * l;
L_1 = UA / UA_R_temp;
// 냉매 중간 영역 엔탈피
i_x = R1270_1.Enthalpy - m_dot_CO2 / m_dot_R1270 * (CO2i.Enthalpy - GCO2.Enthalpy); // [kJ/kg]
Quality_x = (i_x - LR1270.Enthalpy) / (R1270_1.Enthalpy - LR1270.Enthalpy);
//>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
// 응축 Nu-conds
h_fg = GCO2.Enthalpy - LCO2.Enthalpy; // [kJ/kg*k]
h_fg_prime = h_fg + 0.375 * LCO2.C_p * (LCO2.Temperature - R1270_8.Temperature); // [kJ/kg*k]
Nu_conds_tmp1 = (LCO2.Densiy * 9.81 * (LCO2.Densiy - GCO2.Densiy) * h_fg_prime * pow(D, 3)) / (LCO2.Viscosity * LCO2.Therm_Cond * (LCO2.Temperature - R1270_8.Temperature));
Nu_conds = 0.555 * pow(Nu_conds_tmp1, 0.25);
h_conds = h_cond(Nu_conds, LCO2.Therm_Cond, D); // [W/m^2*K]
q_conds = case2_m_dot_CO2 * (GCO2.Enthalpy - LCO2.Enthalpy); // [kW]
UA_conds = q_conds / 5; // q_conds / delta T
// 응축 부분 핀효율
ml_conds = l * sqrt(h_conds / (2 * k_al * t));
eta_f_conds = tanh(ml_conds) / ml_conds;
UA_conds_temp = h_conds * (w * N_c + eta_f * N_c * l);
L_2 = UA_conds / UA_conds_temp;
V = W * H * (L_1 + L_2);
q_conv = (k_al * (N_c * w * t) * 5) / (L_1 + L_2);
if ((L_1 + L_2) < 3 && H - 0.005 < W && W < H + 0.005 && W - 0.005 < H && H < W + 0.005) {
printf("%5d %5d ", N_c, N_r);
printf("%20.0f %16.0f %17.0f ", Re_mco2 / N_c, Re(case2_m_dot_CO2, GCO2.Viscosity, D) / N_c, Re(case2_m_dot_CO2, LCO2.Viscosity, D) / N_c);
printf("%5d %12.4f %12.4f %12.4f %6.4f", N, L_1 + L_2, W, H, W * H * (L_1 + L_2));
cout << " " << "CASE2" << " " << q_conv << endl;
}
/*-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------*/
// RCR RCR RCR ... RCR
if (N_r % 3 == 0) {
// cout << "CASE3: RCRRCR...RCR" << endl;
N = N_r * N_c; // 전체 관의 개수
W = (N_c + 1) * delta + N_c * w;
H = (N_r + 1) * t + N_r * l;
D = (4 * (l * w * N_c)) / (l * (N_c + 1) + w * N_c);
double case3_m_dot_CO2 = m_dot_CO2 / (N_r / 3);
double case3_m_dot_R1270 = m_dot_R1270 / (N_r / 3);
// epsilon - NTU
C_co2 = case3_m_dot_CO2 * mCO2.C_p; // [kg/s] * [J/kg*K] = [W/K]
epsilon = (CO2i.Temperature - GCO2.Temperature) / (CO2i.Temperature - R1270_8.Temperature);
NTU = -log(1 - epsilon);
UA = C_co2 * NTU;
// 대류열전달계수
Re_mco2 = Re(case3_m_dot_CO2, mCO2.Viscosity, D);
f_mco2 = f(Re_mco2);
Nu_mco2 = Nu_cond(f_mco2, Re_mco2, mCO2.Prandtl);
h_mco2 = h_cond(Nu_mco2, mCO2.Therm_Cond, D); // [W/m^2*K]
// 핀효율
ml = l * sqrt(h_mco2 / (2 * k_al * t));
eta_f = tanh(ml) / ml;
// 열교환 모델 UA
UA_R_temp = h_mco2 * (w * N_c + eta_f * N_c * l);//w * h_mco2 * N_c + (N_c - 1) * eta_f * h_mco2 * l;
L_1 = UA / UA_R_temp;
// 냉매 중간 영역 엔탈피
// i_x = R1270_8.Enthalpy - m_dot_CO2 / m_dot_R1270 * (CO2i.Enthalpy - GCO2.Enthalpy); // [kJ/kg]
// 응축 Nu-conds
h_fg = GCO2.Enthalpy - LCO2.Enthalpy; // [kJ/kg*k]
h_fg_prime = h_fg + 0.375 * LCO2.C_p * (LCO2.Temperature - R1270_8.Temperature); // [kJ/kg*k]
Nu_conds_tmp1 = (LCO2.Densiy * 9.81 * (LCO2.Densiy - GCO2.Densiy) * h_fg_prime * pow(D, 3)) / (LCO2.Viscosity * LCO2.Therm_Cond * (LCO2.Temperature - R1270_8.Temperature));
Nu_conds = 0.555 * pow(Nu_conds_tmp1, 0.25);
h_conds = h_cond(Nu_conds, LCO2.Therm_Cond, D); // [W/m^2*K]
q_conds = case3_m_dot_CO2 * (GCO2.Enthalpy - LCO2.Enthalpy); // [kW]
UA_conds = q_conds / 5; // q_conds / delta T
// 응축 부분 핀효율
ml_conds = l * sqrt(h_conds / (2 * k_al * t));
eta_f_conds = tanh(ml_conds) / ml_conds;
//double UA_conds_temp = w * h_conds * N_c + (N_c - 1) * eta_f_conds * h_conds * l;
UA_conds_temp = h_conds * (w * N_c + eta_f * N_c * l);
L_2 = UA_conds / UA_conds_temp;
V = W * H * (L_1 + L_2);
q_conv = (k_al * (N_c * w * t) * 5) / (L_1 + L_2);
if ((L_1 + L_2) < 3 && H - 0.005 < W && W < H + 0.005 && W - 0.005 < H && H < W + 0.005) {
printf("%5d %5d ", N_c, N_r);
printf("%20.0f %16.0f %17.0f ", Re_mco2 / N_c, Re(case3_m_dot_CO2, GCO2.Viscosity, D) / N_c, Re(case3_m_dot_CO2, LCO2.Viscosity, D) / N_c);
printf("%5d %12.4f %12.4f %12.4f %6.4f", N, L_1 + L_2, W, H, W * H * (L_1 + L_2));
cout << " " << "CASE3" << " " << q_conv << endl;
}
}
// printf("\n");
// cout << "--------------" << endl;
// cout << "--------------" << endl;
}
}
}
double Re(double m, double vis, double D) {
double Reynolds = (4 * m) / (vis * 3.141592 * D);
return Reynolds;
}
double f(double Re) {
double tmp = 0.79 * log(Re) - 1.64;
return pow(tmp, -2);
}
double Nu_cond(double f, double Re, double Pr) {
double tmp1 = (f / 8) * (Re - 1000) * Pr;
double tmp2 = 1.0 + 12.7 * sqrt(f/8) * (pow(Pr, 0.666666667) - 1.0);
return (tmp1 / tmp2);
}
double h_cond(double Nu, double k, double D) {
return (Nu * k) / D;
}
double E(double Q, double rho_L, double rho_G, double Bo) {
double tmpx = Q / (1 - Q);
double ratio_rho = rho_L / rho_G;
double tmp = 1 + 3000 * pow(Bo, 0.86) + 1.12 * pow(tmpx, 0.75) * pow(ratio_rho, 0.41);
return tmp;
}
참고자료6, Plate-Fin Heat Exchangers
추가 고려사항
포집 GCO2의 정제 방법 및 순도 영향
몇 가지 냉매를 사용한 이산화탄소 액화에 대한 연구
본 연구에서는 연소 배기가스 중에서 이산화탄소의 포집은 습식 용매를 이용한 포집 공정과 거식 공정 및 분리막 공정을 이용하여 포집한 배기가스를 활용하였다. 다음은 위의 3가지 이산화탄소 포집 공정을 통해 포집하여 농축된 이산화탄소가 포함된 기상류의 조성을 나타내었다.
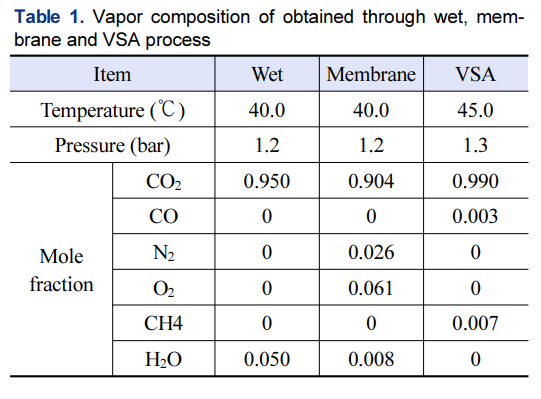
포집한 기체 상태의 이산화탄소를 액화시키는 이유는 저장 및 수송이 쉽기 때문이다. 이산화탄소를 액화시키면 기체 상태일 때에 비해 부피는 상온 및 상압일 때에 비해서 약 550분의 1로 줄어든다. 이것은 같은 공간에 이산화탄소를 기체 상태로 저장할 때에 비해서 액화시키면 550배 더 많이 저장할 수 있다는 것을 의미한다. 또한 이산화탄소를 기체 상태로 수송하는 것에 비해서 액체 상태로 수송하게 되면 압축기 동력에 비해 상대적으로 더 낮은 펌프의 소요 동력으로 수송할 수 있으며 파이프라인의 직경을 줄일 수 있어서 초기 투자 비용이 절감된다.
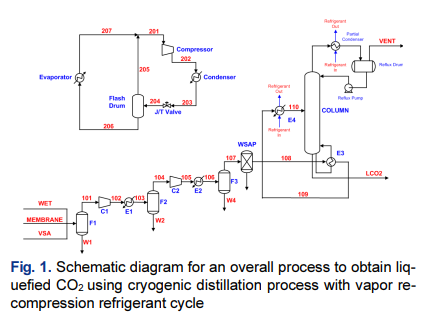
위는 냉매를 이용한 냉동사이클과 고순도 이산화탄소를 얻기 위한 이단 압축공정과 심냉공정을 포함하는 전체 공정에 대한 개요도를 나타내었다. 중간에 냉각기를 가지는 이단 압축공정을 이용해서 이산화탄소를 25bar까지 가압한 다음에 후단 냉각기를 이용해서 냉각수가 냉각시킬 수 있는 온도인 $45^{\circ}\mathrm{C}$ 까지 냉각시킨 후에 몇 가지 냉매를 이용한 증기 재압축 냉동사이클을 이용해서 $-30^{\circ}\mathrm{C}$까지 냉각시켜서 액화시킨다. 다음은 이단 압축 공정에 대한 개요도를 나타내었다.
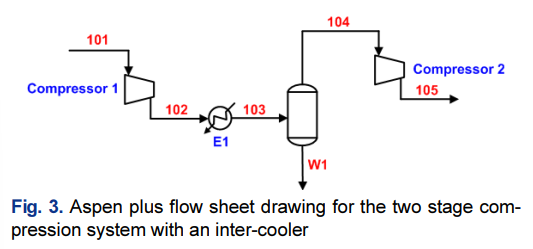
이산화탄소 수송을 위한 압축 및 액화 공정 설계 및 비용 평가
ICARUS를 이용하여 각 장치들의 필요 크기 및 비용이 추정되었으며 각각의 공정에 대하여 압축에 필요한 전기에너지와 함께 다음 표에 나타내었다.(*로 표시한것은 전기 에너지 이외에 열에너지가 필요한 공정이다.)

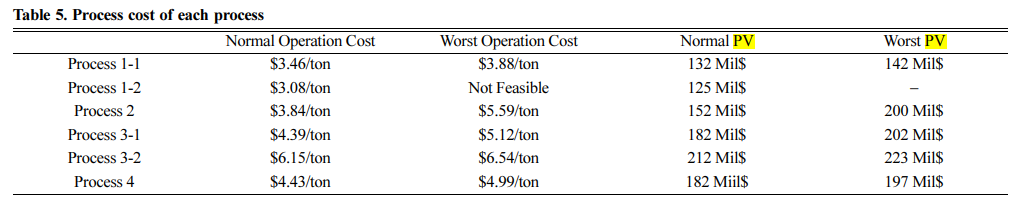
공정 1-2는 $40^{\cdot}\mathrm{C}$로 공정 3-2는 $116^{\cdot}\mathrm{C}$ 에서의 열에너지를 필요로 한다. 일반케이스의 경우 143.1 kWh/ton, 고온 케이스의 경우 152.22 kWh/ton의 총 에너지가 필요하게 된다.
2012년 6월 기준 유연탄 연료 발전단가 49.41won/kWh을 적용하고 환율 1150원/달러 를 적용하였다. 들어오는 이산화탄소의 가격은 0으로 했다.
Project year는 20년으로 했다. 그렇게 해서 이산화탄소 액화공정 각각에 대하여 톤 당 가격 및 현재가를 추산하였다. 이자율은 12%로 가정되었다. 혼합 냉매를 사용하는 경우에 한 가지 냉매를 사용하는 공정에 비하여 평소에는 더 높은 비용을 고온기에서는 더 낮은 비용을 나타냄을 알 수 있다. 참고로 국내 초임계 이산화탄소의 포집 비용은 41.3달러/ton으로 산출되었다.
혼합냉매 증기압축 냉동 사이클 및 기체 냉동 사이클 ------ **천연 가스 액화 공정**
댓글남기기