열역학 11장 기체 혼합물
Updated:
이상기체 혼합물
N개 순수 물질의 일반적인 혼합물에서 전체 질량과 전체 몰수는 다음과 같다.
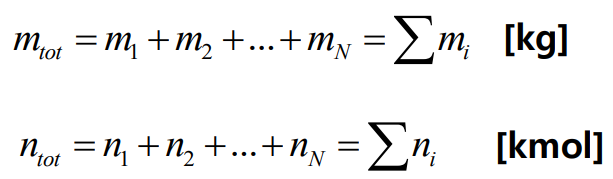
이 혼합물은 보통 각 성분의 질량 분율(mass fracrion) 또는 농도(concentration)인 $c_i$ 또는 각 성분의 몰분율(mole fraction) $y_i$로 나타낸다.

이 두 가지는 분자량 $M_i$[kg/kmol]를 통해 서로 관련되는데, 즉 $m_i = n_iM_i$이다. 따라서 다음과 같은 식이 성립한다.
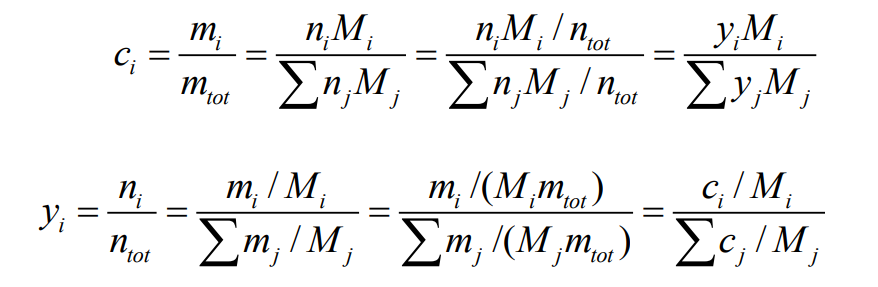
혼합물에 대한 분자량은 다음과 같다.
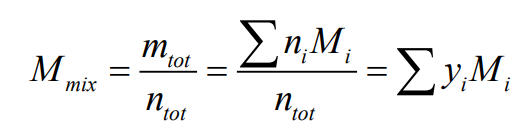
다음 예제를 보자.
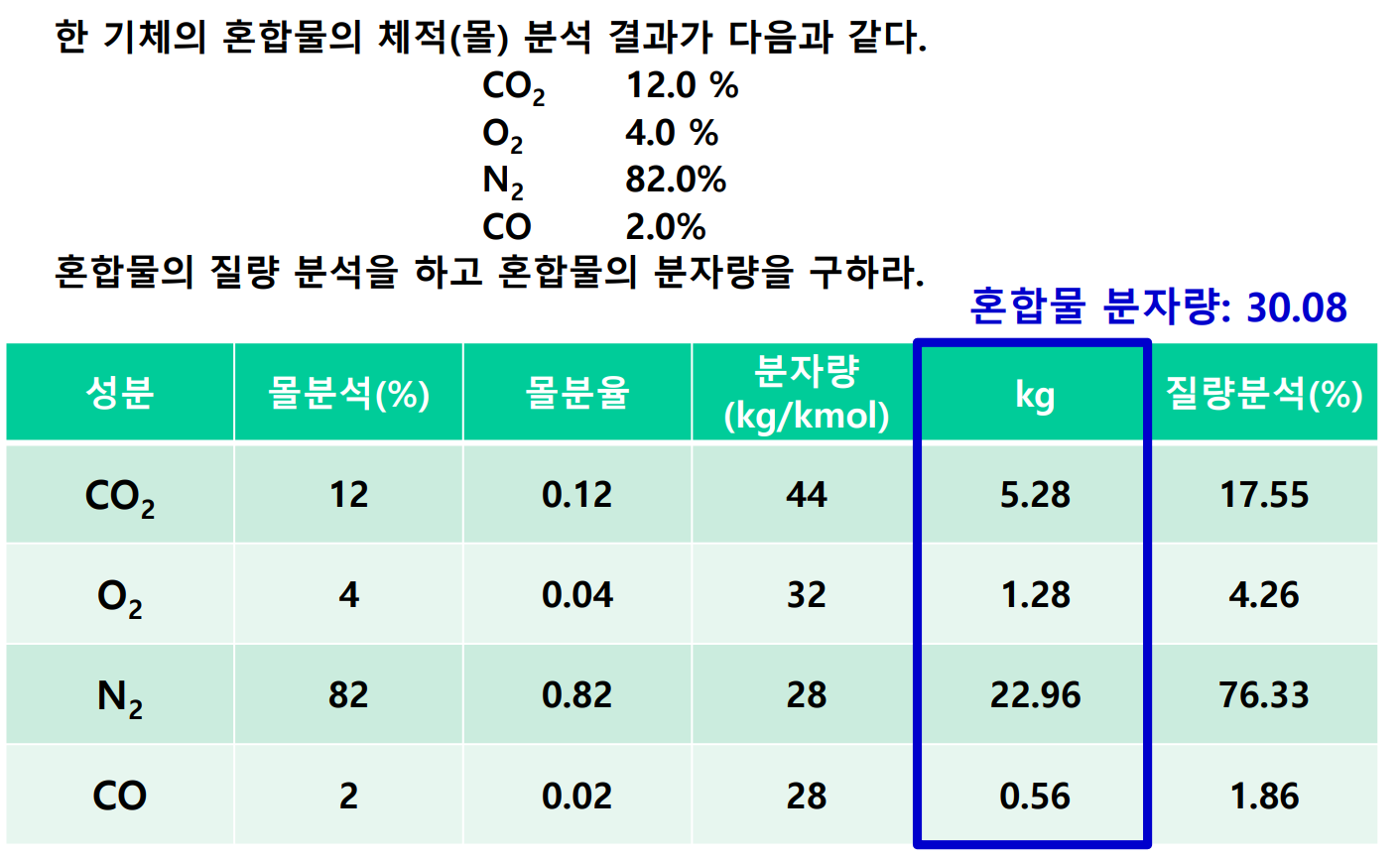
두 기체의 혼합물을 생각해보자. 이는 “습공기”(공기 + 수증기) 문제에 적용된다. 기체 혼합물을 해석하기 위해 Dalton 모델을 고려한다.
Dalton 모델
기체 혼합물에 대한 Dalton 모델에서는 각 성분이 다음과 같이 혼합물과 동일한 온도와 체적에서 분리되어 있고 독립적인 것으로 간주하여 각 성분의 상태량을 다룬다.
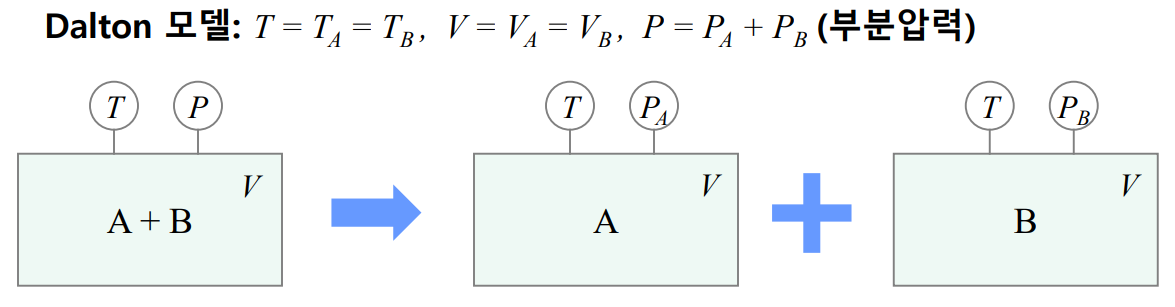
혼합물과 각 성분에 대해서 각각 다음과 같은 식이 성립한다.
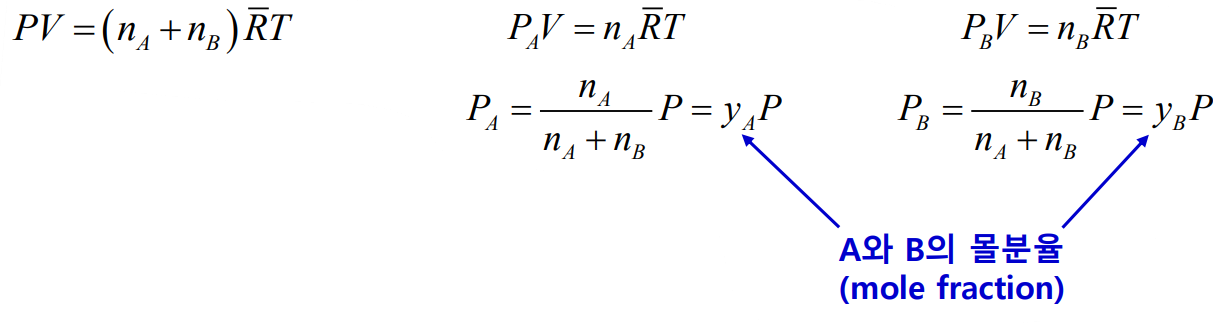
위 식에서 $y_A + y_B = 1$이고 분압 $P_A$와 $P_B$는 전체 압력의 분율이 되므로 $P_A + P_B = P$가 된다.
질량 기준으로 이상기체 혼합물의 상태 방정식은 다음과 같다.
여기서 다음과 같은 식들이 성립한다.
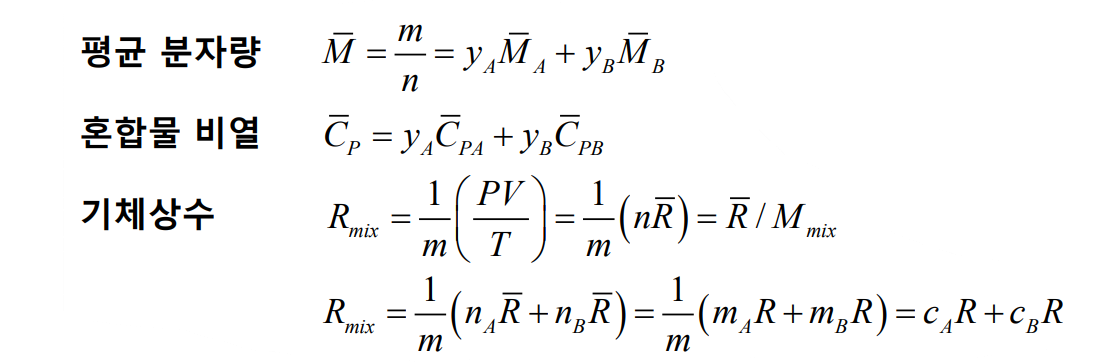
이상기체 혼합물의 내부 에너지, 엔탈피, 엔트로피를 결정하는 데 있어서, 각 성분이 전체 체적을 차지하고 있다고 가정하는 Dalton 모델이 유용하다. 따라서 내부 에너지, 엔탈피, 엔트로피는 각 성분이 혼합물 안에서 존재하고 있는 상태(조건)에서의 구성 기체의 각 상태량들의 합으로 계산할 수 있다. 이상기체의 내부 에너지와 엔탈피는 온도만의 함수고 내부 에너지, 엔탈피, 엔트로피는 다음과 같다.
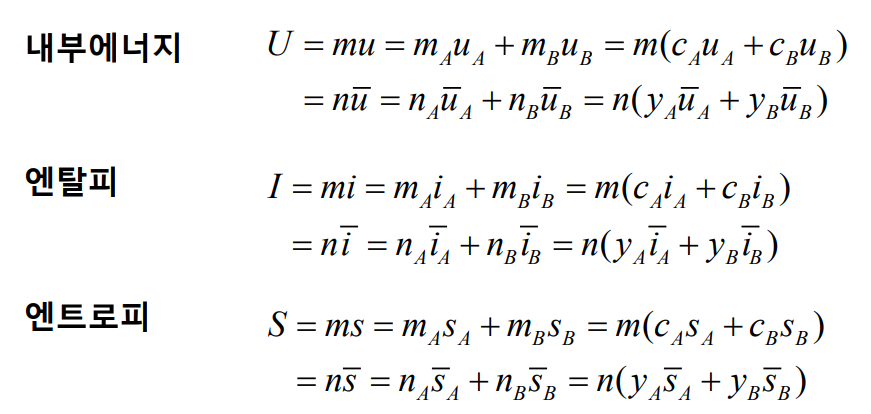
참고로 이상기체($C_v, C_p$ 일정)에 대해 다음과 같은 식들이 성립한다.
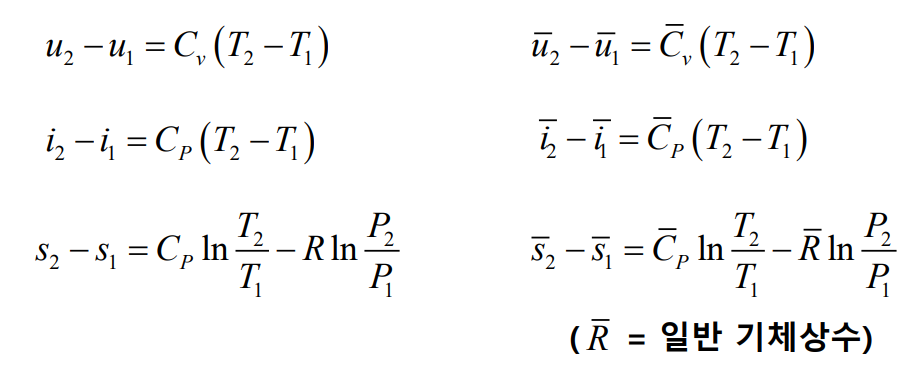
다음 예제를 보자.

기체-증기 혼합물(습공기, 공기 + 수증기)에 대한 단순 모델
이상기체 혼합물에 대해 건공기의 물리량은 다음과 같다.
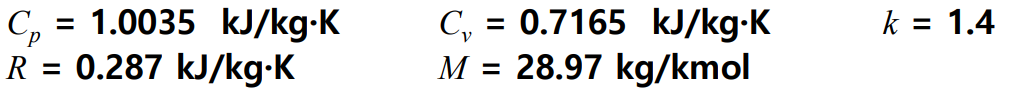
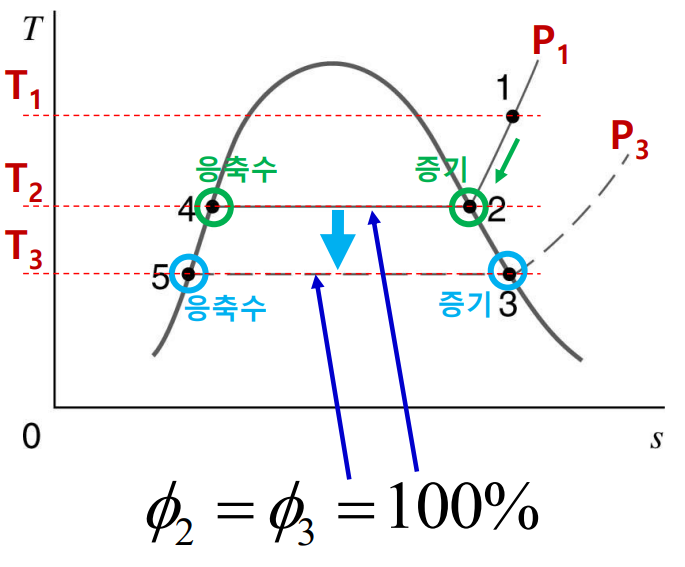
이슬점(dew point)은 일정한 압력하에서 냉각될 때 증기가 응축되거나 응고되는 온도이다. 이슬점 온도는 $T_{dp} = T_{sat}(P_{\mathrm{v}}) = T_{sat}(y_{\mathrm{v}}P)$로 표현된다. 다음 $T$-$s$선도를 보자.
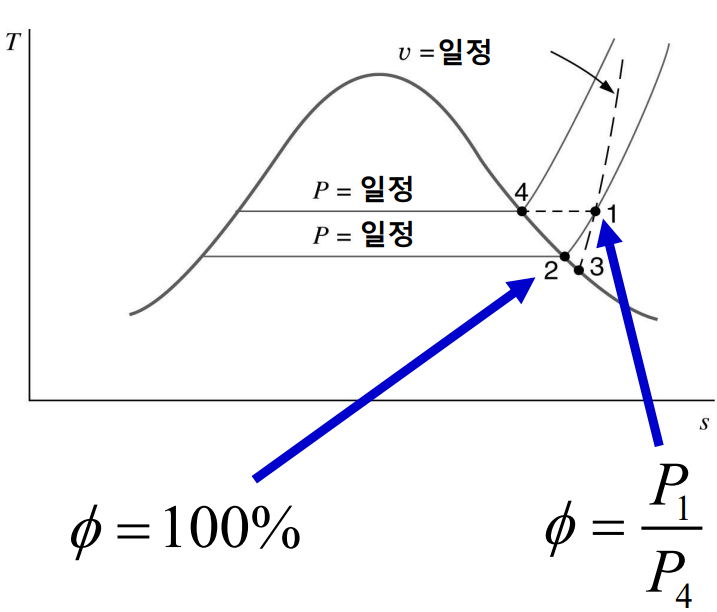
증기는 기체 혼합물의 온도 및 증기의 부분압하에서 과열 상태 1에 있다고 볼 수 있다. 혼합물이 정압(constant pressure)냉각이 되면 증기의 부분압은 점 2에 도달할 때까지 일정하고 그 후에는 응축이 시작된다. 상태 2의 온도가 이슬점 온도이다. 선도상의 곡성 $1-3$은 혼합물이 정적(constant volume)냉각이 될 때의 과정이며 응축이 시작되는 상태 3의 온도는 이슬점 온도보다 약간 낮다.
상대 습도(relative humidity) $\phi$는 혼합물에서 증기의 몰분율과 포화 혼합물에서의 증기의 몰분율의 비로 정의한다. 증기를 이상기채로 간주하므로 상대 습도는 혼합물에서의 증기의 부분압 $P_{\mathrm{v}}$와 그 온도에서의 증기의 포화 압력 $P_{sat}(T)$의 비로 계산할 수 있다.
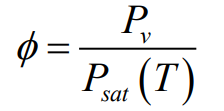
공기-수증기 혼합물의 절대 습도 또는 습도비(humidity ratio) $\omega$는 수중기의 질량 $m_{mathrm{v}}$와 건공기(dry air)의 질량 $m_a$의 비로 정의한다. 비습도(specific humidity)와 절대 습도(absolute humidity)는 습도비와 동의어로 사용한다.
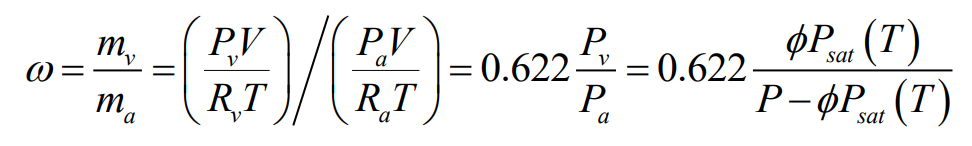
최대 습도비는 상대 습도 100%에 해당하며, 전체압과 $P_g$에 따른 온도로 정해지는 함수가 된다. 이 관계는 온도의 함수로 다음과 같다.
다음 예제를 보자.


기체-증기 혼합물에 대한 에너지 방정식
유동이 있는 조건에서 습공기 제 1법칙은 다음과 같다.
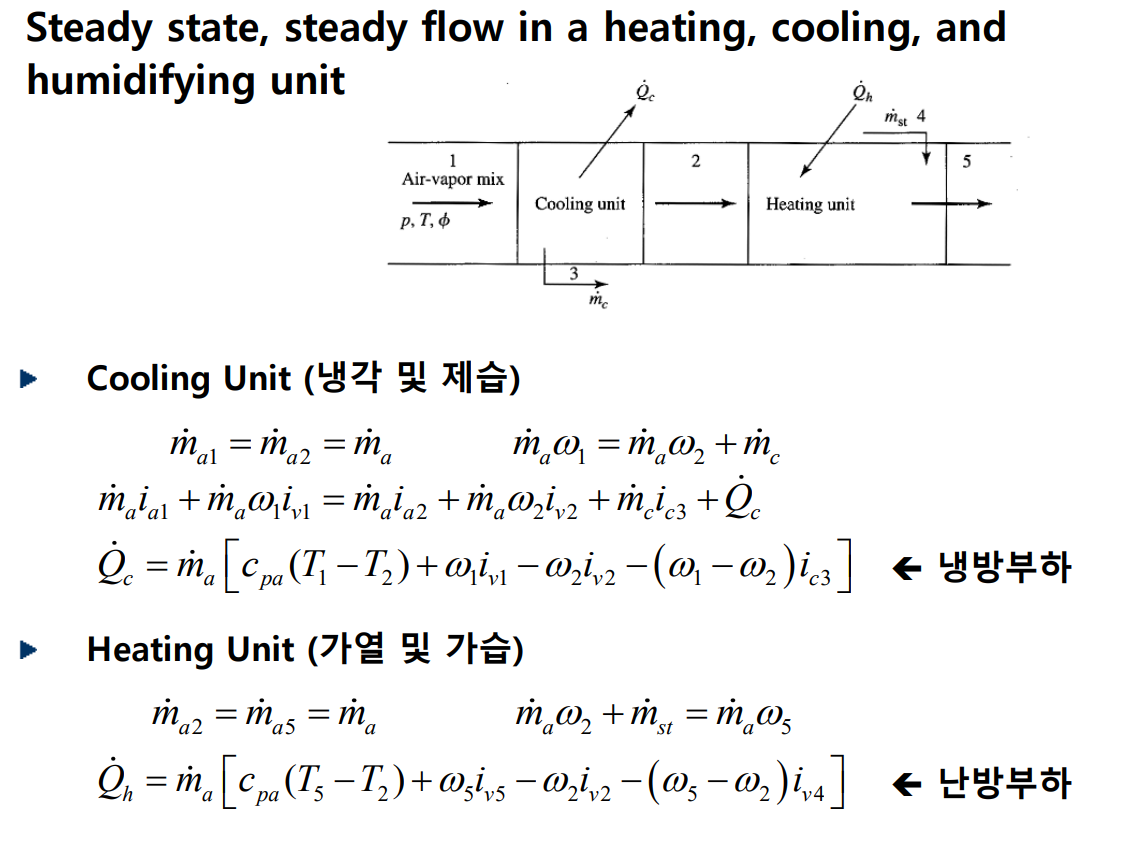
다음 예제를 보자.
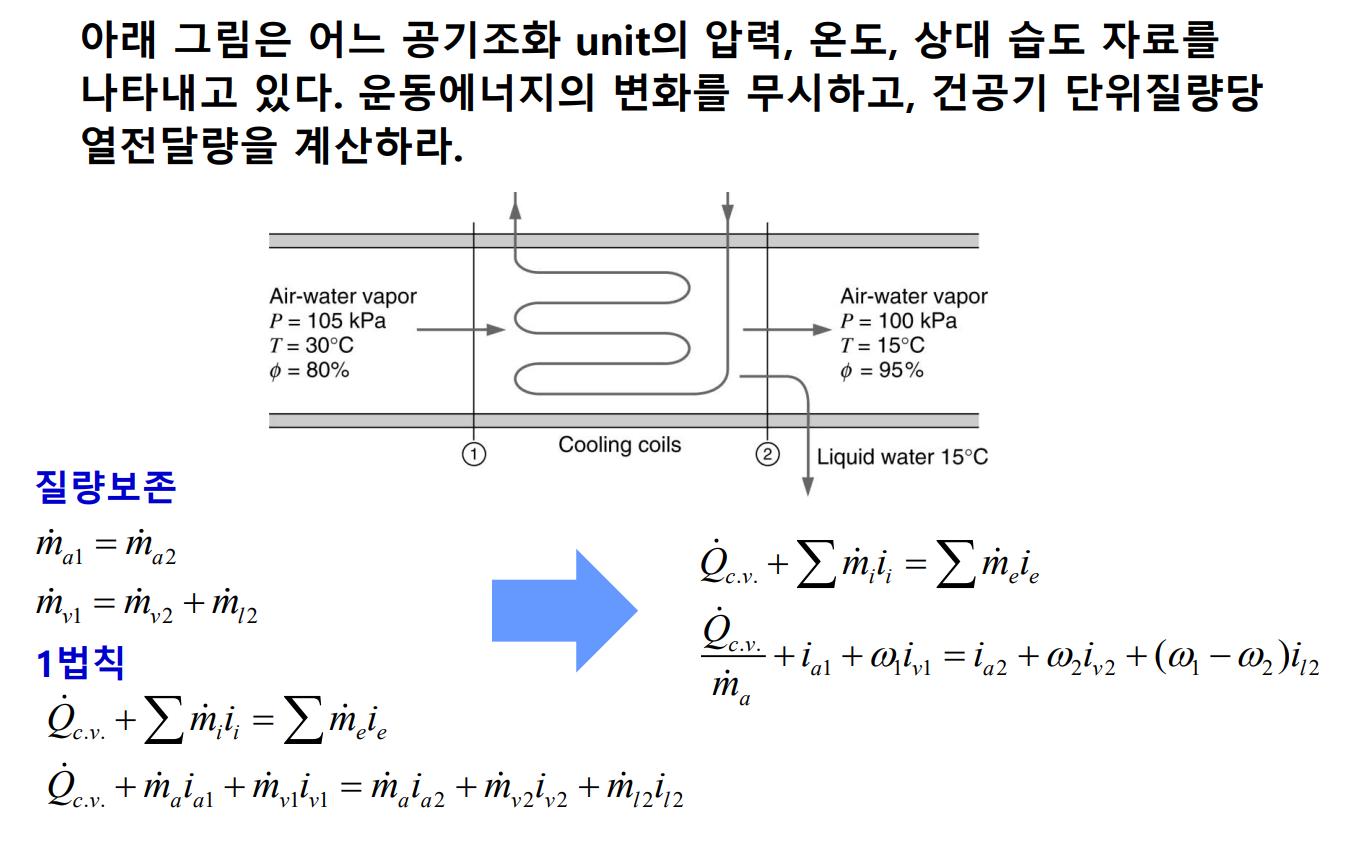
단열 포화 과정
공기-수증기 혼합물으 중요한 과정으로 단열 포화 과정(adiabatic saturation process)이 있다. 이 과정에서는 공기-수증기 혼합물이 다음과 같이 완전하게 단열된 덕트에서 물과 접촉한다.
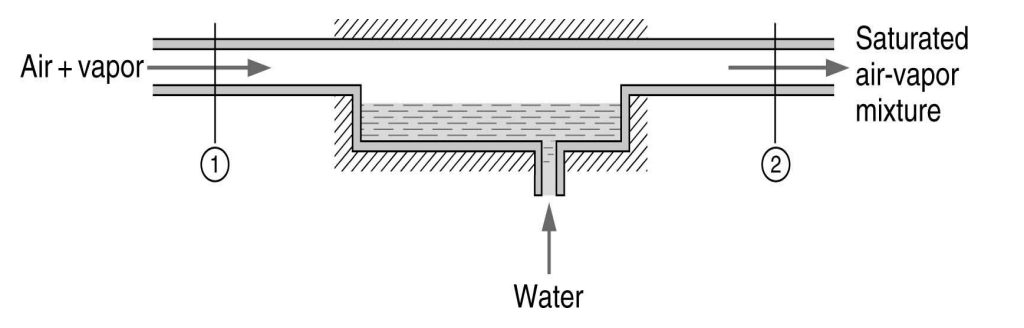
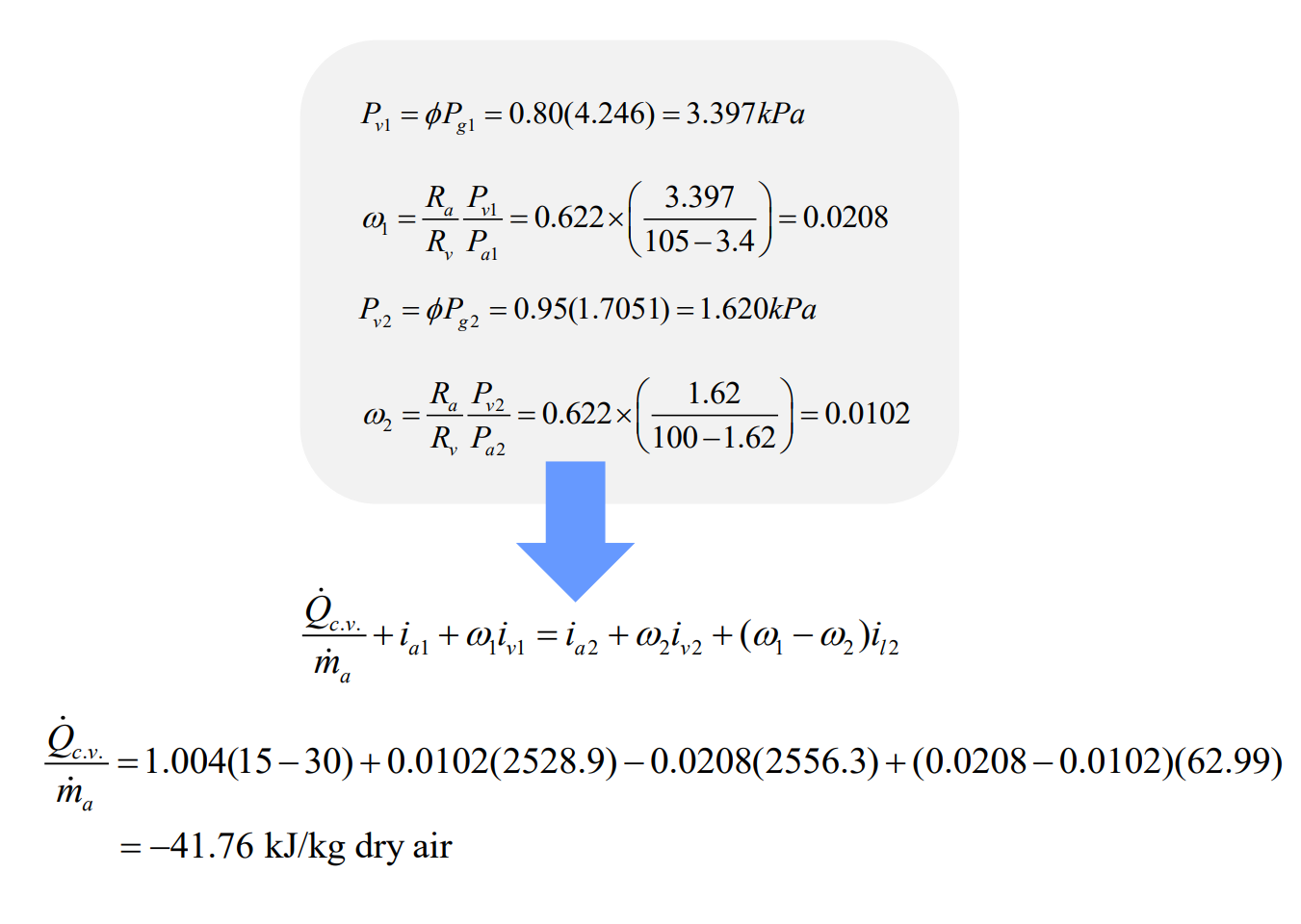
입수의 상대 습도가 100% 미만이면 물의 일부가 증발할 것이고 공기-수증기 혼합물의 온도는 감소할 것이다. 이 과정으로 덕트 출구에서 혼합물의 포화되었을 때 출구에서의 혼합물의 온도를 단열 포화 온도라 한다. 이 과정에서 정상 유동 과정으로 이루어지기 위해서는 증발되는 물만큼의 보충수(makeup water)를 단열 포화 온도에서 공급해 주어야 한다. 압력은 일정하다고 가정한다.
단열 포화 과정을 운동 에너지와 위치 에너지의 변화가 없는 정상상태, 정상 유동 과정으로 간주하면 열역학 제 1법칙은 다음과 같다.
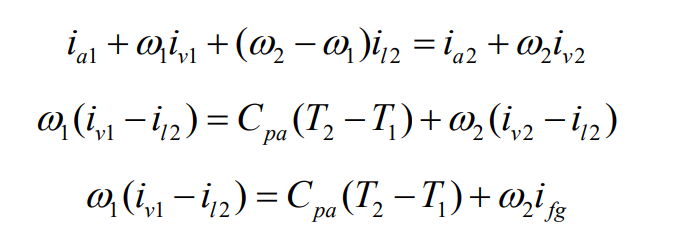
단열 포화 과정에서 가장 중요한 점은 출구에서 혼합물의 온도인 단열 포화 온도가 공기-수증기 혼합물의 입구 압력, 온도, 상대 습도, 그리고 출구 압력의 함수라는 점이다. 따라서 공기-수증기 혼합물의 입구에서의 상대 습도와 절대 습도는 단열 포화기의 입출구 압력, 입출구 온도를 축정하여 결정할 수 있다. 다음 예제를 보자.

습공기 선도
공기-수증기 혼합물의 상태량은 습공기 선도(psychrometric chart)로 나타낸다. 이원 혼합물(binary mixture)의 상태를 기술하기 위해서는 세 개의 독립 상태량이 필요하다. 다음은 습공기 선도이다.
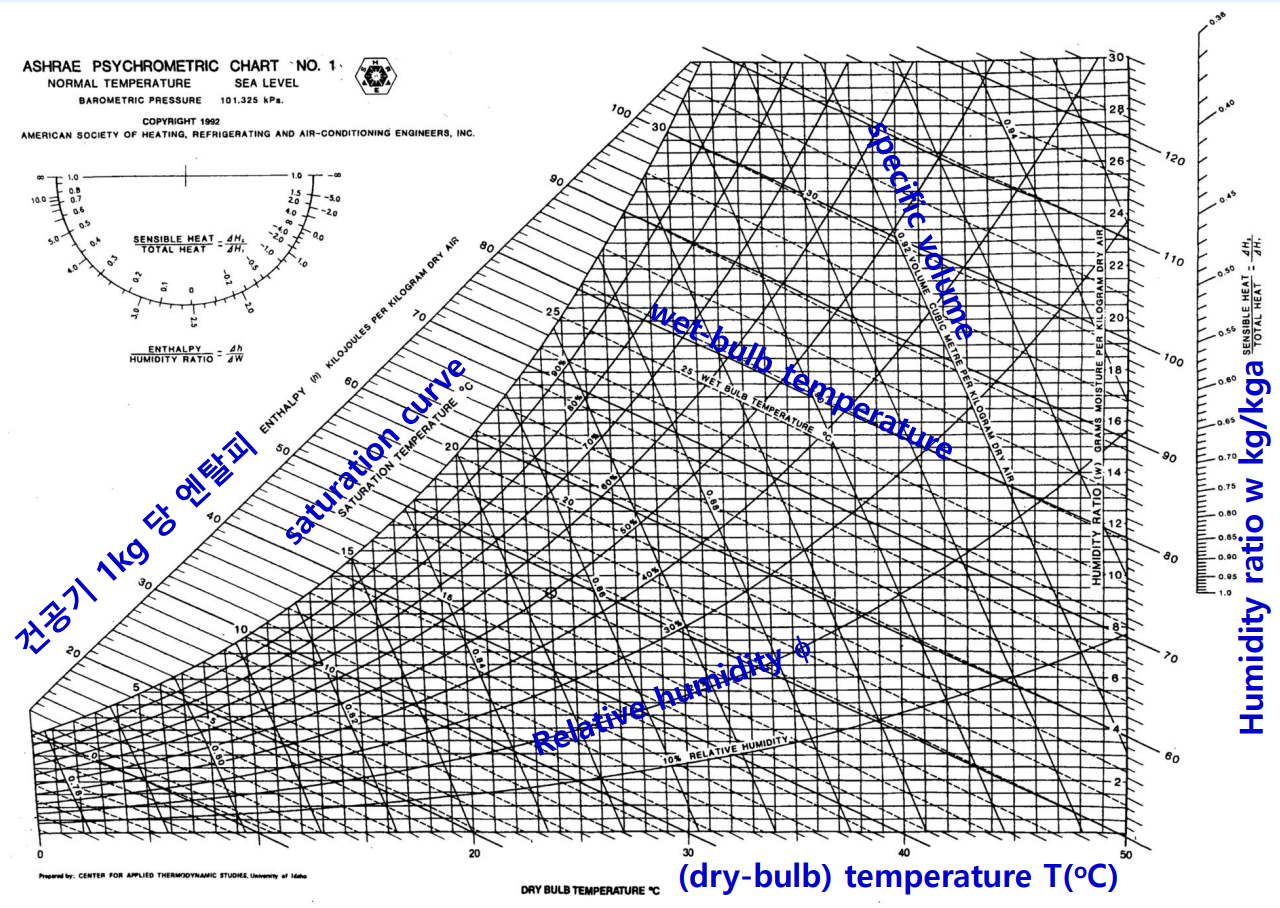
다음은 습공기 선도에서 공기-수증기 혼합물에 대한 여러 가지 과정의 진행 방향을 제시한다.
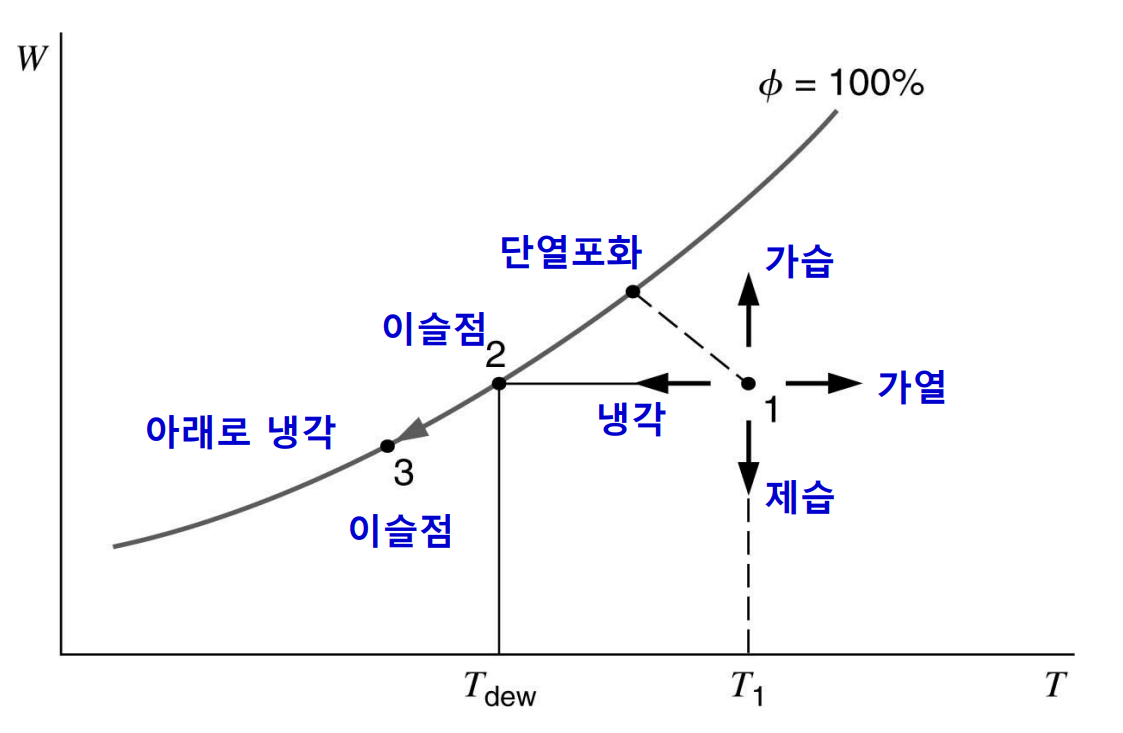
예를 들어, 상태 1에서 출발하는 정압 냉각 과정은 일정한 절대 습도하에서 상태 2의 이슬점까지 진행된 후 계속 하여 냉각하면 포화 곡선(상개 습도 100%)을 따라서 상태 3까지 연속 냉각된다. 유사한 방식으로 다른 과정도 추적할 수 있다. 다음 예제를 보자.
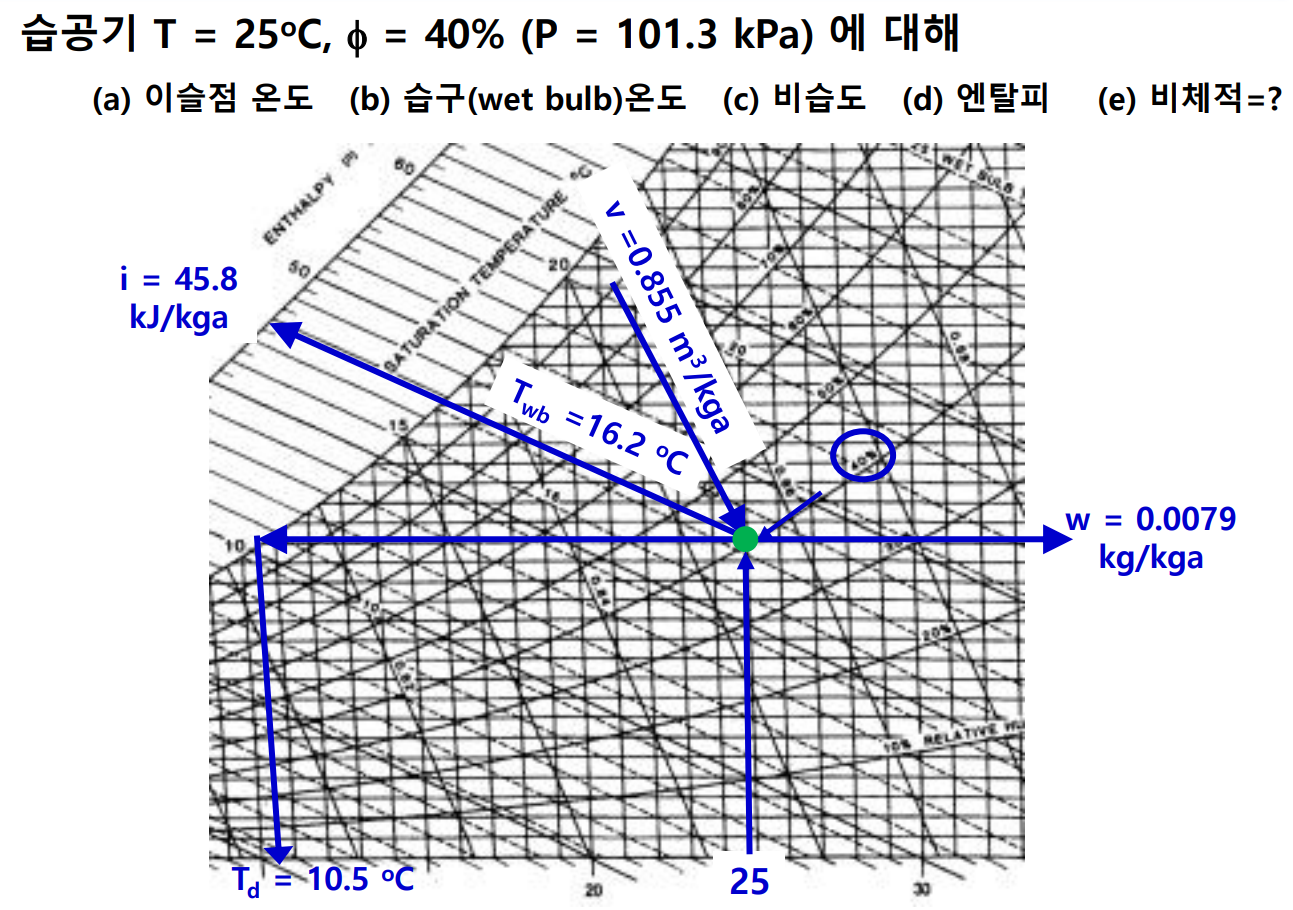
습공기 정리

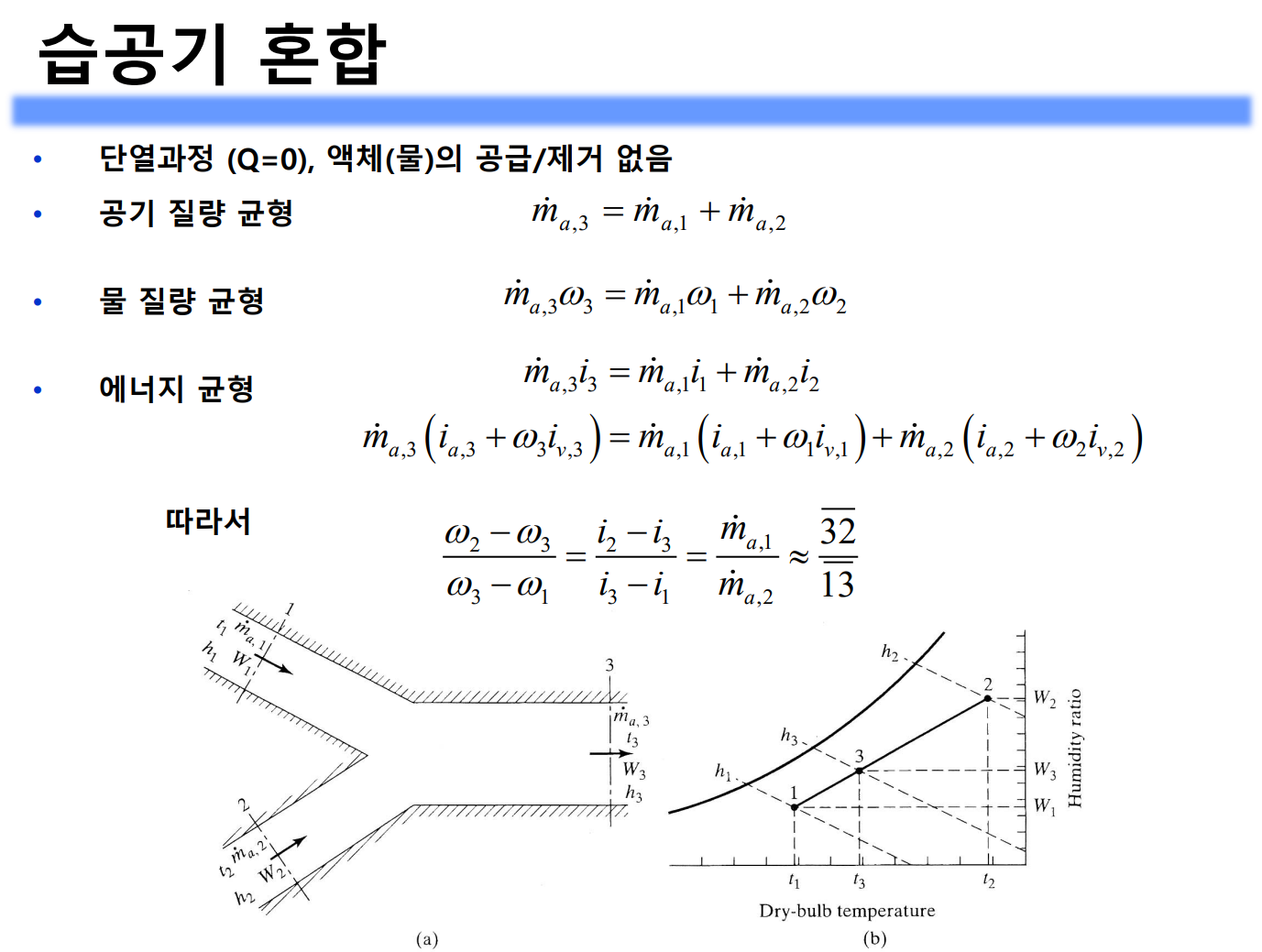

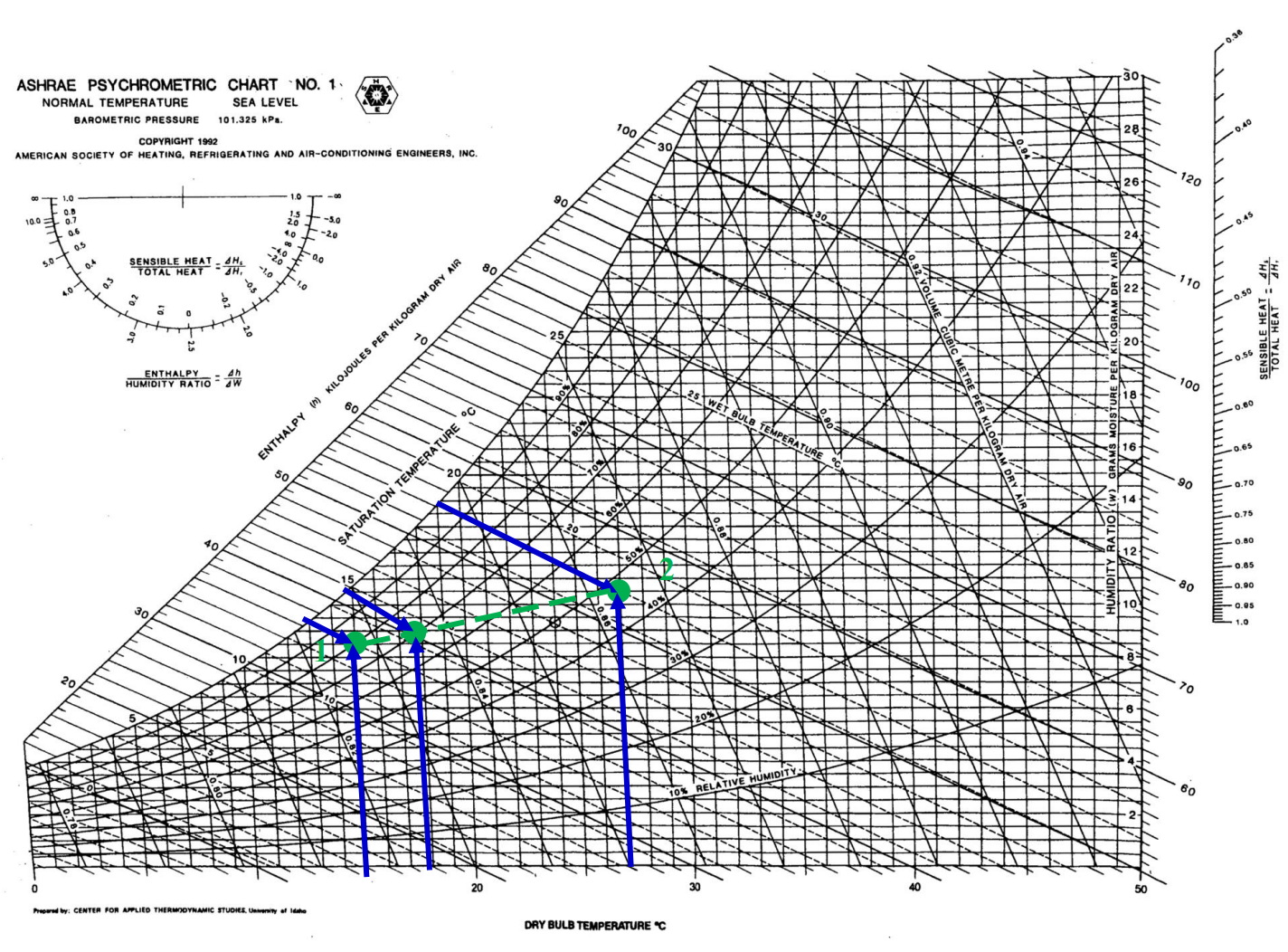
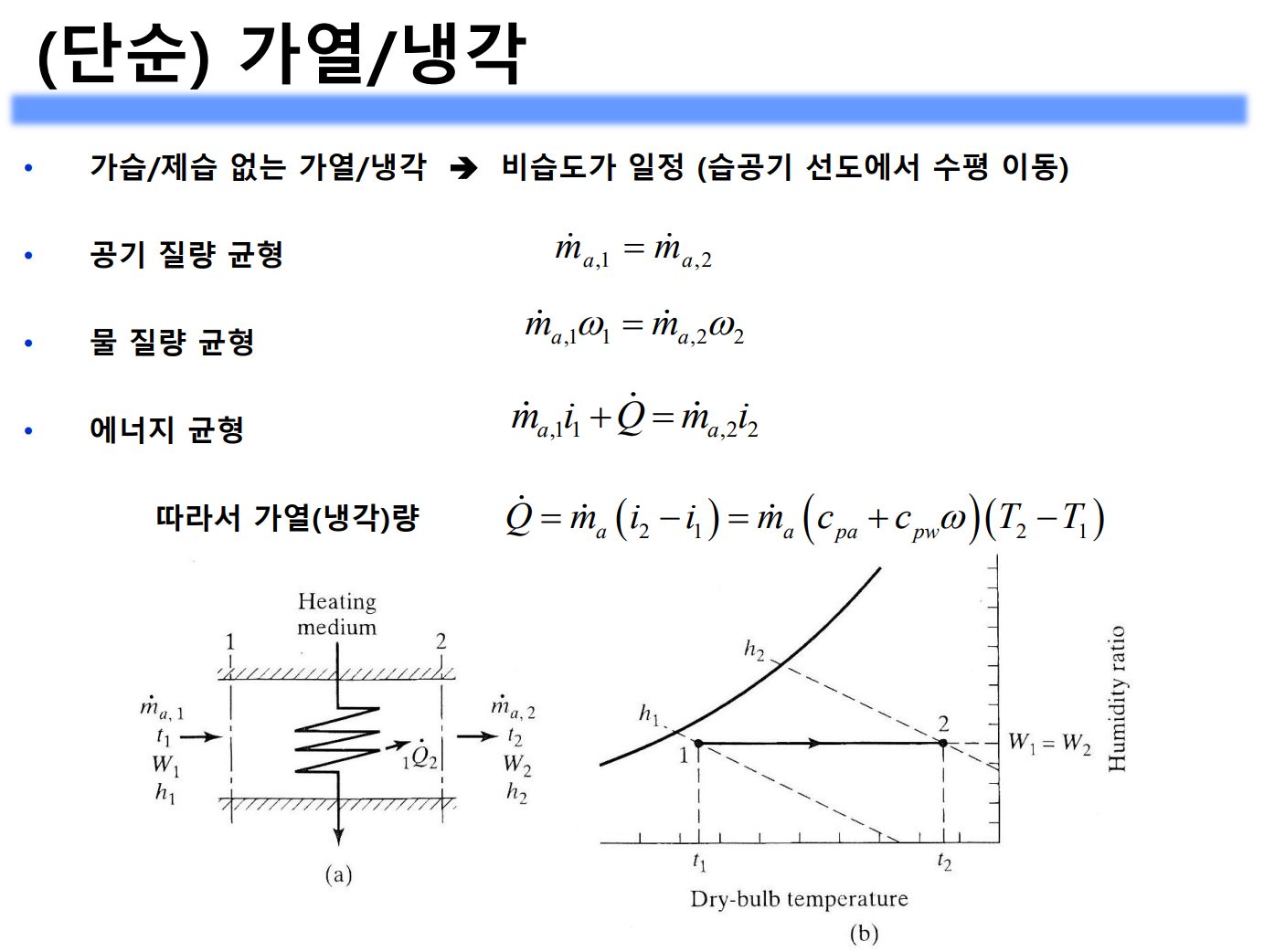
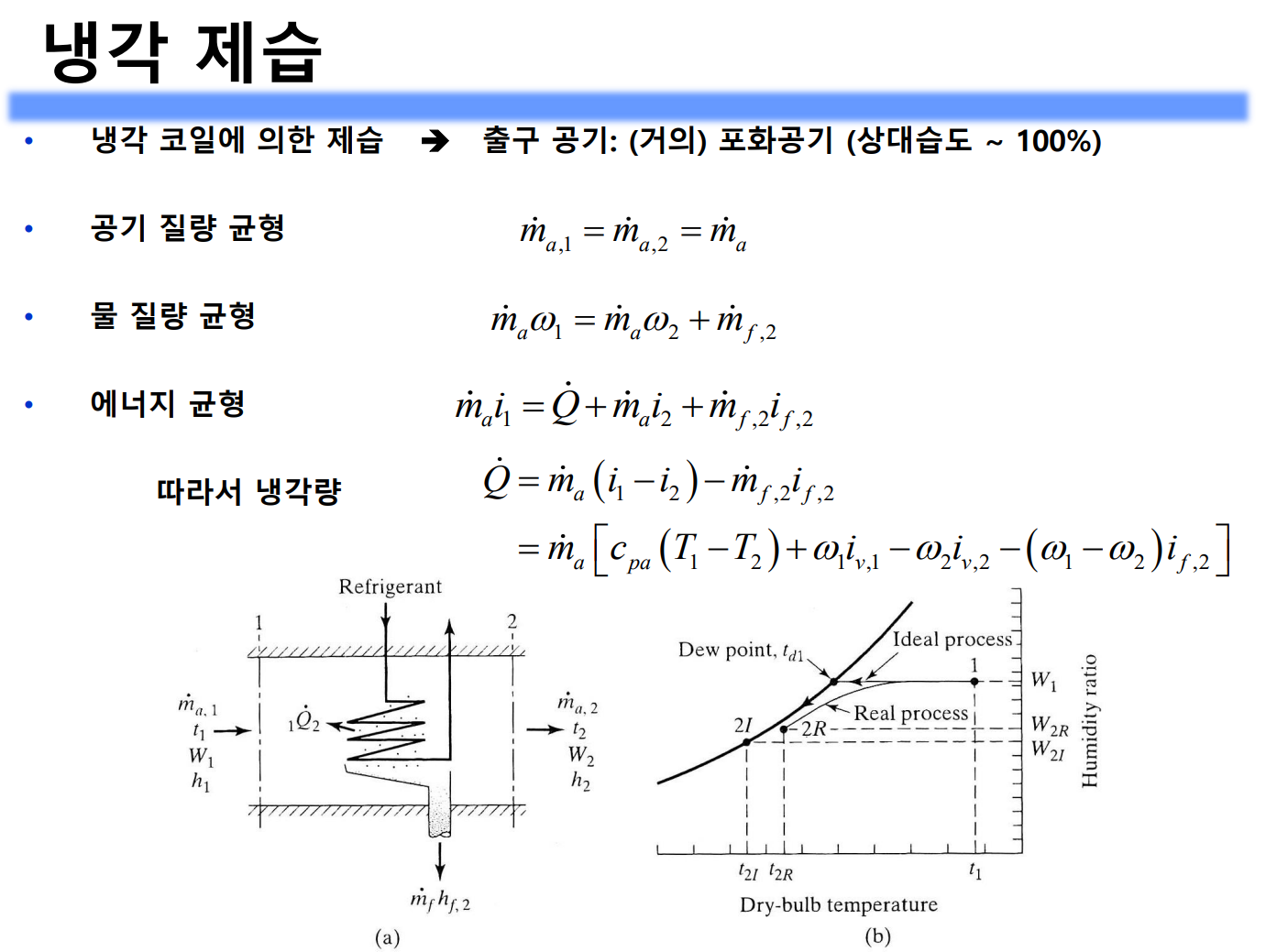
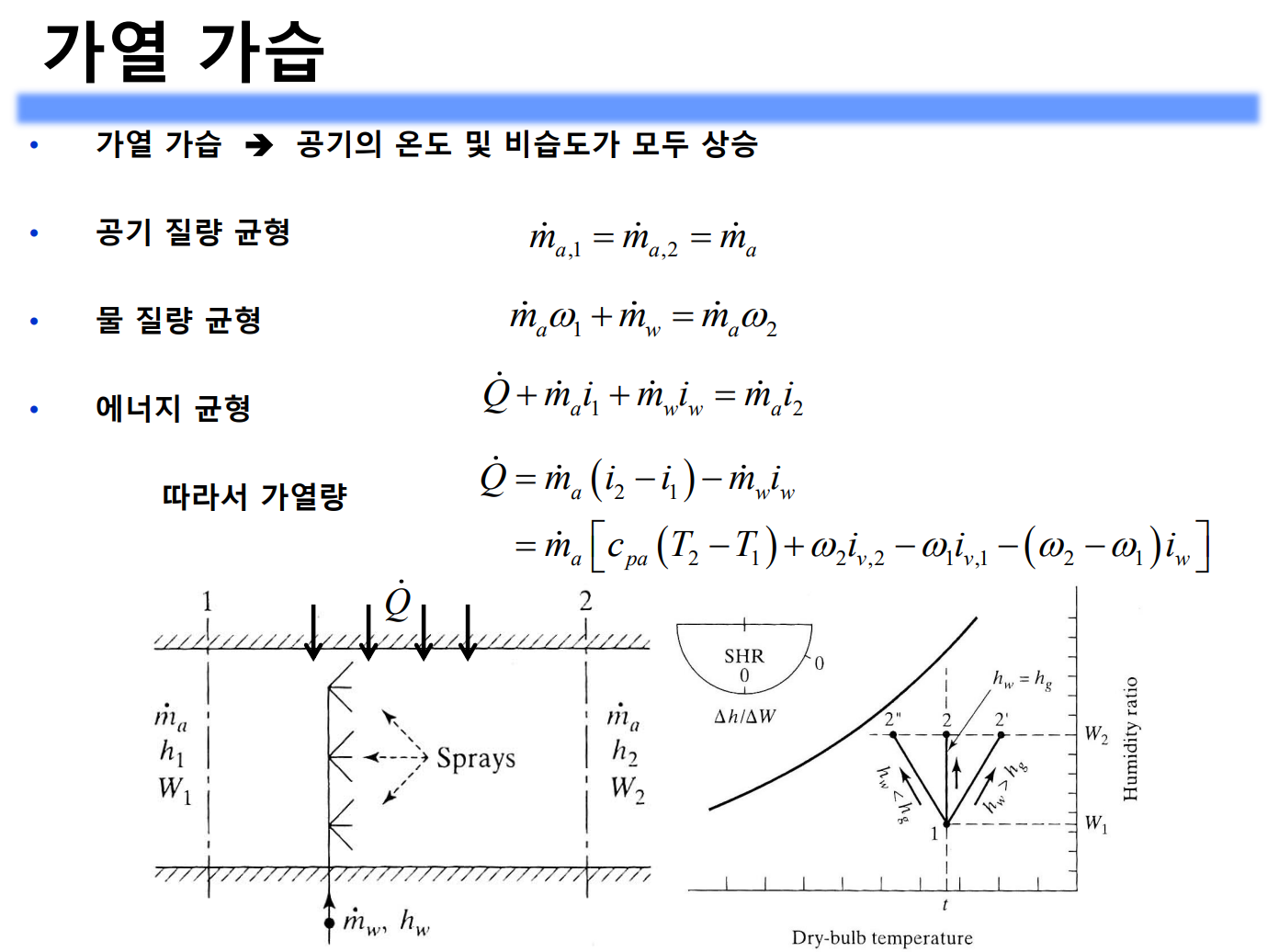
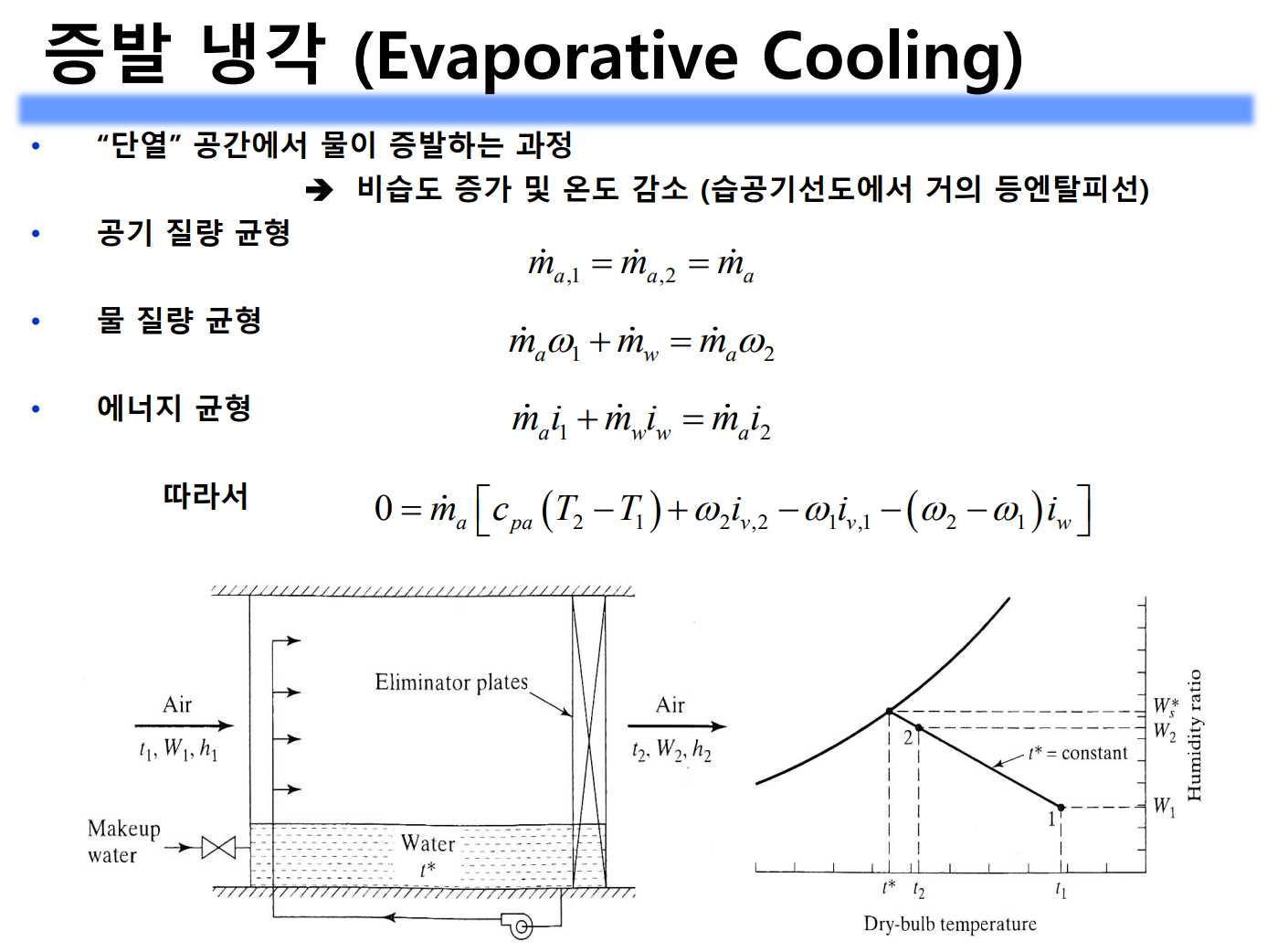
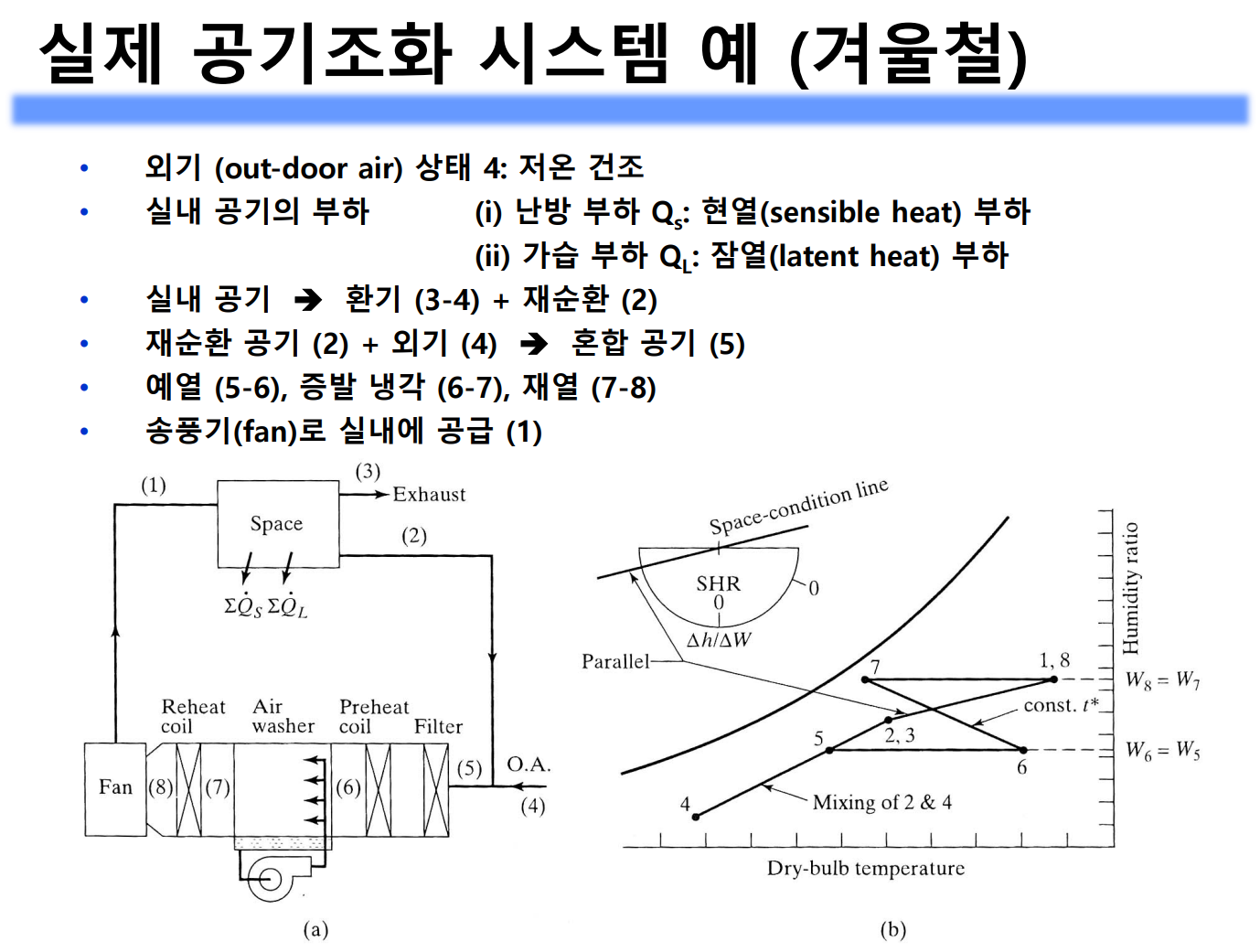
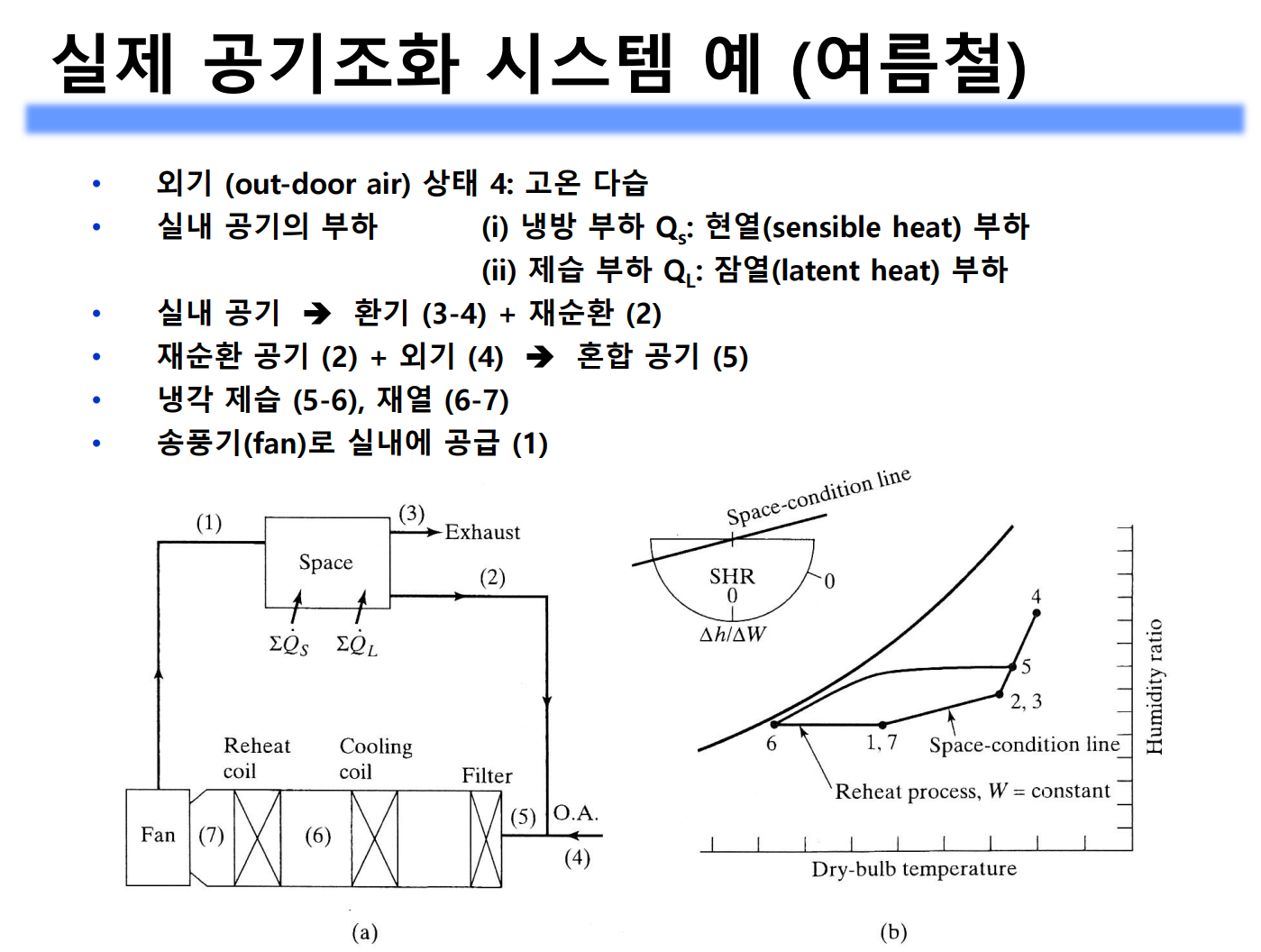
가열, 냉각
댓글남기기