열전달
Updated:
에너지 보존(열역학 제 1법칙)은 “(에너지 변화) = (들어온 에너지) - (나간 에너지)”이다.
열전달은 “온도차”에 의한 에너지 전달이다. 확산(diffusion)은 매질(medium)을 통한 열전달로 상대적으로 느리다. 확산에는 정지한 매질에 의한 열전달인 전도(conduction)와 유동하는 유체에 의한 열전달인 대류(convection)이 있다. 복사(radiation)는 빛(전자기파)에 의한 열전달로 매우 빠르다.
열전달(율)(rate)은 $q$라 하고 단위는 [W]이다. 열유속(heat flux)은 단위 면적당 열전달로 $q^{\prime \prime}$라 하고 단위는 [W/$m^2$]이다.
전도(Conduction)
열전도에 대한 전달률 방정식은 Fourier의 전도법칙으로 알려져 있다.
비례상수 $k$는 열전도율(thermal conductivity, [W/m K])로 알려진 전달 물성치이며 대표적으로 다음과 같다.

열유속이 벡터량인 것을 감안하면, 보다 일반적인 전도 전달률 방정식(Fourier의 법칙)의 표현은 다음과 같이 쓸 수 있다.
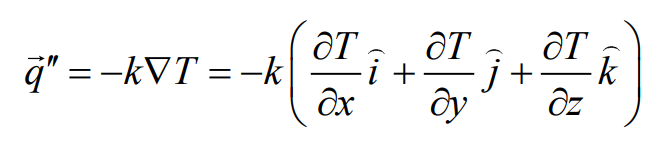
위 식에서 열유속 벡터는 등온 표면에 수직이다.
1차원 전도
평면벽에서의 1차원 전도에서, 온도는 $x$ 좌표만의 함수이며 열은 이 방향으로만 전달된다.
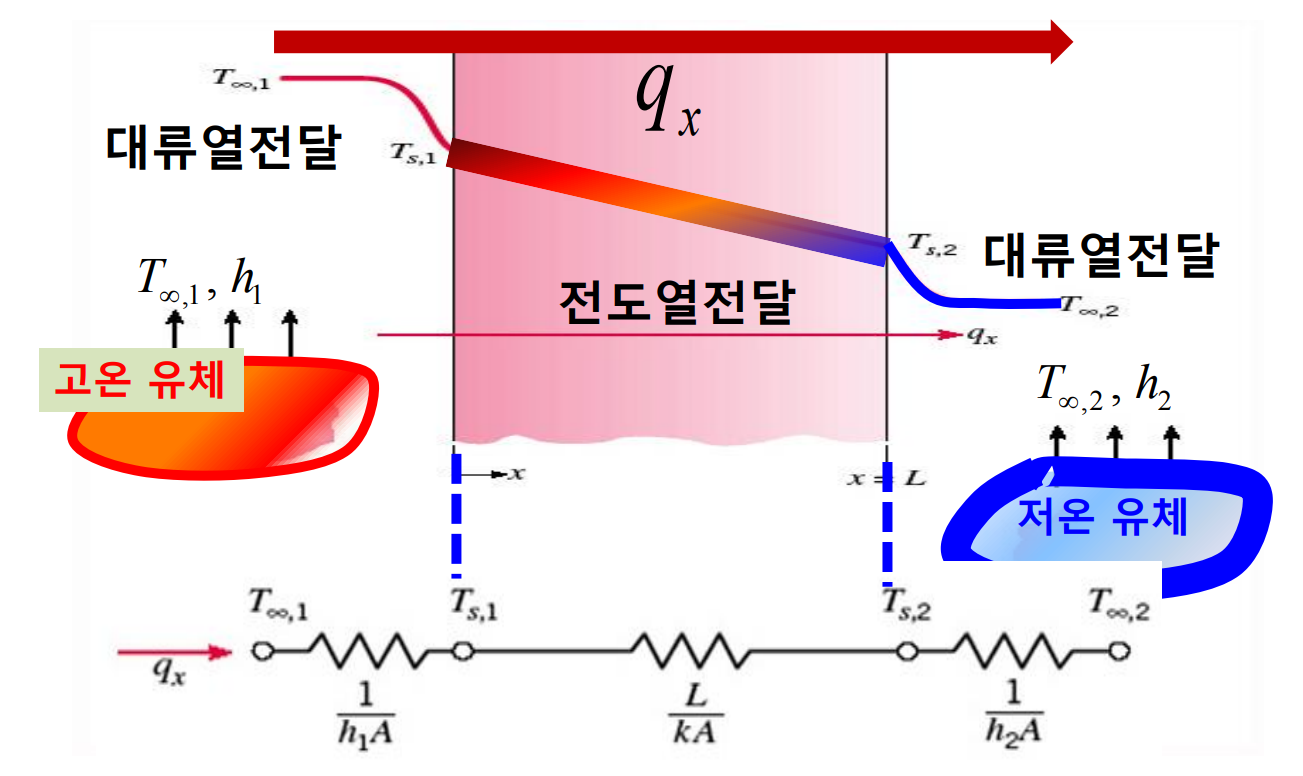
열전달률을 구하기 위해 Fourier의 법칙을 사용하면 다음과 같다.
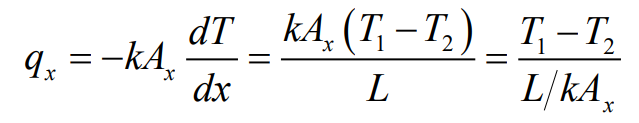
원통벽에서 열전달률 $q_r$은 다음과 같이 반지름 방향으로 일정하다.
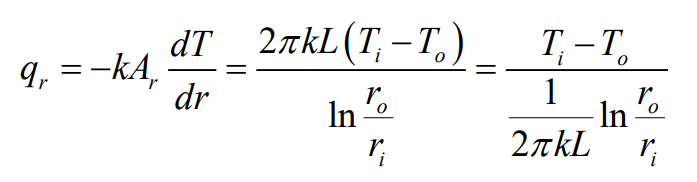
열전달률은 다음과 같은 형태로 표현될 수 있다.
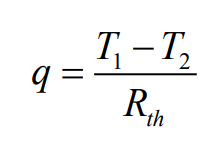
여기서 $R_{th}$로 표현된 양은 열저항(thermal resistance)이라고 부르며 열전달의 방식에 따라 다음과 같이 다른 형태를 가지고 있다.

다음 예제를 보자.
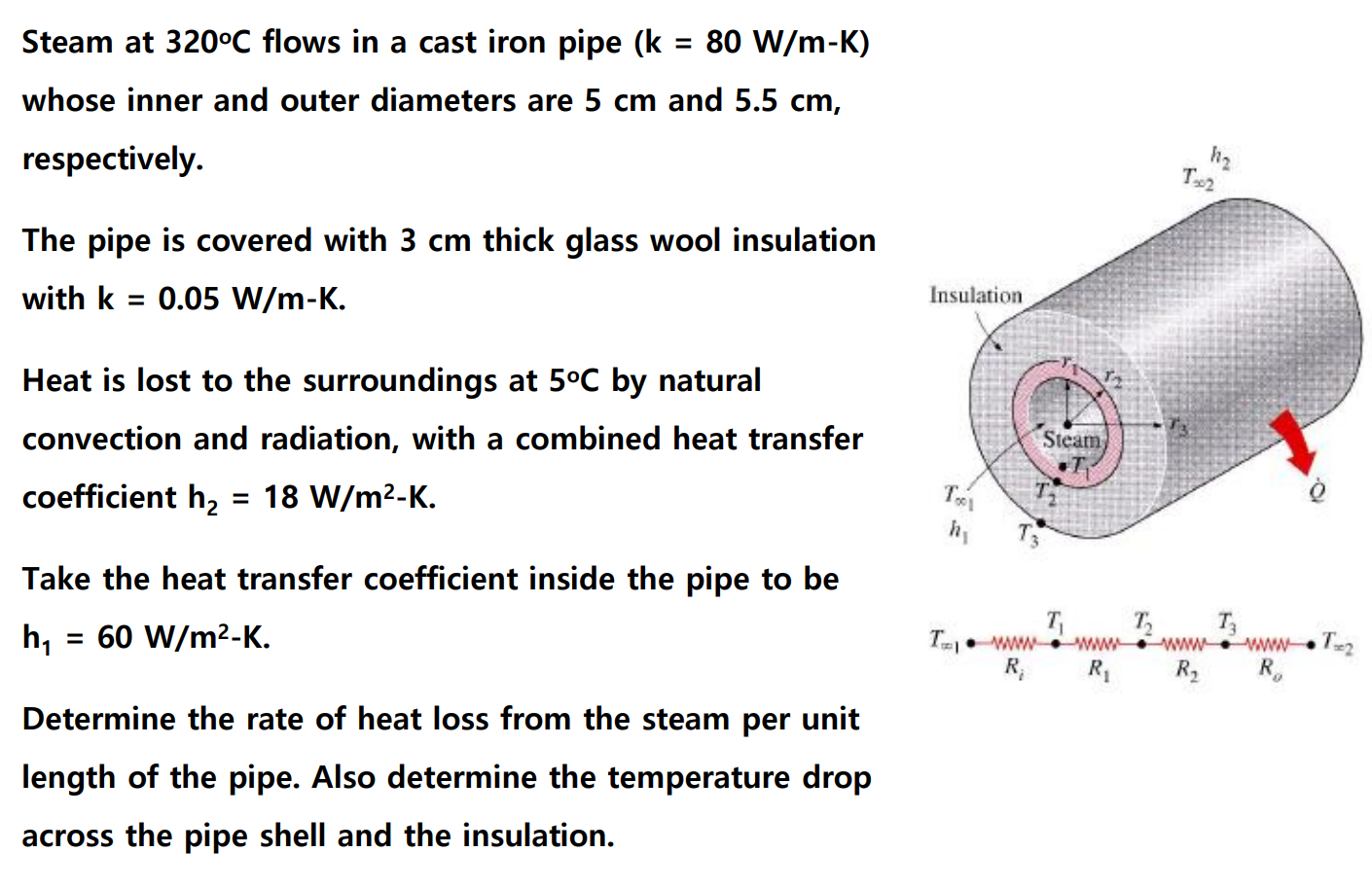

복합계에 있어서 열관류계수(overall heat transfer coefficient) $U$를 사용하는 것이 편리하다.
여기서 $\Delta T$는 총합 온도차이다. 열관류계수는 총 열저항과 관련되어 있으며 $UA = 1 / R_{tot}$이다. 다음과 같은 복합벽을 보자.
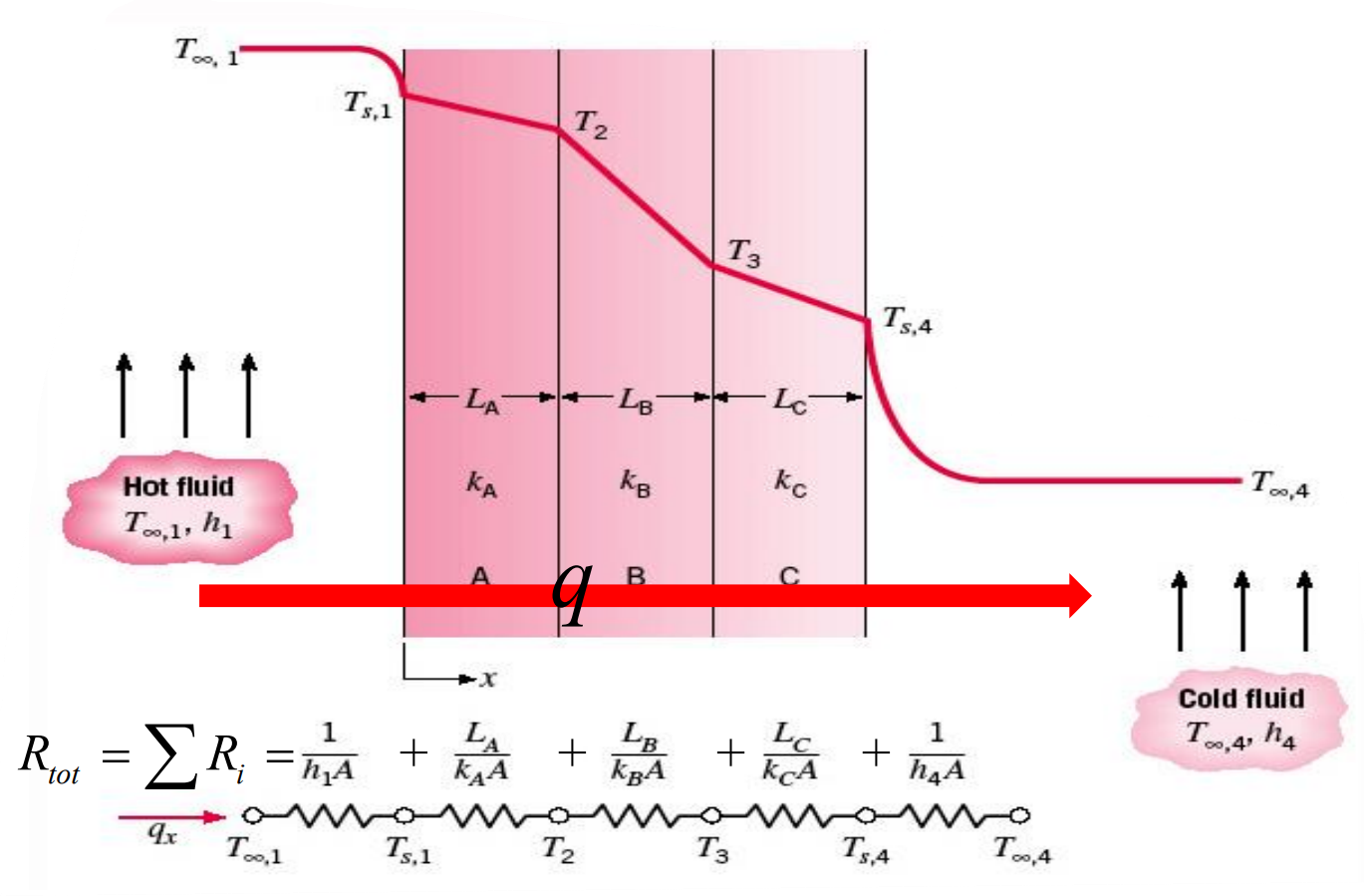
위에서 열관류계수는 다음과 같다.
일반적으로 다음과 같이 쓸 수 있다.
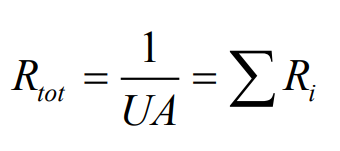
원형관에서 다음과 같은 복합계를 생각해보자.
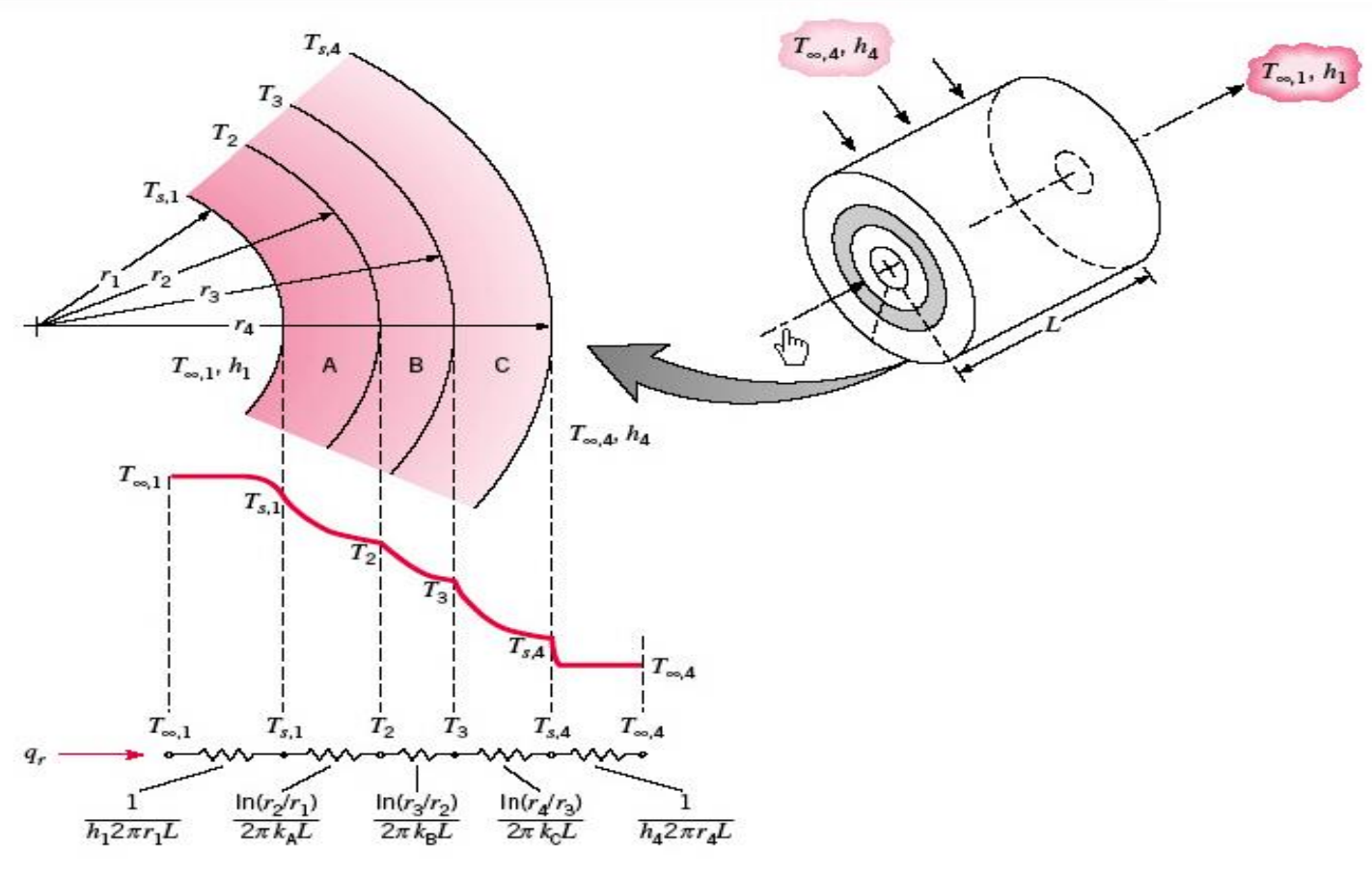
열전달률은 다음과 같이 나타낼 수 있다.
위 결과를 열관류계수의 항으로 나타낼 수 있다.
확장표면
확장표면(extended surface)은 대류 열전달을 증가시키기 위해 추가되는 열전달 면이다. 이러한 확장표면을 휜(fin)이라 한다. 휜에서는 다음과 같은 식들이 성립한다.

다음 예제를 보자.
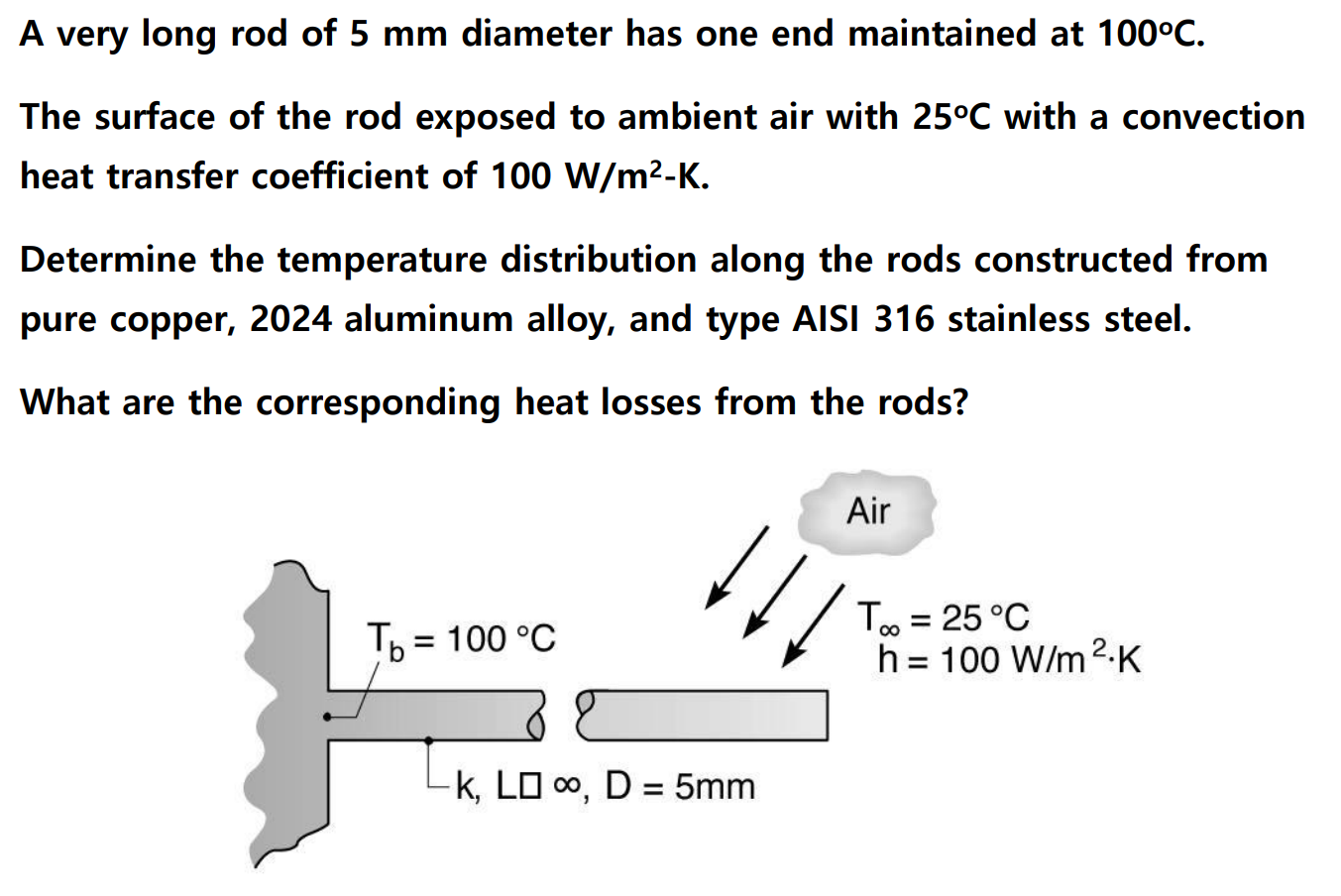
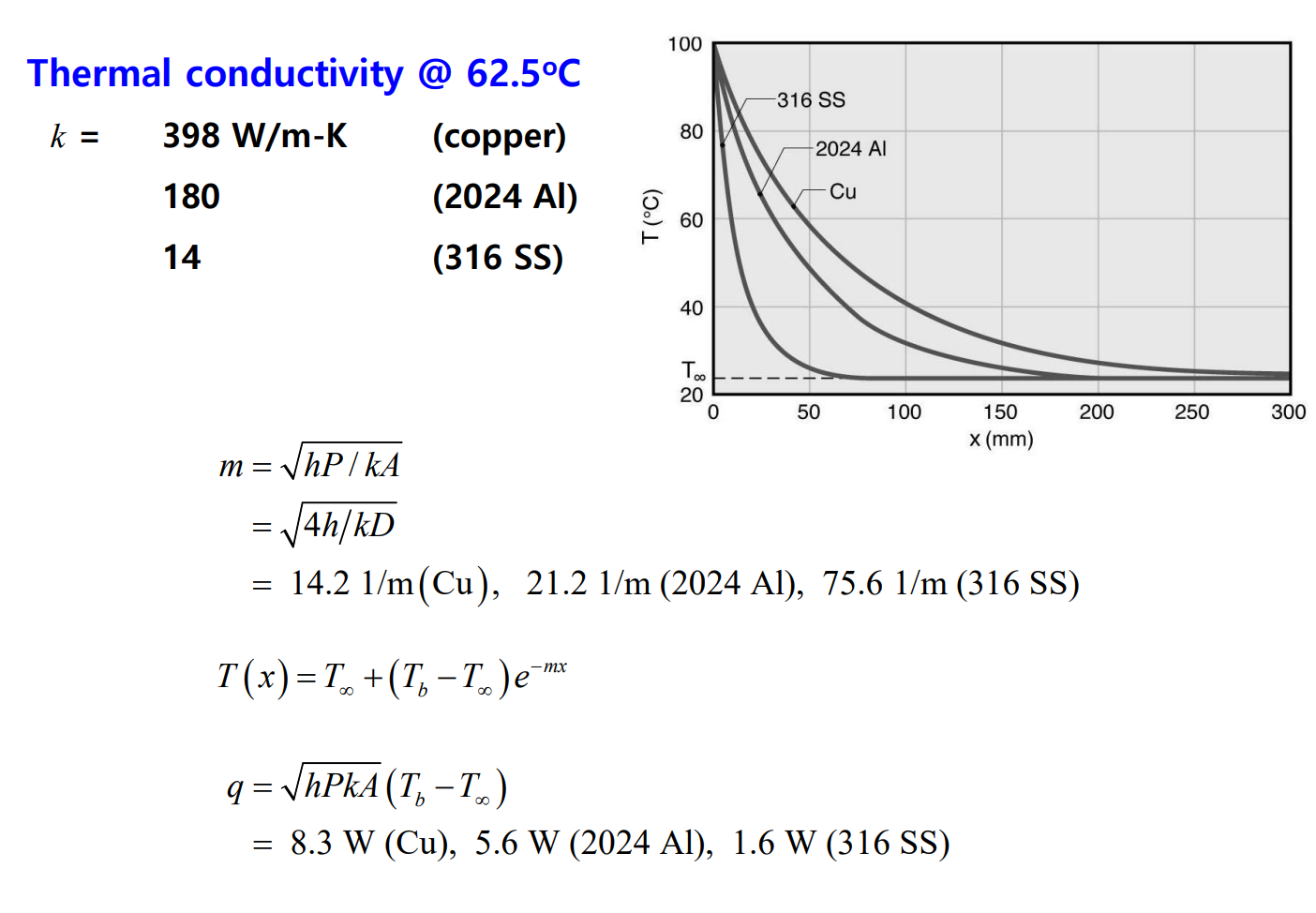
대류(Convection)
대류열전달의 방정식의 형태는 다음과 같다.
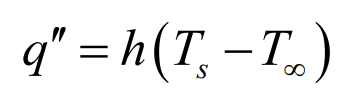
여기서 대류 열유속 $q^{\prime\prime}$(W/$m^2$)은 표면온도 $T_s$와 유체온도 $T_{\infty}$ 사이의 온도차에 비례한다. 이 식을 Newton의 냉각법칙(Newton`s law of cooling)이라 하고 비례상수 $h$([W/$m^2$K])를 대류열전달계수(convection heat tracsfer coefficient)라 한다.
대류계수에서부터 다음과 같은 무차원 매개변수를 정의할 수 있다.

이 식을 Nusselt 수라고 하는 무차원 매개변수라고 한다.
대류 열전달은 다음과 같이 분류할 수 있다.

강제 외부대류
열전달 관계식은 다음과 같다.

평판위에서 Re 수에 따른 Nu 수는 다음과 같은 관계를 가지고 있다.
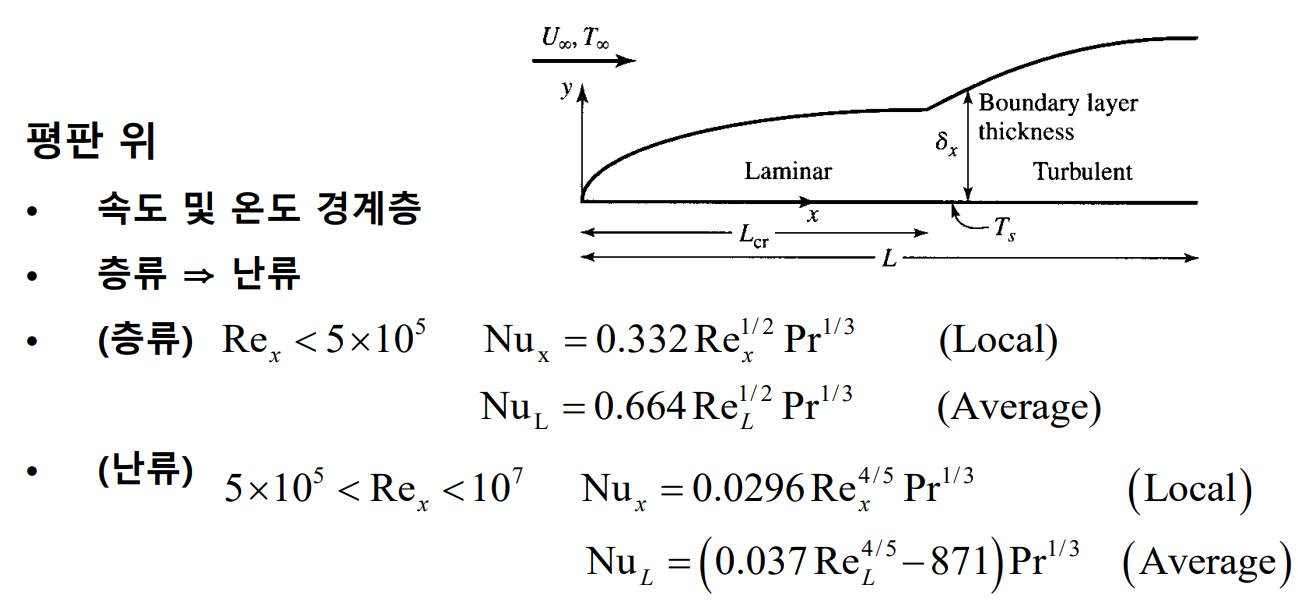
원통의 축에 수직인 유체흐름을 생각해보자.
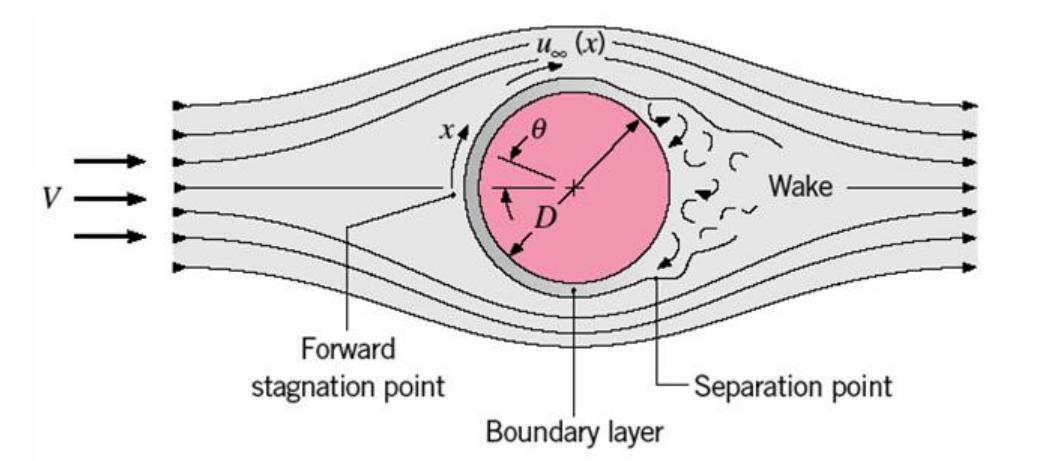
유체는 압력의 증가와 함께 전방 정체점(forward stagnation point)에서 정지하게 된다. 평판 위의 평행 유동 조건과 달리 $u_{\infty}$는 정체점으로부터의 거리 $x$에 의존한다. 유체가 감속됨에 따라 표면 위치에서 속도구배는 결국 0이 될 것이다. 이 점을 박리점(separation point)이라 하며, 이 위치에서부터 유체는 압력구배를 극복하기 위한 운동량이 부족해서, 하류로의 계속적인 흐흠은 불가능하게 된다. 또한 뒤따라 오는 유체가 상류로의 흐름을 방해하기 때문에 경계층 박리(boundary layer separation)가 일어나게 된다. 이것이 경계층이 표면으로부터 이탈되는 조건이며, 이후의 하류영역에서는 후류(wake)가 생성된다.
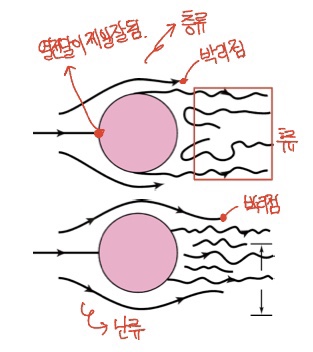
국소 Nusselt 수에 대한 상관식은 다음과 같이 얻어질 수 있고 상수 $C$와 $m$은 다음과 같다.

관군을 가로지르는 유동을 생각해보자.
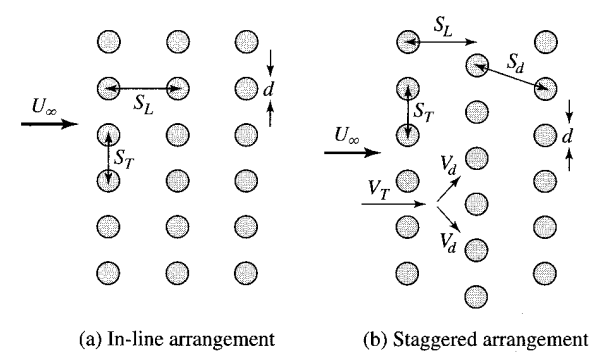
관군의 열(row)은 유체속도($U_{\infty}$)의 방향에서 엇갈림(staggered)으로 놓여 있거나 정렬(aligned)되어 놓여 있다. 배열은 관 지름 $d$, 관 중심 사의를 측정한 가로피치(transverse pitch) $S_T$와 세로피치(longitudinal pitch) $S_L$에 의한 특성을 갖는다. 관군 내의 흐름조건은 경게층 박리의 영향과 후류의 상호작용에 의하여 지배되며, 결과적으로 대류열전달에 영향을 미친다.
$S_L$이 큰 경우에는 상류의 열에 대한 영향이 적어지고 후류열들의 열전달도 덜 촉진된다. 이와 같은 이유로, $S_T/S_L < 0.7$인 정렬배열인 관군에서는 운전이 바람직하지 않다. 엇갈림 배열의 경우에는, 주흐름의 결오가 굴곡을 이루고 정렬배열의 관 배열에 비해 직교유동 우체의 혼합이 증가한다. 일반적으로 엇갈림 배열에서 흐름이 더욱 많이 꼬불꼬불해질수록 열전달의 촉진 면에서 유리하다.
전체 관군에 대한 평균 열전달계수를 알아보자.
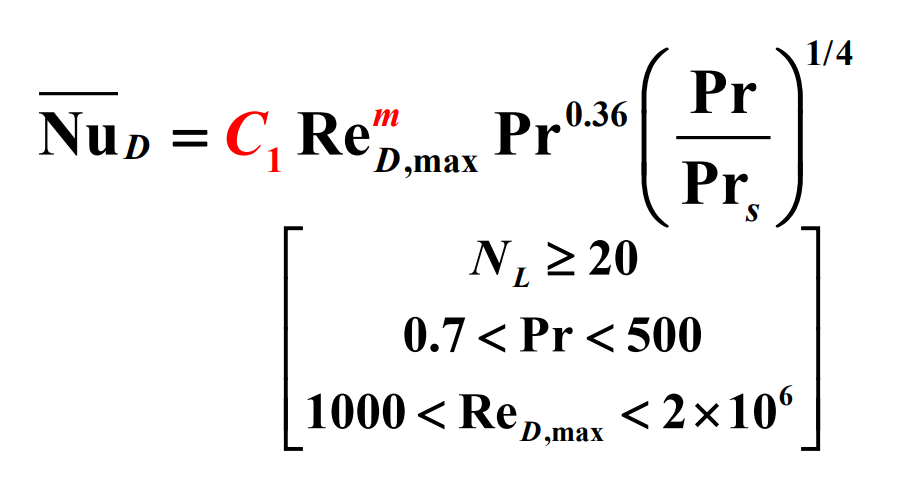
여기서 $N_L$은 관 열의 수이고, $Pr_s$를 제외한 모든 물성치들은 유체의 입구온도($T_i = T_{\infty}$)와 출구온도($T_o$)의 산술평균 온도에서의 값이다. 만약 관 열의 개수가 20개 또는 그 이하인 경우, 평균 열전달계수는 일반적으로 더 많은 관을 갖는 관군에 비해 상대적으로 감소하는데, 다음과 같은 수정계수를 사용할 수 있다.
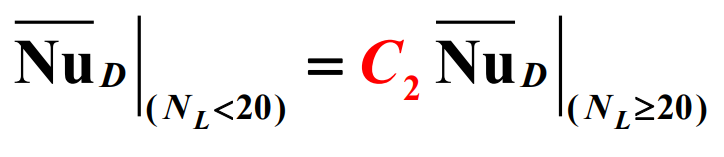
상수 $C_1$과$C_2$, $m$은 다음과 같다.
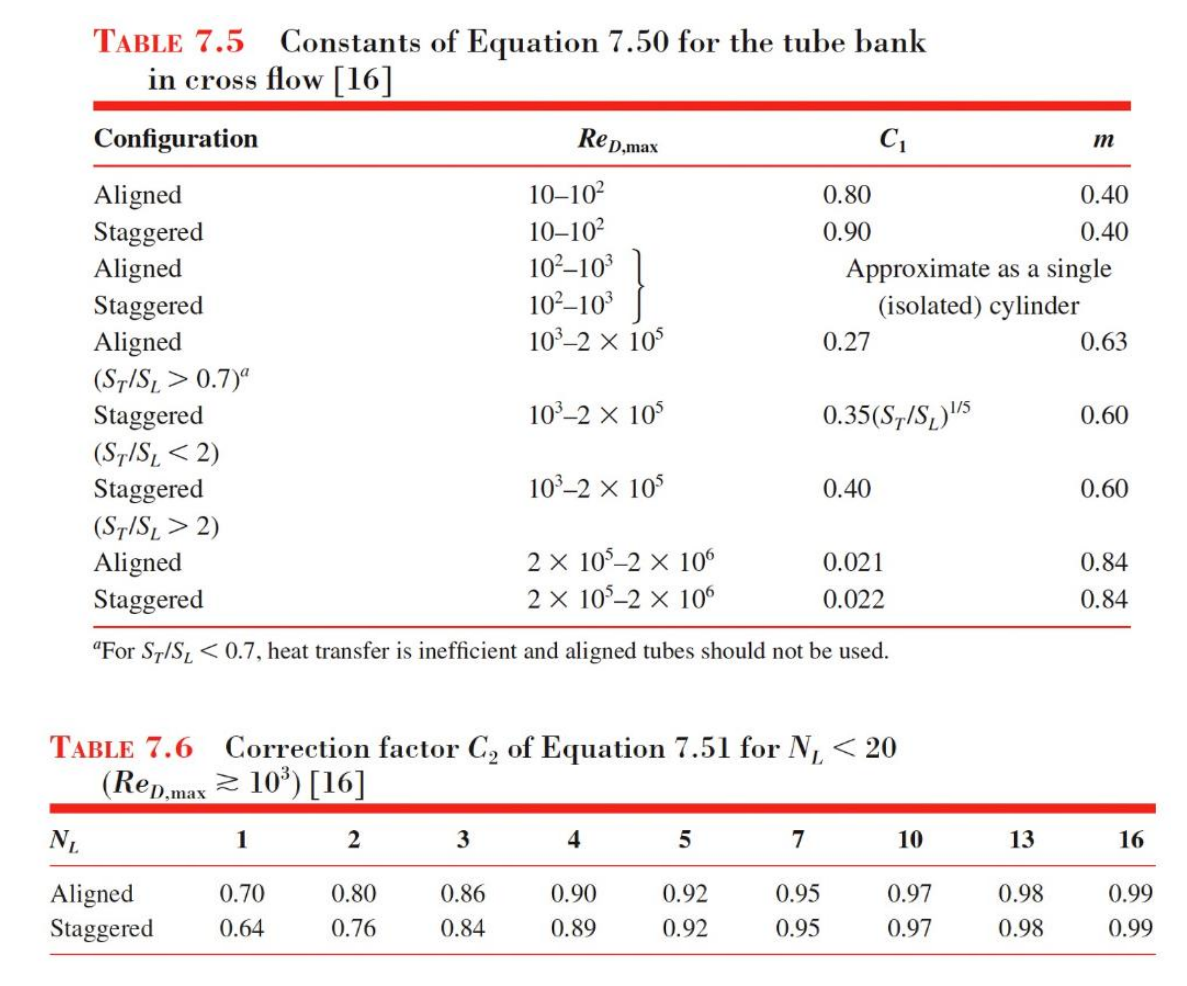
위 상관식들에 대한 Reynolds 수 $Re_{D, max}$는 관군 내에서 일어나는 최대 유체속도에 기초를 둔 것이다. 정렬배열에서 $V_{max}$는 다음과 같이 $A_1$에서 일어나며, 값은 다음같다.
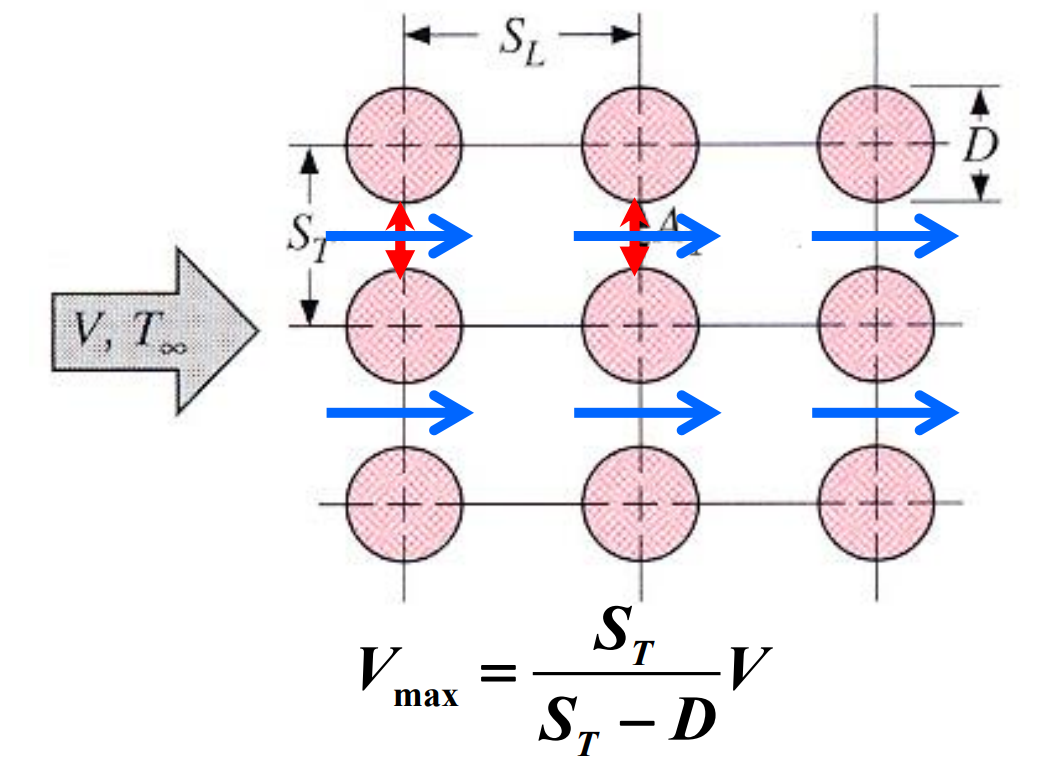
엇갈림 배열에서 최대속도는 횡단면 $A_1$ 또는 대각선면 $A_2$에서 일어날 수 있다.
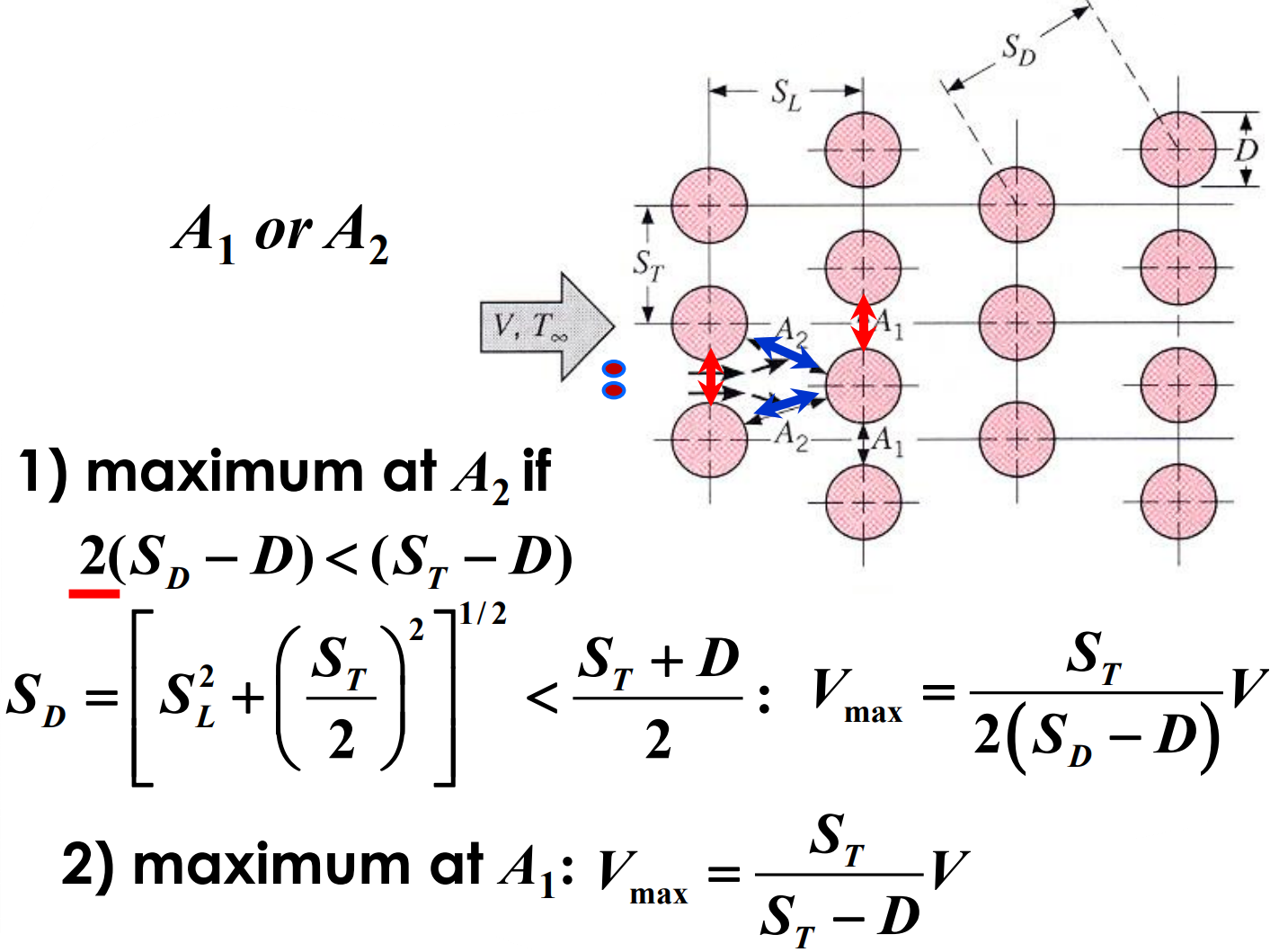
유체가 관군을 지나는 동안 온도변화가 크므로 Newton의 냉각법칙에서 온도차로서 $\Delta T = T_s - T_{\infty}$를 사용하면, 열전달률이 과도하게 예측될 수도 있다. 유체가 관군을 통과할 때, 유체의 온도는 $T_s$에 접근하고 $|\Delta T|$는 감소한다. $\Delta T$의 적절한 형식은 대수평균 온도차(log-mean temperature difference)로 다음과 같다.
여기서 $T_i$와 $T_o$는 유체가 각각 관군으로 들어올 때와 관군에서 나갈 때의 유체온도이다. $\Delta T_{lm}$을 결정하는 데 필요한 출구온도는 다음 식으로부터 얻을 수 있다.
여기서 $N$은 관군 내의 관의 총수이며, $N_T$는 횡단면에서의 관의 수이다. $\Delta T_{lm}$을 알게 되면, 관들의 단위 길이당 열전달률은 다음 식으로부터 계산될 수 있다.
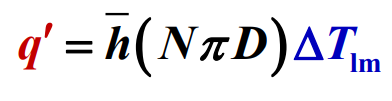
일반적으로, 관군을 지나는 흐름과 관련된 열관류율(overall heat transfer rate)과 함께 이와 관련된 압력강하에도 큰 관심이 있다. 관군을 지나는 유체를 흐르게 하는 데 필요한 동역은 운전경비의 대부분을 차지하며, 이것은 다음 식에서 보여 주는 바와 같이 압력강하에 정비례한다.
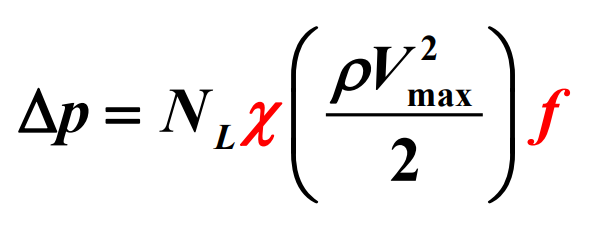
마찰계수(friction factor) $f$와 수정계수(correction factor) $\chi$는 다음과 같다.
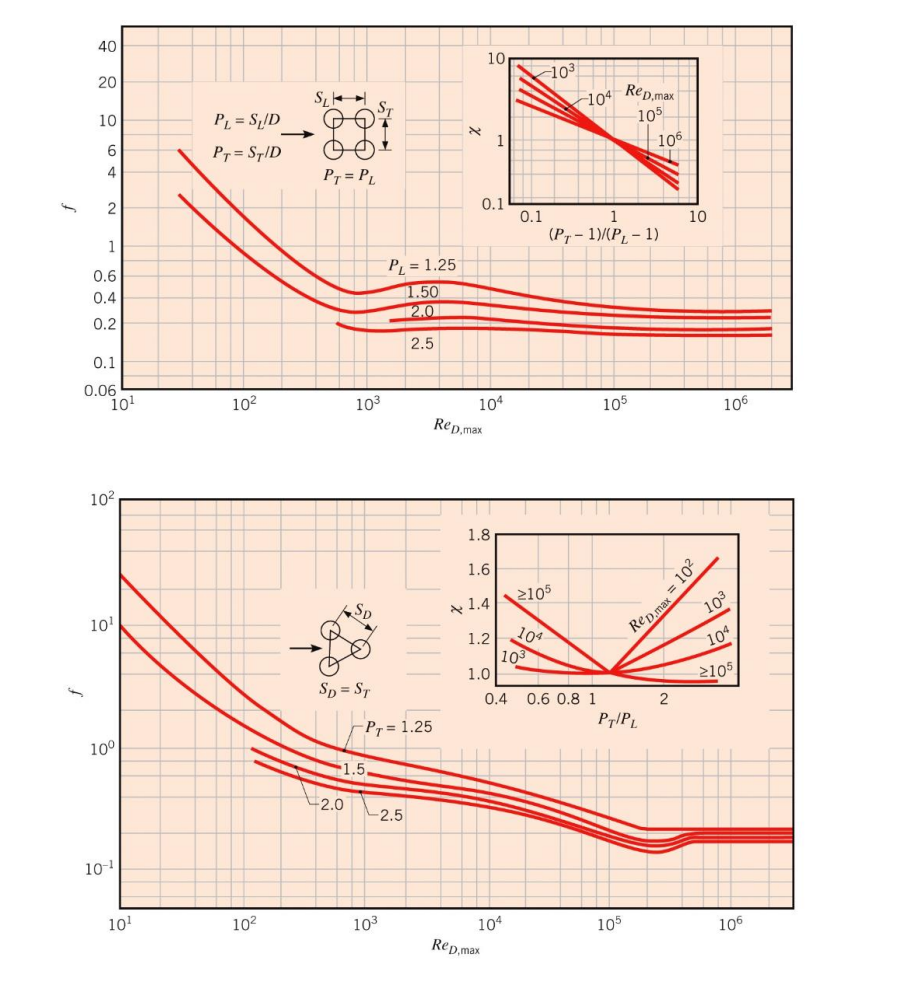
다음 예제를 보자.

강제 내부대류
평균온도 $T_m$은 내부유동에서 편리한 기준 온도로서, 외부유동에서의 자유유동 온도 $T_{\infty}$와 똑같은 역할을 한다. 따라서 Newton의 냉각법칙은 다음과 같이 표현될 수 있다.
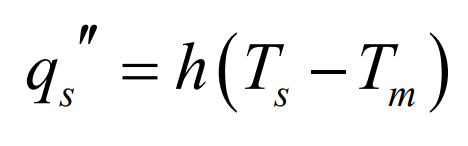
여기서 $h$는 국소 대류열전달계수이다.
원형관 내의 층류유동에서 대류 상관식은 다음과 같다.

위 식에서 $\mathrm{Nu}_D = 4.36$은 균일 표면열유속, 층류, 완전발달한 조건 등을 특성으로 하는 원형관에서 성립하고 일정 표면온도의 층류, 완전발달 조건들에 대해서는 $\mathrm{Nu}_D = 3.66$이 성립한다.
원형관 내의 난류유동에서 대류 상관식은 다음과 같다.
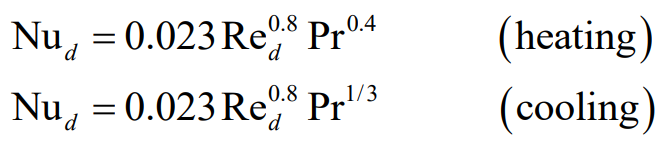
위 식에서 $\mathrm{Pr}$의 지수의 경우 가열에 대해서 $0.4$이며, 냉각에 대해서는 $0.3$이다.
입구 길이는 다음과 같이 구할 수 있다.
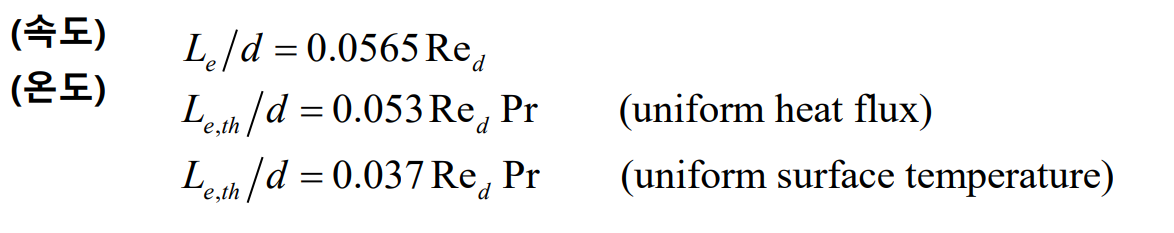
다음 예제를 보자.


자연대류
강제속도가 없는경우에 유체 중에 대류유동이 존재하는 상황에 대하여 고려해 보자. 이러한 상황을 자유대류(free convection) 또는 자연대류(natural convection)라 하며, 이들은 밀도구배(density gradient)가 존재하는 유체에 체적렬(body force)이 작용할 때 발생한다. 자연대류의 유동속도는 일반적으로 강제대류에 의한 것보다 훨씬 작으므로, 이에 대응하는 대류전달률도 작다.
자연대류에 대한 열전달 관게식은 다음과 같다.

외부 자유대류 유동중 수직평판에 대해 알아보자. 전체 영역이 $\mathrm{Re}_L$에 대하여 적용할 수 있는 상관식은 다음과 같다.
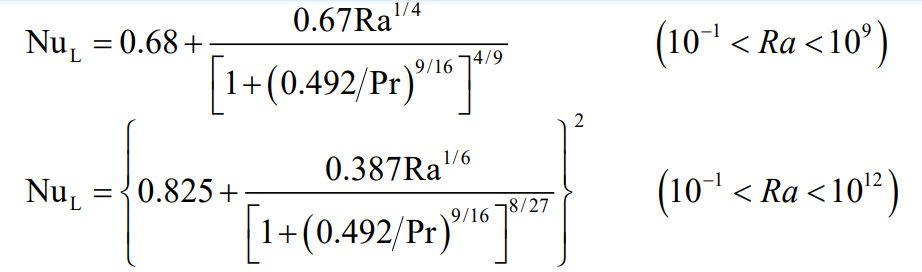
위 결과는 등온평판(일정 $T_s$)에 대하여 얻어진 것이다. 표면조건이 균일한 열유속(일정 $q_s^{\prime \prime}$) 이면, 온도차($T_s - T_{\infty}$)는 선단에서 0의 값에서부터 증가하면서 $x$에 따라 변화할 것이다. 이 변화에 대한 근사적 방법은 $\bar{\mathrm{Nu_L}}$과 $\mathrm{Ra_L}$을 평판의 중간지점에서의 온도차 $\Delta T_{L/2} = T_s(L/2) - T_{\infty}$를 사용하여 정의하면, 등온평판에 대하여 구해진 $\bar{Nu_L}$ 상관식을 근사로 이용할 수 있다.
수평평판에 적용할 수 있는 상관식은 다음과 같다.

수평평판에서는 Nusselt 수를 이용하기 위해 특성길이를 정의해야 한다. 특성길이를 $L = \frac{A_s}{P}$로 정의하면 한가지 종류의 상관식이 여러 다른 모양의 평판에 적용될 수 있다. 여기에서 $A_s$는 평판의 한쪽 면의 표면적이며 $P$는 주변길이(perimeter)이다.
긴 수평 원통(실린더)에 대해서는 다음 식을 사용할 수 있다.
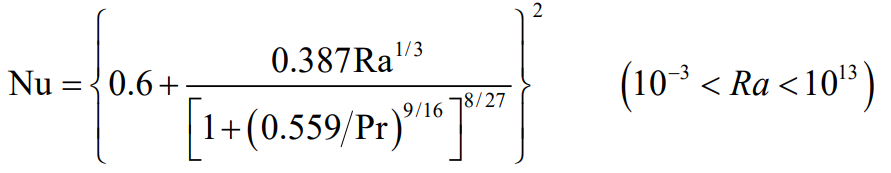
위 식에서는 $\mathrm{Ra_D}$와 $\bar{\mathrm{Nu_D}}$는 원통지름에 기초를 두었다.
열교환기
서로 다른 온도와 고체벽으로 분리된 두 유체들 사이의 열교환 과정은 많은 공업 응용분야애서 일어나고 있다. 이 열교환을 수행하는 장치를 열교환기(heat exchanger)라 하며 난방, 공기조화, 동력발생, 폐열회수 그리고 화학공정 등에서 찾아볼 수 있다.
열교환기의 형식
열교환기는 유동배열(flow arrangement)과 구조의 형태(type of construction)에 따라 분류된다. 가장 간단한 열교환기는 동심관(concentric) 또는 이중관(double pipe) 구조에서 고온의 유체와 저온의 유체가 같은 방향 또는 반대 방향으로 흐르는 열교환기이다.
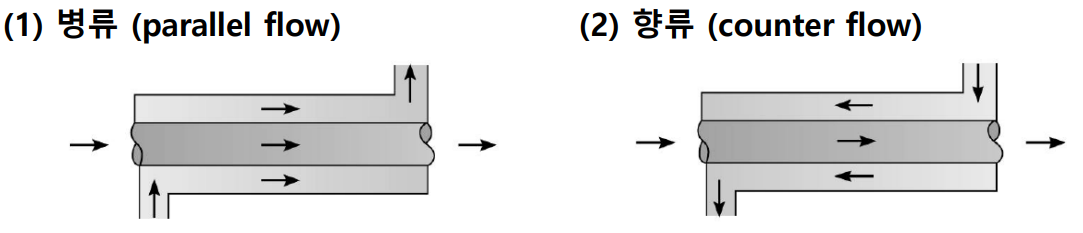
위에서 (1)의 평행유동(parallel-flow) 배열에서는 고온 및 저온의 유체들이 같은 끝면에서 들어와서, 같은 방향으로 흐르고, 같은 끝면으로 나간다. (2)의 대항유동(counterflow) 배열에서는 유체들이 반대쪽 끝면에서 들어와서 반대 방향으로 흐르고, 서로 반대측 끝면으로 나간다.
위의 경우와 달리 휜이 있거나 휜이 없는 관형 열교환기들에 의해 표시된 것처럼 유체들이 직교유동(cross flow, 서로 수직)으로 흐를 수도 있다. 두 장치는 관의 바깥을 지나는 유체가 혼합되지 않았는가(unmixed), 혼합되었는가(mixed)에 따라 구별된다.
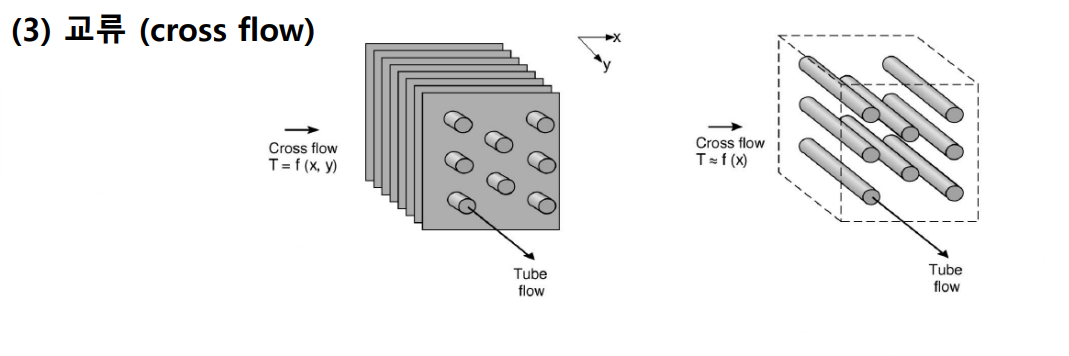
위 그림의 왼쪽에서 휜이 주유동방향($x$)을 가로지르는 방향($y$)으로의 유동을 막기 때문에 유체는 혼합되지 않았다고 말한다. 이 경우, 유체온도는 $x$와 $y$에 따라 변한다. 반면에 오른쪽의 휜이 없는 관군에서는 가로지르는 방향으로 유체의 운동으로 인해 혼합이 가능하며 온도변화는 주로 주유동방향에 따른다. 관유동은 혼합되지 않으므로 휜이 있는 열교환기에서는 두 유체 모두 혼합되지 않으며, 휜이 없는 열교환기에서는 한 유체는 혼합되고 다른 유체는 혼합되지 않는다. 혼합조건의 성질은 열교환기 성능에도 큰 영향을 미칠 수 있다.
열교환기의 해석 및 설계 방법은 다음과 같다.

대표적인 열교환기는 다음과 같다.
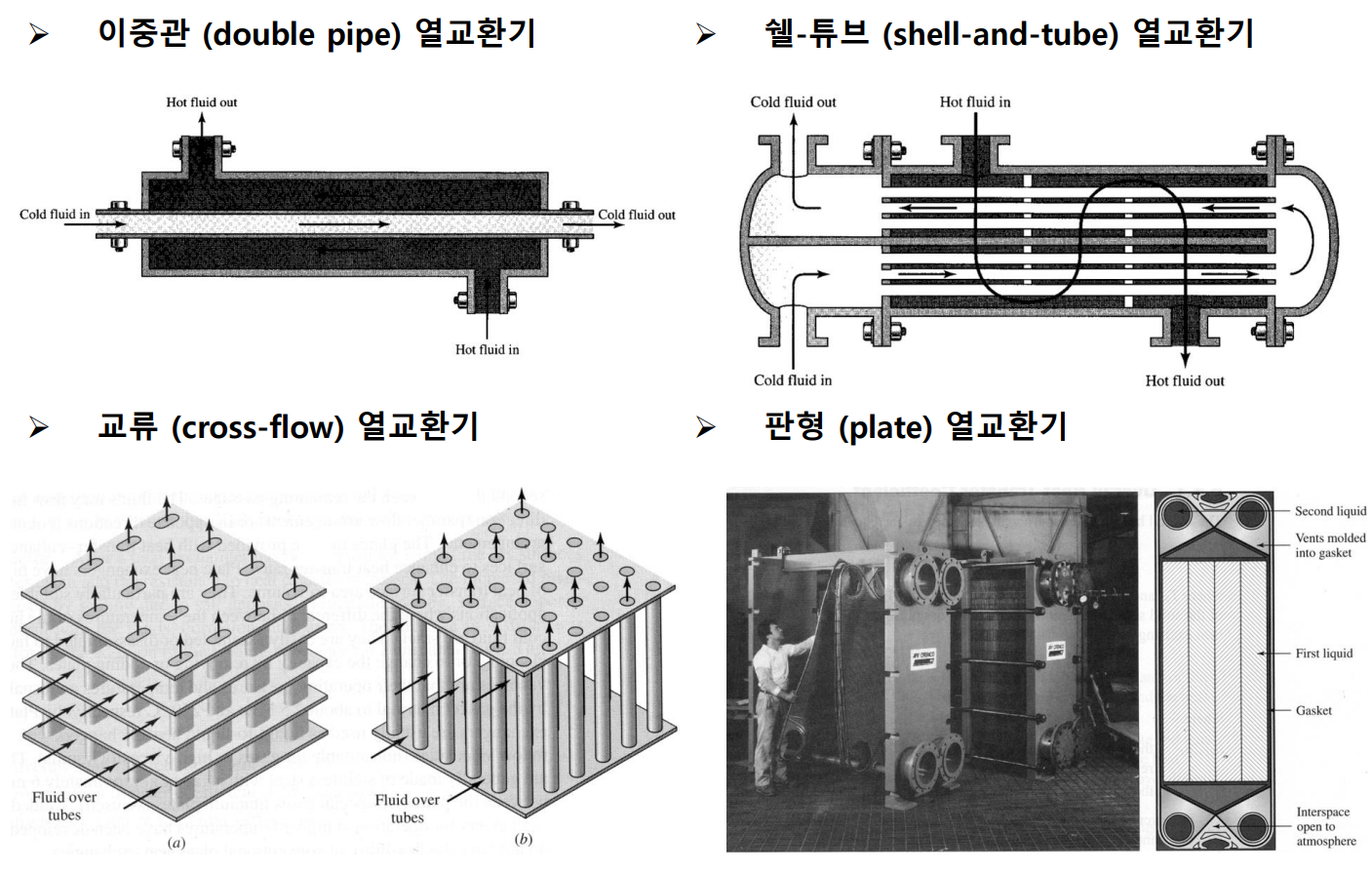
열관류계수
모든 열교환기의 해석에 있어서 필수적이지만, 종종 가장 불확실한 부분은 열관류계수(overall heat transfer coefficient, 총합 열전달계수)를 결정하는 일이다. $R_{tot} = \frac{\Delta T}{q} = \frac{1}{UA}$ 로부터, 이 계수는 두 유체들 사이의 열전달에 대한 전체 열저항으로 정의된다. $U = \frac{1}{R_{tot}A} = \frac{1}{[(1/h_1) + (L_A/k_A) + (L_B/k_B) + (L_C/k_C) + (1/h_4)]}$과 $U_1 = \frac{1}{\frac{1}{h_1} + \frac{r_1}{k_A}\ln(\frac{r_2}{r_1}) + \frac{r_1}{k_B}\ln(\frac{r_3}{r_2}) + \frac{r_1}{k_C}\ln(\frac{r_4}{r_3}) + \frac{r_1}{r_4} \frac{1}{h_4}}$에서 이 계수는 각각 복합 평면벽과 복합 원통형 벽에 의해 분리된 유체들 사이의 전도저항과 대류저항을 고려하여 결정된다. 두 유체 흐름으로 분리된 벽면에 대한 열관류계수는 다음과 같다.
아래첨자 $c$와 $h$는 각각 고온과 저온의 유체를 의미한다. 전도저항 $R_w$는 평판에 관한 식 $R_{t, cond} = \frac{T_{s,1} - T_{s,2}}{q_x} = \frac{L}{kA}$로부터 또는 원통 벽면에 대한 식 $R_{t, cond} = \frac{\ln (r_2/r_1)}{2\pi L k}$으로부터 얻어진다.
불결계수(fouling factor) $R_f$로 정의된 추가적인 열저항은 열교환기를 장시간 운전시, (특히 액체와 접하는) 표면에 생성된 퇴적물(scale, deposits), 부식(corrosion) 등에 의해 추가되는 열저항이다.

열교환기의 기본 해석
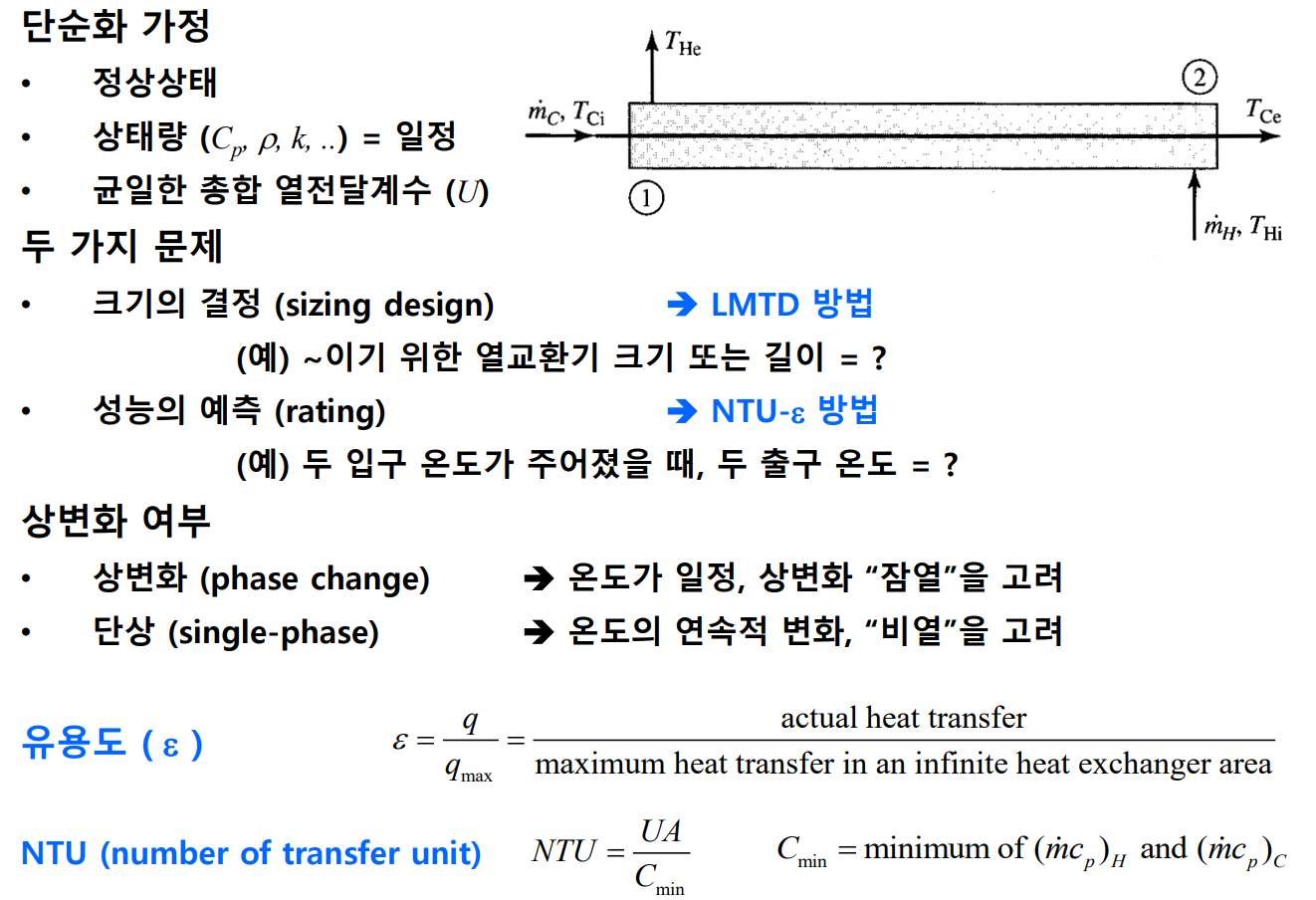
LMTD(로그평균 온도차) 방법
열교환기를 설계하거나 성능을 예측하기 위해서는 총 열전달률을 입구와 출구의 유체온도, 열관류계수 그리고 열전달을 위한 총 표면적의 양과 관련시키는 것이 필수적이다. 이와 같은 관계는 다음과 같은 고온유체와 저온유체에 총 에너지평형을 적용시킴으로써 쉽게 얻을 수 있다.
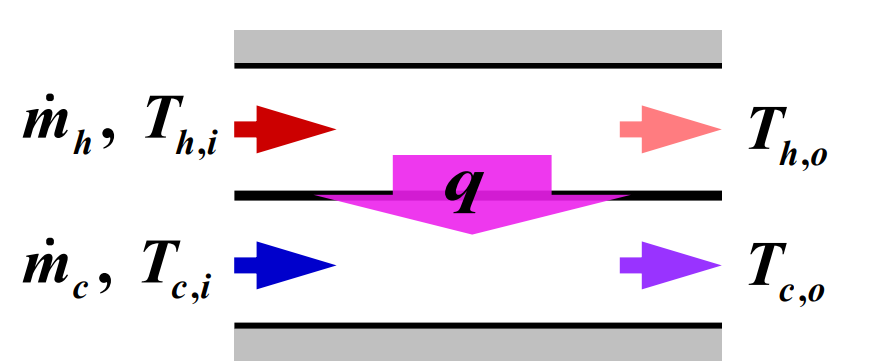
$q$가 고온유체와 저온유체 사이의 총 열전달률이고, 열교환기와 그 주변 사이의 열전달을 무시할 수 있으며, 위치에너지와 운동에너지의 변화들도 무시할 수고 유체가 상변화를 일으키지 않고 비열들이 일정하다고 가정하면 에너지평형식은 다음과 같다.
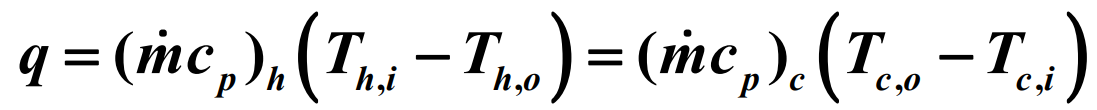
총 열전달률 $q$를 고온유체와 저온유체 사이의 온도차 $\Delta T = T_h - T_c$와 연관지어 식을 얻을 수 있다. 대류열전달계수 $h$ 대신에 열관류계수 $U$를 사용한 Newton의 냉각법칙을 확장하면 다음과 같다.
여기서 $\Delta T_m = \Delta T_{lm} = \frac{\Delta T_1 - \Delta T_2}{\ln(\frac{\Delta T_1}{\Delta T_2})}$이다. 교류 및 쉘-튜브 등에는 수정계수(correction factor)를 이용한다. 다음 예제를 보자.
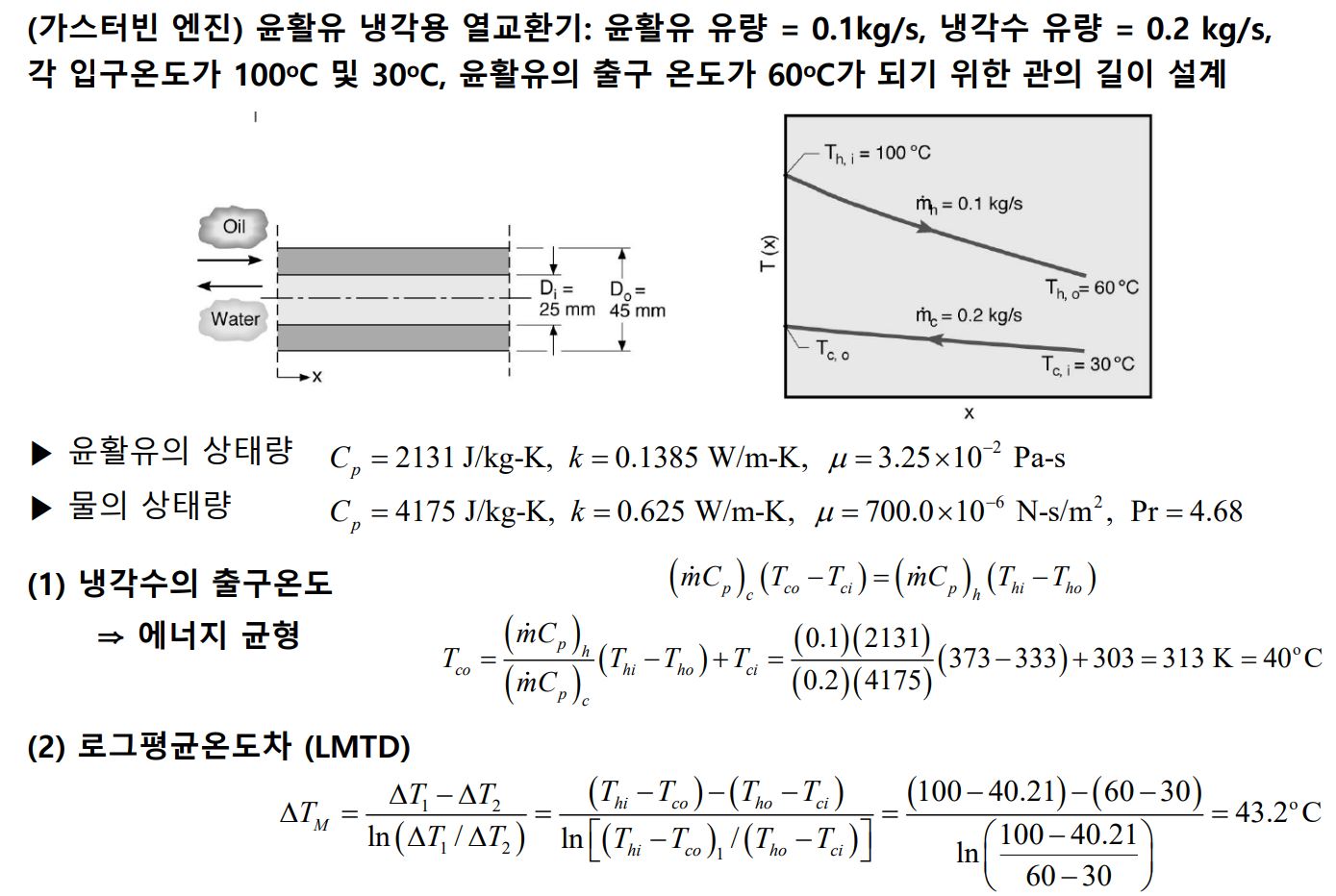

NTU-유용도 방법
유체의 입구온도들이 제시되어 있고, 유체의 출구온도들이 주어지거나 에너지평형식으로부터 쉽게 구할 수 있을 때 LMTD 방법을 사용하면 쉽게 열교환기 해석을 수행할 수 있다. 그러나 단지 입구온도들만이 주어져 있다면 LMTD 방법을 사용할 때에 반복계산을 해야한다. 이러한 경우 유용도-NTU 법(effectiveness-NTU method)이라 불리는 또 다른 방법을 사용하는 것이 바람직하다.
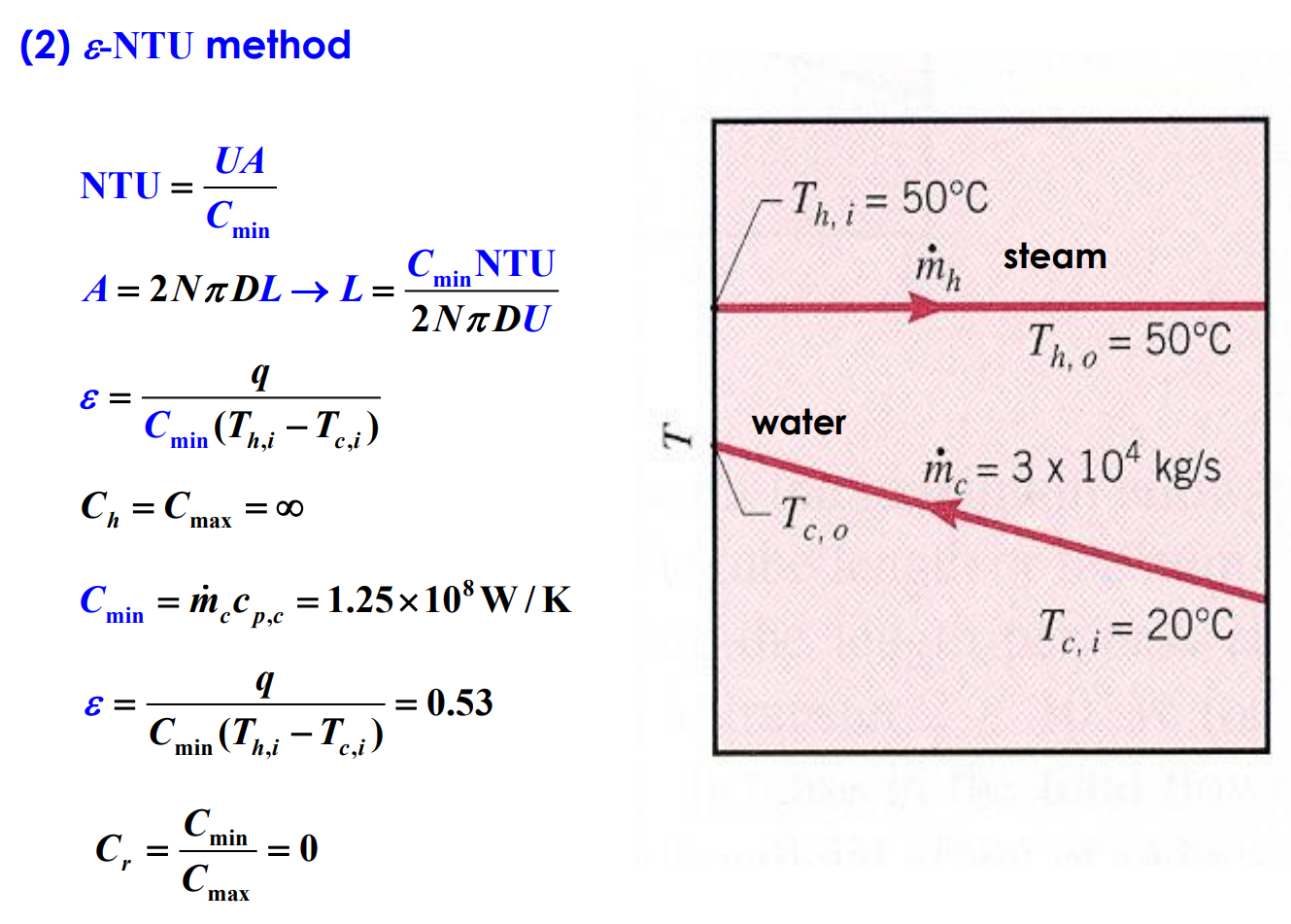
열교환기의 유용도를 정의하기 위해 먼저 열교환기에 대한 최대 가능 열전달률 $q_{max}$를 결정해야한다. 열교환기에서 유체들 중의 한 유체는 최대 가능 온도차 $T_{h, i} - T_{c, i}$를 가질 수 있다. 이는 용량 유량($C = mc_p$)이 작은 유동으로 결정된다.
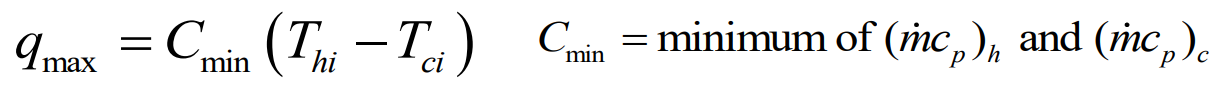
유용도 $\varepsilon$을 열교환기에 대해 최대 가능한 열전달률에 대한 실제 열전달률의 비로서 정의하는 것이 적절하다.
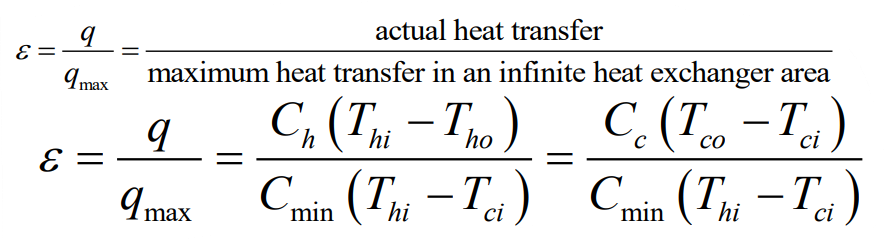
실제 열전달률은 다음 식으로부터 쉽게 결정할 수 있다.
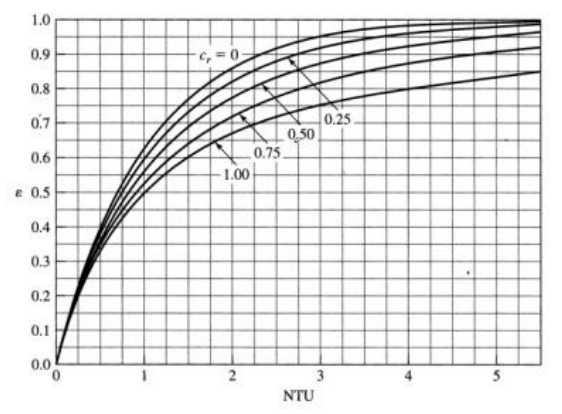
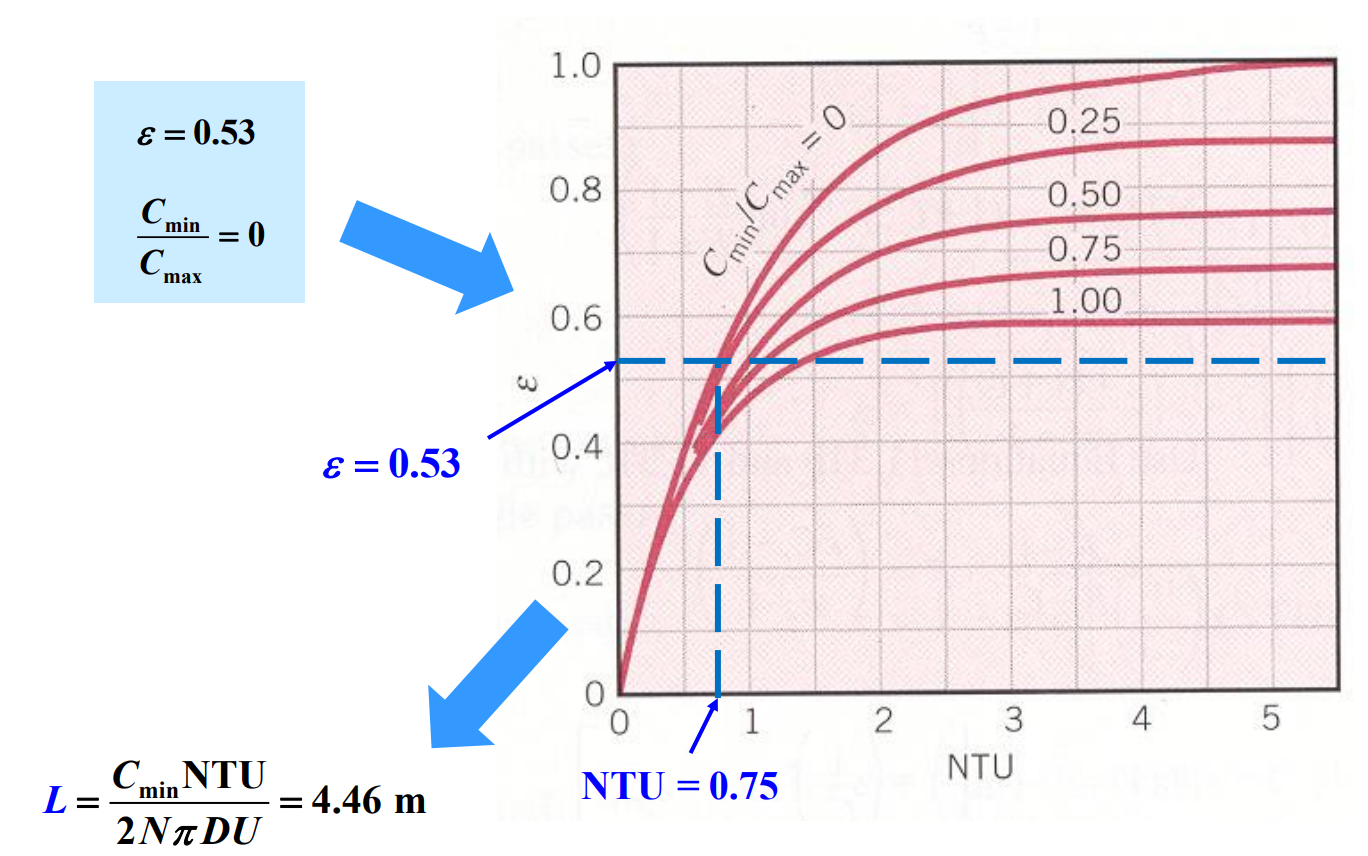
열교환기에 대해서 $\varepsilon = f(\mathrm{NTU}, C_r)$로 표시할 수 있는데 여기서 $C_r = C_{min} / C_{max}$이다. 전달단위수(NTU, number of transfer unit)는 열교환기의 해석에서 널리 사용되는 무치원 매개변수이며, 다음과 같이 정의된다.
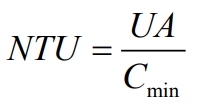
유용도는 대향유동(향류, counter flow)에 대해 다음과 같이 구할 수 있다.
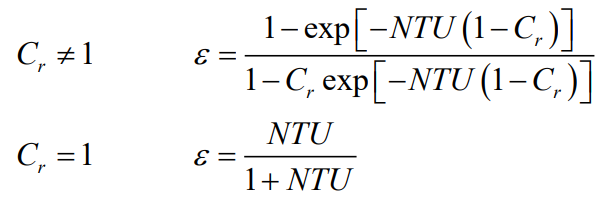
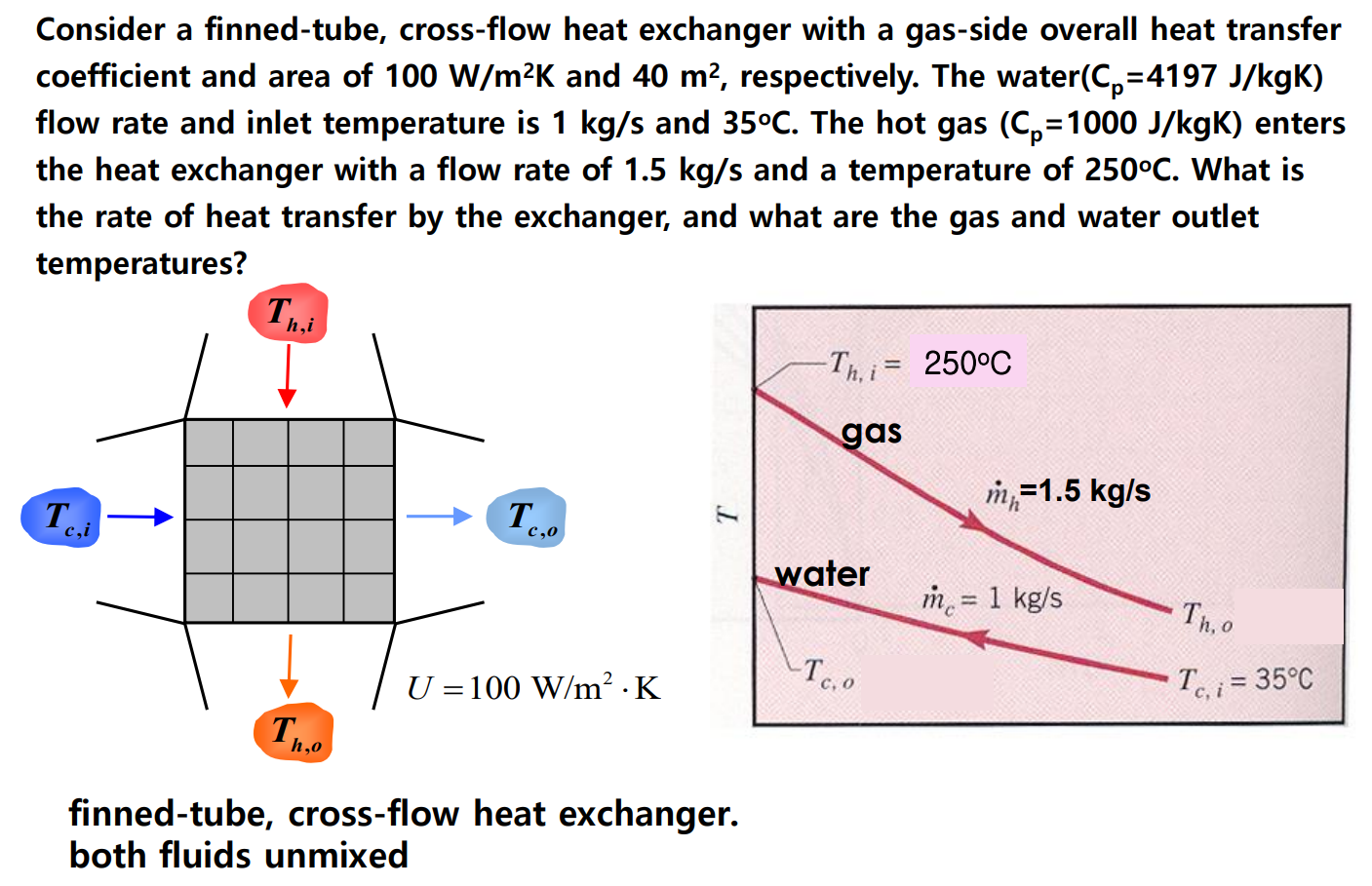
다음 예제를 보자.


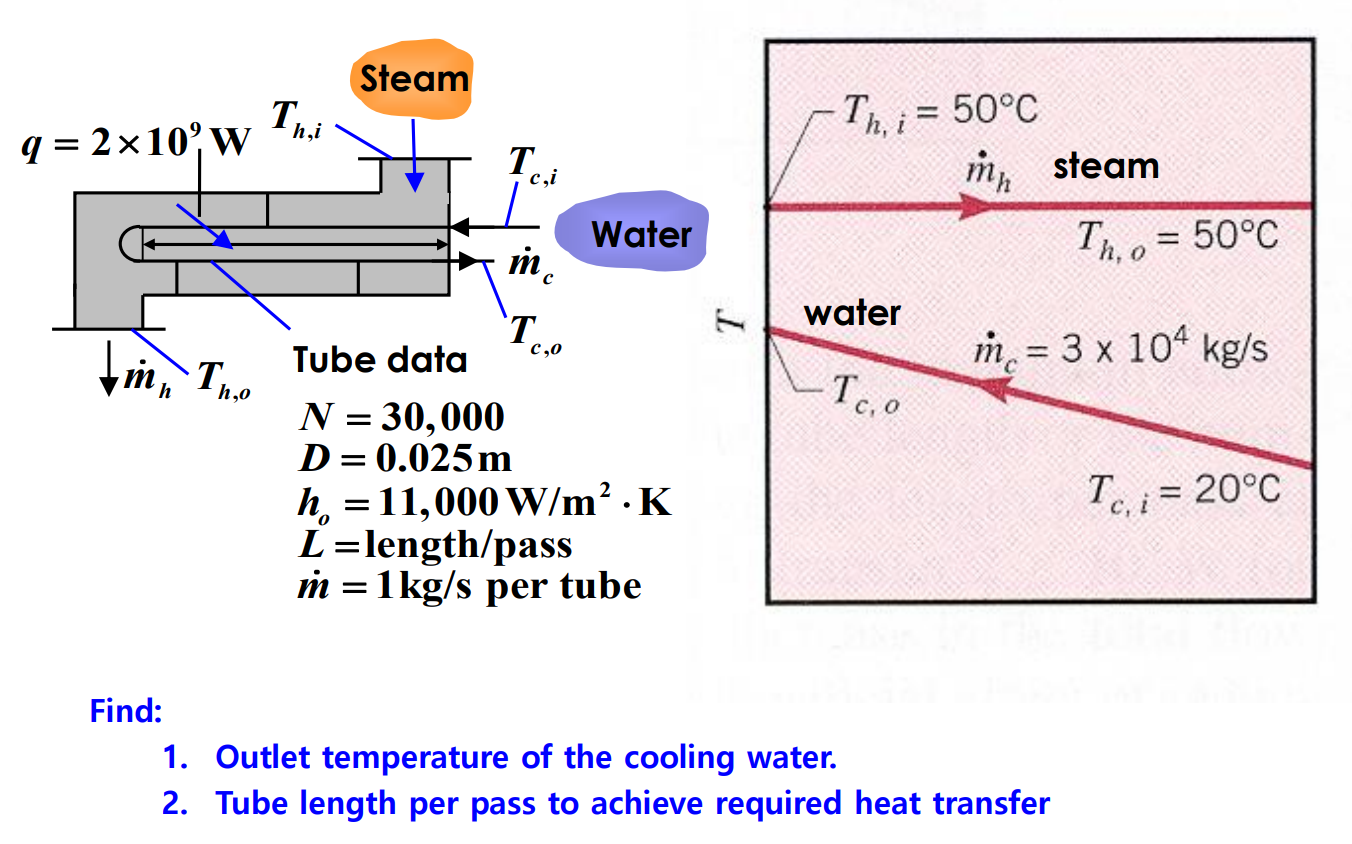

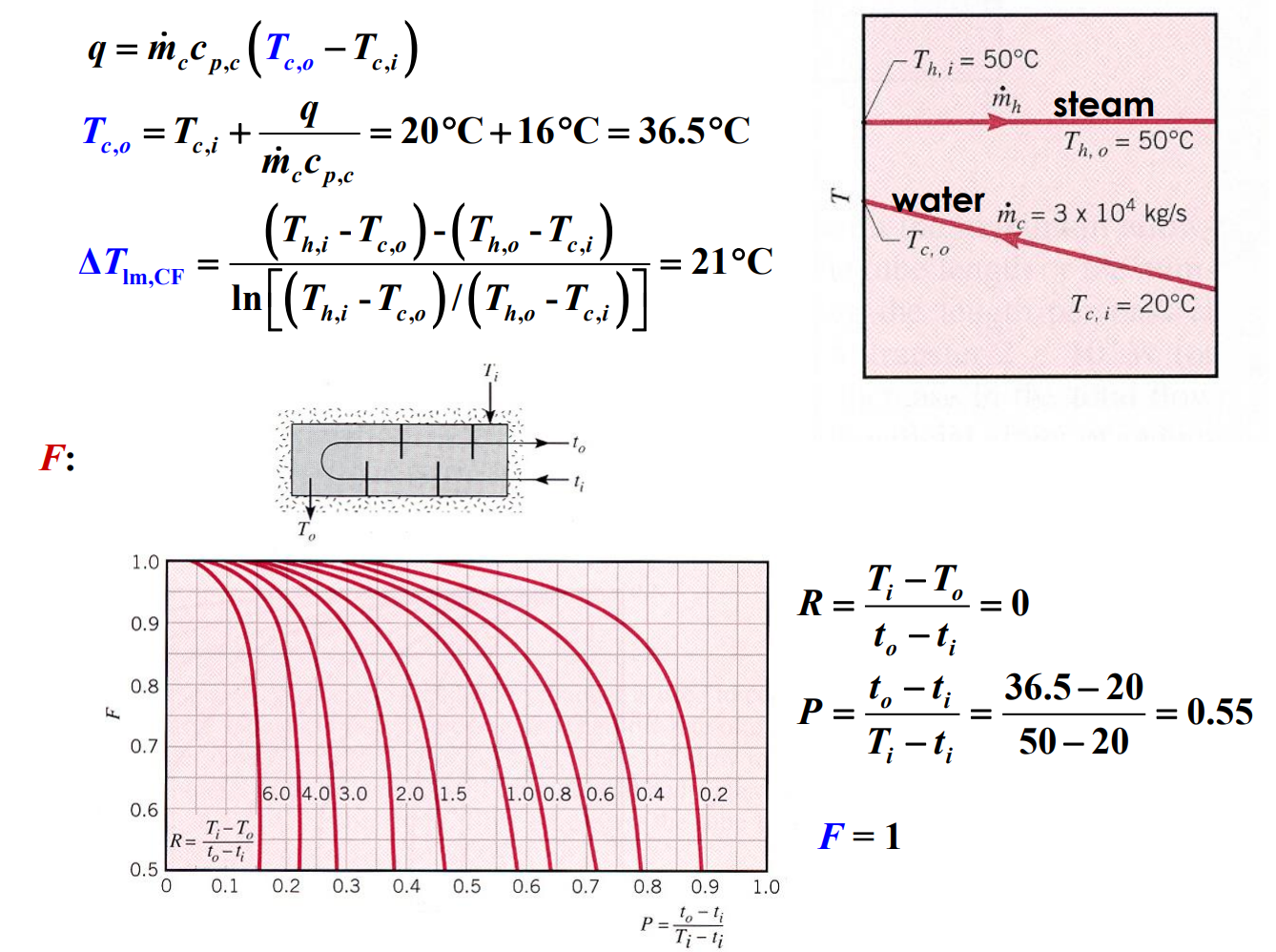

댓글남기기