유체역학
Updated:

정지 유체의 압력은 중력장에서 ${dp \over dz} = -\rho g$이다.
Bernoulli 식

내부 유동
관 내의 유동과 같은 내부유동은 유체가 표면에 의해 구속된 유동이다. 따라서 경계층은 궁극적으로 제약 없이 발달되어 나갈 수 없다. 내부유동을 고려할 때, 유동이 층류인지 난류인지를 알아보는 것이 필요하고 입구(enterence) 영역과 완전발달된(fully developed) 영역의 존재도 고려해야한다.
비원형덕트
비원형관(noncircular tube)에서 특성길이를 유효지름(effective diameter)으로 사용함으로써 원형관에 대한 많은 결과들을 사용할 수 있다. 이것을 수력지름(hydraulic radius)이라 하며 다른 equivalent diameter들과 함께 다음과 같이 정의한다.

다음 예제를 보자.
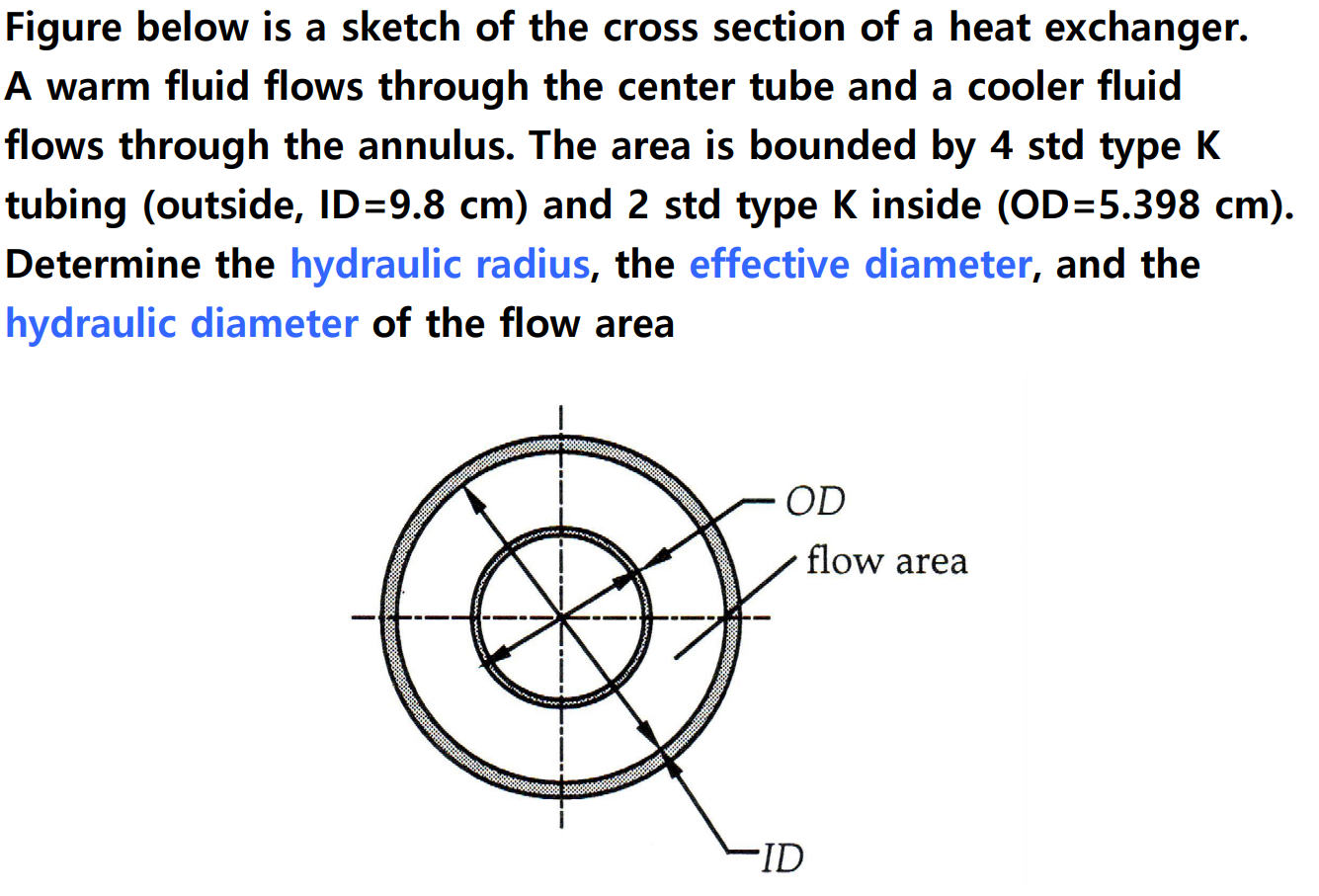
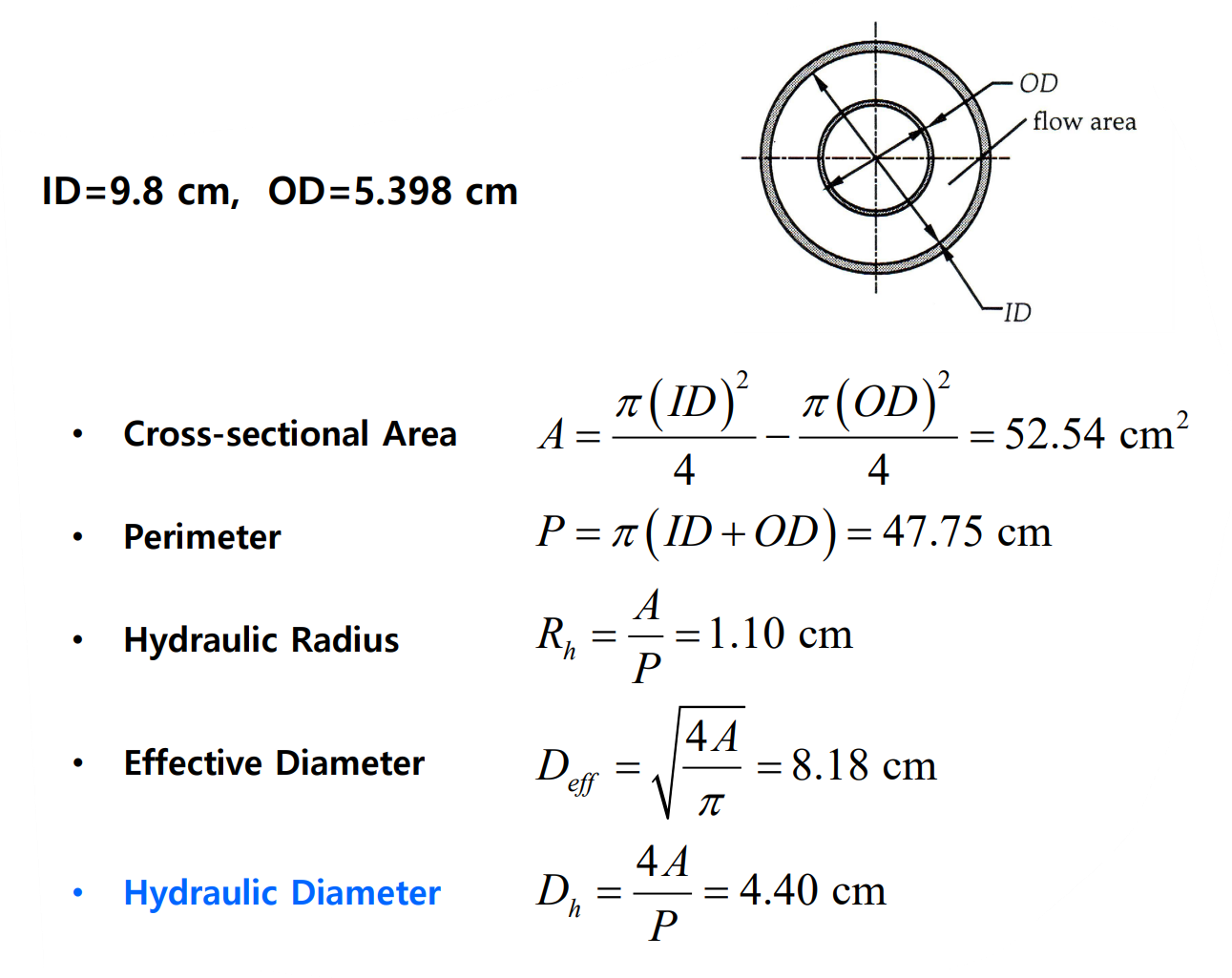
내부 유동의 손실
유동에 대해서 에너지 고찰을 하면, 두 점 사이의 비입축성, 정상유동에 대해 수정된 Bernoulli 방정식은 다음과 같다.
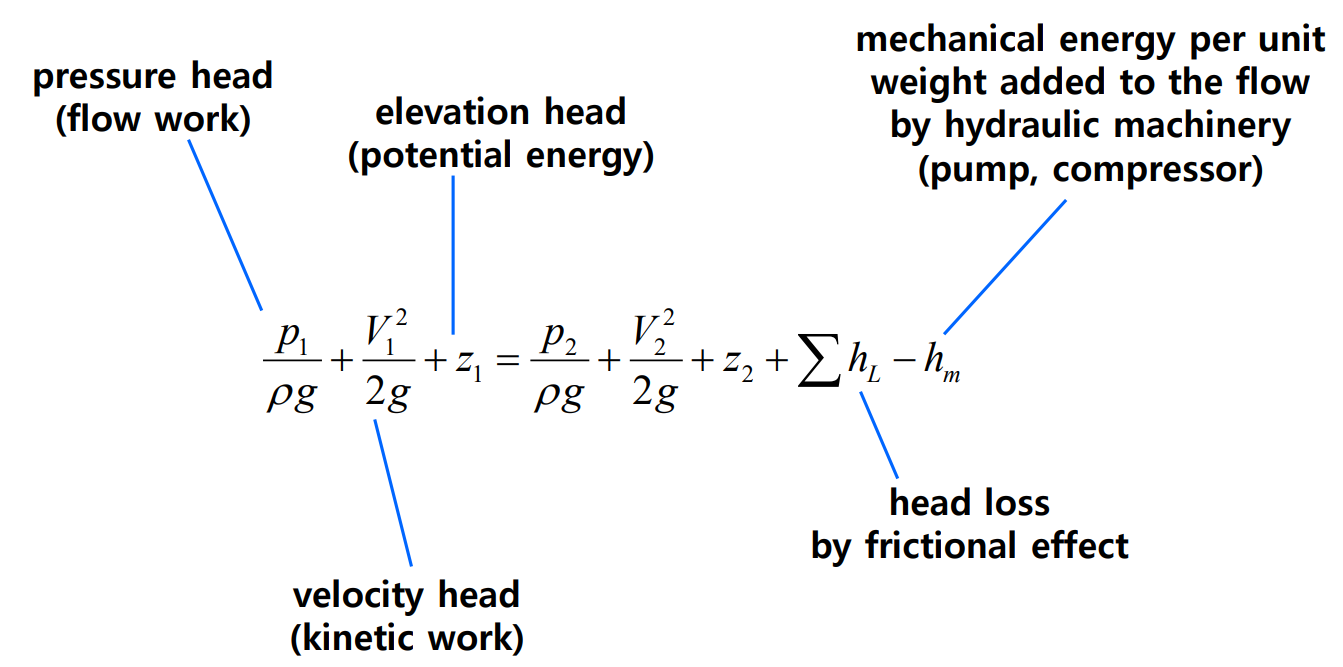
덕트에서 유체의 운동 방정식들은 다음과 같다.
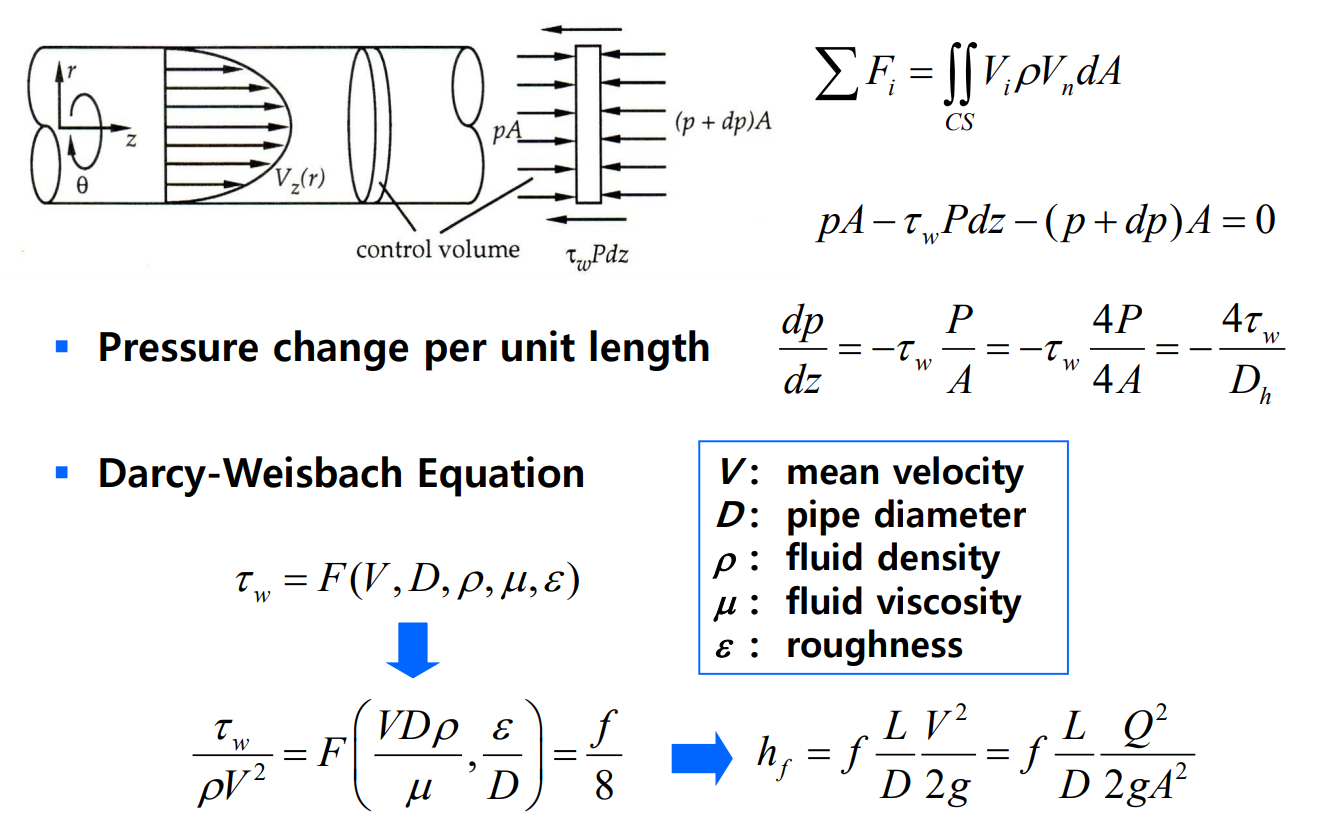
다음은 $f$와 Re와 $\epsilon / \mathrm{D}$에 대한 함수 관계를 나타낸 것으로 Moody 선도(Moody chart)라고 한다.
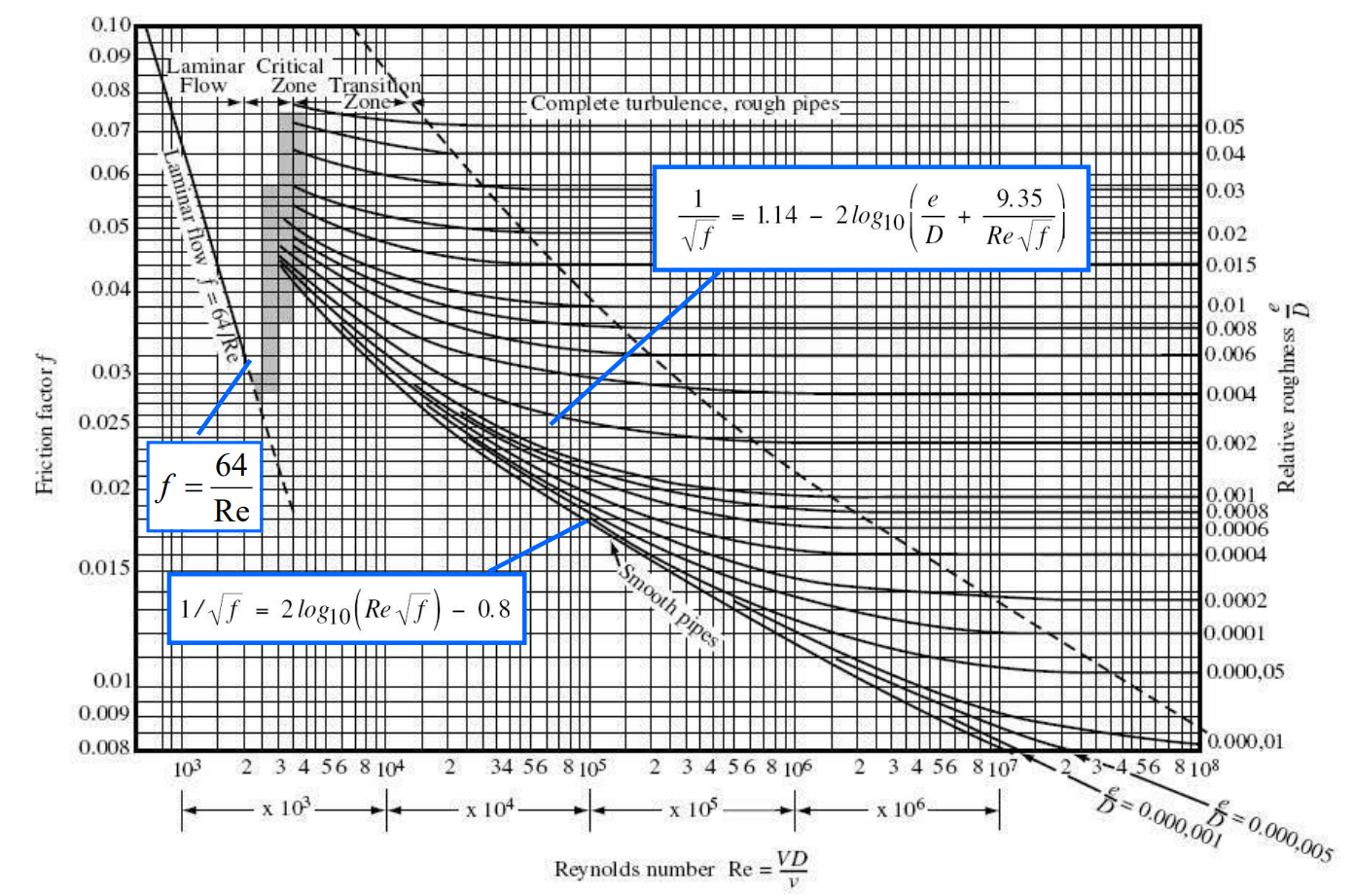
다음 예제를 보자.


대부분의 배관계에서는 직선 파이프뿐만 아니라 다른것들도 많다. 배관계에 추가로 들어간 부품들(밸브, 벤드, 티 등)은 전반적으로 수두손실을 높이는데 이와 같은 손실을 부차적손실(minor losses)라고 하고 $h_{L minor}$로 표현한다. 따라서 Bernoulli 방정식은 다음과 같이 표현할 수 있다.
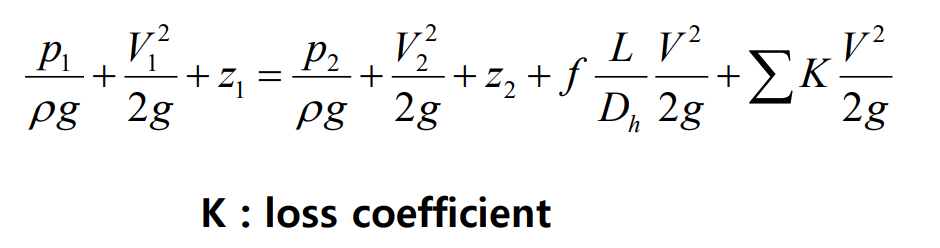
다음 예제를 보자.
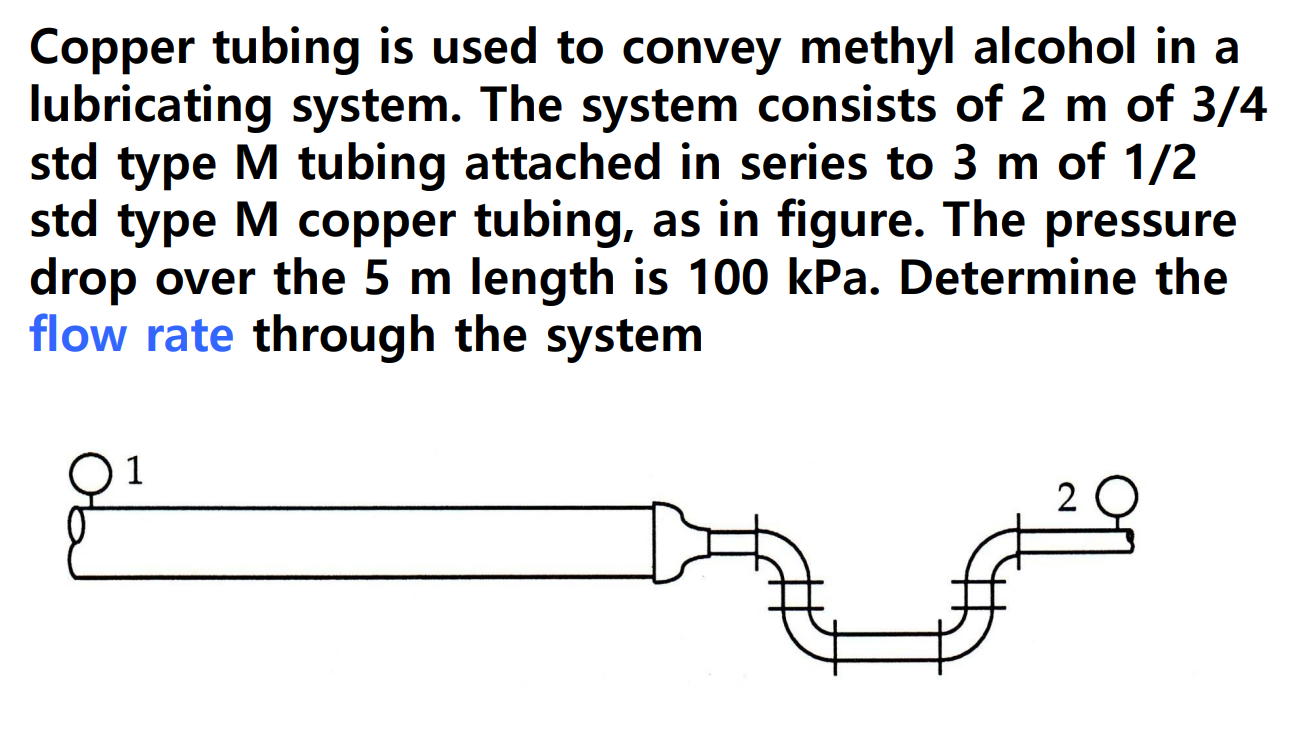
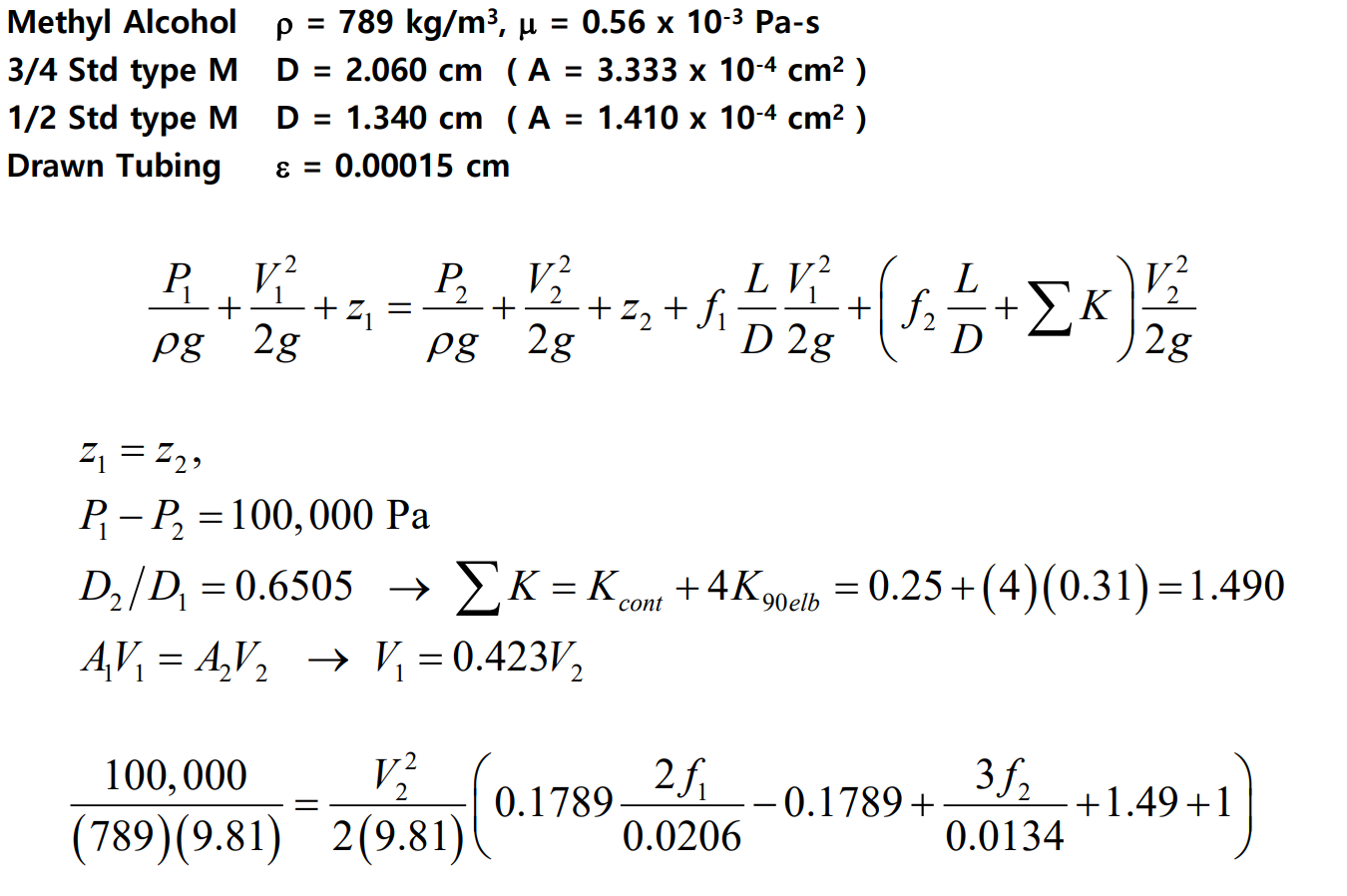
외부 유동
점성, 비압축성유체가 다음과 같이 무한히 긴 평판 위를 흐를 때 형성되는 경계층(가장 단순한 상황)에 대해 살펴보자.
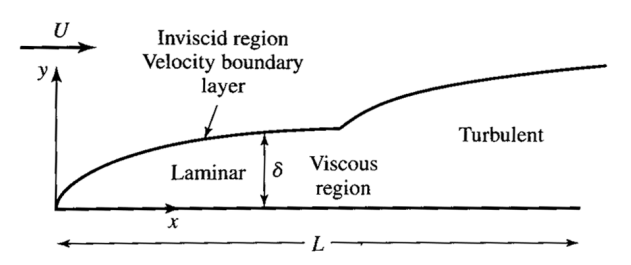
평판의 길이가 무한히 긴 경우는 앞전으로부터 거리 $x$를 특성길이로 사용하며, Reynolds 수는 다음과 같이 정의한다.

전방 층류(laminar)는 상사(서로 비슷한) 속도 분포를 가진다.
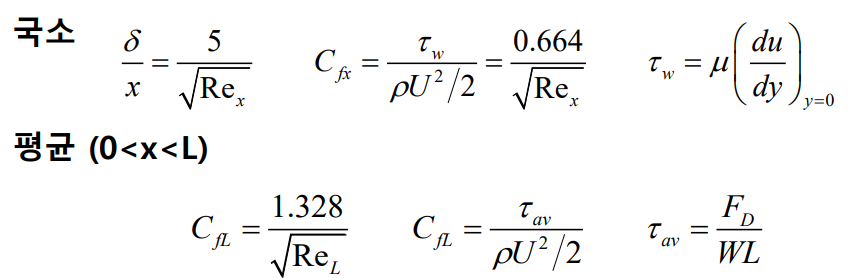
위 식에서 $\delta$는 경계층 두께(boundary layer thickness)를 나타내며 $C_{fx}$는 국소마찰계수, $C_{fL}$은 마찰항력계수(friction drag coefiicient)를 의미한다.
후방 난류(turbulent)는 벽근처의 급격하 속도구배를 가진다. 난류 유동에서 평판 항력 계수에 대한 식은 다음과 같다.
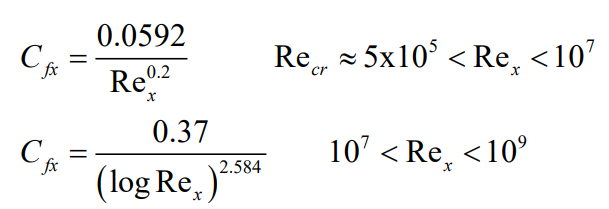
일반적으로 항력계수 $C_D$는 다음과 같이 나타낸다.
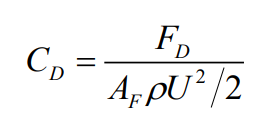
실린더 또는 구에서 Renolds 수에 의한 항력 계수는 다음과 같다.
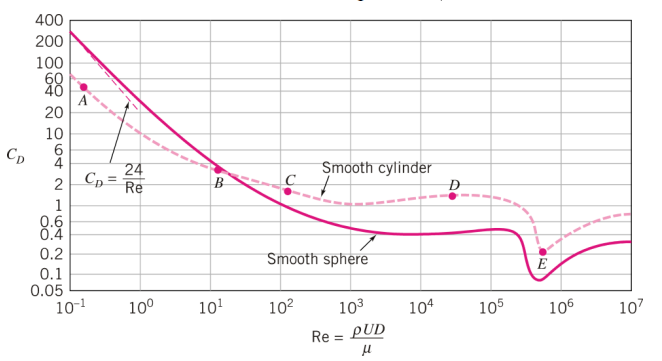
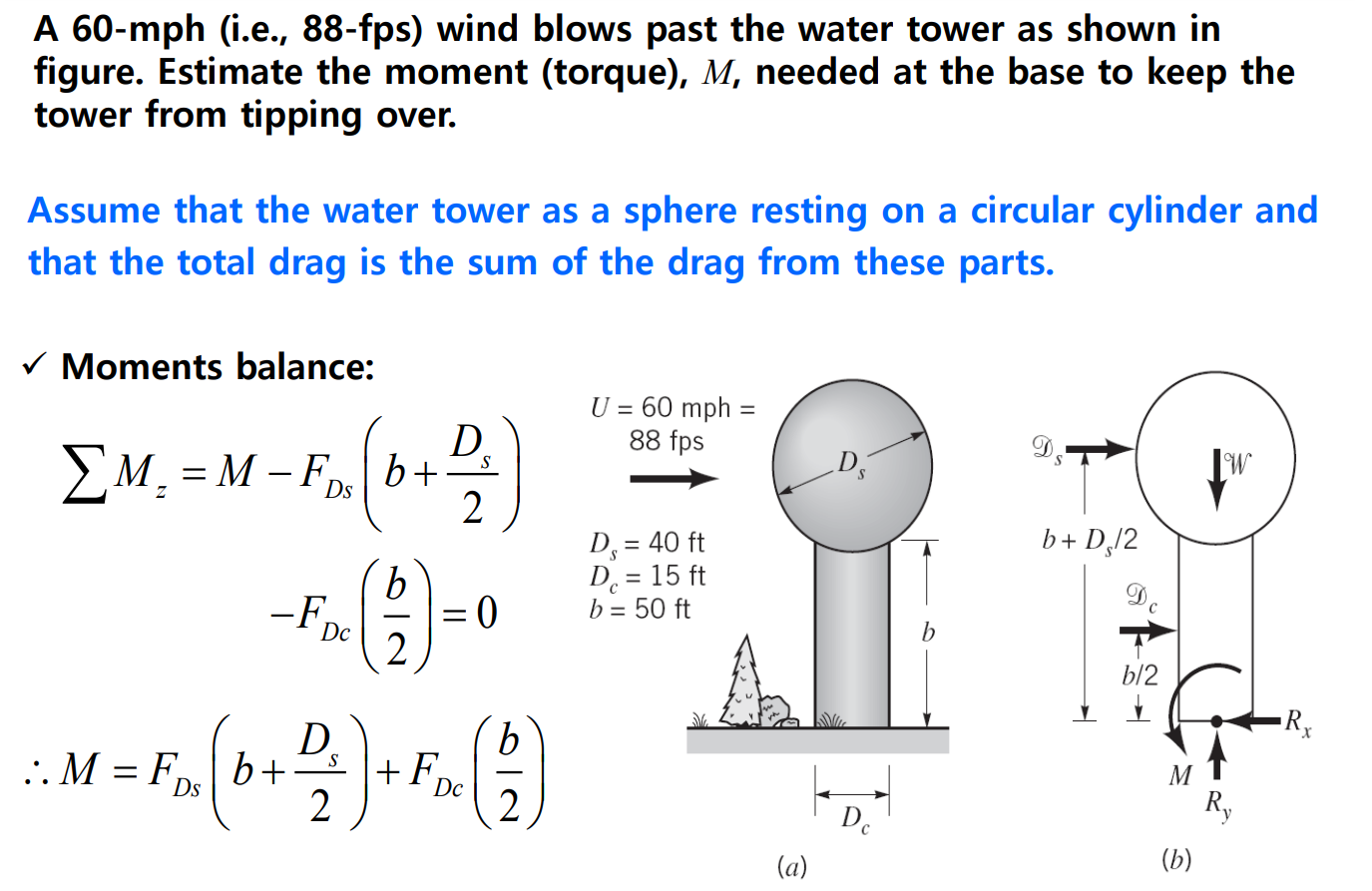
다음 예제를 보자.
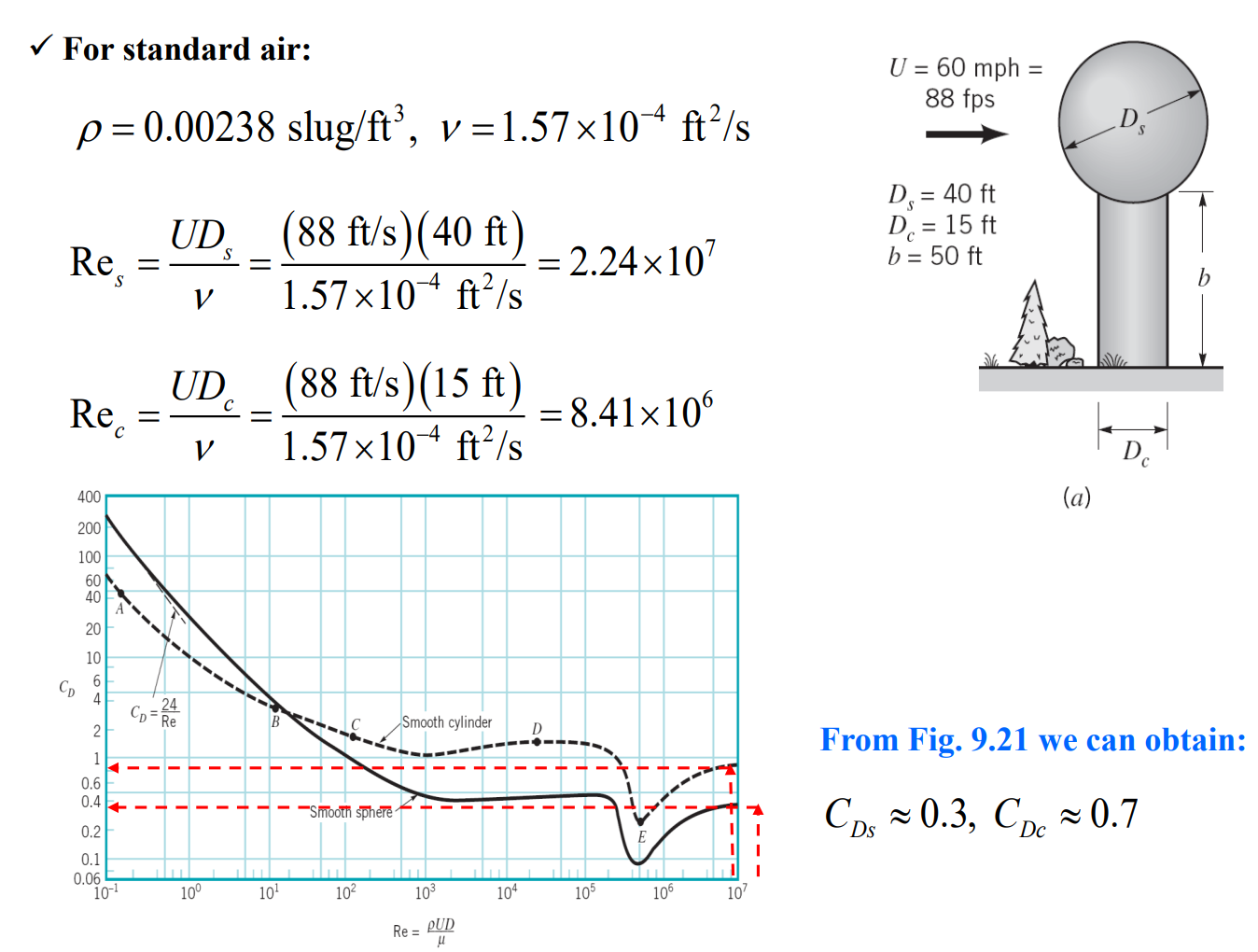

댓글남기기